Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Mar 21.
Published in final edited form as: J Biomech. 2013 Dec 24;47(5):1151–1156. doi: 10.1016/j.jbiomech.2013.12.009

Biaxial Mechanical Testing of Posterior Sclera using High-Resolution Ultrasound Speckle Tracking for Strain Measurements

Benjamin Cruz-Perez 1, Junhua Tang 1, Hugh J Morris 1, Joel R Palko 2, Xueliang Pan 3, Richard T Hart 1, Jun Liu 1,4
PMCID: PMC3951139  NIHMSID: NIHMS552443  PMID: 24438767

Abstract

This study aimed to characterize the mechanical responses of the sclera, the white outer coat of the eye, under equal-biaxial loading with unrestricted shear. An ultrasound speckle tracking technique was used to measure tissue deformation through sample thickness, expanding the capabilities of surface strain techniques. Eight porcine scleral samples were tested within 72 hours postmortem. High resolution ultrasound scans of scleral cross-sections along the two loading axes were acquired at 25 consecutive biaxial load levels. An additional repeat of the biaxial loading cycle was performed to measure a third normal strain emulating a strain gauge rosette for calculating the in-plane shear. The repeatability of the strain measurements during identical biaxial ramps was evaluated. A correlation-based ultrasound speckle tracking algorithm was used to compute the displacement field and determine the distributive strains in the sample cross-sections. A Fung type constitutive model including a shear term was used to determine the material constants of each individual specimen by fitting the model parameters to the experimental stress-strain data. A non-linear stress-strain response was observed in all samples. The meridian direction had significantly larger strains than the circumferential direction during equal-biaxial loadings (P’s<0.05). The stiffness along the two directions were also significantly different (P=0.02) but highly correlated (R2=0.8). These results showed that the mechanical properties of the porcine sclera were nonlinear and anisotropic under biaxial loading. This work has also demonstrated the feasibility of using ultrasound speckle tracking for strain measurements during mechanical testing.

Keywords: Biaxial testing, ultrasound speckle tracking, sclera, strain, anisotropy

1. Introduction

Glaucoma is the second leading cause of blindness worldwide (Quigley, 1999). The optic nerve head (ONH) is the principal site of damage in glaucoma, and the mechanical properties of the posterior sclera could strongly influence the stresses and strains experienced by the ONH during intraocular pressure (IOP) elevations (Norman et al., 2011; Sigal et al., 2005). It is thus an important goal to characterize the mechanical properties of sclera in order to better understand their involvement in the pathogenesis of glaucoma.

Uniaxial mechanical tests (Downs et al., 2005; Elsheikh, 2010; Girard et al., 2007; Palko et al., 2011; Schultz et al., 2008) and inflation tests (Coudrillier et al., 2012; Fazio et al., 2012; Girard et al., 2009c; Tang and Liu, 2012) have been used to study the mechanical responses of the sclera. Biaxial mechanical testing has been used to mimic inflation tests (Gere, 2004; Sacks, 2000) by loading a planar square specimen along two orthogonal axes to characterize the mechanical properties of an anisotropic tissue. The main assumptions for this test are planar deformation (Sacks, 1999) and incompressibility (Wang et al., 2006). Eilaghi et al. (2010) reported the first biaxial mechanical tests on human scleral specimens using a quasi-static, shear-restricting setup. Their results showed non-linear stress-strain relationships, but no difference was found in the responses along the two loading directions which were aimed to align with the material axes, i.e., the anatomical circumferential and meridian directions of the posterior sclera. Sacks (1999) developed a method using a system of pulleys and sutures to ensure equal forces at each loading point while allowing the tissue sample to shear during biaxial loading, thereby better mimicking in situ physiological conditions. This shear-allowing biaxial setup also eliminated the need for the precise alignment between the material axes of the specimen and the test axes, and reduced the inter-sample variability associated with the misalignment (Sacks, 2000). In the present study, we adopted a biaxial setup allowing unrestricted shear to characterize the anisotropic responses of the posterior porcine sclera.

Our laboratory has developed an ultrasound speckle tracking technique to measure the through-thickness distribution of strains in a cross-section of the sclera during IOP elevations (Tang and Liu, 2012). This technique entails tracking of the intrinsic ultrasonic interference patterns (i.e., speckles) of the tissue under an applied load (Ophir et al., 1999) or motion (O’Donnell et al., 1994). Our previous work has demonstrated a high accuracy and resolution of this approach when implemented with high-frequency ultrasound (Tang and Liu, 2012). In the present study, the ultrasound speckle tracking technique was adopted for measuring the tissue deformation through the sample thickness during biaxial testing. This technique enables direct measurements of the three orthogonal normal strains and delineates their distribution throughout the sample thickness. In addition, the ultrasound measurement can be conveniently achieved by submerging the samples in an aqueous environment to maintain physiological hydration.

The objective of this study was to investigate the anisotropic responses of porcine sclera in the presence of shear and characterize the material constants along the loading axes. The secondary goal was to implement a new strain measurement technique, i.e., ultrasound speckle tracking, during mechanical testing of soft tissue.

2. Methods

2.1 Sample preparation

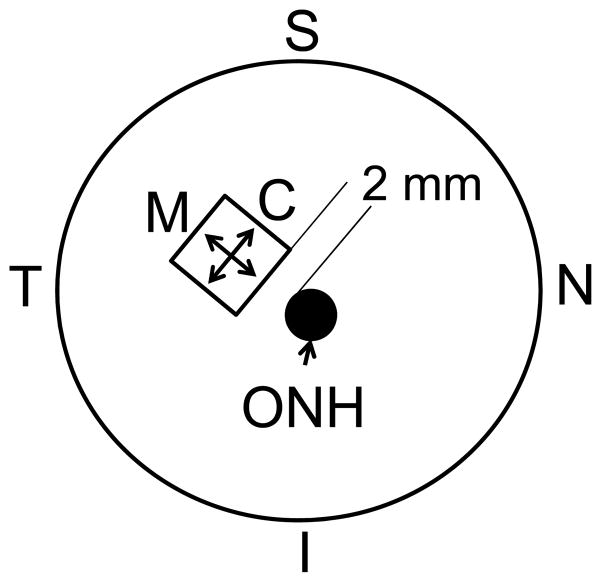
Eight porcine eyes were obtained from SiouxPreme Packing Co. (Sioux City, IA) within 24 hours postmortem. The globes were stored in phosphate buffered saline (PBS) at 4 °C until use. All testing was completed within 72 hours postmortem (Girard et al., 2007). Before mechanical testing, the globes were allowed to equilibrate at room temperature for at least one hour. A 7 mm by 7 mm square specimen was excised from the superotemporal region of the posterior sclera (Figure 1) using a custom made cutting tool. Sixteen hooks, 4 per side, were placed along the edges of the specimen ensuring an equal distance between the hooks and a gauge length of about 5 mm in both directions. Hooks were looped in pairs using a 3-0 silk suture to fit the pulley system in a trampoline-like manner that allows free shear during equal-biaxial loadings (Sacks, 1999) (Figure 2). Distance between hooks in opposite sides was measured with a caliper and used as the gauge length.

Figure 1.

Figure 1

Open in a new tab

A schematic posterior view of the sample location (C: Circumferential; M: Meridian; ONH: optic nerve head; S: superior; I: inferior; T: temporal; N: nasal).

Figure 2.

Figure 2

Open in a new tab

Trampoline-like sclera sample mount using a pulley-suture system. The sample was immersed in saline at room temperature during the tests. The ultrasound transducer was placed on top of the sample with no direct contact.

2.2 Biaxial mechanical testing

A biaxial mechanical testing system (ElectroForce Planar Biaxial TestBench, Bose Corp., Eden Prairie, MN) was modified to include custom-made fixtures which support the load cells and pulleys. The load axis was concentric with the motor axis preventing residual torques. The pulleys were made of Teflon to reduce friction on sutures and avoid interference during potential sample shearing. The mechanical testing system was placed on an isolation table (Newport, Irvine, CA) to reduce external vibrations. The WinTest 7 software (Bose Corp., Eden Prairie, MN) was used to control the biaxial system.

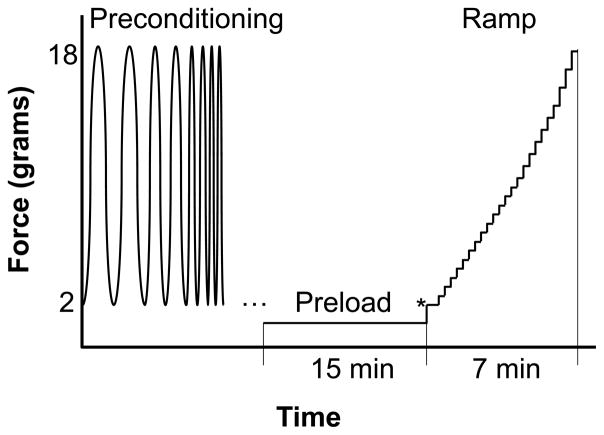
The sample was immersed in 0.9% saline during all tests. A flotation device (i.e., a small piece of foam) was placed underneath the sample to balance out the weight of the sample, hooks and suture and make it neutrally buoyant (Sacks, 2000). The sample was first preloaded to 1 gram to ensure full contact and flatten the curvature. A built-in sine wave frequency sweep (TuneIQ) with a load ranging from 2 to 18 grams was used as preconditioning along both axes. After preconditioning, the sample was allowed to equilibrate at 1 gram preload for at least 15 minutes. It was then ramped in 25 equal biaxial load-controlled steps ranging from 2 to 18 grams representing an estimated IOP range of 5 to 45 mmHg (computed from Laplace law for a globe radius of 12 mm). The experimental protocol is graphically outlined in Figure 3. The initial point of testing (marked by an “*” in Figure 3) was considered as zero stress and zero strain. The ramp was repeated to measure the normal strains along three directions using ultrasound speckle tracking: two along the loading axes and one along an angle (~ 45°) in-between the loading axes. Measurement of three normal strains allows the calculation of in-plane shear strains following the method of a strain gauge rosette (Gere, 2004) (details are described in Subsection 2.4). Fifteen seconds were allowed at each loading level for the completion of the ultrasound scans. Fifteen minutes equilibration at 1 gram preload was allowed between the ramps.

Figure 3.

Figure 3

Open in a new tab

Experimental protocol for biaxial testing of scleral samples.

A repeatability test was performed on three additional sclera samples acquired and prepared in the same way as the experimental samples to examine whether re-ramping resulted in significantly different mechanical responses.

2.3 Ultrasound speckle tracking for strain measurements

A high-resolution ultrasound system (55 MHz, Vevo 660, VisualSonics Inc., Toronto) was used to acquire the radiofrequency (RF) data of the cross-sectional scans. The probe was held in place using a linear precision stage (Newport, Irvine, CA). The sample was placed within the focal zone of the ultrasound beam during all tests. The RF data was processed using an ultrasound speckle tracking algorithm as described previously (Tang and Liu, 2012). Briefly, a cross-correlation based method was used to compute the displacement fields comparing the reference image and the deformed image. The cross-correlation coefficients were interpolated using spline functions to obtain sub-pixel tracking. A least-square strain estimator (Kallel and Ophir, 1997) was then used to calculate the strain maps within the tissue cross-section. E11 denotes the average normal strain within the cross-section along the circumferential direction, E22 denotes that along the meridian direction, E33 denotes the average compressive strains along the circumferential direction, and E′33 denotes that along the meridian direction. Sample thickness was calculated from the ultrasound data assuming a speed of sound of 1,640 m/s (Palko et al., 2011).

2.4 Constitutive modeling

Assuming small planar deformations (Sacks, 1999), the stress-strain data from each sample was fit to a reduced Fung type strain energy function (Equation 1)

W=C2(eA1E112+A2E222+2A3E122-1) (1)
Sij=∂W∂Eij (2)

where W is the strain energy, Eij’s are the Green strains, Sij’s are the second Piola-Kirchoff stresses, and C and Ai’s are the material constants. The interactions between the shear and normal strains were assumed negligible according to Sacks and Sun (2003). The interactions between the normal strains were also assumed negligible to avoid over-parameterization in the fitting of a small number of samples.

Shear strain (E12) was found using the following equation of a strain gauge rosette (Gere, 2004):

EN=E11cos2θ+E22sin2θ+E12sinθcosθ (3)

where EN is the third normal strain along the angle θ from E11 (Figure 4).

Figure 4.

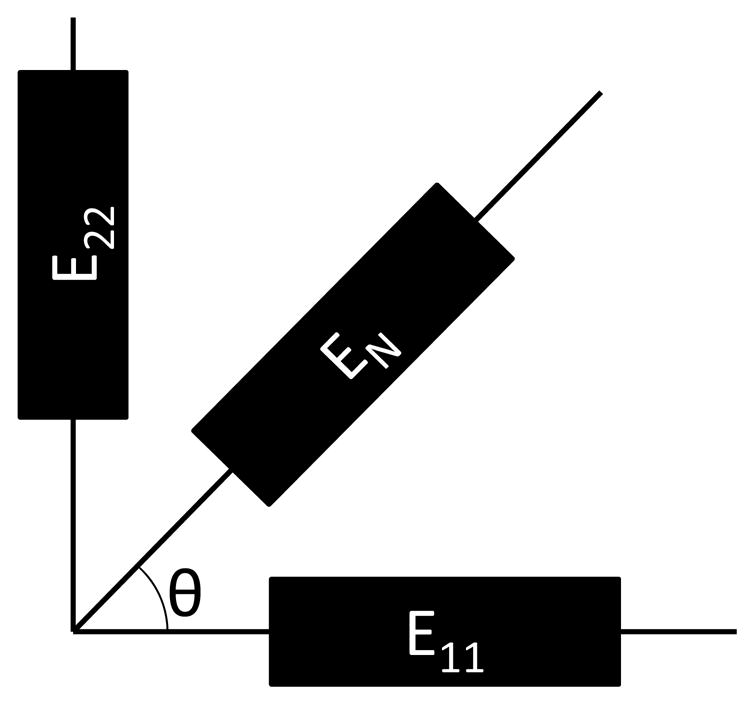
Figure 4

Open in a new tab

Schematics for the strain gauge rosette.

Lagrangian stresses (Tij) were computed from the sample dimensions (gauge length and sample thickness) and the force readings from the load cells. Second Piola-Kirchoff stresses (Sij) were computed from the measured Lagrangian stresses (Tij) and the deformation gradient F using the following relationship (Sacks, 1999):

Sij=TikFjk-1 (4)

where T12 = T21 = 0 (Sacks, 2000). The deformation gradient F was calculated from the Green strains by assuming that this tensor is symmetric and that:

2Eij=FikFjkT+I (5)

where I is the identity matrix.

An unconstrained non-linear minimization algorithm based on the subspace thrust region method (MATLAB, The MathWorks Inc., MA, USA) was applied to determine the best fitting material constants that reproduce the experimentally obtained stress/strain curves according to Equation 2. To verify the independence from the initial guesses, the initial value for each parameter was varied across several orders of magnitude. No dependency on the initial guess was found for any case tested. Another minimization method, the Levenberg-Marquardt algorithm, was also used to reprocess the data to evaluate whether the parameter convergence was dependent on the search algorithm. R2 values were used to evaluate the goodness of fit for each case.

2.5 Statistical Analysis

Statistical analysis was performed using SAS 9.3 software package (SAS Institute Inc., Cary, NC). The average circumferential and meridian strains at several pre-selected stress levels were compared using paired t-tests. For the repeatability test, the pooled standard deviation for the three repeated measurements in three scleral samples was computed at a stress level of 20 kPa and compared to the overall sample standard deviation. Paired t-tests were used to detect if there was a significant difference between the fitted material constants A1 and A2, as well as the products C·A1 and C·A2. The correlation between C·A1 and C·A2 was evaluated by linear regression. Sensitivity analyses were conducted to confirm the conclusions using mixed models to account for the associations of the measures from the same eye.

3. Results

A cross-sectional ultrasound image of the porcine superotemporal posterior sclera is presented in Figure 5, showing the typical intrinsic ultrasound speckle patterns in sclera. The strain images at different levels of loadings in one sample are presented in Figure 6. Within the central region of the sample (as indicated by the rectangular region of interest), the strains were usually homogeneous. Within the full cross-section, strains displayed some level of heterogeneity. For example, the compressive strains (E33 and E′33) were greater in the outer and inner layers of the sclera compared to the middle layer.

Figure 5.

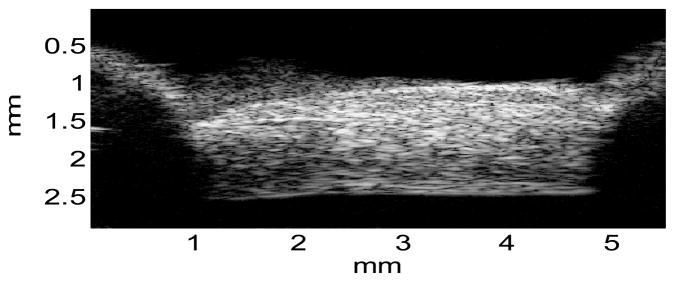
Figure 5

Open in a new tab

A representative ultrasound image of the porcine posterior sclera noted with the actual physical dimensions, showing the typical intrinsic ultrasound speckle patterns, adequate sample flattening, and the locations of sample mount (shadows on both sides).

Figure 6.

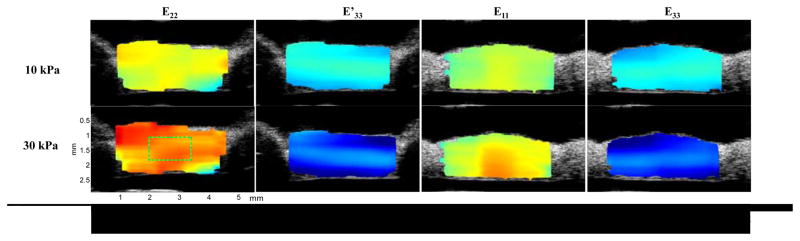
Figure 6

Open in a new tab

Strain distribution for a sclera sample at two stress levels (10 kPa and 30 kPa). Typical region of interest for average strain analysis is shown in the bottom left subfigure.

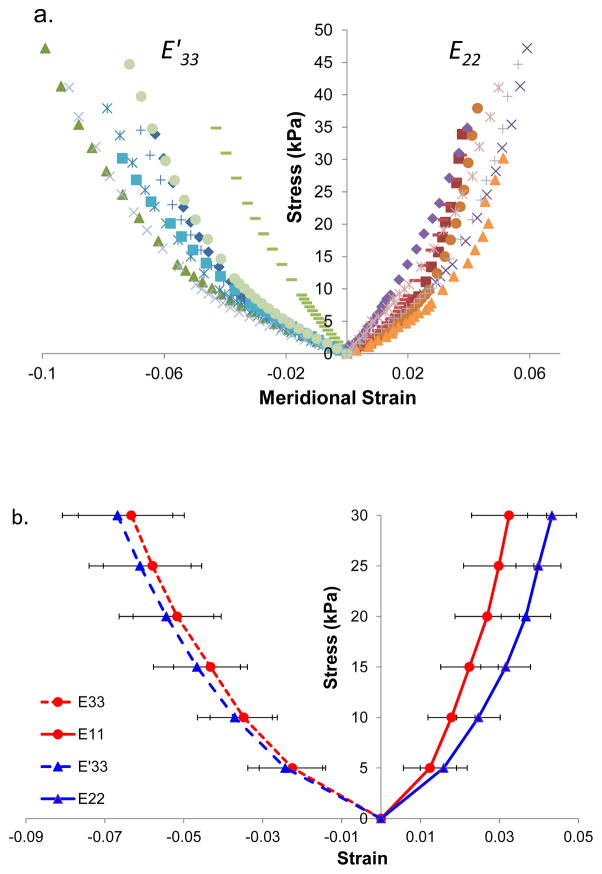
The individual stress-strain data along the meridian direction for all tested scleral samples are shown in Figure 7a, demonstrating nonlinear responses. The average stress-strain curves are presented in Figure 7b. The tensile strains were significantly higher in the meridian direction as compared to the circumferential direction at stress levels of 10, 15, 20, 25, and 30 kPa (P = 0.011, 0.003, 0.005, 0.006, and 0.008, paired t-tests). Compressive strains did not show significant differences along the two anatomical directions at these stress levels (P = 0.065, 0.068, 0.214, 0.102, and 0.102, respectively). However, they were significantly larger in magnitude than their respective tensile strains at all stress levels (all P’s < 0.05).

Figure 7.

Figure 7

Open in a new tab

a. Individual stress-strain responses in porcine posterior sclera along the meridional direction during biaxial testing. The response of each sample is indicated by a type of marker (different color is used to differentiate E33 vs E′33). b. Average stress-strain responses along both circumferential and meridian directions.

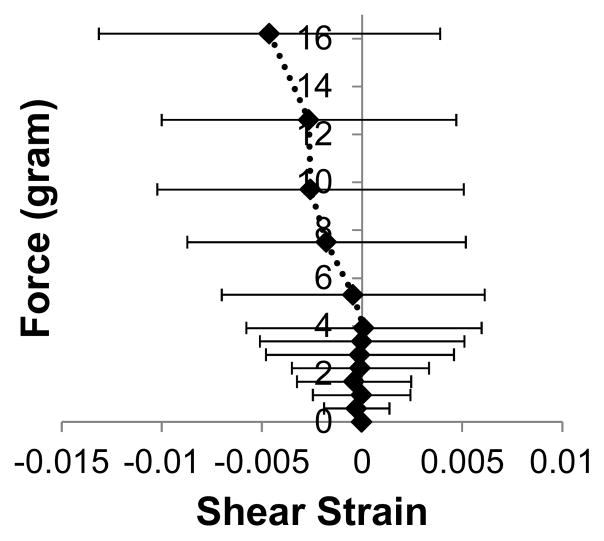
Shear strains (E12) at different loading levels were calculated from the three normal strains following the method of a strain gauge rosette. The shear strains were small compared to the normal strains (about 25% in average) with a large variance across samples (Figure 8). The calculated shear stresses (S12) were also about one order of magnitude lower than the normal stresses.

Figure 8.

Figure 8

Open in a new tab

Average shear strains for different biaxial loading levels.

The pooled standard deviation of the measured strains in the three repeated biaxial ramp tests (the variation of the repeated measures) was much smaller than the inter-sample variance (the variation among samples). For example, at the stress level of 20 kPa, the ratios between the standard deviation in all measured scleral samples and the pooled standard deviation during the repeatability test were 6.1, 5.1, 8.2, and 8.2, for E11, E22, E33, and E′33, respectively. Similar ratios were found at other stress levels (data not shown), suggesting adequate agreement during three repeated biaxial ramps.

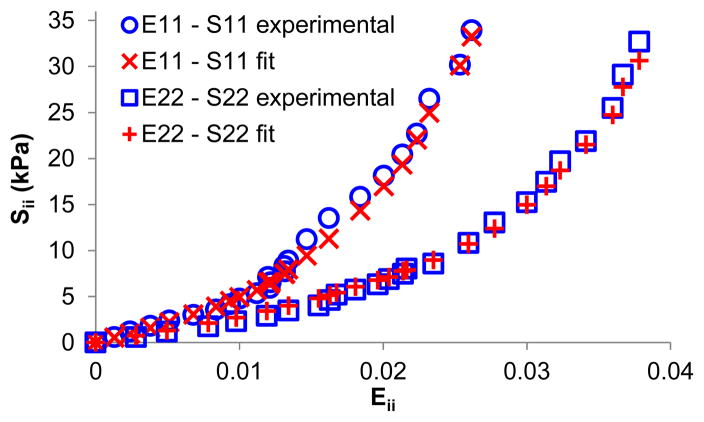
The material constants obtained from the fitting of a Fung-type model using the subspace thrust region method are displayed in Table 1. Both search algorithms yielded the same results (within 0.01% difference), but the Levenberg-Marquardt algorithm was substantially slower in reaching convergence. The R2 values (goodness of fit) were above 0.99 for all samples. Figure 9 presents a comparison of the experimental data with the model fitting in one sample, showing excellent agreement.

Table 1.

Material constants obtained from model fitting in 8 porcine scleral specimens.

Specimen C (kPa) A1 A2 A3 C·A1 (kPa) C·A2 (kPa)
1 0.566 720.2 465.0 −11.0 407.7 263.2
2 1.850 154.4 159.3 −6.3 285.7 294.7
3 0.934 256.1 281.4 −9.5 239.1 262.7
4 1.454 426.4 276.1 −9.9 620.0 401.5
5 4.054 227.5 144.5 −4.5 922.2 585.7
6 1.246 251.4 180.4 −7.7 313.3 224.8
7 3.260 159.3 136.3 −2.9 519.4 444.2
8 1.360 374.9 205.3 −7.1 509.7 279.1
Mean 1.841 321.3 231.0 −7.4 477.1 344.5
SD 1.201 187.1 109.6 2.8 222.4 122.9
Open in a new tab

Figure 9.

Figure 9

Open in a new tab

Circumferential and meridian tensile stress-strain curves (i.e., E11-S11 and E22-S22) in one scleral sample showing excellent agreement between experimental data and model fitting.

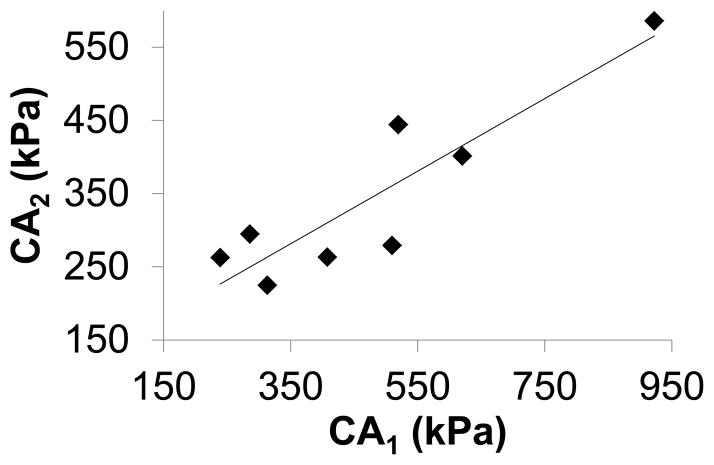
Constant A1 (circumferential) was significantly larger than A2 (meridian) (P=0.03, paired t-test). C·A1 was significantly larger than C·A2 (477±222 kPa vs 344±123 kPa, P=0.02, paired t-test). There was a strong correlation between C·A1 and C·A2 (R2=0.8, Figure 10).

Figure 10.

Figure 10

Open in a new tab

C·A1 was significantly larger than (P=0.02) and highly correlated with C·A2 (R2=0.8).

4. Discussion

This study presented heterogeneous, nonlinear, and anisotropic biomechanical properties in the posterior porcine sclera. Both tensile and compressive strains displayed a nonlinear relationship with the corresponding stresses. Ultrasound speckle tracking revealed a non-uniform strain distribution within the cross-section of the tissue samples through their thickness. The tensile strains along the meridian direction (E22) were significantly larger than those along the circumferential direction (E11) (P<0.05). Fitting with a Fung-type model also showed significantly larger material constants along the circumferential direction (P<0.05), demonstrating an anisotropic behavior of the posterior sclera in the porcine eye.

The biomechanical properties of the sclera are influenced by its biochemical composition as well as microstructural features such as collagen fiber organization and orientation. The difference in the tensile strains under equal-biaxial loading along the meridian and circumferential directions, as well as the difference in the fitted material constants along these two directions, was likely due to the preferred collagen fiber alignment along the circumferential direction in the posterior sclera close to the optic nerve head (ONH) (Pijanka et al., 2012; Yan et al., 2011). Circumferential arrangement of collagen fibers around the ONH was shown to significantly reduce canal expansion (Girard et al., 2009c; Grytz et al., 2011), which is protective of the structural stability of the ONH.

The compressive strains resulting from sample thinning during biaxial stretch were higher in magnitude than the tensile strains, and the outer and inner layers of the sclera had larger compressive strains than the middle layer (Figure 6). These results were consistent with what we observed during inflation tests of porcine posterior sclera (Tang and Liu, 2012). It is known that the outer and inner sclera has thinner and smaller collagen bundles as compared to the middle layer of the sclera (Komai and Ushiki, 1991; Watson and Young, 2004), which may partially contribute to the through-thickness heterogeneity in compressive strains. Other microstructural components such as proteoglycans (as well as hydration levels) may also influence the compressive responses of the sclera (Cheng and Pinsky, 2013).

The ratios of the shear strain to normal strain were 0.25±0.23 in average. This is approximately 3.7 times larger than what was reported for human sclera using inflation testing (0.067±0.052) (Coudrillier et al., 2012). The inflation tests required clamping to a pressurization chamber, while the biaxial testing allowed unrestricted shear. In addition, in Coudrillier et al’s study, the shear/normal ratio was averaged over a circular sector around the ONH, while the present study only tested the superotemporal quadrant which could differ from the other quadrants (Fazio et al., 2012). Species and age differences might also play a role.

The model fitting showed a significant difference between A1 and A2, confirming an anisotropic behavior in posterior sclera. We found a strong linear correlation (R2 = 0.8) between C·A1 and C·A2 (Figure 9). The slope of this regression (C·A2/C·A1) was 0.55. Girard et al found a similar ratio of modulus between the circumferential and meridian directions in monkey posterior sclera using an inverse finite element method combining inflation tests and an anisotropic hyperelastic constitutive model with preferred fiber alignment (Girard et al., 2009a; Girard et al., 2009b). Compared to the results from the biaxial testing of the human sclera (Eilaghi et al., 2010), the stiffness of the porcine posterior sclera was about 85% less than that of the human posterior sclera (477 kPa and 344 kPa in porcine vs. 2.9 MPa and 2.8 MPa in human). Interestingly, this comparison was remarkably similar to what was reported in a previous study showing a 75% lower stiffness in porcine sclera compared to in human sclera using uniaxial testing (Schultz et al., 2008). Besides biological differences between species, the age at tissue harvest was markedly different between these two groups. The average age of the animals used in the present study was 6 months, while the average age of the human donors was 55.4 years in Eilaghi’s study (Eilaghi et al., 2010). Since age is positively associated with collagen cross-linking, which largely determines the tensile stiffness of tissue (Reddy, 2004), the older age in the human donors likely contributed to the larger stiffness in the scleral tissue. Specifically, recent studies have reported age-associated stiffening of human sclera shown as reduced scleral strains during inflation tests (Coudrillier et al., 2012; Fazio et al., 2013).

Eilaghi et al. (2010) included an interaction term in their model fitting of the biaxial testing data, and found negligible effects of the interaction between E11 and E22. Holzapfel et al. (2000) proposed a convexity requirement for effectively fitting biaxial stress-strain data. These requirements included that C, A1, A2, and Ai (which is the coefficient for the interaction term) are all greater than 0 and that A1·A2 >Ai2. We found (data not shown) that the parameters in five out of the eight porcine scleral samples tested in this study did not satisfy the second condition, when the interaction term was included in the fitting. These considerations confirmed the choice of not including the interaction term in the current model fitting.

This study is limited in several aspects. First, only three ultrasound cross-sections were acquired in each sample. A full 3D-volume scan combined with a 3D ultrasound speckle tracking algorithm would allow the computation of the 3D strain tensor for the full field analysis of the mechanical response of the sclera during biaxial testing. Second, the samples were immersed in saline for the duration of the test which was about 2 hours. This may have resulted in some level of swelling, particularly at the exposed edges of the samples. A previous computational study showed that the characteristics of the sample apron did not significantly affect the mechanical behavior during biaxial testing (Eilaghi et al., 2009). Thus, the outcome of the current study was likely not altered by the potential larger swelling in the aprons. Third, the true material axes were unknown in the present study. Future microstructure analysis is needed to determine preferential collagen fiber alignment in the tested samples for a microstructure-informed interpretation and analysis of the mechanical data. Fourth, the sclera has a natural curvature which introduces uneven pre-strains through the thickness when it is flattened prior to biaxial testing. This heterogeneous pre-strain may have affected the through-thickness strain distribution during biaxial loading as compared to that during inflation.

In summary, this study has demonstrated the feasibility of combining high resolution ultrasound speckle tracking with biaxial mechanical testing to characterize the stress-strain response of the sclera. During biaxial tensile stretch, the porcine posterior sclera displayed nonlinear and anisotropic mechanical properties and the circumferential direction was significantly stiffer than the meridian direction.

Supplementary Material

01

Acknowledgments

This project was funded by NIH grants RO1EY020929 and RO1EY020929-S1. Dr. Paul Weber is gratefully acknowledged for helpful discussions on sample preparation.

Footnotes

Conflict of Interest Statement:

All authors declare no conflict of interest.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Cheng X, Pinsky PM. Mechanisms of self-organization for the collagen fibril lattice in the human cornea. Journal of the Royal Society, Interface/the Royal Society. 2013;10:20130512. doi: 10.1098/rsif.2013.0512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Coudrillier B, Tian J, Alexander S, Myers KM, Quigley HA, Nguyen TD. Biomechanics of the Human Posterior Sclera: Age- and Glaucoma-Related Changes Measured Using Inflation Testing. IOVS. 2012;53:1714–1728. doi: 10.1167/iovs.11-8009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Downs JC, Suh JKF, Thomas KA, Bellezza AJ, Hart RT, Burgoyne CF. Viscoelastic Material Properties of the Peripapillary Sclera in Normal and Early-Glaucoma Monkey Eyes. IOVS. 2005;46:540–546. doi: 10.1167/iovs.04-0114. [DOI] [PubMed] [Google Scholar]
  4. Eilaghi A, Flanagan JG, Brodland GW, Ethier CR. Strain Uniformity in Biaxial Specimens is Highly Sensitive to Attachment Details. Journal of Biomechanical Engineering. 2009:131. doi: 10.1115/1.3148467. [DOI] [PubMed] [Google Scholar]
  5. Eilaghi A, Flanagan JG, Tertinegg I, Simmons CA, Wayne Brodland G, Ross Ethier C. Biaxial mechanical testing of human sclera. Journal of Biomechanics. 2010;43:1696–1701. doi: 10.1016/j.jbiomech.2010.02.031. [DOI] [PubMed] [Google Scholar]
  6. Elsheikh A. Finite element modeling of corneal biomechanical behavior. J Refract Surg. 2010;26:289–300. doi: 10.3928/1081597X-20090710-01. [DOI] [PubMed] [Google Scholar]
  7. Fazio MA, Grytz R, Bruno L, Girard MJA, Gardiner S, Girkin CA, Downs JC. Regional Variations in Mechanical Strain in the Posterior Human Sclera. IOVS. 2012 doi: 10.1167/iovs.12-9668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fazio MA, Grytz R, Morris JS, Bruno L, Gardiner SK, Girkin CA, Downs JC. Age-related changes in human peripapillary scleral strain. Biomechanics and modeling in mechanobiology. 2013 doi: 10.1007/s10237-013-0517-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Gere JM. Mechanics of Materials. 6. Brooks/Cole-Thomas Learning; Belmont, CA: 2004. [Google Scholar]
  10. Girard M, Suh J-KF, Hart RT, Burgoyne CF, Downs JC. Effects of storage time on the mechanical properties of rabbit peripapillary sclera after enucleation. Curr Eye Res. 2007;32:465–470. doi: 10.1080/02713680701273792. [DOI] [PubMed] [Google Scholar]
  11. Girard MJ, Downs JC, Bottlang M, Burgoyne CF, Suh JK. Peripapillary and posterior scleral mechanics--part II: experimental and inverse finite element characterization. J Biomech Eng. 2009a;131:051012. doi: 10.1115/1.3113683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Girard MJ, Suh JK, Bottlang M, Burgoyne CF, Downs JC. Scleral biomechanics in the aging monkey eye. Invest Ophthalmol Vis Sci. 2009b;50:5226–5237. doi: 10.1167/iovs.08-3363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Girard MJA, Downs JC, Bottlang M, Burgoyne CF, Suh JKF. Peripapillary and Posterior Scleral Mechanics—Part II: Experimental and Inverse Finite Element Characterization. Journal of Biomechanical Engineering. 2009c:131. doi: 10.1115/1.3113683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Grytz R, Meschke G, Jonas JB. The collagen fibril architecture in the lamina cribrosa and peripapillary sclera predicted by a computational remodeling approach. Biomechanics and modeling in mechanobiology. 2011;10:371–382. doi: 10.1007/s10237-010-0240-8. [DOI] [PubMed] [Google Scholar]
  15. Holzapfel GA, Gasser TC, Ogden RW. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
  16. Kallel F, Ophir J. A least-squares strain estimator for elastography. Ultrason Imaging. 1997;19:195–208. doi: 10.1177/016173469701900303. [DOI] [PubMed] [Google Scholar]
  17. Komai Y, Ushiki T. The three-dimensional organization of collagen fibrils in the human cornea and sclera. Invest Ophthalmol Vis Sci. 1991;32:2244–2258. [PubMed] [Google Scholar]
  18. Norman RE, Flanagan JG, Sigal IA, Rausch SMK, Tertinegg I, Ethier CR. Finite element modeling of the human sclera: Influence on optic nerve head biomechanics and connections with glaucoma. Experimental Eye Research. 2011;93:4–12. doi: 10.1016/j.exer.2010.09.014. [DOI] [PubMed] [Google Scholar]
  19. O’Donnell M, Skovoroda AR, Shapo BM, Emelianov SY. Internal displacement and strain imaging using ultrasonic speckle tracking. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control. 1994;41:314–325. [Google Scholar]
  20. Ophir J, Alam SK, Garra B, Kallel F, Konofagou E, Krouskop T, Varghese T. Elastography: Ultrasonic estimation and imaging of the elastic properties of tissues. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 1999;213:203–233. doi: 10.1243/0954411991534933. [DOI] [PubMed] [Google Scholar]
  21. Palko JR, Pan X, Liu J. Dynamic testing of regional viscoelastic behavior of canine sclera. Experimental Eye Research. 2011;93:825–832. doi: 10.1016/j.exer.2011.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pijanka JK, Coudrillier B, Ziegler K, Sorensen T, Meek KM, Nguyen TD, Quigley HA, Boote C. Quantitative Mapping of Collagen Fiber Orientation in Non-glaucoma and Glaucoma Posterior Human Sclerae. IOVS. 2012;53:5258–5270. doi: 10.1167/iovs.12-9705. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Quigley HA. Neuronal death in glaucoma. Progress in Retinal and Eye Research. 1999;18:39–57. doi: 10.1016/s1350-9462(98)00014-7. [DOI] [PubMed] [Google Scholar]
  24. Reddy GK. Cross-linking in collagen by nonenzymatic glycation increases the matrix stiffness in rabbit achilles tendon. Experimental diabesity research. 2004;5:143–153. doi: 10.1080/15438600490277860. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Sacks MS. A Method for Planar Biaxial Mechanical Testing That Includes In-Plane Shear. Journal of Biomechanical Engineering. 1999;121:551–555. doi: 10.1115/1.2835086. [DOI] [PubMed] [Google Scholar]
  26. Sacks MS. Biaxial Mechanical Evaluation of Planar Biological Materials. Journal of Elasticity. 2000;61:199–246. [Google Scholar]
  27. Sacks MS, Sun W. Multiaxial Mechanical Behavior of Biological Materials. Annual Review of Biomedical Engineering. 2003;5:251–284. doi: 10.1146/annurev.bioeng.5.011303.120714. [DOI] [PubMed] [Google Scholar]
  28. Schultz DS, Lotz JC, Lee SM, Trinidad ML, Stewart JM. Structural factors that mediate scleral stiffness. Invest Ophthalmol Vis Sci. 2008;49:4232–4236. doi: 10.1167/iovs.08-1970. [DOI] [PubMed] [Google Scholar]
  29. Sigal IA, Flanagan JG, Ethier CR. Factors Influencing Optic Nerve Head Biomechanics. IOVS. 2005;46:4189–4199. doi: 10.1167/iovs.05-0541. [DOI] [PubMed] [Google Scholar]
  30. Tang J, Liu J. Ultrasonic Measurement of Scleral Cross-Sectional Strains During Elevations of Intraocular Pressure: Method Validation and Initial Results in Posterior Porcine Sclera. Journal of Biomechanical Engineering. 2012:134. doi: 10.1115/1.4007365. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Wang C, Garcia M, Lu X, Lanir Y, Kassab GS. Three-dimensional mechanical properties of porcine coronary arteries: a validated two-layer model. Am J Physiol Heart Circ Physiol. 2006;291:H1200–H1209. doi: 10.1152/ajpheart.01323.2005. [DOI] [PubMed] [Google Scholar]
  32. Watson PG, Young RD. Scleral structure, organisation and disease. A review. Exp Eye Res. 2004;78:609–623. doi: 10.1016/s0014-4835(03)00212-4. [DOI] [PubMed] [Google Scholar]
  33. Yan D, McPheeters S, Johnson G, Utzinger U, Vande Geest JP. Microstructural differences in the human posterior sclera as a function of age and race. Invest Ophthalmol Vis Sci. 2011;52:821–829. doi: 10.1167/iovs.09-4651. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS552443-supplement-01.pdf (44.8KB, pdf)

RESOURCES