A Bayesian Extension of the Hypergeometric Test for Functional Enrichment Analysis

Summary

Functional enrichment analysis is conducted on high-throughput data to provide functional interpretation for a list of genes or proteins that share a common property, such as being differentially expressed (DE). The hypergeometric P-value has been widely used to investigate whether genes from pre-defined functional terms, e.g., Gene Ontology (GO), are enriched in the DE genes. The hypergeometric P-value has three limitations: 1) computed independently for each term, thus neglecting biological dependence; 2) subject to a size constraint that leads to the tendency of selecting less-specific terms; 3) repeated use of information due to overlapping annotations by the true-path rule. We propose a Bayesian approach based on the non-central hypergeometric model. The GO dependence structure is incorporated through a prior on non-centrality parameters. The likelihood function does not include overlapping information. The inference about enrichment is based on posterior probabilities that do not have a size constraint. This method can detect moderate but consistent enrichment signals and identify sets of closely-related and biologically-meaningful functional terms rather than isolated terms. We also describe the basic ideas of assumption and implementation of different methods to provide some theoretical insights, which are demonstrated via a simulation study. A real application is presented.

1 Introduction

In traditional high-throughput data analysis such as microarray analysis the focus has been on identifying differentially expressed (DE) genes. Researchers have found that the list of identified DE genes are usually difficult to reproduce and bear little unifying biological theme (Subramanian et al., 2005). Many methods have been proposed to incorporate biological knowledge accumulated in public databases to detect enriched and pertinent biology (Khatri et al., 2002; Hosack et al., 2003; Zhang et al., 2004; Subramanian et al., 2005; Kathri and Draghici, 2005; Efron and Tibshirani, 2007; Newton et al., 2007). Many annotation resources have been utilized, including Gene Ontology (GO), protein-protein interactions (e.g., KEGG, Kanehisa and Goto, 2000), protein functional domains, disease associations, bio-pathways, sequence features, homology, gene functional summaries, gene tissue expression, literature, transcription factors, miRNAs, structural motifs, drug targets, etc.

The GO database (Gene Ontology consortium, 2000) is one of the most popular gene description databases used in enrichment analyses, with GO terms (each annotating a group of genes) as the building block. Gene Ontology consists of biological processes, cellular components, and molecular functions. In this paper we generically refer to GO terms as functional terms with the understanding that they are also applicable to the other two components. GO terms are organized in a directed acyclic graph (DAG) of parent-child relationship. A child represents a more specific biological classification. The GO DAG is different from a traditional classification tree in that a GO term is allowed to have more than one parent, a feature known as multiple inheritance. The GO database also follows the true-path rule: genes annotated by a child node are automatically annotated by its parent nodes, and subsequently, by all the ancestral nodes.

Many existing procedures to detect enrichment are based on the hypergeometric test (or its variants including the binomial and Fisher’s exact tests). We briefly review the classical hypergeometric test. In a high-throughput experiment, let g be the number of genes annotated to a certain GO term, and let f and d be the total numbers of genes evaluated and DE genes detected, respectively. The number of DE genes annotated to this GO term, denoted by n, indicates the representation of the GO term in the list of DE genes. The null hypothesis is that the functional term is irrelevant to the experiment, which means that a gene being annotated by the GO term and this gene being DE are independent events. Given (g, f, d), we can model n by a hypergeometric distribution under the null hypothesis, and the P-value measuring the significance of enrichment is the tail probability of observing n or more DE genes annotated to the GO term,

$$P-\text{value}=\sum _{k=n}^{min(g,d)}\frac{\left(\begin{array}{c}g\\ k\end{array}\right)\left(\begin{array}{c}f-g\\ d-k\end{array}\right)}{\left(\begin{array}{c}f\\ d\end{array}\right)},$$ (1)

where $\left(\begin{array}{c}m\\ n\end{array}\right)=\frac{m!}{n!(m-n)!}$ is the binomial coefficient.

Due to its computational simplicity and straightforward interpretation, the hypergeometric P-value and its variants have become popular in functional enrichment analysis. However, researchers have noticed some drawbacks of the hypergeometric P-value. For example, the hierarchical structure of the GO DAG can be informative but it is ignored in the hypergeometric test. Suppose we observe an enrichment signal at a particular GO term (a biological function). Examining this term by itself, it might be difficult to determine whether this signal arises from biological truth, experimental error, or random noise. On the other hand, biological functions are interconnected. The activity of a particular function requires supply of inputs and utilization of outputs by other functions. Also, the stimulus activating a function might be effective on other closely related functions. Such biological dependence suggests that if a GO term is truly enriched, we would expect some of the neighboring terms to show similar signals. In short, when we take the inter-relationship of biological functions (represented by the hierarchical structure in the GO DAG) into consideration, moderate but consistent signals from a neighborhood of related GO terms might be more trustworthy than a “strong” signal from an isolated single term.

We use Figure 1 to illustrate the above point. It depicts the hierarchical structure of 19 terms {G_j, j = 1, ···, 19} from a small region of the GO DAG. We use F = {a, b, ···, z} to denote the full list of genes, and among them the set of 8 DE genes, denoted by D, are marked by boldface (i.e., f = 26 and d = 8). Each arrow indicates a parent-child pair. Each rectangle contains the subset of genes annotated by a GO term, where (g_j, n_j) are listed in the first row under each rectangle, together with the hypergeometric P-values based on (1), denoted as P(·). For example, G₂ annotates g₂ = 11 genes and n₂ = 6 of them are DE. The hypergeometric P-value is 0.034. Figure 1 exhibits some important features of the GO DAG, such as the true-path rule and multiple inheritance (e.g., G₁₅ is the child of G₁₁ and G₁₂ simultaneously).

Figure 1.

Illustration of different enrichment measures based on a small region of GO DAG. The full list of genes (F) are denoted as lowercase letters; the genes in set D are marked by boldface. The rectangles contain the subset of genes annotated by each node. Under each rectangle, the first row lists (g_j, n_j) and the P-value presented in P(). The second row lists ( $g_j^{\ast },n_j^{\ast }$) and the B-value presented in B(). In the third row, the parent-child P-value (Grossmann et al., 2007) is presented in G() and the elim P-value (Alexa et al., 2006) is presented in A(), and the posterior probability under MGSA (Bauer et al., 2010) is presented in M(). Note that stronger enrichment is indicated by greater values of B(·) and M(·), and smaller values of P(·), A(·), and G(·).

Enrichment analysis based on the hypergeometric test has some limitations. First, it can not distinguish GO terms with the same (g_j, n_j). In Figure 1, nodes G₈, G₁₈, and G₁₉ have the same P-value because they have identical (g_j, n_j) = (1, 1). Examining the whole graph, we might consider G₈ more likely to be enriched because of the stronger evidence of enrichment in its neighborhood (related biological functions). This limitation stems from treating GO terms as isolated entities and ignoring the hierarchical structure. Second, the hypergeometric P-value has a size constraint. For a GO term of size g_j, the smallest possible P-value is attained when all the annotated genes are DE (i.e., n_j = g_j). This lower bound is reversely associated with g_j. For example, with (f = 26, d = 8), the hypergeometric P-value is 0.005 when (g_j = n_j = 4) and 0.046 when (g_j = n_j = 3). If we set the significance level at 0.01, any term with a size less than 4 will be automatically excluded from the inference. From a biologist’s point of view, detecting more specific GO terms, which usually have a smaller size (g_j), might be more desirable because they provide more detailed information. The third limitation is the repeated use of information. Due to the true-path rule, the genes annotated by a GO term are involved in the tests for all of its ancestors. For example, the information of gene a being DE is used seven times, in the hypergeometric tests for each of (G₂, G₃,···, G₈). The information of gene z being non-DE, however, is used only once (G₃). It is desirable for a test procedure to appropriately distribute evidence from each gene among GO terms according to the hierarchical structure.

A number of new methods have been proposed trying to address the limitations of the hypergeometric test. Carmona-Saez et al. (2006) extracted combinations of annotations that appear in at least a pre-specified number of genes. Then a statistical test is applied to access enrichment. Lewin and Grieve (2006) proposed to group closely related GO nodes and compute a hypergeometric P-value for each group. Alexa et al. (2006) evaluated enrichment from leaf to root, downweighting genes annotated by child terms which have already been declared significantly enriched. Grossmann et al. (2007) evaluated each GO term conditional on the enrichment at the parent(s). Falcon and Gentleman (2007) developed a R package on a conditional hypergeometric test to utilize parent-child relationship. Goeman and Buhlmann (2007) investigated methodological issues in the analysis of gene expression data in terms of gene sets. Lu et al. (2008) developed a probabilistic generative model for GO enrichment analysis. Bauer et al. (2010) analyzed functional terms in a Bayesian network which assumes gene responses to be directly associated with the activation of biological functions. Zhang et al. (2010) proposed a Bayesian method to model the DE status of individual genes with a hierarchical prior on relevance parameters to account for the GO structure. Stingo et al. (2011) developed a Bayesian model which uses information on pathways and gene networks. Wang et al. (2011) presented a network-based ontology analysis method. Wei and Pan (2012) investigated integrative modeling of multiple gene networks and diverse genomic data to identify targeted genes of transcription factor. Huang et al. (2009a) reviewed existing enrichment tools and classified them into three categories: 1) singular enrichment analysis, which calculates enrichment P-value for each term separately based on a pre-selected gene list; 2) gene set enrichment analysis, which directly uses gene experimental values (no need to pre-select genes); 3) modular enrichment analysis, which utilizes the inter-relationship among terms to assess enrichment. Some modular enrichment tools allows researchers to simultaneously incorporate multiple annotation resources (e.g., DAVID (Huang et al. 2009b), GENECODIS (Nogales-Cadenas et al, 2009), and GeneTerm Linker (Fontanillo et al, 2011)). For example, DAVID covers over 40 annotation categories.

We propose a Bayesian extension of the hypergeometric test which naturally incorporates the GO structure into enrichment analysis. Like the traditional hypergeometric test, the Bayesian method assumes that if a GO term is not enriched, the number (n_j) of DE genes annotated to the term follows the hypergeometric distribution. If the term is enriched, n_j tends to have a greater value, deviating from the hypergeometric distribution. Such deviation has been described by the non-central hypergeometric distribution (Harkness, 1965). We construct a Bayesian non-central hypergeometric model and the GO structure is incorporated through a hierarchical prior on the non-centrality parameters. According to Huang et al. (2009a), the proposed method belongs to the category of modular enrichment analysis. Subramanian et al. (2005), on the other hand, would refer to it as enrichment analysis of annotations. We demonstrate that the proposed method can overcome the aforementioned limitations of the hypergeometric P-value and produce biologically meaningful results.

2 Method

Researchers have used the example of picking colored balls at random from an urn to explain the idea of the non-central hypergeometric distribution. Suppose we pick d balls without replacement from an urn containing a total of f balls, among which g are red and (f − g) are black. When the sampling is unbiased, each ball has an equal chance of being selected and the number of red balls picked follows the hypergeometric distribution. The non-central hypergeometric distribution arises where the sampling is biased. For example, due to differences in size, weight, or texture, a red ball might have a greater chance of being picked than a black ball. In this case, the number of red balls picked can be modeled by the non-central hypergeometric distribution (Harkness, 1965; Fog, 2008). Denote the number of red/black balls picked as Y_r and Y_b, respectively, and Y_r ~Binomial(g, p_r) and Y_b ~Binomial(f − g, p_b). Then the conditional probability of Y_r given Y_r + Y_b = d is

$$\begin{array}{l}P(Y_r=n\mid Y_r+Y_b=d)=\frac{P(Y_r=n)P(Y_b=d-n)}{{\sum }_{i}P(Y_r=i)P(Y_b=d-i)}\\ =\frac{\left(\begin{array}{c}g\\ n\end{array}\right)p_r^n{(1-p_r)}^{g-n}\left(\begin{array}{c}f-g\\ d-n\end{array}\right)p_b^{(d-n)}{(1-p_b)}^{[(f-g)-(d-n)]}}{{\sum }_i\left(\begin{array}{c}g\\ i\end{array}\right)p_r^i{(1-pr)}^{g-i}\left(\begin{array}{c}f-g\\ d-i\end{array}\right)p_b^{(d-i)}{(1-pb)}^{[(f-g)-(d-i)]}}\\ =\frac{\left(\begin{array}{c}g\\ n\end{array}\right)\left(\begin{array}{c}f-g\\ d-n\end{array}\right){\theta }^n}{{\sum }_{i=l}^s\left(\begin{array}{c}g\\ i\end{array}\right)\left(\begin{array}{c}f-g\\ d-i\end{array}\right){\theta }^i},\end{array}$$ (2)

where parameter $\theta \equiv \frac{p_r/(1-p_r)}{p_b/(1-p_b)}$ is called the non-centrality parameter, effectively the odds ratio measuring the sampling bias. The valid summation boundaries in the denominator are l = max(0, d−(f −g)) and s = min(g, d). For the special case of θ = 1, or equivalently p_r = p_b, it can be shown that the denominator reduces to $\left(\begin{array}{c}f\\ d\end{array}\right)$, and (2) becomes a hypergeometric probability. Equation (2) provides a flexible model to accommodate biased sampling where θ ≠ 1. In the context of enrichment analysis, for GO term G_j, we consider the red and black balls in the urn as the groups of genes annotated and not annotated by G_j in the full list, with sizes g_j and (f − g_j), respectively. Hence the enrichment of G_j can be modeled through the non-central hypergeometric distribution for n_j with parameter θ_j. We declare G_j to be enriched if the estimated non-centrality parameter θ_j is significantly greater than 1.

In reality, researchers are usually interested in evaluating the whole DAG simultaneously instead of a single GO term. We propose a Bayesian non-central hypergeometric model to addresses the limitations of the traditional hypergeometric P-value: 1) genes annotated by a GO term is repeatedly used in the test of enrichment for all of its ancestors; 2) there is no sharing of information among related GO terms; and 3) it has a size constraint.

We address Limitation 1) by only including the additionally-contributed information by term G_j into the likelihood. Let $g_j^{\ast }$ be the number of genes that are most specifically annotated to term G_j, among which, $n_j^{\ast }$ are DE genes. In other words, the $g_j^{\ast }$ genes are annotated by G_j, but not by any of its child terms. In Figure 1 the most specifically annotated genes by G₅, G₇ and G₈ are (c, s, u), (b, d, t), and (a), and we have $(g_5^{\ast }=3,n_5^{\ast }=1),(g_7^{\ast }=3,n_7^{\ast }=2)$ and ( $g_8^{\ast }=1,n_8^{\ast }=1$). Corresponding to ( $g_j^{\ast },n_j^{\ast }$), we define $f_j^{\ast }=f-(g_j-g_j^{\ast })$ and $d_j^{\ast }=d-(n_j-n_j^{\ast })$. Here ( $g_j-g_j^{\ast }$) and ( $n_j-n_j^{\ast }$) represent information that has been used in the tests of off-spring terms of G_j. Then the likelihood from G_j is

$$P(n_j^{\ast }\mid f_j^{\ast },d_j^{\ast },g_j^{\ast },{\theta }_j)=\frac{\left(\begin{array}{c}{g}_j^{\ast }\\ n_j^{\ast }\end{array}\right)\left(\begin{array}{c}{f}_j^{\ast }-g_j^{\ast }\\ d_j^{\ast }-n_j^{\ast }\end{array}\right){\theta }_j^{n_j}}{{\sum }_{i-l^{\ast }}^{s^{\ast }}\left(\begin{array}{c}{g}_j^{\ast }\\ i\end{array}\right)\left(\begin{array}{c}{f}_j^{\ast }-g_j^{\ast }\\ d_j^{\ast }-i\end{array}\right){\theta }_j^i}.$$ (3)

Accordingly, the lower and upper bounds for summation are $l^{\ast }=\mathit{max}(0,d_j^{\ast }-(f_j^{\ast }-g_j^{\ast }))$ and $s^{\ast }=\mathit{min}(g_j^{\ast },d_j^{\ast })$.

We address Limitation 2) by incorporating the GO hierarchical structure through a prior model on the set of non-centrality parameters. First we define φ_j ≡ log(θ_j), hence −∞ < φ_j < ∞. We set φ₁ = 0 for the root node. From top to bottom, we assume the following conditional distribution of φ_j (j = 2, ···, J) given the non-centrality parameters of its parent nodes, denoted by φ_Pj = {φ_k : G_k ∈ P_j},

$${\phi }_j\mid {\phi }_{P_j},{\sigma }^2~\sum _{k:G_k\in P_j}\frac{1}{\mid P_j\mid }N({\phi }_k,{\sigma }^2).$$ (4)

Here P_j denotes the set of parent nodes of G_j and |P_j | is the number of GO terms in P_j. Model (4) assumes that φ_j arises from a mixture distribution of |P_j | components, each being a normal distribution centered at the non-centrality parameter of one of its parents. With an equal mixing probability 1/|P_j | we assume a priori that each parent has equal influence on φ_j. Parameter σ² characterizes the variability among child nodes. The joint prior of φ = {φ_j : j = 2, ···, J} is obtained by the product of (4) over j = 2, ···, J. This prior provides a mechanism to share information among GO terms based on the DAG structure. It also accommodates multiple inheritance. We assign an inverse gamma prior IG(0.01, 0.01) to σ², which has been used extensively in Bayesian models (Gelman et al., 2003).

We infer the enrichment of term G_j based on the posterior distribution of φ_j, denoted by [φ_j | (f*, d*, g*, n*)], where $({\mathit{f}}^{\ast },{\mathit{d}}^{\ast },{\mathit{g}}^{\ast },{\mathit{n}}^{\ast })=\left\{(f_j^{\ast },d_j^{\ast },g_j^{\ast },n_j^{\ast }),j=2,\cdots ,J\right\}$. Specifically, we use B_j ≡P(φ_j > 0 | (f*, d*, g*, n*)), denoted as the B-value, to measure the enrichment of a GO term. It is the posterior probability of G_j being enriched in the DE gene list D. By using the B-value, we overcome Limitation 3), because the B-value has a support of (0,1) and it does not have a size constraint like the hypergeometric P-value.

A Markov Chain Monte Carlo (MCMC) sampling algorithm is employed to simulate random samples from the joint posterior distribution. The full conditional distribution of σ² is an inverse gamma distribution. A Metropolis-Hasting algorithm is implemented to sample from the full conditional distribution of φ_j. See Web Appendix A and B for more details on the MCMC algorithm and the calculation of the B-value.

The B-value measures the strength of enrichment evidence at each GO term. We can use it as a screening tool to rank GO terms to help researcher select terms for further investigation. To answer questions such as “what should be the cutoff value for the B-value”, the Bayesian FDR (Newton et al., 2004) has been widely used to account for multiplicity: $E(\mathit{FDR}\mid \mathit{data})=\frac{\sum {\delta }_j(1-B_j)}{D}$, where D = Σ_j δ_j is the number of selected GO terms, indicator δ_j = 1 if the jth term is identified as enriched (its B-value ranks among the top D terms), and δ_j = 0 otherwise. E(FDR|data) is the posterior proportion of false discoveries in the identified enriched terms. The Bayesian FDR has been used extensively in Bayesian highthroughput data analysis (Storey, 2002; Do et al., 2005). Examples of other developments in Bayesian paradigm to address statistical significance in multiple comparison include Muller et al. (2006) and Scott and Berger (2010). Due to the complexity in the biological data-mining environment (e.g., gene-gene and function-function correlation, annotation redundancy, etc.), the sensitivity and specificity of existing enrichment methods are not yet in the optimal state (Goeman et al., 2007). We agree with the idea that the B-value, like other enrichment scores including the P-value, should be treated as a scoring system that plays an advisory role such as ranking and suggesting possible relevant annotations, as opposed to an absolute, decision-making role (Huang et al., 2009b). The important guideline to help users in adjusting analytic thresholds is the notion that enriched terms should make sense based on a priori biological knowledge of the study (Huang et al., 2009a).

3 Comparison with Existing Methods

Based on Figure 1, we compare the proposed method with a number of existing methods: the hypergeometric P-value, the elim P-value (Alexa et al., 2006), the parent-child P-value (Grossmann et al., 2007), and a Bayesian model-based gene set analysis (Bauer et al., 2010), denoted as MGSA. They have different assumptions and tend to detect different features. With the biological truth unknown, there is no gold standard to compare methods in real studies (Grossmann et al., 2007). We try to demonstrate and understand the distinctive characteristics of each method. In Figure 1 we present ( $g_j^{\ast },n_j^{\ast }$) and the B-value in the second row under each term. We also use A(·), G(·), and M(·) to present the elim P-value, the parent-child P-value, and the posterior probability of activation under MGSA, respectively. Stronger enrichment is indicated by larger values of B(·) and M(·), and smaller values of P(·), A(·), and G(·).

Compared with the hypergeometric P-value, the B-value has several advantages. First, it can distinguish GO terms with the same (g_j, n_j). The three nodes G₈, G₁₈, and G₁₉, all with (g_j, n_j) = (1, 1) and thus equal hypergeometric P-values, are differentiated by their B-values (B₈ = 0.861, B₁₈ = 0.404, and B₁₉ = 0.315). Due to intrinsic noises in high-throughput data collection and processing, there can be errors in DE detection, which affects the accuracy of the hypergeometric P-values. The proposed method recognizes that neighboring terms on the GO DAG represent related biological functions. Thus enrichment detected in a neighborhood might be more reliable than that detected in an isolated term. The larger B-value for G₈ is attributed to the stronger evidence of enrichment in its neighbors. Second, the proposed method mitigates the undue influence of GO term size. The hypergeometric P-value identifies G₂ as the most enriched term, although its enrichment level, n₂/g₂ = 6/11 = 0.55, is modest. Because it is one of the largest terms (g₂ = 11) in Figure 1, it has the smallest P-value of 0.034. If we exclude evidence already accounted for in the off-springs, its marginal evidence of enrichment is ( $g_2^{\ast }=3,n_2^{\ast }=2$), the same as G₇. The B-value takes into account marginal evidence and enrichment in the neighborhood: for G₇, both of its parent $G_5(g_5^{\ast }=3,n_5^{\ast }=1)$ and off-spring $G_8(g_8^{\ast }=1,n_8^{\ast }=1)$ contribute supporting evidence, which is not the case for G₂. Thus the B-value considers G₇ to have stronger evidence of enrichment.

Both the elim P-value (Alexa et al., 2006) and the parent-child P-value (Grossmann et al., 2007) attempt to address the “dependency problem” caused by overlapping annotations between parent-child pairs. The elim method tests GO terms from leaf to root, and removes all genes annotated to a significantly enriched term from its ancestors. Thus the elim P-value tends to identify highly enriched GO terms that remain significant even after removing enrichment evidence from their offsprings. Considering the small size of Figure 1, we set the P-value cutoff at 0.10. Thus G₇ is considered significantly enriched and genes (a, b, d, t) are removed from its ancestors (G₂, ···, G₆). The elim P-value considers G₇ the most significantly enriched. Due to the removal of genes (a, b, d, t), none of G₇’s ancestors are significant, and the previously top-ranking term G₂ (by both the B-value and the hypergeometric P-value) now ranks even behind G₁₈ and G₁₉. The parent-child P-value works from root to leaf, computing the hypergeometric P-value for each term in the context of its parent (treating the genes annotated by its parent as the full gene list). This approach identifies GO terms that show stronger enrichment compared to their parents. Effectively it penalizes terms for having highly enriched parents. Take G₈ and G₁₉ for example, which have the same (I_A, n_A). Based on the parent-child P-value, G₁₉ is more enriched than G₈ because G₁₉’s enrichment (1 out of 1) is stronger relative to its parent G₁₇ (1 out of 6), than G₈ (1 out of 1) relative to its parent G₇ (3 out of 4). The B-value accounts for parent-child relationship through hierarchical prior (4). It puts greater emphasis on consistent enrichment signal from neighborhoods of related GO terms. As a result, G₈ has a larger B-value than G₁₉ because the enrichment in G₈ is corroborated by its neighbors.

MGSA evaluates all terms at once using a Bayesian network (Bauer et al., 2010), assuming that in an experiment, a limited number of terms are activated which activate the genes they annotate (i.e., the true states of these genes become DE). Thus a gene is assumed to be truly DE if and only if at least one of its annotations is activated. The observed status are noisy observations of the true gene states, subject to a false positive rate α and false negative rate β. The inference is based on the posterior probability of each term being activated (enriched). MGSA does not use the GO DAG structure other than the true-path rule. One of its advantages is parsimony because a gene being DE is assumed to be fully explained by the activation of one of its annotations. Declaring additional terms to be active is discouraged because the likelihood function remains the same but a penalty is imposed by the prior. In Figure 1 MGSA identifies G₇, G₁₈ and G₁₉ as most likely to be enriched, because they efficiently explain the DE status of five genes (a, b, d, g, h) at the cost of one false negative gene (t). Although G₈ shows the same evidence of enrichment as G₁₈ and G₁₉, MGSA assigns a smaller score to G₈ because once G₇ is declared active, declaring G₈ active only leads to penalty by the prior. In contrast, the proposed method assigns a greater B-value to G₈ than G₁₈ and G₁₉ because it does not emphasize parsimony. Instead, it emphasizes the detection of subareas in GO where neighboring terms show consistent enrichment signals. Under this rationale, G₁₈ and G₁₉ have smaller B-values because their enrichment was not corroborated by their neighbors. Both MGSA and B-value address overlapping annotations, but via different approaches: MGSA by imposing that overlapping annotations lead to no gain in likelihood but penalty in prior; B-value by only including marginal evidence (excluding genes annotated by child terms) into likelihood (3).

In summary, all methods have their strength and weakness. The elim P-value and parentchild P-value tend to identify highly enriched terms that stand out from their background. These highly enriched terms might bear important biological meaning, but they are vulnerable to random noise or experimental error. MGSA tends to identify a small number of terms among which there is little overlap, and jointly they best account for the DE genes. It is advantageous in parsimony but it might suffer the problem of “not seeing the forest for the tree”. That is, MGSA does not detect joint terms which may contain unique biological information that is not held by individual terms (Huang et al., 2009a). The B-value tends to identify neighborhoods of related terms where moderate but consistent signals are considered more trustworthy than strong signals from isolated terms. In addition, sharing information among neighbors may mitigate the impact of mis-classified genes on the inference of individual terms. However, it might miss some highly enriched but isolated functions. Incorporating the GO graphical structure via prior implies that mistakes in the GO database might adversely affect its performance.

4 Simulation to Assess Performance

We conduct a simulation to compare the performance of different methods in detecting enriched GO subareas. Based on the DAG in Figure 1, we simulated data (the DE status of genes) following a generative scheme similar to that of Bauer et al. (2010). First, we assume the region containing (G₂, ···, G₈) to be active (truly enriched). Genes annotated by active terms are set to be non-DE and DE with probabilities β and 1−β, respectively. Genes annotated by inactive terms are set to be non-DE and DE with probabilities 1−α and α. We set α = β = 0.3 and generated 100 datasets. In Figure 2.A we present the precision/recall plot where precision=TP/(TP+FP) and Recall=TP/(TP+FN). Here TP, FP, and FN are the numbers of true positives, false positives, and false negatives, respectively. In Figure 2.B we present the ROC plot. This simulation is not a comparison of overall performance among the enrichment methods. Instead, by setting a subarea as truly enriched, it specifically evaluates the ability of different methods in identifying neighborhoods of related terms. It is no surprise that B-value performs best because it is designed to identify related terms. The parent-child P-value performs poorly on this task for a simple reason: In order to identify related GO terms, moderate but consistent signal in a neighborhood is considered stronger evidence than extreme signals from isolated terms. The parent-child P-value is designed to do exactly the opposite, detecting highly enriched terms that stand out from their parents. Here we assume that related functions tend to be activated together, thus we specified truly enriched terms as a subarea. This assumption implicitly favors the proposed B-value. We conduct a second simulation which adopts the assumption of MGSA that DE genes are determined by the activation of a limited number of terms among which there is minimum overlap (see Web Appendix C). Under this simulation truth MGSA has the best performance while the hypergeometric P-value has the poorest performance. Thus we caution against over-interpreting Figure 2 as the comparison of overall performance among different methods.

Figure 2.

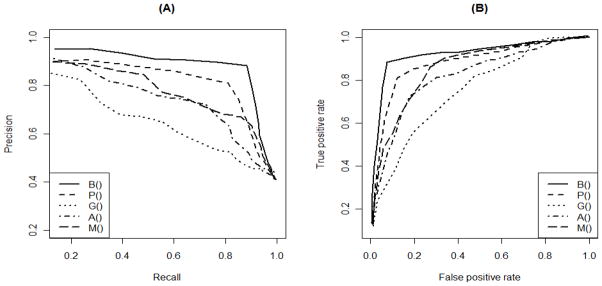
Benchmarking on simulated datasets, where P() represents the hypergeometric P-value, B() the B-value, G() the parent-child P-value, A() the elim P-value, and M() the MGSA posterior probability. The left panel shows the precision/recall plot, and the right panel shows the ROC curve.

With biological knowledge still evolving, inevitably there are some mistakes and incompletions in existing annotation systems. We conduct a third simulation to assess the performance of enrichment methods under imperfect annotations. We first generate data following the generative scheme described above. At this stage we assume perfect annotations. Then we introduce two types of imperfection: one by switching the annotations of two randomly selected genes, which attempts to mimic potential mistakes in existing annotations; the other by randomly removing a gene from its annotations, which attempts to mimic incompletions in existing annotations. We find that imperfect annotations does lead to poorer performance for all the methods, but their relative performance remains unchanged. It shows that different enrichment methods can produce useful results despite some imperfections in the existing annotation system. Please see Web Appendix D for simulation under the imperfect annotations.

5 Application

5.1 Dataset

We use a microarray data set to demonstrate the proposed Bayesian method. Researchers evaluated the effect of three stimulus on a B cell lymphoma cell line: the B cell antigen receptor (BCR), CD40, and a combination of the two (Basso et al., 2005). The expression data was processed using the SAM approach (Tusher et al., 2001). The full list contains f = 3952 genes and a cluster of d =196 genes was identified. Genes in this cluster shared a particularly interesting expression pattern: they were all upregulated in response to BCR signaling alone, but this upregulation was suppressed when CD40 signaling was included. These treatment conditions mimic important biological responses of immature B cells (Hsueh and Scheuermann, 2000), which must distinguish between signals delivered by authentic pathogen-derived antigens and by self antigens. In the former case, B cells need to respond by productive proliferation and differentiation into immune effector cells. In the later case, B cell responses need to be suppressed either through the induction of unresponsiveness or apoptotic cell death. It is hypothesized that B cells receiving only one signal, through the BCR, will proliferate and die, but B cells receiving two signals, through the BCR combined with a co-stimulatory receptor like CD40, will proliferate and survive. Thus, genes in the identified cluster are suppressed with the addition of CD40 signaling and could thus be involved either in the cell death response or in the induction of unresponsiveness.

5.2 Result

The full list of 3952 genes are annotated by J =6768 GO terms. We compare the top 100 GO terms selected by the hypergeometric P-value (denoted as the P-list) and by the B-value (denoted as the B-list). First, we examine which method tends to identify sets of related terms instead of isolated ones. We define a GO-set to be a group of GO terms connected through parent-child links. For example, in Figure 1, if we set the threshold of B-value at 0.75, then four terms are above this threshold (G₂,G₅,G₇,G₈). They form two GO-sets, one containing (G₅,G₇,G₈) and the other by G₂ itself. Larger GO-sets might contains more reliable enrichment signals than isolated single terms. Table 1 indicates that the B-value tends to identify larger GO-sets. Specifically, 25 terms in the P-list are isolated single terms, while there are only 7 such terms in the B-list. In addition, there are 15 GO-sets of size 2 (parent-child pairs) in the P-list. Among them, 9 pairs have parent terms with $(g_j^{\ast },n_j^{\ast })=(0,0)$, meaning that those parent terms contribute no additional evidence, and their small P-values are purely due to repeated use of information that has already been used in the test of their off-springs. By comparison, the B-list has far fewer such overlapping cases because the method is based on ( $g_j^{\ast },n_j^{\ast }$) instead of (g_j, n_j). Furthermore, the B-value has identified 3 large GO-sets each with more than 10 GO terms, while the largest GO-set in the P-list is of size 8.

Table 1.

Comparison of GO-sets identified in the P-list and the B-list

Size of GO-sets	1	2	3	4	5	7	8	12	22	31
P-list	25	15	6	2	3	1	1	0	0	0
B-list	7	0	3	4	0	1	0	1	1	1

Next we compare the biological functional groups identified by GO-sets of size ≥ 2 in the P-list and the B-list. A functional group is defined as a region in DAG that is associated with a relatively coherent biological theme and contains at least one such GO-set. Table 2 lists those functional groups identified and the number of GO terms from each list. First, the P-list has identified 5 functional groups (groups A – E) and the B-list has identified 2 additional functional groups (groups F, G). Among groups A – E, three groups (A, C, and E) are represented by similar numbers of GO terms in both lists. For the other two groups (B and D), the number of GO terms from the B-list substantially exceeds that from the P-list. Second, the two additional functional groups (F and G) identified by the B-list are represented by neighborhoods of 7 and 16 GO terms, indicating strong signals of enrichment that otherwise would have been missed by the hypergeometric P-value. For example, Figure 3 shows the regional DAG of functional group G. Among these 16 GO terms from the top 100 B-value list, only two disconnected terms (GO:0048167 and GO:0032230) are selected by the P-list, providing trivial evidence for this functional group. Group G, which is synaptic transmission, can be biologically associated with the experiment. Specifically, B cell receptor is one of the cell surface receptors that can activate phospholipase C enzymes to govern the opening of calcium ions channel in endoplasmic and reticulum and plasma membrane, and changes in intracellular calcium concentration is an established mechanism to regulate synaptic transmission (Wang et al., 2000; Dutting, Brachs, and Mielenz, 2011). In addition, disruption of mitochondrial membrane potential (Group F) has been found to be one of the main causes of BCR-medicated cell cycle arrest and apoptosisi in simulated immature B cells (Katz et al., 2001). We also include biological implications of functional groups A–E in Web Appendix E.

Table 2.

Functional groups identified in the P-list and the B-list

Group	#(P)	#(B)	Representing GO term
A	3	3	GO:0005764 (lysosome)
B	15	31	GO:0051049 (regulation of transportation)
C	9	7	GO:0016021 (integral to membrane)
D	2	22	GO:0016757 (transferase activity, transferring glycosyl groups)
E	11	9	GO:0007188 (G-protein signaling, coupled to cAMP nucleotide second messenger)
F	0	7	GO:0051881 (regulation of mitochondrial membrane potential)
G	0	16	GO:0051969 (regulation of synaptic transmission)

The seven functional groups are represented by letters A to G. #(P) and #(B) represent the number of GO terms in the P-list and the B-list that appear in each functional group, respectively. The last column lists the GO terms that represent the corresponding functional groups, which are the root terms (the least-specific terms) in the groups, respectively.

Figure 3.

The regional DAG of the biological functional group G. The rectangles in the DAG denote the GO terms in the group. The first row lists (g_j, n_j) and the P-value, an the second row lists ( $g_j^{\ast },n_j^{\ast }$) and the B-value.

Finally we illustrate that B-value can distinguish GO terms with the same (g_j, n_j) by incorporating evidence from neighboring terms. There are eight GO terms with (g_j, n_j) = (2, 2) that have the same hypergeometric P-value of 0.0024. All of them are in the top-100 P-list. The B-value suggests that these terms are very different. For example, GO:0007217 (tachykinin signaling pathway) has a B-value of 0.948 and it is in the top-100 B-list. In contrast, GO:0051319 (G2 phase) has a B-value of 0.397 and its rank based on the B-value is 5196. To shed light on their difference in B-values, we compare their regional DAGs in Figure 4 and 5. The parent of GO:0007217 has stronger enrichment than that of GO:0051319. In addition, GO:0007217 has 9 siblings, 6 of which have genes represented in the identified cluster (n_j > 0). By comparison, GO:0051319 has 6 siblings, none of which has genes represented in the cluster. The support from related GO terms is substantially higher for GO:0007217 than for GO:0051319, and thus GO:0007217 is considered more likely to be associated with the identified list D. We conducted a literature search and could not find experimental evidence for the involvement of G2 phase (GO:0051319) in the regulation of B cell function. On the other hand, tachykinin (GO: 0007217) has been found to be secreted during the differentiation of B cell precursors thereby regulating their development (Milne et al., 2004). Thus, GO:0007217 does appear to be biologically relevant.

Figure 4.

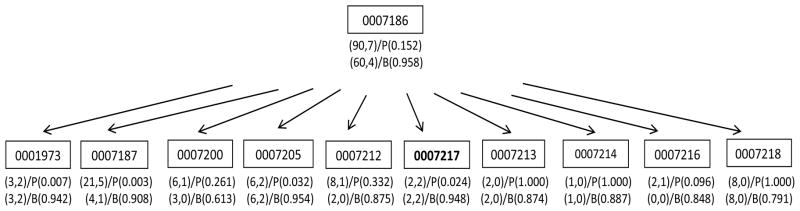
The regional DAG of GO:0007217. The rectangles in the DAG denote the GO terms in the neighborhood of GO:0007217. The first row lists (g_j, n_j) and the P-value, an the second row lists ( $g_j^{\ast },n_j^{\ast }$) and the B-value.

Figure 5.

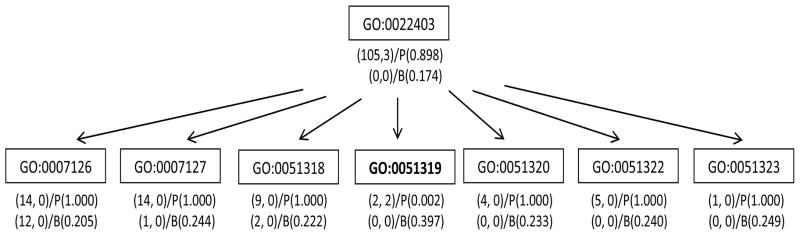
The regional DAG of GO:0051319. The rectangles in the DAG denote the GO terms in the neighborhood of GO:0051319. The first row lists (g_j, n_j) and the P-value, an the second row lists ( $g_j^{\ast },n_j^{\ast }$) and the B-value.

6 Discussion

We have proposed a Bayesian approach to detecting enriched annotations based on a non-central hypergeometric model. To address the issue of repeated use of information, we only include additionally contributed information from each GO term in the likelihood. We encourage sharing of evidence among related biological functions by specifying a hierarchical prior on the non-centrality parameters based on the dependence structure of GO DAG. We also use the B-value, which does not have a size constraint, to measure enrichment. The proposed method is a natural extension of the hypergeometric test, which provides a straightforward connection with the conventional test. More importantly, the mechanism induced by the Bayesian model to share information among related GO terms strengthens the detection of moderate but consistent enrichment signals which helps researchers to identify sets of related terms rather than individual isolated terms.

Currently annotation databases like GO are imperfect and still evolving, which means that mistakes in GO annotations might adversely affect functional enrichment analysis. This is a challenge faced by all enrichment analysis methods. Many studies have demonstrated that although imperfect, incorporating annotation information may help researchers achieve more meaningful results. The proposed method may mitigate the impact of mis-annotations in GO. For example, the hypergeometric test accesses each GO terms separately, thus a mis-annotated gene will greatly impact the P-value of a small term. Furthermore, this mis-annotation affects all the ancestors due to the true-path rule. The proposed Bayesian method can reduce the impact of mis-annotation in two ways: First, in likelihood (3), only the additional genes are included. Thus mis-annotation at a GO term does not directly affect its ancestors’ likelihood. Second, the hierarchical prior (4) allows borrowing strength among neighboring terms, which considers moderate but consistent signals from a neighborhood stronger evidence than isolated strong signals from individual terms. It is reasonable to believe that a false signal due to mis-annotation at a GO term would not be consistent with the true signals from its neighbors, which would be down-weighted by the Bayesian model.

The proposed Bayesian model is constructed based on the GO DAG structure. In this paper we could not investigate all possible structures of functional terms. However, our paper provides a framework that can be easily extended to account for other structures, where only the prior model (4) needs to be modified accordingly. For example, to make inference on KEGG functional terms which are organized as pathways, a possible choice of the prior is the conditional auto-regressive (CAR) model (Gelfand and Vounatsou, 2003) to incorporate the spatial relationship between KEGG terms. On the other hand, a number of methods have been proposed to measure the similarity between terms from semantic, topological, and functional perspectives (Schlicker et al., 2006; Lerman and Shakhnovich, 2007). Incorporating similarity measures into enrichment analysis might be another interesting topic in modular enrichment methodological research, especially in the Bayesian paradigm.

Some state-of-the-art enrichment tools allow researchers to utilize different sources of annotation simultaneously, including DAVID (Huang et al., 2009b), GENECODIS (Nogales-Cadenas et al., 2009), and GeneTerm Linker (Fontanillo et al., 2011). One type of tools, such as DAVID and GENECODIS, first organize and condense heterogeneous annotation content (such as GO terms, protein pathways, etc.) into term classes based on biological co-occurrences. Then enrichment tests are performed on those term classes. For this type of tools, the proposed Bayesian approach can be implemented at the second stage to account for inter-relationship among newly constructed term classes, if such inter-relationship can be established. Another type of tools, such as GeneTerm Linker, first perform enrichment analysis in different annotation spaces and the outputs are filtered and linked to produce metagroups of coherent biological significance. For this type of tools, the proposed Bayesian method can be implemented at the first stage to improve the accuracy and robustness of individual enrichment analysis.