Modeling the impact of hepatitis C viral clearance on end-stage liver disease in an HIV co-infected cohort with Targeted Maximum Likelihood Estimation

Summary

Despite modern effective HIV treatment, hepatitis C virus (HCV) co-infection is associated with a high risk of progression to end-stage liver disease (ESLD) which has emerged as the primary cause of death in this population. Clinical interest lies in determining the impact of clearance of HCV on risk for ESLD. In this case study, we examine whether HCV clearance affects risk of ESLD using data from the multicenter Canadian Co-infection Cohort Study. Complications in this survival analysis arise from the time-dependent nature of the data, the presence of baseline confounders, loss to follow-up, and confounders that change over time, all of which can obscure the causal effect of interest. Additional challenges included non-censoring variable missingness and event sparsity.

In order to efficiently estimate the ESLD-free survival probabilities under a specific history of HCV clearance, we demonstrate the doubly-robust and semiparametric efficient method of Targeted Maximum Likelihood Estimation (TMLE). Marginal structural models (MSM) can be used to model the effect of viral clearance (expressed as a hazard ratio) on ESLD-free survival and we demonstrate a way to estimate the parameters of a logistic model for the hazard function with TMLE. We show the theoretical derivation of the efficient influence curves for the parameters of two different MSMs and how they can be used to produce variance approximations for parameter estimates. Finally, the data analysis evaluating the impact of HCV on ESLD was undertaken using multiple imputations to account for the non-monotone missing data.

1. Introduction

The hepatitis-C virus (HCV) is a common co-infection for people infected with HIV, in particular amongst injection-drug users (Alter, 2006). While HIV can be successfully managed through highly active antiretroviral therapy, simultaneous treatment of both infections is challenging. Effective treatment for HCV exists, and unlike HIV, HCV can be cleared from the system both spontaneously and through HCV treatment (Sulkowski and Thomas, 2005).

For those who fail to clear the virus, infection with HCV will become chronic and may lead to cirrhosis, hepatocellular carcinoma and End Stage Liver Disease (ESLD), the condition signaling imminent liver failure. ESLD is characterized clinically by the presence of ascites, bleeding esophageal varices, spontaneous bacterial peritonitis and/or hepatic encephalopathy. Co-infection with HIV has been shown to accelerate the natural history of HCV (Merwat, 2011). Due to the reduction in mortality for co-infected patients who are treated for HIV, ESLD and its complications have emerged as primary causes of morbidity and mortality in the modern HIV treatment era (Operskalski and Kovacs, 2011). There is evidence that highly active anti-retroviral therapy might negatively affect HCV-related outcomes due to long term liver toxicity (Operskalski and Kovacs, 2011; Moodie et al., 2009).

The Canadian Co-Infection Cohort (CCC) study (Klein et al., 2010) follows a group of HIV and HCV co-infected participants over time, with follow-up appointments every six months. Our scientific question of interest is whether clearance of HCV has a causal effect on ESLD-free survival. Some of the statistical challenges involved in such an analysis include identifying and adjusting for variables (baseline or time-varying) that affect both HCV clearance and ESLD. In addition, various types of missing data might be caused by factors closely related to ESLD. In this manuscript, we will refer to HCV clearance as our exposure of interest, and ESLD as the survival outcome or failure event. In accordance with the causal inference literature, a time-dependent variable affecting HCV clearance and ESLD status at subsequent time-points will be called a time-dependent confounder.

Due to the concerns outlined above, standard survival modeling was deemed an inappropriate approach. Kaplan-Meier and Cox proportional hazards modeling both rely on the unlikely assumption that censoring and survival are independent. In addition, these methods either ignore or over-adjust for time-dependent confounders affected by previous exposure (Robins, 1986). Anti-retroviral therapy is one such confounder, as subjects may inconsistently follow anti-retroviral therapy that affects both viral clearance (Cooper and Cameron, 2002) and liver function (Operskalski and Kovacs, 2011), and previous knowledge of HCV status may affect the prescription of anti-retroviral therapy in the CCC study.

Marginal structural models (MSM) (Robins et al., 2000) have been developed to correctly model the effect of time-dependent exposure on the outcome in the presence of time-dependent confounders that are affected by previous exposure. In the survival context, MSMs have been developed for the parameters of a Cox proportional hazards model (Hernán et al., 2000). Weighting methods such as inverse probability of treatment weighting (IPTW) (Cole and Hernán, 2008; Xie and Liu, 2005) and substitution estimators such as G-computation (Robins, 1987) have been developed to fit MSMs. These methods properly account for baseline and time-dependent confounders.

Targeted Maximum Likelihood Estimation (TMLE, van der Laan and Rubin 2006) is a general framework that produces semiparametric efficient estimators. TMLE offers potential improvements over double-robust efficient estimating equation methodology (such as Adjusted-IPTW, Robins and Rotnitzky 1992), in that it will never produce multiple solutions, and that it can be constructed to preserve the natural bounds of the parameter of interest in estimation. The flexibility of the estimating framework allows improvements in estimation that can give TMLE an additional advantage in challenging situations such as data sparsity (Gruber and van der Laan, 2010). TMLE has been used to produce estimators for survival parameters (van der Laan and Gruber, 2012; Stitelman et al., 2012), general longitudinal parameters (van der Laan, 2010; Rosenblum and van der Laan, 2010b; Schnitzer et al., 2013; van der Laan and Gruber, 2012), and history-adjusted MSMs for longitudinal data (Rosenblum and van der Laan, 2010a). A review of influence curves, TMLE and a description of variance estimation is provided in the Supplementary Materials.

In this paper, we demonstrate an extension of a TMLE for longitudinal data to estimate survival curves under different histories of viral clearance. In addition, we develop a TMLE for the hazard model and derive the efficient influence curve. These techniques are then applied to analyze the effect of viral clearance on ESLD. Variance estimation is made possible using efficient influence curve inference, which produces a closed-form large-sample approximation of the variance of the different estimators (i.e. a sandwich estimator for the variance).

2. Modeling theory and procedures for the CCC study

In the CCC study, participants are scheduled for appointments every six months, with data collected on risk behaviours, treatment status (on/off), lab tests describing disease progression, and drug and alcohol use at each follow up visit. The HCV clearance time was defined as the first visit where a subject was found to be RNA negative. In order to assess the effect of clearing HCV, we are interested in estimating the probability of having ESLD depending on when the patient has cleared the virus. Since we obtain time-dependent data, the probability of ESLD can be calculated at each time point, which produces a survival curve for each clearance time. We could then compare, for example, the difference in survival curves for clearing HCV at the second time point versus clearing two years (or four time points) later. In this example, the representation of viral clearance at time two is (0, 1, 1, …, 1) since we are defining “first viral clearance” as a monotone process. To correspond with the longitudinal causal analysis literature, we will also refer to clearance time as exposure pattern. An exposure pattern up until time k − 1 representing a clearance history will be denoted as ${\stackrel{‒}{a}}_{k-1}\equiv (a_0,a_1,\dots ,a_{k-1})$.

We choose a semiparametric estimator because it requires the parametrization of only a component of the data generating density, thereby reducing our modeling assumptions. If a semiparametric estimator is regular and asymptotically linear (RAL), it has an associated influence curve. The influence curve is the unique function that determines the asymptotic properties of the estimator, including the variance. An estimator associated with the efficient (or minimal-variance) influence curve will also have minimal asymptotic variance amongst RAL semiparametric estimators, and is therefore called semiparametric efficient (van der Laan and Robins, 2003; Bickel et al., 1998). Estimating the density components of the influence curve while solving the empirical mean of the influence curve set equal to zero for the parameter of interest will produce an efficient estimator when this influence curve is efficient. Semiparametric efficient estimators in causal inference have been produced in the survival context (Robins and Rotnitzky, 1992; Scharfstein et al., 1999; Bang and Robins, 2005). These efficient causal estimators often have the added advantage of double-robustness where only a component of the underlying density must be correctly specified for asymptotic unbiasedness (van der Laan and Robins, 2003).

The following section describes the development of a TMLE for a survival curve under a given clearance time. Next, we develop theory and a procedure for estimating a marginal model for the hazard of obtaining ESLD. As shown in D'Agostino et al. (1990), when the event rate at all time points is small, as was true for our situation, this model is approximately equivalent to a Cox model (as the estimated odds ratio provides a good approximation of the hazard ratio). In the Supplementary Materials, we also demonstrate the simpler construction of an MSM for the log-odds of survival.

2.1 TMLE for a survival outcome

In this subsection, we adapt the methodology of van der Laan and Gruber (2012) to obtain an estimate of the marginal survival curve and the influence curve of the estimator. The influence curve is used to approximate the variance of the estimator. Let $T^{\stackrel{‒}{a}}$ denote the ESLD-free survival time that a subject would have obtained if they had experienced exposure pattern $\stackrel{‒}{a}=(a_0,a_1,\dots ,a_{K-1})$ and remained uncensored, defined according to the Neyman-Rubin counterfactual model (Rubin, 1974). The parameters of interest are the survival probabilities $S_{\stackrel{‒}{a}}\left(t\right)\equiv P(T^{\stackrel{‒}{a}}>t)$ for a fixed exposure pattern $\stackrel{‒}{a}$ at discrete time points t = 1, …, K. We will refer to $S_{\stackrel{‒}{a}}\left(t\right)$ as the survival curve under exposure $\stackrel{‒}{a}$ at time t. The survival curve can also be constructed separately for individual patient subgroups, V, if that is of interest.

Suppose we observe independent and identically distributed discretized survival times, T, and censoring times, C, for n subjects. In addition, we have information about a time-dependent exposure of interest (HCV status) and potentially confounding covariates at each time point. A corresponding censored observed data structure (without other variable missingness) can be described as O (L₀, A₀, Y₁, L₁, A₁, Y₂, …, A_K−1, Y_K), where the subscripts indicate a time-ordering. The vector-variable L₀ contains the baseline variables, including all potential baseline confounders which we considered to be age, HIV duration, HCV duration, gender, and education. The bivariate intervention nodes A_t ≡ {A_t(1), A_t(2)}, t = 0, …, K − 1 indicate categorical exposure and censoring status, respectively, at each time point. Specifically, A_t(2) = 0 indicates that a subject is uncensored at time t (i.e. C > t), and A_t(2) = 1 indicates censoring prior to or at time t (C ≤ t). The variables L_t, t = 0, …, K − 1 are time-dependent confounders. For instance, in our study, this includes CD4 cell count, antiretroviral therapy, HCV treatment status, and whether the participant had reported drinking alcohol in the past six months. Y_t, t = 1, …, K is the survival status at time t where Y_t = 1 indicates continued ESLD-free survival (so that Y_t = 1 if and only if T > t). We also let ${\stackrel{‒}{A}}_t$, ${\stackrel{‒}{L}}_t$ and ${\stackrel{‒}{Y}}_t$ indicate the variable history up to and including time t.

In order to describe the formulation of the efficient influence curve first developed by Bang and Robins (2005) and used by van der Laan and Gruber (2012) to develop the TMLE, fix a time t ≤ K and define the conditional probability of survival under a fixed history of exposure as

$$Q_t^{\stackrel{‒}{a}}\left(t\right)\equiv P\{T^{\stackrel{‒}{a}}>t\mid {\stackrel{‒}{A}}_{t-1}(1)={\stackrel{‒}{a}}_{t-1},A_{t-1}(2)=0,{\stackrel{‒}{L}}_{t-1},Y_{t-1}\}.$$

Note that this conditional probability is zero if there was failure at the previous time point, i.e. if Y_t−1 = 0. Recursively define the conditional probabilities of the $Q_t^{\stackrel{‒}{a}}(j-1)\mathrm{s}$ (going backwards starting with j = t) as

$$Q_t^{\stackrel{‒}{a}}(j-1)\equiv E\left\{Q_t^{\stackrel{‒}{a}}\right(j)\mid {\stackrel{‒}{A}}_{j-2}(1)={\stackrel{‒}{a}}_{j-2},A_{j-2}(2)=0,{\stackrel{‒}{L}}_{j-2},Y_{j-2}\},j=t,\dots ,2.$$

Each $Q_t^{\stackrel{‒}{a}}(j-1)$ is therefore defined by taking the previous conditional expectation, $Q_t^{\stackrel{‒}{a}}\left(j\right)$ and marginalizing over the intermediate covariate L_j−1 and Y_j−1. Finally, the parameter $S_{\stackrel{‒}{a}}\left(t\right)$ can be identified as $E\left\{Q_t^{\stackrel{‒}{a}}\right(1\left)\right\}$. Therefore, this target parameter is defined as a function of the sequential conditional means. We can fit a model for the conditional probability of being ESLD free, specified through the Q functions, and produce an estimate of the target parameter by taking an empirical mean of the predicted values ${\widehat{Q}}_t^{\stackrel{‒}{a}}\left(1\right)$ for each subject.

For each time-point, define $g_{\stackrel{‒}{a}}\left(t\right)$ as the probability of being uncensored and exposed according to $\stackrel{‒}{a}$ and in terms of the covariate history among the at-risk population (i.e. for those uncensored and ESLD-free at time t − 1). This quantity can be decomposed as

$$\begin{array}{cc}\hfill g_{\stackrel{‒}{a}}\left(t\right)\equiv \prod _{j=1}^t& \mathit{Pr}\left\{A_j\right(1)=a_j\mid {\stackrel{‒}{A}}_{j-1}(1)={\stackrel{‒}{a}}_{j-1},A_j(2)=0,{\stackrel{‒}{L}}_{j-1},Y_{j-1}=1\}\hfill \\ \hfill & \mathit{Pr}\left\{A_j\right(2)=0\mid {\stackrel{‒}{A}}_{j-1}(1)={\stackrel{‒}{a}}_{j-1},A_{j-1}(2)=0,{\stackrel{‒}{L}}_{j-1},Y_{j-1}=1\}.\hfill \end{array}$$

Set $Q_t^{\stackrel{‒}{a}}(t+1)\equiv Y_t$ for notational convenience. Then the efficient influence curve, $D_{\stackrel{‒}{a},t}$ for the parameter $S_{\stackrel{‒}{a}}\left(t\right)=P(T^{\stackrel{‒}{a}}>t)$ can be written as the sum of the t + 1 components

$$\begin{array}{cc}\hfill & D_{\stackrel{‒}{a},t}\left(j\right)\equiv \frac{I\{{\stackrel{‒}{A}}_{j-2}={\stackrel{‒}{a}}_{j-2},A_{j-2}(2)=0\}}{g_{\stackrel{‒}{a}}(j-2)}\left\{Q_t^{\stackrel{‒}{a}}\right(j)-Q_t^{\stackrel{‒}{a}}(j-1\left)\right\}\text{for}j=t+1,\dots ,2,\hfill \\ \hfill & D_{\stackrel{‒}{a},t}\left(1\right)\equiv Q_t\left(1\right)-S_{\stackrel{‒}{a}}\left(t\right)\hfill \end{array}$$ (1)

so that $D_{\stackrel{‒}{a},t}\equiv {\sum }_j{D}_{\stackrel{‒}{a},t}\left(j\right)$. We refer the interested reader to van der Laan and Gruber (2012) for a derivation of this quantity. Inference performed using this influence curve will be double robust: the estimator is consistent if either each $g_{\stackrel{‒}{a}}(j-2)$, j = t + 1, …, 2or each $Q_t^{\stackrel{‒}{a}}\left(j\right)$ j = t, …, 1contain the truth.

2.2 Fitting procedure for the TMLE

For a given time, t and HCV-clearance pattern, $\stackrel{‒}{a}$, a TMLE estimate for ESLD-free probability of survival, $S_{\stackrel{‒}{a}}\left(t\right)$ can be obtained by modifying the procedure given in van der Laan and Gruber (2012). Start with j = t. For convenience of notation, set $Q_t^{\stackrel{‒}{a},\ast }(j+1)\equiv Y_t=I(T>t)$ (the *-notation will indicate an updated fit produced according to the TMLE methodology). Fit the conditional expectation $Q_t^{\stackrel{‒}{a}}\left(j\right)=E\left\{Q_t^{\stackrel{‒}{a},\ast }\right(j+1)\mid {\stackrel{‒}{A}}_{j-1}(1)={\stackrel{‒}{a}}_{j-1},A_{j-1}(2)=0,{\stackrel{‒}{L}}_{j-1},Y_{j-1}\}$ as the initial fit. Let ${\widehat{Q}}_t^{\stackrel{‒}{a}}\left(j\right)$ be the predicted outcome for all subjects (zero for those not at-risk). In this case study, we used logistic regression to fit the model using all at-risk subjects with any exposure history. Then, the predicted outcome under fixed pattern $\stackrel{‒}{a}$ was made for each subject.

To update the fit for those at-risk, let $Q^{\stackrel{‒}{a},\ast }$ be a perturbation of ${\widehat{Q}}_t^{\stackrel{‒}{a}}\left(j\right)$ by ∊_t(j):

$$\mathrm{logit}\left\{Q_t^{\stackrel{‒}{a},\ast }\right(j\left)\right\}\equiv \mathrm{logit}\left\{{\widehat{Q}}_t^{\stackrel{‒}{a}}\right(j\left)\right\}+{∊}_t\left(j\right)\frac{1}{g_{\stackrel{‒}{a}}(j-1)}.$$ (2)

To fit the update by obtaining an estimate for ∊_t(j), perform a regression, amongst those at-risk, of ${\widehat{Q}}_t^{\stackrel{‒}{a},\ast }(j+1)$ with offset ${\widehat{Q}}_t^{\stackrel{‒}{a}}\left(j\right)$ and unique covariate $I\left\{{\stackrel{‒}{A}}_{j-1}\right(1)={\stackrel{‒}{a}}_{j-1},A_{j-1}(2)=0\}∕{\widehat{g}}_{\stackrel{‒}{a}}(j-1)$. Set ${\widehat{∊}}_t\left(j\right)$ to be the estimate of the coefficient of this covariate. Then update the original fit by plugging ${\widehat{∊}}_t\left(j\right)$ into Equation (2) and obtain a fit for all at-risk subjects (the fit for those who previously failed remains zero). The updated conditional expectation for all subjects is ${\widehat{Q}}_t^{\stackrel{‒}{a},\ast }\left(j\right)$. This update is only be performed once for each time point j.

Repeat the above procedure for j = t − 1, …, 1. The final fit ${\widehat{Q}}_t^{\stackrel{‒}{a},\ast }\left(1\right)$ is predicted for all n subjects. The parameter estimate ${\widehat{S}}_{\stackrel{‒}{a}}\left(t\right)$ is the mean of ${\widehat{Q}}_t^{\stackrel{‒}{a},\ast }\left(1\right)$ over all subjects. The result of this procedure is that the perturbed densities ${\widehat{Q}}_t^{\stackrel{‒}{a},\ast }\left(j\right)$ and the estimate ${\widehat{S}}_{\stackrel{‒}{a}}\left(t\right)$ jointly solve the efficient influence curve (1). This can be seen by noting that each logistic regression update solves the empirical mean of $I\{{\stackrel{‒}{A}}_{j-2}={\stackrel{‒}{a}}_{j-2},A_{j-2}(2)=0\}∕g_{\stackrel{‒}{a}}(j-2)\left\{{\widehat{Q}}_t^{\stackrel{‒}{a},\ast }\right(j)-{\widehat{Q}}_t^{\stackrel{‒}{a},\ast }(j-1\left)\right\}$ set equal to zero.

This procedure can be repeated for each time point t = 1, …, K to obtain an estimate of the survival curve $S^{\stackrel{‒}{a}}\left(t\right)$ for all values of t. One can then estimate different survival curves for each fixed exposure pattern of interest. Let each possible combination of $\stackrel{‒}{a}=(a_0,\dots ,a_{K-1})$ be uniquely identified as ${\stackrel{‒}{a}}^l$. Let a given exposure pattern ${\stackrel{‒}{a}}^l$ up until time t be denoted ${\stackrel{‒}{a}}_t^l$. Let M represent the number of unique truncated exposure patterns ${\stackrel{‒}{a}}_t^l$, t = 0, …, K − 1. We can calculate M survival estimates, one for each truncated exposure pattern, ${\stackrel{‒}{a}}_t^l$.

2.3 MSM for the hazard function

In addition to estimating each survival curve separately for each exposure pattern, we are interested in modeling ESLD-free survival at the population level as a function of time and the exposure pattern. Following common practice, we chose to specify a logistic model for the discrete hazard function, ${\lambda }_{\stackrel{‒}{a}}\left(t\right)\equiv P(T^{\stackrel{‒}{a}}=t\mid T^{\stackrel{‒}{a}}\ge t)$. This corresponds to a marginal structural mean model and can be written as

$${\lambda }_{\stackrel{‒}{a}}\left(t\right)=\mathrm{logit}\left[\frac{\{1-S_{\stackrel{‒}{a}}(t\left)\right\}}{S_{\stackrel{‒}{a}}(t-1)}\right]=X_{l,t}^T\beta$$

for all unique patterns ${\stackrel{‒}{a}}_t^l$. X is the design matrix of column vectors representing the covariates in the model which only includes combinations of time, t, and ${\stackrel{‒}{a}}_t^l$ (or time since clearance). Let X_l,t represent the R-dimensional row of the design matrix corresponding with exposure ${\stackrel{‒}{a}}_t^l$ and time t, represented as a column vector. For example, if the MSM was a linear model with an intercept and a linear term for time, then for each unique pattern ${\stackrel{‒}{a}}_{t^{\ast }}^l$ for the time point t*, X_l,t* = (1, t*)^T. The design matrix can also contain subgroups if S was calculated separately for the components of a categorical variable, V, and although we do not include conditioning in our notation, the following development easily extends to such a case. Finally, let β denote the vector of coefficients corresponding with the columns of the design matrix. Therefore, since there are M estimates for the survival function, the dimension of the matrix X is R by M, corresponding with a β-vector of length R.

The parameter β can be defined as

$$\beta \equiv {\mathrm{argmax}}_{\beta }E\sum _{l,t}\log \left[{\left\{\text{expit}\right(X_{l,t}^T\beta \left)\right\}}^{I\left(T^{{\stackrel{‒}{a}}^l=t}\right)}{\{1-\text{expit}(X_{l,t}^T\beta \left)\right\}}^{I\left(T^{{\stackrel{‒}{a}}^l>t}\right)}\right]$$

or the value that maximizes the log-likelihood of a logistic model with marginal mean specification $\text{expit}\left(X_{l,t}^T\beta \right)$. Only subjects with $T^{{\stackrel{‒}{a}}^l}>t$ contribute to the likelihood at a given time point. By passing the expectation through the linear expression, this simplifies to

$${\text{argmax}}_{\beta }\sum _{l,t}{S}_{{\stackrel{‒}{a}}^l}(t-1)\left[{\lambda }_{{\stackrel{‒}{a}}^l}\right(t\left)\log \right\{\text{expcit}\left(X_{l,t}^T\beta \right)\}+\{1-{\lambda }_{{\stackrel{‒}{a}}^l}\left(t\right)\left\}\log \right\{1-\text{expcit}\left(X_{l,t}^T\beta \right)\left\}\right]$$

where $S_{{\stackrel{‒}{a}}^l}\left(0\right)=1$. This corresponds to the maximum log-likelihood for a logistic regression with outcome ${\lambda }_{{\stackrel{‒}{a}}^l}\left(t\right)$ and weights $S_{{\stackrel{‒}{a}}^l}(t-1)$.

The efficient influence curve (derived in the Supplementary Materials) is

$$D_{\beta }={\left[\sum _{l,t}{S}_{{\stackrel{‒}{a}}^l}(t-1)X_{l,t}{X}_{l,t}^T\frac{\text{exp}\left(X_{l,t}^T\beta \right)}{{\{1+\text{exp}(X_{l,t}^T\beta \left)\right\}}^2}\right]}^{-1}$$

$$\sum _{l,t}\left[X_{l,t}-\sum _{m:\{{\stackrel{‒}{a}}_t^l\subset {\stackrel{‒}{a}}_{t+1}^m\}}{X}_{m,t+1}\{1+\text{expit}(X_{m,t+1}^T\beta \left)\right\}\right]D_{{\stackrel{‒}{a}}^l,t}.$$

The inside summation is taken over all m for which the truncated exposure pattern ${\stackrel{‒}{a}}_t^l$ is a subset of the pattern ${\stackrel{‒}{a}}_{t+1}^m$ (or, equivalently, ${\stackrel{‒}{a}}_t^m={\stackrel{‒}{a}}_t^l$). The efficient influence function components can be numerically evaluated for each of the n subjects, producing an influence matrix of dimension n × R, representing the joint influence components for β.

To obtain the point estimates of the MSM parameters, first calculate the hazard functions for each exposure pattern and time using ${\lambda }_{{\stackrel{‒}{a}}^1}\left(t\right)=\left\{S_{{\stackrel{‒}{a}}^l}\right(t)-\{S_{{\stackrel{‒}{a}}^l}(t-1)\}∕S_{{\stackrel{‒}{a}}^l}(t-1)$. Then, using these M values as outcome measurements, fit the logistic regression of interest, with weights equal to $S_{{\stackrel{‒}{a}}^l}(t-1)$. This will produce the point estimate of β. To obtain variance estimates, fit the efficient influence curve for β for each subject by estimating each of the components. Then, for each of the R columns of the resulting matrix the empirical variance is the estimated variance for the corresponding MSM coefficient estimate of β.

3. The impact of HCV clearance on ESLD

At the time of data extraction, the CCC study had collected data on 1,055 individuals. At the time of cohort entry, 778 had not cleared HCV and had not yet been diagnosed with ESLD. Thirty-eight participants had hepatitis B and were excluded from the analysis as chronic hepatitis B is itself a very strong risk factor for progressive liver disease, leaving 740 subjects in the analysis. The median follow-up in this subgroup was two years after baseline, sometimes including missed visits.

Potential baseline confounders considered were age, HIV duration, HCV duration, gender, and education. Potential time-dependent confounders (collected at baseline and at subsequent visits) were CD4 cell count, whether the participant was receiving antiretroviral therapy, HCV treatment status, and whether the participant had reported drinking alcohol in the past six months.

Characteristics of the sample used in the analysis are given in Table 1. The population was primarily composed of patients who had been infected with HCV and HIV for a long duration. While most were receiving antiretroviral therapy to control their HIV infection, few received treatment for HCV. Approximately 25% of the sample was female.

Table 1.

Characteristics at baseline of the 740 subjects analyzed from the Canadian Co-infection Cohort Study.

Characteristic	Summary		N. Missing
Numeric variables	Median	IQR
Age (years)	44	(39,50)	2
HIV duration (years)	11	(6,16)	20
HCV duration (years)	18	(11,25)	4
CD4 cell count	380	(242,540)	16
Binary variables	N.	%
Female	227	25	1
Education: ≥ high school	760	83	0
Taking antiretroviral drugs	735	80	1
Currently treated for HCV	28	3	0
Alcohol in past 6 months	455	50	3

ARV is antiretroviral therapy; IQR is the inter-quartile range.

We performed the analysis using six visits after the baseline visit (equivalent to a follow-up of three years), as the data were excessively sparse for longer follow-ups. Subjects often missed their biannual visits, and in addition, the time-varying covariates, exposure and development of ESLD were all subject to irregular (i.e. non-monotone) missingness. We defined exposure as first clearance of HCV and outcome as diagnosis of ESLD. A subject was assumed to be censored if they missed three visits in a row, or died from a cause unrelated to ESLD. If a subject died from liver complications, they were considered to have experienced the event. Table 2 reports the number of subjects at risk and the failure incidence at each time point, by exposure status (when known, and when unknown). The time-dependent exposure status is defined as having cleared HCV at some previous time. From this table, it is clear that there is limited information about subjects who have cleared HCV.

Table 2.

Number at-risk and failure incidence by time point and exposure status (when known)

Status	Visit	1	2	3	4	5	6
Unexposed	N. at-risk	380	294	214	159	102	78
	N. failed	22	16	12	4	4	4
Exposed	N. at-risk	29	62	80	85	84	76
	N. failed	0	3	1	1	1	2
Unknown	N. at-risk	320	325	216	195	197	162
	N. failed	14	9	10	4	5	3

Due to the relatively large amount of missing data in the data set (in particular, due to many missed visits), we chose to employ multiple imputations (Rubin and Schenker, 1986) as part of our analytical strategy to account for non-censoring missingness. The validity of multiple imputations in this context relies on the sequential randomization assumption, or that the missing data depends on the full data process only through the observed past and the validity of the imputation model. We built the imputation model using all of the variables included in the analysis. The imputation models chosen allowed each variable to be imputed conditional on all previously or simultaneously collected variables so that future information was never used following, for example Shortreed and Moodie (2012). Multivariate Imputation by Chained Equations (MICE) was performed using the R package mice (van Buuren and Groothuis-Oudshoorn, 2011). After a burn-in of 20 draws, 50 imputations were drawn with 20 lagged iterations each. Logistic regression was used to impute all binary variables, and Bayesian linear regression was used for all continuous variables (including CD4 cell count, which was log-transformed throughout). The analytical method was performed on each imputed data set, and the estimates and standard errors obtained were combined according to Rubin and Schenker (1986) to produce the final inference.

The probabilities of survival at each time point for a given exposure pattern were calculated using the Kaplan-Meier estimator, the (stabilized) Adjusted Kaplan-Meier Estimator (AKME; Xie and Liu 2005) which is an inverse probability of treatment weighted estimator, and the TMLE described above. Due to the sparsity of failures among the exposed subjects, we used all at-risk subjects in the outcome models for the TMLE procedure and included the complete exposure history in the model. All censoring and exposure probabilities were estimated with logistic regression using covariates at the baseline and previous time point, and an indicator of whether or not the visit was missing in each model. Limiting these models to omit time-varying covariates prior to the current time point (while including baseline) was partially justified through exploratory analysis which was greatly limited by data sparsity.

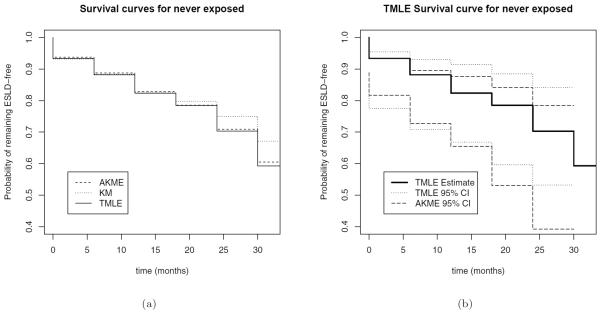
Figure 1(a) shows the survival curves under “never-exposed” estimated by each of the three methods. The curves can be interpreted as estimates of the marginal probability of remaining ESLD-free at each time point for a subject who is exposed according to pattern $\stackrel{‒}{a}=(0,0,0,0,0,0)$, i.e. never clearing HCV. For later time points, the Kaplan-Meier estimator appears to overestimate the probability of remaining ESLD-free. Figure 1(b) displays pointwise 95% confidence intervals for the TMLE and AKME. For this exposure pattern, the AKME has smaller standard errors than the TMLE, but similar point estimates.

Figure 1.

Survival curves under no exposure (a) calculated with adjusted Kaplan-Meier (AKME), unadjusted Kaplan-Meier (KME), and Targeted Maximum Likelihood Estimation (TMLE), and (b) calculated with TMLE and including confidence intervals for TMLE and AKME. Confidence intervals were calculated using a normality assumption on the logit-transformed parameter and then transformed back to the (0,1) scale. The variance for each imputation was calculated using the sandwich estimator for TMLE, and the bootstrap for AKME.

An MSM for the hazard of developing ESLD was defined using a logistic mean model: $\mathrm{logit}{\lambda }_{\stackrel{‒}{a}}\left(t\right)={\gamma }_0+{\gamma }_{1}a(t-1)+{\gamma }_{2}t$ where a(t − 1) is the lagged binary exposure status at time t − 1, and ${\lambda }_{\stackrel{‒}{a}}\left(t\right)$ is the marginal hazard at time t. The parameters of the logistic model were estimated using the three different methods shown in Table 3, each incorporating the multiple imputations. The unadjusted pooled logistic regression was fit, with an empirical sandwich estimator to estimate the standard error of each coefficient (using R library sandwich; Zeileis 2006). The MSM was fit using IPTW (adjusting for both non-randomized exposure and censoring) with stabilized weights, and with the TMLE described in Section 2.3.

Table 3.

CCC results: Logistic model for hazard of developing end-stage liver disease as a function of HCV clearance. Naïvt refers to unweighted logistic regression. Variance estimates were obtained using a robust sandwich estimator for tht Naïve and IPTW methods and the efficient influence curve for the TMLE. Each method was performed on 50 imputed datasets and the inference combined.

Method	Est	SE	95% CI
γ2 Intercept
Naïve	−3.05	0.29	(−3.62,−2.49)
IPTW	−3.30	1.03	(−5.32,−1.27)
TMLE	−3.37	0.68	(−4.70,−2.04)
γ1 Coefficient of exposure status
Naïve	−0.12	0.37	(−0.85,0.62)
IPTW	−0.44	0.82	(−2.05,1.17)
TMLE	−0.35	0.46	(−1.26,0.55)
γ2 Coefficient of time
Naïve	0.10	0.07	(−0.05,0.24)
IPTW	0.22	0.22	(−0.21,0.66)
TMLE	0.22	0.15	(−0.08,0.52)

The results for γ₁ indicate that the coefficient for exposure status was estimated as −0.12 but not significantly different than zero at the 0.05 level when using the naïve method (which does not adjust for confounding or informative dropout). TMLE and IPTW estimated greater effect magnitudes of −0.44 and −0.35, respectively, consistent with a protective effect of clearance on ESLD. TMLE had a 44% smaller standard error than IPTW, but neither estimator found a significant effect of HCV clearance. All of the models yielded a positive (but not significant) parameter estimate for γ₂, suggesting a higher risk of ESLD over time. Here again, the IPTW standard error was substantially larger than the TMLE standard error. The large standard errors in this analysis were a result of the sparsity of the events across exposure patterns. The small difference between the adjusted and unadjusted methods may be due to the multiple imputations already adjusting for some of the informative missingness in the analysis. We anticipate more power as the study continues to accrue events.

4. Discussion

The science and treatment of HIV/HCV co-infection is an active area of research. In this paper we used sequential longitudinal TMLE to estimate survival curves under a fixed history of HCV clearance and modeled the hazard of obtaining ESLD in order to evaluate the marginal effect of clearing HCV on the risk of ESLD. We found a clinically but not statistically significant protective effect of the clearance of HCV on ESLD, adjusting for time in the model. A protective effect of HCV clearance on ESLD is consistent with studies that have shown curative HCV therapy greatly reduces progression to ELSD, hepatic decompensation, transplantation, hospitalisation and death (Berenguer et al., 2009).

Clearance of HCV occurs both spontaneously and due to HCV treatment, and the subsequent risk of liver damage might differ depending on the reason for clearance. The causal relationship of viral clearance on ESLD may indeed be more complicated than was represented in our simple MSM. With additional power, further analyses could also consider the different ethnic groups participating in the study, including the Aboriginal subpopulation (representing 15% of our sample) who may clear HCV more readily than the general population (Minuk et al., 2003; Scott et al., 2006) and could have a different risk of ESLD.

The TMLE for the hazard model estimates the same parameter as the well-known IPTW method for the estimation of the parameters of an MSM with pooled logistic regression. This is demonstrated theoretically and through simulation in the Supplementary Materials. When the hazard at all time points is small, these MSM coefficients are approximately equal to the coefficients of a marginal structural Cox model (Hernán et al., 2000; D'Agostino et al., 1990; Xiao et al., 2010). TMLE is an asymptotically efficient method, and it produced substantially smaller standard errors than IPTW for the coefficients of the logistic model. However, in finite samples, TMLE is not always more efficient than IPTW.

A major challenge particular to the TMLE was the need to fit outcome models for failure at every time point. The rarity of events in the CCC data made this difficult, even with multiple imputations. We adjusted our initial estimation plan by smoothing over exposure pattern and thereby using all at-risk subjects in the estimation of each outcome model.

The validity of a causal interpretation of this analysis relies on the assumption that all confounders were measured and incorporated in the analysis. Omission of strong confounders can potentially lead to bias. While we believe that we have captured the strongest predictors of ESLD (and therefore most confounding variables), some confounders may have been overlooked. In particular, intravenous drug usage was omitted due to event sparsity. To make a causal claim, it must also be assumed that directly intervening to set the exposure status of a patient would result in an outcome identical to that if the exposure had occurred naturally. However, current knowledge does not allow for direct manipulation of HCV presence, but the existence of such an underlying data generating system could be assumed. If one is not willing to accept these causal assumptions, the interpretation of the parameter of interest is limited to a statistical effect that controls for all measured confounders.

Multiple imputations were used for the missing values. This methodology was fundamental in allowing us to use as much of the information in the data set as possible. The missingness included both incomplete covariates and intermittent missing visits. We preferred to use multiple imputations over last-observation-carried-forward which requires stronger (and untenable) assumptions about the nature of the missing data (Beunckens et al., 2005). We found complete case analysis to be impossible as very few subjects had complete data. Multiple imputations have been proposed for and used in causal inference studies (Rubin, 2004; Taylor and Zhou, 2009; Shortreed and Moodie, 2012; Shortreed and Forbes, 2009).

This is the first application of the sequential TMLE method in a survival context. We also derived the efficient influence curve of an MSM for the hazard with discrete covariates and describe one approach to fitting the model using TMLE. This is the first derivation of a TMLE for an unsaturated MSM that can evaluate the effect of setting a fixed exposure at multiple time points. Assessments of the performance of the TMLE for estimating marginal longitudinal or survival parameters described in this paper and comparisons to other causal methods have also been obtained through simulation study in van der Laan and Gruber (2012) and Schnitzer et al. (2013). In the simulation study in the Supplementary Materials, we confirmed the unbiasedness of this TMLE under misspecification of the outcome model when estimating the survival curve (a partial demonstration of its double-robustness). We also numerically confirmed the unbiasedness and efficiency of the extension of the method for estimating the parameters of a marginal structural model, again under misspecification of the outcome models. Our contribution adds to the growing literature demonstrating the promise and practicality of TMLE in longitudinal and time-to-event scenarios.