Semiparametric Bayesian commensurate survival model for post-market medical device surveillance with non-exchangeable historical data

Summary

Trial investigators often have a primary interest in the estimation of the survival curve in a population for which there exists acceptable historical information from which to borrow strength. However, borrowing strength from a historical trial that is non-exchangeable with the current trial can result in biased conclusions. In this paper we propose a fully Bayesian semiparametric method for the purpose of attenuating bias and increasing efficiency when jointly modeling time-to-event data from two possibly non-exchangeable sources of information. We illustrate the mechanics of our methods by applying them to a pair of post-market surveillance datasets regarding adverse events in persons on dialysis that had either a bare metal or drug-eluting stent implanted during a cardiac revascularization surgery. We finish with a discussion of the advantages and limitations of this approach to evidence synthesis, as well as directions for future work in this area. The paper’s Supplementary Materials offer simulations to show our procedure’s bias, mean squared error, and coverage probability properties in a variety of settings.

1. Introduction

Post-market device surveillance trials often have a primary interest in the estimation of the survival curve for various subgroups in a population for which there exists acceptable historical information as defined by Pocock (1976, p.177). Acceptable historical information may arise from previous phases in a trial setting, or in a database with information about an experimental treatment in a seemingly exchangeable population. Borrowing strength from acceptable historical data promises to facilitate greater efficiency in the investigation process, especially with small sample sizes. However, assuming exchangeability between data from historical and current sources ignores potential unexpected differences, risking biased estimation of concurrent effects. When historical information is used for the purpose of improving efficiency in a current population, inference should derive from flexible statistical models that account for inherent uncertainty while increasingly favoring the current information as evidence for between-source heterogeneity arises. In contrast, models for inference on population averaged effects, such as a meta-analytic review of non-exchangeable current and historical sources, need not favor one source over another since between-source effects are of interest.

One setting that is frequently accompanied by historical information is that of post-market surveillance. In fact, a recent FDA guidance document encourages borrowing strength from previous phases or large external databases in the post-market surveillance setting (Center for Devices & Radiological Health, 2010). Post-market surveillance studies generally commence after pivotal trials (used to gain regulatory approval), and are often concerned with improving the precision of an estimate of safety beyond what was seen in the pivotal trial data, and comparing this with that of an established treatment option. The safety measure might be the percentage of patients experiencing a serious adverse event associated with the product within the first year of use. On the one hand, we would like to get as precise an estimate as possible of the occurrence of serious adverse events over time by using the maximum amount of available data. On the other hand, the broad population of patients and physicians using the new product after it has been approved might differ markedly from the narrow population of physicians and patients that took part in the earlier pivotal trial. Additionally, the population receiving the standard of care is likely changing over time as the novel intervention popularizes and disease management practices evolve. What is needed is an objective means of evidence synthesis for combining the data from both sources, to produce a fair and accurate safety estimate that is appropriate for both current and future populations.

Currently, there exist very few highly flexible methods for combining non-exchangeable current and historical survival data. Plante (2009) develops a weighted Kaplan-Meier estimator to borrow strength across non-exchangeable populations, though it is not clear how an investigator should specify the control parameters that non-trivially impact the resulting estimate. Another approach is the highly flexible power prior framework discussed in Ibrahim et al. (2001, p.24). The power prior approach assumes that the two sources of data are exchangeable, and constructs a prior by down-weighting the historical likelihood contribution using a weight estimated by empirical or fully parametric Bayes. This approach satisfies certain optimality properties, however it often requires burdensome computational requirements in the development of the Markov chain Monte Carlo (MCMC) sampling algorithms due to the weighted historical likelihood term, rendering it impractical for wider consumption (Ibrahim et al., 2003). Hobbs et al. (2012) extend Pocock (1976) to develop a “commensurate prior” framework for generalized linear mixed models that accommodates non-exchangeable sources, but in the context of the often insufficiently flexible parametric Weibull survival model. Hobbs et al. (2013) extends this framework to the flexible piecewise exponential model, but they employ an independent gamma prior process on the hazard pieces that, as discussed by Ibrahim et al. (2001, Section 3.1), restricts the number of hazard pieces that can be estimated reliably. Here we increase the flexibility of a piecewise exponential commensurate prior approach by implementing a correlated prior process (Ibrahim et al., 2001, Section 3.1), but doing so substantially complicates the formulation. In contrast to power priors, our method jointly models current and historical data assuming the two sources are non-exchangeable. Furthermore, our method is fully Bayesian and can be readily implemented in standard software, such as JAGS (Plummer, 2003) or OpenBUGS (Lunn et al., 2009). As such, our novel method should provide investigators with a choice that is more general yet also more practical than similar methods already developed.

The pair of datasets we use to illustrate our method contain information about Medicare patients on dialysis that had either a bare metal stent (BMS) or a drug-eluting stent (DES) implanted during their incident in-hospital percutaneous coronary revascularization between 2008 and 2009 (Shroff et al., 2013). The endpoint considered is a composite of time to a second in-hospital cardiac revascularization or death, with follow up lasting through December 31st, 2010. We are interested in comparing the survival distributions in the small sub-population of persons on peritoneal dialysis (PD) with BMS versus DES placement during 2009, while borrowing strength from persons on PD with BMS placement during 2008. The two cohorts were constructed retrospectively from the USRDS (United States Renal Data System, 2011). Persons undergoing these procedures and their endpoints were determined from inpatient, outpatient, or Part B Medicare claims. Eligible persons must have initiated dialysis at least 90 days prior to revascularization to ensure the necessary Medicare claims would be captured in the USRDS. Follow-up times are censored for persons that received a kidney transplant or were lost to follow up. The baseline covariates collected at the time of revascularization are race, age, time since onset of end-stage renal disease (ESRD), and primary cause of ESRD.

Before we apply our methods to the heart stent data, we develop semiparametric statistical methods for automatically incorporating both historical and current information for survival analysis while allowing possibly different model parameters in each source. Specifically, Section 2 develops a semiparametric Bayesian Cox-type survival model using a piecewise exponential baseline hazard with a correlated prior process, time dependent covariate adjustment, and commensurate priors to jointly model current and historical data. In Section 3 we illustrate the mechanics of our methods by applying them to the heart stent data, both with and without covariate adjustment. Finally, Section 4 discusses potential extensions for joint models of current and historical survival data.

2. Piecewise Exponential Commensurate Prior Model

We approach the problem of having current and historical data by developing statistical methods that jointly model the two sources of data. Specifically, we develop a fully model-based Bayesian method that relies on flexible piecewise exponential likelihoods with correlated prior processes, time dependent covariate adjustment, and commensurate priors to facilitate borrowing of strength from the historical data. A commensurate prior distribution centers the parameters in the current population likelihood on their historical counterparts, and “facilitates estimation of the extent to which analogous parameters from distinct data sources have similar (‘commensurate’) posteriors” (Hobbs et al., 2013). Commensurate priors borrow strength from historical data in the absence of strong evidence for between source heterogeneity.

Following the notation used in Hobbs et al. (2011), we let L(θ, θ₀|D, D₀) denote the joint likelihood for the current and historical data. We assume the current and historical data are independent conditional on their associated parameters, that is L(θ, θ₀|D, D₀) = L(θ|D)L(θ₀|D₀). The first term in the product denotes the current likelihood, whereas the second term denotes the historical likelihood, with θ and θ₀ denoting the parameters that characterize the current likelihood and historical likelihoods, respectively.

Typically, the components of θ have parallel components in θ₀, although θ may contain components without a parallel in θ₀. For example, when a subset of the current population is exposed to some novel treatment, θ will contain an element that characterizes the novel treatment effect and has no counterpart in θ₀. As such, we decompose these parameters into the following components θ = (α, β, γ), where α characterizes the baseline hazard, β characterizes the effect of baseline covariates observed in both data sources, and γ characterizes the effect of exposures only observed in the current data. We also let θ₀ = (α₀, β₀), where α₀ and β₀ are defined analogously to α and β, respectively.

2.1 Likelihood

To maintain flexibility in a time to event setting, we avoid fully parametric specifications of L(θ|D) and L(θ₀|D₀). We instead use a generalized Cox-type model that assumes a semiparametric piecewise exponential formulation of the baseline hazard, with possibly time dependent covariate adjustment. The generalized distinction refers to the possible time dependencies in the regression coefficients, with proportional hazards being a special case when the regression coefficients are held constant over time. In practice, the piecewise exponential baseline hazard formulation with a vague prior process is a flexible and broadly applicable choice that provides regression coefficient estimates similar to the Cox model (Kalbeisch, 1978; Ibrahim et al., 2001, Section 3.4). Thus, it provides a useful choice when an investigator does not feel confident in any particular parametric form of the hazard, even if the underlying hazard is believed to be smooth.

To specify a piecewise exponential baseline hazard we first partition the time axis into K intervals, (0, κ₁], (κ₁, κ₂], …, (κ_K−1, κ_K], 0 = κ₀ < κ₁ < … < κ_K, with κ_K equal to the maximum observation time in the current dataset. We next assume the baseline hazard in each interval is constant, so that the baseline hazard function is given by h*(t;α) = exp(α_k) for t ∈ I_k = (κ_k−1, κ_k]. We adjust the baseline hazard for covariates X and Z in the following manner, h(t;α, β, γ, X, Z) = h*(t;α) exp(X′β_k + Z′γ_k) = exp(α_k + X′β_k + Z′γ_k) for t ∈ I_k (cf. Ibrahim et al., 2001, Section 3.4). To simplify prior specification later, we distinguish between X, the baseline covariates with historical counterparts that correspond to parameters β, and Z, the baseline exposures only observed in the current data that correspond to parameters γ. Note that the coefficients may be time dependent, since they are allowed to change across the time axis partition. Taking β_k ≡ β or γ_k ≡ γ results in a proportional hazards model. For the remainder of this document, we take β_k ≡ β, and assume Z is univariate while allowing for time dependencies (i.e., γ_k).

For this setting, D = (y, δ, x, z) consists of possibly right censored observations and baseline covariates. Here y = (y₁,…,y_n) is the set of follow up times, δ = (δ₁,…,δ_n) is the corresponding set of event indicators, $\mathit{x}=({\mathit{x}}_1^{\prime },\dots ,{\mathit{x}}_n^{\prime })\prime$ are the baseline covariates observed in both data sources, and z = (z₁,…,z_n) are indicators for a novel treatment only observed in the current data. Following Klein and Moeschberger (2003, Section 3.5), the likelihood for a set of possibly right censored observations can be formulated as:

$$L(\mathit{\theta }|\mathit{D})=\prod _{i=1}^n[h{(y_i;\mathit{\theta },{\mathit{x}}_i,z_i)}^{{\delta }_i}\times \text{exp}\{-\underset{0}{\overset{y_i}{\int }}h(t;\mathit{\theta },{\mathit{x}}_i,z_i)dt\}].$$

Letting α = (α₁,…,α_K) and plugging in the piecewise exponential with generalized Cox-type covariate adjustment formulation of h(t; θ, x, z) = h*(t;α) exp(x′β + zγ_k) for t ∈ I_k, we can rewrite the likelihood function for the current population as

$$L(\mathit{\theta }|\mathit{D})=\prod _{i=1}^n\prod _{k=1}^K[\text{exp}\{I(y_i\in I_k)({\delta }_i{\mu }_{ik}-(y_i-{\kappa }_{k-1})e^{{\mu }_{ik}}+\sum _{\ell =1}^{k-1}({\kappa }_{\ell }-{\kappa }_{\ell -1})e^{{\mu }_{i\ell }}\left)\right\}],$$ (1)

where ${\mu }_{ik}={\alpha }_k+{\mathit{x}}_i^{\prime }\mathit{\beta }+z_i{\gamma }_k$ and I(y_i ∈ I_k) is an indicator function. We retain the same time axis partition to model the historical data, D₀ = (y₀, δ₀, x₀) where y₀ = (y_0,1,…,y_0,n0), δ₀ = (δ_0,1,…,δ_0,n0), and ${\mathit{x}}_0=({\mathit{x}}_{0,1}^{\prime },\dots ,{\mathit{x}}_{0,n_0}^{\prime })\prime$. By retaining the same time axis partition, we just replace (D, α, β) in (1) with its historical counterpart (D₀, α₀, β₀) and omit z_iγ_k from μ_ik to obtain L(θ₀|D₀).

Conducting a simulation study of our procedure’s properties requires an automated strategy for a time axis partition that is computationally feasible but still provides consistently good model fit. To avoid computationally intensive methods like adaptive knot selection (Sharef et al., 2010) or AIC optimization (Hobbs et al., 2013) for constructing a time axis partition, we partition the time axis into a relatively large number of intervals with approximately equal numbers of events in each. To resist overfitting, a correlated prior process is used to smooth the baseline hazard functions (Besag et al., 1995; Fahrmeir and Lang, 2001). This method has been shown to work well when the underlying baseline hazard is continuous, and exhibit robustness against small shifts in the κ_k’s (Ibrahim et al., 2001, p.48). Formally, we employ the following time axis partition strategy: let $K=\text{max}\{5,\text{min}(\frac{r}{8},20)\}$ where r is the total number of events in the current population, and let ${\kappa }_k={(100*\frac{k}{K})}^{th}$ percentile of the current event times, k = 1,…,K, with κ₀ = 0. This strategy is motivated by the spline literature (cf. Ruppert et al., 2003, p.126) and a similar strategy is used by Sharef et al. (2010). In practice, a model should be fit with a few different choices of K to assess sensitivity and to ensure K is large enough. Inference under excessively small K risks failure to account for potentially important temporal features.

2.2 Priors

The other key aspect of this fully Bayesian approach is the choice of prior distributions. The likelihood contains parameters α and α₀ that characterize the current and historical populations’ baseline hazards, respectively. It also contains parameters β and β₀ that adjust the baseline hazards for baseline covariates. Finally, it contains parameters γ that adjust the current population’s baseline hazard for exposures only observed in the current population. In what follows, we use the same distributional notations throughout, where 𝒩(μ, τ) denotes a normal distribution with mean μ and precision τ, and 𝒰(a, b) denotes an uniform distribution with positive support on the interval (a, b).

The Bayesian framework affords the ability to construct a prior that hierarchically connects the two sources of data through their parallel parameters. To do so, we extend the commensurate prior approach described in Hobbs et al. (2011, Section 2), which constructs π(θ|D₀, τ) by integrating the product of three components over the historical parameters: the historical likelihood L(θ₀|D₀), a non-informative prior on the historical population parameter π₀(θ₀), and a commensurate prior π(θ|θ₀, τ) which centers the current population parameter at its historical counterpart and facilitates inter-source smoothing through the additional parameters τ. Formally,

$$\pi (\mathit{\theta }|{\mathit{D}}_{\mathbf{0}},\mathit{\tau })\propto \int \pi (\mathit{\theta }|{\mathit{\theta }}_{\mathbf{0}},\mathit{\tau })\frac{L({\mathit{\theta }}_{\mathbf{0}}|{\mathit{D}}_{\mathbf{0}}){\pi }_0({\mathit{\theta }}_{\mathbf{0}})}{\int L({\mathit{\theta }}_0|{\mathit{D}}_{\mathbf{0}}){\pi }_0({\mathit{\theta }}_{\mathbf{0}})d{\mathit{\theta }}_{\mathbf{0}}}d{\mathit{\theta }}_{\mathbf{0}}.$$ (2)

Here we consider L(θ₀|D₀) in (2) to be a part of the likelihood, not a component in the prior. This minor discrepancy means that our proposed method is interpreted as a joint model for the two sources of information, whereas commensurate priors Hobbs et al. (2011) and power priors Ibrahim et al. (2001) are interpreted as methods for constructing an informative prior from historical data. Regardless, the motivation does not change for the commensurate prior in (2), π(θ|θ₀, τ), which still facilitates the borrowing of strength from historical data.

In what follows, we motivate our prior choices for π₀(θ₀) and π(θ|θ₀, τ). Since π₀(θ₀) represents the prior that would be used in an analysis of the historical data on its own, it will often be vague. Therefore, we assume the parameters that characterize the historical baseline hazard are a priori independent of the regression coefficients, i.e., π₀(θ₀) = π₀(α₀)π₀(β₀). We further assume ${\pi }_0({\mathit{\beta }}_0)=\prod _{p=1}^P{\pi }_0({\beta }_{0,p})$ with β_0,p ~ 𝒩(0, 10⁻⁴), p = 1,…,P where P is the number of columns in x. We adopt a correlated prior process for π₀(α₀) = π₀(α₀|η₀)π₀(η₀) that introduces an intra-source smoothing parameter η₀ and is described in Fahrmeir and Lang (2001) and Ibrahim et al. (2001, Section 4.1.3). Specifically, we use a first order random walk prior process on the log-hazards, defined as

$${\alpha }_{0,1}~𝒩(0,{10}^{-4})\text{and}{\alpha }_{0,k}|{\eta }_0,{\alpha }_{0,k-1}~𝒩({\alpha }_{0,k-1,}{\eta }_0),k=2,\dots ,K.$$ (3)

As noted in Fahrmeir and Lang (2001), the diffuse prior on α_0,1 initializes the random walk, and the remaining hazards are then shrunk toward the hazard in the previous interval by the intra-source smoothing parameter η₀, which effectively temporally smooths the baseline hazard function $h_0^{*}(t;{\mathit{\alpha }}_0)$ and resists overfitting, a danger when K is relatively large. We opt for a vague uniform prior on the standard deviation scale, taking ${\eta }_0^{-2}\sim U(0.01,100)$, having investigated other non-informative options and finding posterior estimation to be fairly insensitive to π₀(η₀). This choice allows the data to primarily inform the amount of intra-source smoothing across intervals. A large number of other correlated prior processes have been explored for piecewise exponential models; many alternatives can be found in Ibrahim et al. (2001, Sections 3.5–7). There are also a number of options for specifying η₀: Ibrahim et al. (2001, Section 4.1.6) discuss strategies for choosing a particular value, whereas Fahrmeir and Lang (2001) and Besag et al. (1995) add another level to the hierarchy, specifying a hyperprior π(η₀) as we do here.

Our choice for π(θ|θ₀, τ) needs to facilitate borrowing of strength from the historical data. Again we assume the parameters that characterize the current baseline hazard are a priori independent of the regression coefficients, i.e., π(θ|θ₀, τ) = π(α|α₀, τ_α, η)π(β, γ|β₀, τ_β). We further assume $\pi (\mathit{\beta },\mathit{\gamma }|{\mathit{\beta }}_0,{\mathit{\tau }}_{\mathit{\beta }})=\pi (\mathit{\gamma })\prod _{p=1}^P\pi ({\beta }_p|{\beta }_{0,p},{\tau }_{{\beta }_p})$. When allowing for time dependencies in γ we use a random walk prior process as in (3), otherwise we assume γ ~ 𝒩(0, 10⁻⁴). The former choice adds an additional smoothing parameter, ξ, which we model as uniform on the standard deviation scale, ξ⁻² ~ 𝒰(0.01, 100). In order to borrow strength from the historical data, we employ location commensurate priors for β_p|β_0,p, τ_βp, p = 1,…,P. Formally, we assume β_p|β_0,p, τ_βp ~ 𝒩(β_0,p, τ_βp), and place a “spike and slab” distribution on τ_βp, p = 1,…,P developed by Mitchell and Beauchamp (1988) and applied by Hobbs et al. (2012). The “spike and slab” distribution is defined as,

$$f_{\tau }(t)=\{\begin{array}{cc}{p}_0\left(\frac{t}{{𝒮}_u-{𝒮}_l}\right),\hfill & {𝒮}_l\le t\le {𝒮}_u\hfill \\ 1-p_0,\hfill & t=ℛ\hfill \end{array}$$ (4)

where 0 ≤ 𝒮_l ≤ 𝒮_u < ℛ and 0 ≤ p₀ ≤ 1. This distribution is uniform between 𝒮_l and 𝒮_u with probability p₀ and concentrated at ℛ otherwise. Hobbs et al. (2012) show that the spike and slab family of distributions offers a flexible framework for estimating the commensurability parameters (i.e., τ_βp’s) through information that is supplied by the data about these precision components. The interval, (𝒮_l, 𝒮_u), or “slab”, is placed over a range of values characterizing strong to moderate levels of heterogeneity. The “spike”, ℛ, is fixed at a point corresponding to practical homogeneity. The hyperparameter, p₀, denotes the prior probability of that τ is in the slab.

For π(α|α₀, τ_α, η), we devise a flexible prior distribution that is amenable to evidence of heterogeneity with the historical information, favoring the concurrent information in the presence of incongruence while still temporally smoothing the hazards in adjacent intervals. We extend the commensurate prior employed in Hobbs et al. (2013) to

$${\alpha }_1|{\alpha }_{0,1},{\tau }_{\alpha }~𝒩({\alpha }_{0,1},{\tau }_{\alpha }),{\alpha }_k|{\alpha }_{k-1},{\alpha }_{0,k},{\tau }_{\alpha },\eta ~𝒩\left\{\right(\frac{{\tau }_{\alpha }}{{ℛ}_{\alpha }}){\alpha }_{0,k}+(1+\frac{{\tau }_{\alpha }}{{ℛ}_{\alpha }}){\alpha }_{k-1},(\frac{{\tau }_{\alpha }}{{ℛ}_{\alpha }}){\tau }_{\alpha }+(1-\frac{{\tau }_{\alpha }}{{ℛ}_{\alpha }}\left)\eta \right\},$$ (5)

for k = 2,…,K, where ℛ_α is the “spike” from the prior placed on τ_α discussed below. Note that we use only one τ_α, which reduces model complexity and ensures that inter-source homogeneity is defined with respect to congruency over the entire baseline hazard curve, rather than case-by-case for each interval. Here η controls the intra-source smoothing of the current hazard function across adjacent intervals. Taking the fully Bayesian approach, we let η⁻² ~ U(0.01, 100), again having investigated other non-informative options and finding posterior estimation to be fairly insensitive to π(η).

We place a “spike and slab” distribution defined in (4) on the inter-source smoothing parameter τ_α. With 𝒮_u << ℛ_α, when τ_α = ℛ_α we see that (5) directly facilitates inter-source hazard smoothing; otherwise, (5) still facilitates intra-source smoothing on the current hazard, as in (3). With no covariates, taking τ_α = ℛ_α = ∞ results in full borrowing from the historical data with estimation driven by the piecewise exponential model, where π(α|η) is given by (3) and π(η) is unaffected. Alternatively, taking τ_α = 𝒮_l = 0 results in ignoring the historical data completely. The former method assumes exchangeability a priori, ignoring the possibility of non-exchangeable sources, while the latter assumes complete heterogeneity, effectively discarding the historical data.

3. Dialysis Patient Heart Stent Application

We now apply our methods to data constructed retrospectively from the United States Renal Data System (2011) on heart stent placements in PD patients undergoing their first in-hospital percutaneous coronary revascularization. The USRDS was used to identify 119 PD patients with BMS placement and 159 with DES placement between 2008–2009. Recall, the outcome of interest is a composite endpoint of time to a second revascularization or death, with follow up through December 31st, 2010 (Shroff et al., 2013). Naturally, we consider the 2008 cohort to be the historical data, and the 2009 cohort to be the current data. Based on the demographic characteristics in Table 1, the 2008 BMS cohort is older and slightly more white than the other three cohorts, but all four cohorts are relatively similar. Nevertheless, there may always exist unobservable sources of heterogeneity that are the accumulation of small changes in the population and underlying disease management practices over time. Thus, even if we adjust for all observable sources of heterogeneity, there may still be unexplained heterogeneity between the two sources of data. Our method will borrow more strength when there is little evidence of inter-source heterogeneity that cannot be explained by the covariates.

Table 1.

Demographics of BMS and DES cohorts in 2008 and 2009. (Percentages for subgroups with a sample size less than 10 have been masked with an asterisk for privacy reasons)

	BMS (2008)	BMS (2009)	DES (2008)	DES (2009)
N	62	57	78	81
Number of events	37	28	30	39
Mean follow up (years)	0.403	0.496	0.639	0.575
Race (%)
White	80.6	77.2	73.1	76.5
Black	*	*	16.7	17.3
Other	*	*	*	*
Age (%)
20–64	25.8	52.6	41.0	40.7
65–74	40.3	28.1	37.2	33.3
≥75	33.9	19.3	21.8	25.9
Primary cause of disease (%)
Other	19.4	19.3	19.2	18.5
Diabetes mellitus	43.5	50.9	50.0	45.7
Hypertension	37.1	29.8	30.8	35.8
Dialysis duration in years (%)
<2	37.1	40.3	39.7	49.3
2–5	58.1	43.9	50.0	38.3
6–10	*	*	*	*
≥11	*	*	0.0	*

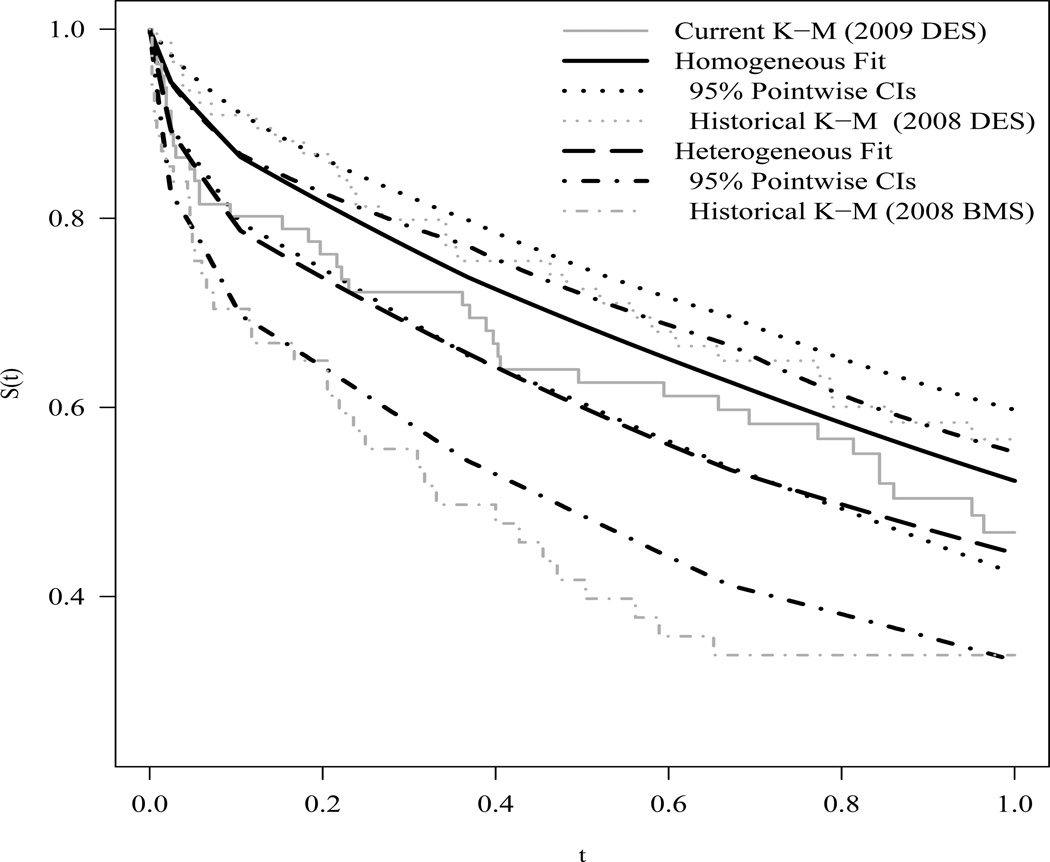
We begin by illustrating the essential mechanics of our method, that is less inter-source borrowing as heterogeneity increases. For now, we ignore the covariates and fit our method to two different pairs of datasets. We first take the 2009 and 2008 DES cohorts as the current and historical datasets, respectively. By contrast, we next pair the 2009 DES cohort with the 2008 BMS cohort, taking the latter as the historical dataset. After preliminary investigations via simulation into the bias-variance tradeoffs that different specifications of the spike and slab distribution can provide, we chose 𝒮_l = 10⁻⁴, 𝒮_u = 2, ℛ_α = 200, and p₀ = 0.9. This specification of hyperparameters represents much skepticism regarding exchangeability of the two sources of information, with a prior probability of just 0.1 for strong borrowing. Based on preliminary investigations, we know the first pairing is more homogeneous than the second pairing. Thus, we refer to our model fit to the first and second pairings as the homogeneous and heterogeneous fits, respectively. We ran three MCMC chains in JAGS (Plummer, 2003) for 2,000 iterations of burn-in, followed by 500,000 posterior samples thinned every fifty draws for estimation, and obtained the posterior survival curves displayed in Figure 1. For the homogeneous pairing, the posterior mean survival curve (solid black) interpolates the two K-M estimators fit to the 2009 DES data alone and to the 2008 DES data alone. For the heterogeneous pairing, the fitted survival curve (dashed black) follows slightly below the K-M estimator fit to the 2009 data alone and appears modestly influenced by the 2008 BMS data. Another notable difference between these two fits is the width of the 95% pointwise credible intervals. For t > 0.2 the homogeneous fit has tighter intervals, indicating that more strength is being borrowed from the historical data. In fact, the posterior for the inter-study smoothing parameter τ is in the spike for greater than 95% of the posterior draws for the homogeneous case, but less than 65% for the heterogeneous case. For a link to JAGS code and a thorough simulation-based investigation of the mechanics of our method, please see the Web Appendix A.

Figure 1.

Posterior survival curves for homogeneous (solid black) and heterogeneous (dashed black) dataset pairings with their 95% pointwise credible intervals. For reference, the Kaplan-Meier estimator fit to the 2009 DES data alone (solid grey) and to the corresponding homogeneous 2008 DES (dotted grey) and heterogeneous 2008 BMS (dot-dashed grey) data alone.

We now fit our covariate adjusted model to the heart stent data, accounting for all the covariates listed in Table 1. We borrow strength from the 2008 BMS cohort through the baseline hazard and the covariate adjustment parameters, but ignore the 2008 DES data for the sake of illustration. The specification we choose for the spike and slab distributions placed on the β’s is 𝒮_l = 10⁻⁴, 𝒮_u = 2, ℛ_β = 200, and p₀ = 0.9. We used three MCMC chains each with 500,000 posterior samples thinned every fifty samples for posterior estimation following 2,000 samples of burn-in. We first fit our proposed model taking γ_k ≡ γ, k = 1,…,K, and compare the posterior estimates for β and γ with those of a Cox proportional hazards model fit the 2009 data alone (Current PH), the 2008 data alone (Historical PH), and to the pooled 2008 and 2009 data (Pooled PH). Results from these four approaches are reported in Table 2. Note that the posterior mean hazard ratios from the proposed method are similar to those of the Cox proportional hazards models. In fact, these estimates from the proposed method are generally intermediate to the Current PH and Historical PH models. This indicates that the proposed method is borrowing strength from the historical data. The posterior means of the commensurability parameters analogous to the β parameters (i.e., τ_βp’s) are between 18 and 47, indicating partial borrowing. The τ_βp with the largest posterior mean (i.e. greatest borrowing) corresponds to the dialysis duration of 2 – 5 years covariate, which has very similar hazard ratio estimates in both the Current and Historical PH models. Furthermore, the 95% posterior credible intervals for the proposed method are generally tighter than those from the Current PH model, but not quite as tight as those from the Pooled PH model. For example, the effect of DES has a credible interval of (0.51, 1.33) for the proposed method versus (0.50, 1.36) from the Current PH model and (0.48, 1.08) from the Pooled PH model. This tighter credible interval can primarily be attributed to borrowing information on the baseline hazard function, with a posterior mean for the inter-study smoothing parameter, τ_α, of 187.

Table 2.

Results from the proposed method with no time varying covariates and three Cox proportional hazards models fit to the current data alone (Curr PH), historical data alone (Hist PH), and the pooled data (Pool PH). Covariates above the line are associated with β, while those below the line are associated with γ.

	Proposed	Curr PH	Hist PH	Pool PH
	Hazard Ratio (95% CI)
Race
White (ref)	–	–	–	–
Black	0.58(0.27, 1.13)	0.52(0.24, 1.11)	1.39(0.49, 3.96)	0.77(0.43, 1.38)
Other	0.83(0.27, 2.15)	1.02(0.36, 2.88)	0.46(0.06, 3.50)	0.85(0.34, 2.14)
Age
20–64 (ref)	–	–	–	–
65–74	1.21(0.67, 2.13)	1.08(0.59, 1.98)	1.87(0.66, 5.33)	1.32(0.80, 2.19)
≥75	2.22(1.21, 3.98)	1.97(1.05, 3.69)	3.62(1.37, 9.54)	2.55(1.56, 4.18)
Cause of disease
Other (ref)	–	–	–	–
Diabetes	1.32(0.73, 2.51)	1.32(0.65, 2.68)	1.17(0.43, 3.16)	1.23(0.71, 2.13)
Hypertension	0.86(0.44, 1.70)	0.84(0.39, 1.84)	0.96(0.36, 2.55)	0.89(0.50, 1.57)
Dialysis duration
<2 yrs	–	–	–	–
2–5 yrs	1.29(0.78, 2.12)	1.31(0.77, 2.23)	1.18(0.56, 2.48)	1.28(0.84, 1.94)
6–10 yrs	1.81(0.81, 3.79)	1.90(0.87, 4.15)	2.19(0.21, 22.7)	1.75(0.85, 3.59)
≥11 yrs	1.48(0.30, 5.09)	1.37(0.31, 6.09)	3.61(0.30, 42.9)	2.21(0.66, 7.41)
Stent Type
BMS	–	–	–	–
DES	0.82(0.51, 1.33)	0.83(0.50, 1.36)	–	0.72(0.48, 1.08)

Lastly, we fit our proposed method allowing a time varying effect for DES relative to BMS placement. The resulting posterior mean estimates for β remained very similar to the results reported in Table 2. The γ_k, k = 1,…,8 estimates suggest a slightly decreasing effect of DES versus BMS over time, with DES being most effective during the first week following placement (posterior mean hazard ratio of 0.8), and showing little benefit over BMS after about 9 months (posterior mean hazard ratio of 1.0). However, none of the posterior credible intervals excluded a hazard ratio of 1. The diminishing benefit of DES over BMS has been shown to exist in larger dialysis populations, and (though not shown here) can clearly been seen when fitting the proposed model to a much larger dataset that also includes persons on hemodialysis, as discussed in Shroff et al. (2013).

4. Future Work

The methods developed in this work allow more efficient use of available data while we determine an evolving picture of the risk-benefit ratio for medical therapies. They also improve flexibility over existing methods and set the stage for further advances with respect to knot selection and baseline hazard modeling as in Sharef et al. (2010). Future research also includes the possibility of generalizing the smoothing commensurate prior developed in Section 2 to borrow strength in the estimation of covariate effects modeled flexibly with splines discussed by Ruppert et al. (2003). We will continue to look for ways to improve efficiency while making valid inference on safety outcomes.