Mathematical model of adult stem cell regeneration with cross-talk between genetic and epigenetic regulation

Significance

This paper examines how adult stem cells maintain their ability to carry out a complex set of tasks, including tissue regeneration and replacement of defective cells. To do so, stem cell populations must coordinate differentiation, proliferation, and cell death (apoptosis) to maintain an appropriate distribution of epigenetic states. Using the tools of applied mathematics, and borrowing from the theory of intergenerational transfer of resources, this paper shows how control strategies during cell division should be chosen to maximize expected performance, utilizing cross-talk between genetic and epigenetic regulation and performance criteria during homeostasis. Heterogeneous proliferation, a mixed strategy in which not all cells have the same proliferation probability, is shown to increase robustness, and hence long-term performance.

Abstract

Adult stem cells, which exist throughout the body, multiply by cell division to replenish dying cells or to promote regeneration to repair damaged tissues. To perform these functions during the lifetime of organs or tissues, stem cells need to maintain their populations in a faithful distribution of their epigenetic states, which are susceptible to stochastic fluctuations during each cell division, unexpected injury, and potential genetic mutations that occur during many cell divisions. However, it remains unclear how the three processes of differentiation, proliferation, and apoptosis in regulating stem cells collectively manage these challenging tasks. Here, without considering molecular details, we propose a genetic optimal control model for adult stem cell regeneration that includes the three fundamental processes, along with cell division and adaptation based on differential fitnesses of phenotypes. In the model, stem cells with a distribution of epigenetic states are required to maximize expected performance after each cell division. We show that heterogeneous proliferation that depends on the epigenetic states of stem cells can improve the maintenance of stem cell distributions to create balanced populations. A control strategy during each cell division leads to a feedback mechanism involving heterogeneous proliferation that can accelerate regeneration with less fluctuation in the stem cell population. When mutation is allowed, apoptosis evolves to maximize the performance during homeostasis after multiple cell divisions. The overall results highlight the importance of cross-talk between genetic and epigenetic regulation and the performance objectives during homeostasis in shaping a desirable heterogeneous distribution of stem cells in epigenetic states.

Adult stem cells are present in most self-renewing tissues, including skin, intestinal epithelium, and hematopoietic systems. Stem cells provide regeneration through proliferation, differentiation, and apoptosis; therefore, the accumulation of undesirable epigenetic changes, which are independent of the genetic instructions but heritable at each cell division, can lead to the causation or progression of diseases (1, 2). Epigenetic effects such as the stochastic partitioning of the distribution of regulatory molecules during cell division may change the capability of the cell to undergo differentiation or proliferation (3), and the accumulation of DNA errors (or damages) can result in carcinogenesis (4–6).

Many stem cells are heterogeneous in their ability to proliferate, self-renew, and differentiate, and they can reversibly switch between different subtypes under stress conditions. Specifically, hematopoietic stem cells (HSCs) (see ref. 7 for a review of HSC heterogeneity) have distinguished subtypes (such as lymphoid deficient, balanced, or myeloid deficient) whose distribution depends on their heterogeneity during the differentiation process (7, 8). HSCs can reversibly acquire at least three proliferative states: a dormant state in which the cells are maintained in the quiescent stage of the cell cycle, a homeostatic state in which the cells are occasionally cycling, and an injury-activated state in which the cells are continuously cycling (9, 10). Each state is likely associated with a unique microenvironment (10, 11). Dormant and homeostatic HSCs are anchored in endosteal niches through interactions with a number of adhesion molecules expressed by both HSCs and niche stromal cells (10, 12). Furthermore, injury-activated HSCs are located near sinusoidal vessels (the perivascular niche). In response to the loss of hematopoietic cells, surviving dormant HSCs located in their niches develop into injury-activated HSCs to undergo self-renewing divisions. In the recovery stage, injury-activated HSCs either differentiate into multipotential progenitor cells or migrate to their osteoblastic niches to reestablish the dormant and homeostatic HSC pools (10, 13).

The growth and regeneration of many adult stem cell pools are tightly controlled with feedback regulation at different levels. For example, HSC self-renewal and differentiation are regulated by direct HSC–niche interactions and cytokines secreted from stromal cells through various feedback signals (9–11). Adult intestinal stem cells residing in a niche in the crypt are regulated by the paracrine secretion of growth factors and cytokines from surrounding mesenchymal cells (14–16). In addition, the mammalian olfactory epithelium, a self-renewing neural tissue, is regulated through negative feedback signals involving the diffusive molecules GDF11 and activin (17).

Independent of division modes, symmetric or asymmetric cell divisions may lead to daughter cells with genetic or epigenetic states different from the normal states. The enormous functional demands and longevity of stem cells suggest that stem cells, particularly the cells from highly regenerative tissues (e.g., epithelium or blood), may be equipped with effective repair mechanisms to ensure genomic integrity over a lifetime (18). Stem cells often respond differently to genetic or epigenetic errors at different proliferation phases (19). Studies regarding the population response to DNA damage of HSCs have suggested that the system selects for the least damaged cells, and the competition between different cells is controlled by the level of p53 proteins (20, 21). Highly regenerative adult stem cells (e.g., HSCs) need to possess effective strategies that balance long-term regeneration with protection from mutagenesis (for example, cell proliferation or differentiation may be affected by the DNA damage response) (20, 22).

Previous modeling studies based on the cell population dynamics have indicated that feedback regulation to the proliferation is important to maintain the homeostasis of tissue growth (23–25). The exploration and analysis of models that include transit-amplifying progenitor cells and terminally differentiated cells have suggested that multiple feedback mechanisms at different lineage stages can influence the speed of tissue regeneration for better performance (17, 26–28). These population dynamic models could include age structure (29), evolution (27, 30), and stochasticity (30, 31); and these models could also be applied to the regulation of cancer (32). Studies based on spatial modeling have found that diffusive and regulatory molecules involved in feedback mechanisms regulating the differentiation capabilities of the cells are important in maintaining the stem cell niche and shaping tissue stratification (33, 34).

During the tissue self-renewal process driven by adult stem cells, how do stem cells maintain a desirable distribution of epigenetic states over their lifetimes despite many perturbations or accidental changes? What are the controlling strategies that enable a cell to maximize its performance at each cell cycle while contributing positively to the entire cell population during tissue growth? Additionally, are these control strategies able to guide genetic evolution to achieve high tissue performance over a long period? Without considering any molecular details, we present a dynamic programming model that includes stochastic transitions between cell cycles. The model is defined by the combination of a performance function at each cell division and a fitness function during tissue homeostasis. We sought optimal controlling strategies involving proliferation, differentiation and apoptosis that naturally and collectively emerge from achieving performance objectives as well as optimizing fitness. The model, which represents stem cells as a distribution of a state variable, emphasizes the cross-talk between genetic evolution and epigenetic states and their stochastic transitions at each cell cycle. The analysis and computation of the model suggest the existence of several critical controlling strategies that regulate proliferation and apoptosis and are highlighted by heterogeneous dependence on the epigenetic states in the feedback regulation.

Results

A Model of Stem-Cell Regeneration with Epigenetic Transition.

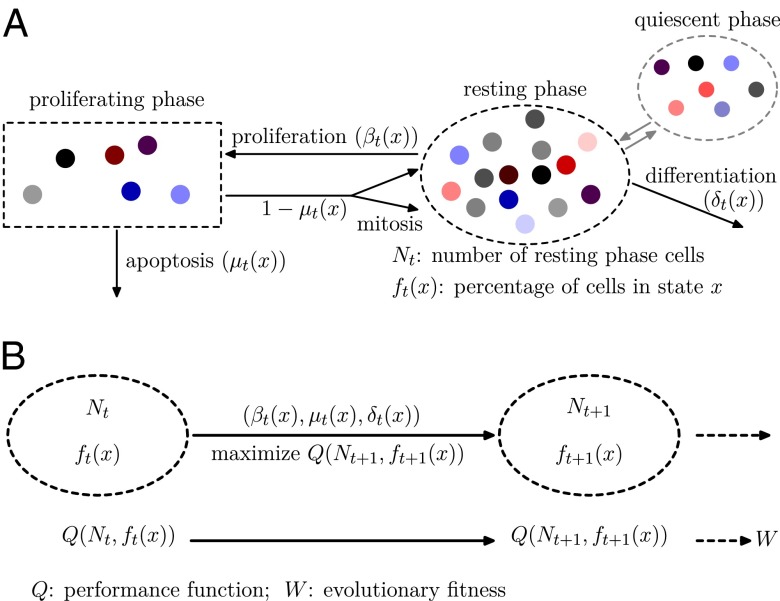
The model is based on the G₀ cell cycle model (35, 36) and a dynamic programming approach for intergenerational resource transfer (37, 38) together with evolutionary dynamics (39). Stem cells at cell cycling are classified into resting (G₀) or proliferating (G₁, S, and G₂ phases and mitosis) phases (Fig. 1A) (35). During each cell cycle, a cell in the proliferating phase either undergoes apoptosis or divides into two daughter cells; however, a cell in the resting phase either irreversibly differentiates into a terminally differentiated cell or returns to the proliferating phase. In some tissues, resting phase cells (e.g., HSCs) may undergo a reversible transition to a quiescent phase with preserved self-renewal, which results in two distinct cell populations.

Fig. 1.

Model Illustration. (A) At the tth cell cycle, cells in the resting phase either enter the proliferating phase with the probability of 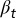, or differentiate into other cell types with the probability of 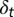. The proliferating cells undergo apoptosis with the probability of 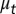. Resting phase cells occasionally migrate to the quiescent phase and vice versa under stress. (B) The performance function 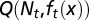quantifies how well the tissue fits to its physiological properties. The changes in the tissue state 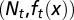at each cell cycle are determined by the three quantities 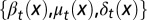chosen to maximize the performance at the next cycle to give 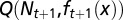. An evolutionary fitness function at homeostasis, denoted by W, is the limit of 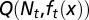when .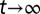

To study the heterogeneity of cell responses, we denote x as the epigenetic state of a cell, which, for example, can be the expression levels of one or multiple genes, the number of nucleosome modifications of a DNA region, or the positions of DNA methylation. In short, x represents one or several intrinsic cellular states that may change during cell division. Here, only epigenetic states that are significant for cell differentiation, proliferation, or apoptosis are considered. Consequently, the three processes have dependences on the epigenetic state x: 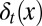, , 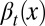and 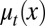, where the subscript t indicates the tth cell cycle (Fig. 1).

The distribution density of stem cells during the resting phase, whose total population is denoted as N_t, with different epigenetic states x, is characterized by 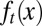. 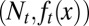undergoes a transformation from one cell cycle to the next (Fig. 1B):

During each cell cycle, 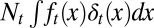cells leave the resting phase due to differentiation, and 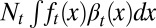cells enter the proliferating phase. Each cell in the proliferating phase either undergoes apoptosis with a probability of 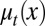or produces two daughter cells. Hence, the cell population after mitosis is

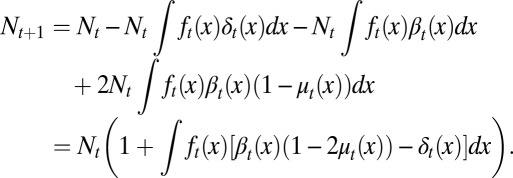The integrals are taken over all possible epigenetic states. In this derivation, the reversible transition between the resting phase and the quiescent phase is regarded as perfectly balanced for an equilibrium, which may occur during homeostasis. In this paper, we only considered the effect of this transition for regeneration in response to a severe loss of differentiated cells (SI Text, section S3).

We define the observed proliferation probability as

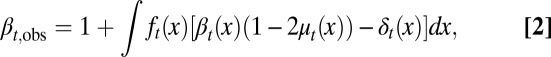then

Here 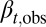is the ratio of the cell population numbers between two consecutive cell cycles.

To account for stochastic effects during the inheritance of epigenetic states that lead to variability of daughter cells in each cell division (3, 40, 41), we introduced an inheritance probability 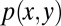, which represents the probability that a daughter cell of state x comes from a mother cell of state y. Therefore, for any y. Similarly to the above argument, we obtained (SI Text, section S1)

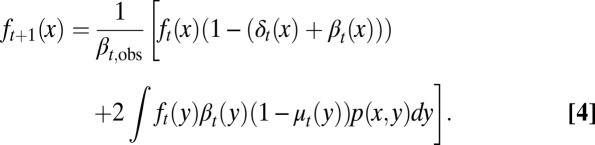Eqs. 3 and 4 define a transformation between two cell cycles.

During the tissue homeostasis, Eq. 3 indicates that the observed proliferation satisfie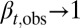s as 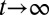. Otherwise, either uncontrolled growth 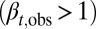or tissue degeneration 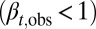occurs. Hence, cell proliferation, differentiation, and apoptosis (i.e., 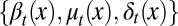) must be dynamically controlled at each cell cycle, for example, through signal molecules released from downstream cell lineages (17, 32). This dynamic regulation leads to a limited distribution at homeostasis,

which describes the stem cell distribution as a function of epigenetic states, and is termed “tissue epigenetics” for short.

One possible control strategy for this type of growth may follow evolution akin to natural selection (42). To model this selection, we first introduced a tissue performance function Q depending on the population of stem cells through a function φ as well as the distribution of epigenetic states x in the tissue through a cell performance function , so that the performance at the tth cell cycle is given by

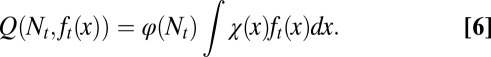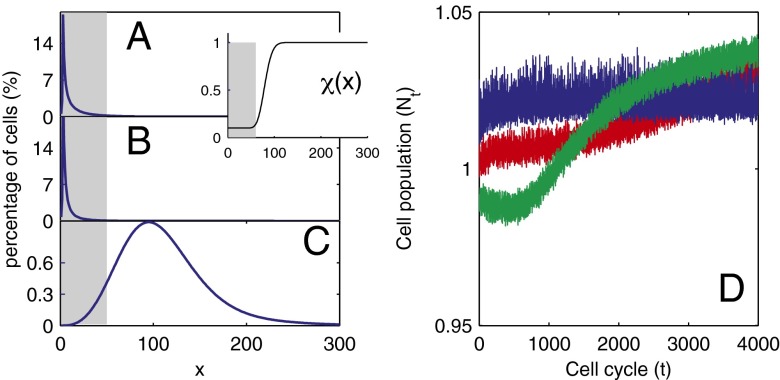
The cell performance 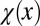measures the capability of a cell with given epigenetic state x in accomplishing its physiological functions (see Fig. 2 as an example). A larger value corresponds to better performance.

Fig. 2.

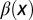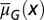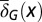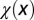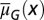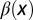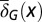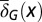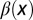Distribution of cells at homeostasis under three different combinations of the epigenetic regulation. (A) Both and are independent of x, and changes with x. (Inset) The performance function is shown. (B) is independent of x, and and change with x. (C) Both and are independent of x, and 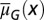changes with x. Shadow regions 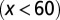represent defective states. (D) Time course of N_t under the three conditions (red, green, and blue for conditions A–C, respectively). (See SI Text, section S5 for details on simulations.)

We assumed that two layers of regulation occur between two cell cycles: one at the epigenetic level that occurs at each cell division, and one at the genetic level that is selected by mutations over a long time scale of many cell divisions. In particular, the probability of proliferation 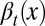varies at each cell cycle by epigenetic regulation, while the apoptosis probability 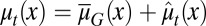, in which 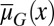is the average probability at homeostasis and is selected through genetic mutations over a long time scale and 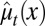is random at each cell cycle due to epigenetic modulations. Similarly, the differentiation probability takes the form of 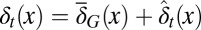in which 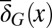is the average probability at homeostasis and 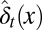represents epigenetic uncertainty. With these mechanisms of regulation, the performance Q after cell division depends, through Eqs. 2–4, on the proliferation 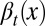as well as the stochasticities in apoptosis 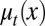and differentiation 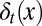. Thus, we can write the performance function after cell division as (SI Text, section S1)

During each cell cycle, the proliferation 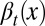is controlled to achieve maximum tissue performance after cell division in the face of uncertainties in apoptosis 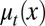and differentiation 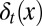, which leads to solving the corresponding Bellman condition (38, 43–45)

where 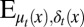is the expectation with respect to apoptosis and differentiation probabilities during cell division.

The evolutionary fitness function is defined as the performance at homeostasis after multiple cell divisions (i.e., 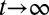; see also Fig. 1B):

While the tissue performance function Q is subject to epigenetic regulation at each cell cycle, the fitness function W is genetically regulated and dependent on the apoptosis 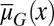and the differentiation 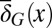. Evolution selects 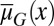and 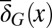through mutations to maximize the fitness W. The overall model defines a principle of a control strategy that incorporates cross-talk between genetic and epigenetic regulation in stem cell regeneration and evolution.

Heterogeneous Apoptosis Can Improve the Maintenance of Tissue Epigenetics.

During growth, the accumulation of stochastic modifications in epigenetic states may produce defective cells that need to be effectively repaired or removed. Here, we show that heterogeneous apoptosis is advantageous in controlling tissue epigenetics.

First, the epigenetic function 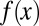, when we take 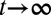in Eqs. 3 and 4 with an assumption of no epigenetic uncertainty in differentiation and apoptosis, satisfies the following integral equation (SI Text, section S2):

where 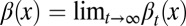satisfies

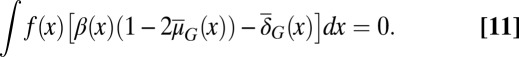Analysis of a simplified model based on Eqs. 10 and 11 shows that homogenous apoptosis [i.e., 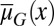is independent of x] easily leads to abnormal or disease conditions for a tissue (SI Text, section S2). This observation is further confirmed by direct simulations of Eqs. 10 and 11 under the condition in which apoptosis probability 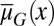is either dependent on or independent of x (Fig. 2). Whenever the apoptosis 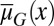is independent of x, most cells accumulate in low-performance states (Fig. 2 A and B). In contrast, if 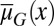is dependent on x so that the cells with lower performance have a greater probability of apoptosis, only a small number of low-performance cells are present during homeostasis (Fig. 2C). These results suggest that heterogeneity in apoptosis can improve the maintenance of acceptable tissue epigenetics during a long lifespan.

Furthermore, we find that heterogeneity in the cell performance function 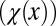is important for successful natural selection of apoptosis strategies, and epigenetic transition during cell division is helpful for robust tissue epigenetics during homeostasis with respect to accidental changes in the tissue lifespan (SI Text, section S3). Interestingly, despite apparent differences in tissue epigenetics, homogeneous or heterogeneous apoptosis yields similar dynamics in the cell population N_t (Fig. 2D), demonstrating the importance of introducing the function 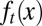for epigenetic states into the model. The cell population model alone may be insufficient to study the control strategies of stem cell regeneration.

An Optimal Control for Proliferation During Each Cell Cycle Depends on Complex Feedback Regulation Involving the Epigenetic States and the Size of the Total Cell Population.

Optimal control at each cell cycle involves identifying the proliferation probability to maximize the performance Q in Eq. 8 after cell division. To study the system analytically, we considered two cases based on either homogeneous or heterogeneous proliferation.

Homogeneous proliferation (strategy A).

When 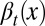is independent of the epigenetic state x, meaning that all cells in the tissue are alike in their ability to undergo cell cycle reentry, the optimal proliferation (strategy A) is governed by 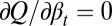, which yields

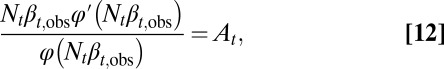where A_t is a quantity determined by 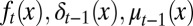(SI Text, section S3). The proliferation 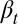is obtained from Eq. 12 by solving 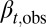. In particular, when N_t is near the value 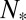that maximizes the function φ, 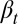can be approximated by

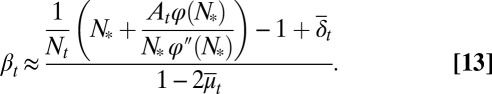Here 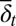and 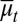are average probabilities of differentiation and apoptosis, respectively. Examples of tissue dynamics based on strategy A are shown in SI Text, section S3.

A direct consequence of Eq. 13 is that the proliferation 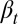decreases with the cell population, resulting in a negative feedback control. We note that the tissue epigenetics in the next cell generation 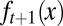depends on the current generation proliferation 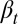through Eq. 4, leading to complex negative feedback regulation during each cell cycle.

Heterogeneous proliferation (strategy B).

Next, we considered the case of cells having two distinct proliferation probabilities. In these two distinct states, denoted by 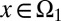or 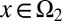, we assumed

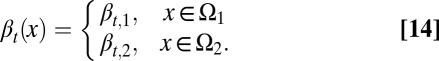In addition, we assumed that type I cells, defined as cells with 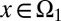, are unmodulated at each cell cycle (i.e., 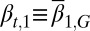is genetically regulated), and type II cells, defined as cells with 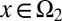, are modulated such that 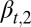changes at each cell cycle. Biologically, this assumption corresponds to the situation in which, for example, certain growth factor receptors are active (or expressed) only in type II but not type I cells; however, the receptors are required to respond to external signals to control proliferation.

The probability 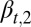(strategy B) is determined by 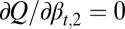, which yields an equation for 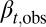similar to Eq. 12. In particular, when N is close to the value 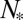(SI Text, section S3), one has

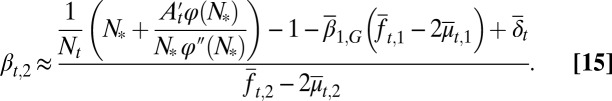All bar terms are averages over cell epigenetic states, with a subscript 1 for type I cells 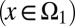and a subscript 2 for type II 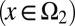. Similarly to 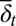and 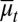in Eq. 13, these average terms incorporate genetic and epigenetic regulation in differentiation and apoptosis. Examples of tissue dynamics based on strategy B are shown in SI Text, section S3.

Eq. 15 shows that is a decreasing function of the cell population, resulting in a complex negative feedback regulation with respect to cell populations and the epigenetic states of the tissue cells. We note that the heterogeneous proliferation probability 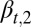for the type II cells also depends on the probability of the type I cells, which suggests that an appropriate selection of the unmodulated proliferation 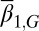can improve the performance at homeostasis in comparison with homogenous cells (SI Text, section S3).

Simple feedback via the size of the cell population (strategy C).

Optimal controls of proliferation based on our model lead to the negative feedback regulation of proliferation through the cell population. Similar regulatory mechanisms with negative feedback have been explicitly introduced in many stem cell population models (17, 27, 36, 46) by use of a Hill function (strategy C) such as

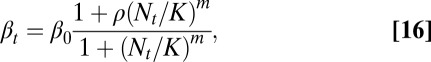where 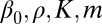are constants.

A major difference between Eqs. 16 and 13 or 15 based on our model is that the coefficients in Eq. 16 are constants and independent of the tissue epigenetics. Thus, strategy C is a simple feedback mechanism involving only the cell population; however, both strategies A and B are complex feedback mechanisms incorporating both cell population and tissue epigenetics. The importance of epigenetic states has recently been implicated during the stem cell self-renewal and differentiation processes (47, 48). This epigenetic dependence of feedback mechanisms, as shown in the next section, can improve the robustness in tissue dynamics.

Heterogeneous Proliferation Is Important for the Robustness of Growth with Respect to Sudden Changes.

During the lifespan of an organism, many unexpected alterations to stem cell systems occur at various levels, such as the loss of stem cells (e.g., injury or marrow donation) and temporal changes in cell differentiation and apoptosis capabilities (several studies have reported a 20-fold increase in the differentiation activity of HSCs under the administration of G-CSF) (49). In many situations, stem cell tissues recover in a timely manner after these types of changes. For example, most marrow donors complete recovery within a few weeks (50, 51) (see also http://bethematch.org), corresponding to ∼10 cell cycles of HSCs (each cell cycle is approximately 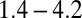d according to ref. 24). Many donors even recover in less than 5 d (51). Therefore, a physiologically reliable control strategy should induce fast adaptation and robust recovery against these changes.

Here, we studied the three different strategies (A, B, and C) in response to changes in the stem cell population. Two types of changes were studied: a sudden decrease in the cell population and a temporary increase in the differentiation probability. First, we examined the recovery dynamics after a sudden loss of the cell population to approximately half of the normal level (all cell types were equally lost). Both strategies A and B induced fast recovery of the cell populations in ∼10 cell cycles (Fig. 3). However, using strategy C, the recovery process was significantly slower even with a very large Hill coefficient (e.g., 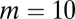). For the cases with small Hill coefficients (e.g., 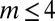) that are commonly used in stem cell modeling (17, 32), more than 50 cell cycles were needed to recover the stem cell population to a level near the levels observed in A and B. These results indicate that complex feedback mechanisms incorporating epigenetic states provide faster recovery after sudden damage in stem cell tissues.

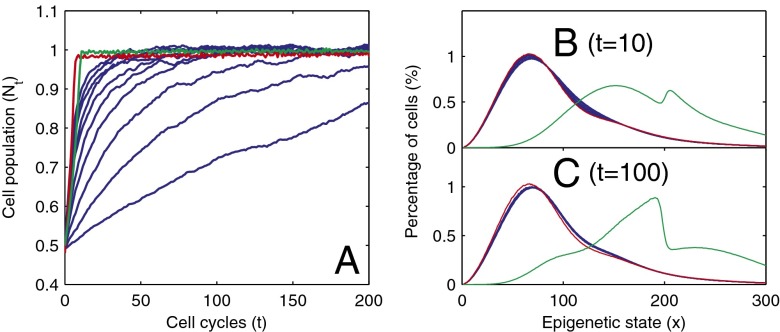
Fig. 3.

Recovery of the cell population and distribution of epigenetic states after a sudden loss of half of the total population of cells. (A) Cell population time courses. (B) The function 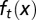at 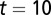cell cycles after the sudden loss. (C) The function 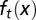at 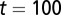cell cycles after the sudden loss. Three different controls are shown: strategy A (red), B (greed), and C (blue). For strategy C, the Hill coefficient m varies from 1 to 10 (from bottom to top in A). The cell populations at homeostasis are normalized to their maximum levels. See SI Text, section S5 for other parameters used in simulations.

We also note that the distributions of the cell epigenetic states show different dynamics for homogeneous or heterogeneous proliferation probabilities. If the proliferation is homogeneous (strategies A and C), the cell distributions remain unchanged during the process. When the proliferation is heterogeneous (strategy B), the cell distribution reshapes after a decrease in cell population and then regains its original form; however, this period is longer than the recovery time of the population (Fig. 3 B and C).

Next, we induced a temporary increase in the differentiation probability. Physiologically, this type of increase can be induced by a decrease in differentiated cells through a negative feedback mechanism regulating the differentiation process (see refs. 52 and 53 for examples of HSC). We study the three strategies to determine which ones induce a response to effectively replenish the lost cells.

The three strategies yielded different dynamics regarding cell populations. Strategy B provided less variation in the total cell population, a higher level of differentiated cells during the increasing phase of differentiation, and a faster recovery to the normal level after the differentiation probability regained its value (Fig. 4 A and B). Moreover, for the homogenous proliferating cells, strategy A induced a better response compared with strategy C in terms of smaller variance in the cell population and a higher level of differentiated cells during the increase of the differentiation probability (Fig. 4 A and B, red and blue lines). These results indicate that an optimal control strategy proposed here with the heterogeneous proliferation probability can lead to good adaptation to temporal changes in the differentiation probability to sustain the cell population and effectively replenish decreases in downstream differentiated cells.

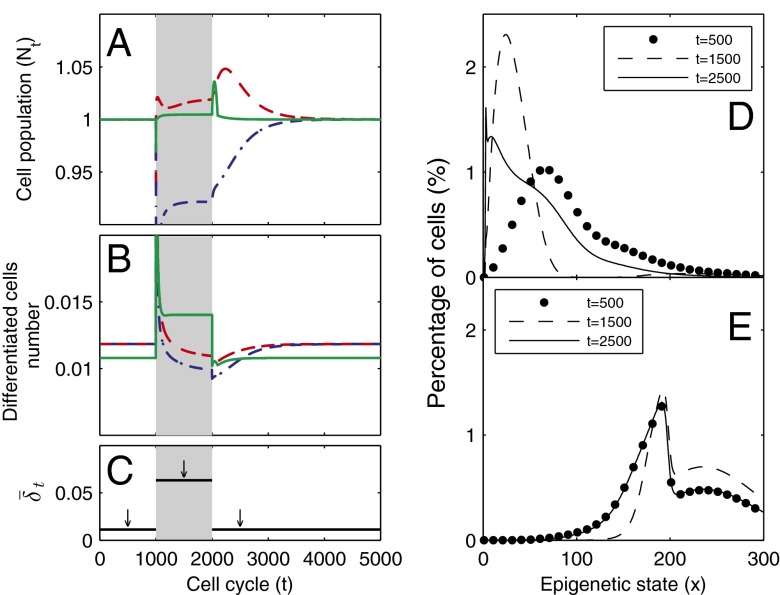
Fig. 4.

Tissue response to temporal changes in differentiation. (A) Cell population time courses under three different strategies for proliferation. The red dashed line represents strategy A, the green solid line strategy B, and the blue dashed/dotted line strategy C with the Hill coefficient 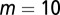. (B) Time course of the number of differentiated cells 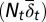. (C) Time course of average differentiation 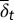. Shadows indicate the time window of increasing differentiation. (D) Cell distributions (strategy A) at three time points (marked with arrows in C), before (filled circles, 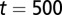), during (dashed line, 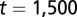), and after (solid line, 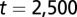) the temporal change of differentiation. (E) Same as D but using strategy B.

The three strategies also yielded different dynamics for tissue epigenetics 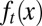. For strategies A and C, a clear shift in 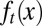occurred toward the low-performance region (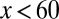, see Fig. 2, Inset for the performance function) during the increases in differentiation, and a slow recovery occurred after the differentiation level returned to its normal level (Fig. 4D). For strategy B, the tissue epigenetics shifted to its higher performance region 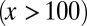and recovered quickly after the differentiation level returned to normal (Fig. 4E). These results suggest that an optimal control strategy using heterogeneous proliferation can lead to a better robust response in the epigenetic states of resting phase stem cells after a sudden increase in differentiation.

In response to the severe loss of hematopoietic cells, dormant HSCs may shift their niches and become injury-activated HSCs (10). We modeled this effect by introducing an increase in the resting phase cell population along with an increase in differentiation probability (SI Text, section S3). In comparison with the case in Fig. 4, only a minor difference in the transient dynamics is observed with the similar long-time dynamics between the two cases, and the results regarding the characteristics of the three strategies remain the same.

In addition, we also examined the tissue response to temporal increases in apoptosis, which is often observed in diseases or clinical treatments (e.g., during chemotherapy). The simulations again showed that an optimal control strategy based on heterogeneous proliferation leads to less variation in cell populations (SI Text, section S3). The overall results demonstrate the apparent advantages of the control strategy of heterogeneous proliferation in robust responses to perturbations during tissue growth.

Successful Evolution Depends on the Selection of both Epigenetic States and Cell Populations.

When mutation occurs, the fitness function W varies with evolutionary time. For simplicity, we only considered mutations affecting the apoptosis and the proliferation probability 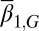(see SI Text, section S5 for simulation details) and ignore their effects on the differentiation 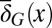. Assuming mutations of higher fitness are more likely to survive, we investigated the evolution of apoptosis to maximize the evolutionary fitness.

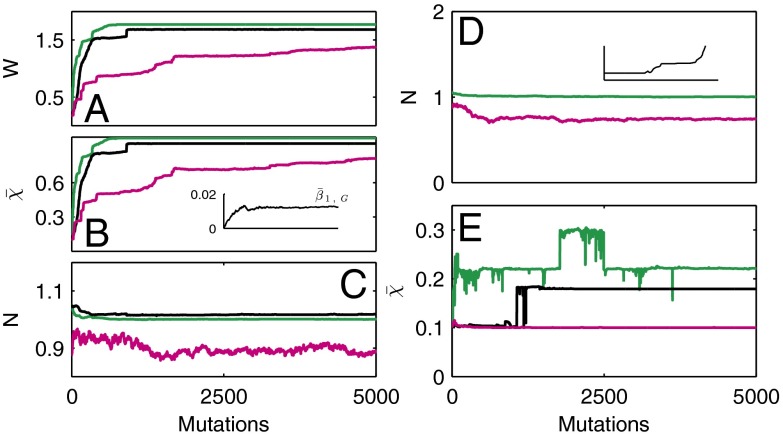
First, we studied the three different strategies (A, B, and C) with the apoptosis probability being initialized as a constant and with low performance at the beginning of the evolution period (Fig. 2B). Following the evolution of apoptosis, all three strategies caused high performance and stable cell populations (Fig. 5 A–C). In comparison with the traditional simple feedback (strategy C), the optimal control strategies (A and B) showed faster evolutionary dynamics and less fluctuations in the cell population. During the evolution period, the average cell performance function 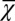obviously increased, but only a small change in the cell population was observed. The dynamics originate from genome mutations that alter the apoptosis 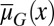, and the performance 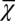during homeostasis is a consequence of the optimal control of proliferation that depends on the epigenetic states during each cell cycle. Thus, the increasing of 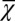during evolution indicates that cross-talk occurs between genetic and epigenetic regulation.

Fig. 5.

Evolution dynamics for different control strategies. Time is measured by the number of mutations. Results for strategies A (green), B (black) and C (magenta) are shown using the average of 10 independent sample evolution dynamics. (A) Fitness during evolution. (B) The cell performance function 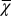. Inset shows 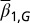based on strategy B. (C) Cell population N. (D) The cell population when 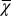is used as the evolutionary fitness. Inset shows the dynamics for strategy B in which the population size markedly increases after 1,000 mutations. 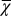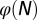(E) Time course of when is used as the evolutionary fitness.

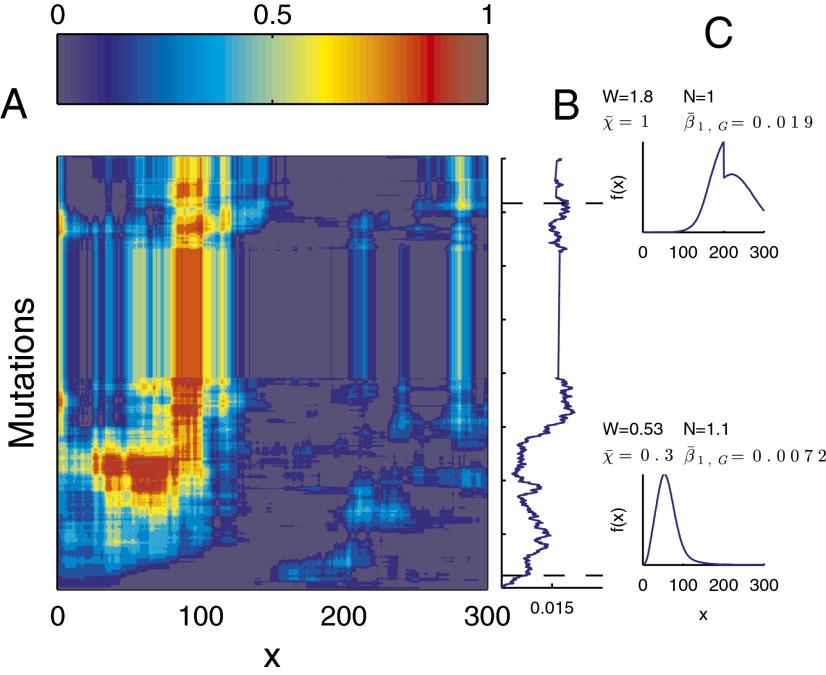
An example of the evolution in apoptosis using strategy B is shown in Fig. 6, and this example suggests the tendency to choose a high apoptosis probability for cells with low performance and low apoptosis probability for cells with high performance. Consequently, the tissue epigenetics 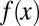during homeostasis shifts from a profile of low-performance cells dominating at the beginning to the profile of high-performance cells dominating at the end during evolution. These results indicate that the evolutionary fitness function W automatically leads to an evolution of effective apoptosis that eliminates low-performance cells and maintains high tissue performances. The evolutionary dynamics using strategy A show similar results, and the resulting apoptosis 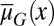is insensitive to its initial probability and the differentiation 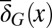(SI Text, section S4).

Fig. 6.

An example of evolutionary dynamics of the apoptosis 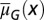and the proliferation 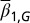following strategy B. (A) The evolution of 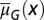, with the initial 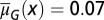for each x. (B) The proliferation 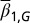that is initiated from 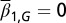. (C) The density 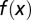during homeostasis at two time points of mutations, indicated by dashed lines in B. Evolutionary fitness W, population number N, cell performance 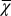, and proliferation probability 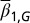are also given in each case.

Finally, we investigated whether it is possible to have successful evolution based on a fitness function defined only with epigenetic states or with cell populations. To this end, we replaced the fitness function W with eithe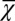r or 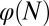. When only the epigenetics 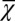were considered, strategy A and C produced successful evolution of high performance and persistent cell populations (Fig. 5D). However, strategy B caused a marked increase in the cell population (Fig. 5D, Inset) that originated from the proliferation 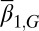, which changed at each mutation but was not selected in the evolution process. In contrast, when 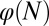was chosen as the evolutionary fitness, all three strategies failed to select an apoptosis probability function to produce high performance due to the absence of cross-talk between the genetic control and the epigenetics regulation. This finding is shown in Fig. 5E in which 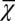remains a small value in the evolutionary process.

Conclusions and Discussion

Adult stem cells in self-renewing tissues are persistent over a long lifespan despite stochastic perturbations and accidental changes. How can stem cells regulate their regeneration during each cell cycle such that the tissue performances (e.g., size of cell populations and cell distributions in epigenetic states) are maintained over the lifetime of tissues? How can stem cells recover robustly after sudden changes? In this paper, we developed a generic modeling framework based on the dynamic programming approach to obtain control strategies that govern the probabilities of proliferation, differentiation, and apoptosis of stem cells. One important feature of the model is its capability of incorporating the performance functions of stem cells at two distinct time scales: the time of one cell cycle and the lifetime of the tissue. Another noteworthy attribute of the model is the representation of stem cells in their epigenetic states to allow cells that are programmed to perform the same functions to exhibit variability and heterogeneity, a characteristic often observed in stem cells.

Using these modeling techniques, we identified controlling strategies that maintain the performance of regeneration tissues (e.g., the desirable distributions of stem cells in their epigenetic states) that are subject to random fluctuations during each cell division. One optimal control inherently emerging from maximizing the performance during each cell cycle is a feedback regulation that controls proliferation through both the cell population and heterogeneous dependence on the epigenetic states. The strategy has an additional advantage compared with the typical feedback regulation that depends only on the size of the cell population, and the advantage entails the speedy recovery of tissue functions after a sudden loss in cells or temporal perturbations in differentiation capability.

While a regenerative tissue needs to reproduce cells in an accurate quantity as well as in a faithful distribution of their epigenetic states within a reasonable time window, the tissue also needs an ability of removing cells that have genetic or epigenetic errors due to mutations or stochastic cellular events. By maximizing the fitness function, our model naturally selects an apoptosis strategy to eliminate the cells with errors. The control strategy regarding proliferation depends on apoptosis at each cell cycle; therefore, the derived apoptosis regulation demonstrates that cross-talk occurs between epigenetic regulation occurring at a short time scale of one cell cycle and genetic evolution occurring at a long time scale. Recent observations provide strong evidences of how the DNA variant influences the epigenetics (54–56). At the center of the epigenetic-dependent control strategies is the dependence of proliferation on differentiation and apoptosis through a complex feedback mechanism.

The current study is intended to introduce a simple and generic modeling framework without involving any molecular or mechanistic descriptions. To investigate specific functions of one particular type of stem cells, one can add an additional layer of complexity into the model by incorporating corresponding genetic and molecular regulation into the quantities of proliferation, differentiation, and apoptosis. The transition between quiescent and resting phase can also be added to the model for tissues with quiescent stem cells. Additionally, we can study the effect of apoptosis in response to differentiation and proliferation within the same framework, as well as the effect of aging, by introducing a time-dependent performance function. Cell lineages consisting of different cell types along with different performance objectives may also be included in this type of modeling framework. The derived control strategies in this work lack molecular details; however, the qualitative relationships found between the epigenetic states and the three control probabilities can be scrutinized closely using experiments. For example, the three quantities may be estimated using techniques such as fluorescence-activated cell sorting (FACS) if the epigenetic states (e.g., through levels of transcriptional factors) can be marked by fluorescence labels. The distributions of epigenetic states of stem cells at both resting and proliferating phases can be obtained at different times through FACS to estimate the dynamics of the cell population distribution in terms of the epigenetic states. Through these experimental connections, the present work sheds light on how stem cells use proliferation, differentiation, and apoptosis collectively to manage many challenges that regenerative tissues face during each cell cycle and during their lifetime, which may lead to new therapeutic strategies in medical practice. For example, one may control the distribution of stem cell populations using drugs targeting epigenetic components (e.g., special forms of DNA methylation) or alternating the physiological environment so the cells favor particular epigenetic states for better proliferation or better differentiation in an unhealthy tissue.

In this study, the performance function Q, which measures the physiological performance of stem cells, is usually difficult to quantify in real biological tissues because the function is dependent on the complex physiological environment. Nevertheless, it may be possible to estimate the relative performance when two or more types of stem cells compete for a common resource or a niche by which growth factors and other survival signals are provided. The performance of each type of cell depends on the populations as well as the common resource and niches; and therefore, the control strategies for different stem cells affect each other. For this case, the game theoretic approach may be very useful. In general, evolutionary adaptation ensures healthy biological functions and robust response to accidental changes of tissues controlled by stem cells, suggesting that evolution shapes the population biology of stem cells. The methods from population biology and evolutionary theory are helpful in understanding stem cells and their epigenetic regulation.