Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Jul 16.
Published in final edited form as: Cell. 2013 Dec 19;156(0):183–194. doi: 10.1016/j.cell.2013.11.028

The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity

Bradley R Parry 1,¥, Ivan V Surovtsev 1,2,¥, Matthew T Cabeen 1,†, Corey S O’Hern 3,4,5, Eric R Dufresne 4,5,6,7, Christine Jacobs-Wagner 1,2,8,*
PMCID: PMC3956598  NIHMSID: NIHMS559716  PMID: 24361104

SUMMARY

The physical nature of the bacterial cytoplasm is poorly understood even though it determines cytoplasmic dynamics and hence cellular physiology and behavior. Through single-particle tracking of protein filaments, plasmids, storage granules and foreign particles of different sizes, we find that the bacterial cytoplasm displays properties characteristic of glass-forming liquids and changes from liquid-like to solid-like in a component size-dependent fashion. As a result, the motion of cytoplasmic components becomes disproportionally constrained with increasing size. Remarkably, cellular metabolism fluidizes the cytoplasm, allowing larger components to escape their local environment and explore larger regions of the cytoplasm. Consequently, cytoplasmic fluidity and dynamics dramatically change as cells shift between metabolically active and dormant states in response to fluctuating environments. Our findings provide insight into bacterial dormancy and have broad implications to our understanding of bacterial physiology as the glassy behavior of the cytoplasm impacts all intracellular processes involving large components.

INTRODUCTION

In eukaryotes, active transport (including ATP-dependent diffusive-like motion) involves protein motors and cytoskeletal filaments. In the absence of cytoskeletal motor proteins, (micrometer-sized) bacteria are thought to primarily rely on diffusion for molecular transport and cytoplasmic mixing. Diffusion is therefore considered an integral part of bacterial life; it determines the mobility of cytoplasmic constituents and hence sets the limits at which molecular interactions (and thereby biological reactions) can occur. Diffusion is also essential for cell proliferation by promoting a homogeneous distribution of cytoplasmic components and the equal partitioning of solutes between daughter cells. While diffusion in general has been extensively studied theoretically and experimentally, the bacterial cytoplasm bears little resemblance to the simple liquids usually considered. First, the bacterial cytoplasm is an aqueous environment that is extremely crowded (Cayley et al., 1991; Zimmerman and Trach, 1991). Second, the cytoplasm is highly polydisperse, with constituent sizes spanning several orders of magnitude, from subnanometer (ions, metabolites) to nanometers (proteins) to tens and hundreds of nanometers (ribosomes, plasmids, enzymatic megacomplexes, granules, microcompartments) to micrometers (protein filaments, chromosomes). Third, metabolic activities drive the cytoplasm far from thermodynamic equilibrium. Furthermore, as a resistance mechanism, the cell can reversibly shut down metabolism in response to environmental stresses How these features affect the physical properties of the cytoplasm is poorly understood. Such an understanding is critical because the physical nature of the cytoplasm determines the dynamics of cytoplasmic components and therefore impacts all intracellular processes.

Both normal and anomalous diffusive motions have been reported for cytoplasmic components (Bakshi et al., 2011; Coquel et al., 2013; English et al., 2011; Golding and Cox, 2006; Niu and Yu, 2008; Weber et al., 2010), and a unifying picture about the physical nature of the cytoplasm has yet to emerge. We show here that the bacterial cytoplasm exhibits physical properties typically associated with glass-forming liquids approaching the glass transition. Glass-forming liquids, which are intensively studied in condensed matter physics, encompass many materials, including molecular glasses (vitreous glass) and dense suspensions of colloidal particles (colloidal glasses) (Hunter and Weeks, 2012). We found that the glassy behavior of the bacterial cytoplasm affects the mobility of cytoplasmic components in a size-dependent fashion, providing an explanation for the previous seemingly conflicting reports. Strikingly, metabolic activity abates this glassy behavior such that, in response to environmental cues, cytoplasmic fluidity and dynamics are dramatically altered through modulation of cellular metabolism.

RESULTS

The motion of crescentin-GFP structures and PhaZ-GFP-labeled storage granules is reduced in metabolically inactive C. crescentus cells

Our study began with a serendipitous observation while studying the bacterial intermediate filament protein crescentin. Under native conditions, crescentin self-associates to form a stable (i.e., having no detectable subunit exchange) membrane-bound filamentous structure that generates the namesake curvature of the bacterium Caulobacter crescentus (Ausmees et al., 2003). A specific modification of the cell envelope (Cabeen et al., 2010) or addition of a bulky tag (e.g., GFP) to crescentin (Ausmees et al., 2003) causes the crescentin structure to detach from the membrane; these non-functional structures display random motion in the cytoplasm (Cabeen et al., 2009). While imaging GFP-labeled crescentin structures in a filamentous mutant strain growing on an agarose pad made with nutrient-containing medium (M2G), we observed, to our surprise, that crescentin-GFP structure movement suddenly stopped when the cells simultaneously arrested growth (Movie S1). The reason for the abrupt growth arrest was unknown, but the ensuing drop in crescentin-GFP structure mobility raised the intriguing possibility that metabolic activity may play a role in the motion of freely diffusing cytoplasmic components.

A possible link between metabolism and cytoplasmic dynamics would be important to investigate as bacteria in the wild are able to shift between metabolically active and dormant states in response to changing environments (Lennon and Jones, 2011). Dormancy is a survival strategy that can be triggered by many external insults, including nutrient limitation and late stationary phase. To examine whether dormancy can affect cytoplasmic dynamics, we first tracked crescentin-GFP structures (replacing wild-type crescentin structures) in otherwise wild-type cells (using custom two-dimensional tracking methods for non-diffraction-limited objects; see SI, Fig. S1A–F), and compared their mobility in actively growing cells to their mobility in cells subjected to prolonged carbon starvation. In cells actively growing on M2G medium, crescentin-GFP structures displayed motion and were able to sample the cytoplasm in minutes (Fig. 1A, Movie S2) by taking large, seemingly random steps (Fig. 1B). In contrast, carbonstarved cells were unable to grow, and crescentin-GFP structures rarely left their original locations (Fig. 1A–B; Movie S3) for the entire duration of the experiment (up to 9 h; data not shown). We observed similar spatial confinement in late stationary-phase cells (Fig. 1B) and under treatment with 2,4-dinitrophenol (DNP; Fig. 1B, Movie S4), an oxidative phosphorylation uncoupling agent that rapidly depletes cells of ATP and GTP.

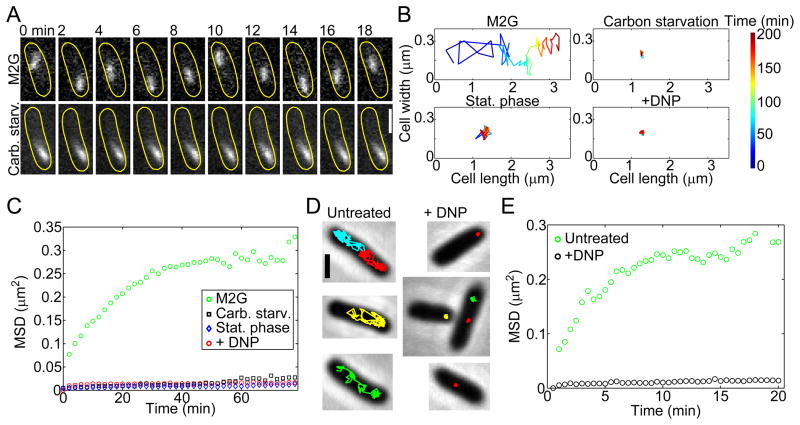
Figure 1. The mobility of crescentin-GFP structures and GFP-LacI-labeled mini-RK2 plasmids is affected by metabolism.

Figure 1

Open in a new tab

(A) Time-lapse montages of crescentin-GFP structures acquired under conditions of growth (M2G) and carbon source depletion. C. crescentus cells (CJW1265) were grown and imaged in M2G, a glucose-based medium (top montage). For carbon starvation, cells were washed into M2 buffer (lacking glucose) and incubated for 3 h before imaging (bottom montage). The scale bar is 1 μm.

(B) Two-dimensional trajectories representing 200 min of crescentin-GFP tracking from single C. crescentus cells (CJW1265) under metabolically active (M2G) and metabolically depleted (carbon starvation, late stationary phase, + DNP) conditions.

(C) MSD of crescentin-GFP structures in metabolically active (M2G, n = 1,796 trajectories) and energy-depleted (carbon starvation, n = 861 trajectories; stationary phase, n = 718 trajectories; and +DNP, n = 1,943 trajectories) conditions. C. crescentus cells (CJW1265) from late stationary phase cell cultures (OD660 ≥ 1.7) were imaged on agarose pads made with stationary-phase culture supernatant instead of M2G.

(D) Two-dimensional trajectories of GFP-LacI-labeled mini-RK2 plasmids overlaid on corresponding phase-contrast images of metabolically active and DNP-treated E. coli cells (JP924). Scale bar is 1 μm.

(E) MSD of mini-RK2 plasmids under metabolically active (untreated, n = 497 trajectories) and energy-depleted (+DNP, n = 488 trajectories) conditions.

See also Figs. S1–2 and Movies 1–6

To quantitatively analyze crescentin-GFP structure mobility at the population level, we calculated the mean square displacement (MSD) over large numbers of trajectories (n = 718 – 1943). The MSD averages, over all objects, the square of the distance between an object’s current position and its original position (see SI). Comparison of one-dimensional (along cell length) MSDs among experimental conditions confirmed the dramatic loss of mobility in metabolically reduced cells (carbon-starved, stationary-phase and DNP-treated populations; Fig. 1C). Thus, the metabolic state of the cell had a dramatic effect on crescentin-GFP structure mobility.

Crescentin-GFP forms large structures, with an average apparent length of 900 nm (Fig. S1G). To test whether the motion of other large cytoplasmic components is affected, we tracked the motion of polyhydroxyalkanoate (PHA) granules labeled with PhaZ-mCherry. PhaZ is a PHA depolymerase that binds to PHA storage granules (Maehara et al., 2002; Qi and Rehm, 2001). Consistent with this binding, PhaZ-mCherry formed fluorescent foci (1–2 per cell) that moved inside active (untreated) C. crescentus cells (Fig. S2A). Metabolic depletion by DNP treatment dramatically reduced motion (Fig. S2A), similar to what we observed with crescentin-GFP structures.

Plasmid motion is also reduced in Escherichia coli when cellular energy is depleted

To examine whether this metabolism-dependent motion is unique to C. crescentus, we switched to E. coli and examined the motion of engineered low-copy-number mini-RK2 plasmids. These plasmids have an estimated radius of gyration of 150 nm based on measurements of plasmids with similar base-pair lengths (Latulippe and Zydney, 2010). Mini-RK2 lacks a partitioning system and hence is not actively partitioned or constrained in space (Derman et al., 2008). This plasmid also contains a lacO array for visualization via GFP-LacI labeling. Mini-RK2 plasmids were imaged every 30 sec on agarose pads containing M9-glycerol (M9G) medium to sustain cellular activity. Under these conditions, mini-RK2 plasmids were able to travel the cell length within one minute, leaving their previous location from frame to frame (Fig. 1D, Movie S5) as previously observed (Derman et al., 2008). In contrast, depletion of cellular energy by DNP treatment drastically limited their spatial exploration (Fig. 1D, Movie S6), which was confirmed at the population level in MSD plots (Fig. 1E; n = 488 – 497 trajectories). Thus, mini-RK2 plasmids exhibit metabolism-dependent motion in E. coli, similar to crescentin-GFP structures and PHA granules in C. crescentus. As E. coli and C. crescentus diverged over a billion years ago, the effect of metabolism on cytoplasmic dynamics is likely to be an ancient and common feature of the bacterial cytoplasm.

Development of a genetically encoded probe to study cytoplasmic dynamics

Specific interactions with other cellular components are known to affect the motion of components endogenous to the cytoplasm, altering motion in an unpredictable manner (Nenninger et al., 2010) and making normal diffusion appear anomalous (Dix and Verkman, 2008). Therefore, to characterize the physical nature of metabolism-dependent motion, we needed a probe that is completely foreign to the cell (unlike crescentin, PHA granules and plasmids), and thus unlikely to make any specific interactions with components of the bacterial cytoplasm. As the direct injection methods used in eukaryotic cells cannot be used with micron-sized bacteria, we attempted to introduce non-biological probes (quantum dots, dextrans, or gold particles) into the bacterial cytoplasm with biolistic and electroporation techniques. None of these attempts were successful. As an alternative, we sought a genetically encoded probe that is foreign to the bacterial cytoplasm and capable of self-assembly into particles. Several eukaryotic viruses are known to replicate in cytoplasmic factories that require a matrix made of self assembling viral proteins. The avian reovirus protein μNS is an example of such a self-assembling protein (Broering et al., 2002), and a C-terminal fragment is sufficient to form globular cytoplasmic particles, even when fused to GFP (Broering et al., 2005). These GFPlabeled particles, referred to as GFP-μNS particles here, are unlikely to make specific interactions with components of the bacterial cytoplasm given the evolutionary divergence between bacteria and the avian reovirus host.

Induction of GFP-μNS synthesis in E. coli usually resulted in a single fluorescent focus per cell (Fig. S3A). The foci exhibited significant motion in metabolically active cells, but became spatially confined with DNP treatment (Fig. 2A–C, Movie S7), recapitulating our results with plasmids, PHA granules and crescentin-GFP structures. Depletion of cellular energy through treatment with carbonylcyanide-m-chlorophenylhydrazone (CCCP) instead of DNP had the same negative effect on GFP-μNS mobility (data not shown). Collectively, these results further support the notion that metabolism-dependent motion is a general property of the bacterial cytoplasm.

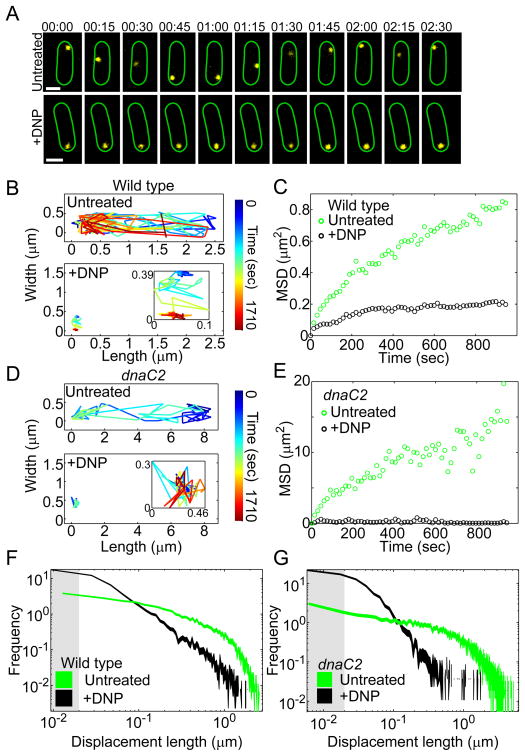
Figure 2. GFP-μNS probe dynamics are affected by cellular metabolism.

Figure 2

Open in a new tab

(A) Representative time-lapse montages of GFP-μNS particles (yellow) in E. coli cells (CJW4617) acquired under untreated and DNP-treated conditions (+DNP). The scale bar is 1 μm. Time is min:sec.

(B) An example of a two-dimensional trajectory of a GFP-μNS particle in an E. coli cell (CJW4617) with or without DNP treatment.

(C) MSD of GFP-μNS particles in metabolically active (untreated, n = 729 trajectories) and DNP-treated (+DNP, n = 643 trajectories) E. coli cells (CJW4617).

(D) Two-dimensional trajectory of a GFP-μNS particle in a filamentous E. coli dnaC2 cell (CJW4619) at the restrictive temperature (37ºC) with or without DNP treatment.

(E) MSD of GFP-μNS particles in filamentous E. coli dnaC2 cells (CJW4619) at their restrictive temperature with (+DNP, n = 118 trajectories) or without (untreated, n = 192 trajectories) DNP treatment.

(F) Histogram of GFP-μNS particle displacements in E. coli cells (CJW4617) with or without DNP treatment. Line width indicates Poisson counting error, and the gray shading delineates the estimated tracking error. Displacements were measured over 15-sec intervals.

(G) Histogram of GFP-μNS particle displacements in E. coli dnaC2 cells (CJW4619) at the restrictive temperature (37ºC) with or without DNP treatment. Line width indicates Poisson counting error, and the gray shading delineates the estimated tracking error. Displacements were measured over 15-sec intervals.

See also Figs. S2–5 and Movie 7.

Metabolism-dependent motion is not driven by known motor-like activity or chromosome dynamics

The observation that the motion of cytoplasmic components depends on metabolic activity was surprising as it appeared inconsistent with diffusion, which is a passive process. ATP-dependent motion was recently reported for chromosomal loci in E. coli (Weber et al., 2012). However, chromosomal loci are distinct from free cytoplasmic components as they remain confined within a small space (where they “jiggle”) by virtue of their attachment to the rest of the chromosome. As a consequence, the motion of chromosomal loci depends not only on the cytosolic environment but also on the DNA structure. Using DAPI staining, we found that energy depletion by DNP treatment has a strong effect on the shape and hence structure of the chromosome (Fig. S4A–B), and likely contributes to the change in chromosomal locus dynamics. Consistent with this notion, the mobility of chromosomal loci is also ATP dependent in eukaryotic nuclei (Heun et al., 2001; Levi et al., 2005) and this ATP dependence has been attributed to reduced activity of DNA-remodeling proteins (Soutoglou and Misteli, 2007).

While our cytoplasmic probes do not associate with the chromosome, it remained possible that their metabolism-dependent motion results from a change in chromosome structure and dynamics (for example, through probe entrapment; see SI). We found that the chromosome affected the spatial distribution of GFP-μNS particles (see SI). However, experiments with dnaC2 mutant cells, which produce large DNA-free regions, showed that metabolism-dependent motion occurs independently of the DNA (see SI, Figs. 2D–E and S2B). These experiments exclude a predominant role for the chromosome in the metabolism-dependent motion of free cytoplasmic components.

In eukaryotes, agitation of the pervasive cytoskeletal meshwork by the activity of motor proteins can produce diffusive-like motion in the cytoplasm in an ATP-dependent manner (Brangwynne et al., 2009). This process is often referred to as “active diffusion”. However, bacteria lack motor proteins like dyneins, myosins and kinesins, and their cytoskeletal elements are primarily membrane-associated. Furthermore, metabolism-dependent motion still occurred when the polymerization of MreB (bacterial actin homolog) or FtsZ (tubulin homolog) was disrupted (see SI, Fig. S3B and Fig. 2D–E; note that FtsZ rings do not form in filamentous dnaC2 cells). Thus, the mechanism producing the metabolism-dependent motion in bacteria appears different from the cytoskeletal motor-based “active diffusion” observed in eukaryotes.

Through drug inactivation of transcription, translation or peptidoglycan wall synthesis, we also showed that metabolism-dependent motion does not originate from the sole (motor-like) action of RNA polymerases, ribosomes or penicillin-binding proteins on their DNA, mRNA or peptidoglycan substrates (see SI, Fig. S3C–E).

Increase in frequency of large displacements contributes to metabolism-dependent motion

To gain insight into the origin of metabolism-dependent motion, we sought to characterize this motion more precisely. An interesting characteristic of energy-depleted cells is that while GFP-μNS particles remained largely confined in space in these cells, they still appeared to display small displacements over the imaging interval (15 sec); this was true in wild-type and dnaC2 cells (see Fig. 2B,D for example trajectories). Through control experiments and simulations (see SI; Fig. S5), we determined that our single-particle tracking method can distinguish small (>20 nm) displacements. Therefore, even after accounting for potential localization errors, GFP-μNS particles displayed discernible motion in DNP-treated cells as shown by the distributions of displacement lengths (Fig. 2F for wild-type cells and Fig. 2G for dnaC2 cells, with gray shading denoting our estimated tracking error; see SI). Under both untreated and DNP-treated conditions, small displacements were more frequent than large ones (Fig. 2F and Fig. 2G). However, the frequency of long displacements was much greater in metabolically active cells. This higher frequency of long displacements is likely responsible for the ability of GFP-μNS particles to explore more cytoplasmic area in active cells. In other words, GFP-μNS particles are able to sample the cytoplasm of active cells with large displacements, while they remain spatially confined in inactive cells because the largest displacements disappear.

The effect of metabolism on cytoplasmic dynamics depends on particle size

Recent fluorescence recovery after photobleaching (FRAP) measurements from our laboratory have shown only a nominal difference in the diffusion coefficient of free GFP between untreated and DNP-treated C. crescentus cells (Montero Llopis et al., 2012). Because GFP (size ≈ 3 nm) is smaller than mini-RK2 plasmids, PHA granules, and crescentin-GFP filaments, this observation raised the possibility that the influence of metabolism on motion may depend on particle size. To examine this possibility, we took advantage of our titratable GFP-μNS system in which GFP-μNS synthesis can be tuned to different levels by varying the inducer (IPTG) concentration and the induction time. By doing so, we obtained GFP-μNS particles with a wide range of fluorescence intensities and hence sizes (Fig. S6A–B). We then plotted MSDs of particles binned by fluorescence intensities (bins 1–9), and found that MSDs of both untreated and DNP-treated cell are inversely correlated with fluorescence intensity (Fig. 3A–B shows selected bins on a log-log scale for clarity), as anticipated. When we compared the distribution of displacement lengths between untreated and DNP-treated conditions across discrete bins of particle fluorescence intensities, we found that the difference between the two conditions is accentuated with fluorescence intensity and hence particle size (Fig. 3C, Fig. S7).

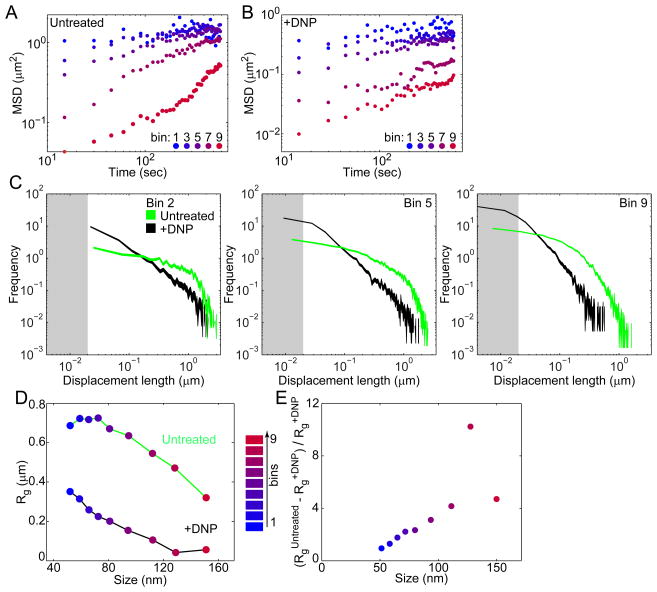
Figure 3. Effect of metabolism on cytoplasmic motion depends on particle size.

Figure 3

Open in a new tab

(A) MSD of GFP-μNS particles of varying binned fluorescence intensities in E. coli cells (CJW4617) under normal growth conditions (M2G).

(B) Same as A, but for GFP-μNS particles in E. coli cells (CJW4617) under DNP treatment.

(C) Histograms of GFP-μNS particle displacements under untreated and DNP-treated conditions for selected bins. Displacements were measured over 15-sec intervals. Line width indicates Poisson counting error, and the gray shading delineates the estimated tracking error.

(D) Mean radius of gyration (Rg) of all trajectories from GFP-μNS particles of a given binned size is plotted as a measure of spatial exploration for untreated and DNP-treated cells.

(E) The ratio (RgUntreated-Rg+DNP)/Rg+DNP is plotted as a function of particle size.

See also Figs. S6–7.

To estimate the absolute size of particles from their fluorescence intensity, we measured the diffusion coefficients of GFP-μNS particles in solution after cell lysis and compared these values to those of fluorescent beads of known size (see SI, Fig. S6C–D). From these measurements, we obtained a calibration curve (see SI), which we used to estimate the particle size (in nm). We then characterized the relationship between particle size and metabolism-dependent motion by calculating the radius of gyration (Rg; along the long axis of the cell) of each trajectory. Rg is the root mean square distance from the center of the trajectory (see SI) and measures the average space a particle explores. Rg analysis showed that both cellular energy depletion (+DNP) and increasing particle size leads to increasing spatial confinement (Fig. 3D). By calculating the ratio (RgUntreated-Rg+DNP)/Rg+DNP (which compares the difference in space explored in metabolically active conditions relative to energy-depleted conditions) as a function of particle size (Fig. 3E), we found that the ratio is significantly greater than zero and increases with increasing particle size (except perhaps for the largest size bin, possibly because these particles may be too big to move even in active cells). This trend supports a size dependence for metabolism-dependent motion. Of equal interest, the ratio (RgUntreated-Rg+DNP)/Rg+DNP decreased toward 0 as size decreased (Fig. 3E), with an estimated intercept near 30–40 nm assuming a linear relationship. This finding suggests that cytoplasmic components smaller than this estimated size are not affected by metabolism-dependent motion.

The distribution of displacements is non-Gaussian

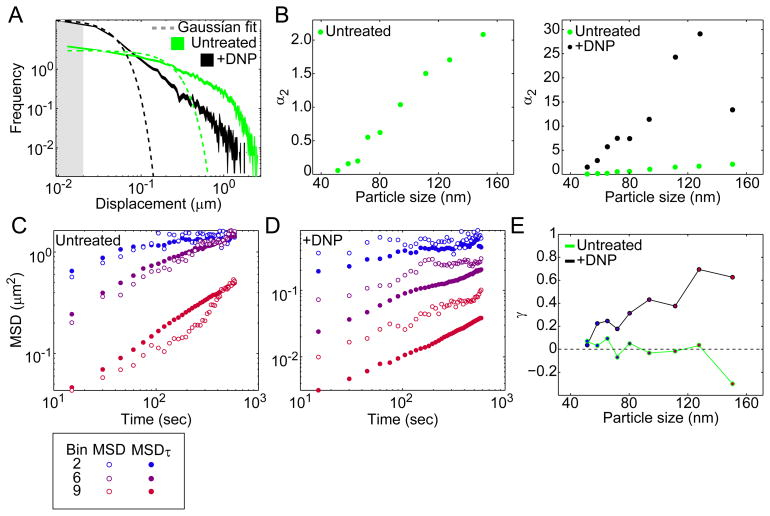
In normal diffusion, the diffusing particles will exhibit a Gaussian distribution of displacements. In contrast, the displacement distributions of GFP-μNS particles under both untreated and DNP-treated conditions diverged from the expected Gaussian distribution (Fig. 4A shows bin 5 as an example) as signified by long tails. We quantified deviations from a Gaussian distribution by calculating the non-Gaussian parameter α2 (see SI). The α2 value of a Gaussian distribution is zero, and grows as the tail of the measured distribution increases. First, we found that in metabolically active cells, the α2 values of GFP-μNS displacement distributions grew with increasing GFP-μNS particle size (Fig. 4B), indicating that non-Gaussian behavior increases with particle size. Second, the non-Gaussian behavior was dramatically stronger for particles in metabolically inactive cells, where α2 grew much faster with particle size than in active cells (Fig. 4B).

Figure 4. GFP-μNS particles display non-Gaussian and non-ergodic behavior in the cytoplasm.

Figure 4

Open in a new tab

(A) Experimental distributions of GFP-μNS particle displacements for E. coli cells (CJW4617) under untreated and DNP-treated conditions for a selected size bin (bin 5). Dashed lines are the best fit to a Gaussian distribution. Line width indicates Poisson counting error, and the gray shading delineates the estimated tracking error. Time interval is 15 sec.

(B) Non-Gaussian parameter α2 of particle displacement distributions is plotted as a function of particle size for E. coli cells (CJW4617) with or without DNP treatment.

(C) Comparison of MSD and MSDτ for selected size bins for cells under untreated conditions.

(D) Same as C, but for cells under DNP treatment.

(E) The parameter γ is plotted as a function of particle size for cells with or without DNP treatment.

Non-ergodicity increases with energy depletion and particle size

Notably, deviations from Gaussian statistics for particle displacements have been reported in various non-living physical systems including glass-forming liquids near the glass transition. Colloidal suspensions have proven to be instructive model systems to characterize the dynamics of glass-forming liquids (Hunter and Weeks, 2012). Dense colloidal suspensions (also known colloidal glasses) are metastable near the glass transition, changing from liquids to amorphous solids with small changes in colloid concentration. At low concentration (low crowding), colloidal particles exhibit diffusive behavior. Increasing the concentration of particles results in a strong increase in viscosity and decrease in particle mobility, ultimately driving the system through the glass transition to a disordered solid-like state (Pusey and van Megen, 1986). The approach to the glass transition is accompanied by several distinct features. For example, the non-Gaussian parameter α2 increases as the system approaches the glass transition (Kegel and van Blaaderen, 2000; Marcus et al., 1999; Weeks et al., 2000). Additionally, the system becomes non-ergodic (Cipelletti and Ramos, 2005). In ergodic systems, time averages are equivalent to ensemble averages. For example, to measure probe diffusion in cells, one could either track a probe in a single cell over a very long time and average over all times, or track many probes in different cells over a short time and average over all probes. The two methods produce the same result if the system is ergodic. Non-ergodicity can arise from caging or aging phenomena, where the probe becomes trapped in a given region or the system slowly moves from one region of configuration space to another.

If the cytoplasm were ergodic, we would expect ensemble-averaged MSDs of many GFP-μNS trajectories to coincide with the time-averaged MSD of a single trajectory. Obtaining the time-averaged MSD of a trajectory in a single cell with sufficient statistics for this comparison requires acquisition of an extremely long trajectory, which was not possible for GFP-μNS particles due to technical limitations (photobleaching and phototoxicity). Instead, we compared ensemble-averaged MSDs with an MSD (MSDτ) that is both time- and ensemble-averaged (see SI). If the system were ergodic, MSD and MSDτ would be equivalent. We found relatively close agreement between the MSD and its corresponding MSDτ for GFP-μNS particles in untreated cells (Fig. 4C), except perhaps for the largest particles. However, in DNP-treated cells, MSD and MSDτ were significantly different for all particle sizes, and this difference was greatest for the largest GFP-μNS particles (Fig. 4D). We defined a parameter γ to measure the difference between the MSD and MSDτ (see SI), with γ = 0 indicating equivalency between MSD and MSDτ. For GFP-μNS particles in metabolically active cells, γ fluctuated near zero except for GFP-μNS particles of the largest size bin (Fig. 4E). However, under metabolic depletion, γ grew in response to increasing GFP-μNS particle size (Fig. 4E). These differences cannot be explained by the finite number of trajectories or their limited duration (see SI). These results suggest that the bacterial cytoplasm becomes increasingly non-ergodic with both energy depletion and increasing particle size.

The cytoplasm displays dynamic heterogeneity

While non-Gaussian statistics and ergodicity breaking are consistent with glassy dynamics, a hallmark of glassy systems is dynamic heterogeneity, which is characterized by regions of high particle mobility coexisting with regions of low particle mobility (Berthier, 2011). Due to crowding, particles in colloidal suspensions can become trapped by their nearest neighbors, resulting in small random displacements of the particles. Over longer times, the “cage” formed by their neighbors can spontaneously rearrange through collective motion, allowing the particles to escape with large displacements. Particles in regions with different cage rearrangement times will exhibit different dynamics.

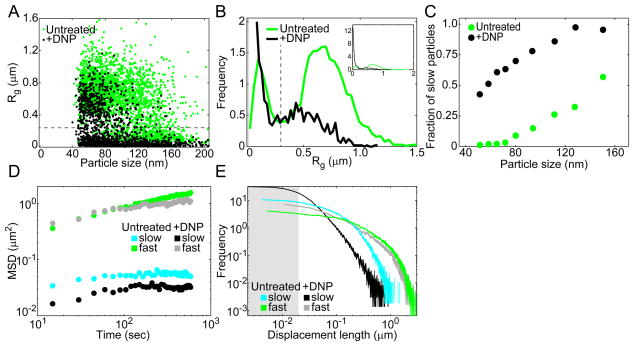
To examine whether heterogeneity in particle dynamics exists in the GFP-μNS tracking experiments, we plotted Rg measurements of individual GFP-μNS trajectories as a function of particle size (Fig. 5A). Interestingly, the Rg values split GFP-μNS particles into two distinct subpopulations at an Rg value of 0.3 μm, irrespective of particle size or metabolic state of the cell. This can be easily seen in the distributions of Rg (Fig. 5B). Because Rg is a measure of how much space a particle explores on average, we will refer to the two populations as “slow” (Rg < 0.3 μm) and “fast” (Rg > 0.3 μm) particles. While fast and slow particles were found in both active and inactive cell populations, their fraction differed, with the fraction of slow particles being low in the active (untreated) cell population and high in the inactive (+DNP) cell population (Fig. 5B). This trend was observed across the 9 bins of particle sizes (Fig. 5C). Thus, the fraction of slow and fast particles appears to be the primary reason for the difference in dynamics between active and inactive cells. Note that the presence of fast particles in the DNP-treated cell population was not due to cell growth by DNP-resistant cells, as no DNP-treated cells (out of 4 × 109 cells) were able to form a colony after overnight incubation.

Figure 5. Two subpopulations of GFP-μNS particles exist in both active and inactive cells.

Figure 5

Open in a new tab

(A) Radius of gyration (Rg) of individual trajectories is plotted as a function of GFP-μNS particle size for E. coli cells (CJW4617) under untreated and DNP-treated conditions. The horizontal dashed line delimits slow (Rg<0.3 μm) and fast (Rg>0.3 μm) particles.

(B) Histogram of Rg for cells under untreated and DNP-treated conditions. The vertical dashed line delimits slow (Rg<0.3 μm) and fast (Rg>0.3 μm) particles. The gray shading delineates the estimated tracking error.

(C) Fraction of slow particles (Rg<0.3 μm) for trajectories in each size bin for cells with or without DNP treatment.

(D) MSD of slow (Rg<0.3 μm) and fast (Rg>0.3 μm) GFP-μNS particles.

(E) Distribution of displacements for slow (Rg<0.3 μm) and fast (Rg>0.3 μm) GFP-μNS particles under untreated and DNP-treated conditions. The line width indicates Poisson counting error, and the gray shading delineates the estimated tracking error.

The slow and fast particle populations from both active and inactive cells exhibited markedly different behavior, as evident from their MSDs (Fig. 5D) and displacement distributions (Fig. 5E). Fast particles not only explored more cytoplasmic space on average, but did so with displacements from distributions shifted toward longer lengths. Most striking was the observation that fast particles from both untreated and DNP-treated conditions behave similarly, with virtually overlapping MSDs and displacement length distributions (Fig. 5D–E). Although not to the same degree, the behavior of slow particles was also close between metabolically active and energy-depleted conditions. This suggests that particles from the fast population and to a lesser extent particles from the slow population experience a similar local environment regardless of metabolic status.

The difference in particle dynamics (slow and fast) may reflect dynamic heterogeneity within the cytoplasm. Similar to glass-forming liquids, the slow particles would be caged by neighboring macromolecules and have a low probability of escape, whereas the probability of escape through collective rearrangement of neighboring macromolecules would be greatly increased for fast particles. The collective effect of all ongoing metabolic activities in active cells would facilitate cage turnover, which would explain the observed higher fraction of fast particles in active cells (Fig. 5B–C). Alternatively, the two populations in particle dynamics may stem from heterogeneity among cells: some cells would have slow particles while others would have fast particles. In this latter case, two particles in the same cell would always behave similarly (slow or fast), whereas in the first scenario (heterogeneity within the cytoplasm), slow and fast dynamics could co-exist in a single cell. To test this, we sought to identify instances of cells containing two particles of similar size (within 10%). Cells with two GFP-μNS foci were rare and tended to be observed only under greater induction conditions of GFP-μNS synthesis, which led to larger and thus slower particles. Despite the bias toward slower particles, we still found that fast (Rg > 0.3 μm) particles could coexist with slow (Rg < 0.3 μm) particles (Fig. 6A–B), arguing that the difference in dynamics primarily comes from dynamic heterogeneity within the cytoplasm of individual cells.

Figure 6. Double-particle tracking and correlation of displacements are consistent with dynamic heterogeneity in the cytoplasm.

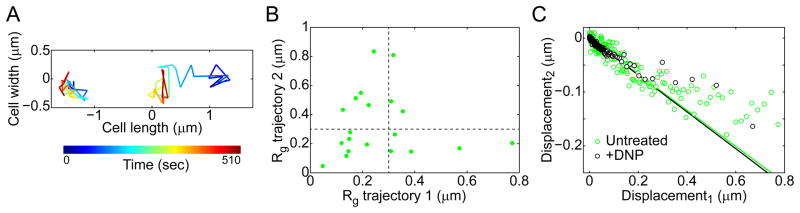
Figure 6

Open in a new tab

(A) Example of two-dimensional trajectories of two GFP-μNS particles in a single E. coli cell (CJW4617). The trajectory of the left particle has a radius of gyration Rg = 0.12 μm and the particle has an estimated size d = 144 nm, while Rg = 0.43 μm and d = 158 nm for the right particle.

(B) Radius of gyration (Rg) of individual trajectories for pairs of GFP-μNS particles in individual E. coli cells (CJW4617) under metabolically active conditions. Only the results for particle pairs with a difference of particle size of less than 10% are shown. The horizontal dashed line delimits slow (Rg<0.3 μm) and fast (Rg>0.3 μm) particles.

(C) Plot showing the average displacement length (displacement2) following an initial displacement (displacement1) of a given length for GFP-μNS particles in E. coli cells (CJW4617) under untreated and DNP-treated conditions. The second displacement was signed positive if it was in the same direction as the initial displacement and negative otherwise. Each point represents the average of 700 displacements. Solid lines represent the best fit (displacement2 = − 0.34 displacement1) to the data where displacement1 < 0.2 μm. The time interval is 15 sec.

Local caging is mitigated by cellular metabolism

In dense colloidal suspensions, local caging is evident in correlation analysis of consecutive displacements (Doliwa and Heuer, 1998; Weeks and Weitz, 2002). For small displacements, the local caging results in a negative linear correlation between consecutive displacements. The linear relationship does not hold for longer displacements, which indicates the escape of the particle from its cage, presumably through collective rearrangement of its neighbors. To examine whether the dynamics of GFP-μNS particles are linked to caging, we calculated the average displacement length following an initial displacement of a given length (signed positive if the second displacement was in the same direction as the initial displacement and negative otherwise). An object trapped in a container with perfectly reflecting walls exhibits an apparent negative correlation between two subsequent steps with a correlation coefficient c = −0.5 (Doliwa and Heuer, 1998). If the object has a non-zero probability of escaping the cage, the correlation coefficient is expected to be between 0 and −0.5. For small initial displacements (< 200 nm), we observed a strong negative correlation (c = −0.34 for both untreated and DNPtreated cells; Fig. 6C), in agreement with local caging. Around 250 nm, this linear relationship breaks, consistent with cage escape. The break in linearity provides an estimation of the cage size (Weeks and Weitz, 2002). The higher number of displacements above 250 nm in untreated cells than in DNP-treated cells (reflected by the greater number of data points > 250 nm in Fig. 6C) suggests more frequent cage escape and thus higher cage turnover under metabolically active conditions, consistent with the greater proportion of fast particles in the active cell population (Fig. 5B–C). This result suggests that cellular metabolism facilitates long-distance motion by increasing cage rearrangement (see Discussion).

DISCUSSION

Our findings fundamentally alter the way we view the bacterial cytoplasm. We show that at a certain size scale (ca. ≥ 30 nm), the bacterial cytoplasm behaves differently from a simple (viscous) fluid. Instead, it displays striking features (such as non-Gaussian distributions of displacements with long tails, non-ergodicity, caging, and dynamic heterogeneity; Figs. 4B, 4E, 5A, 6) that are characteristic of colloidal glasses (Cipelletti and Ramos, 2005; Hunter and Weeks, 2012). The cytoplasm behaves as a liquid for small particles while it increasingly behaves as a glass-forming liquid approaching the glass transition with increasing particle size. This size dependence provides an explanation for previous, seemingly conflicting reports of normal and anomalous diffusion (see SI, Fig. S6E–G). In dense colloidal suspensions containing particles of two sizes, the smaller particle can be mobile, perceiving the environment as a liquid, while the larger one can display glassy dynamics (Zaccarelli et al., 2005). This is in line with the size-dependent dynamics that we observed for GFP-μNS particles. As their size increases, GFP-μNS particles would become increasingly constrained by other surrounding components of the cytoplasm.

Remarkably, the glassy dynamics are partially suppressed by metabolic activity in a size-dependent manner. In other words, our data suggest that cellular metabolism enhances the motion of cytoplasmic components by ‘fluidizing’ the cytoplasm, and this effect increases with component size.

What is the origin of the glassy behavior?

Aspects of glassiness have been reported in eukaryotic cells, but have been attributed to the mechanical response of their extensive cytoskeletal network (Fabry et al., 2001). Bacteria lack such a pervasive cytoskeletal meshwork and its associated motors. However, the bacterial cytoplasm is more similar to colloidal glasses by being more crowded than the eukaryotic cytoplasm based on the diffusion coefficient of free GFP being about three times smaller in E. coli than in eukaryotic cells (Elowitz et al., 1999; Swaminathan et al., 1997). Since crowding in dense colloidal suspensions is responsible for their glassy dynamics, it is likely that the glassy behavior of the bacterial cytoplasm originates from its extreme crowding (Cayley et al., 1991; Zimmerman and Trach, 1991). While measuring crowding inside bacterial cells is technically difficult and subject to uncertainties, estimates suggest that macromolecules occupy 20 to 40% of the bacterial cytoplasm (Cayley et al., 1991; Zimmerman and Trach, 1991). An additional ~20% of the cytoplasm consists of “bound” water, presumably as a hydration layer to macromolecules (Cayley et al., 1991), suggesting that the total excluded volume may range between 40 and 60%. Colloidal suspensions can exhibit glassy dynamics over a wide range of volume fractions depending on the properties of the system. For example, monodisperse suspensions of non-interactive colloidal particles vitrify at volume fractions near 58% (Hunter and Weeks, 2012). Importantly, elements of glassy dynamics are observable at lower (e.g. 45%) volume fractions (Kegel and van Blaaderen, 2000; Weeks et al., 2000). If the colloidal particles are interacting, glassy dynamics can occur at even lower volume fractions (Dawson, 2002). Furthermore, glass transition occurs at lower density in a confined geometry (Fehr and Lowen, 1995).

How can cellular metabolism fluidize the cytoplasm to enhance motion?

The nucleoid affects the distribution of large components (Coquel et al., 2013), and the dynamics of individual chromosomal loci change with ATP depletion (Weber et al., 2012). However, we found that metabolic depletion results in the confinement of both GFP-μNS and mini-RK2 plasmids, even when they are located in the large DNA-depleted regions of filamentous dnaC2 cells (Figs. 2D–E and S2B). Thus, DNA dynamics, DNA-related processes (e.g., transcription) or agitation of the DNA mesh from DNA-associated activities cannot be the driving factor underlying metabolism-dependent motion and the proposed increase in cage turnover in active cells. We also ruled out a predominant role for MreB (Fig. S3B) or FtsZ (Figs. 2D–E and S2B, note that filamentous dnaC2 cells do not make FtsZ rings). Inhibiting translation or peptidoglycan synthesis had little, if any, measurable effect on metabolism-dependent motion (Figs. S3C, E). This suggests that any of these processes cannot alone account for the observed metabolism-dependent motion. However, there are a multitude of cellular processes occurring simultaneously inside metabolically active cells. We envision that these processes collectively promote cage turnover, as opposed to a single process being solely responsible.

How could cellular activities collectively increase cage turnover? Spitzer and Poolman argued that from a physical chemistry perspective, hydrophobic and screened electrostatic interactions, together with macromolecular crowding, must result in the formation of overcrowded regions of macromolecules separated by a more-fluid phase of less crowded cytosol (nanopools) (Spitzer, 2011; Spitzer and Poolman, 2009). Their theory also stipulates that metabolic reactions, by altering the hydrophobicity and charge of molecules, would continuously remodel the topology of nanopools and overcrowded regions within the cytoplasm. Following this view, it is conceivable that large particles would become caged in the overcrowded regions or nanopools, and that the metabolism-dependent rearrangement of these domains would promote their long-range motion. A second, non-exclusive way by which metabolism could promote cage turnover does not require microphase separation, and is based on the notion that cellular activities cause agitations to the system. A remarkable property of liquids near a glass transition is that small changes in the system can dramatically modify its fluidity. In a colloidal glass, particles are caged by surrounding neighbors. However, agitation can fluidize the system by increasing the rate of cage rearrangements (Petekidis et al., 2002). We provide evidence that cellular metabolism promotes cytoplasmic fluidization (Figs. 1–5) and uncaging (Fig. 6C). Metabolic activity can cause a variety of perturbations (conformational changes, fluid displacements, non-equilibrium fluctuations, etc.), that collectively influence cage rearrangement, allowing cage escape and long-distance motion. When all metabolic activities are abolished, rearrangement of the local domain (cage) would become rare (as in non-living glassy materials), leading to particle confinement.

What are the biological implications?

Current models of bacterial processes generally consider the cytoplasm as a simple fluid. However, even in active cells, the cytoplasm retains glassy features in a component size-dependent manner (Figs. 4B, 5A–C, and 6C). Based on our rough critical size estimation, we expect that cytoplasmic constituents ≥ 30 nm will be subject to metabolism-dependent motion. This implies that proteins, which typically have a size < 10 nm, will not be affected, consistent with the minimal effect of DNP on the apparent diffusion of free GFP in C. crescentus (Montero Llopis et al., 2012). However, larger cellular components such as plasmids (Fig. 1D–E), protein filaments (Fig. 1A–C), storage granules (Fig. S2A) and the multitude of other large components populating the cytoplasm (e.g., polyribosomes, chromosomes, enzymatic megacomplexes, intracellular organelles, phage capsids and genomes, microcompartments, etc.) will be impacted by the glassy behavior of the cytoplasm and the metabolic state of the cell. Many of these large components are involved in processes that are essential for life and fitness in natural environments and their functions depend on their ability to move in the cytoplasm. For example, while the origin region of the chromosome segregates via an active mechanism, the bulk of the chromosome has been proposed to partition passively through an entropy-driven mechanism (Jun and Wright, 2010) that implies diffusion. Similarly, multi-copy plasmids and some storage granules require motion for their partitioning (which is essential for their propagation). Low-copy plasmids typically have a dedicated partitioning system, but even then, some plasmid partitioning systems have been proposed to rely on an active diffusion-ratchet mechanism (Hwang et al., 2013; Vecchiarelli et al., 2013) in which plasmid diffusion is an essential element. We even expect phages to be impacted by the physical nature of the cytoplasm as the assembly of their genomes and capsids depends on their ability to interact.

Our data suggest that cellular metabolism fluidizes the cytoplasm, allowing larger cellular components to escape local environments and sample cytoplasmic space that they otherwise could not. This metabolism-induced fluidization may help the cell achieve the delicate balance of attaining extremely high concentrations of biomolecules (to increase metabolism and cell proliferation) without severely compromising macromolecular motion. Ultimately, during the course of evolution, the glassy properties of the cytoplasm may have set upper limits to the size of molecular components and the degree of molecular crowding a cell can have. Higher crowding could result in particles of smaller sizes (such as proteins) ‘perceiving’ the cytoplasm as more glass-like, severely impacting biochemical reactions. Consistent with this idea, the mobility of free GFP becomes disproportionally reduced compared to a smaller molecule (e.g., glucose derivative) when high osmotic stress increases cytoplasmic crowding (Mika et al., 2010).

Another interesting outcome of the metabolic effect on cytoplasmic fluidity is that fluctuations in the environment can modulate cytoplasmic dynamics by affecting metabolism. Metabolic dormancy is widespread in the wild; for example, the fraction of quiescent cells ranges from 20% in the human gut to over 80% in soil samples (Lennon and Jones, 2011). Dormancy has generated considerable interest in the scientific community, notably because of its links to both pathogenesis and antibiotic resistance (Coates, 2003). Dormancy is a survival strategy that bacteria in both environmental and clinical settings use to respond to stress such as starvation, antibiotic exposure, and high cell density (Lennon and Jones, 2011). We show that the motion of large components drops under metabolic depletion, and this occurs under natural conditions such as prolonged carbon starvation and late stationary phase (Fig. 1B–C). This implies that the fluidity of the cytoplasm in dormant cells is very different compared to active cells, a difference that has not, to our knowledge, been considered. It would be interesting to examine in the future whether the vitrification of the dormant cytoplasm helps preserve subcellular architecture during quiescent periods, while still allowing diffusion of proteins and metabolites to permit a quick restart of growth when conditions improve.

EXPERIMENTAL PROCEDURES

Strains, plasmids and growth conditions

A list of strains and methods of construction is provided in Table S1 of the Supporting Information (SI). Exponentially growing cell cultures were used in all experiments (OD600 ≤ 0.3 for E. coli and OD660 ≤ 0.25 for C. crescentus), except where noted.

C. crescentus strains were grown at 30°C in defined minimal M2G medium (Ely, 1991), and supplemented with antibiotics when appropriate.

E. coli strain JP924 was grown at 30°C in M9 glycerol medium supplemented with casamino acids (M9G), 50 μg/mL of ampicillin and 2 μg/mL of chloramphenicol. GFP-LacI expression was accomplished by spotting cells on agarose pads containing a concentration gradient of L-arabinose prior to imaging. CJW4386 (carrying dnaC2) was grown at 30°C in M9G, 50 μg/mL ampicillin and 2 μg/mL chloramphenicol. Ninety minutes prior to imaging, the culture was shifted to 37°C, and L-arabinose was added (to a final concentration of 0.02%) 45 min prior to imaging.

E. coli strains CJW4617 and CJW4619 were grown at 30°C in M9G supplemented with 50 μg/mL kanamycin. GFP-μNS synthesis was induced by addition of isopropyl β-D-1-thiogalactopyranoside (IPTG) to 50–200 μM. After 30–120 min at 30°C, induction was stopped by washing cells into IPTG-free M9G medium. CJW4619 (carrying dnaC2) cells were incubated at 37°C for 2–3 h to obtain filamentous cells.

Light microscopy

Cells were imaged on agarose-padded slides supplemented with indicated media; see SI for further details. Cell outlines were obtained from phase contrast images using open source software MicrobeTracker (Sliusarenko et al., 2011). Fluorescent spots were detected and tracked using SpotFinder (Sliusarenko et al., 2011) and custom-built scripts in Matlab (The MathWorks Inc.) as described in SI.

Supplementary Material

01
02
Download video file (2.9MB, mp4)
03
Download video file (2.7MB, mp4)
04
Download video file (1.7MB, mp4)
05
Download video file (2MB, mp4)
06
Download video file (1.4MB, mp4)
07
Download video file (1.6MB, mp4)
08
Download video file (2.3MB, mp4)
09

HIGHLIGHTS.

  • The motion of large cytosolic components is drastically reduced upon metabolic arrest.

  • Dynamics and apparent fluidity of the cytosol depend on metabolism and particle size

  • The bacterial cytoplasm displays properties characteristic of glass-forming liquids. Research Highlights (for ACCEPTED papers only)

Acknowledgments

We are grateful to Jason Hocking for the construction of strains CJW4617 and CJW4619. We thank Dr. Anuradha Janakiraman, Dr. Max Nibert and Dr. Cammie Lesser for providing the template for the construction of the IPTG-inducible allele that encodes GFP-μNS. We also thank Dr. Joe Pogliano for providing JP924 strain, and Dr. Manuel Campos for sharing the information about nucleoid expansion in response to DNP treatment. We also thank all members of the Jacobs-Wagner lab for critical reading of the manuscript and for fruitful discussions. B.R. Parry was in part supported by the National Institutes of Health (T32HG 003198). This work was supported by the National Institutes of Health (GM065835 to C.J.-W.). C.J.-W. is a Howard Hughes Medical Institute investigator.

Footnotes

SUPPORTING INFORMATION

Procedures used for imaging, strains construction, single-particle tracking, trajectory analysis, tracking precision estimation, image analysis, parameter determination (Rg, MSD, MSDτ, α2, γ), and particle size estimation are described in SI. Additionally, SI includes supplementary figures and their legends, supplementary results, the strain table and relevant references.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errorsmaybe discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Ausmees N, Kuhn JR, Jacobs-Wagner C. The bacterial cytoskeleton: an intermediate filament-like function in cell shape. Cell. 2003;115:705–713. doi: 10.1016/s0092-8674(03)00935-8. [DOI] [PubMed] [Google Scholar]
  2. Bakshi S, Bratton BP, Weisshaar JC. Subdiffraction-limit study of Kaede diffusion and spatial distribution in live Escherichia coli. Biophys J. 2011;101:2535–2544. doi: 10.1016/j.bpj.2011.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berthier L. Dynamic heterogeneity in amorphous materials. Physics. 2011;4:42. [Google Scholar]
  4. Brangwynne CP, Koenderink GH, MacKintosh FC, Weitz DA. Intracellular transport by active diffusion. Trends Cell Biol. 2009;19:423–427. doi: 10.1016/j.tcb.2009.04.004. [DOI] [PubMed] [Google Scholar]
  5. Broering TJ, Arnold MM, Miller CL, Hurt JA, Joyce PL, Nibert ML. Carboxyl-proximal regions of reovirus nonstructural protein muNS necessary and sufficient for forming factory-like inclusions. J Virol. 2005;79:6194–6206. doi: 10.1128/JVI.79.10.6194-6206.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Broering TJ, Parker JS, Joyce PL, Kim J, Nibert ML. Mammalian reovirus nonstructural protein microNS forms large inclusions and colocalizes with reovirus microtubule-associated protein micro2 in transfected cells. J Virol. 2002;76:8285–8297. doi: 10.1128/JVI.76.16.8285-8297.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cabeen MT, Charbon G, Vollmer W, Born P, Ausmees N, Weibel DB, Jacobs-Wagner C. Bacterial cell curvature through mechanical control of cell growth. EMBO J. 2009;28:1208–1219. doi: 10.1038/emboj.2009.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cabeen MT, Murolo MA, Briegel A, Bui NK, Vollmer W, Ausmees N, Jensen GJ, Jacobs-Wagner C. Mutations in the Lipopolysaccharide biosynthesis pathway interfere with crescentin-mediated cell curvature in Caulobacter crescentus. J Bacteriol. 2010;192:3368–3378. doi: 10.1128/JB.01371-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cayley S, Lewis BA, Guttman HJ, Record MT., Jr Characterization of the cytoplasm of Escherichia coli K-12 as a function of external osmolarity. Implications for protein-DNA interactions in vivo. J Mol Biol. 1991;222:281–300. doi: 10.1016/0022-2836(91)90212-o. [DOI] [PubMed] [Google Scholar]
  10. Cipelletti L, Ramos L. Slow dynamics in glassy soft matter. J Phys Condens Mat. 2005;17:R253–R285. [Google Scholar]
  11. Coates ARM. Dormancy and low-growth states in microbial disease. Cambridge; New York: Cambridge University Press; 2003. [Google Scholar]
  12. Coquel AS, Jacob JP, Primet M, Demarez A, Dimiccoli M, Julou T, Moisan L, Lindner AB, Berry H. Localization of protein aggregation in Escherichia coli is governed by diffusion and nucleoid macromolecular crowding effect. PLoS Comp Biol. 2013;9:e1003038. doi: 10.1371/journal.pcbi.1003038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dawson KA. The glass paradigm for colloidal glasses, gels, and other arrested states driven by attractive interactions. Curr Opin Coll Int Sci. 2002;7:218–227. [Google Scholar]
  14. Derman AI, Lim-Fong G, Pogliano J. Intracellular mobility of plasmid DNA is limited by the ParA family of partitioning systems. Mol Microbiol. 2008;67:935–946. doi: 10.1111/j.1365-2958.2007.06066.x. [DOI] [PubMed] [Google Scholar]
  15. Dix JA, Verkman AS. Crowding effects on diffusion in solutions and cells. Ann Rev Biophys. 2008;37:247–263. doi: 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
  16. Doliwa B, Heuer A. Cage effect, local anisotropies, and dynamic heterogeneities at the glass transition: A computer study of hard spheres. Phys Rev Lett. 1998;80:4915–4918. [Google Scholar]
  17. Elowitz MB, Surette MG, Wolf PE, Stock JB, Leibler S. Protein mobility in the cytoplasm of Escherichia coli. J Bacteriol. 1999;181:197–203. doi: 10.1128/jb.181.1.197-203.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Ely B. Genetics of Caulobacter crescentus. Meth Enzymol. 1991;204:372–384. doi: 10.1016/0076-6879(91)04019-k. [DOI] [PubMed] [Google Scholar]
  19. English BP, Hauryliuk V, Sanamrad A, Tankov S, Dekker NH, Elf J. Single-molecule investigations of the stringent response machinery in living bacterial cells. Proc Nat Acad Sci USA. 2011;108:E365–E373. doi: 10.1073/pnas.1102255108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ. Scaling the microrheology of living cells. Phys Rev Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
  21. Fehr T, Lowen H. Glass-transition in confined geometry. Phys Rev E. 1995;52:4016–4025. doi: 10.1103/physreve.52.4016. [DOI] [PubMed] [Google Scholar]
  22. Golding I, Cox EC. Physical nature of bacterial cytoplasm. Phys Rev Lett. 2006;96:098102. doi: 10.1103/PhysRevLett.96.098102. [DOI] [PubMed] [Google Scholar]
  23. Heun P, Laroche T, Shimada K, Furrer P, Gasser SM. Chromosome dynamics in the yeast interphase nucleus. Science. 2001;294:2181–2186. doi: 10.1126/science.1065366. [DOI] [PubMed] [Google Scholar]
  24. Hunter GL, Weeks ER. The physics of the colloidal glass transition. Rep Prog Phys. 2012;75:066501. doi: 10.1088/0034-4885/75/6/066501. [DOI] [PubMed] [Google Scholar]
  25. Hwang LC, Vecchiarelli AG, Han YW, Mizuuchi M, Harada Y, Funnell BE, Mizuuchi K. ParA-mediated plasmid partition driven by protein pattern self-organization. EMBO J. 2013;32:1238–49. doi: 10.1038/emboj.2013.34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Jun S, Wright A. Entropy as the driver of chromosome segregation. Nat Rev Microbiol. 2010;8:600–607. doi: 10.1038/nrmicro2391. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kegel WK, van Blaaderen A. Direct observation of dynamical heterogeneities in colloidal hard-sphere suspensions. Science. 2000;287:290–293. doi: 10.1126/science.287.5451.290. [DOI] [PubMed] [Google Scholar]
  28. Latulippe DR, Zydney AL. Radius of gyration of plasmid DNA isoforms from static light scattering. Biotechnol Bioeng. 2010;107:134–142. doi: 10.1002/bit.22787. [DOI] [PubMed] [Google Scholar]
  29. Lennon JT, Jones SE. Microbial seed banks: the ecological and evolutionary implications of dormancy. Nat Rev Microbiol. 2011;9:119–130. doi: 10.1038/nrmicro2504. [DOI] [PubMed] [Google Scholar]
  30. Levi V, Ruan Q, Plutz M, Belmont AS, Gratton E. Chromatin dynamics in interphase cells revealed by tracking in a two-photon excitation microscope. Biophys J. 2005;89:4275–4285. doi: 10.1529/biophysj.105.066670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Maehara A, Taguchi S, Nishiyama T, Yamane T, Doi Y. A repressor protein, PhaR, regulates polyhydroxyalkanoate (PHA) synthesis via its direct tnteraction with PHA. J Bacteriol. 2002;184:3992–4002. doi: 10.1128/JB.184.14.3992-4002.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Marcus AH, Schofield J, Rice SA. Experimental observations of non-Gaussian behavior and stringlike cooperative dynamics in concentrated quasi-two-dimensional colloidal liquids. Phys Rev E. 1999;60:5725–5736. doi: 10.1103/physreve.60.5725. [DOI] [PubMed] [Google Scholar]
  33. Mika JT, van den Bogaart G, Veenhoff L, Krasnikov V, Poolman B. Molecular sieving properties of the cytoplasm of Escherichia coli and consequences of osmotic stress. Mol Microbiol. 2010;77:200–207. doi: 10.1111/j.1365-2958.2010.07201.x. [DOI] [PubMed] [Google Scholar]
  34. Montero Llopis P, Sliusarenko O, Heinritz J, Jacobs-Wagner C. In vivo biochemistry in bacterial cells using FRAP: insight into the translation cycle. Biophys J. 2012;103:1848–1859. doi: 10.1016/j.bpj.2012.09.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Nenninger A, Mastroianni G, Mullineaux CW. Size dependence of protein diffusion in the cytoplasm of Escherichia coli. J Bacteriol. 2010;192:4535–4540. doi: 10.1128/JB.00284-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Niu L, Yu J. Investigating intracellular dynamics of FtsZ cytoskeleton with photoactivation singlemolecule tracking. Biophys J. 2008;95:2009–2016. doi: 10.1529/biophysj.108.128751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Petekidis G, Moussaid A, Pusey PN. Rearrangements in hard-sphere glasses under oscillatory shear strain. Phys Rev E. 2002;66:051402. doi: 10.1103/PhysRevE.66.051402. [DOI] [PubMed] [Google Scholar]
  38. Pusey PN, van Megen W. Phase-behavior of concentrated suspensions of nearly hard colloidal spheres. Nature. 1986;320:340–342. [Google Scholar]
  39. Qi QS, Rehm BHA. Polyhydroxybutyrate biosynthesis in Caulobacter crescentus: molecular characterization of the polyhydroxybutyrate synthase. Microbiol. 2001;147:3353–3358. doi: 10.1099/00221287-147-12-3353. [DOI] [PubMed] [Google Scholar]
  40. Sliusarenko O, Heinritz J, Emonet T, Jacobs-Wagner C. High-throughput, subpixel precision analysis of bacterial morphogenesis and intracellular spatio-temporal dynamics. Mol Microbiol. 2011;80:612–627. doi: 10.1111/j.1365-2958.2011.07579.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Soutoglou E, Misteli T. Mobility and immobility of chromatin in transcription and genome stability. Curr Opin Gen Dev. 2007;17:435–442. doi: 10.1016/j.gde.2007.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Spitzer J. From water and ions to crowded biomacromolecules: in vivo structuring of a prokaryotic cell. Microbiol Mol Biol Rev. 2011;75:491–506. doi: 10.1128/MMBR.00010-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Spitzer J, Poolman B. The role of biomacromolecular crowding, ionic strength, and physicochemical gradients in the complexities of life’s emergence. Microbiol Mol Biol Rev. 2009;73:371–388. doi: 10.1128/MMBR.00010-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Swaminathan R, Hoang CP, Verkman AS. Photobleaching recovery and anisotropy decay of green fluorescent protein GFP-S65T in solution and cells: cytoplasmic viscosity probed by green fluorescent protein translational and rotational diffusion. Biophys J. 1997;72:1900–1907. doi: 10.1016/S0006-3495(97)78835-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Vecchiarelli AG, Hwang LC, Mizuuchi K. Cell-free study of F plasmid partition provides evidence for cargo transport by a diffusion-ratchet mechanism. Proc Nat Acad Sci USA. 2013;110:E1390–7. doi: 10.1073/pnas.1302745110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Weber SC, Spakowitz AJ, Theriot JA. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys Rev Lett. 2010;104:238102. doi: 10.1103/PhysRevLett.104.238102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Weber SC, Spakowitz AJ, Theriot JA. Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc Nat Acad Sci USA. 2012;109:7338–7343. doi: 10.1073/pnas.1119505109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Weeks E, Weitz D. Properties of cage rearrangements observed near the colloidal glass transition. Phys Rev Lett. 2002;89:095704. doi: 10.1103/PhysRevLett.89.095704. [DOI] [PubMed] [Google Scholar]
  49. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science. 2000;287:627–631. doi: 10.1126/science.287.5453.627. [DOI] [PubMed] [Google Scholar]
  50. Zaccarelli E, Mayer C, Asteriadi A, Likos C, Sciortino F, Roovers J, Iatrou H, Hadjichristidis N, Tartaglia P, Löwen H, et al. Tailoring the flow of soft glasses by soft additives. Phys Rev Lett. 2005;95:268301. doi: 10.1103/PhysRevLett.95.268301. [DOI] [PubMed] [Google Scholar]
  51. Zimmerman, Trach Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J Mol Biol. 1991;222:599–620. doi: 10.1016/0022-2836(91)90499-v. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS559716-supplement-01.pdf (12.4MB, pdf)
02
Download video file (2.9MB, mp4)
03
Download video file (2.7MB, mp4)
04
Download video file (1.7MB, mp4)
05
Download video file (2MB, mp4)
06
Download video file (1.4MB, mp4)
07
Download video file (1.6MB, mp4)
08
Download video file (2.3MB, mp4)
09
NIHMS559716-supplement-09.pdf (2.6MB, pdf)

RESOURCES