A novel significance score for gene selection and ranking

Abstract

Motivation: When identifying differentially expressed (DE) genes from high-throughput gene expression measurements, we would like to take both statistical significance (such as P-value) and biological relevance (such as fold change) into consideration. In gene set enrichment analysis (GSEA), a score that can combine fold change and P-value together is needed for better gene ranking.

Results: We defined a gene significance score π-value by combining expression fold change and statistical significance (P-value), and explored its statistical properties. When compared to various existing methods, π-value based approach is more robust in selecting DE genes, with the largest area under curve in its receiver operating characteristic curve. We applied π-value to GSEA and found it comparable to P-value and t-statistic based methods, with added protection against false discovery in certain situations. Finally, in a gene functional study of breast cancer profiles, we showed that using π-value helps elucidating otherwise overlooked important biological functions.

Availability: http://gccri.uthscsa.edu/Pi_Value_Supplementary.asp

Contact: xy@ieee.org, cheny8@uthscsa.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

In this article, we introduce a gene significance score, π-value, for robust selection of differentially expressed (DE) genes, and demonstrate its application in gene set enrichment analysis (GSEA). In developing the concept, we are inspired by two facts. First, there is discrepancy between the statistical and biological meanings of differential expression. Second, a proper score is required to evaluate and rank genes in GSEA.

It was pointed out in McCarthy and Smyth 2009 that statistically speaking, genes showing systematic difference between two conditions are considered DE, whereas in biological term, DE means the difference in gene expression is sufficiently large. In some biological applications, DE genes were selected by gene expression level change (such as using 2-fold change as cutoff), and the variability of gene expression was not taken into account. Meanwhile, some statistical methods consisted of finding ‘informative genes’ whose expression levels correlate with or are predictive of class labels, such as in Ambroise and McLachlan 2002; Golub et al. 1999. These approaches usually found not all DE genes, but a subset of DE genes that distinguished sample classes. To detect all DE genes, we usually conduct hypothesis testing of μ₀ = μ₁ against μ₀ ≠ μ₁ or the like, such as methods based on expression ratio statistic Chen et al., 1997, distinctness by Kolmogorov–Smirnov distance and similarity of expression profiles by Pearson's correlation coefficient Huang et al., 2010, t-statistic and its variants Smyth, 2004; Tusher et al., 2001.

In hypothesis test-based statistical methods, P-value of the test statistic is the basis of gene selection, as a result of which, we face the following two issues:

• The ‘small fold change, small variance’ (SFSV) issue. When a gene's variance is small, a slight expression level change may result in significant P-value and conclusion of statistical significance. However, a small expression change has questionable biological justification, which frequently leads to false discovery.

• The ‘large fold change, large variance’ (LFLV) issue. A gene with considerable fold change (FC) may possess a large variance, such as dysregulated genes in a disease condition. In such a situation, a large expression change may be accompanied by a non-significant P-value, making it possible for us to miss biologically meaningful but highly volatile changes.

Since variance estimation is part of the issues, which is often worsened by small sample size, improvements were proposed to adjust estimated variance, such as SAM test Tusher et al., 2001, empirical Bayes method (moderated t-test) Smyth, 2004 and regularized t-test Baldi and Long, 2001. Nevertheless, even with accurate variance estimation, problem may arise when we select genes solely by P-value resulting from a hypothesis test.

To address the SFSV issue, it is common to combine P-value and FC criteria, such as 2-fold change and P ≤ 0.05. Such approach is ad hoc Cui and Churchill, 2003; Yanofsky and Bickel, 2010. Meanwhile, methods that incorporate or improve the original FC criterion were proposed, such as a better defined FC limit Mutch et al., 2002, a better statistical model Fu et al., 2006, or variable threshold according to intensity measurement Mariani et al., 2003; Yang et al., 2002. Methods that directly incorporate FC criterion into test statistics provide significant improvement to meet the practical needs McCarthy and Smyth, 2009; Montazeri et al., 2010. In McCarthy and Smyth, 2009, TREAT, a hypothesis test relative to a FC threshold, was proposed with H₀: |μ₀ − μ₁| ≤ τ and H₁: |μ₀ − μ₁| > τ. TREAT requires that a threshold τ be chosen prior to the test, and if τ changes, all genes need to be tested again and P-values re-calculated. While TREAT has adequately addressed the SFSV issue, the LFLV issue remains a problem, which is fairly common in human clinical studies where patient-to-patient variation far exceeds that of well-controlled cell culture or animal studies, and better variance estimation does not help Wu et al., 2010.

Motivated by aforementioned difficulties, we propose a gene significance score called π-value, which combines FC and P-value into one score. It provides a decision trade-off between FC and P-value, and offers a new means to rank and select genes. Our unique contributions are as follows: (i) π-value does not introduce any new statistical test, and its computation is simple; (ii) it is convenient to adjust the number of selected DE genes by changing the threshold, and no re-computation is needed; (iii) it addresses both SFSV and LFLV issues. Unlike most existing methods, this approach may retain some genes with large FCs but non-significant P-values, because they may be biologically important and worthy of further investigation; and (iv) π assigns one single score to a gene by its FC and P-value, and thus it is useful in gene ranking and can be naturally applied to GSEA.

2 MATERIALS AND METHODS

2.1 Definition

Given pre-processed and normalized microarray data of two sample classes (C₁ and C₂) corresponding to two biological conditions (such as test and control groups), we assume there are M₁ and M₂ samples under C₁ and C₂, respectively, and N probe sets on each array. Each probe set usually represents a gene, and we will use probe set and gene interchangeably unless specified otherwise. Let g_(k)ij be log₂-transformed expression level of the i-th gene in the j-th sample of class C_k (k = 1, 2), then the entire processed microarray data can be represented in two data matrices, G₁ and G₂, where

Let the mean expression of the i-th gene in sample class C_k be g_(k)i·, then the log-ratio (LR) and log-fold change (LFC) of this gene's expression are denoted as x_i = g_(1)i· − g_(2)i· and φ_i = |g_(1)i· − g_(2)i·|, respectively. In the literature, FC refers to the quantity 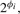and an alternative definition is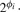

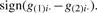
To select DE genes between two sample classes, we can employ one of the following decisions:

1. Correlation decision: selection of genes based on their correlation between expression levels and the corresponding phenotypes.

2. FC decision.

3. P-value decision associated with equal-mean hypothesis test. Usually a t-test or its variants is applied, and when multiple genes are involved, P-values are often adjusted to account for the effect of multiple testings, such as the Benjamini–Hochberg method Benjamini and Hochberg, 1995.

4. Decision cascade: a common ad hoc combination of two or more decisions.

5. A priori information fusion, such as incorporating FC threshold into t-test in TREAT McCarthy and Smyth, 2009.

Here we propose a posteriori information fusion scheme, to combine FC and P-value into one score after their individual evaluation, rather than fuse them earlier. Given φ_i and p_i, LFC and P-value of the i-th gene resulting from a hypothesis test, we define π-value as

(1)

π-value is non-negative, and the larger it is, the more significant gene expression change is. The unique combination of FC and P-value is motivated by our intention to transform P-value by FC, while still maintaining the characteristics of P-value. To see what π suggests, we observe that

(2)

thus 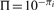can be viewed as a transformed P-value, and 0 ≤ Π ≤ 1. When φ_i = 1, namely 2-fold change, we will have Π = p_i, and Π equals the regular P-value. For φ_i < 1, namely less than 2-fold change, we have Π > p_i and P-value is penalized; for φ_i > 1, namely more than 2-fold change, we have Π < p_i, P-value is enhanced. Therefore, by defining π to be the product of LFC and log-transformed P-value, we adjust gene's statistical significance by the amount of FC. A discussion of decision boundaries of FC, P-value and π-value on volcano plot is provided in Section 2.3. IN Supplementary Materials

In Equation (1), p_i can be P-value from regular t-test, SAM Tusher et al., 2001 or moderated t-test Smyth, 2004. Moreover, π is not tied with specific hypothesis testing; for instance, it can be based on test of variance (such as F-test) or TREAT. Finally, p_i can be raw P-value or adjusted P-value. These facts make π a versatile gene significance score and suited for other applications such as GSEA. In this article, we will simply use P-value of the regular t-test in π.

2.2 Statistical characterization

Assuming LR follows a normal distribution, P-value follows a uniform [0,1] distribution, and LR and P-value are independent, we can show that the probability density function (PDF) of π is (Section 1.1 in Supplementary Materials),

(3)

where λ = ln 10, and σ² is the variance of LR. In reality, LR and P-value are dependent. The distribution of π under independence and dependence assumptions are shown in Figure 1 (simulation details are provided in Section 1.1 in Supplementary Materials). In either case, the PDF of π peaks at 0, decreases monotonically with π and decreases approximately exponentially when π is sufficiently large. The dependent PDF drops less steeply than the independent case, although they have similar trends.

Fig. 1.

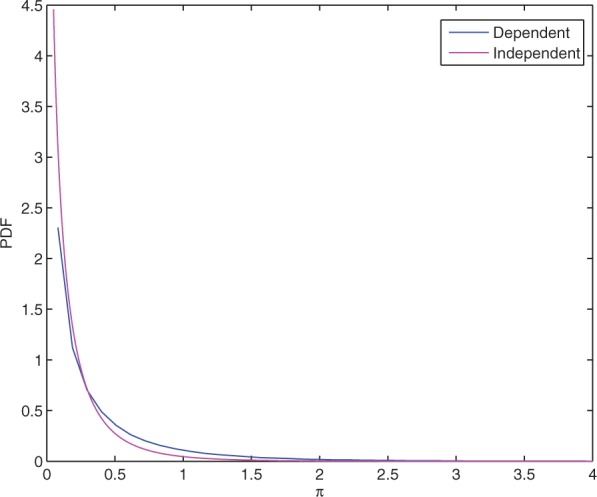
PDF of π when LFC and P-value are dependent (blue) or independent (magenta).

To use π for detecting DE genes at a given significance level α, we need to determine its critical value with respect to α. P-value's distribution does not change by dataset and platform. However, LR follows a normal distribution whose variance σ² can vary by dataset and platform, which impacts the distribution of π as well as critical values. The method of computing critical values under independence or dependence is provided in the Supplementary Materials. Table 1 shows an example of the critical values of π with respect to different α's under the independence and dependence assumptions (σ = 0.48 for the LR), respectively, and the simulation details are in the Supplementary Materials. Table 1 is not a generalized result, but rather a demonstration of the difference between the dependence and independence conditions. We have implemented a significance assessment tool for dependence condition given any input microarray dataset (Supplementary Material).

Table 1.

CV of π under dependence or independence

α	CVdep	CVind	α	CVdep	CVind
0.2	0.4079	0.2572	0.001	3.8434	2.1281
0.1	0.7319	0.4292	0.0005	4.4122	2.4503
0.05	1.1082	0.6274	0.0002	5.1559	2.8988
0.02	1.6657	0.9246	0.0001	5.7964	3.2543
0.01	2.1270	1.1733	0.0001	6.4407	3.6233
0.005	2.6138	1.4408	0.00002	7.1713	4.1308
0.002	3.2939	1.8213	0.00001	7.7298	4.5291

CV, critical value.

2.3 GSEA

In the original GSEA Subramaniana et al., 2005, a set of genes are first ranked by P-value or FC, then a Kolmogorov–Smirnov test is performed to evaluate the significance of differential expression as a whole set. Later, generalized GSEA methods were developed Ackermann and Strimmer, 2009; Jiang and Gentleman, 2007, such as in Tian et al. 2005, where a t-statistic based enrichment score (ES) is suggested for a set of n genes,

(4)

where N is the total number of genes, and I_i is an indicator function, with 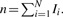Similarly, we can use P-value for enrichment score. To follow the convention that a larger score indicates higher enrichment, we can define

(5)

A discussion of ES_t and ES_p is provided in Section 1.3 in Supplementary Materials.

π-value can be employed in GSEA in two ways: the first is to use the original GSEA method, but rank genes by π-value instead of P-value or FC; and the second is to use generalized GSEA by defining

(6)

Whichever GSEA method we adopt, π-value-based algorithm has the advantage of combining FC and P-value information.

In generalized GSEA, a gene set is considered enriched if the statistical significance (P-value) of its enrichment score is below a threshold, and a method to compute P-value of ES is provided in Algorithm S4 of the Supplementary Materials.

2.4 Data resampling methods

Given a gene expression dataset, which usually contains both non-DE and DE genes, it is useful to extract or generate a dataset that satisfies null hypothesis, called background data or null data. Null data can be used for obtaining the empirical distribution and critical values of π-value, for instance. We can also impose differential expression on pre-chosen genes on the null data, and regard the pre-chosen DE genes as the ground truth. This technique is useful in evaluating the performance of gene selection criterion where true DE genes must be known in order to compute sensitivity and FDR. Two algorithms are developed for generating background data from a real dataset. The first algorithm, maResampling, is based on resampling and suitable for large unbalanced samples. The second one, maBootstrapping, is a parameterized bootstrapping scheme for small or large balanced samples. They are listed as Algorithms S2 and S3 in the Supplementary Materials.

2.5 Datasets

Dataset 1 (Breast Cancer Data): a total of 286 lymph node-negative primary breast cancer samples (GSE2034) described in Wang et al. 2005 were downloaded from GEO (http://www.ncbi.nih.gov/geo), and more details are provided in the Supplementary Materials. To derive a null dataset from it, we used the resampling method in Algorithm S2 in Supplementary Materials, (G₁, G₂) = maResampling (G, 50, 50). To add DE genes, we randomly chose 1114 (5%) genes and make them DE by adding Δμ_i to randomly selected 557 genes in data matrix G₁, and adding Δμ_i to the remaining 557 genes in G₂. Each Δμ_i is uniformly distributed in [0.5, 4].

Dataset 2 (Burn Injury Data): in a recent study on burn injured rats, we have obtained 68 gene expression profiles, from which a data matrix G consisting of five replicate arrays is taken for further manipulation (Section 1.5 in Supplementary Materials). To generate a null dataset from G, we adopted Algorithm S3 in Supplementary Materials and used function (G₁, G₂) = maBootstrapping (G, 5, 5). Adding DE genes to the null data is similar to Dataset 1.

3 RESULTS

3.1 Identification of DE genes

To test π-value in the identification of DE genes, we use the Breast Cancer Data derived null dataset (M₁,M₂ = 50) described before, with 1114 (5%) artificially designed DE genes as the known truth, whose mean differential expression levels are uniformly distributed in [0.2, 2]. We use receiver operating characteristic (ROC) curve as performance measure, and compare the following gene selection criteria. The moderated t-test, shrinkage t-test and TREAT are available in R package. The ROC curves are obtained from the average result of 100 times of simulations.

• (1) π-value: π-value is computed from P-value of regular t-test.

• (2) LFC: Log-fold change criterion;

• (3) RegPval: P-value criterion using regular t-test;

• (4) ModPval: P-value criterion using moderated t-test;

• (5) TREAT: P-value criterion using TREAT with LFC threshold τ = 0.5; and

• (6) ShrPval: P-value criterion using shrinkage t-test.

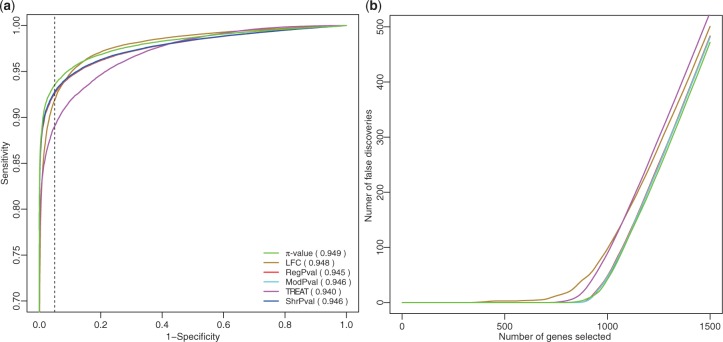
Figure 2a shows that π-value criterion generally outperforms other criteria with the largest area under curve (AUC). The π-value criterion performs best in the high specificity region. For example, when specificity equals 0.95, indicated by a dashed line in Figure 2a, π-value has the highest sensitivity, 0.94. Regular t-test, moderated t-test and shrinkage-t are less sensitive, with FC criterion and TREAT being the least sensitive. The number of false discoveries among the top n selected genes for each criterion is shown in Figure 2b. π-value, regular t-test, moderated-t and shrinkage-t have similar performance and have fewer false discoveries than FC and TREAT. When n < 920 and n ≥ 1000, π-value has the lowest FDR among all criteria. The robustness of π-value criterion is further demonstrated in Supplementary Figure S2 when we reduce the synthetic DE genes' differential expression Δμ_i to the range of [0.1, 1]. π-value still has higher sensitivity in the high specificity region [0.8, 1] (left of the dashed line, Supplementary Fig. S2a and the lowest FDR Supplementary Fig. S2b). We have also evaluated the capability of π-value through an additional simulated dataset and an empirical dataset (Section 2.2 in Supplementary Materials). In simulations adopted from a hierarchical model Smyth, 2004, π-value has comparable performance as moderated-t, TREAT and shrinkage-t in similar and balanced variances conditions. Simulation results on an empirical dataset again demonstrate that π-value has comparable or better performances. It is especially noteworthy that (in the hierarchical model simulations), although FC and regular t-test do not perform robustly in the condition of similar and balanced variances, π-value, which integrated the two methods, has good FDR and AUC values competitive to other more complex methods (moderated-t, TREAT and shrinkage-t) which need extra prior assumption and complicated computations. All the above results indicate that π-value is a desirable criterion for DE gene selection.

Fig. 2.

ROC curves and FDR for various gene selection criteria. (a) ROC curves. AUC for each ROC curve is provided in the parentheses. DE genes have Δμ_i uniformly distributed in [0.2, 2]. (b) Number of false discoveries among top n selected genes.

3.2 Application to GSEA

π-value provides a new ranking method for genes based on combination of expression change and statistical significance, and it can be readily applied to GSEA.

We use Burn Injury Data derived dataset to demonstrate the application of π-value to generalized GSEA [Equation (6]), and the procedure is summarized in the Supplementary Materials. t-statistic, P-value and π-value based enrichment scores are denoted by ES_t, ES_p and ES_π, respectively.

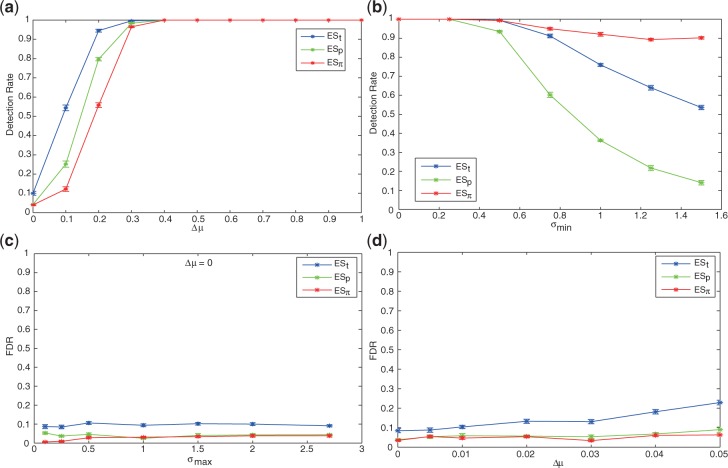
π-based enrichment score is less sensitive to low FC but equally sensitive when LFC ≥ 0.4. To study the sensitivity of enrichment scores with respect to LFCs of genes in GSEA, we designed the following experiment. We created several gene sets, each containing 20 genes. In each gene set, 10 genes have different mean expressions in class C₁ and C₂, with g_(1)ij∼𝒩(μ_i,σ_i), g_(2)ij∼𝒩(μ_i + Δμ, σ_i), and Δμ varies from 0.0 to 1.0 across the gene sets. The detection rates of t-, P- and π-based enrichment scores with respect to Δμ are shown in Figure 3a. As expected, the higher the LFC Δμ is, the more sensitive a enrichment score is to detect enrichment. ES_π is less sensitive than ES_t and ES_p when Δμ < 0.4; however, it is equally sensitive when Δ μ ≥ 0.4, and all three enrichment scores achieve near 100% detection rate. Finally, it is noted that when Δμ is near 0, the gene set is probably not truly enriched, a low detection rate is thus desirable. Figure 3 shows ES_π has the lowest detection rate when Δμ∼0, indicating the lowest FDR.

Fig. 3.

Top figures: detection rates with respect to (a) varied LFC and (b) varied minimum variance. In (a), x-axis denotes LFC Δμ; in (b), x-axis denotes the minimum SD σ_min, with Δμ = 0.5 fixed. Bottom figures: false discovery rates (FDRs) with respect to (c) zero-fold change and varied maximum variance, and (d) slight FC. In (c), Δμ = 0, and x-axis denotes the upper limit of SD σ_max; in (d), Δμ varies from 0.0 to 0.05, and σ_max is not restricted.

π-based enrichment score is robust with respect to intrinsic variance. To study how gene variance affect the detection of enriched gene sets, we designed genes sets similar to the previous experiment, but with fixed differential expression and controlled minimum variance. In particular, we fixed Δμ to be 0.5 to guarantee the high confidence of enrichment, and let the DE genes have g_(1)ij∼𝒩(μ_i, min(σ_i,σ_min) and g_(2)ij∼𝒩(μ_i + Δμ,min(σ_i,σ_min). σ_min varied from 0.0 to 1.5 across the gene sets. As expected and shown in Figure 3b, when σ_min = 0 (no minimum gene variance is imposed), all three enrichment scores have near perfect detection rate. However, when σ_min gradually increases to 1.5, ES_π can still maintain about 90% detection rate, while the detection rate of ES_t drops to <60%, and ES_p has the worst detection rate, <20%.

π-based enrichment score protects against false discovery. The FDR can be assessed when Δμ = 0 or is very small (Fig. 3c and d). Figure 3c shows the result of an experiment where we designed several gene sets with no FC and varied maximum variance (similar to previous experiments, we controlled σ_max of 10 selected genes in each gene set). The FDR for ES_π is consistently <5%, almost always smaller than ES_t and ES_p, and ES_t has the largest FDR. Since Δμ → 0 constitutes a heavy penalty on π-value, a highest degree of protection against FDR is observed when σ_max is smaller ( ≤ 0.5), such that smaller variance is correlated with larger t and smaller P-value, leading to higher ES_t and ES_p. The protection of ES_π against FDR can be further extended when FC is non-zero but too small for the gene set to be considered enriched. In an extended experiment, we let Δμ vary from 0 to 0.05 without variance control, and observed again that ES_π has a consistent lower FDR than ES_t and ES_p (Fig. 3).

3.3 Application to gene expression profiling of estrogen receptor sensitive breast cancer

In the previous sections, we based our simulations on controlled datasets where differential expressions were artificially added to null dataset (satisfying null hypothesis), for convenient evaluation of performance. Now we will apply π-value to the original breast cancer dataset.

The breast cancer dataset (GSE2034) contains 77 estrogen receptor negative (ER − ) and 209 estrogen receptor positive (ER + ) samples of breast tumor, and we use it as the reference to compare three enrichment scores, ES_t, ES_p and ES_π. It is well documented that ER + and ER − breast cancer patients respond to drugs differently and have distinct prognosis, and it is shown that estrogen regulates pathway in breast cancers Lewis-Wambi and Jordan, 2009. Therefore, we choose an estrogen-related Gene Ontology term ‘response to estrogen stimulus’ (GO:0043627) to form our interested gene set. Using 1091 biological process terms (each term corresponding to a gene set) recorded in the Gene Ontology database, we have conducted a generalized GSEA using the method outlined in Section 2.4 in Supplementary Materials. Results in Table 2 (top 3 rows) show that our interested gene set (estrogen stimulus) is highly enriched with high rankings among 1091 gene sets for all three enrichment scores ES_t, ES_p and ES_π. The rankings (rank_ref) of the gene set among all gene sets using ES_t, ES_p and ES_π are 67, 47 and 27, respectively. The P-values (p_ref) of ES_t, ES_p and ES_π are 0.003, 0.002 and 0.001, respectively.

Table 2.

Results of GSEA

Estrogen stimulus	ESt	ESp	ESπ
rankref	67	47	27
pref	0.003	0.002	0.001
rankavg	138	130	58
pavg	0.03	0.03	0.007
Enrichment rate (%)	60.0	60.8	94.3

Rank refers to the ranking of a gene set's ES score in descending order. Average P-value of ES is obtained from 1000 times of simulations. Enrichment rate is determined by the percentage of the gene set satisfying the criterion P-value of ES  ≤ 0.05, in 1000 times of simulations.

In order to test the performance of different enrichment scores in small sample setting, we used the original 283 samples as a pool, and randomly drew a subsample consisting of 27 ER + and 10 ER − profiles 1000 times, to which we applied GSEA based on the three scores. The results are listed in Table 2 (bottom 3 rows). Among three enrichment scores, ES_π provides the highest average ranking (rank_avg = 58) of the interested gene set and also has the most significant average P-value (p_avg). Using P < 0.05 as an enrichment criterion, ES_π has the highest enrichment rate in 1000 times of simulations. These results show that π-value has desirable performance in GSEA, especially in small sample setting.

4 DISCUSSION

We defined π-value as a gene significance score combining FC and P-value, and derived its distribution. To identify DE genes by π-value, we can specify a significance level α and use the corresponding critical value as threshold. Under certain assumptions, critical values can be obtained theoretically; otherwise, they can be estimated from simulation, as shown in the Supplementary Materials.

One may choose ad hoc π threshold of 1.3 or 2.0, noting that at 2-fold change, P = 0.05, 0.01 translate to π = 1.3, 2.0, and the thresholds are also close to the dependent CVs at α = 0.05, 0.01 (Table 1). Moreover, the definition of π-value in Equation (1) implies that 2-fold change is a neutral position: a smaller FC will penalize P-value, and a larger FC will boost P-value. As an extension to this concept, if we consider n-FC as a reasonable decision boundary for DE genes, we can adopt an alternative definition of π = (φ/log₂n)·( − log₁₀p), and choose decision threshold accordingly. Further comparison of π-value, P-value and FC to serve as DE gene selection criteria is discussed in the Supplementary Materials.

Among various selection criteria for identifying DE genes, π-value is the most robust. We have found that

• π-value performs well at the high specificity region, and its ROC curve stays above all other criteria in the region. π-value also has the lowest FDR when the number of selected genes increases.

• Overall, π outperforms other criteria by having the largest AUC (area under curve) of ROC.

In the simulations, π-value was computed based on regular t-test, therefore its computational complexity is less than moderated t-test, TREAT, or some other improvements to the regular t-test.

In generalized GSEA, π-based enrichment score is also more robust than t-statistic and P-value based scores. In the experiments, we designed half of the genes in a gene set to be DE, to mimic the real world scenario. We have found that

• ES_π has comparable detection rate of enriched gene sets as ES_t and ES_p when differential gene expression Δμ ≥ 0.4, although it is less sensitive when Δμ < 0.4.

• ES_π has a robust high detection rate when DE genes in an enriched gene set have increased variance.

• ES_π protects against false discovery when Δμ is close to zero, especially when part of the genes have low variance.

In the application to breast cancer, we utilized various scoring methods of GSEA to evaluate the performance on small subsets of ER + and ER − breast tumor samples. Based on 1000 times of simulations, we have found that π-value based enrichment score provides higher ranks of the estrogen-related GO term, higher enrichment rate and smaller P-values. The results demonstrate the advantages of π-value to serve as enrichment score in GSEA applications.

In conclusion, we find that π-value is a robust score for detecting DE genes, reflected in the ROC curve consisting of sensitivity versus specificity and the false discovery rate plot. In generalized GSEA, π-value based enrichment score has a comparable performance with P-value and t-statistic based enrichment scores in general. In special situations, ES_π behaves more robustly than ES_p and ES_t, in that it improves sensitivity in the LFLV situation, and protects against false discovery in the SFSV situation. When applied to breast cancer data, π-value also shows its potential in identifying enriched gene sets involved in key biological functions. Most existing microarray analysis infrastructure, including software and public domain databases, provide FC and P-value information. FC is an important factor in biological discovery, which represents the variation of mRNA abundance across different biological conditions. P-value of t-test signifies the confidence of difference between case and control, based on which null hypothesis will be rejected or accepted. By integrating the two factors, π-value can improve the performance of microarray analysis without using prior information or recalculating a new statistic. Therefore, it provides us an option to improve on the current infrastructure without major changes. Not limited to regular-t test, π-value can be extended to integrate other kinds of P-values, such like moderated t-test, ANOVA or linear regression, to satisfy various demands in microarray analysis.