Numerical simulation of a susceptible–exposed–infectious space-continuous model for the spread of rabies in raccoons across a realistic landscape

Abstract

We introduce a numerical model for the spread of a lethal infectious disease in wildlife. The reference model is a Susceptible–Exposed–Infectious system where the spatial component of the dynamics is modelled by a diffusion process. The goal is to develop a model to be used for real geographical scenarios, so we do not rely upon simplifying assumptions on the shape of the region of interest. For this reason, space discretization is carried out with the finite element method on an unstructured triangulation. A diffusion term is designed to take into account landscape heterogeneities such as mountains and waterways. Numerical simulations are carried out for rabies epidemics among raccoons in New York state. A qualitative comparison of numerical results to available data from real-world epidemics is discussed.

AMS Subject Classifications: 65Mxx; 65N30; 92D30; 92D40

1. Introduction

Epidemiologists have long used mathematical models to simulate the transmission of a disease throughout populations. These models allow for an understanding of the processes at work and for predicting future epidemics. The large majority of these epidemiological models have a compartmentalized design and are composed of a system of ordinary differential equations in time. Though some aspects of compartmentalized models are extremely well developed (such as the rate of infection and stability of solutions for simple cases), these models do not always account for the movement of individuals from one region to another. This can be a significant limitation, especially when dealing with wildlife diseases, as the daily movement and seasonal migration of animals can have major effects on the transmission of the disease itself. Describing the movement of individuals across a region in a mathematically rigorous and epidemiologically tractable way has been done following different approaches [14, 18]. The canonical procedure is to discretize the population and the geography into geopolitical units and to consider the movement of individuals from unit to unit [18, 29]. Although better than ignoring movement, this approach suffers from several limitations. The average movement of animals generally does not fit the scale and shape of geopolitical units, requiring the introduction of artifacts such as long-distance translocations [30], whose features can be difficult to interpret. Moreover, geopolitical subdivision is of little efficacy when one wants to include the geographical heterogeneities of the landscape.

In this article, we model movement as a continuous process across the geographical region of interest by means of a time-dependent diffusion process. This results in a system of partial differential equations (PDEs) of parabolic form [14, 17, 28]. Parabolic (diffusion) PDE's can be regarded as a macroscopic representation of Brownian motion and are therefore a natural candidate for modelling the movement of wild animals. Our aim is to describe the spread of the infection in a real two-dimensional region of interest Ω, with no simplifying assumptions on the shape of the region. Simple finite difference schemes, as used for instance by Miller Neilan and Lehnart [22], cannot incorporate realistic geographic features. Instead, we turn to unstructured discretization grids, which naturally lead to using finite elements in space, as they are well suited for these kinds of triangulations. Other researchers have used finite elements for the diffusion of age-structured populations [1, 7, 12, 19, 23], but carried out numerical tests only on simple geometries such as rectangles or one-dimensional intervals. Finite elements in an epidemiological context are considered by Kim and Park [20], but they focus only on proving stability and convergence results for the scheme and do not provide numerical results.

For illustration purposes, we focus throughout this article on the diffusion of rabies among raccoons in the state of New York in the USA. A representation of the region of interest has been retrieved by satellite maps, and the specific geographical features are included in the coefficients of the diffusive terms. Rabies, a viral encephalomyelitis, has the longest extant record of reports of any zoonotic disease in the USA. Raccoons (Procyon lotor) are a major carrier of the disease across North America, together with foxes, bats and skunks [26, 31]. While a successful vaccine for humans and other mammals against rabies exists, and human fatalities are rare, the economic cost of widespread animal vaccination and the danger of rabies to threatened species makes understanding the spread of rabies in wildlife hosts important to epidemiologists [27, 31]. It is worth noticing, however, that the results we provide can be extended to other types of infectious diseases in wildlife and to different regions of interest.

The structure of the article is as follows. In Section 2, we introduce the Susceptible–Exposed–Infectious (SEI) model with diffusion. We describe in Section 3 how we incorporate spatial heterogeneities of the landscape in the diffusion coefficients. Section 4 introduces the space and time discretization of the associated system. Finally, in Section 5, we provide a proof of concept of our numerical model by simulating the disease in New York. We first perform a sensitivity study with respect to the parameters of the model. Subsequently, in order to investigate a practical application, we simulate the spread of an epidemic of rabies in raccoons from 1990 to 1994, and compare those results qualitatively with the available public health data [25].

1.1. Notation

Let Ω ⊂ ℝ² be a two-dimensional domain of interest with coordinates x, y. We denote by s(x, y, t), e(x, y, t), and i(x, y, t) the densities of the susceptible (individuals that can be infected by the disease), exposed (individuals that have been exposed to the virus but do not have evident symptoms yet), and infectious populations, respectively, at location (x, y) and time t. The total number of SEI individuals at time t are given by

respectively. We introduce the auxiliary variable,

representing the population density at location (x, y) and time t, and the total population at time t is given, therefore, by

The vector of unknowns [s, e, i]^T (x, y, t) will be denoted by u(x, y, t).

In this article, we refer to the variational formulation of the SEI model, which relies upon the definition of proper functional spaces. In particular, we denote by L²(Ω) the space of functions f of x, y such that ∫_Ω(f(x, y))² dx dy < ∞. If, in addition, ||f||₁² ≡ ∫_Ω(f² + (∂_xf)² + (∂_yf)²) dxdy < ∞, we say that the function belongs to the Sobolev space H¹(Ω). When f is also function of time, the quantity ||f||₁ depends on time. If this function is such that ∫₀^T ||f||²₁(t)dt < ∞, we say that f ∊ L²(0, T;H¹(Ω)). We use the same notation with bold font for vector functions whose components each belong to this space. Bold characters will be used generally for vectors or vector functions (according to the specific context).

2. The SEI model with diffusion

The SEI model divides the population into SEI individuals. In more general cases, a fourth group of recovered individuals could be considered (resulting in an SEIR model). For simplicity, we do not include the effect of vaccination in this work, and so the recovered class is empty in this setting, since rabies is lethal for raccoons. We point out, however, that the following arguments can be straightforwardly extended to an SEIR model.

We model the spread of an epidemic in Ω by the following nonlinear system of reaction–diffusion equations of parabolic type:

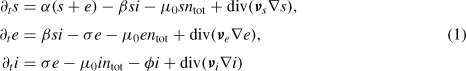for all (x, y, t) ∊ Ω × (0, T). Here, we assume that only susceptible and exposed individuals are able to reproduce, and we denote by α the (constant) reproduction rate. Such an assumption is quite reasonable, since on the one hand, the expected survival of a rabid raccoon is much too short to carry on a pregnancy, and on the other hand, even in the case a pregnant rabid female is able to deliver, her offspring are very unlikely to survive, as the mother is going to die shortly. In a more general epidemic, where the life expectancy of an infectious individual is longer, such an assumption can be relaxed, and the birth term can be replaced by αn_tot. In Equation (1), β denotes the infectiveness of a contact between a susceptible and an infectious individual, σ the reciprocal of the latency period, and ϕ the reciprocal of the life expectancy of a rabid raccoon. We assume a density-dependent mortality rate in the absence of epidemic μ₀n_tot. The diffusion coefficients are organized in three 2 × 2 tensors, v_s, v_e, v_i, designed to take into account the heterogeneities of the landscape, and are thus dependent on the spatial location. The epidemiological parameters above (β, σ, ϕ) can be considered constant for a well-studied and understood disease. Concerning the parameters of the vital dynamics, the mortality rate μ₀ depends on the carrying capacity of the environment, it can vary from one region to another to account for hospitality of different areas, but it can be considered constant within the regions. It can also change in time to model abrupt variations in the environment itself (flood, drought, fires). Finally, the reproduction rate α can be either considered constant to average births along the year or time-dependent to introduce seasonality in the process.

The vector compact representation of system (1) reads

with

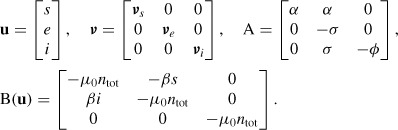This representation points out that our system is in fact a vector generalization of the well-known (scalar) normalized Fisher's equation

that has been introduced in [10] for genetic studies. An analysis of this equation and, more specifically, of its travelling waves solutions (i.e. solutions of the form u(x, t) = g(x − γt), for g(·) a function and γ a scalar number to be identified) can be found in [28].

System (1) is completed by some suitable initial conditions

for (x, y) ∊ Ω, and by boundary conditions to be prescribed over the entire boundary ∂Ω. If we assume that the region of interest is isolated, we prescribe homogeneous Neumann boundary conditions

Other boundary conditions could be considered as well. For instance, a non-zero function of time in the Neumann conditions corresponds to some (known) migratory flux. To instead force s = e = i = 0 (homogeneous Dirichlet conditions) would assume that outside the region of interest, the habitat is so hostile that no individual survives. Alternatively, a non-homogeneous Dirichlet condition would assume that data on the actual size of the different populations at the region boundary are available. Robin conditions could also be used to have the migration dynamics depend on the population itself.

Hereafter, we consider an isolated system (homogeneous Neumann conditions).

2.1. Variational formulation of the problem

The finite element solution of the problem relies upon its variational formulation. Let v(x, y, t) be an arbitrary three-component vector in H¹(Ω). We multiply Equation (2) by v and integrate over Ω to get

where we have exploited the Green formula and the homogeneous Neumann conditions. The variational formulation of the problem we consider can be stated as: Find u(x, y, t) ∊ L² (0, T; H¹(Ω)) such that Equation (3) holds with the initial condition u(x, y, 0) = u₀(x, y). Note that if Ω has a Lipschitz continuous boundary, each term of this formulation is well defined, since thanks to the Sobolev embedding theorem, the product of two functions belonging to H¹(Ω) in two dimensions is in L²(Ω), and so ∫_Ω(A − B(u))u · ν dω is integrable [21].

3. Modelling of landscape heterogeneities

In this work, we consider two kinds of geographical heterogeneity in the region of interest that are modelled in two different ways.

• (1)Localized heterogeneous effects, such as the close proximity of a major waterway that locally drives the movement of the wild animals.
• (2)Extended heterogeneous regions, where the dynamics of the infection are significantly affected by particular features. This is the case of lakes, for instance.

In the latter case, we consider a splitting of the domain of interest into homogeneous subregions. In the former one, we modify the diffusivity tensors to describe the effects of the heterogeneity on the population dynamics.

3.1. Localized heterogeneous effects

Some features of the region of interest can induce local modifications to the dynamics. This can be modelled by a proper dependence of the coefficients in Equation (1) on the geographical coordinates x, y. For instance, we can argue that mobility of the animals in the mountains is reduced by the presence of physical obstacles. We therefore set a reduced value for the diffusivity in these zones.

Rivers also present an obstacle, as movement across the waterway is restricted. Since their dimension is small in comparison with the region of interest, we do not introduce a bidimensional description of the rivers to avoid useless computational burdens. Instead, we resort to a monodimensional representation, where the waterways’ impact on the raccoons’ dynamics is represented by a modification of the diffusivity coefficient. More precisely, we reduce the mobility of raccoons across the rivers by a diffusion reduction in the direction normal to the river. In practice, to each point of the river, we associate a local tangent/normal frame of reference (Figure 1, left) with unit vectors e_τ, e_n, respectively. In a neighbourhood Σ of width 2ε of the river the diffusivity is gradually decreased, as indicated in Figure 1, right. Denoting by _k (k = s, e, i), the quantities evaluated in the normal/tangent frame of reference, respectively, we have in Σ

Figure 1.

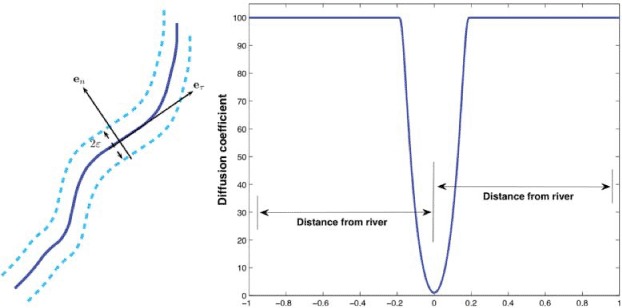
Left: normal/tangent reference frame along the river. Right: diffusion coefficient in the normal direction to the river, with v_H = 100, v_L = 1, and ∊ = 0.2.

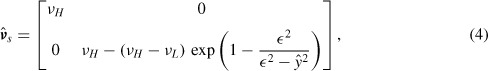where ŷ is the distance from the river along the local normal direction, v_H and v_L are the high and low diffusivity values, the former being the ‘regular’ value and the latter being the diffusivity at the river. The function decreases the value of the diffusion coefficient v from v_H to v_L.

The tensor (4) is then transformed to the Cartesian global frame of reference, by means of the rotation matrix R, which aligns the local frame of reference to the global one. By standard vector calculus manipulations, we have that

Similar arguments are used for the diffusivity tensors v_e and v_i.

In particular, we have applied this to the Hudson and Mohawk rivers in our New York state, for example.

Note that in such framework, the diffusivity tensor is a function of the space coordinates only in the neighbourhood of the river, while it is (piecewise) constant in the rest of the domain. As a consequence, the divergence term in the model introduces a convection in the raccoons dynamics induced by the waterways.

3.2. Strongly heterogeneous subregions

In some subregions, we can postulate that the population dynamics are significantly different, due to geographical heterogeneities or other specific reasons that require modifications to Equation (1). For instance, if we assume that wild animals are subject to a strong hunting activity in a specific part of the geographical domain, we should locally correct the equations to include the effect of the predators. In the presence of large bodies of water, we can eliminate the region from the domain of interest under the assumption that no significant dynamics are occurring there. In our case, we have introduced an internal boundary to the domain of interest corresponding to lakes, with Neumann boundary conditions describing no flux of animals across the basin.

In general, when different dynamics are coupled, from the numerical standpoint, it is convenient to split the domain into subdomains where each problem is solved separately, in a globally iterative framework [33]. A more specific testing of domain decomposition techniques in the context of population dynamics was investigated in [12].

In the numerical tests of this article, we have considered only the presence of the two major Finger Lakes (Seneca and Cayuga), by excluding them from the computational domain.

4. Numerical approximation

A numerical solution of Equation (3) is obtained after a proper discretization of space and time derivatives. The finite element method (FEM) is particularly suitable for complex geometries such as the ones represented by the geographical regions we are interested in. Space discretization is therefore performed with FEM while a classical finite difference discretization is carried out for the time discretization [9].

Let us consider a regular triangulation of the domain Ω and assume that the numerical solution denoted by u_h is piecewise linear on each element of the grid. The mesh has N nodes and h denotes a representative dimension of each element. The solution can be written as

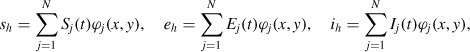and u_h = [s_h, e_h, i_h]^T, where φ_j(x, y) are the piecewise linear functions equal to 1 on the jth node of the mesh and equal to 0 in all the other nodes. The finite element formulation is obtained by plugging this representation of the solution into Equation (3) and selecting alternatively v = [φ_i, 0, 0]^T, v = [0, φ_i, 0]^T, v = [0, 0, φ_i]^T for i = 1, …, N. We obtain a 3N × 3N nonlinear ordinary differential system in the form

where U = [[S_i]_{i=1, …, N}, [E_i]_{i=1, …, N}, [I_i]_{i=1, …, N}] and

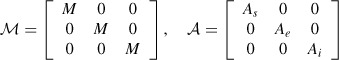with

and

Finally, ℱ(U) = ∫_Ω(A − B(u_h))u_h · vdω when v is selected as stated above.

Let us introduce now a time step Δt and the instants tⁿ = nΔt, where we collocate the semidiscrete problem (5). In particular, the incremental ratio

is an approximation of the time derivative either in tⁿ⁺¹ or tⁿ, with an associated numerical error proportional to Δt. If we collocate it at tⁿ⁺¹, we have the implicit Euler method, and we have to solve the nonlinear algebraic system

This can be done with iterative methods, which, however, rapidly increase the computational costs, since iterations are nested in the time loop. If we collocate the derivative at tⁿ (explicit Euler), the system to be solved is simply (Uⁿ is known by the previous time step or the initial condition)

The drawback of this method is that Δt is subject to restrictions from numerical stability. In this case, this restriction is proportional to h², so it can be significantly limiting for fine reticulations.

This is related to the explicit treatment of the (so called) stiffness term 𝒜Uⁿ. To circumvent the drawbacks of the two approaches, we resort to a mixed implicit/explicit (IMEX) approach, where the stiffness is treated implicitly and the nonlinear term is treated explicitly. At each time step, we solve then

This is a linear system and the stability constraints induced by the explicit treatment of the nonlinear term are less restrictive than the ones induced by the stiffness. In our simulations, we have been in practice free to select the time step in a reasonable range of values for the application at hand. For a more extensive discussion and application of the IMEX method, see [11].

5. Numerical results

To prove the effectiveness of our proposed methodology, we apply it to the diffusion of rabies among raccoons in New York state. The simulations throughout this session are done with a self-developed code¹ running in MATLAB® 7.11.0. Due to the temporal scale of epidemic dynamics, we consider the month as the time unit measure, and in the simulations, we use a time step Δt = 0.1, roughly corresponding to 3 days. Table 1 summarizes the values of the epidemiological parameters of the model, that have either been drawn from published values and US Department of Agriculture sources (http://www.usda.org), or estimated indirectly. In particular, the birth rate α, the contact rate β, the latency period 1/σ, and the infectious period 1/ϕ are taken from the literature [2–4, 6, 16], while the rate of density-dependent mortality, μ₀, is estimated indirectly to produce a disease-free equilibrium within the range of reported densities for raccoon populations for the eastern US (5–17 animals/km²; see Section 5.3.1 below for a more detailed discussion on this aspect) [32, 34].

Table 1.

Coefficients of the SEI model (1).

α	Birth rate	2.67 k/f/y
β	Contact rate	1e–4 (ad)−1
1/σ	Latency period	50 Days
1/ϕ	Infectious period	14 Days

5.1. The computational domain: main waterways, lakes, and mountains

We derived the computational domain from a satellite image of the state of New York with the ImageJ [15] software. The coordinates of the computational domain will be expressed throughout this section in Longitude and Latitude. The movement across the finger lakes in west-central New York has been completely eliminated. We include the Hudson and Mohawk rivers as main waterways by forcing mesh nodes along them. Figure 2 (left) illustrates the computational domain with the included main waterways. The computational domain is then discretized by a regular triangulation with Netgen [24], consisting of 64,759 nodes and 127,360 triangles, plotted in Figure 2 (right).

Figure 2.

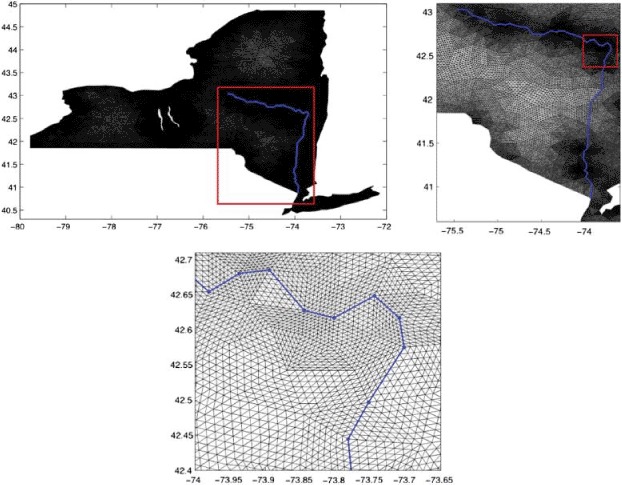
The computational domain including finger lakes and main waterways and its finite elements triangulation.

The diffusion tensors are taken as isotropic diagonal tensors far from the Hudson and the Mohawk rivers and the mountains, with the same value along x and y given by ν_H = 0.01. The mountain region is identified as the interior of the circle centred at (–74.5, 44) with radius 0.7, where we assume the diffusivity ν_M = 5 × 10^–3 × ν_H. These values have been tuned with a trial-and-error approach (with respect to real available data). Around the major rivers, we compute the tensors as described in Section 3.1. We plot in Figure 3 the resulting diffusion coefficients.

Figure 3.

Left to right: diffusion in the x-direction, cross-diffusion, and diffusion in the y-direction (ν_H = 0.01, ν_L = 5 × 10^–3 × ν_H).

As expected, the off-diagonal terms vanish everywhere except in a narrow neighbourhood of the river, following the turns of the river itself.

The computational domain we consider obviously does not take into account all of the heterogeneities of the New York landscape. Woods and mountains in the southern region, as well as interstates and major highways could also be included. However, the treatment of such heterogeneities would not differ too much from what we proposed so far. In particular, interstates and highways can be treated in the same manner as rivers, although expecting a far less significant reduction in the normal diffusion coefficient (raccoons are not good swimmers and actually are more likely able to cross interstates).

5.2. Simulation of a fictitious epidemics

To evaluate the effectiveness of our modelling of the landscape, we first simulate a fictitious epidemic starting in the centre of the state. We assume that, at the beginning of the epidemic, the raccoon population is at equilibrium at the carrying capacity. From available data in the literature, we assume that the raccoon density is 11 animals/km² [32]. We consider homogeneous Neumann boundary conditions and we introduce an initial density of infectious and exposed individuals, i₀ = 0.5 and e₀ = 1.5 animals per km², respectively, localized in a circle of radius 0.1 with centre (−75, 42.5), which is near Oneonta in Otsego County. We consider an isotropic diffusion coefficient across the whole domain Ω, except along the rivers, with the following baseline values:

In the northern mountain region, identified as the interior of the circle centred in (−74.5,44) with radius 0.7, we consider the diffusion coefficient v_M = 5 × 10⁻³ × v_H, and we reduce the carrying capacity to 8 animals/km².

We denote by U_base = [S_base, E_base, I_base]^T the solution associated with the above baseline values. We plot in Figure 4 the spread of the infectious wave: the shielding effect of the river and the influence of the presence of lakes are clearly visible.

Figure 4.

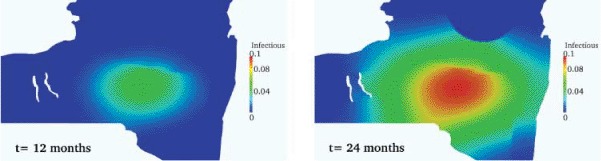
Infectious wave spread. Shielding effect of river, lakes and mountains on the propagation front of I_base at different times (v_H = 10 × v_L). Left to right: 12, and 24 months after infection.

To study the sensitivity of the numerical approximation to the modelling parameters of the major rivers, we consider the following solutions:

• (1)U_noRiver = [S_noRiver, E_noRiver, I_noRiver]^T, computed with a constant diffusion coefficient
  
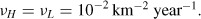
• (2)U_τ = [S_τ, E_τ,I_τ]^T, obtained by modifying the diffusion coefficient across the river, but keeping the baseline value of the distance ∊ unchanged:
  
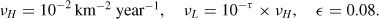
• (3)U_∊ = [S_∊, E_∊, I_∊]^T, obtained by modifying the value of the distance ∊, while keeping the baseline value of the diffusion across the river unchanged:
  

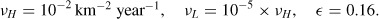
We plot in Figure 5 the difference between the spread of an infection with uniform diffusion coefficients and the one with the landscape heterogeneities included, namely the infectious densities difference I_noRiver − I_base at different times after insurgence (12, 24, and 36 months). The significant difference in the propagation speed follows from the shielding action of the river and can be appreciated by the bottom row in Figure 5, where we plot the relative difference between I_base and I_noRiver.

Figure 5.

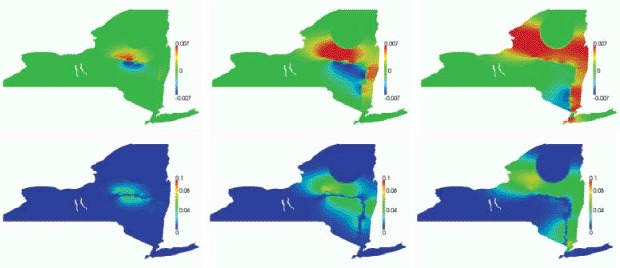
Effect on the propagation front of including landscape heterogeneities at (left to right) 12, 24, and 36 months. Top row: I_noRiver − I_base. Bottom row: relative difference (I_noRiver − I_base)/I_noRiver.

In Figure 6, we highlight the sensitivity of the shielding effect of the river to the reduction factor between the normal and the tangential diffusion along the river. We plot the differences between the infectious density in the baseline solution and the infectious density in U_τ for τ = 7. The expected monotonicity of the shielding effect with respect to the ratio v_H/v_L is confirmed by the numerical simulation.

Figure 6.

Effect of diffusion reduction normal to the river on the propagation front at (left to right) 12, 24, and 36 months: I_base − I₇.

Finally, in Figure 7, we show the effect of the threshold parameter in the definition of the diffusion tensor across the river, by plotting the difference between the infectious density of the baseline solution, and the solution computed with a doubled threshold parameter (I_base − I_∊). Again, as expected, the larger the threshold, the larger the shielding effect in the propagation of the infection.

Figure 7.

Effeczt of the distance ε on the propagation front at (left to right) 12, 24, and 36 months: I_base − I_∊.

These results highlight the relevance of the presence of rivers on an epidemic. The relative difference in infectious population density in the presence and absence of rivers is 10%. The numerical values of the parameters have an impact of at most 3% on the results, in the presence of variations in the threshold. A far less significant impact is associated with changes in the ratio ν_H/ν_L.

5.3. Simulation of the New York state epidemic outbreak (1990–1994)

In order to test our method with a more realistic problem, we simulate an epidemic spread that is inspired by the raccoon rabies epizootic that spread in the state of New York from the early 1990s. Since World War II, three major regional epidemics of rabies in animals have appeared and are still ongoing. Two of them (one in Europe, one in Canada) are primarily associated with red fox (Vulpes vulpes), while the third one is occurring in the USA, and appears to have multiple hosts. The east coast of the USA has experienced an epidemic of rabies among raccoons (Procyon lotor) since the early 1970s. The epidemic began at the boundary between Virginia and West Virginia and spread northeast through Pennsylvania and Connecticut and southeast to North Carolina.

On 4 May 1990, the first case of a rabid raccoon was recorded in the state of New York, in the township of Addison, Steuben County, on the New York/Pennsylvania border. By the end of 1994, the epidemic had propagated across a great part of the state.

5.3.1. Initial and boundary conditions

We assume the population to be at the carrying capacity at the beginning of the epidemic. One of the major difficulties in studying epidemics in wildlife is the scarcity of available information about the actual size of the at-risk population under investigation, and the raccoon population in New York is no exception to this.

The best estimates in the literature report raccoon density in eastern USA to be in the range of 5–17 animals per km² [32, 34]. However, according to the New York State Department of Environmental Conservation [25], raccoons are more keen to live in areas where the human presence is larger. To study the impact of the population distribution on the epidemic spread, we consider two possible initial conditions, one assuming uniform density of animals across the state, and the other one considering heterogeneous density. In the former case, we assume everywhere the reported average raccoon density of 11 animals per km². In the latter one, we assume the homogeneous case as baseline and we add a correction to this distribution that takes into account the human population density. As a consequence, we obtain an initial population density between 8 and 14 animals per km², where the highest values are associated with the most populated areas, such as New York City and its surroundings, Albany, Ithaca, and Syracuse, while the lowest values are associated with the less populated ones, such as Clinton, Franklin, and Hamilton Counties, for instance. We plot in Figure 8 (left) the heterogeneous initial condition across the whole state.

Figure 8.

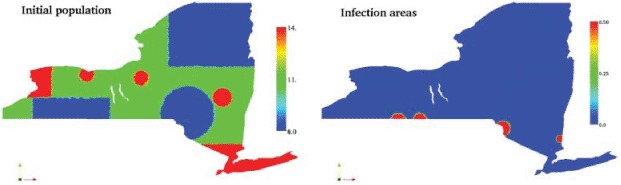
Initial conditions for the total raccoon population, and epidemic outbreak locations.

We also prescribe homogeneous Neumann boundary conditions on the border of the state. Note that if the assumption of an isolated environment makes perfect sense for the portion of boundary lying along water (Erie and Ontario lakes, Saint Lawrence and Hudson river, the Atlantic ocean around Long Island), it may be questionable when applied to the portion of boundary that borders Pennsylvania, Connecticut, and Vermont. However, since we do not have information about the actual movement of raccoons across those borders, we chose to consider New York state as an isolated environment. We describe the epidemic wave propagating north from Pennsylvania and west from Vermont by including source terms in the areas where the first cases have been reported.

5.3.2. Qualitative comparison with real data

To best reproduce the real-world data, the source terms for the epidemic were placed at the three locations highlighted in Figure 8 (right). These locations correspond to the first confirmed case of rabies in three areas of the state. Each source term was added at the month corresponding to the first confirmed case in that region. The central-western source term, centred at (−77.24,41.80), is at the location of the first confirmed case in the state, in Steuben county, thus it is introduced at t = 0. Also at t = 0, the south-central source in Sullivan county is introduced, centred at (−75.01,41.67). Both of these first two source terms have a circular radius of 0.2. The next source terms are the western source, centred at (−77.80,41.80) with radius 0.2 and introduced at t = 4, as well as the south-eastern source, centred at (−73.61, 41.33) with radius 0.1 and introduced at t = 11. These times (4 and 11 months) correspond to the moment when the epidemic reached Cattaraugus and Westchester counties, respectively.

We use the model values from Table 1 and the coefficients of the baseline simulation of the previous section (9). To take into account the separation of Long Island from the mainland, we also reduce the diffusion across the East River, by considering a normal diffusion coefficient ν_ER = 10⁻⁸ × ν_H, still combined with a threshold parameter ∊ = 0.08.

The model we simulate does not take into account the oral vaccination policies implemented in reality in Clinton, Essex, and Franklin counties beginning in the fall 1995. Thus, we limit our comparison with real data to the early stage of the epidemic outbreak (1990–1994). We run simulations both assuming a uniform raccoon population density and assuming the population distribution plotted in Figure 8. We plot in Figure 9 the spread of the infectious wave, together with the corresponding available data [25]. The epidemic waves match qualitatively, suggesting that even a moderate mesh like the one used here (the average area of each element is 1.10 km²) is enough for the problem at hand.

Figure 9.

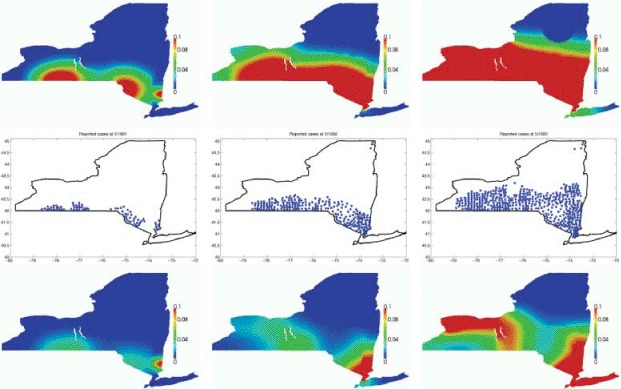
Propagation of a realistic rabies epidemics in New York state at different times (left to right: 1, 2, and 3 years after infection). Top: uniform initial population. Middle: reported data [25]. Bottom: heterogeneous initial population.

A more quantitative comparison is not readily feasible, as the available data are counts of reported rabies cases, while our model provides the density of rabid raccoons in a given area. Moreover, the high uncertainty surrounding the actual total raccoon population would spoil such comparison of all meaning. On the qualitative side, the propagation of the infection wave is quite well captured, in the uniform initial population case, in the north-northeast direction, but it seems too fast in the westbound direction. In the case of heterogeneous initial population, on the other hand, the westbound spread appears too fast towards the Buffalo area and the Ontario Lake, and at the same time too slow in the area close to the state southern border. This latter behaviour is likely a consequence of the homogeneous Neumann boundary conditions along the southwest border. The epidemic wavefront is actually part of a larger epizootic moving north from Pennsylvania, and the appearance of infectious cases along the border should be taken into further account.

Both simulations feature an infection spread in the Long Island area, where no rabid cases were reported in the period under consideration. Soon after the wavefront reaches the area, the high raccoon population density triggers an outbreak even in the presence of a small density of infectious. This is particularly evident in the heterogeneous population case: the higher the raccoon density, the larger the error. Since the wavefront reaches Long Island in a time consistent with the data, the problem can be addressed in a twofold manner. On the one hand, one could further reduce the normal diffusion across the East River. On the other hand, the high human population density in the area results in high levels of surveillance [13], and so infectious animals are more easily identified and removed. Thus, another possibility could be to reduce the infection rate in the area as a consequence of the high level of surveillance.

The comparison in Figure 9 does not really take into account the dynamics of the epidemic itself, as it focuses more on the propagation speed of the infection wave. To have a more accurate comparison, we considered not only the location of the reported cases, but also their quantity. We thus compared the results obtained with both the uniform and the heterogeneous population with the cumulative reported cases aggregated by county and in time, that we report in Figure 10. From this last comparison, it appears that the heterogeneous initial population, despite suffering from the problems highlighted above, performs better in identifying spatial clusters of infectious individuals that clearly emerge from reported data.

Figure 10.

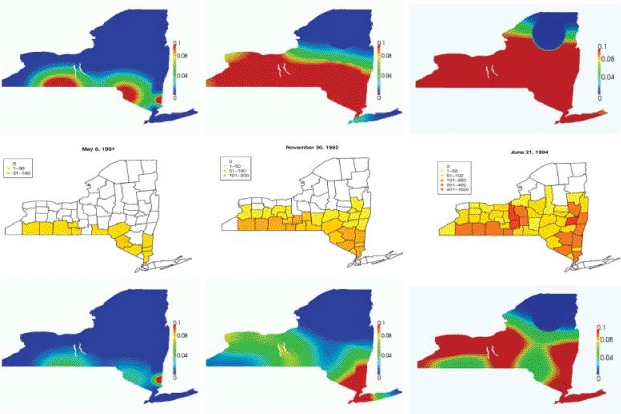
Propagation of a realistic rabies epidemics in New York state at different times (left to right: May 1991, November 1992, and June 1994). Top: uniform initial population. Middle: total reported data aggregated per county [25]. Bottom: heterogeneous initial population.

5.3.3. Computational cost

The discrete problem is reasonably well conditioned and its numerical solution does not present any significant difficulty. The mass and stiffness matrices are pre-assembled and the resulting linear system is associated with a (194, 277 × 194, 277) matrix. The simulation of 10 years of epizootic took about 3h45'on a desktop computer with 3.2 GHz Intel Core i3 dual processor and 4GB 1333MHz DDR3.

6. Conclusions

We present here a numerical model to simulate the spread of a lethal, infectious disease across a heterogeneous and continuous landscape. We introduced heterogeneities by including lakes, mountains, and main waterways in a finite element settings that allow the use of unstructured grids, which are better suited to represent a complex geographical domain. We provided a numerical simulation showing the effectiveness of such modelling. In addition, the method proves to be viable in reproducing the outbreak of a real epidemic of rabies among raccoons in the state of New York from 1990 to 1994. This aspect has a major potential, as it renders such modelling a solid tool, both in terms of accuracy in prediction and landscape description, and, most of all, CPU time. Moreover, such modelling requires the tuning of a small number of parameters in comparison to SEIR models based on geopolitical units [8, 26], where also a full mixing matrix has to be estimated.

However, further work still needs to be done. In this work, for instance, the diffusion coefficients have been tuned empirically. Data assimilation procedures [5], that is, the parameter tuning based on a rigorous minimization of the misfit between results and available measures, is anticipated to improve the knowledge of such a crucial parameter. In a forthcoming article, we will introduce a parameter estimation procedure of Bayesian type, based on the available observed data, which is currently under investigation.

Acknowledgements

The authors thank L.A. Real (Emory University) for some fruitful discussions on the topic. The first author has been partially supported by NIEHS grant T32 ES015459. The second author has been supported by the NIH grant RO1-AI047498 to L.A. Real during his stay at the Center for Disease Ecology, Emory University, 2010–2011.