Analysis of genetic population structure in Acacia caven (Leguminosae, Mimosoideae), comparing one exploratory and two Bayesian-model-based methods

Abstract

Bayesian clustering as implemented in STRUCTURE or GENELAND software is widely used to form genetic groups of populations or individuals. On the other hand, in order to satisfy the need for less computer-intensive approaches, multivariate analyses are specifically devoted to extracting information from large datasets. In this paper, we report the use of a dataset of AFLP markers belonging to 15 sampling sites of Acacia caven for studying the genetic structure and comparing the consistency of three methods: STRUCTURE, GENELAND and DAPC. Of these methods, DAPC was the fastest one and showed accuracy in inferring the K number of populations (K = 12 using the find.clusters option and K = 15 with a priori information of populations). GENELAND in turn, provides information on the area of membership probabilities for individuals or populations in the space, when coordinates are specified (K = 12). STRUCTURE also inferred the number of K populations and the membership probabilities of individuals based on ancestry, presenting the result K = 11 without prior information of populations and K = 15 using the LOCPRIOR option. Finally, in this work all three methods showed high consistency in estimating the population structure, inferring similar numbers of populations and the membership probabilities of individuals to each group, with a high correlation between each other.

Introduction

Evaluating population genetic structure is of considerable interest because it is a precursor to addressing many other issues, such as estimating migration, identifying conservation units, and specifying phylogeographical patterns (Manel et al., 2005).

Various statistical approaches can be used to form genetic groups of populations or individuals. For statistical inferences, model-based approaches are more suitable. Bayesian clustering (Manel et al., 2005) based on Hardy-Weinberg and linkage equilibrium, as implemented in the STRUCTURE (Pritchard et al., 2000) or GENELAND (Guillot et al., 2005) programs, is widely used for this purpose. These programs can also consider coordinates of sampling locations. For example, when STRUCTURE is applied to population genetics, it is often useful to classify individuals of a sample into populations. In one scenario, the investigator starts with a sample of individuals, aiming to determine something about the properties of populations. In a second scenario, the investigator begins with a set of predefined populations, aiming to classify individuals of unknown origin. Using the estimated allele frequencies, it is then possible to compute the likelihood of a given genotype having originated in each population. Individuals of unknown origin can be assigned to populations according to these likelihoods. Therefore, STRUCTURE uses a Bayesian clustering approach to assign individuals (probabilistically) to populations. A model is assumed in which there are K populations (where K may be unknown), each of which is characterized by a set of allele frequencies at each locus. This method attempts to assign individuals to populations on the basis of their genotypes, while simultaneously estimating population allele frequencies. The method can be applied to various types of markers, but it assumes that the marker loci are unlinked and in linkage equilibrium with one another within the populations. It also assumes that the populations are in Hardy-Weinberg equilibrium (Pritchard et al., 2000). In other words, the method assumes that any disequilibrium found is attributable to population structuration.

For cases in which the geographic locations of individuals are known and sampling is relatively even in space, spatial model-based clustering methods such as GENELAND (Guillot et al., 2005) are available to identify clusters of individuals. Assuming that populations occupy geographically delimited areas, the use of spatial information increases the power of correctly detecting the underlying population structure (Bonin et al., 2007). The statistical model implemented in GENELAND helps inferring and locating genetic discontinuities between populations in space from individual multilocus genetic data. The central assumption is that some spatial dependence is often present among individuals. Based on this sensible assumption, a hierarchical spatial model was developed in which a priori information on how the individuals are spatially organized is formally injected. In addition to detecting genetic discontinuities between populations, the method also addresses other points, such as denoising blurred coordinates of sampled individuals, estimating the number of populations in the studied area, quantifying the amount of spatial dependence in the data, assigning individuals to their population of origin, and detecting individual migrants between populations (Guillot et al., 2005).

One of the shortcomings of Bayesian clustering methods is related with the assumption of Hardy-Weinberg and linkage equilibrium within populations. However, in many cases, this assumption is not tenable. A technical yet critical limitation is the considerable computation time required for analyzing large datasets. In order to satisfy the need for less computer-intensive approaches, multivariate analyses seem particularly appealing, as they are specifically devoted to extracting information from large datasets. This is how the Discriminant Analysis of Principal Components (DAPC) was developed. DAPC is based on data transformation, using principal components analysis (PCA) as a prior step to discriminant analysis (DA), which ensures that variables submitted to DA are perfectly uncorrelated, and that their number is less than that of the analyzed individuals. Without necessarily implying a loss of genetic information, this transformation allows DA to be applied to any genetic data. Two options for DAPC are offered, depending on whether group priors are known or not (Jombart et al., 2010).

In this context, since plant populations are not randomly arranged assemblages of genotypes, but are structured in space and time, the above mentioned programs allow a fine-scale study of the genetic structure of these populations. This genetic structure may be manifested among geographically distinct populations, within a local group of plants, or even in the progeny of individuals. Ecologic factors affecting reproduction and dispersal are likely to be particularly important in determining genetic structure. Also, spatial and genetic patterns are often assumed to result from environmental heterogeneity and differential selection pressures (Loveless and Hamrick, 1984).

In this paper, we describe a study on natural Argentinean populations of the plant species Acacia caven (Leguminosae, Mimosoideae). This species is an extremely wide-ranging one that probably originated in the warm temperate to subtropical biogeographic region known as the Gran Chaco of southern South America, due to its great morphologic diversity. This small legume species is found in six countries and is considered to have certain potential as a managed silvopastoral crop (Aronson and Ovalle, 1989). Fruit size and shape are highly variable in A. caven. In 1992, Aronson recognized six varieties for this species, including A. caven var. caven, A. caven var. dehiscens, A. caven var. sphaerocarpa, A. caven var. stenocarpa, A. caven var. microcarpa and A.caven var. macrocarpa, based on both morphologic traits (Aronson 1992; Pometti et al., 2007) and molecular markers (Pometti et al., 2010). Argentina is the only country where all varieties cohabit (Aronson, 1992).

In this context, the main objective of the present work was to study the genetic structure of 15 populations of the six varieties of Acacia caven, using a dataset of AFLP markers. To accomplish this objective, we used two model-based approaches (STRUCTURE and GENELAND) and the exploratory method DAPC for estimating genetic structure and compared the consistency of the three methods.

Materials and Methods

Description of the dataset

In this study, a real dataset was used to compare the results of genetic structure analyses made by alternative approaches. This dataset consists of AFLP patterns of 224 individuals of the six varieties of Acacia caven (Leguminosae, Mimosoideae), collected from 15 sampling sites (Table 1). The distances between the sampling sites are shown in Table 2.

Table 1.

Populations of Acacia caven sampled in this study.

Variety	Eco-region	Population	Population code	Latitude (ºS)	Longitude (ºW)	Number of individuals analyzed
A. caven var caven	Pampa	Costanera Sur	CS	34°38′10.71″	58°42′44.08″	14
A. caven var caven	Pampa	Gualeguaychú	GY	33°22′4.00″	58°44′3.00″	22
A. caven var caven	Puna	Coiruro	CI	23°53′34.00″	65°27′30.00″	18
A. caven var caven	Puna	Campo Quijano	CQ	24°55′12.00″	65°39′0.00″	13
A. caven var caven	Puna	Ruta Nueve	RN	24°39′48.00″	65°22′49.00″	14
A. caven var macrocarpa	Puna	El Carril	EC	25° 4′58.80″	65°28′1.20″	16
A. caven var macrocarpa	Puna	Tolombón	TO	26°11′8.00″	65°56′7.00″	14
A. caven var microcarpa	Wet Chaco	Vivero Forestal	VF	26°16′0.00″	58°17′41.64″	12
A. caven var stenocarpa	Wet Chaco	Formosa	FS	26°16′13.20″	58°17′7.92″	12
A. caven var stenocarpa	Wet Chaco	YPF	YP	26°11′26.76″	58° 9′23.82″	12
A. caven var sphaerocarpa	Espinal	Iberá	IB	28°15′40.13″	56°30′20.38″	18
A. caven var dehiscens	Dry Chaco	Las Gemelas	LG	30°53′26.10″	64°30′13.50″	14
A. caven var dehiscens	Dry Chaco	Pan de Azúcar	PA	31°15′58.90″	64°20′28.60″	12
A. caven var dehiscens	Dry Chaco	Vaquerías	VA	31°23′38.93″	63°51′30.87″	12
A. caven var dehiscens	Dry Chaco	Valle Hermoso	VH	31° 7′1.20″	64°28′58.80″	21

Table 2.

Pairwise geographic distances in kilometers between Acacia caven sampling sites.

Pop	CQ	CS	EC	FS	GY	IB	LG	PA	RN	TO	VA	VF	VH	YP
CI	111.00	1348.53	123.80	768.28	1226.00	1017.75	809.44	832.00	79.21	263.14	833.53	771.49	856.92	780.57
CQ		1280.00	25.00	752.46	1166.50	982.49	700.00	749.50	39.28	159.26	744.23	751.00	750.71	764.50
CS			1238.29	910.82	185.00	745.31	655.00	645.00	1273.21	1155.11	650.00	911.38	664.42	932.57
EC				730.82	1121.00	961.09	674.07	716.00	50.33	139.09	701.21	729.25	683.00	743.00
FS					777.15	282.15	779.31	801.41	731.84	759.85	780.43	3.00	800.00	15.80
GY						617.17	584.38	574.00	1198.25	1046.00	593.30	770.79	593.50	793.76
IB							832.84	827.86	976.03	964.59	794.48	283.43	838.96	282.15
LG								43.50	738.31	547.38	29.40	783.78	35.20	809.13
PA									798.50	576.00	21.00	795.39	22.44	823.54
RN										194.06	767.15	730.38	727.22	745.00
TO											593.13	759.56	565.74	774.56
VA												775.78	4.00	797.27
VF													799.00	16.41
VH														824.37

The AFLP assay was performed as described by Vos et al. (1995), with a slight modification, as described in Pometti et al. (2012). This technique was used to investigate genetic variation within and among natural populations of A. caven from five eco-regions: Wet Chaco, Dry Chaco, Espinal, Pampa and Puna (Burkart et al., 1999). From the individuals studied by means of AFLP markers, 225 bands were obtained. Each AFLP band was considered as a single biallelic locus with one amplifiable and one null allele. Bands with the same migration distance were considered homologous. Data were scored manually as band presence (1) or absence (0).

Methods to assess population structure

As mentioned before, different approaches were used here to identify spatial structure in A. caven populations: two Bayesian-model-based and one exploratory method. The first one was the spatial cluster model implemented in the GENELAND package (Guillot et al., 2005) of the R program (R Development Core Team, 2011). Different sets of parameters (MCMC, thinning and burn-in) were used in different test runs, in order to find the optimal parameters by the time taken for the run. Finally, following the recommendation of the user’s manual, the Markov chain Monte Carlo (MCMC) repetitions were set at 100,000, thinning was set at 100, and the burn-in period was set at 200 (we eliminated the first 200 iterations whenever the curve was not constant); the number of groups (K) to be tested was set at 1–15. All individuals were assigned to K populations (1≤ K ≤ 15) based on their multilocus genotype and the spatial coordinates. To ensure that the run was long enough, we obtained 10 different runs and compared the parameter estimates (K, individual population membership, maps). The best result was chosen, based on the highest average posterior probability. The other Bayesian-model-based cluster analysis was performed using the STRUCTURE program version 2.3.3 (Pritchard et al., 2009). This analysis was performed twice: once without prior information of the populations to which the individuals belonged, and once with prior information on the populations (LOCPRIOR model). In both cases, the burn-in period and the number of MCMC repetitions were set, respectively, at 50,000 and 100,000. An admixture model was used, with correlated allele frequencies. K was set at 1–15, and the highest K value was identified as the run with the highest likelihood value, as recommended by Pritchard et al. (2000). In addition, K values were averaged across 10 iterations. The exploratory Discriminant Analysis of Principal Components (DAPC) was applied, using the adegenet package (Jombart, 2008) (function dapc) for software R (R Development Core Team, 2011). This analysis was also performed both with and without prior information on individual populations. Whenever group priors were unknown, the number of clusters was assessed using the find.clusters function, which runs successive K-means clustering with increasing number of clusters (k). For selecting the optimal number of clusters, we applied the Bayesian Information Criterion (BIC) for assessing the best supported model, and therefore the number and nature of clusters, as recommended by Jombart el al. (2010).

Comparison of individual groupings in the different methods

The probabilities of posterior population membership of individuals obtained by all grouping methods used were converted into between-individual Euclidean distances. Pairwise comparisons of these distance matrices were performed by means of the Mantel test using the ade4 package of R (Chessel et al., 2004).

Results

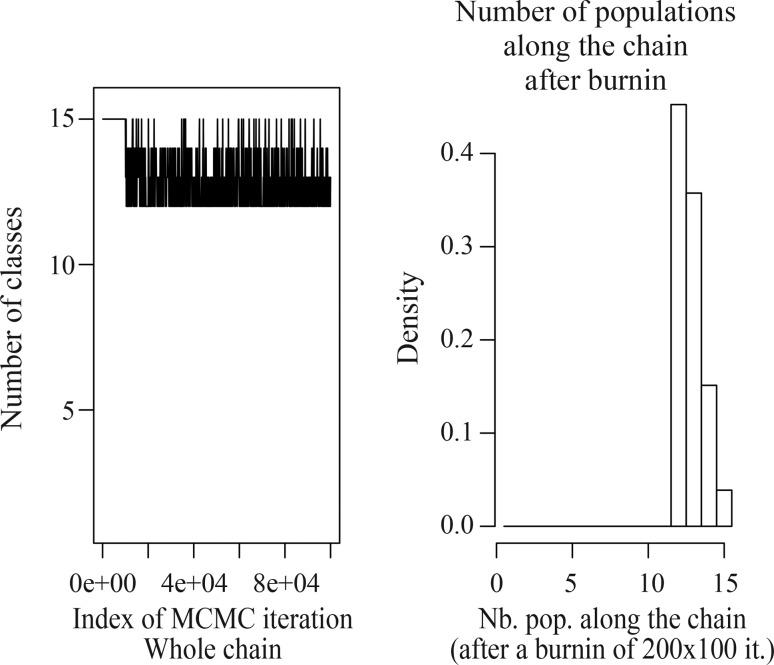
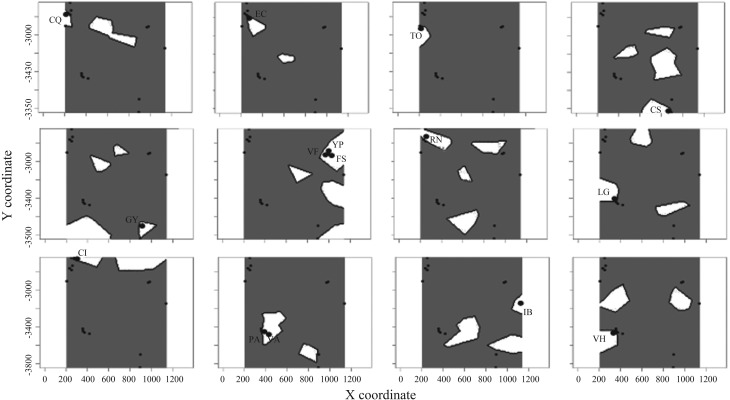
Analysis of the Acacia caven AFLP dataset obtained using GENELAND yielded a modal number of populations of 12, varying from 11–13 in different runs (Table 3). The run with the highest average posterior probability was chosen to base the conclusions on. The number of populations simulated from posterior distribution (Figure 1) displays a clear mode at K = 12. MCMC clearly converges within the first 10,000 iterations (Figure 1). Two populations, VA and PA (belonging to var. dehiscens), were included in one of the groups produced by GENELAND (Figure 2, row 3, column 2), and the other group identified comprises the VF, FS, and YP populations (belonging to vars. microcarpa and stenocarpa) (Figure 2, row 2, column 2). In both cases, the populations grouped together are geographically very close to each other. Each of the remaining groups corresponds to a single sampling site. The comparison of posterior probability of assignment of individuals to populations led to unequivocal results, assigning each individual to the population to which it belongs, except for those previously mentioned individuals that are in the same group of populations (100% of correct assignation).

Table 3.

Multiple runs for inferring the number of populations using GENELAND software.

Run	Modal number	% of modal number	Mean of probability density
1	12	37.20	−62443.26
2	12	37.80	−60538.68
3	11	38.90	−60964.61
4	13	32.80	−60583.12
5	11	36.80	−61215.83
6	13	33.40	−60874.19
7	12	36.40	−60953.19
8	12	36.20	−59999.66
9	12	36.80	−61164.86
10	12	36.00	−60860.80

In bold: highest average posterior probability.

Figure 1.

Plot of the number of populations simulated from the posterior distribution obtained with GENELAND.

Figure 2.

Spatial distribution of each group defined by GENELAND at K = 12. Population codes are given in Table 1.

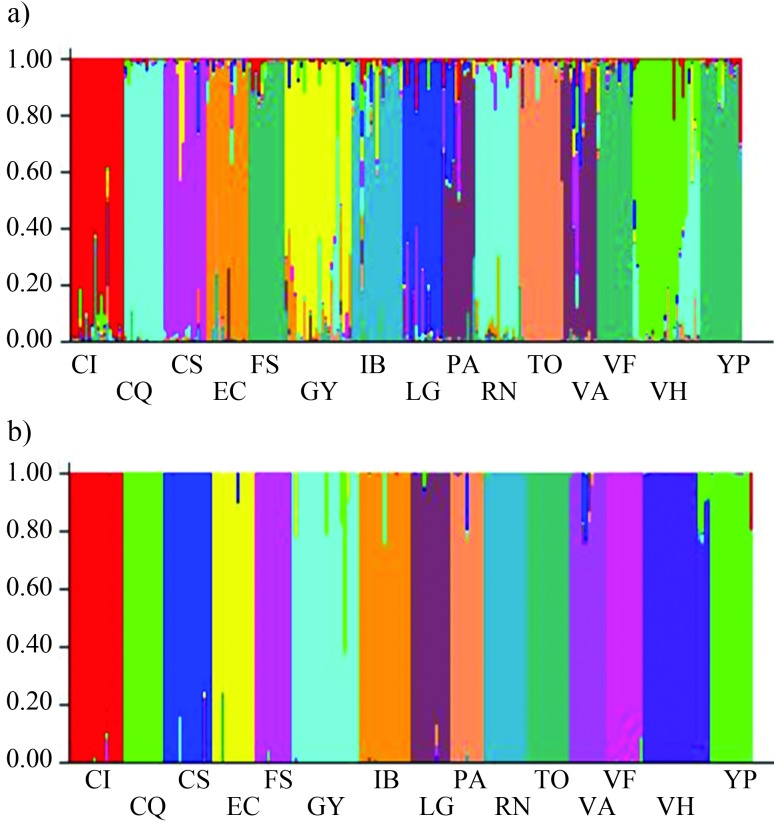
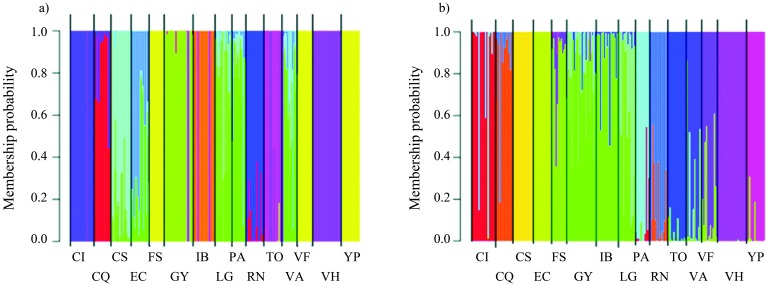
Data analysis using STRUCTURE with no prior distribution specified revealed that K = 11 had the highest mean probability of density value (Ln P(D) = −16832.60), after which this value plateaus, suggesting that the optimal number of K was 11. In this analysis (Figure 3a), individuals of populations FS, VF, and YP are grouped together, the same occurs with individuals of populations PA and VA, and a third group joins together individuals of populations CQ and RN that belong to the var. caven and are both located in the Puna eco-region (Figure 3a). The assignation of individuals to populations was 96.4% correct.

Figure 3.

Clustering of individuals by STRUCTURE. Each individual is represented by a vertical bar that is partitioned into colored segments that represent the individual’s estimated membership fractions. Same color in different individuals indicates that they belong to the same cluster. a) K = 11, estimated with no prior distribution of populations; b) K = 15, estimated with LOCPRIOR option. Population codes are given in Table 1.

When the LOCPRIOR option was used, K = 15 had the highest mean probability of density value (Ln P(D) = −17065.30), suggesting that each population corresponded to a single sampling site (Figure 3b). Moreover, the STRUCTURE results detected admixture of individuals in all populations with both models (Figure 3 a, b). The assignation of individuals to populations was 94.2% correct.

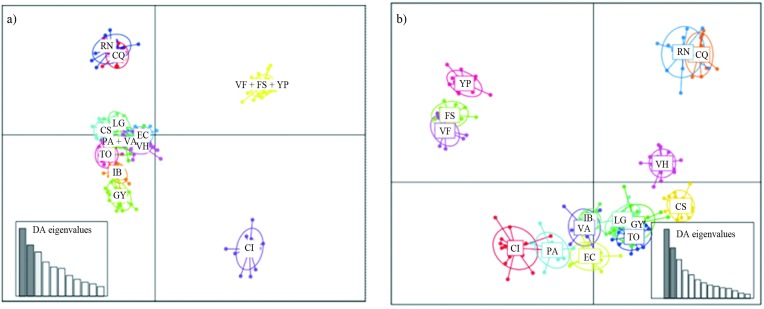
DAPC analysis was first made without any a priori group assignment. To obtain the optimal number of clusters with the find.clusters function, 70 axes that represented more than 88% of the total variance were retained. The program covered a range of possible clusters from 1 to 15. The lowest BIC value (1137.35) corresponded to K = 12. For DAPC analysis, 70 PCA axes and three discriminant functions were retained (52.3% of variance). One of the clusters included individuals of populations VF, FS, and YP, a second cluster joined PA and VA, and the remaining clusters were rather consistent with the rest of the sampling sites. The scatterplot of individuals on the two principal components of DAPC (Figure 4a) showed that the 12 clusters formed four groups. The consistency between prior and posterior assignment was 84.8%.

Figure 4.

Scatterplot of individuals on the two principal components of DAPC. The graph represents the individuals as dots and the groups as inertia ellipses. Eigenvalues of the analysis are displayed in inset: a) obtained with the find.clusters option, b) with clusters defined a priori according to the sampling site. Population codes are given in Table 1.

In the second analysis, the clusters were defined a priori, according to the sampling site. Also in this case, 70 axes of the PCA were retained for DAPC, corresponding to more than 88.8% of the variance, and three discriminant functions were obtained (53.9% of the variance). The scatterplot shows overlapping between the a priori defined groups (Figure 4b); the consistency between prior and posterior assignment was 88.8%.

The results obtained from the two approaches can also be compared with the posterior probability plots corresponding to the groups defined by the find.clusters procedure (Figure 5a) and with the groups defined by the sampling site (Figure 5b).

Figure 5.

STRUCTURE-like plot of DAPC analysis for a global picture of the clusters composition. Each individual is represented by a vertical colored line. Same color in different individuals indicates that they belong to the same cluster. a) K = 12, obtained with find.clusters option; b) K = 15, obtained with a priori information of sampling sites. Population Codes are given in Table 1.

Regarding the consistency between prior and posterior assignment of individuals to groups (Table 4), the maximum corresponded to GENELAND (100%), whereas the lowest consistency was obtained by DAPC without information on population membership (84.8%). Pairwise comparison of distances between individuals obtained from the probabilities of posterior assignment of population membership of individuals resulting from all five grouping methods (Table 4) revealed highly significant correlations (p < 0.0005, based on 2000 permutations) in all cases. The highest consistency value (r = 0.811) corresponded to the groupings obtained by GENELAND and STRUCTURE for the admixture model without prior information on population membership. The grouping obtained by DAPC without prior information on population membership showed the lowest correlation estimates when compared with most of the other grouping methods.

Table 4.

Pairwise comparison of distances between individuals obtained from the probabilities of posterior population membership of individuals, obtained by all five grouping methods. K = number of clusters; r = correlation coefficient; p < 0.0005; STR 1= STRUCTURE analysis without prior information; STR 2 = STRUCTURE analysis with LOCPRIOR option; DAPC 1= DAPC analysis with find.clusters option; DAPC 2 = DAPC analysis with a priori information of populations.

	r
	K	% of correct assignment	GENELAND	STR 1	STR 2	DAPC 1	DAPC 2
Sampling sites	15	-
GENELAND	12	100	-
STR 1	11	96.4	0.811	-
STR 2	15		0.726	0.710	-
DAPC 1	12	84.8	0.612	0.616	0.577	-
DAPC 2	15	88.8	0.769	0.673	0.716	0.607	-

Discussion

The analysis of genetic diversity within species is vital for understanding the evolutionary processes, both at the population and at the genomic levels. Several statistical packages recently developed which offer a panel of standard as well as more sophisticated analyses have been reviewed by Excoffier and Heckel (2006). Most data analyses require the use of more than one program and should start with generalist packages to uncover the basic properties of the data, followed by the use of specialized methodologies to address more specific questions (Excoffier and Heckel, 2006).

In line with this recommendation, we evaluated the consistency of different methodological approaches for analyzing genetic properties of Acacia caven populations, a shrub widely distributed in South America. This species plays an important role in arid ecosystems, as it contributes to the fixation of atmospheric nitrogen, provides fruits and leaves to herbivores, and stabilizes soils by fixing dunes. In addition, it is an appreciated natural resource for local settlers, because it provides fire wood, charcoal and forage for livestock. Due to its great plasticity, it is used in the reforestation of degraded ecosystems (Karlin et al., 1997).

In this work, we chose one exploratory and two Bayesian-model-based methods to infer the genetic structure of A. caven species from 15 sampling sites. The exploratory method used here was DAPC that seeks synthetic variables, the discriminant functions, which show differences between groups as best as possible, while minimizing variation within clusters (Jombart, 2012). Using the find.clusters option in this analysis, the number of populations inferred was K = 12, grouping together VF, FS, and YP and also PA and VA. DAPC analysis is preferred when groups are often unknown or uncertain and there is a need for identifying genetic clusters before describing them. In this work, we found that those sampling sites that grouped together in the same cluster were the geographically closer ones. When we defined the prior groups for the DAPC analysis, the inferred K was 15, the same as the number of sampling sites. In both cases, the percentage of variance explained by the three discriminant functions was < 54%. This could be attributed to the reduction of variables achieved by DAPC; in other words, we had 225 loci or variables, and this method reduced (in this case) the number of composed variables to the 70 more informative axes.

Additionally, two Bayesian analyses were applied to the data to study the genetic structure of the samples (GENELAND and STRUCTURE). When STRUCTURE was run with the LOCPRIOR option, the K estimated was coincident with the number of data sampling sites (K = 15). When using STRUCTURE, it is usually assumed that all partitions of individuals are a priori approximately equally likely. Since the number of possible partitions is immense, it takes highly informative data for STRUCTURE to conclude that any particular partition of individuals into clusters has compelling statistical support. In contrast, the LOCPRIOR models assume that, in practice, individuals from the same sampling location often come from the same population. Therefore, the LOCPRIOR models are set up to expect that the sampling locations may be informative about ancestry. If the data suggest that the locations are informative, then the LOCPRIOR models allow STRUCTURE to use this information (Pritchard et al., 2010).

GENELAND analysis in turn showed that the 15 A. caven populations studied could be grouped into K =12 independent groups, indicating that each sampling site represented a single Mendelian population, with the exception of VA and PA, and FS, YP, and VF, which would correspond to two clusters. STRUCTURE analysis without prior information of populations showed that the optimal number of populations was K = 11, joining together populations CQ and RN. The other 10 groups constituted were coincident with those detected by GENELAND. The slight difference between analyses regarding the detection of the number of K could be attributed to the model chosen, since GENELAND was run with previous information of geographic coordinates, tending to favor partitions that are spatially organized, while STRUCTURE was not. Similar differences in behavior between GENELAND and STRUCTURE were noted by Guillot et al. (2005) when comparing the dataset of Montana wolverines (Gulo gulo) recorded by Cegelski et al. (2003), as STRUCTURE inferred K = 3, whereas GENELAND inferred K = 4. In our case, GENELAND grouped together A. caven populations that were geographically and genetically closer and located in the same eco-region, such as VA and PA, and FS, VF, and YP. On the other hand, STRUCTURE detected the genetically similar groups. Variety caven is the most widespread (a generalist, in terms of ecology range), and here we analyzed five of its populations from two eco-regions. One could expect to find these populations grouped together according to the eco-region and the variety they belong to. However, the results of the Puna eco-region suggest that there the populations are less connected to each other by gene flow than the populations of the other eco-regions, since CI was not grouped together with CQ and RN in the STRUCTURE analysis. A possible explanation for this clustering could be that the geographic distances between CQ and RN were smaller than that from CI, and the genetic and geographic distances among the populations studied here have shown to be significantly correlated (Pometti et al., 2012). Moreover, although these three populations belong to the same variety and the same eco-region, they were found at different altitudes: RN at 1305 m o.s.l., CQ at 1511 m o.s.l., and CI at 2089 m o.s.l. This results in an environment of patchy vegetation, because of the presence of mountains that separate CI from RN and CQ. It has been well documented that marginal populations are often less variable than populations within the primary range (Blows and Hoffmann, 1993; Deng et al., 2009). The results obtained for the variety caven from the Puna eco-region could be explained by the observations of Hamrick and Godt (1990) and Maguire et al. (2000) that populations located at range margins are more isolated from sources of immigrants and are thus more prone to genetic bottlenecks.

When comparing the number K of populations estimated in the three methods, DAPC using the find.clusters option proved as accurate in detecting population clusters as STRUCTURE without prior information of populations and GENELAND.

When prior groups were defined, the DAPC results were coincident with those obtained by STRUCTURE with the LOCPRIOR option, where K = 15. As previously explained, in both cases the sampling locations were informative about ancestry.

A significant degree of genetic differentiation among A. caven populations was observed using the three methods, since K ranged from 11 to 15, showing a high level of structuration in the 15 sampling sites studied. The most evident associations among populations were found for PA and VA, and FS, VF and YP in all analyses, and for CQ and RN with STRUCTURE. No other association between populations by eco-region or variety was observed consistently with the tree methods used.

The three methods used here to infer population structure also provide coefficients of membership probabilities of each individual to the different groups, based on the retained discriminant functions in the case of DAPC, or based on ancestry in the case of STRUCTURE and GENELAND. While DAPC coefficients are different from the admixture coefficients of softwares like STRUCTURE or GENELAND, they can still be interpreted as proximities of individuals to the different clusters. Membership probabilities also provide indications of how clear-cut genetic clusters are (Jombart, 2012). The highest membership probabilities of each individual for the different groups were obtained by GENELAND, followed by STRUCTURE with prior definition of groups, STRUCTURE without population information, DAPC with prior definition of groups, and the lowest membership probabilities were those observed by DAPC without information on population membership. This means that the three methods and their variants provided accurate assignments of individuals, ranging from 84.8% for DAPC using the find.clusters option to 100% for GENELAND.

In conclusion, of the three methods used here, DAPC proved to be the fastest one, showing accuracy in inferring the K number of populations and the membership probabilities of each individual for the different groups in a short computational time (only a few minutes, while STRUCTURE and GENELAND needed four or five days to perform the analysis). So, DAPC should be preferred as a starting point when working with large datasets and several sampling sites, as recommended by Excoffier and Heckel (2006). GENELAND, on the other hand, provides information on the area of membership probabilities for individuals or populations in space, when coordinates are specified; moreover, the number of population units is treated as an unknown parameter (Guillot et al., 2005). STRUCTURE, in addition to inferring the number of K populations and the membership probabilities of individuals based on ancestry, allows a hierarchical analysis of sampling sites from K =2 to K = n, where n is the number of populations estimated with the highest mean probability of density value (Tishkoff et al., 2009; Pometti et al., 2012). The two latter analyses present the disadvantage of being more time-consuming and relying on assumptions, such as the type of population subdivision and Hardy-Weinberg and linkage equilibrium inside populations. Finally, in this work, all three methods showed high consistency in estimating the population structure of A. caven, inferring similar numbers of populations and membership probabilities of individuals to each group, with a high correlation between each other. This consistency may be interpreted in a similar way as the consistency between phenetic and cladistic analyses, which, although being based on different assumptions, reveal in many cases similar associations between phylogenetically related groups.