Abstract
Determination of the local configuration of interacting defects in a crystalline, periodic solid is problematic because defects typically do not have a long-range periodicity. Uranium dioxide, the primary fuel for fission reactors, exists in hyperstoichiometric form, UO2+x. Those excess oxygen atoms occur as interstitial defects, and these defects are not random but rather partially ordered. The widely-accepted model to date, the Willis cluster based on neutron diffraction, cannot be reconciled with the first-principles molecular dynamics simulations present here. We demonstrate that the Willis cluster is a fair representation of the numerical ratio of different interstitial O atoms; however, the model does not represent the actual local configuration. The simulations show that the average structure of UO2+x involves a combination of defect structures including split di-interstitial, di-interstitial, mono-interstitial, and the Willis cluster, and the latter is a transition state that provides for the fast diffusion of the defect cluster. The results provide new insights in differentiating the average structure from the local configuration of defects in a solid and the transport properties of UO2+x.
Uranium dioxide is the principal fuel of nuclear reactors. One of the unique properties of UO2 is its ability to accommodate a variable stoichiometry, depending on temperature and oxygen pressure1,2. The excess oxygen atoms in hyperstoichiometric uranium dioxide (UO2+x) occur as interstitial defects3,4,5,6,7,8,9,10,11. Positions and dynamics of these excess oxygen atoms control many important properties, such as thermal conductivity12,13,14, fission-product accommodation and transport15, micro-structure evolution16,17, and corrosion behavior18,19. These properties are closely related to the performance of the fuel in a reactor and its behavior in a geologic disposal. For UO2+x at low x values, the interstitial O atoms occur as isolated point defects. As x increases, individual defects interact with each other increasingly and form clusters3,4,5,20,21. Various experimental and theoretical studies have shown that these clusters are not random but rather structured with well-defined configurations3,4,5,6,11,22,23. However, the defect structures are difficult to quantify experimentally using diffraction techniques because the clusters are local structures and lack long-range periodicity. Based on early neutron-diffraction studies, a defect cluster model, the so-called 2:2:2 Willis type, was proposed for UO2.11–2.13 over fifty years ago3. Since then, this has remained the dominant conceptual model in the literature. Although slightly modified later by the original author and the collaborators4,5, the proposed oxygen configuration remains the same4,5. The acceptance of the model is largely based on the neutron diffraction data. However, recent first-principles calculations and empirical potential molecular dynamics show that the Willis cluster is not stable11,22,23,24,25. Upon optimization, it spontaneously relaxes to a split di-interstitial or tri-oxygen cluster sharing a vacancy (V3O”)11,22,23,24,25. The essential question is whether the Willis defect is an appropriate model for UO2+x or whether it is a limitation of static first-principles calculations being performed at the athermal limit that cannot account for finite temperature effects on the defect structure. In order to overcome the limitations related to zero temperature and the accuracy of empirical potentials in the previous theoretical calculations11,22,23,24,25, first-principles molecular-dynamics simulations at high temperatures are employed here. These results provide a self-consistent explanation of the Willis cluster model that is based on neutron diffraction data and the atomistic-scale structure that is derived from recent theoretical calculations. The simulations also improve the understanding of different defect types and reveal the role of the Willis defect model in the transport of the oxygen defect clusters in UO2+x.
Results and discussion
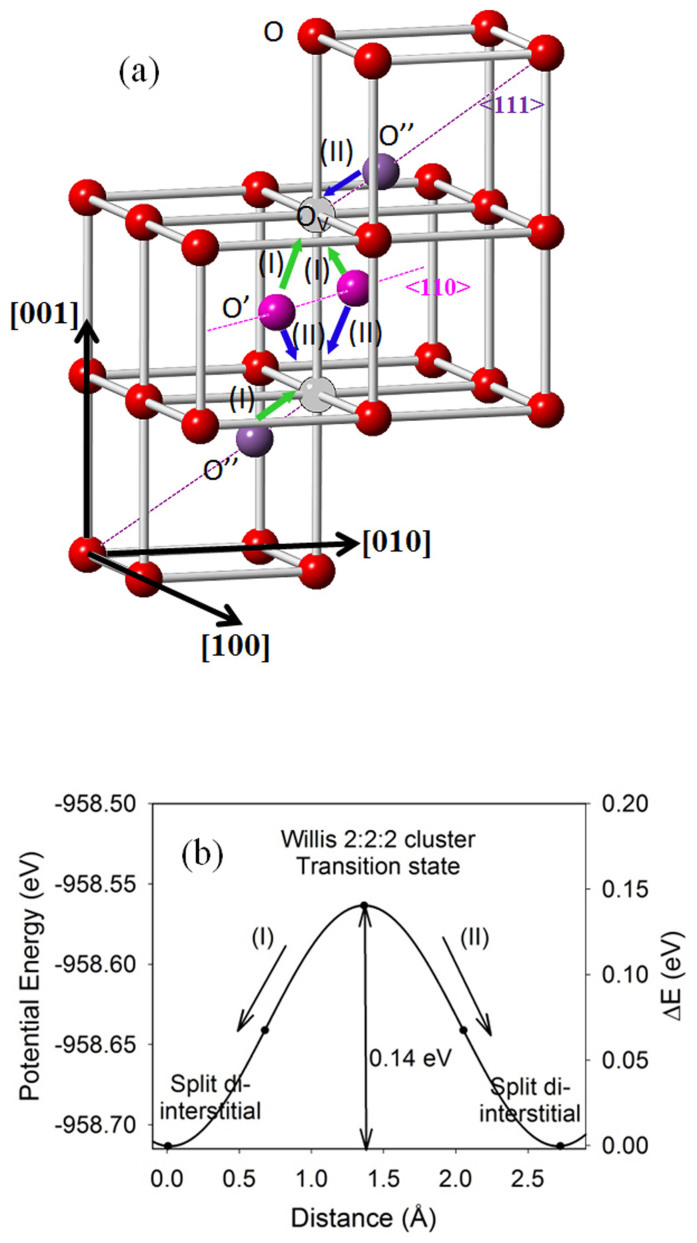
Uranium dioxide has the isometric fluorite structure (Fm3m). The 4a site is occupied by uranium, the 8c site by oxygen, and 4b site is empty in UO2. The Willis 2:2:2 defect cluster consists of two vacancies (Vo) at the O 8c site, two O interstitials displaced in <110> directions (O') from the 4b site, and two other O interstitials displaced in <111> (O”) from the 4b site (Figure 1a)3,4,5. Starting with this configuration without constraints, the cluster was optimized to a split di-interstitial defect (V3O”). Depending on how the Willis defect is perturbed by a small change in geometry, one of the <111> oxygen interstitials (O”) moves back to one vacant lattice 8c site while the other O” and two O' move away from their initial positions towards to the other vacant lattice 8c site. This split di-interstitial defect (V3O”) consists of three interstitial O atoms sharing an oxygen 8c site. This result confirms the instability of the Willis defect cluster repeatedly reported in recent first-principles studies using similar computational methods22,23,24,25. Geometry optimizations starting from the Willis defect configuration (Figure 1a) and with a constraint to allow the two <110> O atoms to move only in the (001) plane result in a only slightly modified Willis cluster configuration. However, when the constraint is removed, the structure relaxes to a split di-interstitial defect. This result suggests that, although the Willis cluster is unstable, it could provide a transition path for cluster migration from one location to another, very different from previously studied paths for oxygen di-interstitial diffusion11,23,25. In order to check the energy barrier of the transition path, the Climbing Image-Nudged Elastic Band (CI-NEB) method26 was applied to estimate the barrier for the Willis cluster configuration as a transition state. The calculated migration energy is ~0.14 eV (Figure 1b), which is low, about 5 times kBT at ambient temperature. Similar migration energies were estimated using empirical potential models and temperature-accelerated molecular-dynamics simulations but assuming different transition paths11,25. A recent DFT calculation estimated a higher migration barrier of 0.47 eV for a split di-interstitial assuming a different path23. Since static diffusion calculations often have to presume a transition path, one may question whether the paths and calculated values at the athermal limit represent the properties of the diffusion at the finite temperatures at which experiments with UO2+x are often performed.
Figure 1.
Schematic structure of Willis 2:2:2 defect cluster (a), which relaxes to either one of the split di-interstitial defects, depending on the path I or II respectively. The arrows indicate the direction of the movements of the atoms. (b) Potential energy surface of the migration of a split di-interstitial defect cluster. Migration energy barrier: 0.14 eV. Arrows in (b) show relaxation directions. Spheres are O atoms. Uranium atoms are not shown. Red stands for lattice 8c O atoms, purple and pink for oxygen interstitials displaced along <111> <110>, respectively, and grey circles for the oxygen vacancy at the 8c site.
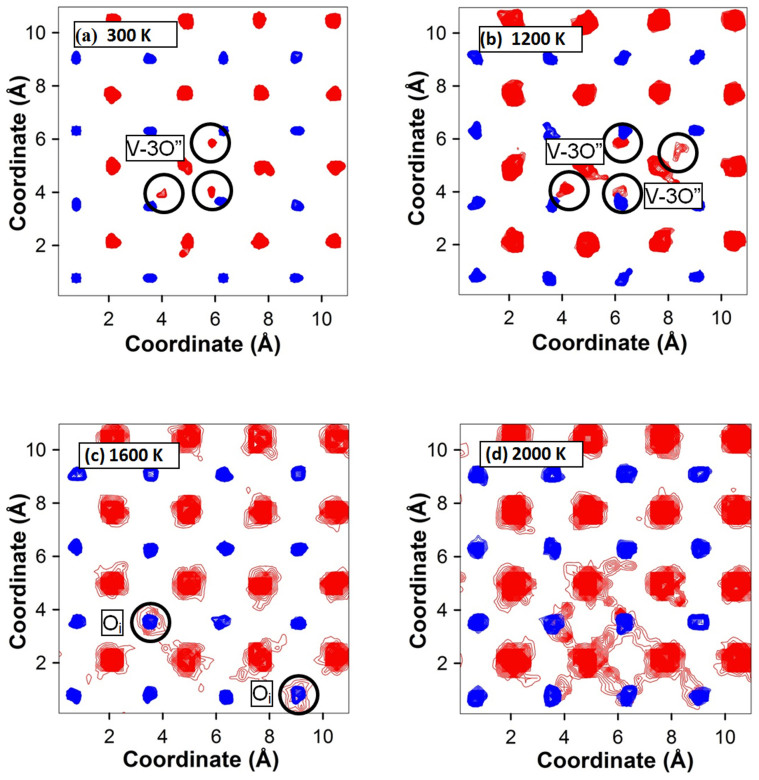
In order to reconcile the structure of the Willis defect and to directly reveal the migration of a split di-interstitial defect cluster, first-principles molecular-dynamics (MD) simulations were carried out at 300 K, 500 K, 800 K, 1200 K, 1600 K, and 2000 K. It was expected that thermal energy at higher temperatures activates the cluster migration and increases the effectiveness of probing the phase space of the cluster migration, giving its low migration energy barrier. The simulations started with one split di-interstitial in the computational supercell (UO2.06). At low temperatures (300 K–800 K), the split di-interstitials remain at their initial location with a configuration of the two interstitials displaced from the octahedral 4b sites, pushing a lattice 8c oxygen atom towards the other octahedral 4b site, resulting in three interstitials sharing an oxygen lattice 8c site. Figure 2a shows the atomic density probability contour maps at 300 K projected on (001) plane. Similar results were observed at 500 K and 800 K. At 1200 K, one of the interstitial O atoms is moved back to its lattice site while another oxygen interstitial appears, resulting in a new split di-interstitial defect cluster at a different location (Figure 2b). At 1600 K, the cluster has become two separate mono-interstitials (Figure 2c). After the dissociation, the two mono-interstitial defects remain relatively immobile for the rest of the molecular dynamics simulation. As the temperature increases to 2000 K, the cluster becomes highly mobile and goes through multiple transformations at different locations (Figure 2d).
Figure 2. Atomic density probability contour maps of UO2.06 (U32O66) projected onto (100) plane, calculated from the MD trajectories at different temperatures (a: 300 K, b: 1200 K, c: 1600 K, d: 2000 K).
Circles indicate the locations of the interstitial O atoms.
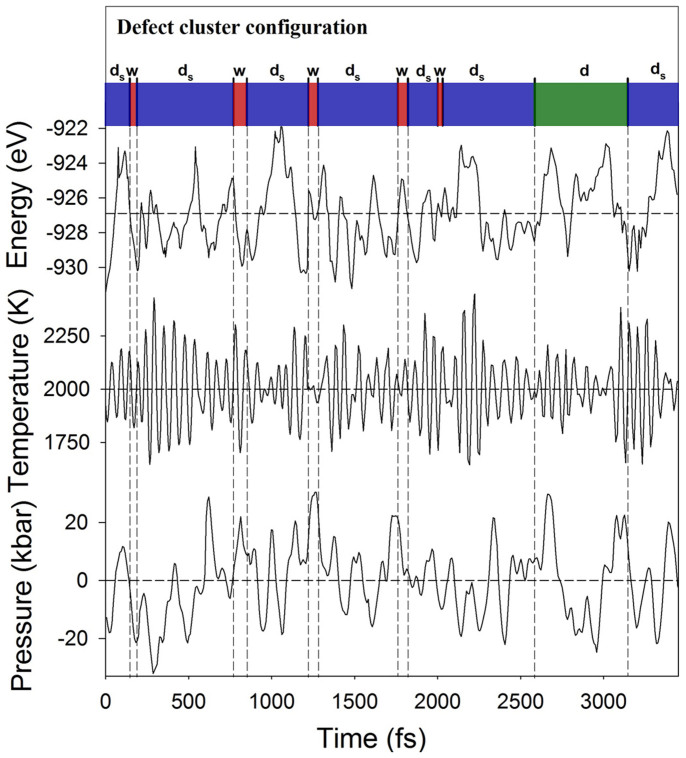
A careful analysis of the trajectory of UO2.06 at 2000 K shows that, as the split di-interstitial cluster migrates, it is transformed from one to another of the same kind. During the transition, the defect cluster passes quickly through a transition state with two 8c site vacancies (Vo), two <110> interstitials (O'), and two <111> interstitials (O”), which resembles the 2:2:2 Willis defect cluster. Between the transitions, the split di-interstitials cluster remain relatively stable. At some point during the MD run, the split di-interstitial cluster was temporarily transformed into a di-interstitial (i.e., two mono-interstitials at neighboring locations), but transformed back to a split di-interstitial cluster, which does not involve the 2:2:2 Willis configuration. Figure 3 shows the MD profiles of the potential energy, temperature, and pressure with time as the cluster migrates. Split di-interstitial clusters constitute the majority of the simulation time, and the Willis cluster is only a transition state occurring in a small percentage of the time. In order to check how individual split di-interstitials clusters interact with each other, similar molecular-dynamics simulations of UO2.13 and UO2.19 were completed at 2000 K with two and three di-interstitials in a 2×2×2 supercell, respectively. At the beginning of the simulations, each individual cluster behaved similarly to a single split di-interstitial cluster. However, once they were in contact and aggregated, the mobility of the clusters slowed because of complex interactions between them. During the migration of the interacting clusters, one of the split di-interstitial clusters had to be activated to a transition state similar to the Willis cluster. One important result of the simulations of single and multiple di-interstitial clusters is that the 2:2:2 Willis defect configuration is actually a transition state for migrating clusters at all of the x values investigated.
Figure 3. Potential energy, temperature, and pressure profiles over the course of a ~3.5 ps MD simulation of UO2.06 (U32O66) at 2000 K.
Top panel shows defect cluster configurations of different types: ds: split di-interstitial (blue), w: Willis 2:2:2 defect cluster (red), d: di-interstitial (green).
While the oxygen defect clusters migrate, the uranium atoms are immobile. With the excess oxygen atoms in the structure, some uranium atoms are oxidized from U4+ to U5+ by transferring an electron from uranium to oxygen. An interesting observation is that, at low temperatures (300 K–800 K), the U5+ atoms are mostly adjacent to the defect cluster, while at temperatures above 1200 K, the 5+ oxidation state occurs at all uranium lattice sites over the course of the simulation time of the 3 ps as shown in Figure S1. The fact that the location of U5+ is not constrained by the interstitial O atoms at temperatures lower than the temperatures at which the di-interstitial cluster becomes mobile suggests that the charge mobility is decoupled from the interstitial oxygen mobility. It seems that the oxidation state of U atoms changes between U4+ and U5+ at a faster rate than oxygen cluster migration through the U lattice.
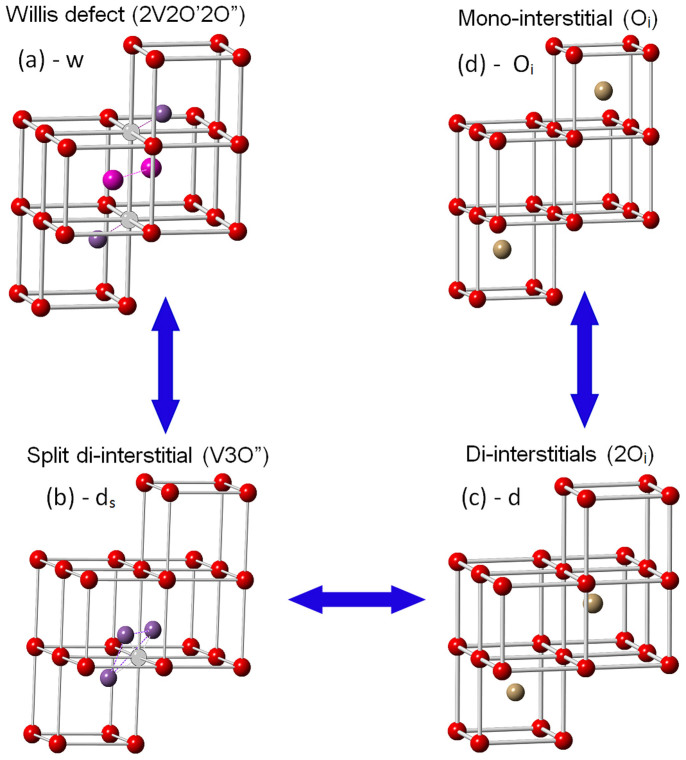
In order to reconcile these computational results with the early neutron diffraction data, average occupancy numbers and displacements of O' and O” interstitials were calculated over the trajectory for each composition and are listed in Table 1. For UO2.06, at low temperatures, the interstitials are mainly displaced along <111>. As the temperature increases, the O'/O” ratio increases. As expected, the displacements increase with temperature as well. As x increases from 2.06, 2.13, to 2.19 at 2000 K, the O'/O” ratio increases because the interstitial O atoms joining neighboring di-interstitial clusters are mainly displaced along <110>. The calculated ratios of O' and O” occupancies for UO2.13, 0.15:0.09, is consistent with the experimental values of 0.08–0.33:0.10–0.16 for UO2.11–UO2.13 based on neutron diffraction3,4,5. The calculated displacements for UO2.13 are 0.77 ± 0.21 Å and 0.92 ± 0.20 Å along <110> and <111>, respectively, as compared with experimental values of 0.85 ± 0.08 Å and 1.04 ± 0.10 Å for UO2.12 at 1073 K4. Note that the calculations were done at a higher temperature for the composition, which is necessary to have adequate statistical averages in a short MD simulation. However, the temperature only has a small effect on the values of both the O'/O” ratio and displacements as the temperature increases from 1200 K to 2000 K as shown in Table 1 for UO2.06. The lower temperature is comparable to the experimental temperature conducted at 1073 K4. The probability distributions of the angle between <111> and the displacement direction of interstitial oxygen atom are shown in Figure S2. The calculated result suggests that the 2:2:2 Willis cluster model for UO2.11–13 does account for the numerical fraction of the O' and O” interstitials. However, the Willis model does not represent the local defect configuration of defect clusters. The often assumed Willis 2:2:2 defect configuration is, in fact, a transition state for the migration of a split di-interstitial cluster in the hyperstoichiometric UO2. A careful review of all the trajectories shows that the average structure of UO2+x involves a combination of defect structures including the split di-interstitial, di-interstitial, mono-interstitial, and Willis cluster, and the latter serves as a transition state for a fast diffusion of the defect cluster (Figure 4). Spectroscopic techniques such as vibrational spectroscopy can be used to validate local structure configuration of different types of defect clusters, and property measurements such as electron and ionic conductivity can be used to test if the charge transport between U4+ and U5+ is activated at a lower temperature than the oxygen migration.
Table 1. Average occupancy numbers and displacements of <110> and <111> interstitial O atoms in UO2+x with different x values at different temperatures. v is the displacement in <110> directions and w is in the <111> directions.
| Composition | UO2.06 (U32O66) | UO2.13 | UO2.19 | ||
|---|---|---|---|---|---|
| Temperature | 300 K | 1200 K | 2000 K | 2000 K | 2000 K |
| O/O'/O” | 1.97/0.00/0.09 | 1.95/0.05/0.06 | 1.95/0.06/0.05 | 1.89/0.15/0.09 | 1.90/0.19/0.10 |
| v <110> | 0.67 ± 0.07 | 0.71 ± 0.18 | 0.74 ± 0.27 | 0.77 ± 0.21 | 0.72 ± 0.24 |
| w <111> (Å) | 0.78 ± 0.09 | 0.87 ± 0.19 | 0.90 ± 0.25 | 0.92 ± 0.20 | 0.90 ± 0.24 |
Figure 4. Defect models for oxygen interstitials in UO 2+x.
The Willis defect cluster (a) serves as a transition state for rapid diffusion of the split di-interstitial defect (b). The latter can also migrate through a di-interstitial (c). Di-interstitial can dissociate to two immobile mono-interstitials (d).
Methods
The first-principles calculations were based on the Density Functional Theory and plane wave basis sets as implemented in VASP27. The Projector-Augmented Wave method and exchange-correlation as parameterized by the Perdew-Wang 91 functional were applied in the Generalized Gradient Approximation28,29. For U, 14 electrons are treated as valence electrons and the core electrons have [Xe, 5d, 4f] configuration. For O, 6 electrons are treated as valence electrons and the core has [He]. On-site Coulomb interaction (U = 4.5, J = 0.51) with the rotational invariant Liechtenstein approach30, fully relativistic calculation for the core-electrons, and the scalar relativistic approximation for the valence electrons were employed to account for electron correlation and relativistic effects31. The U and J values are based on the experiment32, and these values have been used in a number of most recent publications of DFT+U studies of UO26,33,34. However, other different U and J values have also been used in the literature35,36, depending on how U and J values were determined. We have used U = 3.8 eV and J = 0.4 eV in previous publications36,37, the results are comparable with those using U = 4.5 eV and J = 0.51 eV. In this study, for the reason of comparison and consistency with the majority of the literature, the values based on the experiment were used. The details and performance of the methods on the calculations of crystal structure and electronic structure of UO2+x are summarized in a previous publication36. All the calculations were performed with a supercell of 2×2×2 unit cells of UO2 and the energy cut-off for the plane-wave basis was set to 520.00 eV. 3×3×3 k-point grids were used for the static calculations and Γ point for the molecular dynamics simulations. Ferromagnetic ordering without spin-orbit coupling was used in the molecular-dynamics simulations. Antiferromagnetic and ferromagnetic configurations were both used in the static calculations to test the effect of the spin configurations on the calculations. The optimized volumes were used for static calculations. For dynamics simulations, both optimized volumes and relaxed volumes at 1 bar and high temperatures were used. Molecular-dynamics simulations were performed using a NVT ensemble with the Nosé-thermostat for 2–3 ps for equilibration, which was checked by monitoring a number of parameters including temperature, pressure, potential energy of the systems, and kinetic energy of both U and O sublattices. The time step is 0.5 fs for low-temperature simulations (300–800 K) and 0.25 fs for high-temperature (1200–2000 K). It is necessary to carry out the simulations at high temperatures, at which multiple migration events can be observed and statistical meaningful averages can be obtained in short molecular dynamics simulations. The total energy drift was ~ (2–8) meV/atom/ps at low temperatures and increased to ~25 (15–50) meV/atom/ps at high temperatures. For UO2+x with unpaired 5f electrons, it was extremely challenging to achieve both high accuracy and adequate sampling with enough statistics of the systems. Extensive tests were performed to balance between the accuracy and duration of the simulations by systematically tuning simulation parameters including those related to convergences, real space projection, and time step. After equilibrations, simulations run up to 4 ps for statistical analysis.
Author Contributions
J.W., R.C.E., and U.B. participated in conceiving and designing the computations. J.W. carried out the computations. J.W., R.C.E., and U.B. have reviewed, discussed and approved the results and conclusions of this report.
Supplementary Material
Willis-defect-dynamics-supp-R1.pdf
Acknowledgments
This work was supported by the Center for the Materials Science of Actinides, an Energy Frontier Research Center, funded by the U.S. Department of Energy (DE-SC0001089). The computational work was supported by NERSC (DE-AC02-05CH11231) and XSEDE (TG-DMR080047N and TG-DMR100034).
References
- Olander D. R. Mechanistic interpretations of UO2 oxidation. J. Nucl. Mater. 252, 121–130 (1998). [Google Scholar]
- Thompson W. T. et al. Thermodynamic treatment of uranium dioxide based nuclear fuel. Int. J. Mater. Res. 98, 1004–1011 (2007). [Google Scholar]
- Willis B. T. M. Positions of Oxygen Atoms in UO2.13. Nature 197, 755–& (1963). [Google Scholar]
- Willis B. T. M. Defect Structure of Hyper-Stoichiometric Uranium-Dioxide. Acta Crystallogr., Sect. A: Found. Crystallogr. 34, 88–90 (1978). [Google Scholar]
- Murray A. D. & Willis B. T. M. A neutron-diffraction study of anion clusters in onstoichiometric uranium-dioxide. J. Solid State Chem. 84, 52–57 (1990). [Google Scholar]
- Geng H. Y. et al. Point defects and clustering in uranium dioxide by LSDA+U calculations. Phys. Rev. B 77, 104120 (2008). [Google Scholar]
- Andersson D. A. et al. Cooperativity among defect sites in AO2+x and A4O9 (A = U,Np,Pu): Density functional calculations. Phys. Rev. B 79 (2009). [Google Scholar]
- Dorado B. et al. Stability of oxygen point defects in UO2 by first-principles DFT plus U calculations: Occupation matrix control and Jahn-Teller distortion. Phys. Rev. B 82, 035114 (2010). [Google Scholar]
- He H. & Shoesmith D. Raman spectroscopic studies of defect structures and phase transition in hyper-stoichiometric UO2+x. Phys. Chem. Chem. Phys. 12, 8108–8117 (2010). [DOI] [PubMed] [Google Scholar]
- Crocombette J.-P., Torumba D. & Chartier A. Charge states of point defects in uranium oxide calculated with a local hybrid functional for correlated electrons. Phys. Rev. B 83, 184107 (2011). [Google Scholar]
- Bai X. M. et al. Migration mechanisms of oxygen interstitial clusters in UO2. J. Phys.: Condens. Matter 25, 015003 (2013). [DOI] [PubMed] [Google Scholar]
- Fink J. K. Thermophysical properties of uranium dioxide. J. Nucl. Mater. 279, 1–18 (2000). [Google Scholar]
- Stan M. Multi-Scale Models and Simulations of Nuclear Fuels. Nucl. Eng. and Technol. 41, 39–52 (2009). [Google Scholar]
- White J. T. & Nelson A. T. Thermal conductivity of UO2+x and U4O9−y. J. Nucl. Mater. 443, 342–350 (2013). [Google Scholar]
- Grimes R. W. & Catlow C. R. A. The stability of fission-products in uranium-dioxide. Philos. Trans. R. Soc. London, A 335, 609–634 (1991). [Google Scholar]
- Lucuta P. G. et al. Microstructural features of simfuel - simulated high-burnup UO2-based nuclear-fuel. J. Nucl. Mater. 178, 48–60 (1991). [Google Scholar]
- Nogita K. & Une K. Thermal recovery of radiation defects and microstructural change in irradiated UO2 fuels. J. Nucl. Sci. Technol. 30, 900–910 (1993). [Google Scholar]
- Shoesmith D. W. Fuel corrosion processes under waste disposal conditions. J. Nucl. Mater. 282, 1–31 (2000). [Google Scholar]
- He H. M. et al. Determination of local corrosion kinetics on hyper-stoichiometric UO2+x by scanning electrochemical microscopy. J. Electrochem. Soc. 156, C87–C94 (2009). [Google Scholar]
- Catlow C. R. A. Point-defect and electronic properties of uranium-dioxide. Philos. Trans. R. Soc. London, A 353, 533–561 (1977). [Google Scholar]
- Crocombette J. P. et al. Plane-wave pseudopotential study of point defects in uranium dioxide. Phys. Rev. B 64, 104107 (2001). [Google Scholar]
- Geng H. Y. et al. Ab initio investigation on oxygen defect clusters in UO2+x. Appl. Phys. Lett. 93 (2008). [Google Scholar]
- Andersson D. A. et al. Role of di-interstitial clusters in oxygen transport in UO2+x from first principles. Phys. Rev. B 80 (2009). [Google Scholar]
- Govers K. et al. Comparison of interatomic potentials for UO2. Part I: Static calculations. J. Nucl. Mater. 366, 161–177 (2007). [Google Scholar]
- Ichinomiya T. et al. Temperature accelerated dynamics study of migration process of oxygen defects in UO2. J. Nucl. Mater. 384, 315–321 (2009). [Google Scholar]
- Henkelman G., Uberuaga B. P. & Jonsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000). [Google Scholar]
- Kresse G. & Furthmuller J. Vienna ab-initio simulation package (Universitat Wein., 2004). [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
- Perdew J. P. et al. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687 (1992). [DOI] [PubMed] [Google Scholar]
- Liechtenstein A. I., Anisimov V. I. & Zaanen J. Density-Functional Theory and Strong-Interactions - Orbital Ordering in Mott-Hubbard Insulators. Phys. Rev. B 52, R5467–R5470 (1995). [DOI] [PubMed] [Google Scholar]
- Hafner J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 29, 2044–2078 (2008). [DOI] [PubMed] [Google Scholar]
- Dudarev S. L., Manh D. N. & Sutton A. P. Effect of Mott-Hubbard correlations on the electronic structure and structural stability of uranium dioxide. Philosophical Magazine B-Physics of Condensed Matter Statistical Mechanics Electronic Optical and Magnetic Properties 75, 613–628 (1997). [Google Scholar]
- Meredig B. et al. Method for locating low-energy solutions within DFT plus U. Phys. Rev. B 82, 195128 (2010). [Google Scholar]
- Andersson D. A. et al. U and Xe transport in UO2±x: Density functional theory calculations. Phys. Rev. B 84, 054105 (2011). [Google Scholar]
- Yu J. G., Devanathan R. & Weber W. J. First-principles study of defects and phase transition in UO2. Journal of Physics-Condensed Matter 21, 435401 (2009). [DOI] [PubMed] [Google Scholar]
- Wang J., Ewing R. C. & Becker U. Electronic structure and stability of hyperstoichiometric UO2+x under pressure. Phys. Rev. B 88, 024109 (2013). [Google Scholar]
- Wang J. & Becker U. Activation energetics of actinide diffusion in UO2 from first-principles calculations. J. Nucl. Mater. 433, 424–430 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Willis-defect-dynamics-supp-R1.pdf