Orchestration of cooperative events in DNA synthesis and repair mechanism unraveled by transition path sampling of DNA polymerase β's closing

Abstract

Our application of transition path sampling to a complex biomolecular system in explicit solvent, the closing transition of DNA polymerase β, unravels atomic and energetic details of the conformational change that precedes the chemical reaction of nucleotide incorporation. The computed reaction profile offers detailed mechanistic insights into, as well as kinetic information on, the complex process essential for DNA synthesis and repair. The five identified transition states extend available experimental and modeling data by revealing highly cooperative dynamics and critical roles of key residues (Arg-258, Phe-272, Asp-192, and Tyr-271) in the enzyme's function. The collective cascade of these sequential conformational changes brings the DNA/DNA polymerase β system to a state nearly competent for the chemical reaction and suggests how subtle residue motions and conformational rate-limiting steps affect reaction efficiency and fidelity; this complex system of checks and balances directs the system to the chemical reaction and likely helps the enzyme discriminate the correct from the incorrect incoming nucleotide. Together with the chemical reaction, these conformational features may be central to the dual nature of polymerases, requiring specificity (for correct nucleotide selection) as well as versatility (to accommodate different templates at every step) to maintain overall fidelity. Besides leading to these biological findings, our developed protocols open the door to other applications of transition path sampling to long-time, large-scale biomolecular reactions.

Capturing large-scale, long-time conformational rearrangements in biomolecular systems is a well appreciated central objective in structural and computational biophysics. Such motions are involved in drug binding, enzyme catalysis, protein folding, ion permeation through membrane channels, macromolecular assembly, and chromatin condensation. In many cases, experimental data are available on key structural states, kinetic measurements (e.g., rate of catalysis, effect of salt on reaction), and related mutant or variant systems. Modeling and simulation are thus important to complement experimental data by bridging macroscopic kinetic data with all-atom structures through insights into detailed local motions.

Standard approaches for biomolecules (1), molecular dynamics, Monte Carlo, and other specialized techniques,† can generate a rich amount of information concerning structural and dynamic properties for complex systems and connect structure and function through a wide range of thermally accessible states. However, sampling the complex configurational space of biomolecules remains a challenge.

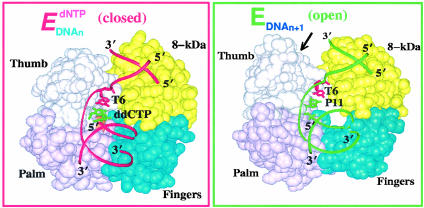
Here we describe the application of transition path sampling (TPS; ref. 18) (for an overview, see Appendix 1, which is published as supporting information on the PNAS web site) to a long-time, large-scale biomolecular transition, namely “thumb closing” before chemistry in DNA polymerase β (pol β) complexed to primer/template DNA. This pol β conformational change has been inferred from crystallographic structures (19) for pol β (Fig. 1) and is thought to be key in organizing the active site for DNA synthesis (extension of primer strand by one base) and thereby helping the enzyme discriminate a correct rather than incorrect nucleotide (e.g., C rather than A opposite a G). Because mechanistic details are difficult to obtain experimentally, modeling and simulation, subject to the usual approximations and imperfections of force fields, can help describe events at the atomic level and offer insights into rate-limiting conformational and chemical steps.

Fig. 1.

pol β in open (Right) and closed (Left) states (19).

Mammalian pol β is ideal for studying polymerase mechanisms for efficient and faithful DNA synthesis: it is the smallest eukaryotic cellular DNA polymerase (20), its activity is thought to be governed by an “induced-fit” mechanism in which the correct incoming base triggers a conformational change (19, 21–26), and a wealth of structural and kinetic data are available. Indeed, this induced-fit mechanism (19, 21–26) between the DNA-bound polymerase and the substrate, in which the correct substrate leads to a “closed,” tightly bound enzyme/substrate complex where catalytic groups are aligned as required for proper synthesis (“fidelity”), whereas the incorrect unit misaligns components so that repair is hampered (and can lead to “infidelity”), is supported by a large body of structural and kinetic data for polymerases such as the Klenow fragment, Klentaq 1, and HIV-1 reverse transcriptase. After synthesis or repair, which involves a chemical incorporation of the nucleotide in DNA by means of phosphodiester bond formation, the enzyme complex returns to its “open” state, releasing the DNA to allow translocation for the next cycle of polymerization.

Our path sampling of pol β's closing before the chemical reaction employs the state-of-the-art charmm force field and is subject to the well documented limitations of modern force fields; nonetheless, the details we unravel, which tie well with a large body of experimental as well as modeling studies, refine polymerase mechanisms by presenting a more detailed and complex view of polymerase kinetic cycles. Specifically, we identify key slow motions and interpret their significance in the context of pol β's reaction pathway. Namely, the calculated reaction profile reveals a cascade of subtle conformational rearrangements rather than subdomain motion per se that brings the DNA/protein system to a state nearly competent for the chemical reaction. This complex orchestration of events introduces checks and balances in the enzyme complex and likely helps in fidelity discrimination.

Shaped like a hand, with thumb, palm, and fingers subdomains (Fig. 1), pol β fills single-stranded gaps in DNA with relatively high accuracy (fidelity): it recruits the nucleotide unit (dNTP, 2′-deoxyribonucleoside 5′-triphosphate) complementary to the template base (e.g., C opposite G) about 1,000 times more often than the incorrect unit (e.g., T opposite G) (27–33). Closed and open conformations of pol β have been solved by x-ray crystallography by Wilson and coworkers (19, 34) and are related by a large subdomain motion (≈6 Å) of the thumb (Fig. 1, arrow). Kinetic data (28–30, 35–43) suggest slow conformational changes (milliseconds to seconds) before and after the chemical reaction, but their identity is unknown. Prior simulations by molecular and Langevin dynamics simulations, as well as targeted molecular dynamics (TMD), have suggested that key residues in the enzyme active site (e.g., Phe-272 and Arg-258) exhibit subtle conformational rearrangements during the thumb subdomain's motion (14, 15, 44). While these suggestions tie well with, and refine, recent experimental studies (45), details of the reaction pathway (Fig. 6, which is published as supporting information on the PNAS web site) explaining fidelity of the repair or synthesis process remain unknown.

Our goal is to delineate at atomic resolution the sequence of events in the overall catalytic mechanism of DNA polymerases along with energetic estimates and possibly to refine the schematic view of Fig. 6, which focuses on subdomain motions. This refinement is not possible with standard simulation methods that capture short-time dynamics, techniques that employ biasing potentials (13), or approaches that are subject to the approximations of transition-state theory in locating transition-state regions. TPS developed in the Chandler group (18) yields true dynamics at transition states by a clever sampling that conserves equilibrium distributions and the fluctuation-dissipation theorem (46): complete reaction profiles, transition states, barrier free energies, and reaction rates, for the system can ultimately be obtained. However, path sampling has been applied only to relatively small systems [alanine dipeptide isomerization (47), dissociation of water in the condensed phase (48), methanol coupling in zeolites, ice nucleation (49), folding of oligomers modeled as hard spheres (50), and β-hairpin folding (51)]. The challenge of applying TPS to a macromolecular system is certainly practical, to detect and then piece in correctly all the biochemically relevant transition regions, but new procedures are required to assess convergence and estimate free energy barriers. By addressing these computational issues for macromolecules in explicit solvent (our complete protocol is in Appendix 2, which is published as supporting information on the PNAS web site), we delineate here key transition-state regions and the associated cooperative dynamics in DNA pol β's closing before the chemical reaction; we also discuss how this collective cascade of subtle conformational changes may play a critical role in pol β's function.

Computational Method

System Preparation. Two models of solvated pol β/DNA/dCTP complexes were prepared from 1BPX (open binary) and 1BPY (closed ternary) crystal structures (19). Hydrogen atoms were added by charmm's subroutine hbuild (52). The open complex was modified by incorporating the incoming unit dCTP (deoxyribocytosine 5′-triphosphate) with nucleotide-binding Mg²⁺, producing the 1BPX ternary complex.

Also added were the following: a hydroxyl group to the 3′ terminus of the primer DNA strand, missing residues 1–9 of pol β, and specific water molecules coordinated to the catalytic Mg²⁺ (missing in the ternary complex).

Cubic periodic domains for both initial models were constructed by using simulaid and pbcaid (53). To neutralize the system at an ionic strength of 150 mM, water molecules with minimal electrostatic potential at the oxygen atoms were replaced by Na⁺, and those with maximal electrostatic potential were replaced with Cl^–. All Na⁺ and Cl^– ions were placed more than 8 Å away from any protein or DNA atoms and from each other. The electrostatic potential for all bulk oxygen atoms was calculated with delphi. The resulting system (see Lower Center image in Fig. 4) has 40,238 atoms (including 11,249 water molecules). Consistent with a pH value of 7.0, we assume deprotonated states (i.e., –1 charge each) for Asp-190, Asp-192, and Asp-256, as assumed recently (54). Appendix 3, which is published as supporting information on the PNAS web site, provides protonation states of titratable side chains and a brief related discussion. These settings produce a net charge of +7 for pol β, –29 for DNA, and –4 for the dCTP. There are 42 Na⁺ ions, 20 Cl^– ions, and 2 Mg²⁺ ions, producing an overall neutral system.

Fig. 4.

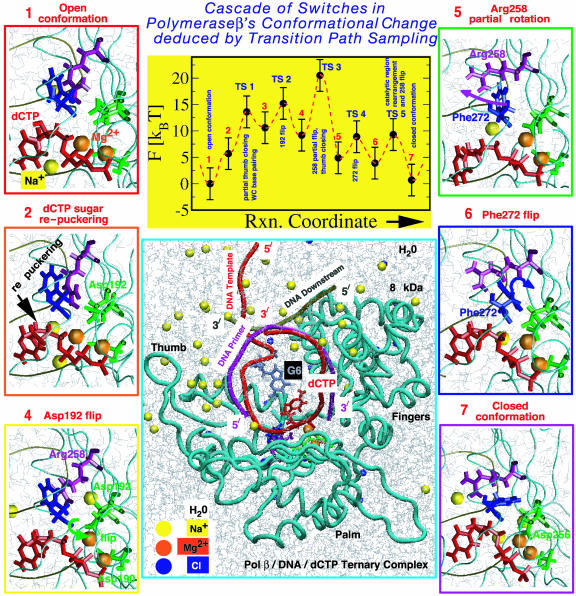
(Upper Center) Overall captured reaction kinetics profile from TPS for pol β's closing transition (for a G·C system) from the open state and estimated energies in units of k_BT (product of Boltzmann constant and absolute temperature). Different barrier regions (TS) and metastable basins along the reaction coordinate are illustrated (images 1, 2, 4–6, and 7). (Lower Center) Structure of pol β/DNA/dCTP ternary complex.

Initial Runs. To generate configurations for initiating path sampling, targeted dynamics were conducted with charmm C28a2 (52), implemented with a restraint constant K = 2,000 kcal/(mol·Å²) on heavy atoms of pol β (see Appendix 2). With a decrease from 5 to 0 Å in the offset distance (d₀) over 100 ps, the conformational change is driven from open to closed states. Although unphysical, the targeted trajectory helps suggest transition-state regions. Namely, histograms of geometric variables, dihedral angles associated with key residues 192, 258, and 272 (flip of Asp-192, rotation of Arg-258, and flip of Phe-272), and the thumb's helix N displacement (residues 275–295) that display bimodality lead us to propose candidates for the path sampling order parameters {χ_i}, as described in Table 1 and Fig. 2.

Table 1. Order parameters for each transition state (TS) and associated simulation details.

TS	Event	χ-order parameter*	χmax state A	χmin state B	Length, ps TPS/CPD†	No. of trajectories	τmol, ps‡
1	Partial thumb motion, Watson—Crick pairing of dCTP	rms deviation of residues 275-295 with respect to closed form	3.4 Å	2.7 Å	100/100	150	70 ± 10
2	Asp-192 flip	Dihedral angle Cγ—Cβ—Cα—C	100°	140°	10/20	200	4 ± 1
3	Arg-258 rotation, thumb closing	Dihedral angle Cγ—Cδ—Nε—Cζ	120°	160°	10/20	200	4 ± 1
4	Phe-272 flip	Dihedral angle Cδ1—Cγ—Cβ—Cα	-25°	15°	10/20	200	3 ± 1
5	Arg-258 rotation, ion motion	Distance: nucleotide-binding Mg2+ to O1α of dCTP	—	—	—	—	-

^*Our coverage of each TS is given by χ_min, χ_max, along with lengths τ of TPS simulations and of additional runs for convergence (see Figs. 2 and 7).

^†CPD, commitment probability distribution function (see Fig. 7).

^‡See Fig. 7 for estimating τ_mol.

Fig. 2.

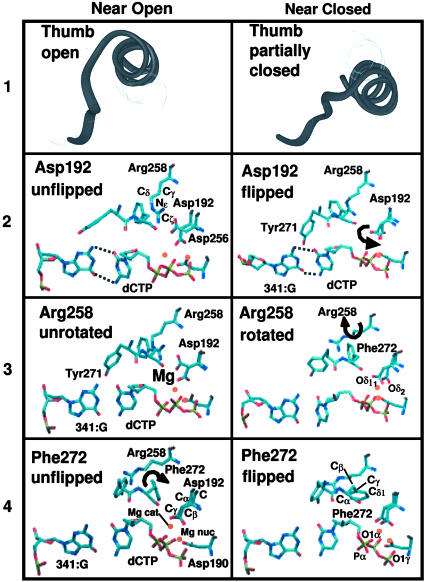
Molecular snapshots near open (Left) and closed (Right) states for four transition state regions. (1) Partial thumb closing. (2) Asp-192 flip. (3) Arg-258 partial rotation. (4) Phe-272 flip.

Identifying Transition-State Regions. The existence of transitionstate regions 2, 3, and 4 was confirmed by calculating the commitment probability distribution (CPD) (47) by using several short (20–100 ps), unrestrained dynamics trajectories. The CPD describes the partitioning of trajectories in proximal free-energy basins near each transition state region (47) (Appendix 2) from the transition state ensemble. For example, barrier region 3, partial rotation of Arg-258, corresponds to the dihedral-angle window between the dashed lines for χ₃'s evolution in Fig. 7, which is published as supporting information on the PNAS web site (see also Fig. 8 in Appendix 1). For each configuration in such a barrier region, four trajectories were initiated with a randomly chosen set of momenta from a Maxwell distribution, and the commitment probability P_B is determined as the fraction of trajectories committing to basin B (i.e., χ₃ > 160°; see Table 1); thus, resolution of the commitment probability is 0.25. From P_B, the probability distribution P(P_B) yields the CPD function of Fig. 7. In general, the initial (unphysical) trajectory (Fig. 7) does not lead to a unimodal function and lacks the peak at 1/2 indicating correct barrier crossing (18) (where P_B ∼ P_A ∼ 0.5). Because the ensemble for Arg-258 committed to an intermediate value of χ₃, the existence of a different barrier region (TS 5) was suggested.

Performing Path Sampling. Our protocol (Appendix 2) was performed by using a perl script that interfaces charmm C28a2 (52) and handles multiple transition-state regions characterized by sets of arbitrary dihedral angles, distances, and any calculable configurational quantity. charmm's Verlet integrator with a time step of 1 fs is used for generating symplectic dynamics trajectories, with electrostatic and van der Waals interactions smoothed to 0 at 12 Å and cubic periodic boundary conditions enforced. The truncation of long-range electrostatic interactions makes the computation of our 40,238-atom system tractable; studies on DNA (e.g., ref. 55) conclude that this approach is satisfactory.

Path segments corresponding to barrier regions (generated as described above, Fig. 7) were used to initiate four different path sampling runs corresponding to TS regions 1–4 (Table 1). Trajectories in each region were harvested by using the shooting algorithm (56) (Appendix 1 and Fig. 8 Inset) to connect by an ensemble two metastable states A and B by means of a Monte Carlo protocol in trajectory space. States A and B are defined by our order parameters (Table 1): for TS 1, χ₁ > χ_max ∈ A and χ₁ < χ_min ∈ B; for TS 2–4, χ_i < χ_max ∈ A and χ_i > χ_min ∈ B. In each shooting run, the momentum perturbation size (dP ≈ 0.002 for TS 1, and 0.005–0.01 for TS 2–4, in units of atomic mass units ×Å/fs) yields an acceptance rate of 30–40%.

Monitoring Adequate Sampling and Convergence. Five sample harvested trajectories (of 150–200 total trajectories in each ensemble; see Table 1) capturing the dynamics for each region 1–4 are shown in Fig. 7. The ergodicity and convergence of each run were monitored by calculating the autocorrelation function of the order parameter 〈χ_i(0)χ_i(t)〉 (Fig. 7, Top Right). The gradual decrease for χ₁ and increase for χ₂, χ₃, and χ₄ indicate the decorrelation of the generated trajectories in each TPS run; strongly correlated trajectories would lead to an abrupt change in the correlation function for the chosen values of τ. The characteristic relaxation time τ_mol associated with the crossing of each transition-state region is given by the time taken for the gradual transition of the autocorrelation function 〈χ_i(0)χ_i(t)〉 and can be estimated graphically, to yield values in Table 1. The sampling quality was also assessed by calculating order-parameter correlation functions in path space and found to be very satisfactory (see Appendix 2).

The convergence of the overall harvested path (collection of 150–200 trajectories in each region) was verified by recalculating commitment probability distribution functions (Fig. 7 Right). Unimodal distribution peaks around 1/2 reflect the true saddle nature of the transition state region. The striking contrast between the distributions of the converged path sampling runs and those for the initial trajectory reveals the system's relaxation along coordinates orthogonal to the reaction coordinate, to reach true saddle regions, as discussed in ref. 18.

Piecing Entire Reaction Path. The combined path sampling simulations (750 trajectories of length 10–100 ps) were extended by 20 dynamics simulations of lengths 500 ps to 1 ns to ensure that pol β open and closed structures were visited‡ and trajectories ergodically sampled the phase space between the five barrier regions (see Fig. 3). The decorrelation from the initial path during our path sampling is significant, indicating independence from initial conditions (see Fig. 9 in Appendix 2).

Fig. 3.

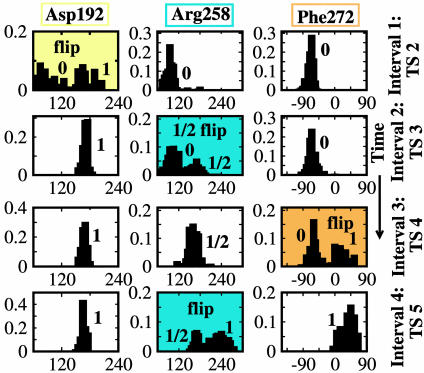
Normalized probability distributions of dihedral angles (in degrees) characterizing flips of pol β residues. Each column represents a dihedral angle distribution and each row represents a time interval capturing the dynamics in a barrier region. Labels 0, 1/2, and 1 refer to unflipped, partially flipped, and fully flipped states. Highlighted bimodal plots correspond to flipping events.

TS region 5 was discovered when extending the trajectories associated with TS region 4. In overcoming TS region 5, the fully rotated state of Arg-258 is stabilized, and the ligands coordinating the nucleotide binding Mg²⁺ ion undergo subtle rearrangements (see Results).

Normalized probability distributions (i.e., unit areas) for the dihedral angles characterizing the flips Asp-192, Arg-258, and Phe-272 are calculated in Fig. 3, from the harvested trajectories. The nonoverlapping nature of the distribution for each residue (i.e., within each column) confirms independence of the motions; the transient time τ_mol (Table 1) to cross each transitionstate region is much shorter than the time separating the events, justifying performing independent runs for each flip. The combined distribution of dihedral angles for each residue samples the dihedral space between the open and closed conformations of pol β, further ensuring that we have captured intermediate configurations between the barrier regions. The dihedral-angle distributions clearly show that the Asp-192, partial-Arg-258, Phe-272, and full-Arg-258 flip events are local barrier regions in the free energy surface.

The order of the transition states along the pathway (see Fig. 4) was determined by ranking the values of the order parameters in the metastable states. For example, because χ₂ changes from unflipped (in open) to flipped (in closed) values while χ₃, χ₄, and χ₅ remain at values of the open structure (see Fig. 3), we know that TS 2 precedes TS 3–5. The independence of flips associated with barrier regions 2–5 suggests that key residues of the enzyme act discretely to trigger a cascade of subtle changes resulting in systematic assembly of the catalytic region. Near the open and closed states (see Fig. 2) the χ_i values range as follows: χ₁ from ≈6 to 1.5 Å, χ₂ from ≈90° to 180°, χ₃ from ≈100 to 260°, χ₄ from ≈–50° to 50°, and χ₅ from ≈3.2 to 1.8 Å.

The combined simulations involved an aggregate time of ≈85 ns, requiring 10 months of central processing unit time (approximately half of which was spent on the free energy calculations) on 24 processors of an Origin 3000, 120-MHz processor Silicon Graphics machine at New York University.

Results: Sequence of Conformational Changes

Fig. 4 illustrates the sequence of changes along the pathway: 1, partial thumb closing; 2, flip of Asp-192; 3, partial rotation of Arg-258; 4, flip of Phe-272; and 5, rearrangement of catalytic region and stabilization of Arg-258 in the fully rotated state. The approximate free energies shown were calculated by using our method BOLAS (unpublished work and Appendix 2), separate from the path sampling protocol.

The conformational landscape that emerges reveals highly cooperative events. Starting from the open ternary complex, the system traverses metastable basin 2 as the thumb subdomain begins to close, during which repuckering of the sugar ring of dCTP occurs: the pseudorotation phase angle changes from about 160° (C2′-endo) to 25° (C3′-endo) (57) (with mean puckering amplitude, 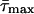, constant at ≈44°), facilitating the pairing of dCTP with the guanine template partner. Crossing TS 1 leaves the system in metastable basin 3, in which the thumb is partially closed. The partial thumb closing corresponds to a large subdomain motion during which the rms deviation of helix N residues with respect to the closed structure changes from around 6 to 2.5 Å. The associated dynamics reveal cooperative motion among helix N (thumb) residues, incoming dCTP, guanine template partner, and conserved residue Tyr-271, resulting in the Watson–Crick pairing of dCTP with the template G. Thus, TS 1 selects and helps discriminate the correct incoming dNTP. A similar motion coupling, with biological significance, has been inferred in a recent study involving DNA polymerase I of the A family (58), where the thumb moves in concert with the conserved tyrosine residue (Tyr-714 in DNA polymerase I); this cooperativity has been suggested to block and unblock a preinsertion site that likely shields the template partner against inducing frameshift mutations, thereby enhancing fidelity. Our results for pol β (which lacks such a preinsertion site) suggest that the cooperativity of the thumb motion with Tyr-271, dCTP, and template partner acts similarly as a signaling network for correct nucleotide selection.

TS regions 2–5 define a cascade of global and side-chain motions that (i) transition the catalytic region from a disordered arrangement to one nearly ready for the two-metal-ion (Mg²⁺)-catalyzed phosphoryl transfer reaction (59); and (ii) stabilize the polymerase in the closed (active) form. With Asp-192's flip (TS 2), the system reaches basin 4. Asp-192's flip occurs concomitantly with the breaking of the salt bridge between Asp-192 and Arg-258 and facilitates the aspartate oxygens O^δ1 and O^δ2 to coordinate the catalytic and nucleotide-binding magnesium ions (see Fig. 4 4). Interestingly, the path sampling snapshots in Fig. 4 indicate that the Na⁺ ions are mobile in the vicinity of the active site (ions were initially placed 8 Å from each other and from the enzyme/DNA/dCTP complex), as also supported by separate modeling studies (L. Yang, K. Arora, and T.S., unpublished work).

The partial rotation of Arg-258 occurs in crossing TS 3, during which the thumb assumes the fully closed position; the rms deviation (χ₁) decreases from ≈2.4 to 1.7 Å between metastable basins 4 and 5. Once in basin 5, Arg-258 interchanges between the partially and fully rotated positions. After crossing TS 4, the flipped state of Phe-272 (χ₄ = 50°) sterically clashes with Arg-258 in its partially rotated state. Thus, metastable basin 6 is a precursor for stabilizing Arg-258 in its fully rotated state. Metastable basin 7 (after crossing TS 5) is characterized by the stabilization of Arg-258 in its fully rotated state, where it participates in a salt bridge with residues Tyr-296 and Glu-295.

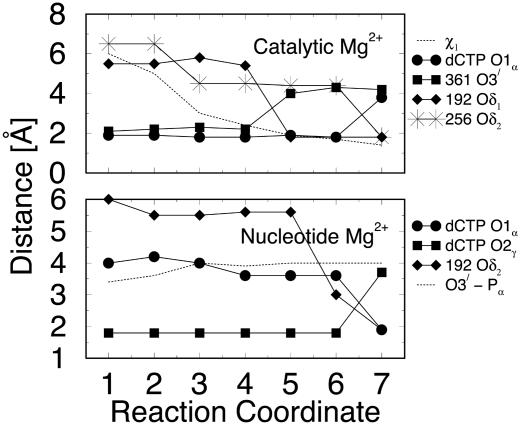
Concomitant to the motion in crossing transition states 2–5, the position and coordination of the catalytic Mg²⁺ ion undergo subtle, yet systematic, transformations (Fig. 5) that evolve the system toward the catalytically active configuration. The three conserved aspartate residues (190, 192, and 256 in pol β) coordinate the Mg²⁺ ions, creating a tight binding pocket for the metal ions. The formation of two octahedral complexes (involving the Mg²⁺ ions and their respective ligands), and the transformation to a nearly reaction-competent state [as envisioned in the two-metal-ion catalytic mechanism (59)], is completed in a cascade of changes involving the aspartate oxygens of Asp-192 and Asp-256 and the Mg²⁺ ions (TS 2–4), and in a subtle rearrangement of the Mg²⁺ ions (TS 5), as evident from Fig. 5.

Fig. 5.

Evolution of average distances of ligands coordinating the catalytic and nucleotide-binding Mg²⁺ ions along the reaction coordinate. For atom types, see Fig. 2. States 1–7 correspond to Fig. 4. The extent of thumb closing (χ₁ in Upper), and a crucial distance for the chemical reaction (O3′ of last primer residue to P^α of dCTP in Lower) are also provided.

Additional transition state regions, outside of the reaction coordinate considered in Fig. 4, cannot be excluded. For instance, in our open starting conformation, the DNA was already bound to pol β, and the two Mg²⁺ ions along with the dCTP molecule were already in the vicinity of the catalytic region. The binding events of dCTP, Mg²⁺ ions, and DNA could represent additional transition states, although experimental evidence from kinetic studies suggests that they are not rate limiting (27).

Discussion: Rate-Limiting Steps and Implications for Polymerase Efficiency and Fidelity

The developed divide-and-conquer procedure described here for trajectory generation and analysis makes possible the application of TPS to biomolecular systems. Of course, all such simulations are vulnerable to uncertainties in force field parameters, even in the carefully developed and tested charmm package, and require careful assessment with respect to available experimental and modeling studies. Although the generated trajectories differ from each other in microscopic details, the collective picture that emerges here suggests a dominant pathway for the closing of the pol β/DNA complex for the correct (G·C) system. This pathway is consistent with the biological relevance of the pol β conformational transition (i.e., selection of incomer dNTP, followed by assembling of the catalytic region for nucleotidyl transfer reaction). The unraveled complex cascade of subtle conformational rearrangements also introduces “checks and balances” on the nucleotide incorporation process.

Our findings of subtle residue motions rather than subdomain motion per se tie well with a large body of experiments that reveal reduced catalytic efficiency of the enzyme (19, 21–26, 45) when some of these key residues (258, 192, and 272) and those associated with the metastable nearby basins (such as 271) are altered. However, our specific description of sequential conformational events and associated energetics (see below) pieces together and extends these kinetic data and findings of prior modeling studies by suggesting a global significance of these collective local changes: a tight orchestration of events at the active site may be essential to the enzyme's function. This view refines the catalytic cycle of Fig. 6 by extending the mechanisms beyond simple subdomain motions. Significantly, a cascade of events guides the enzyme toward the chemistry step; different conditions at the active site may sensitively affect this delicate steering process. Indeed, we expect that the process for a mismatched system (e.g., G·A) at the primer/template terminus will result in multiple pathways rather than a dominant pathway as found for our G·C system here; these alternatives may hamper the closing transition, allowing removal of the incorrect nucleotide unit near the active site.

Significantly, our estimated free energy values along the closing pathway (Fig. 4) suggest that the rate-limiting step is associated with TS 3, namely the partial rotation of Arg-258 (overall barrier of 20.5 ± 3 k_BT). This value is lower but comparable to the overall rate of the reaction (25–28 k_BT), as obtained from experimental kinetic data [k_pol, the overall rate of nucleotide incorporation of 3–90 s^–1 (27–33)]. This rate-limiting conformational barrier in the same order of the overall (conformational and chemical steps) reaction profile immediately suggests site-specific mutant experiments on Arg-258 to assess Arg-258's effect on reaction efficiency and fidelity. For example, we expect that the substitution of Ala for Arg will reduce the TS 3 barrier and possibly accelerate the conformational closing (i.e., lead to a higher synthesis efficiency and lower k_pol value).

Ongoing work in our laboratory combined with a tour de force study of the chemical reaction in T7 DNA polymerase (54) also suggest that chemical-reaction barriers define the overall rate-limiting step, consistent with analysis of Showalter and Tsai (60). Still, even in the chemical barrier identified (54), crucial motions of selected residues such as conserved acidic groups in the active site emerge. Thus, while the identification of the single, overall rate-limiting step, as well as events leading up to it or affecting it, have important biological implications for fidelity (60), our results underscore the parallel need to understand at atomic resolution the complex sequence of events in the overall catalytic mechanism of DNA polymerases and to refine the somewhat simplistic kinetic pathway (Fig. 6). These refinements may ultimately lead to design of site-specific therapeutic agents that address diseases caused by DNA polymerase malfunction such as skin cancer and premature aging.

Possible extensions of path sampling to treat the chemical reaction by a combined molecular/quantum mechanical treatment can also be envisioned to further illuminate polymerase mechanisms. Application of other long-time methods that have potential for capturing large-scale motion in biomolecules and associated free energy profiles, such as the stochastic path approach of Elber et al. (10, 61), enhanced sampling using Tsallis statistics (62), and the adaptive sampling approach of Vanden-Eijnden and coworkers (E. Weinan, W. Ren, and E. Vanden-Eijnden, personal communication) may also be fruitful.