Landmark Estimation of Survival and Treatment Effect in a Randomized Clinical Trial

Summary

In many studies with a survival outcome, it is often not feasible to fully observe the primary event of interest. This often leads to heavy censoring and thus, difficulty in efficiently estimating survival or comparing survival rates between two groups. In certain diseases, baseline covariates and the event time of non-fatal intermediate events may be associated with overall survival. In these settings, incorporating such additional information may lead to gains in efficiency in estimation of survival and testing for a difference in survival between two treatment groups. If gains in efficiency can be achieved, it may then be possible to decrease the sample size of patients required for a study to achieve a particular power level or decrease the duration of the study. Most existing methods for incorporating intermediate events and covariates to predict survival focus on estimation of relative risk parameters and/or the joint distribution of events under semiparametric models. However, in practice, these model assumptions may not hold and hence may lead to biased estimates of the marginal survival. In this paper, we propose a semi-nonparametric two-stage procedure to estimate and compare t-year survival rates by incorporating intermediate event information observed before some landmark time, which serves as a useful approach to overcome semi-competing risks issues. In a randomized clinical trial setting, we further improve efficiency through an additional calibration step. Simulation studies demonstrate substantial potential gains in efficiency in terms of estimation and power. We illustrate our proposed procedures using an AIDS Clinical Trial Protocol 175 dataset by estimating survival and examining the difference in survival between two treatment groups: zidovudine and zidovudine plus zalcitabine.

1 Introduction

In many research settings with an event time outcome, it is often not feasible to fully observe the primary event of interest as these outcomes are typically subject to censoring. In the presence of noninformative censoring, the Kaplan Meier (KM) estimator (Kaplan & Meier, 1958) can provide consistent estimation of the event rate. However, such a simple estimate may not be extremely precise in settings with heavy censoring. To improve the efficiency, many novel procedures have been proposed to take advantage of available auxiliary information. For example, when the auxiliary information consists of a single discrete variable W, it has been shown that the nonparametric maximum likelihood estimator of survival is n⁻¹∑_i F̂_T|W(t|W_i) where F̂_T|W is the KM estimate of survival based on the subsample with W = W_i (Rotnitzky & Robins, 2005). Murray & Tsiatis (1996) considered a nonparametric estimation procedure to incorporate a single discrete covariate and provided theoretical results on when such augmentation enables more efficient estimation than the KM estimate. However, when multiple and/or continuous covariates are available, such fully nonparametric procedures may not perform well due to the curse of dimensionality.

Additional complications may arise when auxiliary variables include intermediate event information observed over time. In many clinical studies, information on non-fatal intermediate events associated with survival may be available in addition to baseline covariates. For example, in acute leukemia patients, the development of acute graft-versus-host disease is often monitored as it is predictive of survival following bone marrow or stem cell transplantation (Lee et al., 2002; Cortese & Andersen, 2010). The occurrence of bacterial pneumonia provides useful information for predicting death among HIV-positive patients (Hirschtick et al., 1995). In these settings, incorporating intermediate event information along with baseline covariates may lead to gains in efficiency for the estimation and comparison of survival rates.

In the aforementioned examples, the primary outcome of interest is time to a terminal event such as death and the intermediate event is time to a non-terminal event. This setting is referred to as a semi-competing risk setting since the occurrence of the terminal event would censor the non-terminal event but not vice versa. With a single intermediate event and no baseline covariates, Gray (1994) proposed a kernel smoothing procedure to incorporate such event information in order to improve estimation of survival. Parast et al. (2011) proposed a nonparametric procedure for risk prediction of residual life when there is a single intermediate event and a single discrete marker. Parast et al. (2012) extended this procedure to incorporate multiple covariates using a flexible varying-coefficient model. However, such methods cannot be easily extended to allow for both multiple intermediate events and baseline covariates due to the curse of dimensionality (Robins & Ritov, 1997).

Most existing methods for analyzing semi-competing risk data focus on estimation of relative risk parameters and/or the joint distribution of events under semiparametric models (Fine et al., 2001; Siannis et al., 2007; Jiang et al., 2005). These semiparametric models, while useful in approximating the relationship between the event times and predictors, may not be fully accurate given the complexity of the disease process. Therefore, marginal survival rates derived under such models may be biased and thus lead to invalid conclusions (Lin & Wei, 1989; Hjort, 1992; Lagakos, 1988). To overcome such limitations, we propose a two-stage procedure by (i) first using a semiparametric approach to incorporate baseline covariates and intermediate event information observed before some landmark time; and (ii) then estimating the marginal survival nonparametrically by smoothing over risk scores derived from the model in the first stage. The landmarking approach allows us to overcome semi-competing risk issues and the smoothing procedure in the second stage ensures the consistency of our survival estimates.

In a randomized clinical trial (RCT) setting, there is often interest in testing for a treatment difference in terms of survival. Robust methods to incorporate auxiliary information when testing for a treatment effect have been previously proposed in the literature. Cook & Lawless (2001) discuss a variety of statistical methods that have been proposed including parametric and semiparametric models. Gray (1994) adopted kernel estimation methods which incorporate information on a single intermediate event. To incorporate multiple baseline covariates, Lu & Tsiatis (2008) used an augmentation procedure to improve the efficiency of estimating the log hazard ratio, β, from a Cox model and testing for an overall treatment effect by examining the null hypothesis β = 0 and demonstrated substantial gains in efficiency. However, if the Cox model does not hold, the hazard ratio estimate converges to a parameter that may be difficult to interpret and may depend on the censoring distribution. It would thus be desirable to use a model-free summary measure to assess treatment difference. Furthermore, none of the existing procedures incorporate both intermediate event and baseline covariate information. In this paper, we use our proposed two-stage estimation procedure, which utilizes all available information, to make more precise inference about treatment difference as quantified by the difference in t-year survival rates.

The rest of the paper is organized as follows. Section 2 describes the proposed two-stage estimation procedure in a one-sample setting. Section 3 presents a testing procedure using these resulting estimates. We present an additional augmentation step which takes advantage of treatment randomization to further improve efficiency in an RCT setting. Simulation studies given in Section 4 demonstrate substantial potential gains in efficiency in terms of estimation and power. In Section 5 we illustrate our proposed procedures using an AIDS Clinical Trial comparing the survival rates of HIV patients treated with zidovudine and those treated with zidovudine plus zalcitabine.

2 Estimation

For the ith subject, let T_𝕃i denote the time of the primary terminal event of interest, T_𝕊i denote the vector of intermediate event times, Z_i denote the vector of baseline covariates, and C_i denote the administrative censoring time assumed independent of (T_𝕃,T_𝕊i,Z_i). Due to censoring, for T_𝕃i and T_𝕊i, we could potentially observe X_𝕃i = min(T_𝕃i, C_i), X_𝕊i = min(T_𝕊i, C_i) and δ_𝕃i = I(T_𝕃i ≤ C_i), δ_𝕊i = I(T_𝕊i ≤ C_i). Due to semi-competing risks, T_𝕊i is additionally subject to informative censoring by T_𝕃i, while T_𝕃i is only subject to administrative censoring and cannot be censored by T_𝕊i. Let t₀ denote some landmark time prior to t. Our goal is to estimate S(t) = P(T_𝕃i > t) using intermediate event collected up to t₀ and baseline covariate information, where t is some pre-specified time point such that P(X_𝕃 > t | T_𝕃 ≥ t₀) ∈ (0, 1) and P(T_𝕃 ≤ t₀, T_𝕊 ≤ t₀) ∈ (0, 1).

2·1 Two-stage estimation procedure

For t > t₀, S(t) = P(T_𝕃i > t) can be expressed as S(t | t₀)S(t₀), where

$$S(t|t_0)=P(T_{𝕃i}>t|T_{𝕃i}>t_0)=P(T_{𝕃i}>t|X_{𝕃i}>t_0)\text{and}S(t_0)=P(T_{𝕃i}>t_0).$$ (2·1)

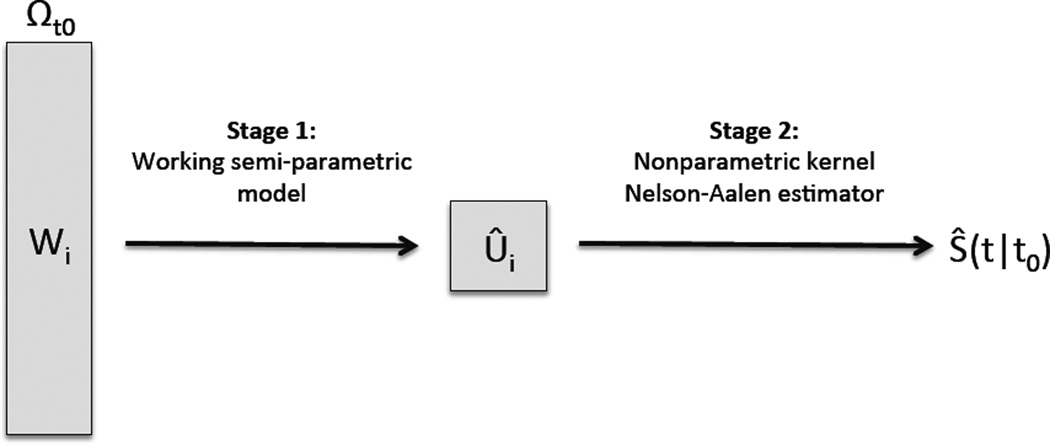
We first consider estimation of S(t | t₀) with a two-stage procedure using subjects in the subset Ω_t0 = {i : X_𝕃i > t₀} as illustrated in Figure 1. Note that conditional on X_𝕃i > t₀, T_𝕊i is observable up to T_𝕊i ∧ t₀ and I(T_𝕊i ≤ t₀) is always observable. Let ${\mathbf{W}}_i={[{\mathbf{Z}}_i^{\mathrm{T}},I({\mathbf{T}}_{𝕊\mathbf{i}}\le t_0),\text{min}({\mathbf{T}}_{𝕊\mathbf{i}},t_0)]}^{\mathrm{T}}$ for all subjects in Ω_t0. Note that for any function of W, ζ(·),

$$S(t|t_0)=P(T_{𝕃i}>t|X_{𝕃i}>t_0)=E\{S_{\zeta (\mathbf{W})}(t|t_0)\},$$ (2·2)

where S_ζ(W)(t | t₀) = P{T_𝕃i > t | X_𝕃i > t₀, ζ(W_i)}. Hence if Ŝ_ζ(W)(t | t₀) is a consistent estimator of S_ζ(W)(t | t₀), S(t | t₀) can be estimated consistently with $n_{t_0}^{-1}{\sum }_{i\in {\mathrm{\Omega }}_{t_0}}{Ŝ}_{\zeta ({\mathbf{w}}_i)}(t|t_0)$ where $n_{t_0}={\sum }_{i=1}^{n}I(X_{𝕃i}>t_0)$. When T_𝕊i consists of a single intermediate event and Z consists of a single discrete marker, the nonparametric estimation procedure proposed in Parast et al. (2011) can be used to obtain a consistent estimator of S_W(t | t₀) with ζ(W) = W. However, when the dimension of W is not small, such nonparametric estimation of S_W(t | t₀) may not behave well (Robins & Ritov, 1997). Instead, we propose to reduce the dimension of W by first approximating S_W(t | t₀) where ζ(W) = W with a working semiparametric model and use the model to construct a low dimensional function that is then used to derive an estimator for S(t | t₀). A useful example of such a model is the landmark proportional hazards model (Van Houwelingen & Putter, 2008; Van Houwelingen, 2007; Van Houwelingen & Putter, 2012)

$$S_{\mathbf{w}}(t|t_0)=\text{exp}\{-{\mathrm{\Lambda }}_0^{t_0}(t)\text{exp}({\mathit{\beta }}^{𝖳}\mathbf{w})\},t>t_0$$ (2·3)

where ${\mathrm{\Lambda }}_0^{t_0}(·)$ is the unspecified baseline cumulative hazard function for T_𝕃i among Ω_t0 and β is an unknown vector of coefficients. This is referred to as our Stage 1. Let β̂ be the maximizer of the corresponding log partial likelihood function and ${\mathrm{\Lambda ̂}}_0^{t_0}(t)$ be the Breslow-type estimate of baseline hazard (Breslow, 1972). When (2·3) is correctly specified, ${Ŝ}_{\mathbf{w}}(t|t_0)=\text{exp}\{-{\mathrm{\Lambda ̂}}_0^{t_0}(t)\text{exp}({\mathit{\beta ̂}}^{𝖳}\mathbf{w})\}$ could consistently estimate S_W(t | t₀). However, if (2·3) is not correctly specified, Ŝ_W(t | t₀) would not longer be a consistent estimator of S_W(t | t₀) and thus $n_{t_0}^{-1}{\sum }_{i=1}^{n_{t_0}}{Ŝ}_{{\mathbf{W}}_i}(t|t_0)$ may be a biased estimate of S(t | t₀) (Lagakos, 1988; O’neill, 1986). On the other hand, the risk score Û_i ≡ β̂^𝖳W_i may still be highly predictive of T_𝕃i. This motivates us to overcome the difficulty arising from model misspecification and multi-dimensionality of W_i by using $\zeta (\mathbf{W})={\mathit{\beta }}_0^{𝖳}\mathbf{W}$. Therefore, S(t | t₀) = E{S_Ui(t | t₀)}, where S_u(t | t₀) = P(T_𝕃i > t | T_𝕃i > t₀, U_i = u), $U_i={\mathit{\beta }}_0^{𝖳}{\mathbf{W}}_i$ and β₀ is the limit of β̂, which always exists (Hjort, 1992). In essence, we use the working Cox model as a tool to construct $\zeta (\mathbf{W})=U={\mathit{\beta }}_0^{𝖳}\mathbf{W}$ in stage 1 and estimate S(t | t₀) as $Ŝ(t|t_0)=\frac{1}{n_{t0}}{\sum }_{i\in {\mathrm{\Omega }}_{t_0}}{Ŝ}_{{Û}_i}(t|t_0)$, where Ŝ_u(t | t₀) is a consistent estimator of S_u(t | t₀) obtained in stage 2.

Figure 1.

Illustration of proposed two-stage procedure

To estimate S_u(t | t₀) in stage 2, we use a nonparametric conditional Nelson-Aalen estimator (Beran, 1981) based on subjects in Ω_t0. Specifically for any given t and u, we use the synthetic data {(X_𝕃i, δ_𝕃i, Û_i), i ∈ Ω_t0} to obtain a local constant estimator for the conditional hazard Λ_u(t | t₀) = −log S_u(t | t₀) as

$${\mathrm{\Lambda ̂}}_u(t|t_0)={\int }_{t_0}^t\frac{{\sum }_{i\in {\mathrm{\Omega }}_{t_0}}{K}_h({\mathrm{D̂}}_{ui})d{N}_i(z)}{{\sum }_{i\in {\mathrm{\Omega }}_{t_0}}{K}_h({\mathrm{D̂}}_{ui})Y_i(z)}$$

as in Cai et al. (2010), where Y_i(t) = I(T_𝕃i ≥ t), N_i(t) = I(T_𝕃i ≤ t)δ_𝕃i, D̂_ui = Û_i − u, K(·) is a smooth symmetric density function, K_h(x) = K(x/h)/h, and h = O(n^−υ) is a bandwidth with 1/2 > υ > 1/4. The resulting estimate for S_u(t | t₀) is Ŝ_u(t | t₀) = exp{−Λ̂_u(t | t₀)}. The uniform consistency of Ŝ_u(t | t₀) in u for S_u(t | t₀) can be shown using similar arguments as in Cai et al. (2010) under mild regularity conditions. Note that this consistency still holds when $U_i={\mathit{\beta }}_0^{𝖳}{\mathbf{W}}_i$ is discrete as long as it takes only a finite number of values (Du & Akritas, 2002). Finally, we propose to estimate S(t | t₀) as

$$Ŝ(t|t_0)=\frac{1}{n_{t_0}}\sum _{i\in {\mathrm{\Omega }}_{t_0}}{Ŝ}_{{Û}_i}(t|t_0)=\frac{1}{n_{t_0}}\sum _{i\in {\mathrm{\Omega }}_{t_0}}\text{exp}\{-{\mathrm{\Lambda ̂}}_{{Û}_i}(t|t_0)\}.$$

The uniform consistency of Ŝ_u(t | t₀) along with the consistency of β̂ for β₀ ensures the consistency of Ŝ(t | t₀) for S(t | t₀). This approach is similar to the semiparametric dimension reduction estimation procedure proposed in Hu et al. (2011) and Hu et al. (2010) for estimating the conditional mean response in the presence of missing data.

Now that we have obtained an estimate of S(t|t₀) in (2·1), an estimate for S(t₀) follows similarly from this same two-stage procedure replacing W_i with Z_i and Ω_t0 with all patients. More specifically, let β̂^* be the maximizer of the partial likelihood function corresponding to the Cox model:

$$P(T_{𝕃i}\ge t|{\mathbf{Z}}_i)=\text{exp}\{-{\mathrm{\Lambda }}_0(t)\text{exp}({\mathit{\beta }}^{*\mathrm{T}}{\mathbf{Z}}_i)\}$$ (2·4)

where Λ₀(·) is the baseline cumulative hazard function and β^* is a vector of coefficients. We then define ${Û}_i^{*}\equiv {\mathit{\beta ̂}}^{*𝖳}{\mathbf{Z}}_i$ and use a local constant estimator, Λ̂_u(t₀), to obtain $Ŝ(t_0)=\frac{1}{n}{\sum }_{i=1}^n{Ŝ}_{{Û}_i^{*}}(t_0)$ where ${Ŝ}_{{Û}_i^{*}}(t_0)=\text{exp}\{-{\mathrm{\Lambda ̂}}_{{Û}_i^{*}}(t_0)\}$ is a consistent estimator of $S_u(t_0)=P(T_{𝕃i}>t_0|U_i^{*}=u)$. An estimate for our primary quantity of interest S(t) incorporating intermediate event and covariate information follows as Ŝ_LM(t) ≡ Ŝ(t | t₀)Ŝ(t₀) where LM indicates that we have used a landmark time to decompose our estimate into two components.

2·2 Theoretical Properties of the Two-Stage Estimator

In this section, we provide theoretical results on how the proposed estimator compares to the standard KM estimator denoted by Ŝ_KM(t). We also aim to investigate how various components of the proposed procedure contribute to the gain in efficiency. To this end, we first show in Supplementary Appendix A that the variability of β̂ and β̂^* can be ignored when making inference about Ŝ_LM(t). In Appendix I, we show that the influence functions of Ŝ(t₀), Ŝ(t|t₀), and Ŝ_LM(t) can be decomposed as the influence function corresponding to the full data without censoring plus an additional component accounting for variation due to censoring.

To examine the potential gain in efficiency of our proposed estimator over the KM estimator, in Appendix II, we show that the reduction in variance is always non-negative taking the form

$$\frac{S(t_0)}{S_C(t_0)}{\int }_{t_0}^t[E\{S_{U_i}(s|t_0){[S_{U_i}(t|s)-S(t|s)]}^2\}]dG(s|t_0)+S{(t|t_0)}^2{\int }_0^{t_0}\left[E\right\{S_{U_i^{*}}(s){[S_{U_i^{*}}(t_0|s)-S(t|s)]}^2\left\}\right]dG(s)$$

as defined in Appendix II. Obviously, there would not be any gain in the absence of censoring with G(t) ≡ 1. The maximum reduction is achieved when S_Ui(t | t₀) = P(T_𝕃i ≥ t | T_𝕃i ≥ t₀, W_i) and $S_{U_i^{*}}(s)=P(T_{𝕃i}\ge s|{\mathbf{Z}}_i)$. This condition for optimal efficiency is parallel to the recoverability condition described in Hu et al. (2010) for conditional mean response estimation, and is satisfied when the working models in (2·3) and (2·4) are correctly specified. It is important to note that the optimality of the proposed estimator is within the class of estimators constructed based on the specific choice of W and thus depends on t₀. In Sections 4 and 5, we examine the sensitivity of our estimator to the choice of t₀ and propose data-driven rules to further improve the robustness of our approach by combining information from multiple t₀s.

To shed light on where the gain in efficiency is coming from, we show in Supplementary Appendix B.1 that Ŝ_LM(t) ≈ Ŝ_KM(t) + ℛ̂(t), where

$$\mathrm{ℛ̂}(t)=n_{t_0}^{-1}\sum _{i\in {\mathrm{\Omega }}_{t_0}}\{S(t_0){\int }_{t_0}^t[S_{U_i}(t|t_0)\frac{d{M}_{C_i}(s|t_0)}{{\pi }_{U_i}(s|t_0)}-S(t|t_0)\frac{d{M}_{C_i}(u|t_0)}{\pi (u|t_0)}\left]\right\}+n^{-1}\sum _{i=1}^n\{S(t|t_0){\int }_0^{t_0}[S_{U_i^{*}}(t_0)\frac{d{M}_{C_i}(s)}{{\pi }_{U_i^{*}}(s)}-S(t_0)\frac{d{M}_{C_i}(u)}{\pi (u)}]\}.$$

That is, our proposed estimator can also be expressed as the KM estimator augmented by a mean zero martingale ℛ̂(t) corresponding to censoring weighted by baseline covariate and intermediate event information. The term ℛ̂(t) is negatively correlated with Ŝ_KM(t) and improves efficiency by leveraging independent censoring and the correlation between T_𝕃i and {T_𝕊i, Z_i}. The proposed two-stage modeling framework allows us to optimally use this additional information while protecting us against model misspecification. This decomposition also connects our proposed estimator to the existing augmentation procedures such as those considered in Lu & Tsiatis (2008). The advantage of our proposal is that the modeling step naturally estimates the optimal bases without necessitating the correct specification of the model. Variance estimates can be obtained using a perturbation-resampling procedure as described in Supplementary Appendix C.

3 Comparing Survival Between Two Treatment Groups

Consider a two-arm RCT setting where we use 𝒢 to denote treatment assignment with 𝒢 taking a value B with probability p and A otherwise. For 𝒢 ∈ {A, B}, let S_𝒢(t) denote the survival rate of T_𝕃 at time t in group 𝒢 and Ŝ_LM,𝒢(t) denote the aforementioned two-stage estimator based on data from treatment group 𝒢. An estimator for the risk difference, Δ(t) = S_A(t) − S_B(t), may be obtained as Δ̂_LM(t) = Ŝ_LM,A(t) − Ŝ_LM,B(t). The standard error of Δ̂_LM(t) can be estimated as σ̂(Δ̂_LM(t)) using a perturbation-resampling procedure as described in Supplementary Appendix C. A normal confidence interval (CI) for Δ(t) may be constructed accordingly. To test the null hypothesis of H₀ : Δ(t) = 0, a Wald-type test may be performed based on Z_LM(t) = Δ̂_LM(t)/σ̂(Δ̂_LM(t)). To compare this testing procedure to a test based on Ŝ_KM(t) let Δ̂_KM(t) = Ŝ_KM,A(t)− Ŝ_KM,B(t) denote the KM estimate for Δ(t) where Ŝ_KM,𝒢(t) is the KM estimate of survival at time t in group 𝒢.

Through an augmentation procedure in a RCT setting, Lu & Tsiatis (2008) demonstrated substantial gains in power when testing the log hazard ratio under a Cox model. Though Lu & Tsiatis (2008) does not offer procedures to estimate or test for a difference in t-year survival rates, the investigation of their useful and effective procedure is worthwhile in our setting. The augmentation procedure in Lu & Tsiatis (2008) (LT) leads to significant gains in efficiency by leveraging two key sets of assumptions: (1) C is independent of {T_𝕃, Z} given 𝒢 and (2) 𝒢 is independent of Z. The LT procedure takes advantage of such information by explicitly creating functional bases and augmenting over both censoring martingales and I(𝒢 = B) − p, weighted by these specified bases. Similar to the arguments given in Section 2 and Supplementary Appendix B.1, one may interpret Δ̂_LM(t) as augmenting Δ̂_KM(t) with an optimal basis of censoring martingales approximated by the working models. However, our procedure does not require explicit specification of the basis and also leverages information on C being independent of T_𝕊.

However, Δ̂_LM(t) does not yet leverage information on the randomization of treatment assignment (that is, 𝒢 is independent of Z)and hence it is possible to further improve this estimator via augmentation. One may follow similar strategies as the LT procedure by explicitly augmenting over certain basis functions of Z. Specifically, let H(Z) be any arbitrary vector of basis functions. An augmented estimator can be obtained as Δ̂_LM(t; ε, H) = Δ̂_LM(t) + ε^𝖳 ∑_i{I(𝒢_i = B) − p}H(Z_i), where ε is chosen to minimize the variance of Δ̂_LM(t; ε, H). However, a poor choice of bases and/or a large number of non-informative bases might result in a loss of efficiency in finite samples (Tian et al., 2012). Here, we propose to explicitly derive an optimal basis using the form of the influence function for Δ̂_LM(t) and subsequently use our two-stage procedure to estimate the basis. Specifically, in Supplementary Appendix B.2 we derive an explicit form for the optimal choice for H(Z) in this setting as

$${\mathbf{H}}_{\text{opt}}(\mathbf{Z},t)=-\sum _{𝒢\in \{A,B\}}\frac{S_{\mathbf{Z},𝒢}(t)-S_{𝒢}(t)}{{(1-p)}^{I(𝒢=A)}{p}^{I(𝒢=B)}}$$ (3·1)

where S_Zi,𝒢(t) ≡ P(T_𝕃i > t | Z_i, 𝒢_i = 𝒢) for 𝒢 = A, B. There are various ways one may estimate (3·1). We choose to guard against possible model misspecification and consider a robust estimate using the proposed two-stage procedure. Specifically, we first fit a Cox model to treatment group 𝒢 using only Z information to obtain an estimated log hazard ratio, ${\mathit{\beta ̂}}_{𝒢}^{*}$, and then approximate −log S_Z,𝒢(t) as ${\mathrm{\Lambda ̂}}_{\mathbf{Z}\prime {\mathit{\beta ̂}}_{𝒢}^{*},𝒢}({\mathit{\beta ̂}}_{𝒢}^{*},t)$, where Λ̂_u,𝒢(β, t) is obtained similarly to Λ̂_u(β, t) but only using data in the treatment group 𝒢. We denote the resulting estimated basis as Ĥ_opt(Z_i, t). We then obtain an augmented estimator for Δ(t) as Δ̂_AUG(t) = Δ̂_LM(t) − ε̂∑_i{I(𝒢_i = B) − p}Ĥ_opt(Z_i, t),where ε̂ is an estimate of cov{Δ̂_LM(t), ∑_i{I(𝒢_i = B) − p}Ĥ_opt(Z_i, t)}var{∑_i{I(𝒢_i = B) − p}Ĥ_opt(Z_i, t)}}⁻¹ which can be approximated using the perturbation procedure as described in Supplementary Appendix C. Note that we use the proposed two-stage procedure to approximate the optimal basis for augmentation. Therefore, when the working models do not hold, the estimated basis may not be optimal but can still improve efficiency empirically by capturing important associations between T_𝕃i and Z_i. In addition, we estimate ε empirically as ε̂ to guard against model misspecification. Since the variability due to Ĥ_opt and ε̂ has a negligible contribution asymptotically to the variance of Δ̂_AUG(t), such calibration and weighting improve the robustness of our proposed approach. Hence, this approach could ultimately improve the efficiency of Δ̂_AUG(t) even in the presence of model misspecification.

4 Simulations

We conducted simulation studies to examine the finite sample properties of the proposed estimation procedures. If a gain in efficiency is observed over the KM estimate, one may consider whether this advantage is due in part to incorporating covariate information or incorporating T_𝕊 information or both. To address this question, let ${Ŝ}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)={Ŝ}^{T_{𝕊}}(t|t_0){Ŝ}_{\mathrm{K}\mathrm{M}}(t_0)$ denote an estimate of S(t) incorporating only T_𝕊 information where Ŝ^T𝕊(t | t₀) is obtained using the two-stage procedure with W = [I(T_𝕊i ≤ t₀), min(T_𝕊i, t₀)]^𝖳. In addition, let Ŝ^Z(t) denote an estimate of S(t) incorporating only Z information. In our numerical examples, we additionally estimate these quantities for comparison. In an effort to compare our results to those examined previously in the literature, we apply our method to similar simulation settings as in Gray (1994). Three settings were considered: (i) a no treatment effect setting i.e. null setting (ii) a small treatment effect setting (iii) a large treatment effect setting. For illustration, t₀ =1 year and t = 2 years i.e. we are interested in the probability of survival past 2 years. In all settings, censoring, C_i, was generated from a Uniform(0.5,2.5) distribution. For each treatment group, n=1000 and results summarize 2000 replications under the null setting (i) and 1000 replications under settings (ii) and (iii). Variance estimates are obtained using the perturbation-resampling method. Under the null setting (i), the event times for each treatment group (Treatment A and Treatment B) were generated from a Weibull distribution with scale parameter $b_1^{-1/a_1}$ and shape parameter 1/a₁ i.e. as $T_{𝕊}={[-b_1^{-1}\text{log}(1-U_1)]}^{1/a_1}$ where a₁ = 1.5, b₁ = 1, and U₁ ~ Uniform(0,1). The conditional distribution T_𝕃 − T_𝕊 | T_𝕊 was generated from a Weibull distribution with scale parameter $b_2^{-1/a_2}$ and shape parameter 1/a₂ i.e. as ${[-b_2^{-1}\text{log}(1-U_2)]}^{1/a_2}$ where a₂ = 1.5, b₂ = exp(g(T_𝕊)), g(t) = 0.15−0.5t² and U₂ ~ Uniform(0,1). We take the covariate Z to be 0.75U₂ + .25U₃ where U₃ ~ Uniform(0,1). Note that in these simulations, T_𝕊 must occur before T_𝕃 though our procedures do not require this assumption to hold. In this setting, P(X_𝕃i < t, δ_𝕃i = 1) = 0.37 and P(X_𝕊i < t₀, δ_𝕊i = 1) = 0.59 in each group. In setting (ii) the Treatment A event times were generated as shown above and the Treatment B event times were generated similarly but with b₁ = 1.2. In this setting, P(X_𝕃i < t, δ_𝕃i = 1) = 0.39 and P(X_𝕊i < t₀, δ_𝕊i = 1) = 0.65 in the Treatment B group. Finally, in setting (iii) the Treatment A event times were generated as shown above and the Treatment B event times were generated similarly but with b₁ = 1.4. In this setting, P(X_𝕃i < t, δ_𝕃i = 1) = 0.43 and P(X_𝕊i < t₀, δ_𝕊i = 1) = 0.70 in the Treatment B group.

As in most nonparametric functional estimation procedures, the choice of the smoothing parameter h is critical. In our setting, the ultimate quantity of interest is the marginal survival and the estimator is effectively an integral of the conditional survival estimates. To eliminate the impact of the bias of the conditional survival function on the resulting estimator, we also require the standard undersmoothing assumption of h = O(n^−δ) with δ ∈ (1/4, 1/2). To obtain an appropriate h we first use the bandwidth selection procedure given by Scott (1992) to obtain h_opt, and then we let h = h_optn^−c₀ for some c₀ ∈ (1/20, 3/10) to ensure the desired rate for h. In all numerical examples, we chose c₀ = 0.10.

Results from estimation of S(t) are shown in Table 1. The standard error estimates obtained by the perturbation-resampling procedure approximate the empirical standard error estimates well. While all estimators have negligible bias and satisfactory coverage levels, our proposed estimate which incorporates both Z and T_𝕊 information is more efficient than that from the standard Kaplan Meier estimate with relative efficiencies with respect to mean squared error (MSE) around 1.20. Though extensive simulation studies may be performed, we expect that such efficiency gains would not be seen in settings with little censoring or with weak correlation between the intermediate and terminal event (Cook & Lawless, 2001). Note that in all three settings, C_i ~ Uniform(0.5, 2.5) and thus P(C < t₀) = 0.25 and P(C < t) = 0.75. To examine efficiency gains under varying degrees of censoring, we simulated data as in setting (i) but with (a) more censoring where C_i ~ Uniform(0.5, 2.15) and (b) less censoring C_i ~ Uniform(0.5, 3.5). In (a) P(C < t₀) = 0.30 and P(C < t) = 0.90 and the relative efficiency with respect to MSE was 1.40 (not shown). In (b) P(C < t₀) = 0.17 and P(C < t) = 0.50 and the relative efficiency with respect to MSE was 1.10 (not shown).

Table 1.

Estimates of S(t) for t = 2 years in treatment group B in settings (i),(ii) and (iii) using a Kaplan Meier estimator, Ŝ_KM(t), the proposed estimator using Z information only, Ŝ^Z(t), T_𝕊 information only, Ŝ^Z(t), and Z and T_𝕊 information, ${Ŝ}_{\mathrm{L}\mathrm{M}}^{\mathbf{W}}(t)$, with corresponding empirical standard error (ESE), average of the standard error estimates from the perturbation-resampling method (ASE), efficiency relative to Ŝ_KM(t) with respect to mean squared error (MSE) (RE_MSE), and empirical coverage (Cov) of the 95% CIs.

	ŜKM(t)	ŜZ(t)	${Ŝ}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)$	${Ŝ}_{\mathrm{L}\mathrm{M}}^{\mathrm{W}}(t)$
	Setting (i)
Estimate	0.4205	0.4267	0.4238	0.4246
Bias	−0.0004	0.0060	0.0031	0.0039
ESE	0.0225	0.0220	0.0220	0.0207
ASE	0.0231	0.0218	0.0218	0.0206
REMSE	-	1.07	1.04	1.20
Cov	0.95	0.95	0.94	0.95
	Setting (ii)
Estimate	0.3676	0.3745	0.3716	0.3720
Bias	−0.0008	0.006	0.0032	0.0036
ESE	0.0224	0.0222	0.0219	0.0210
ASE	0.0227	0.0213	0.0215	0.0201
REMSE	-	1.07	1.03	1.19
Cov	0.96	0.94	0.94	0.93
	Setting (iii)
Estimate	0.3248	0.3322	0.3289	0.3292
Bias	0.0001	0.0074	0.0040	0.0043
ESE	0.0224	0.0222	0.0218	0.0206
ASE	0.0222	0.0208	0.0210	0.0196
REMSE	-	1.06	1.01	1.20
Cov	0.94	0.94	0.91	0.93

To examine the sensitivity of our estimator to the choice of t₀ and to further improve the robustness of our procedure by combining information from multiple t₀s, we estimate S(t) with t₀ ∈ ℧ = {k_0.25, k_0.50, k_0.75}, where k_p is the pth percentile of {X_𝕊i : δ_𝕊i = 1}, in setting (i). We denote the resulting estimators and corresponding standard errors estimated using the perturbation-resampling procedure as Ŝ_k0.25(t), Ŝ_k0.50(t), Ŝ_k0.75(t) and σ̂_k0.25, σ̂_k0.50, σ̂_k0.75, respectively. One potential data-driven approach to choose t₀ would be to set t₀ as $\widehat{t_0}={\text{arg min}}_{t_0\in \mho }{\mathrm{\sigma ̂}}_{t_0}$ and let ${Ŝ}_{\widehat{t_0}}(t)$ denote the corresponding estimator of S(t). Alternatively, one could consider an optimal linear combination of Ŝ_t0(t) = (Ŝ_k0.25(t), Ŝ_k0.50(t), Ŝ_k0.75(t))^𝖳, ${Ŝ}_{\text{comb}}(t)\equiv {\mathbf{w}}_{\text{comb}}^{𝖳}{\mathbf{Ŝ}}_{{\mathbf{t}}_{\mathbf{0}}}(\mathbf{t})$, where w_comb = 1^𝖳∑̂⁻¹[1^𝖳∑̂⁻¹1]⁻¹ and ∑̂ is the estimated covariance matrix of Ŝ_t0(t) estimated using the perturbation-resampling procedure. The variance of Ŝ_comb(t) can be estimated as 1^𝖳∑̂⁻¹1. Due to the high collinearity of Ŝ_t0(t), we expect that in finite samples, ∑̂⁻¹ may be an unstable estimate of var{Ŝ_t0(t)}⁻¹. Consequently Ŝ_comb(t) may not perform well and 1^𝖳∑̂⁻¹1 may be under-estimating the true variance of Ŝ_comb(t). Another alternative would be an inverse variance weighted (IVW) estimator of S(t), ${Ŝ}_{\mathrm{I}\mathrm{V}\mathrm{W}}(t)\equiv {\mathbf{w}}_{\mathrm{I}\mathrm{V}\mathrm{W}}^{𝖳}{\mathbf{Ŝ}}_{{\mathbf{t}}_{\mathbf{0}}}(\mathbf{t})$ where w_IVW = 1^𝖳diag(Σ̂)⁻¹[1^𝖳diag(Σ̂)⁻¹1]⁻¹. Under the current simulation setting (ii), the empirical standard errors of Ŝ_k0.25(t), Ŝ_k0.50(t), Ŝ_k0.75(t), ${Ŝ}_{\widehat{t_0}}(t)$, Ŝ_comb(t), and Ŝ_IVW(t) are 0.0215, 0.0210, 0.0207, 0.0210, 0.0206,and 0.0206 respectively. Although asymptotically the variance of ${Ŝ}_{\widehat{t_0}}(t)$ should be the same as that of Ŝ_k0.75(t), due to the similarity among {σ̂_t0, t₀ ∈ ℧}, the variability in $\widehat{t_0}$ does contribute additional noise to ${Ŝ}_{\widehat{t_0}}(t)$. As expected, using 1^𝖳∑̂⁻¹1, the average variance of Ŝ_comb(t) is estimated as 0.0202, which is slightly lower than the empirical variance of Ŝ_comb(t). For Ŝ_IVW(t), the average of the estimated variance is 0.0204, which is close to the empirical variance. The empirical coverage levels of the 95% confidence intervals using Ŝ_comb(t) and Ŝ_IVW(t) are 0.945 and 0.943, respectively, indicating that such estimators perform well when combining across a small number of choices for t₀. This suggests that our proposed estimators are not overly sensitive to the choice of t₀ and a reasonable approach in practice may be to estimate S(t) using the proposed combined or IVW estimator.

For comparing treatment groups, we show results on the estimation precision and power in testing in Table 2. Similar to above, let Δ̂^Z(t) denote the estimate of Δ(t) using Z information only and ${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)$ denote the estimate using T_𝕊 information only. Corresponding test statistics can then be constructed similar to Δ̂_LM(t). With respect to estimation precision for the treatment difference in survival rate, our proposed procedure yields about 49% gain in efficiency compared to the KM estimator. For testing for a treatment difference, under the null setting (i), the type I error is close to the nominal level of 0.05 with ${\mathrm{\Delta ̂}}_{\mathrm{A}\mathrm{U}\mathrm{G}}^{\mathbf{w}}(t)$ having a slightly higher value of 0.0538. When there is a small treatment difference, setting (ii), the power to detect a difference in survival at time t = 2 is 0.374 using a standard Kaplan Meier estimate and 0.457 when using the proposed procedure incorporating Z and T_𝕊 information. We gain more power through additional augmentation which results in a power of 0.520. Similarly, in setting (iii), when there is a large treatment difference, power increases from 0.846 to 0.941 after incorporating Z and T_𝕊 information and augmentation. These results suggest that in this setting, we can gain substantial efficiency by using the proposed procedures.

Table 2.

Results from testing for a difference in survival at time t = 2 years between the two treatment groups using a Kaplan Meier estimator, Δ̂_KM(t), the proposed estimator using Z information only, Δ̂^Z(t), T_𝕊 information only, ${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)$, Z and T_𝕊 information, ${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{\mathbf{W}}(t)$, and the augmented estimator, ${\mathrm{\Delta ̂}}_{\mathrm{A}\mathrm{U}\mathrm{G}}^{\mathbf{W}}(t)$ with corresponding empirical standard error (ESE), average of the standard error estimates from the perturbation-resampling method (ASE), efficiency relative to Ŝ_KM(t) with respect to MSE, and power.

	Δ̂KM(t)	Δ̂Z(t)	${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)$	${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{\mathrm{W}}(t)$	${\mathrm{\Delta ̂}}_{\mathrm{A}\mathrm{U}\mathrm{G}}^{\mathrm{W}}(t)$
Setting (i), no treatment difference
Estimate	−0.0002	−0.0002	−0.0004	−0.0001	0.0003
ESE	0.0323	0.0318	0.0316	0.0300	0.0282
ASE	0.0326	0.0308	0.0309	0.0291	0.0267
REMSE	-	1.12	1.12	1.26	1.49
α	0.0415	0.0462	0.0544	0.0467	0.0538
Setting (ii), small treatment difference
Estimate	0.0525	0.0519	0.0520	0.0523	0.0525
ESE	0.0318	0.0312	0.0312	0.0292	0.0276
ASE	0.0323	0.0305	0.0306	0.0287	0.0263
REMSE	-	1.12	1.11	1.27	1.51
Power	0.3740	0.4110	0.4060	0.4570	0.5200
Setting (iii), large treatment difference
Estimate	0.0954	0.0942	0.0947	0.0952	0.0952
ESE	0.0317	0.0312	0.0310	0.0288	0.0270
ASE	0.0320	0.0301	0.0303	0.0283	0.0259
REMSE	-	1.13	1.11	1.27	1.53
Power	0.8460	0.8690	0.8650	0.9090	0.9410

5 Example

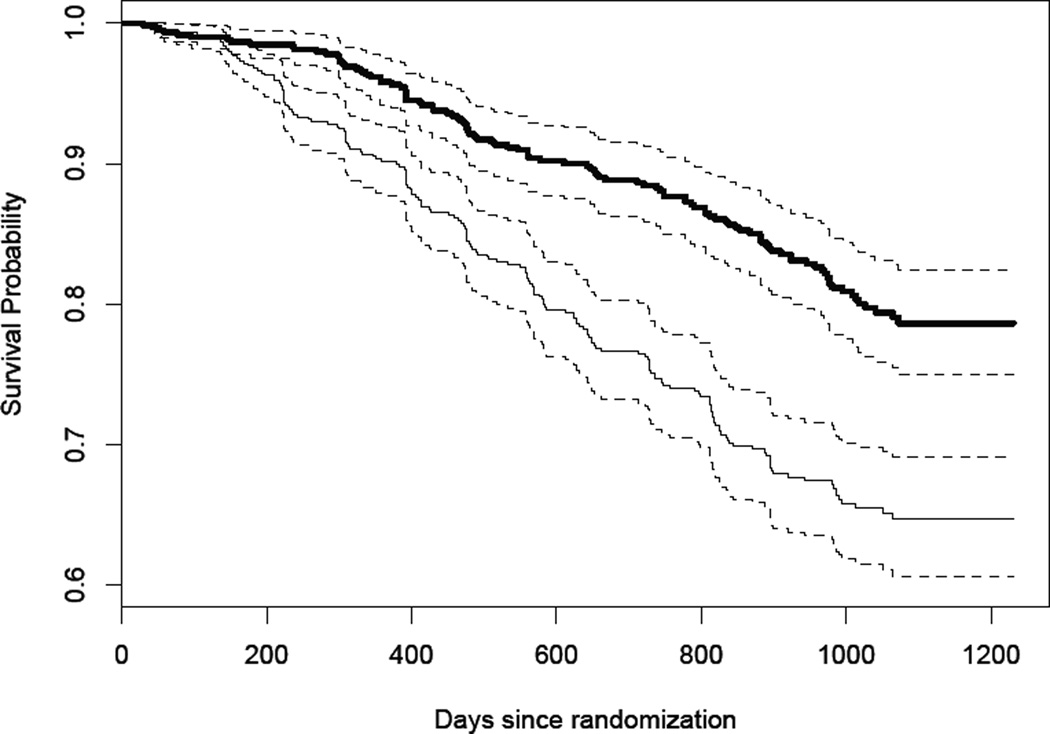
We illustrate the proposed procedures using a dataset from the AIDS Clinical Trial Group (ACTG) Protocol 175 (Hammer et al., 1996). This dataset consists of 2467 patients randomized to 4 different treatments: zidovudine only, zidovudine + didanosine, zidovudine + zalcitabine, and didanosine only. The long term event of interest, T_𝕃, is the time to death and intermediate event information consists of two intermediate events, T_𝕊 = (T_𝕊1, T_𝕊2)^𝖳 where T_𝕊1 = time to an AIDS-defining event e.g. pneumocystis pneumonia and T_𝕊2 = time to a 50% decline in CD4. If a patient experienced multiple intermediate events of one kind, for example multiple AIDS-defining events, the earliest occurrence of the event was used. For illustration, t₀ = 1 year and t = 2.5 years and we examine survival in patients from the zidovudine only (mono group, n=619) and zidovudine + zalcitabine (combo group, n=620) groups. Figure 2 displays the KM estimate of survival in each group. Baseline covariates, Z, include the mean of two baseline CD4 counts, Karnofsky score, age at randomization, weight, symptomatic status, use of zidovudine in the 30 days prior to randomization, and days of antiretroviral therapy before randomization. Results are shown in Table 3. Our proposed procedure leads to a t-year survival rate estimate of 0.926 for the mono group and 0.953 for the combo group. The KM estimate of survival is similar though smaller in both groups.

Figure 2.

Kaplan Meier estimate of survival for the mono group (thin black line) and combo group (thick black line) with corresponding 95% confidence intervals (dashed lines).

Table 3.

Estimates of S(t) for t = 2.5 years in two treatment groups from ACTG Protocol 175 using a Kaplan Meier estimator, Ŝ_KM(t), the proposed estimator using Z information only, Ŝ^Z(t), T_𝕊 information only, Ŝ^Z(t), and Z and T_𝕊 information, ${Ŝ}_{\mathrm{L}\mathrm{M}}^{\mathbf{W}}(t)$, with corresponding standard error from the perturbation-resampling method (SE).

	ŜKM(t)	Ŝz(t)	${Ŝ}_{LM}^{T_{𝕊}}(t)$	${Ŝ}_{LM}^{\mathrm{W}}(t)$
Treatment: Zidovudine
Estimate	0.92	0.93	0.93	0.93
SE	0.0114	0.0108	0.0107	0.0105
Treatment: Zidovudine and Zalcitabine
Estimate	0.95	0.96	0.95	0.95
SE	0.0101	0.0091	0.0094	0.0091

To examine the sensitivity of our estimator to the choice of t₀ in this example, we estimate S(t) with t₀ ∈ ℧ = {k_0.25, k_0.50, k_0.75} = {392, 582, 818}, where k_p is the pth percentile of {X_𝕊1i : δ_𝕊1i = 1, X_𝕊2i : δ_𝕊2i = 1}, X_𝕊ji = min(T_𝕊ji,C_i) and δ_𝕊ji = I(T_𝕊ji ≤ C_i) for j = 1, 2 in the zidovudine only group. Note that when t₀ = 365 as used above, Ŝ(t) = 0.9260 with estimated standard error equal to 0.0105. With t₀ ∈ ℧, our estimates of S(t) are 0.9272, 0.9262, and 0.9262 and estimates of standard error are 0.0106, 0.0105, and 0.0107, respectively. As suggested above, a reasonable alternative approach would be to estimate S(t) using the proposed combined or IVW estimator. Here, Ŝ_comb(t) = 0.9265 and Ŝ_IVW(t) = 0.9266 with standard error estimates 0.0105 and 0.0105, respectively. Therefore, we find that our estimates of survival and corresponding standard error are not sensitive to the choice of t₀ in this example and that both of the combined procedures give similar results on both the point and interval estimators.

We are interested in testing H₀ : Δ(2.5) ≡ S_mono(2.5) − S_combo(2.5) = 0. Results for comparing the two treatment groups are shown in Table 4. Point estimates of Δ(2.5) from various procedures are reasonably close to each other with the KM estimator being 0.0255 and our proposed estimators being 0.0271 and 0.0278 without and with further augmentation, respectively. The proposed procedure provides an estimate which is roughly 19% more efficient than that from the KM estimate. The p-value for this test decreased from 0.0942 to 0.0533 after incorporating information on baseline covariates and T_𝕊. Furthermore, augmentation in addition to the two-stage procedure provides an estimate approximately 49% more efficient than the KM estimate and a p-value of 0.0267.

Table 4.

Results from testing for a difference in survival at time t = 2.5 years between the two treatment groups from ACTG Protocol 175 using a Kaplan Meier estimator, Δ̂_KM(t), the proposed estimator using Z information only, Δ̂^Z(t), T_𝕊 information only, ${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)$, Z and T_𝕊 information, ${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{\mathbf{W}}(t)$, and the augmented estimator, ${\mathrm{\Delta ̂}}_{\mathrm{A}\mathrm{U}\mathrm{G}}^{\mathbf{W}}(t)$ with corresponding standard error from the perturbation-resampling method (SE) and efficiency relative to Ŝ_KM(t) with respect to variance (RE) and p-value

	Δ̂KM(t)	Δ̂Z(t)	${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{T_{𝕊}}(t)$	${\mathrm{\Delta ̂}}_{\mathrm{L}\mathrm{M}}^{\mathrm{W}}(t)$	${\mathrm{\Delta ̂}}_{\mathrm{A}\mathrm{U}\mathrm{G}}^{\mathrm{W}}(t)$
Estimate	0.03	0.03	0.02	0.03	0.03
SE	0.0153	0.0143	0.0143	0.0140	0.0125
RE	1.00	1.13	1.14	1.19	1.49
p-value	0.09	0.04	0.10	0.05	0.03

6 Remarks

We have proposed a semi-nonparametric two-stage procedure to improve the efficiency in estimating S(t) in a RCT setting. We demonstrate with both theoretical and numerical studies that there are substantial potential efficiency gains in both estimation and testing of t-year survival. Our approach can easily incorporate multiple intermediate events, which is appealing when multiple recurrent event information is useful for predicting the terminal events.

This procedure uses the landmark concept developed in Van Houwelingen (2007), Van Houwelingen & Putter (2012) and Parast et al. (2012) to leverage information on multiple intermediate events and baseline covariates, which overcomes complications that arise in a semi-competing risk setting. Existing work on landmark prediction has focused primarily on the prediction of residual life while this paper focuses on improving the estimation of marginal survival. Model misspecification may lead to inaccurate prediction, but would not void the validity of many of the previously proposed prediction procedures. On the contrary, model misspecification of the conditional survival could lead to a biased estimate of the marginal survival. To guard against model misspecification, we use working models to estimate the conditional survival with an additional layer of calibration which ensures the consistency of the marginal survival estimates. We derive asymptotic expansions of the proposed estimator to provide insight into why this method would always improve efficiency compared to the KM estimator and when we would expect to achieve optimal efficiency. The proposed approach can be seen as being related to Bang & Tsiatis (2000) which proposes a partitioned estimator that makes use of the cost history for censored observations to estimate overall medical costs and to Hu et al. (2011) and Hu et al. (2010) which use a semiparametric dimension reduction procedure to estimate the conditional mean response in the presence of missing data.

To avoid any bias due to model specification we use the Cox model only as a tool for dimension reduction followed by a nonparametric kernel Nelson-Aalen estimator of survival to obtain a consistent final estimate of survival. Two conditions required for the consistency of Ŝ_u(t|t₀) are independent censoring and the score derived under a given working model, Û = β̂′W, must converge to a deterministic score U = β′W. This convergence would require the objective function used to derive β̂ to have a unique optimizer. Such an objective function could involve convex functions such as a partial likelihood or an estimating functions with a unique solution such as those considered in Tian et al. (2007) and Uno et al. (2007). In this paper, we have used the Cox model as a working model to obtain β̂ and it has been shown that the Cox partial likelihood has a unique solution even under model misspecification (Hjort, 1992; Van Houwelingen, 2007). Though misspecification of the working model will not affect consistency, it may affect the efficiency of the proposed estimator.

In general, our methods are not restricted to the Cox model being the working model; any working model with this property along with providing root-n convergence of β̂ would be valid and ensure consistency of the final estimate. For example, a proportional odds model or other semi-parametric transformation model could be considered as long as this property holds. However, it is unclear if the maximizer of the rank correlation under the single-index models or the non-parametric transformation model for survival data (Khan & Tamer, 2009) is unique under model misspecification. Therefore, some care should be taken in the choice of the working models. It is interesting to note that it has been shown in some non-survival settings that generalized linear model-type estimators are robust to misspecification of the link function and that the resulting coefficients can be estimated consistently up to a scalar (Li & Duan, 1989). In such settings, even under model misspecification, we would not expect any loss of efficiency due to the link misspecification. Further investigation of this property in a survival setting would be valuable for future research.

The ability to include multiple intermediate events is a desirable property of this proposed procedure. In settings with a small number of potential intermediate events, including all intermediate event information in stage 1 would not affect the efficiency of the overall estimate due to the fact that the variability in β̂ does not contribute to the asymptotic variance (shown in Supplementary Appendix A). However, in finite samples, this additional noise could be problematic and in settings with many potential intermediate events, a regularization procedure (Friedman et al., 2001; Tian et al., 2012) may be considered for variable selection in stage 1.

As in most nonparametric functional estimation procedures, a sufficiently large sample size is needed to obtain stable estimation performance and observe efficiency gains. The degree of efficiency gain using this proposed procedure may be less than expected in small sample sizes. Alternative robust methods should be considered in such settings.

Appendix

Asymptotic properties of Ŝ_LM(t)

We explicitly examine the asymptotic properties of our estimate of survival compared to the KM estimate of survival. Recall that our proposed estimate Ŝ_LM(t) = Ŝ(t | t₀)Ŝ(t₀). Let β̂ and β̂^* be the maximizers of the log partial likelihood functions corresponding to the proportional hazards working models (2·3) and (2·4), respectively. In addition, let β₀ and ${\mathit{\beta }}_0^{*}$ denote the limits of β̂ and β̂^*, respectively. Let $Ŝ({\mathit{\beta }}^{*},t_0)=n^{-1}{\sum }_{i=1}^n{Ŝ}_{{\mathbf{Z}}_i^{\prime }{\mathit{\beta }}^{*}}({\mathit{\beta }}^{*},t_0),Ŝ(\mathit{\beta },t|t_0)=n_{t_0}^{-1}{\sum }_{i=1}^{n_{t_0}}{Ŝ}_{{\mathbf{W}}_i^{\prime }\mathit{\beta }}(\mathit{\beta },t|t_0)$, and Ŝ_LM(β^*, β, t) = Ŝ(β^*, t₀)Ŝ(β, t | t₀), where Ŝ_u(β^*, t₀) = e^{−Λ̂_u(β*,t₀)} Ŝ_υ(β, t | t₀) = e^{−Λ̂_υ(β,t|t₀)}, Λ̂_u(β^*, t₀) and Λ̂_υ(β, t | t₀) are obtained by replacing β̂^* and β̂ in Λ̂_u(t₀) and Λ̂_υ(t | t₀) by β^* and β, respectively. Then Ŝ(β̂^*, t₀) = Ŝ(t₀), Ŝ (β̂^*, t | t₀) = Ŝ(t | t₀), and Ŝ_LM(β̂^*, β̂, t) = Ŝ_LM(t). Furthermore, with a slight abuse of notation, we define $S_u({\mathit{\beta }}^{*},t_0)=P(T_{𝕃i}>t_0|{\mathbf{Z}}_i^{\prime }{\mathit{\beta }}^{*}=u)=e^{-{\mathrm{\Lambda }}_u({\mathit{\beta }}^{*},t_0)}$ and $S_{\upsilon }(\mathit{\beta },t|t_0)=P(T_{𝖳i}>t|{\mathbf{W}}_i^{\prime }\mathit{\beta }=\upsilon ,T_{𝕃i}>t_0)=e^{-{\mathrm{\Lambda }}_{\upsilon }(\mathit{\beta },t|t_0)}$ Hence $S_u(t_0)=S_u({\mathit{\beta }}_0^{*},t_0)$ and S_v(t | t₀) = S_υ(β₀, t | t₀). We will derive asymptotic expansions for ${\mathrm{𝖲̂}}_{\mathrm{L}\mathrm{M}}(t,t_0)\equiv \sqrt{n}\{{Ŝ}_{\mathrm{L}\mathrm{M}}({\mathit{\beta ̂}}^{*},\mathit{\beta ̂},t)-S(t)\}$, which can be decomposed as

$$\sqrt{n}\{{Ŝ}_{\mathrm{L}\mathrm{M}}({\mathit{\beta ̂}}^{*},\mathit{\beta ̂},t)-{Ŝ}_{\mathrm{L}\mathrm{M}}({\mathit{\beta }}_0^{*},{\mathit{\beta }}_0,t)\}+\sqrt{n}\{{Ŝ}_{\mathrm{L}\mathrm{M}}({\mathit{\beta }}_0^{*},{\mathit{\beta }}_0,t)-S(t)\}.$$

In Appendix I below we will express ${\mathrm{𝒲̂}}^{\mathbf{Z}}(t_0)=\sqrt{n}\{Ŝ({\mathit{\beta ̂}}^{*},t_0)-S(t_0)\},{\mathrm{𝖲̂}}^{\mathbf{w}}(t|t_0)=\sqrt{n_{t_0}}\{Ŝ({\mathit{\beta ̂}}^{*},t|t_0)-S(t|t_0)\}$ and 𝒲̂_LM(t, t₀) in martingale notation. Using these martingale representations, in Appendix II we examine the variance of Ŝ_LM(β̂^*, β̂, t) and show that this variance is always less than or equal to the variance of Ŝ_KM(t) and the reduction is maximized when the assumed working models in (2·3) and (2·4) are true.

Assumption A.1 Censoring, C, is independent of {T_𝕃, Z} given treatment assignment, 𝒢.

Assumption A.2 Treatment assignment, 𝒢, is independent of Z.

Regularity Conditions (C.1) Throughout, we assume several regularity conditions: (1) the joint density of {T_𝕃, T_𝕊, C} is continuously differentiable with density function bounded away from 0 on [0, t], (2) ${\mathbf{Z}}^{𝖳}{\mathit{\beta }}_0^{*}$ and W^𝖳β₀ have continuously differentiable densities and Z is bounded, (3) h = O(n^−υ) with 1/4 < υ < 1/2, (4) K(x) is a symmetric smooth kernel function with continuous second derivative on its support and ∫ K̇ (x)²dx < ∞, where K̇ (x) = dK(x)/dx.

Appendix I

Martingale Representation

In Supplementary Appendix A we show that the variability of β̂^* and β̂ is negligible and can be ignored in making inferences on Ŝ(β̂^*, t₀), Ŝ(β̂^*, t|t₀) and ${Ŝ}_{\mathrm{L}\mathrm{M}}({\mathit{\beta }}_0^{*},{\mathit{\beta }}_0,t)$. Therefore, we focus on the asymptotic expansions of 𝒲̃^Z (t₀), 𝒲̃(t | t₀), and 𝒲̃_LM(t, t₀) with ${\mathit{\beta }}_0^{*}$ and β₀ and express these quantities in martingale notation. Throughout, we will repeatedly use the fact that n_t0/n ≈ S_C(t₀)S(t₀), where S_C(t₀) = P(C > t₀).

Theorem 1. Assume A.1, A.2 and Regularity Conditions (C.1) hold. Note that in Supplementary Appendix A it was shown that 𝒲̃_LM(t)) ≈ 𝒲̃_LM(t, t₀).

$${\mathrm{𝒲̃}}_{LM}(t,t_0)\approx n^{-1/2}\sum _{i=1}^n{\varphi }_{1i}(t,t_0)+n^{-1/2}\sum _{i=1}^n{\varphi }_{2i}(t,t_0)$$ (I·1)

$$\mathit{\text{where}}{\varphi }_{1i}(t,t_0)\equiv \frac{I(X_{\mathrm{𝕃}i}>t_0)}{S_C(t_0)}[S_{U_i}(t|t_0){\int }_{t_0}^t\frac{d{M}_{C_i}(s|t_0)}{{\pi }_{U_i}(s|t_0)}+\frac{I(X_{𝕃i}>t)}{S_C(t|t_0)}-S(t|t_0)]$$ (I·2)

$$\mathit{\text{and}}{\varphi }_{2i}(t,t_0)=S(t|t_0)[S_{U_i^{*}}(t_0){\int }_0^{t_0}\frac{d{M}_{C_i}(s)}{{\pi }_{U_i^{*}}(s)}+\frac{I(X_{𝕃i}>t_0)}{S_C(t_0)}-S(t_0)].$$ (I·3)

and 𝒲̃_LM(t) converges to a Gaussian process indexed by t ∈ [t₀, τ].

Proof of Theorem 1. Using a Taylor series expansion and Lemma A.3 of Bilias et al. (1997),

$${\mathrm{𝒲̃}}^{\mathbf{Z}}(t_0)\approx -\int \sqrt{n}\{{\mathrm{\Lambda ̂}}_u({\mathit{\beta }}_0^{*},t_0)-{\mathrm{\Lambda }}_u(t_0)\}{S}_u(t_0)F({\mathit{\beta }}_0^{*},du)+n^{-1/2}\sum _{i=1}^n\{S_{U_i^{*}}(t_0)-S(t_0)\}.$$

Let $M_i(s|u)=N_i(s)-{\int }_0^{t_0}{Y}_i(s)d{\mathrm{\Lambda }}_u(s)$ N_i(s) = I(X_𝕃i ≤ s, δ_𝕃i = 1), Y_i(s) = I(X_𝕃i ≥ s) and ${\pi }_u(s)=P(X_{𝕃i}\ge s|U_i^{*}=u)$. By a martingale representation, $\sqrt{n}\{{\mathrm{\Lambda ̂}}_u({\mathit{\beta }}_0^{*},t_0)-{\mathrm{\Lambda }}_u(t_0)\}=n^{-1/2}{\sum }_{i=1}^n{K}_h(U_i^{*}-u){\int }_0^{t_0}{\pi }_u{(s)}^{-1}d{M}_i(s|u)$. Using a change of variable where $\psi =\frac{u-U_i^{*}}{h}$, and a Taylor series expansion, let ${\xi }_i(t_0|u)={\int }_0^{t_0}\frac{d{M}_i(s|u)}{{\pi }_u(s)}$ and $\eta (U_i^{*}+h\psi )={\xi }_i(t_0|U_i^{*}+h\psi )S_{U_i^{*}+h\psi }(t_0)f({\mathit{\beta }}_0^{*},U_i^{*}+h\psi )$, where f(·) is the probability density function corresponding to S(·),

$$\int \sqrt{n}\{{\mathrm{\Lambda ̂}}_u({\mathit{\beta }}_0^{*},t_0)-{\mathrm{\Lambda }}_u(t_0)\}{S}_u(t_0)F({\mathit{\beta }}_0^{*},du)=n^{-1/2}\sum _{i=1}\int K(\psi )[\eta (U_i^{*})+\eta \prime (U_i^{*})h\psi +O(h^2)]d\psi \approx n^{-1/2}\sum _{i=1}^n{\xi }_i(t_0|U_i^{*})S_{U_i^{*}}(t_0)f({\mathit{\beta }}_0^{*},U_i^{*})=n^{-1/2}\sum _{i=1}^n{\int }_0^{t_0}\frac{d{M}_i(s|U_i^{*})}{{\pi }_{U_i^{*}}(s)}{S}_{U_i^{*}}(t_0)$$

It then follows that

$${\mathrm{𝒲̃}}^{\mathbf{Z}}(t_0)\approx -n^{-1/2}\sum _{i=1}^n{\int }_0^{t_0}\frac{d{M}_i(s|U_i^{*})}{{\pi }_{U_i^{*}}(s)}{S}_{U_i^{*}}(t_0)+n^{-1/2}\sum _{i=1}^n\{S_{U_i^{*}}(t_0)-S(t_0)\}.$$ (I·4)

To understand how Ŝ(β̂^*, t₀) can be viewed as a KM estimator augmented by censoring martingales, we next express the influence function of 𝒲^Z(t₀) in such a form. From (A.2) in Supplementary Appendix A and using martingale representation once again and integration by parts,

$${\mathrm{𝒲̃}}^{\mathbf{Z}}(t_0)\approx n^{-1/2}\sum [-{\int }_0^{t_0}\frac{S_{U_i^{*}}(t_0)}{{\pi }_{U_i^{*}}(s)}d{N}_i(s)-{\int }_0^{t_0}\frac{S_{U_i^{*}}(t_0)}{{\pi }_{U_i^{*}}(s)}{Y}_i(s)\frac{d{S}_{U_i^{*}}(s)}{S_{U_i^{*}}(s)}+S_{U_i^{*}}(t_0)-S(t_0)]=n^{-1/2}\sum [S_{U_i^{*}}(t_0){\int }_0^{t_0}\frac{d{M}_{C_i}(s)}{{\pi }_{U_i^{*}}(s)}+\frac{I(X_{\mathrm{𝕃}i}>t_0)}{S_C(t_0)}-S(t_0)]$$ (I·5)

where $M_{C_i}(t)=N_{C_i}(t)-{\int }_0^t{Y}_i(s)d{\mathrm{\Lambda }}_C(s)$ and Λ_C(s) = −log S_C(s). Using similar arguments, it can be shown that

$$\mathrm{𝒲̃}(t|t_0)\approx -n_{t_0}^{-1/2}\sum _{i\in {\mathrm{\Omega }}_{t_0}}{\int }_{t_0}^t\frac{d{M}_i(s|U_i,t_0)}{{\pi }_{U_i}(s|t_0)}{S}_{U_i}(t|t_0)+n_{t_0}^{-1/2}\sum _{i\in {\mathrm{\Omega }}_{t_0}}\{S_{U_i}(t|t_0)-S(t|t_0)\}$$ (I·6)

$$\mathrm{𝒲̃}(t|t_0)\approx n_{t_0}^{-1/2}\sum _{i\in {\mathrm{\Omega }}_{t_0}}[S_{U_i}(t|t_0){\int }_{t_0}^t\frac{d{M}_{C_i}(s|t_0)}{{\pi }_{U_i}(s|t_0)}+\frac{I(X_{\mathrm{𝕃}i}>t)}{S_C(t|t_0)}-S(t|t_0)]$$ (I·7)

where $M_i(s|U_i,t_0)=N_i(s|t_0)-{\int }_{t_0}^t{Y}_i(s|t_0)d{\mathrm{\Lambda }}_{U_i}(s|t_0)$ and π_Ui(s|t₀) = P(X_𝕃i ≥ υ|U_i = u, X_𝕃i > t₀).

Using (I·5), (I·7) and (A.2) in Supplementary Appendix A, we now examine the form of our complete proposed estimator for S(t), Ŝ_LM(β̂^*,β̂, t), and obtain

$${\mathrm{𝒲̃}}_{\mathrm{L}\mathrm{M}}(t,t_0)\approx S(t_0)\mathrm{𝒲̃}(t|t_0)+S(t|t_0){\mathrm{𝒲̃}}^{\mathbf{Z}}(t_0)\approx n^{-1/2}\sum _{i=1}^n{\varphi }_{1i}(t,t_0)+n^{-1/2}\sum _{i=1}^n{\varphi }_{2i}(t,t_0)$$ (I·8)

$$\text{where}{\varphi }_{1i}(t,t_0)\equiv \frac{I(X_{\mathrm{𝕃}i}>t_0)}{S_C(t_0)}[S_{U_i}(t|t_0){\int }_{t_0}^t\frac{d{M}_{C_i}(s|t_0)}{{\pi }_{U_i}(s|t_0)}+\frac{I(X_{\mathrm{𝕃}i}>t)}{S_C(t|t_0)}-S(t|t_0)]$$ (I·9)

$$\text{and}{\varphi }_{2i}(t,t_0)=S(t|t_0)[S_{U_i^{*}}(t_0){\int }_0^{t_0}\frac{d{M}_{C_i}(s)}{{\pi }_{U_i^{*}}(s)}+\frac{I(X_{\mathrm{𝕃}i}>t_0)}{S_C(t_0)}-S(t_0)].$$ (I·10)

It is interesting to note that these two terms, $n^{-1/2}{\sum }_{i=1}^n{\varphi }_{1i}(t,t_0)$ and $n^{-1/2}{\sum }_{i=1}^n{\varphi }_{2i}(t,t_0)$, converge to two independent normal distributions and that E{ϕ_1i(t, t₀)ϕ_2i(t, t₀)} = 0. Since S_Ui(t|t₀) is a bounded smooth monotone function in t and ${\int }_{t_0}^t\frac{d{M}_{C_i}(s|t_0)}{{\pi }_{U_i}(s|t_0)}$ is a martingale process, $\{S_U(t|t_0){\int }_{t_0}^t\frac{d{M}_{C_i}(s|t_0)}{{\pi }_{U_i}(s|t_0)}t\in [t_0,\tau ]\}$ is Donsker. This coupled with the fact that the simple class {I(X_𝕃i > t)|t} is Donsker, implies that {ϕ_ji(t, t₀)|t}, j = 1, 2 are Donsker by Theorem 9.30 of Kosorok (2008). Therefore 𝒲̂_LM(t)) converges to a Gaussian process indexed by t ∈ [t₀, τ].

Appendix II

Variance of Ŝ_KM(β̂^*,β̂, t)

In this section we compare the variance of the proposed estimator to that of the KM estimator, as described in the next theorem.

Theorem 2. Assume A.1, A.2, and Regularity Conditions (C.1) hold. The proposed estimator, Ŝ_LM(β̂^*, β̂, t), is always at least as efficient as the Kaplan Meier estimate. Specifically,

$$\mathrm{\Delta }{\mathit{\text{Var}}}_{LM}=n\mathit{\text{Var}}\{{Ŝ}_{KM}(t)-S(t)\}-n\mathit{\text{Var}}\{{Ŝ}_{LM}({\mathit{\beta ̂}}^{*},\mathit{\beta ̂},t)-S(t)\}\approx \frac{S(t_0)}{S_C(t_0)}{\int }_{t_0}^t\left[E\right\{S_{U_i}(s|t_0){[S_{U_i}(t|s)-S(t|s)]}^2\}]dG(s|t_0)+S{(t|t_0)}^2{\int }_0^{t_0}E\{S_{U_i^{*}}(s){[S_{U_i^{*}}(t_0|s)-S(t_0|s)]}^2\}dG(s)\ge 0$$

where ΔVar_LM denotes the difference in variance.

Proof of Theorem 2. We first note that it can be shown that Ŝ(β̂^*, t₀) and Ŝ(β̂, t) are asymptotically independent and hence can be handled separately. From (I·4), we can easily examine the variance of Ŝ(β̂^*, t₀) and compare it to the variance of Ŝ_KM(t₀). The resulting form of the difference in variance allows us to make some interesting conclusions regarding the reduction in variance when using the proposed marginal estimate. Note that this result only concerns one component of our complete estimate since Ŝ_LM(β̂^*,β̂, t₀) = Ŝ(β̂^*, t₀)Ŝ(β̂, t|t₀), however we consider the results and conclusions worthy of discussion. Similar to Murray & Tsiatis (1996), we use a simple application of the conditional variance formula along with martingale properties, integration by parts and independent censoring,

$$\text{Var}\{{\mathrm{𝒲̂}}^{\mathbf{Z}}(t_0)\}\approx n^{-1}E\left\{\sum _{i=1}^n{S}_{U_i^{*}}{(t_0)}^2{\int }_0^{t_0}\frac{d{\mathrm{\Lambda }}_{U_i^{*}}(s)}{{\pi }_{U_i^{*}}(s)}\right\}+\text{Var}\{S_{U_i^{*}}(t_0)\}=n^{-1}\sum _{i=1}^{n}E\{S_{U_i^{*}}(t_0)G(t_0)-S_{U_i^{*}}{(t_0)}^2-{\int }_0^{t_0}\frac{G\prime (s)ds}{S_{U_i^{*}}(s)}{S}_{U_i^{*}}{(t_0)}^2\}+\text{Var}\{S_{U_i^{*}}(t_0)\}=S(t_0)G(t_0)-E\left\{{\int }_0^{t_0}\frac{G\prime (s)ds}{S_{U_i^{*}}(s)}{S}_{U_i^{*}}{(t_0)}^2\right\}-S{(t_0)}^2$$ (II·1)

where G(s) = 1/S_c(s). Murray & Tsiatis (1996) showed that $n\text{Var}\{{Ŝ}_{KM}(t_0)-S(t_0)\}=S(t_0)G(t_0)-{\int }_0^{t_0}\frac{G\prime (s)ds}{S(s)}S{(t_0)}^2-S{(t_0)}^2$. Comparing these two variances, we have

$$\mathrm{\Delta }\text{Var}=n\text{Var}\{{Ŝ}_{KM}(t_0)-S(t_0)\}-\text{Var}\{{\mathrm{𝒲̂}}^{\mathbf{Z}}(t_0)\}=-{\int }_0^{t_0}\frac{G\prime (s)ds}{S(s)}S{(t_0)}^2+E\left\{{\int }_0^{t_0}\frac{G\prime (s)ds}{S_{U_i^{*}}(s)}{S}_{U_i^{*}}{(t_0)}^2\right\}={\int }_0^{t_0}\left\{E\right[\frac{S_{U_i^{*}}{(t_0)}^2}{S_{U_i^{*}}(s)}-\frac{S{(t_0)}^2}{S(s)}\left]\right\}dG(s)={\int }_0^{t_0}E\{S_{U_i^{*}}(s){[S_{U_i^{*}}(t_0|s)-S(t_0|s)]}^2\}dG(s)\ge 0$$

Here and in the sequel, for any random variable 𝒰, we use notation S_𝒰(t | s) to denote P(T_𝕃 > t | T_𝕃 > s, 𝒰) and S(t | s) = P(T_𝕃 > t | T_𝒰 > s). Provided that $\text{cov}(U_i^{*},T_{𝕃i}|T_{𝕃i}\le t_0)>0,Ŝ({\mathit{\beta ̂}}^{*},t_0)$ is always more efficient than Ŝ_KM(t₀), asymptotically. Furthermore, ΔVar is maximized when the model used to obtain the score, $U_i^{*}$, is the true model. To see this, we note that if $S_{U_i^{*}}(t)$ is replaced with the true conditional survival S_Zi(t), the corresponding variance reduction over the KM estimator is $\mathrm{\Delta }\text{Var}(\mathbf{Z})\equiv {\int }_0^{t_0}E[I(T_{𝕃i}>s){\{S_{{\mathbf{Z}}_i}(t_0|s)-S(t_0|s)\}}^2]dG(s)$. Comparing the variance reduction using S_Zi(t) versus using an arbitrary function of Z_i, denoted by 𝒰_i, we have

$$\mathrm{\Delta }\text{Var}(\mathbf{Z})-\mathrm{\Delta }\text{Var}(𝒰)={\int }_0^{t_0}E\{I(T_{\mathrm{𝕃}i}>s){[S_{{\mathbf{Z}}_i}(t_0|s)-S_{{𝒰}_i}(t_0|s)]}^2\}dG(s)+{\int }_0^{t_0}2E\{[S_{{𝒰}_i}(t_0|s)-S(t|s)][S_{{\mathbf{Z}}_i}(t_0|s)-S_{{𝒰}_i}(t_0|s)]|T_{\mathrm{𝕃}i}>s\}P(T_{\mathrm{𝕃}i}>s)dG(s)$$

Since E{S_Zi(t₀|s) | T_i > s, 𝒰_i} = E{E(I(T_𝕃i > t)|T_𝕃i > s,Z_i)|T_𝕃i > s, 𝒰_i} = E{T_𝕃i > t|T_𝕃i > s, 𝒰_i} = S_𝒰i(t₀|s), and hence E{[S_𝒰i(t₀|s) − S(t|s)][S_Zi(t₀|s) − S_𝒰i(t₀|s)]|T_𝕃i > s} = 0. Therefore, ΔVar(Z) − ΔVar(𝒰) ≥ 0. Since $P(T_{𝕃i}>s|U_i^{*})=S_{{\mathbf{Z}}_i}(s)$ under the correct specification of the working model, Ŝ^Z(t) achieves maximal efficiency when the fitted Cox model holds.

We next derive the variance form of our complete estimate, 𝒲̃_LM(t, t₀). From (I·8), Var{𝒲̃_LM(t, t₀)} ≈ E [{ϕ_1i(t, t₀) + ϕ_2i(t, t₀)}²] = E{ϕ_1i(t, t₀)²}+E {ϕ_2i(t, t₀)²} since it can be shown that E{ϕ_1i(t, t₀)ϕ_2i(t, t₀)} = 0. It follows from (I·5) and (II·1), that

$$E\{{\varphi }_{2i}{(t,t_0)}^2\}\approx S{(t|t_0)}^2[S(t)G(t)-E\{{\int }_0^{t_0}\frac{G\prime (s)ds}{S_{U_i^{*}}(s)}{S}_{U_i^{*}}{(t_0)}^2\}-S{(t_0)}^2]$$

Using similar arguments as above and the expression in (I·6), we can show that

$$\text{Var}\{\mathrm{𝒲̃}(t|t_0)\}=S(t|t_0)G(t|t_0)-E\{{\int }_{t_0}^t\frac{G\prime (s|t_0)ds}{S_{U_i}(s|t_0)}{S}_{U_i}{(t|t_0)}^2\}-S{(t|t_0)}^2$$

where G(s|t₀) = 1/P(C_i > s|t₀). It follows along with (I·7) that

$$E[{\varphi }_{1i}{(t,t_0)}^2]=\frac{S(t_0)}{S_C(t_0)}[S(t|t_0)G(t|t_0)-E\{{\int }_{t_0}^t\frac{G\prime (s|t_0)ds}{S_{U_i}(s|t_0)}{S}_{U_i}{(t|t_0)}^2\}-S{(t|t_0)}^2]$$

Therefore, Var{𝒲̂_LM(t, t₀)} ≈

$$\frac{S(t_0)}{S_C(t_0)}[S(t|t_0)G(t|t_0)-E\{{\int }_{t_0}^t\frac{G\prime (s|t_0)ds}{S_{U_i}(s|t_0)}{S}_{U_i}{(t|t_0)}^2\}-S{(t|t_0)}^2]+S{(t|t_0)}^2[S(t)G(t)-E\{{\int }_0^{t_0}\frac{G\prime (s)ds}{S_{U_i^{*}}(s)}{S}_{U_i^{*}}{(t_0)}^2\}-S{(t)}^2]$$

Note that Ŝ_KM(t) = Ŝ_KM(t|t₀)Ŝ_KM(t₀) where Ŝ_KM(t|t₀) is the KM estimate of survival at t using only Ω_t0. Similarly to (A.2) in Supplementary Appendix A, using a Taylor series expansion, one can show that Ŝ_KM(t) − S(t) ≈ S(t₀)[Ŝ_KM(t|t₀) − S(t|t₀)] + S(t|t₀)[Ŝ_KM(t₀) − S(t₀)] and thus,

$$n\text{Var}[{Ŝ}_{\mathrm{K}\mathrm{M}}(t)-S(t)]\approx \frac{S(t_0)}{S_C(t_0)}[G(t|t_0)S(t|t_0)-{\int }_{t_0}^t\frac{G\prime (s|t_0)ds}{S(s|t_0)}S{(t|t_0)}^2-S{(t|t_0)}^2]+S{(t|t_0)}^2[G(t_0)S(t_0)-{\int }_0^{t_0}\frac{G\prime (s)ds}{S(s)}S{(t_0)}^2-S{(t_0)}^2]$$

where we have used the independence of Ŝ_KM(t|t₀) and Ŝ_KM(t₀), and KM variance estimates from Murray & Tsiatis (1996). Examining the difference which we denote by ΔVar_LM,

$$\mathrm{\Delta }{\text{Var}}_{\mathrm{L}\mathrm{M}}=n\text{Var}\{{Ŝ}_{\mathrm{K}\mathrm{M}}(t)-S(t)\}-n\text{Var}\{{Ŝ}_{\mathrm{L}\mathrm{M}}({\mathit{\beta ̂}}^{*},\mathit{\beta ̂},t)-S(t)\}\approx \frac{S(t_0)}{S_C(t_0)}{\int }_{t_0}^t\left[E\right\{S_{U_i}(s|t_0){[S_{U_i}(t|s)-S(t|s)]}^2\}]dG(s|t_0)+S{(t|t_0)}^2{\int }_0^{t_0}E\{S_{U_i^{*}}(s){[S_{U_i^{*}}(t_0|s)-S(t_0|s)]}^2\}dG(s)\ge 0.$$

Thus, the proposed estimator, Ŝ_LM(β̂^*, β̂, t), is at least as efficient as the Kaplan Meier estimate. In addition, the reduction is maximized when the assumed working models in (2·3) and (2·4) are true. Note that the gain in efficiency depends on t₀ and the true values of β and β^*. The maximum reduction is within the class of estimators constructed using W and t₀. The amount of reduction would also depend on the magnitude of β and β^*. In particular, if β and β^* are equal to zero, there would be no efficiency gain, but the larger β and β^* are, the more variation we would expect in S_Ui(t|s) and $S_{U_i^{*}}(t_0|s)$ which would lead to a larger expected reduction in variance.