Abstract
The stability of colloidal dispersions is of crucial importance because the properties of dispersions are strongly affected by the degree of coagulation. Whereas the coagulation kinetics for quiescent (i.e., nonstirred) and diluted systems is well-established, the behavior of concentrated dispersions subjected to shear is still not fully understood. We employ the discrete element method (DEM) for the simulation of coagulation of concentrated colloidal dispersions. Normal forces between interacting particles are described by a combination of the Derjaguin, Landau, Verwey, and Overbeek (DLVO) and Johnson, Kendall, and Roberts (JKR) theories. We show that, in accordance with the expectations, the coagulation behavior depends strongly on the particle volume fraction, the surface potential, and the shear rate. Moreover, we demonstrate that the doublet formation rate is insufficient for the description of the coagulation kinetics and that the detailed DEM model is able to explain the autocatalytic nature of the coagulation of stabilized dispersions subjected to shear. With no adjustable parameters we are able to provide semiquantitative predictions of the coagulation behavior in the high-shear regions for a broad range of particle volume fractions. The results obtained using the DEM model can provide valuable guidelines for the operation of industrial dispersion processes.
Introduction
The production of many polymers often involves stages in which the monomer, the polymer, or the intermediate product is dispersed into small particles. This is the case of all polymers produced by suspension or emulsion polymerization. These techniques are undoubtedly advantageous because they provide much easier control of the polymerization and also process safety in terms of a thermal runaway. However, the fact that the system is in the form of a dispersion brings along some difficulties. These are mainly related to the colloidal stability and thus the process of coagulation and fouling (which depending on the situation can be desired or not).
Colloidal systems contain usually two immiscible substances, one forming the continuous phase and the other the dispersed phase. These systems are usually thermodynamically unstable, but so-called kinetic stability can be achieved by several means, such as the electrostatic repulsion due to the charge on the surface of colloidal particles, which creates an electrostatic barrier preventing the particles from coagulating. Although this method sufficiently stabilizes colloidal systems under quiescent conditions (i.e., with no stirring), for systems subjected to shear one has to carefully check whether the energy barrier between particles is sufficiently high to prevent coagulation. The problem of colloidal stability under high-shear conditions is even more complex because collisions of particles are strongly affected by the flow pattern, which might vary significantly throughout the process, especially for turbulent flows.
The behavior of the colloidal mixture is influenced by forces acting on each single particle. These may arise from the interaction of the particle with the surrounding fluid, interactions among particles, or particle-wall interactions. For the latter two types of interactions, there are several models describing the forces and torques. The normal particle-particle interactions represent the basis of the description and can generally be divided into two parts: (i) noncontact forces and (ii) contact forces and torques.
The most widely used approach for the description of noncontact forces of small spheres in electrolytes is the Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory.1 It combines the attractive van der Waals and repulsive electrostatic forces. On the other hand, the contact of adhesive elastic spheres is commonly described by the Johnson, Kendall, and Roberts (JKR) theory proposed by Johnson et al. in 1971.2
The problem of the description of the normal interaction between two particles arises when one wants to satisfactorily describe the interaction force for the entire range of separation distances. In 1998, Hong3 presented a way to overcome this issue by taking the maximum adhesion force from the JKR theory as a limiting value for the DLVO theory, which would otherwise provide infinitely high adhesion force for very small separation distances. We adopted this idea and further developed it to obtain the continuous force–distance profile for the whole range of separation distances.
Mathematical modeling is a way of getting better insight into the dynamics of dispersion systems. Because of the discrete nature of colloids, it is convenient to use the discrete element method (DEM), which is employed also in this work. The main advantage of the DEM lies in the direct incorporation of the interparticle forces and torques into the model.
In 2007, Marshall used DEM models to simulate aerosol particles in a channel flow.4 He concluded that for this nonstabilized system, the channel fouling is strongly dependent on the adhesion forces coming from both particle-particle and particle-wall interactions. This means that the channel with more adhesive particles is more likely to end up with large agglomerates in the flow as well as clusters attached to the wall.
Shear-induced aggregation of charge-stabilized colloids can be described as an activated process.5 The activation energy is given by the balance between the height of the potential barrier (Umax) and the energy of the particles obtained from the flow. The ratio of the energy of the particles from shear to the thermal energy is described by the Péclet number (Pe = 3πRp3ηG/(kBT), where Rp, η, G, kB, and T are the particle radius, fluid dynamic viscosity, shear rate, Boltzmann constant, and absolute temperature, respectively). For the system with an energy barrier between the particles, the critical Peclet number can be expressed as5,6
| 1 |
where α is the flow-specific coefficient. The quantity Pec can be viewed as the energy of the advective motion necessary to overcome the energy barrier between the particles. For values of Pe below the critical value Pec, the system should be stable, while for supercritical values aggregation occurs. It is therefore the interplay between the stabilization and the shearing that defines the behavior of the system.
The above-mentioned approach has one limitation. It is not able to capture the effect of larger numbers of particles contributing to the energy of the collision. In other words, for more crowded systems, the critical Péclet number should depend on the volume fraction of particles (ϕ). This phenomenon was investigated by Zaccone et al.7 in 2010, who used the generalized Kramer’s rate theory. This statistical approach is able to describe the dependence of the characteristic coagulation time (tc) on the volume fraction of the particles. This dependence is added to the model by means of the suspension viscosity (ηs), which is a function of ϕ, and this is known as the effective medium approach.
The rate constant of doublet formation (k1,1) in the turbulent regime was measured experimentally by Sugimoto et al.8 in 2014. Compared with our simulations they reported higher values of the doublet formation rate, but the conditions of the measurements were very different.
In 2013, Soos et al.9 investigated the scaling of the maximum stable aggregate size (Rg) with the maximum shear rate (Gmax). From the results of breakage experiments in a stirred tank and contracting nozzle the value of Rg was determined, while the values of Gmax for the respective geometries were obtained using computational fluid dynamics simulations. Soos et al. reported that Rg follows the same scaling with the maximum shear rate independent of whether the flow pattern is laminar (contracting nozzle) or turbulent (stirred tank). Another important result of this work is the finding that the maximum value of the hydrodynamic stress (related to Gmax) is responsible for the breakage of the aggregates (i.e., not the usually used average value).
In this paper, we propose a new approach for the modeling of colloidal stability. Using the DEM we can incorporate all of the necessary forces and torques. Furthermore, because of the dynamic nature of the model we do not have to restrict ourselves to the statistical description. Our model directly accounts for several phenomena, such as the crowding or stabilization of the particles, without simplifications that are often used.5,7,10 Having particles immersed in water phase, we investigate a different case than Marshall4 in this paper. The electrostatic double layer (EDL) is formed on the surface of the particles as a result of their charge, and this imposes an energy barrier. Also, the shear forces are more pronounced because of the higher dynamic viscosity of water compared with air. Moreover, particles in emulsion polymerization are soft because of their swelling by (co)monomers. Therefore, we utilize the description of the interparticle forces to account for all of these phenomena. The disadvantage of our approach lies in the necessity of computing with a small integration step, which imposes high demand for computational power. The computational feasibility can be improved by optimization of the algorithms and proper design of the simulations.
The main result presented in this paper is the demonstration of the strong dependence of the coagulation kinetics on the particle volume fraction, the surface potential, and the shear rate. We also show that the doublet formation rate is an important but not sufficient measure of the coagulation rate, since at some point larger aggregates are formed and the process becomes autocatalytic. All of these results are obtained with no fitting parameters (i.e., material properties and physical constants are the only inputs into the model).
Structure of the Mathematical Model
The DEM is applicable for the description of either naturally discrete particles or continuous materials discretized into discrete elements. Once defined, the discrete elements (labeled i) are characterized by their masses (mi), positions (xi), velocities (vi), and rotation rates (Ωi). In this work, for the sake of simplicity, the elements are assumed to be spherical with density ρp and radius Rp, which are the same for all of the discrete elements. The particle trajectories are governed by the well-known Newton’s equation of motion:
| 2 |
where Fi represents the sum of all forces acting on the discrete element i. The balance of angular momentum (Li) for each particle can be expressed in the following form:
| 3 |
where Ωi = Li/Ii is the rotation rate of particle i, Mi is the sum of all of the torques acting on particle i, and Ii is the particle momentum of inertia. For a homogeneous solid sphere, we have Ii = (2/5)miRp2 (particle moment of inertia around its center) and mi = 4/3πRp3ρp.
Since we perform simulations in two spatial dimensions, it is sufficient to introduce the rotation rate Ωi of particle i only for rotation in the plane where the particle motion occurs. The resulting direction of Ωi is then perpendicular to this plane.
Forces and torques acting on the particle i can originate from (i) the interaction of the particle with the surrounding fluid (superscript F), (ii) the particle-particle interactions (superscript p-p), or (iii) the particle-wall interactions (superscript p-w). These contributions are assumed to be additive, and the resulting force (Fi) and torque (Mi) can be expressed as follows:
| 4 |
The moment of the particle-wall interactions is not taken into account since a strong noncontact force is employed, thus avoiding the solid-body contact of the particles (cf. Interactions between the Particle and the Wall below).
This defines (when initial conditions are supplied) a set of second-order ordinary differential equations that can be numerically integrated in time to obtain the dynamic behavior of the system. We used the solver LSODE from ODEPACK11 to solve the set of differential equations. This solver uses the multistep Adams method with an adaptable time step. The “external” particle trajectory sampling time step used for the recording of simulations was Δt = 4 × 10–10 s. However, the real time step of the integration method was usually smaller, especially when the problem became stiff (during the solid-body contact of the particles).
Structure of the Computational Domain
The spatially two-dimensional (2D) computational domain was chosen to be rectangular with dimensions L × L/2, and for most of the computations we used L = 12.5 μm. The velocity profile in the domain was assumed to be linear. In our setup, the lower plate stayed still and the upper plate moved with velocity V. Therefore the resulting shear rate profile was constant in the system, corresponding to the model of simple shear (the scheme of the computational domain is shown in Figure S1 in the Supporting Information). The position of zero velocity was at y = −L/2 + Rp, because the force acting on the particle was computed from the position of the particle center, and thus, a particle attached to the wall was not moved in the translational way by the flow but was still exposed to the torque caused by the flow. Particles were initially randomly placed into the domain in a way that avoided solid-body contact. The initial velocities and rotation rates of the particles were set to correspond to the fluid velocity and rotation at the location of the particle.
Forces and Torques in Colloids
Colloidal systems are affected by a wide range of force and torque interactions. In the following text, we introduce only those relevant for our specific system. At first we describe the interaction of the particles with the surrounding fluid and then we introduce the equations for the particle-particle and particle-wall interactions.
Interactions of the Particles with the Flow
Particles immersed in the flowing fluid experience a drag force and are also rotated by the fluid. For the colloidal particles investigated in the current paper, the Reynolds number is always much smaller than 1 because of their small inertia. Therefore, we can describe their interaction with the flow by the simple Stokes’ law. The drag force (FiF) is then
| 5 |
where ηF is the fluid dynamic viscosity, Rp is the radius of the particle, and viF and vi are the velocities of the fluid and the particle, respectively.
If the fluid surrounding the particle rotates locally with angular velocity ω, the corresponding fluid torque (MiF) on particle i is computed as follows:12
| 6 |
The velocity and angular velocity of the fluid are computed from the linear velocity profile (cf. Figure S1 in the Supporting Information). This profile is a result of the system geometry, and the particles are assumed not to alter the profile.
Interactions between the Particles
The most important input for the DEM model is the description of the normal forces between the particles. It is necessary to describe the interaction potential energy (or force) for the entire range of separation distances between particles. The most common description of the noncontact forces is the DLVO theory, while the contact forces can be described by the Born repulsion for hard particles13 or the JKR theory for soft particles.4 The most usual combinations are hard particles with noncontact forces and soft particles without noncontact forces. Our system is specific in the way that we deal with soft (swollen) adhesive particles immersed in water. Therefore, the model of normal interaction must be able to describe (i) the energy barrier between the particles due to the presence of the EDL, (ii) the attraction (adhesion) for short separation distances and during the solid-body contact, and (iii) the elastic repulsion of the soft particles. These phenomena are separately described by the DLVO theory (noncontact interactions) and the JKR theory (contact mechanics), but their combination is not straightforward.3 In the following part, we first introduce and then combine these two theories. Finally, the description of the tangential interactions is given.
DLVO Theory
The DLVO theory is usually expressed in the form of interaction potential energy (U). The corresponding interaction force (F) is the negative of the derivative of U with respect to separation distance (h), that is, F = −dU/dh. For the van der Waals attractive potential energy (UvdW) between two spherical particles of the same radius (Rp), we used the expression1
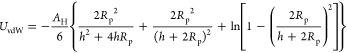 |
7 |
where the separation distance h is given by h = u – 2Rp, where u is the distance between the centers of the two particles. The quantity AH is the Hamaker constant, which characterizes the material of the particles and the surrounding medium.
The electrostatic repulsive potential energy (Uele) of two colloidal particles can be expressed as1
| 8 |
where ε0 is the vacuum permittivity, εr is the relative permittivity of the medium, ψ0 is the surface potential of the particles (assumed to be constant in the model), and κ is the reciprocal of the Debye length.
The DLVO potential energy (UDLVO) is obtained simply as the sum of the two previously mentioned potential energies:
| 9 |
An example of the DLVO potential energy curve and the scaling of the height of the potential barrier (Umax) with the model parameters are shown in Figures S2 and S3, respectively, in the Supporting Information.
JKR Theory
The JKR theory describes the interaction of adhesive, elastic solid bodies. The adhesive force in JKR theory is assumed to act only within the flattened contact region. The equations for JKR theory used in this work were proposed by Johnson et al.2 in 1971 and later slightly modified by Marshall in 2009.12 The equations are valid generally for two spheres with radii Rpi and Rp and the so-called effective radius (R) defined as R = RpiRp/(Rpi + Rp). For contact of a sphere with a plane, the radius Rpj becomes infinite, and R = Rp. When no external force acts on the particles and the force equilibrium is reached, we can define the equilibrium radius of the contact area (a0) as
| 10 |
where γ denotes the surface energy (to be discussed later) and E is the effective Young’s modulus, given by
| 11 |
where Ei and Ej are the Young’s moduli and νi and νj are the Poisson’s ratios of the two interacting bodies.
The equation for the (nonequilibrium) radius of the contact area (a) is implicit:12
| 12 |
where δC is the critical overlap, given by the following equation:
| 13 |
Finally, the magnitude of the normal force between two colliding particles (Fne) can be obtained from the expression
| 14 |
where FC is the magnitude of the critical force, given by
| 15 |
FC corresponds to the maximal adhesive force that can occur between particles described by JKR theory. A typical force–distance curve for the JKR theory is shown in Figure S3 in the Supporting Information.
The precise determination of FC is one of the important tasks in order to obtain reliable results from the model. The maximum adhesion force (cf. eq 15) is directly proportional to the surface energy of the particles (γ), which is experimentally accessible and does not depend on the particle size. We tried to obtain γ from experimental studies that used an atomic force microscope (AFM) for the direct measurement of the force-distance curves using a so-called colloidal probe.14 In these AFM measurements, a colloidal particle is attached to the tip of the AFM cantilever, and the force between the tip particle and the substrate is measured. In 2002, Hodges et al.15 measured the pull-off force between polystyrene particles in water as a function of the size of the particles. Unfortunately, these kinds of measurements usually provide quite scattered results, and the construction of any trends from the published data is very difficult and somewhat ambiguous.15 The theoretical value of γ for polystyrene in air is predicted to be γtheor = 30 mJ m–2.16 However, the presence of water as the surrounding fluid is known to reduce the surface energy by approximately 1 order of magnitude.2,15 Therefore, in this work we used the value γ = 3 mJ m–2, which should correspond to smooth polystyrene particles immersed in water. The effect of surface roughness is known to be more important for large particles.15 Thus, for our case of very small particles (Rp ≈ 50 nm), we assumed the particle surface to be smooth.
Another possibility for obtaining the value of γ would be to use the value of the DLVO potential at a certain cutoff distance (D).17,18 The limitation of this approach lies in the determination of the cutoff distance, which is influenced by many factors, and the resulting value of γ is sensitive to small variations in D. For this reason, the value of γ described in the previous paragraph was chosen.
Connection of the DLVO Theory and the JKR Theory
The previous paragraphs describe well the noncontact and contact interactions in separate theories. A problem arises when one wants to describe the interaction force or potential energy for the entire interval of separation distances. The JKR theory predicts the maximum adhesion force between particles (FC) to occur at the limit radius of the contact area,17alim = 0.63a0 (i.e., at the corresponding limit of the separation distance h; cf. eq 12). The value of FC can be used to constrain the DLVO theory, which is the approach used by Hong in 1998.3 However, the separation distance h for which the maximum adhesive force FC occurs is predicted differently in the DLVO and JKR theories. This inconsistency is caused by different assumptions taken into account for the derivation of the respective theories. The easiest way to overcome this problem without introducing a discontinuity into the force-distance profile is to cut the JKR curve at the point where it crosses the DLVO curve. However, in that case we lose the determination of FC, which is an important characteristics of the system. On the other hand, when we are interested in the agglomeration behavior of the system, the exact position (unlike the value) of the maximum adhesion force is not of crucial importance.14 Therefore, keeping in mind a certain arbitrariness, we decided to overcome the different predictions of the JKR and DLVO theories by shifting the JKR curve in the direction of the x (separation distance) axis in such a way that the maximum adhesion force occurs exactly at the crossing with the DLVO curve.
The resulting potential energy and force profiles are shown in Figure 1. We can see that the potential energy curve describes, apart from the potential barrier already mentioned before, a deep potential well, the so-called primary minimum. Two approaching particles at first experience weak adhesion due to the secondary potential minimum (not apparent in Figure 1) and then repulsion due to the presence of EDL. If their energy is high enough, they overcome the barrier and are brought together by the strong adhesion. When the potential minimum is reached, they are prevented from further approach by elastic repulsion. This behavior, represented in terms of force, is described by the force-distance curve in Figure 1b.
Figure 1.
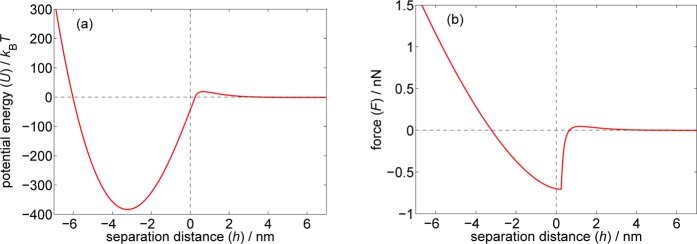
(a) Potential energy U and (b) force F as a function of the separation distance h. The values of the parameters are Rp = 50 nm, AH = 1.3 × 10–20J, ψ0 = −40 mV, κ–1 = 1 nm, γ = 3 mJ m–2, E = 40 MPa, and ν = 0.2.
Dissipation Force
The interaction between the particles is rarely purely elastic because some energy dissipation is likely to occur during the collision.1 This feature can be introduced into the DEM by the addition of a dissipation force (FN d). Let us first define vi as the surface velocity of particle i at the contact point with particle j:
| 16 |
where × denotes the cross product of the vectors and ri = Rpin is the vector pointing from the center of the particle i to the contact point (assuming that n is the unit normal vector pointing from the center of particle i to the center of particle j). For particle j, the corresponding vector is rj = –Rpn. Then the relative velocity of the surfaces of particles i and j at the contact point (vij r) is defined as follows:
| 17 |
Now we can proceed to define the dissipation force as12
| 18 |
in which ηN is the damping coefficient, which can be written as
| 19 |
where m is the mass of the particle, kN is the normal stiffness coefficient (kN = 4/3E√R), and αf is the coefficient of normal friction.
Tangential Interactions
There are several different types of tangential interactions of the particles. Since we restrict ourselves to two spatial dimensions, the twisting of particles is not of concern because it involves rotation of the particles in directions irrelevant for a spatially 2D model. In this work, we employed models for the resistance to sliding and rolling of particles. The formulas for these models are given in the Supporting Information.
Interactions between the Particle and the Wall
The description of the particle-wall interactions is complex and involves most of the interaction types and theories mentioned before in the section about the particle-particle interactions. In this paper, we focused on the behavior of the colloidal particles in the bulk. Therefore, we decided to minimize the influence of the wall on the system behavior.
Colloidal particles immersed in solvent are known to experience the so-called hydration (or solvation) force.17 This force arises from the interactions of the solvent molecules in the so-called hydration shell, but its nature is still not completely revealed.17 Nevertheless, it causes strong short-range repulsion between the involved bodies. In terms of the interaction potential energy (Uh), this repulsion can be phenomenologically described using the following exponential dependence:19
| 20 |
where H is the particle-wall separation distance, F0 is the hydration force constant, and δ0 is the characteristic decay length. We adopted the values of the constants used by Wu et al.,19 as they satisfactorily describe the behavior of the force for colloidal particles. The values of the constants used in our model for the particle-wall interactions were F0 = 2 × 108 N m–2 and δ0 = 3 × 10–10 m.
Coagulation Kinetics
The process of coagulation can be characterized by various quantities, among which the most important are the characteristic time of coagulation (tc) and the rate at which doublets are formed (r1,1). To determine r1,1, we define the number of primary particles contained in doublets as the quantity np,2. The rate of doublet formation can be obtained from the temporal development of np,2 by taking its first derivative with respect to time [i.e., r1,1 ∝ 1/2(dnp,2/dt) because we defined np,2 as the number of primary particles in doublets], and the doublet formation rate constant (k1,1) can be obtained as follows:
| 21 |
where VT is the total volume of the system and N is the number of particles. To eliminate the influence of the initial positions of the particles, we decided to evaluate k1,1 at the point where the growth rate of np,2 reaches its maximum [i.e., the doublet formation rate used for the evaluation of k1,1 was taken to be r1,1max = 1/2 max(dnp,2/dt)].
It is worth noting that the determination of VT in our system is not straightforward. Since the particles are allowed to move only in two spatial dimensions, the appropriate quantity to describe the system would be its total area (AT). However, as we want to be consistent with the common units of k1,1 (m3 s–1), we introduce the following transformation. In three dimensions, the concentration of the particles can be characterized by the volume fraction of the particles, while in two dimensions the corresponding quantity is the “area fraction” of the particles. If we assume that these two are equal (i.e., the ratio between solid and voids is the same for 2D and 3D), we can obtain the VT from the following relation:
| 22 |
where Vp = 4/3πRp3 is the volume of the particle and Ap = πRp2 is the projected area of the particle.
Results and Discussion
The stability of colloidal systems is controlled by the interplay between several influencing factors, of which the most important are (i) the height of the potential barrier (Umax); (ii) the energy inputs, due to either Brownian motion or agitation of the system; and (iii) the particle volume fraction. These factors determine the process of coagulation, which is the main topic of this paper. First we present the results for particle-particle interactions that illustrate the capabilities of the model. Then we show the results of larger simulations dealing with the coagulation kinetics.
Particle-Particle Interactions
To introduce the model behavior, we briefly present the results of two-particle simulations. If not stated otherwise, we used the values of parameters listed in Table 1.
Table 1. Default Values of Model Parameters Used in the Simulations.
| quantity | value | name |
|---|---|---|
| Rp | 50 nm | particle radius |
| AH | 1.3 × 10–20 J | Hamaker constant |
| ηF | 1 × 10–3 Pa s | fluid dynamic viscosity |
| T | 293.15 K | absolute temperature |
| E | 40 MPa | Young’s modulus |
| ν | 0.2 | Poisson’s ratio |
| ρp | 1000 kg m–3 | particle density |
| μeff | 0.5 | effective friction coefficient |
| εr | 80 | relative permittivity of water at T = 293.15 K |
| ψ0p | –30 mV | surface potential of the particles |
| κ–1 | 1 nm | Debye length |
| θcrit | π/4 | critical rolling angle |
| γ | 3 mJ m–2 | surface energy of the particles |
The problem of the stability of colloidal systems always (even for nonsimplified systems) can be reduced to the interactions of primary particles. For dilute systems (ϕ ≪ 1%), this assumption is further developed, and only two-particle collisions are usually assumed to affect the system stability.5 Two aspects are important for the resulting stability: (i) the collision frequency and (ii) the collision efficiency. The first quantity can be statistically determined from the Smoluchowski equation,20 at least for dilute systems. The collision efficiency for two-particle collisions refers to whether the collision results in coagulation or in a rebound and can be expressed in terms of the critical Péclet number (Pec). To determine Pec for a system with two particles, we performed simulations of their direct collision. For this simplified system, Pe is defined as follows:
| 23 |
which means the energy of the collision in the normal direction in units of kBT. The increase in Pec with increasing particle radius is shown in Figure 2. The critical value separates the region where particles rebound (Pe < Pec) from that where they coagulate (Pe > Pec). We have also plotted the values of Pec predicted by eq 1, where the flow-specific coefficient α is equal to unity for this case (i.e., no flow in the system). We can see that the results of the dynamic model correspond almost perfectly with the theoretical prediction, confirming the accuracy of our calculations.
Figure 2.
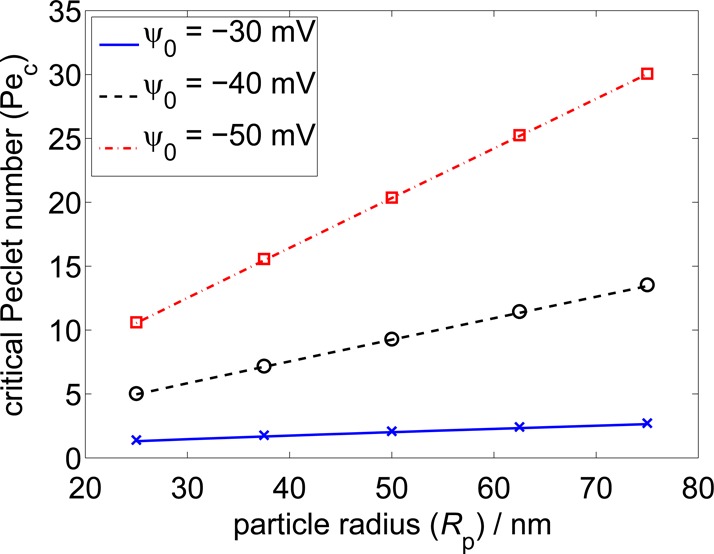
Dependence of the critical Péclet number (Pec) on the particle radius for different values of the surface potential (ψ0). The lines represent the prediction of eq 1, and the points are results of the two-particle dynamic simulations.
Dynamics of Coagulation
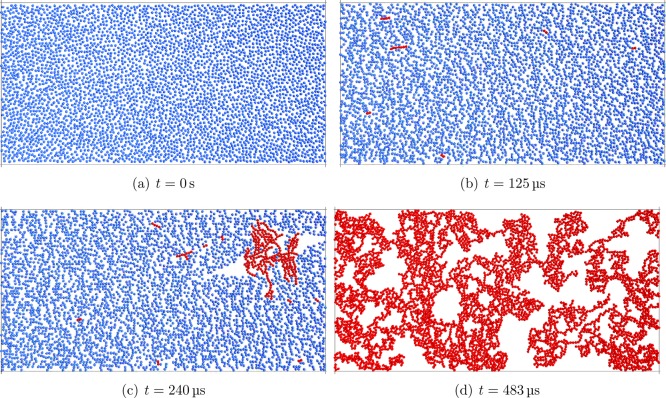
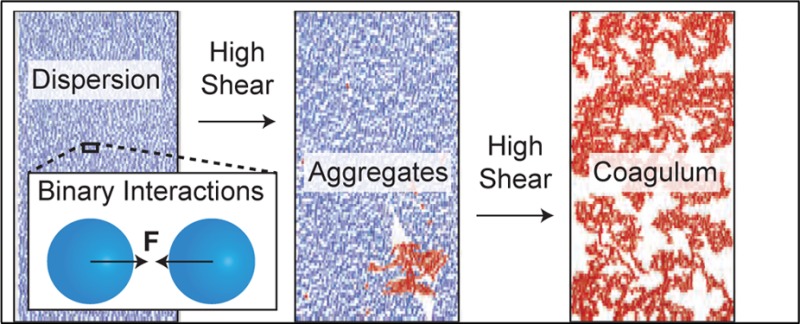
The model used in this work is based on pairwise interactions between two particles (i.e., three-particle forces and torques are not taken into account). These pairwise interactions can be summed up, thus allowing systems with a large number of particles to be studied. One of the big advantages of the DEM model is the possibility directly observing the phenomena taking place in the dynamic system. We performed simulations of the system described in the previous sections for a broad range of volume fractions of the particles (ϕ ∈ ⟨0.19; 0.49⟩). For these very concentrated mixtures, we present the results of their dynamic behavior when exposed to the shear flow. Snapshots from the simulation of the system consisting of 4000 primary particles (ϕ = 0.4) exposed to a shear rate (G) of 6.4 × 104 s–1 at different phases of the aggregation process are shown in Figure 3. We can see that during the initial lag phase, only a small number of small aggregates is formed. The fast aggregation process starts when a larger aggregate is formed in the system. The large aggregate then very quickly coagulates with the remaining primary particles to form dendritic structures. One large interconnected aggregate is present at the end of the coagulation process.
Figure 3.
Snapshots from the simulation for the system with particle volume fraction (ϕ) of 0.4 under a shear rate (G) of 6.4 × 104 s–1.
A movie showing this simulation is available in the HTML version of this paper.
In Figure 4a we show the development of the number of primary particles in aggregates (np) with time. We can see that the curve exhibits a sigmoidal shape with a very slow increase at the beginning. After the lag phase, the onset of coagulum formation occurs, and np linearly increases with time. Finally, np reaches a plateau where all of the particles are contained in the aggregate. This shape (with certain variation) is typical for all of the simulations we performed with shear rates in the range from 6.4 × 104 to 9.0 × 105 s–1.
Figure 4.
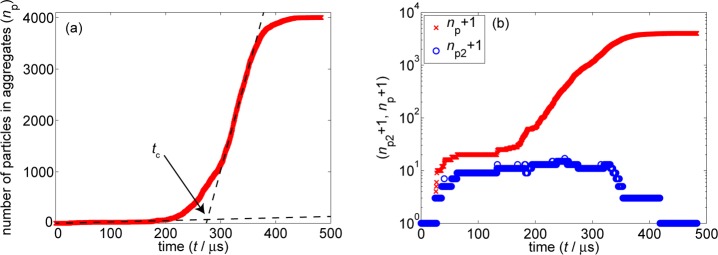
(a) Number of primary particles in aggregates (np) vs time and (b) numbers of primary particles in doublets (np2 + 1) and in all aggregates (np + 1) vs time for the system with ϕ = 0.4 and G = 6.4 × 104 s–1.
The process of coagulation is often characterized by the rate at which doublets are formed. This is usually considered as the measure of the overall rate of coagulation. In Figure 4b we present the number of particles contained in doublets (np,2) as a function of time. The total number of particles in aggregates (np) is also shown for comparison. For the purpose of the logarithmic plot, these quantities are plotted as np,2 + 1 and np + 1. Initially some doublets are formed, but as the coagulation proceeds their number remains more or less constant, and in the later stages np,2 gradually decreases and reaches a value of zero at the end.
Coagulation of primary particles is an important characteristic of the system since doublet formation is the dominant process in the initial phases of the coagulation.8 The rate constant for doublet formation (k1,1) is strongly dependent on both the shear rate G and the volume fraction of particles ϕ, as is apparent from the results of simulations presented in Figure 5. The rate constant k1,1 can be obtained from theory. Considering two equal-sized nonstabilized particles in simple shear flow, we obtain the following relation (a result due to Smoluchowski):
| 24 |
which for our system results in a k1,1t value of ∼1 × 10–16 m3 s–1 (rate constant accounting only for the frequency of the collisions). With the DEM model, we obtained k1,1 values approximately 1–3 orders of magnitude lower (cf. Figure 5). Since the particles are stabilized by the EDL in our model, slower coagulation than for the nonstabilized case is expected. This serves as another justification of the results obtained with our model (also see Figure S5 in the Supporting Information). Considering the very broad range of k1,1 values occurring in real systems and the difficulties in their determination, the values obtained from our simulations can be considered as meaningful.
Figure 5.
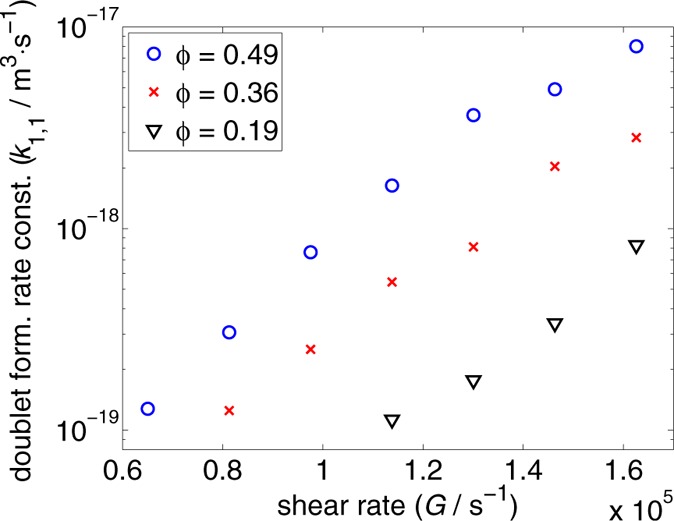
Rate constant of doublet formation (k1,1) as a function of shear rate G for different particle volume fractions ϕ.
It is apparent that the aggregation behavior of the stabilized system exposed to shear is an autocatalytic process, which was also observed experimentally.5,7,21 This means that after the initial lag phase, the system coagulates quickly until all of the primary particles are contained in aggregates. This phenomenon can be explained both in terms of the frequency and the efficiency of the collisions. The explanation of the first one comes naturally from eq 24, if we substitute the radius Rp with the mean radius of two different spheres [(Ri + Rj)/2]. Then, as one of the radii increases, the resulting coagulation rate constant k1,1t grows with the third power of the substituted radius. The efficiency is increased as a result of the higher energy of the collisions. In other words, as a result of the greater momentum of the larger cluster, the resulting Péclet number of the collision increases, while the critical Péclet number remains unaltered (since the same interactions between primary particles exist). This leads to an easier crossing of the potential barrier for the collision of a primary particle with a large cluster.
Another important quantity for the characterization of the coagulation process is the characteristic coagulation time (tc). The coagulation dynamics is typically connected with a sharp increase in the viscosity of the whole system, which makes viscosity (or impeller torque) measurements a convenient tool for the observation of such systems. In 2006, Guery et al.21 proposed a method to determine tc from rheological data. It is based on finding the linear trends in the evolution of viscosity with time in both the lag and growth phases. The intersection of the obtained lines then determines the value of tc. Since the temporal development of the number of particles in aggregates (np) in our simulations exhibits a trend very similar to the trend of viscosity measured by Guery et al.21 and Zaccone et al.,7 we performed the aforementioned procedure for the determination of tc (cf. Figure 4a). The results of this analysis are shown in Figure 6 as the decreasing dependence of tc on the shear rate G in logarithmic and double logarithmic plots. The inverse trend can be observed for the dependence of tc on ϕ (i.e., more concentrated systems coagulate faster). These trends are in agreement with the experimental measurements of Zaccone et al.,7 who proposed an exponential scaling of tc with G. However, it is apparent from Figure 6b that for a broader range of G the dependence rather follows a power-law scaling.
Figure 6.
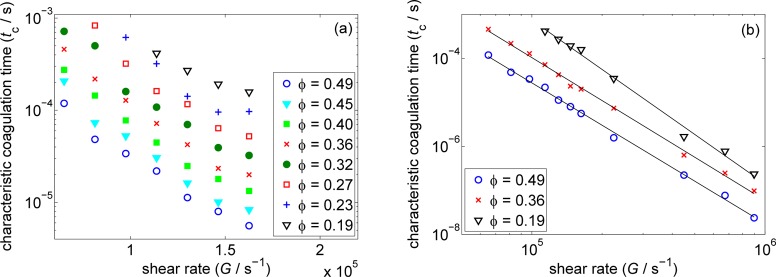
Characteristic coagulation time (tc) as a function of the applied shear rate G for different particle volume fractions ϕ: (a) logarithmic plot; (b) double logarithmic plot (the lines are power-law fits).
It is interesting to compare the characteristic time of coagulation obtained from the global time development of np with the characteristic time of doublet formation (tc,1,1). Since the formation of doublets follows second-order kinetics, the characteristic time of this process can be obtained from the following relation:
| 25 |
where c is the initial number concentration of the particles. From the comparison of tc with tc,1,1 shown in Figure 7, it is apparent that the characteristic time of doublet formation is much larger than the characteristic time for the whole coagulation process. This is the case because the process of coagulation is driven by doublet formation only in the early stage; once a larger aggregate is formed, it grows and the coagulation proceeds much faster.
Figure 7.
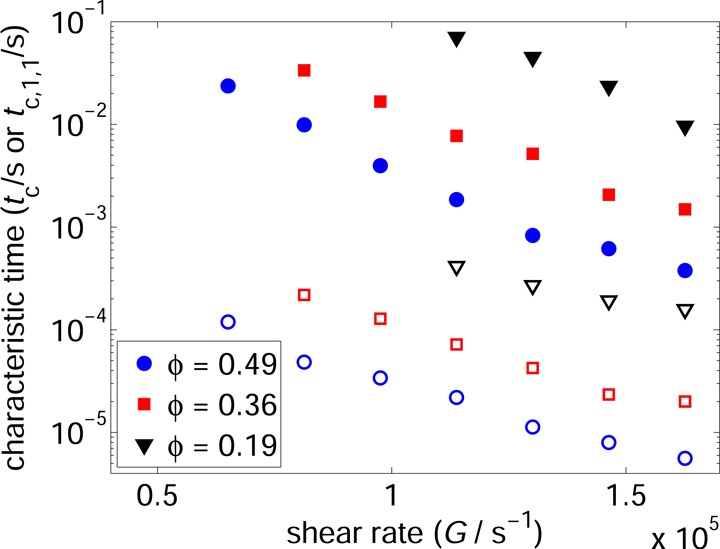
Characteristic times of coagulation (tc, open symbols) and doublet formation (tc,1,1, solid symbols) as functions of the shear rate G for different particle volume fractions ϕ.
The data from Figure 6 can also be plotted as the dependence of the characteristic coagulation time tc on the volume fraction of particles ϕ. We present this graph in Figure 8 as an exponential dependence of tc on ϕ, which varies in the range between 0.19 and 0.49. Through this interval, tc decreases almost by 2 orders of magnitude. Similar behavior has been observed experimentally but for a narrower range of particle volume fractions.7 This suggests a very strong concentration dependence of the behavior of stabilized colloidal systems subjected to shear, which is a very important observation for practical usage.
Figure 8.
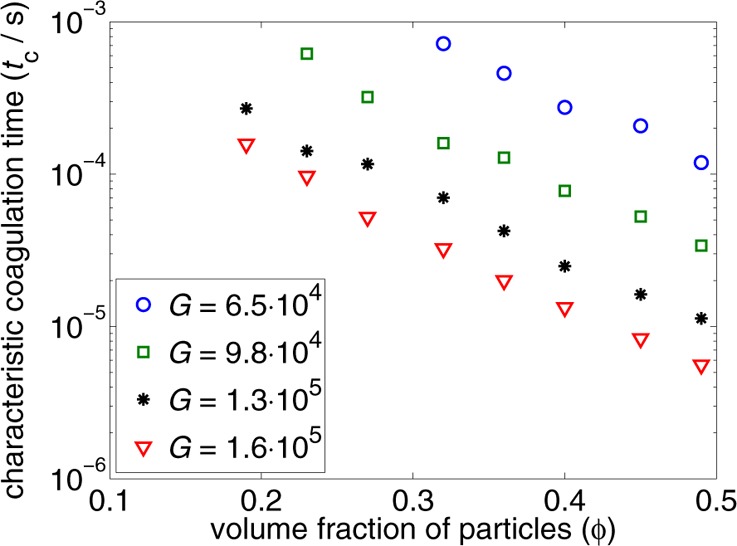
Characteristic time of coagulation tc as a function of particle volume fraction ϕ for different shear rates (G/s–1).
Another important issue is the influence of the surface potential (ψ0) on the behavior of the system. We performed simulations for the values of ψ0/mV ∈ ⟨−50; −30⟩, and the results of this parametric study are shown in Figure 9. It is apparent that tc decreases exponentially with decreasing absolute value of ψ0, as expected because the value of the surface potential is known to influence the behavior of the colloids very strongly.1
Figure 9.
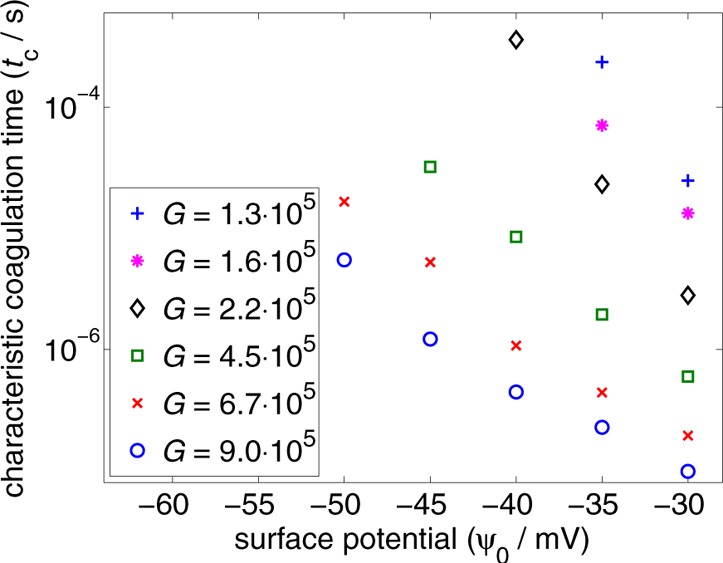
Characteristic time of coagulation tc as a function of surface potential ψ0 for different shear rates (G/s–1).
Variation of the surface energy (γ) produced no significant effect on the doublet formation rate and characteristic coagulation time. It has a serious effect on the shape of the aggregates, but this topic is out of the scope of this paper. A negligible effect on the presented results was observed also for the variation of the parameters of the hydration force (particle-wall interaction).
All of the presented results for the coagulation dynamics deal with systems subjected to high shear rates (G/s–1 ∈ ⟨6.4 × 104; 9.0 × 105⟩). The modeled values of G are higher than in industrial processes, but the choice of large shear rates was necessary for the following reasons. The presented DEM model is based on the interparticle interactions, and the formulations of the forces and torques acting on the particles require only physical constants and material properties as parameters. The formulations are based on the physical laws describing the phenomena of double-layer repulsion, solid-body contact, etc. Such a detailed model, however, requires a very small integration time step (Δt ≈ 1 × 10–10 s). At the same time, a high number of primary particles is needed to obtain statistically relevant results (e.g., for the doublet formation rate). The accessible time scale of the whole process is therefore limited by the computational feasibility of the calculations. To be able to capture the dynamics of the coagulation process within the time scale of our model, we had to consider systems subjected to high shear rates (that are still experimentally accessible6). Most importantly, even with the above-mentioned limitations, our model is able to capture the trends of the coagulation in disperse systems and to provide semiquantitative predictions with no adjustable parameters. A possible approach for accessing the low-shear-rate region with our model could employ an initial configuration with seeds (doublets or triplets) and consequently model the fast-growth stage of coagulation. Unfortunately, in that case we could easily lose the crucial information about the characteristic time of the overall coagulation process.
Conclusions
To the best of our knowledge, we have presented here the first discrete element method (DEM)-based model of concentrated, charge-stabilized disperse systems under shear flow in the liquid phase. Parametric studies of the coagulation considered the influence of the most important parameters, namely, the particle volume fraction (ϕ), the surface potential (ψ0), and the shear rate (G). We quantified the dependence of the coagulation behavior on all of these parameters. A general trend that a more concentrated and less stabilized system subjected to higher shear is more likely to undergo coagulation is in agreement with experimental and theoretical studies. We found that the rate of doublet formation, a commonly used measure of the coagulation rate, is an important characteristic of the process. Moreover, the DEM model employed in this study enabled us to investigate the behavior of the coagulation more in detail, since it was possible to track each single collision and determine the events leading to the coagulation. From these results it is apparent that the autocatalytic nature of the process is the key feature for its understanding. In particular, we have shown that the characteristic time of doublet formation is substantially higher (roughly by 2 orders of magnitude) than the characteristic time of the coagulation itself. This suggests that for the correct description of the coagulation kinetics we have to consider the whole system with its complexity, and the DEM model (even with its simplifications) is a great tool for this purpose. It is worth noting that the model used in this work is completely based on physical laws and mechanisms and contains no adjustable parameters.
The lack of experimental data in the field of the complex fluid rheology does not allow a thorough validation of the quantitative predictions of our DEM model. Nevertheless, we have demonstrated that the model is able to semiquantitatively predict the behavior of concentrated disperse systems subjected to shear. These results are valuable for the operation of industrial processes as well as process models, where they can serve as constraints for the parametric space. An important drawback of our model is its high demand for computational power and time.
In a future paper, the influence of the particle-wall interaction on the process of fouling will be studied in detail with the introduced model. Also, the experimentally observed approach-retraction hysteresis during solid-body contact of the particles (resulting from AFM measurements) will be incorporated into the model.
Acknowledgments
The authors are grateful for support provided by EC FP7 Project COOPOL (NMP2-SL-2012-280827). This work was supported by the Czech Science Foundation (Project GAP106/11/1069).
Supporting Information Available
Scheme of the computational domain and detailed information on the particle-particle interactions. This material is available free of charge via the Internet at http://pubs.acs.org.
A movie showing the simulation for the system with a particle volume fraction (ϕ) of 0.4 under a shear rate (G) of 6.4 × 104 s–1 is available in the HTML version of this paper.
The authors declare no competing financial interest.
Supplementary Material
References
- Hunter R. J.Foundations of Colloid Science, 2nd ed.; Oxford University Press: Oxford, U.K., 2001. [Google Scholar]
- Johnson K. L.; Kendall K.; Roberts A. D. Surface Energy and Contact of Elastic Solids. Proc. R. Soc. London, Ser. A 1971, 324, 301–313. [Google Scholar]
- Hong C. W. From long-range interaction to solid-body contact between colloidal surfaces during forming. J. Eur. Ceram. Soc. 1998, 18, 2159–2167. [Google Scholar]
- Marshall J. S. Particle aggregation and capture by walls in a particulate aerosol channel flow. J. Aerosol Sci. 2007, 38, 333–351. [Google Scholar]
- Zaccone A.; Wu H.; Gentili D.; Morbidelli M. Theory of activated-rate processes under shear with application to shear-induced aggregation of colloids. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2009, 80, 051404. [DOI] [PubMed] [Google Scholar]
- Xie D. L.; Wu H.; Zaccone A.; Braun L.; Chen H. Q.; Morbidelli M. Criticality for shear-induced gelation of charge-stabilized colloids. Soft Matter 2010, 6, 2692–2698. [Google Scholar]
- Zaccone A.; Gentili D.; Wu H.; Morbidelli M. Shear-induced reaction-limited aggregation kinetics of Brownian particles at arbitrary concentrations. J. Chem. Phys. 2010, 132, 134903. [DOI] [PubMed] [Google Scholar]
- Sugimoto T.; Kobayashi M.; Adachi Y. The effect of double layer repulsion on the rate of turbulent and Brownian aggregation: Experimental consideration. Colloids Surf., A 2014, 443, 418–424. [Google Scholar]
- Soos M.; Kaufmann R.; Winteler R.; Kroupa M.; Luthi B. Determination of Maximum Turbulent Energy Dissipation Rate Generated by a Rushton Impeller through Large Eddy Simulation. AIChE J. 2013, 59, 3642–3658. [Google Scholar]
- Henry C.; Minier J. P.; Lefevre G. Towards a description of particulate fouling: From single particle deposition to clogging. Adv. Colloid Interface Sci. 2012, 185, 34–76. [DOI] [PubMed] [Google Scholar]
- ODEPACK Library. http://www.netlib.org/.
- Marshall J. S. Discrete-element modeling of particulate aerosol flows. J. Comput. Phys. 2009, 228, 1541–1561. [Google Scholar]
- Harshe Y. M.; Lattuada M. Breakage Rate of Colloidal Aggregates in Shear Flow through Stokesian Dynamics. Langmuir 2012, 28, 283–292. [DOI] [PubMed] [Google Scholar]
- Butt H. J.; Cappella B.; Kappl M. Force measurements with the atomic force microscope: Technique, interpretation and applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar]
- Hodges C. S.; Cleaver J. A. S.; Ghadiri M.; Jones R.; Pollock H. M. Forces between polystyrene particles in water using the AFM: Pull-off force vs particle size. Langmuir 2002, 18, 5741–5748. [Google Scholar]
- Schmitt F. J.; Ederth T.; Weidenhammer P.; Claesson P.; Jacobasch H. J. Direct force measurements on bulk polystyrene using the bimorph surface forces apparatus. J. Adhes. Sci. Technol. 1999, 13, 79–96. [Google Scholar]
- Israelachvili J.Intermolecular and Surface Forces; Elsevier Science: Amsterdam, 2010. [Google Scholar]
- Li S.-Q.; Marshall J.; Liu G.; Yao Q. Adhesive particulate flow: The discrete element method and its application in energy and environmental engineering. Prog. Energy Combust. Sci. 2011, 37, 633–668. [Google Scholar]
- Wu H.; Tsoutsoura A.; Lattuada M.; Zaccone A.; Morbidelli M. Effect of Temperature on High Shear-Induced Gelation of Charge-Stabilized Colloids without Adding Electrolytes. Langmuir 2010, 26, 2761–2768. [DOI] [PubMed] [Google Scholar]
- Smoluchowski M. Über Brownsche Molekularbewegung unter Einwirkung äußerer Kräfte und den Zusammenhang mit der verallgemeinerten Diffusionsgleichung. Ann. Phys. (Berlin, Ger.) 1915, 353, 1103–1112. [Google Scholar]
- Guery J.; Bertrand E.; Rouzeau C.; Levitz P.; Weitz D. A.; Bibette J. Irreversible shear-activated aggregation in non-Brownian suspensions. Phys. Rev. Lett. 2006, 96, 198301. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.