Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Mar 21;4:4411. doi: 10.1038/srep04411

Information content and analysis methods for Multi-Modal High-Throughput Biomedical Data

Bisakha Ray 1, Mikael Henaff 1,2, Sisi Ma 1, Efstratios Efstathiadis 1, Eric R Peskin 1, Marco Picone 3,4, Tito Poli 5, Constantin F Aliferis 1,6, Alexander Statnikov 1,7,a
PMCID: PMC3961740  PMID: 24651673

Abstract

The spectrum of modern molecular high-throughput assaying includes diverse technologies such as microarray gene expression, miRNA expression, proteomics, DNA methylation, among many others. Now that these technologies have matured and become increasingly accessible, the next frontier is to collect “multi-modal” data for the same set of subjects and conduct integrative, multi-level analyses. While multi-modal data does contain distinct biological information that can be useful for answering complex biology questions, its value for predicting clinical phenotypes and contributions of each type of input remain unknown. We obtained 47 datasets/predictive tasks that in total span over 9 data modalities and executed analytic experiments for predicting various clinical phenotypes and outcomes. First, we analyzed each modality separately using uni-modal approaches based on several state-of-the-art supervised classification and feature selection methods. Then, we applied integrative multi-modal classification techniques. We have found that gene expression is the most predictively informative modality. Other modalities such as protein expression, miRNA expression, and DNA methylation also provide highly predictive results, which are often statistically comparable but not superior to gene expression data. Integrative multi-modal analyses generally do not increase predictive signal compared to gene expression data.

Developing robust predictive models from clinico-molecular data for disease risk, diagnosis, recurrence, survival, and treatment/drug responses are at the core of personalized medicine and next generation diagnostics. Over the last 10–15 years many high-throughput technologies have been introduced and adopted to measure gene expression, miRNA expression, protein expression, DNA methylation, single nucleotide polymorphisms, copy number alterations, somatic mutations, and other molecular features on a genome-scale. Numerous studies have demonstrated success in using each of these high-throughput technologies to build patient classifiers for various phenotypes and outcomes1,2,3,4,5. As these technologies mature and become more accessible to researchers, the next frontier is to collect “multi-modal” data for the same set of subjects and conduct integrative analyses using multi-level views on the same phenomena. The biomedical research community is embracing multi-modal data because it contains distinct biological information that can be used to answer causal and systems biology questions6,7,8. Furthermore, the great promise of such data for diagnosis, prognosis, and treatment personalization is to increase the accuracy of such tests beyond the limits of what was previously feasible with data from a single modality/platform.

At present, the value of multi-modal data for predicting clinical phenotypes and outcomes and, in particular, the unique and shared contributions of each type of input remain unknown. Consider a common research design dilemma of having, for example, a cohort of cancer patients with ability to measure tumor gene expression and GWAS data, and the ultimate goal to predict the recurrence of disease after chemotherapy. It may be the case that GWAS data does not provide any more predictive information than the information contained in the gene expression data or vice versa. Alternatively, a combination of variables from both modalities may be needed to maximize predictive ability.

The best way to use high-throughput multi-modal data for predicting clinical phenotypes and outcomes is a matter of divergent opinions in the literature. One school of thought suggests that using multi-modal data should increase predictivity of patient classifiers9,10,11,12,13,14,15. The National Institutes of Health have established a program PAR-11-203 to support the development of “predictive multiscale models for biomedical, biological, behavioral, environmental and clinical research” (http://grants.nih.gov/grants/guide/pa-files/PAR-11-203.html, accessed on 11/25/2013). Researchers in this group have reported initial promising results and have proposed new analytic methods for handling multi-modal data9,10,11,12,14. For example, a recent study integrated microarray gene expression and copy number data to predict prostate cancer grade, stage, metastasis, and recurrence9. The researchers found that the multi-modal approach improves performance compared to the best models derived from individual data modalities with performance increases ranging from 0.01 to 0.07 AUC. While the above results are promising, they (i) are often derived from few modalities (typically 2); (ii) do not consider a wide range of state-of-the-art predictive analytic approaches, both for uni-modal and multi-modal data; (iii) base their conclusions on the analysis of very few datasets (typically 1–3), often with small sample sizes that are insufficient to determine whether the differences in performance between single and multiple modalities are statistically significant; and (iv) may be consequences of the reporting bias, i.e. only datasets/studies where combination of modalities increases signal are reported. Because of these shortcomings, both the generalizability and the practical significance of these findings are limited.

A different school of thought suggests that one should use the most downstream modality for predicting clinical phenotypes and outcomes16,17,18. Even if the original cause of the disease could have happened in DNA, the information will eventually flow to RNA and proteins and can be detected there. Of course, there may be exceptions to this rule, depending on disease pathogenesis. For example, when a certain number of genetic mutations have to accumulate before significant changes in gene expression appear, using gene expression data may not be useful for early diagnosis and/or risk assessment of disease19,20,21. On the other hand, not all DNA damage leads to disease and thus, everything else being equal, examining disease at the level of DNA has more noise than at the level of the transcriptome. It is also worthwhile to mention that using multiple data modalities leads to a significant increase in the cost of biomedical investigations.

To shed light on this issue, we have used high-throughput data to perform, for the first time, a comprehensive exploration of the information content in individual and multiple modalities. Our study is enabled by multi-modal datasets of varying sample sizes from national and international resources such as The Cancer Genome Atlas (TCGA) and the Molecular Taxonomy of Breast Cancer International Consortium8, which have recently been available.

We used 47 datasets/predictive tasks that in total span over 9 data modalities, with up to 5 modalities measured in the same dataset. We focused on predicting various cancer phenotypes and outcomes such as cancer grade, stage, lymph node involvement, ER status, PR status, lymphatic invasion, neoplasm histologic grade, relapse, and survival at different time points. First, we analyzed each modality separately using uni-modal approaches based on several state-of-the-art supervised classification and feature selection methods. Then, we applied advanced integrative multi-modal classification techniques.

Results

Gene expression microarrays are exhibiting the highest predictive performance among tested data modalities

In order to determine the most predictive individual modality, we computed predictive performance (AUC) for models derived from each modality and dataset/task (Table 1, detailed results are provided in Supplementary File 1). Gene expression had highest AUC averaged over all applicable datasets/tasks compared to other data modalities (Table 2). Protein expression, DNA methylation, miRNA expression, and tumor imaging modalities have lower mean AUCs, but the differences with gene expression are not statistically significant.

Table 1. Comparison of predictivity of various modalities for each dataset/task. Predictivity is measured by the area under ROC curve (AUC). AUC values listed in the table were optimized over uni-modal methods given in Table S3. The highlighting of each cell corresponds to relative predictivity for each dataset/task – the more predictive is modality for a given dataset/task, the darker is its highlighting.

  TCGA_BRCA1.R1 TCGA_BRCA1.R2 TCGA_BRCA1.R3 TCGA_BRCA1.R4 TCGA_BRCA1.R5 TCGA_BRCA1.R6 TCGA_BRCA1.R7 TCGA_BRCA1.R8 TCGA_BRCA2.R1 TCGA_BRCA2.R2 TCGA_BRCA2.R3 TCGA_BRCA2.R4 TCGA_BRCA2.R5 TCGA_BRCA2.R6 TCGA_BRCA2.R7 TCGA_BRCA2.R8 TCGA_OVCA.R1 TCGA_OVCA.R2 TCGA_OVCA.R3 TCGA_OVCA.R4 TCGA_OVCA.R5 TCGA_OVCA.R6 TCGA_OVCA.R7 TCGA_OVCA.R8 TCGA_OVCA.R9 TCGA_OVCA.R10 TCGA_OVCA.R11
Clinical 0.590 0.656 0.646 0.646 0.633 0.630 0.725 0.594 0.578 0.587 0.697 0.689 0.604 0.806 0.759 0.721 0.667 0.690 0.657 0.543 0.650 0.577 0.582 0.549 0.614 0.639 0.652
Gene Expression 0.661 0.637 0.612 0.979 0.969 0.836 0.606 0.764 0.661 0.672 0.721 0.935 0.910 0.860 0.860 0.750 0.744 0.768 0.811 0.734 0.670 0.618 0.608 0.566 0.609 0.714 0.763
Protein Expression 0.650 0.743 0.733 0.983 0.953 0.812 0.713 0.733 0.584 0.618 0.705 0.936 0.881 0.845 0.644 0.716 0.695 0.687 0.688 0.704 0.665 0.592 0.610 0.581 0.602 0.738 0.757
Somatic Mutations 0.589 0.618 0.668 0.845 0.801 0.748 0.636 0.691 0.651 0.659 0.627 0.709 0.716 0.796 0.744 0.759 - - - - - - - - - - -
DNA Methylation 0.695 0.637 0.619 0.983 0.935 0.753 0.681 0.697 0.680 0.688 0.723 0.921 0.821 0.856 0.883 0.713 0.728 0.772 0.745 0.707 0.670 0.642 0.575 0.627 0.590 0.675 0.682
miRNA Expression - - - - - - - - - - - - - - - - 0.761 0.723 0.741 0.803 0.698 0.611 0.584 0.593 0.601 0.658 0.742
Copy Number - - - - - - - - - - - - - - - - - - - - - - - - - - -
Tumor Imaging - - - - - - - - - - - - - - - - - - - - - - - - - - -
GWAS - - - - - - - - - - - - - - - - - - - - - - - - - - -
Open in a new tab

Table 2. Comparison of various modalities with gene expression in terms of mean AUC (computed over datasets/tasks where data from both modalities was available).

    Mean AUC Comparison of mean AUC differences
Modality Number of datasets/tasks where this modality was measured this modality gene expression modality p-value p-value adjusted for multiple comp.
Clinical 47 0.686 <0.788 <10-5 <10−5
Protein expression 27 0.725 <0.742 0.1910 0.2183
Somatic Mutations 16 0.704 <0.777 0.0023 0.0046
DNA Methylation 27 0.730 <0.742 0.1290 0.1720
miRNA Expression 14 0.730 <0.742 0.2585 0.2585
Copy Number 3 0.783 <0.929 <10−5 <10−5
Tumor Imaging 1 0.947 <0.979 0.0502* 0.0803
GWAS 16 0.708 <0.826 <10−5 <10−5
Open in a new tab

*Since there is only one dataset for tumor imaging, significance in difference between AUC was not assessed by permutation testing, but instead was assessed by the method of Delong43.

In the following analyses, we decided to use gene expression as a reference modality and further statistically compare its predictive performance to the remaining 8 data modalities using two different comparison approaches (see Methods section for details). In the first approach, we compared the proportion of datasets where gene expression was ‘statistically optimal’ with that of another modality. In the second approach, we compared the proportion of datasets where gene expression had predictivity at least as good as another modality with the proportion of datasets where another modality had predictivity at least as good as gene expression. The detailed results of comparisons are given in Tables 3 and 4 for the first and second approaches, respectively. Both approaches reveal that gene expression has significantly better predictivity than clinical, copy number, and GWAS modalities. Protein expression, somatic mutations, and DNA methylation modalities are nominally but not statistically significantly outperformed by gene expression using either comparison approach, with the exception of somatic mutations modality that is significantly outperformed by gene expression using the second comparison approach. Finally, miRNA expression and tumor imaging modalities, when compared to gene expression, yield exactly the same proportions of datasets/tasks with either statistically optimal results (for the first comparison approach) or one modality outperforming the other (for the second comparison approach). No modality outperformed gene expression in terms of the above proportions.

Table 3. Comparison of various modalities with gene expression in terms of proportion of dataset/tasks where two modalities achieve ‘statistically optimal’ AUC.

  Number of datasets/tasks Comparison of proportions
Modality where this modality was measured where this modality had ‘statistically optimal’ performance where gene expression had ‘statistically optimal’ performance p-value p-value adjusted for multiple comp.
Clinical 47 15 <43 <10−5 <10−5
Protein expression 27 22 <25 0.2242 0.3587
Somatic Mutations 16 9 <14 0.0493 0.0986
DNA Methylation 27 23 <25 0.3865 0.5153
miRNA Expression 14 14 = 14 1 1
Copy Number 3 0 <3 0.0143 0.0381
Tumor Imaging 1 1 = 1 1 1
GWAS 16 1 <14 <10−5 1.6483·10−5
Open in a new tab

Table 4. Comparison of various modalities with gene expression in terms of proportion of datasets/tasks where one modality performs at least as good as the other.

  Number of datasets/tasks Comparison of proportions
Modality where this modality was measured where this modality had performance ≥ gene expression where gene expression had performance ≥ this modality p-value p-value adjusted for multiple comp.
Clinical 47 21 <45 <10−5 <10−5
Protein expression 27 24 <25 0.6387 0.8516
Somatic Mutations 16 11 <16 0.0149 0.0298
DNA Methylation 27 25 <27 0.1495 0.2393
miRNA Expression 14 14 = 14 1 1
Copy Number 3 0 <3 0.0143 0.0298
Tumor Imaging 1 1 = 1 1 1
GWAS 16 1 <16 <10−5 <10−5
Open in a new tab

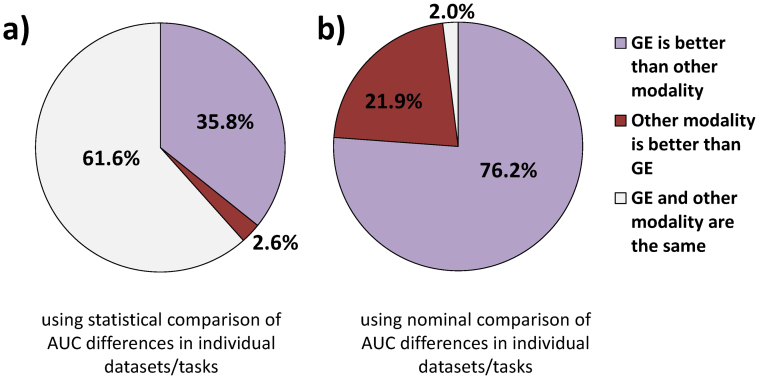
It follows from data in Tables 1–4 that out of all 151 comparisons of gene expression with various modalities for various datasets/tasks, only in 4 (2.6%) comparisons gene expression is statistically significantly outperformed by other modalities in terms of AUC, while in 54 (35.8%) comparisons gene expression statistically significantly outperforms other modalities. In the remaining 61.6% comparisons, gene expression and other modalities have statistically comparable performance. Without consideration of statistical significance of differences in AUC's for each dataset/task, gene expression outperforms other modalities in 115 (76.2%) comparisons, other modalities outperform gene expression in 33 (21.9%) comparisons, and the performance is exactly equal in 3 (2.0%) comparisons. The above results are visualized in Figure 1.

Figure 1. Comparison of predictivity of gene expression microarrays (GE) with other modalities.

Figure 1

Open in a new tab

The results are based on 151 comparisons of gene expression with various modalities for various datasets/tasks. Predictivity is measured by the area under ROC curve (AUC). The results in (a) are obtained using statistical comparison of AUC differences in individual datasets/tasks, while the results in (b) are obtained using nominal comparison of AUC difference in individual datasets/tasks.

The predictive performance of gene expression microarrays cannot be improved by integrating data from multiple modalities

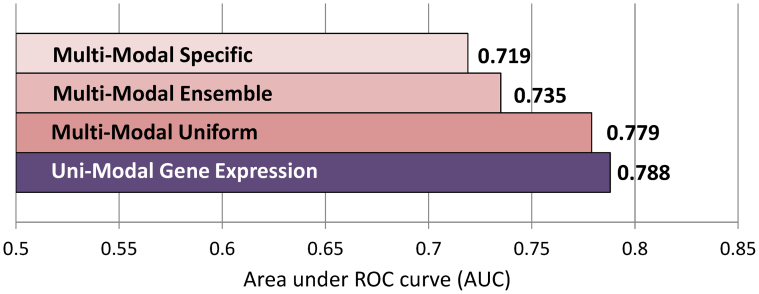
We have established above that gene expression microarrays are exhibiting the highest predictive performance among tested data modalities. Next we assessed whether multiple modalities, combined by an integrative analytics approach, have better predictivity than a single gene expression modality. Figure 2 compares AUC averaged over all 47 datasets/tasks of uni-modal gene expression-based and multi-modal analytic approaches. When gene expression data is analyzed with traditional uni-modal approaches, it leads to AUC = 0.788. Multi-modal uniform approaches, applied to data from multiple modalities, lead to AUC = 0.779 which is nominally but not statistically significantly lower than AUC of gene expression data (p = 0.1333; see also Figure S1 in Supplementary Information). Multi-modal ensemble approaches, applied to data from multiple modalities, lead to AUC = 0.735, which is significantly lower than AUC of gene expression data (p < 10−5; see also Figure S2 in Supplementary Information). Similarly, multi-modal specific approaches, applied to data from multiple modalities, lead to AUC = 0.719, which is significantly lower than AUC of gene expression data (p < 10−5; see also Figure S3 in Supplementary Information).

Figure 2. Comparison of predictivity of various analytic approaches.

Figure 2

Open in a new tab

Predictivity is measured by the area under ROC curve (AUC) and averaged over all 47 datasets/tasks.

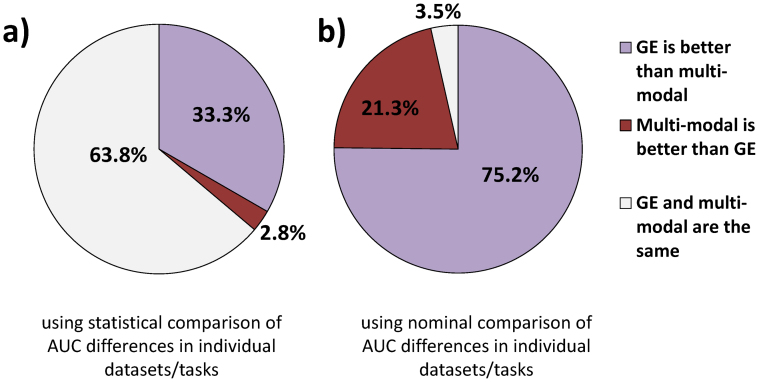
Out of all 141 comparisons of uni-modal approach with gene expression data with 3 multi-modal integrative analytic approaches for 47 datasets/tasks, only in 4 (2.8%) comparisons uni-modal gene expression is statistically significantly outperformed by multi-modal approaches in terms of AUC, while in 47 (33.3%) comparisons uni-modal gene expression statistically outperforms multi-modal approaches. In the remaining 63.8% comparisons, uni-modal gene expression and multi-modal approaches have statistically comparable performance. Without consideration of statistical significance of differences in AUC's for each dataset/task, uni-modal approach with gene expression outperforms multi-modal approaches in 106 (75.2%) comparisons, multi-modal approaches outperform gene expression in 30 (21.3%) comparisons, and the performance is exactly equal in 5 (3.5%) comparisons. The above results are visualized in Figure 3.

Figure 3. Comparison of predictivity of uni-modal gene expression-based approach (GE) with multi-modal approaches.

Figure 3

Open in a new tab

The results are based on 141 comparisons of uni-modal gene expression-based approach with 3 multi-modal approaches for 47 datasets/tasks. Predictivity is measured by the area under ROC curve (AUC). The results in (a) are obtained using statistical comparison of AUC differences in individual datasets/tasks, while the results in (b) are obtained using nominal comparison of AUC difference in individual datasets/tasks.

The results suggest that a model derived solely from microarray gene expression data is unlikely to be improved by integrating data from multiple modalities and applying multi-modal predictive analytics approaches. Furthermore, models derived from only microarray gene expression data in general and on average lead to slightly better performance than models from multiple data modalities combined. Since gene expression data is also utilized in multi-modal approaches, the latter observation can be attributed to the “curse of dimensionality” that is degradation of predictivity due to increased variable-to-sample size ratio that affects even well regularized classifiers22. Another possible and related reason is that differences in high-dimensional distributions of data from various modalities can hinder classifier learning.

Multi-modal uniform approaches are preferred for integrating data from multiple modalities for predictive modeling

In order to find the best performing technique for integrating data from multiple modalities for predictive modeling, we have compared predictivity among three types of multi-modal approaches: uniform, ensemble, and specific (see Methods section for details). Figure 2 reports mean AUC averaged over all 47 datasets/tasks for various multi-modal analytic approaches. Multi-modal uniform approaches achieve AUC = 0.779 and statistically significantly outperform multi-modal ensemble (AUC = 0.735, p = 0.0008; see also Figure S4 in Supplementary Information) and multi-modal specific (AUC = 0.719, p = 0.0001; see also Figure S5 in Supplementary Information). The multi-modal ensemble approaches significantly outperform multi-modal specific approaches (p = 0.0352; see also Figure S6 in Supplementary Information).

Discussion

Performing a definitive exploration of predictive analytics approaches in multi-modal data is challenging in several ways. The conclusions of this study may need to be revised as more modalities become available for each dataset or improved assays for existing modalities become available. For example, while extensive clinical data (patient demographics, electronic medical record, orders, prior history, etc.) is available in most medical centers these days, only a limited set of such variables was accompanying genomic datasets used in this study. Similarly, protein expression data used in the TCGA_BRCA datasets involved measurements of only 166 proteins, while recent proteomics assays can readily capture >10,000 proteins. Also, we could not utilize all modalities measured in TCGA due to limited sample size or small overlap of samples measured by multiple modalities as well as restricted availability of several, primarily genetic modalities. Our dataset inclusion criteria are detailed in the Methods section.

While we performed integration of all available modalities for each dataset/task, some researchers may give preference to integrating selected modalities only, e.g. using only gene expression and protein expression. Since many multi-modal analytics approaches used in this study explicitly performed feature selection, these techniques by design would be able to find the most predictively relevant features in all available modalities, and if needed would focus exclusively on features in a subset of modalities. Therefore, we anticipate that the performance of multi-modal approaches would not increase by using fewer modalities. Table S7 in Supplementary Information provides the results of additional experiments to compare using all 5 modalities versus only gene expression and protein expression (2 modalities) in all TCGA datasets. As can be seen, using only gene expression and protein expression for multi-modal analyses does not improve average predictive performance compared to uni-modal approaches and multi-modal based on all 5 data modalities.

Our results imply that for a large set of 47 datasets/tasks used in this study, on average there is little benefit of integrating multiple modalities for predictive modeling purposes. However, we do not preclude the possibility that in some datasets/tasks not represented by our benchmark collection combining modalities may increase predictive performance over uni-modal approaches. For example, in a dataset TCGA_BRCA2.R4, the best uni-modal approach (based on gene expression data) achieved AUC of 0.860, while the best multi-modal approach (multi-modal uniform) achieved higher AUC of 0.914. Overall, in 66% of datasets/tasks the best uni-modal approach had performance greater or equal than that of the best multi-modal approach, and in 34% of datasets/tasks the best multi-modal approach outperformed the best uni-modal approach (average improvement of AUC was only 0.01). Therefore, we suggest that multi-modal studies should never omit uni-modal analytic approaches.

We also note that it may be possible for researchers to come up with new integrative modeling approaches that would increase performance of existing techniques, and such research would benefit from the benchmark results achieved in our work. We are not particularly optimistic about the likelihood of discovering such approaches however, because both theoretical results and empirical experience of existing multi-modal data analysis methods in other fields of study suggest that the existing methods are very powerful and capable of extracting and combining signals from distinct types of data15,23,24,25.

In conclusion, this study conducted the largest exploration to date of analytics approaches for predicting clinical phenotypes and outcomes with multi-modal high-throughput biomedical data. Using 47 datasets/tasks that span over 9 data modalities in total (with up to 5 modalities measured in the same dataset) and with numbers of patients in each dataset ranging from 52 to 1,950, we found that gene expression is the most predictively informative modality. Other modalities such as protein expression, miRNA expression, and DNA methylation also provide highly predictive results, which are often statistically comparable but not superior to gene expression data. Tumor imaging has high predictivity that is statistically comparable to gene expression data. However, since we have only one dataset/task where both tumor imaging and gene expression were measured, we cannot generalize this result. We also found that various integrative multi-modal analytic approaches differ in performance, but in the majority of cases and on average they do not increase predictive signal compared to uni-modal approach based on gene expression data. While combining modalities and conducting integrative analyses is essential for mechanistic and system biology studies, our results suggest that performing multi-modal high-throughput biomedical studies is in most cases unwarranted for predicting clinical phenotypes and outcomes and special care must be given to analytic methodology.

Methods

Datasets collection and preparation

We obtained 47 datasets/predictive tasks from The Cancer Genome Atlas (TCGA), Memorial Sloan-Kettering Cancer Center, the European NeoMark Project, and the Canada-UK METABRIC Project (see Table 5). To be eligible for inclusion in our study, a dataset/task was required to: (i) address a clinically/pathologically relevant prediction task; (ii) involve human patient samples; (iii) have available data for 3 or more modalities; (iv) have at least 50 samples with complete coverage of data from all available modalities; (v) have at least one modality with high-dimensional/genome-wide data. In addition to the above criteria, we gave preference to datasets with harder predictive tasks (e.g., predicting clinical outcomes versus diagnosis), so that there is “room for improvement” by multi-modal predictive modeling approaches.

Table 5. Characteristics of datasets/tasks used in this study. “N” is number of subjects with complete coverage of data from all available modalities in a given dataset. “N(0)” and “N(1)” denote number of subjects for classes “0” and “1”, respectively. The encoding of classes is given in the second column.

Dataset short name Phenotypic response variable definition and encoding N(0) N(1) Gene Expression miRNA Expression Protein expression Clinical Tumor Imaging GWAS DNA Methylation Somatic Mutations Copy Number
Breast cancer patient samples from The Cancer Genome Atlas (TCGA), N = 240
TCGA_BRCA1.R1 Neoplasm disease stages I*, II* (0) vs. III*, IV* (1) 124 111 X   X X     X X  
TCGA_BRCA1.R2 Lymph node stage N0* (0) vs. N1*, N2*, N3* (1) 183 50 X   X X     X X  
TCGA_BRCA1.R3 Tumor stages T1*, T2* (0) vs. T3*, T4* (1) 203 37 X   X X     X X  
TCGA_BRCA1.R4 Estrogen receptor negative (0) vs. positive (1) 57 176 X   X X     X X  
TCGA_BRCA1.R5 Progesterone receptor negative (0) vs. positive (1) 89 144 X   X X     X X  
TCGA_BRCA1.R6 survived 2 years (0) or not (1) 96 7 X   X X     X X  
TCGA_BRCA1.R7 survived 3 years (0) or not (1) 62 13 X   X X     X X  
TCGA_BRCA1.R8 survived 4 years (0) or not (1) 45 13 X   X X     X X  
Breast cancer patient samples from The Cancer Genome Atlas (TCGA), N = 160
TCGA_BRCA2.R1 Neoplasm disease stages I*, II* (0) vs. III*, IV* (1) 57 101 X   X X     X X  
TCGA_BRCA2.R2 Lymph node stage N0* (0) vs. N1*, N2*, N3* (1) 107 52 X   X X     X X  
TCGA_BRCA2.R3 Tumor stages T1*, T2* (0) vs. T3*, T4* (1) 129 30 X   X X     X X  
TCGA_BRCA2.R4 Estrogen receptor negative (0) vs. positive (1) 39 121 X   X X     X X  
TCGA_BRCA2.R5 Progesterone receptor negative (0) vs. positive (1) 60 100 X   X X     X X  
TCGA_BRCA2.R6 survived 2 years (0) or not (1) 94 6 X   X X     X X  
TCGA_BRCA2.R7 survived 3 years (0) or not (1) 71 9 X   X X     X X  
TCGA_BRCA2.R8 survived 4 years (0) or not (1) 38 14 X   X X     X X  
Ovarian cancer patient samples from The Cancer Genome Atlas (TCGA), N = 397
TCGA_OVCA.R1 Lymphatic invasion present (1) vs. absent (0) 47 87 X   X X     X X  
TCGA_OVCA.R2 Neoplasm histologic grade G1,G2 (0) vs. G3,G4 (1) 52 325 X   X X     X X  
TCGA_OVCA.R3 Tumor stages T1*, T2* (0) vs. T3*, T4* (1) 30 350 X   X X     X X  
TCGA_OVCA.R4 Venous invasion present (1) vs. absent (0) 40 53 X   X X     X X  
TCGA_OVCA.R5 survived 1 year (1) or not (0) 271 32 X   X X     X X  
TCGA_OVCA.R6 survived 2 years (1) or not (0) 206 68 X   X X     X X  
TCGA_OVCA.R7 survived 3 years (1) or not (0) 153 98 X   X X     X X  
TCGA_OVCA.R8 survived 4 years (1) or not (0) 85 148 X   X X     X X  
TCGA_OVCA.R9 survived 5 years (1) or not (0) 55 168 X   X X     X X  
TCGA_OVCA.R10 survived 6 years (1) or not (0) 30 182 X   X X     X X  
TCGA_OVCA.R11 survived 7 years (1) or not (0) 19 189 X   X X     X X  
Prostate cancer patient samples from Memorial Sloan-Kettering Cancer Center (MSKCC), N = 92
MSKCC_PRCA.R1 Lymph node stage N0 (0) vs. N1 (1) 62 12 X X   X         X
MSKCC_PRCA.R2 Primary (0) vs. metastatic (1) 79 13 X X   X         X
MSKCC_PRCA.R3 Tumor stages T1 (0) vs. T2, T3, T4 (1) 53 35 X X   X         X
Oral squamous cell carcinoma patient samples from the European project NeoMark, N = 106
NEOMARK.R1 Recurrence (1) vs. no recurrence (0) of oral squam. cell cancer 71 6 X     X X        
Breast cancer patient samples from the UK-Canada project METABRIC, N = 1950
METABRIC.R1 ER_Expr positive (1) vs. negative (0) 463 1487 X     X   X      
METABRIC.R2 HER2_Expr positive (1) vs. negative (0) 1710 240 X     X   X      
METABRIC.R3 PR_Expr positive (1) vs. negative (0) 920 1030 X     X   X      
METABRIC.R4 Grade 1 (0) vs. 2,3 (1) 167 1783 X     X   X      
METABRIC.R5 Grade 1,2 (0) vs. 3 (1) 1018 932 X     X   X      
METABRIC.R6 Stage 0 (0) vs. Stages 1,2,3,4 (1) 509 1441 X     X   X      
METABRIC.R7 Stages 0,1 (0) vs. Stages 2,3,4 (1) 1005 945 X     X   X      
METABRIC.R8 Stages 0,1,2 (0) vs. Stages 3,4 (1) 1825 125 X     X   X      
METABRIC.R9 Stages 0,1,2,3 (0) vs. Stage 4 (1) 1940 10 X     X   X      
METABRIC.R10 survived 1 year (1) or not (0) 27 1878 X     X   X      
METABRIC.R11 survived 2 years (1) or not (0) 102 1767 X     X   X      
METABRIC.R12 survived 3 years (1) or not (0) 184 1634 X     X   X      
METABRIC.R13 survived 4 years (1) or not (0) 279 1482 X     X   X      
METABRIC.R14 survived 5 years (1) or not (0) 340 1328 X     X   X      
METABRIC.R15 survived 6 years (1) or not (0) 387 1138 X     X   X      
METABRIC.R16 survived 7 years (1) or not (0) 424 1013 X     X   X      
Open in a new tab

TCGA_BRCA1 and TCGA_BRCA2 breast cancer datasets originate from The Cancer Genome Atlas (https://tcga-data.nci.nih.gov/tcga/). The samples in these datasets correspond to patient breast cancer invasive tumors. We accessed TCGA website on 9/13/2012 and downloaded clinical and publicly available genomic data (Level 2) for the following modalities: gene expression, DNA methylation, protein expression, and somatic mutations (Table S1 in Supplementary Information). There were 400 patients with all five measured modalities (four genomic modalities and one clinical). Since DNA methylation data originated from 2 different assaying platforms, we divided the 400 patient dataset into two smaller datasets: one with DNA methylation assayed by HumanMethylation27 platform (denoted as “TCGA_BRCA1”) and another one by HumanMethylation450 platform (“TCGA_BRCA2”). The former dataset contained 240 patients, while the latter 160. We defined 8 phenotypic response variables/predictive tasks given in Table 5. In summary, the responses correspond to neoplasm disease stage, lymph node stage, tumor stage, ER receptor status, PR receptor status, and survival at 2, 3, and 4 years of follow-up. Patients with missing values in the responses (e.g., due to loss of follow-up for survival tasks) were removed from the analysis, resulting in 58–240 patients in TCGA_BRCA1 and 52–160 patients in TCGA_BRCA2 datasets, depending on the response variable/predictive task (see Table 5). Once the responses were defined, we extracted from the clinical data a set of 24 binary or numerical predictors for predictive modeling of the responses (Table S2 in Supplementary Information). We ensured that these predictors in the clinical data do not represent ‘proxies’ or components of any response variable and were not measured after the responses. We have followed this practice for all datasets listed below. For example, we did not want to use patient survival at 3 years of follow-up to predict tumor grade at baseline. Likewise, we did not want to use lymph node stage to predict tumor stage (the former is a component of the definition of the later).

TCGA_OVCA ovarian cancer datasets also originate from TCGA. The samples in these datasets correspond to patient ovarian serous cystadenocarcinoma tumors. We accessed TCGA website on 12/16/2012 and downloaded clinical and publicly available genomic data (Level 2) for the following modalities: gene expression, DNA methylation, protein expression, and miRNA expression (Table S1, Table S2). We did not obtain data for other genomic modalities available on TCGA (e.g., somatic mutations) due to the small number of patients in these data. There were 397 patients with all five measured modalities (four genomic modalities and one clinical). We defined 11 phenotypic response variables/predictive tasks given in Table 5. In summary, the responses correspond to lymphatic invasion, neoplasm histologic grade, tumor stage, venous invasion, and survival at 1, 2, 3, 4, 5, 6, and 7 years of follow-up. Patients with missing values in the responses were removed from the analysis, resulting in datasets with 93–380 patients, depending on the response variable/task (Table 5).

MSKCC_PRCA prostate cancer datasets originate from a study7 performed at Memorial Sloan Kettering Cancer Center. The samples in these datasets correspond to patient prostate cancer tumors. We accessed the MSKCC Cancer Genomics data portal (http://cbio.mskcc.org/cancergenomics/prostate/data/) on 7/27/2012 and downloaded clinical and publicly available genomic data for the following modalities: gene expression, microRNA expression, and copy number (Table S1, Table S2). There were 92 patients with all four measured modalities (three genomic and one clinical). We defined 3 phenotypic response variables/predictive tasks given in Table 5. In summary, the responses correspond to lymph node stage, tumor stage, and primary vs. metastatic tumor classification. Patients with missing values in the responses were removed from the analysis, resulting in datasets with 74–92 patients, depending on the response variable/task (Table 5).

NEOMARK oral squamous cell carcinoma datasets originate from the European NeoMark project26. The samples in these datasets correspond to patient oral squamous cell carcinoma tumors. We obtained clinical, tumor imaging, and gene expression data from the co-authors of this study (M.P. and T.P.) who led the NeoMark project (Table S1, Table S2). There were 106 patients with all three measured modalities. We defined a response variable denoting recurrence of oral squamous cell carcinoma within 12 months after surgery (Table 5). Patients with missing values in the response (due to loss of follow-up) were removed from the analysis, resulting in datasets with 77 patients.

METABRIC breast cancer datasets originate from the UK-Canada METABRIC project8. The samples in these datasets correspond to patient invasive breast cancer tumors. We have accessed the European Genome-Phenome Archive (https://www.ebi.ac.uk/ega/datasets) on 4/5/2013 and downloaded GWAS and gene expression data under the accession numbers EGAD00010000164 and EGAD00010000162, respectively. Clinical data was obtained from the supplement of8 (Table S1, Table S2). There were 1,950 patients with all three measured modalities (two genomic and one clinical). We defined 16 phenotypic response variables/predictive tasks given in Table 5. In summary, the responses correspond to ER receptor status, PR receptor status, HER2 receptor status, tumor grade, tumor stage, and survival at 1, 2, 3, 4, 5, 6, and 7 years of follow-up. Patients with missing values in the responses were removed from the analysis, resulting in datasets with 1,437–1,950 patients, depending on the response variable/task (Table 5).

The obtained genomic and imaging datasets have been processed and normalized by their primary authors. We have only performed rescaling of all data features to [0, 1] range in order to facilitate classifier learning.

For ease of reproducing the results of this study, all datasets (excluding a few ones with special permission requirements which can be requested by their authors) are available online in Matlab format from http://www.nyuinformatics.org/downloads/supplements/MultiModal/.

Predictive analytics approaches

We considered four types of predictive analytics approaches: traditional and well-established approaches for modeling from a single modality data and three state-of-the-art types of approaches for modeling from multiple data modalities. The latter approaches have been used and described in prior literature on multi-modal predictive analytics9,10,11,12,13,14,15,27.

“Uni-modal” approaches apply well-established feature selection and supervised classification (core) methods to a single data modality to obtain a predictive model. Uni-modal approaches cannot capture/combine information from features in multiple data modalities (e.g., gene expression and protein expression or miRNA). These approaches use core methods listed in Table S3 with parameters given in Table S4 in Supplementary Information.

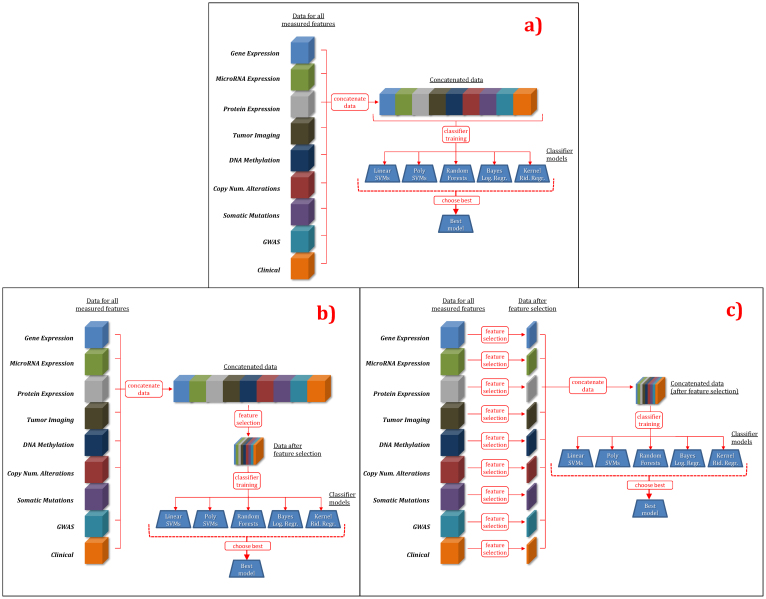
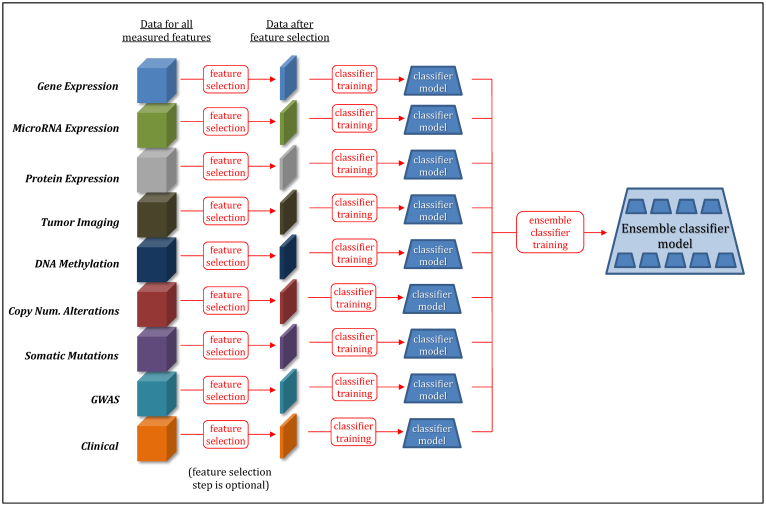
“Multi-modal uniform” (MMU) approaches apply well-established feature selection and supervised classification (core) methods to multiple data modalities to obtain a predictive model. These approaches use the same core methods (listed in Table S3 and with parameters given in Table S4) as in uni-modal approaches, but apply them to multiple modalities while treating data from multiple modalities uniformly. Thus these approaches can capture information from and interactions among features in multiple data modalities. Figure 4 provides a pictorial description of MMU approaches.

Figure 4. Multi-modal uniform (MMU) predictive analytics approaches.

Figure 4

Open in a new tab

(a) MMU w/o feature selection, (b) MMU with feature selection performed on all modalities at once, (c) MMU with feature selection performed independently on individual modalities.

“Multi-modal ensemble” (MME) approaches apply methods to “ensemble” multiple classification models derived from individual data modalities. The classification of subjects is then performed by an ensemble classification model, which is defined as a function of models from individual data modalities. The core MME methods are listed in Table S3 and their parameters are given in Table S4. Figure 5 provides a pictorial description of MME approaches.

Figure 5. Multi-modal ensemble (MME) predictive analytics approaches.

Figure 5

Open in a new tab

“Multi-modal specific” (MMS) approaches apply methods designed specifically for deriving a predictive model from multi-modal data. The core MMS methods are listed in Table S3 and their parameters are given in Table S4.

The choice of conventional supervised classification methods is essential for all uni-modal, multi-modal uniform and multi-modal ensemble approaches (multi-modal specific approaches use other specialized methods for classification). As outlined in Table S3, we used 5 supervised classification methods in our study: support vector machines (SVMs) with linear kernel28, SVMs with polynomial kernel28, kernel ridge regression22,29,30, Bayesian logistic regression31,32, and random forests33. These methods have been chosen because of their: (i) numerous successful empirical applications to datasets from the same or similar domains, (ii) robustness to high variable-to-sample ratio and large number of variables, (iii) ability to efficiently learn complex classification functions, and (iv) overfitting avoidance strategies by employing powerful regularization22,28.

Similarly, the choice of a conventional feature selection method is essential for uni-modal and multi-modal uniform approaches and also plays a role in one tested multi-modal ensemble method (Table S3). We decided to use SVM-RFE34 because of the following considerations. First, unlike other feature selection methods, SVM-RFE has been successfully used in all individual data modalities tested in our study (Table S5 in Supplementary Information). Second, in experiments that involved 8 TCGA_BRCA1 datasets/predictive tasks with 5 modalities, SVM-RFE outperformed in terms of average predictive performance all 16 tested feature selection methods in both uni-modal and multi-modal applications (Table S6 in Supplementary Information).

In order to derive a single performance estimate for each type of approach, we optimized predictive performance over all approach variants and core methods.

Estimation of predictive performance

For model/parameter optimization and estimation of predictive performance, we used a nested repeated 5-fold cross-validation procedure35,36,37,38. The inner loop of cross-validation was used to determine the best parameters and features of the classifier (i.e., values of parameters yielding the best predictive performance for the validation dataset). The outer loop of cross-validation was used for estimating the predictive performance of the model that was built using the previously found best parameters by testing with an independent set of samples. To account for variance in performance estimation, we repeated this entire nested 5-fold cross-validation process for 10 different splits of the data (into 5 cross-validation testing sets) and averaged the results35.

To measure predictive performance (also referred to as “predictivity”), we used the area under the ROC curve (AUC). The ROC curve is the plot of sensitivity versus 1-specificity for a range of threshold values on the outputs/predictions of the classification algorithms39. AUC ranges from 0 to 1, where AUC = 1 corresponds to a perfectly correct classification of samples, AUC = 0.5 corresponds to classification by chance, and AUC = 0 corresponds to an inverted perfect classification. We chose AUC as the predictive performance metric because it is insensitive to unbalanced class prior probabilities, it is computed over the range of sensitivity-specificity tradeoffs at various classifier output thresholds, and it is more discriminative than metrics such as accuracy (proportion of correct classifications), F-measure, precision, and recall40,41.

Statistical comparisons

To test whether the average differences in predictive performance (e.g., across all 47 datasets/tasks) between the approaches are non-random, we used a permutation test, adapted from42. For the comparison of two approaches X and Y, the test involves the following steps: (i) Define the null hypothesis (H0) to be that the average performance (across all applicable datasets/tasks) of the approaches X and Y is the same. Compute the absolute value of the observed average differences between performance of the approaches X and Y (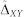Inline graphic). (ii) Repeatedly randomly rearrange the performance values of the approaches X and Y (independently for each dataset/task) and compute the absolute value of the average differences in performance of the approaches X and Y in permuted data. Repeat the above for 100,000 permutations to obtain the null distribution of ΔXY, the estimator of the true unknown absolute value of the average differences in performance of the two approaches. (iii) Compute the cumulative probability (p-value) of ΔXY being greater than or equal to the observed difference 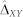Inline graphic over all permutations. If the resulting p-value was considered significant (see last paragraph of this subsection), we rejected H0 and concluded that the data supports that the approaches X and Y do not have the same performance, and this difference is not due to sampling error.

To test whether the differences in predictive performance for a fixed dataset/task between two modalities are non-random, we used U-statistic theory and Delong's test43,44. The nominally best performing modality in each dataset was compared to all other measured modalities. Modalities where the null hypothesis of similar performance could be rejected were designated as ‘statistically optimal’ performing.

To compare two modalities in terms of proportion of datasets (i) where a modality yields ‘statistically optimal’ performance or (ii) where one modality performs at least as good as the other, we used a Chi-squared test with one degree of freedom. The proportions were computed only for datasets/tasks where data from both modalities was available.

The adjustment for multiple comparisons in all statistical tests performed in this work was performed using the methodology of45,46. The statistical significance was determined at 0.05 level using adjusted p-values.

Computing resources and infrastructure

For this project we used four high-performance computing (HPC) clusters available to us. These HPC clusters included the Asclepius and Phoenix clusters of the NYU Langone Medical Center, the Bowery cluster of the New York University main campus, and the BuTina cluster of the New York University Abu Dhabi campus in the United Arab Emirates. Asclepius had ~1,000 Intel x86 processing cores and 4 TB of RAM distributed among the cluster's compute nodes. Phoenix has ~1,200 latest Intel ×86 processing cores and 10 TB of RAM distributed among the compute nodes. Both Asclepius and Phoenix access 585 TB of central disk storage. The Bowery cluster has ~2,500 cores and 9 TB of RAM total among all the nodes. The BuTina cluster has ~6,400 latest Intel ×86 processing cores with a total of 26 TB of RAM.

To make the computations feasible, we divided the problem into many independent jobs, each implemented in Matlab, R, and/or C/C++. The completely independent nature of the jobs enabled linear speedup. We typically used 100–300 cores of the cluster at a time over a calendar year. We estimate that the final results reported here required 50 core-years of computation and were obtained in roughly 4 months of elapsed time.

Author Contributions

A.S., B.R. and C.F.A. designed experiments. A.S., B.R., M.H. and S.M. performed experiments. E.E. and E.R.P. provided computing support and helped to execute experiments. M.P. and T.P. provided NeoMark dataset. B.R., M.H., S.M., C.F.A. and A.S. analyzed results and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep04411-s1.pdf (1.1MB, pdf)
Supplementary Information

Supplementary File 1

srep04411-s2.xls (179KB, xls)

Acknowledgments

This research was supported in part by the grant 1UL1 RR029893 from the National Center for Research Resources, National Institutes of Health. This study uses the data generated by the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC) project, funded by Cancer Research UK and the British Columbia Cancer Agency Branch. The study uses the data generated by the European Union NeoMark project (EU-FP7- ICT-2007-2-22483-NeoMark), funded by the Seventh Framework Programme, The authors also thank Drs. Olivier Gevaert, Anneleen Daemen, and Yves Moreau for providing clarifications on previously predictive analytics multi-modal studies and HIDIDIT software, and Dr. Guillaume Obozinski for SKMsmo software.

References

  1. Golub T. R. et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286, 531–537 (1999). [DOI] [PubMed] [Google Scholar]
  2. Yong F. L., Law C. W. & Wang C. W. Potentiality of a triple microRNA classifier: miR-193a-3p, miR-23a and miR-338-5p for early detection of colorectal cancer. BMC Cancer 13, 280; 10.1186/1471-2407-13-280 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Petricoin E. F., Zoon K. C., Kohn E. C., Barrett J. C. & Liotta L. A. Clinical proteomics: translating benchside promise into bedside reality. Nat. Rev. Drug Discov. 1, 683–695 (2002). [DOI] [PubMed] [Google Scholar]
  4. Poage G. M. et al. Identification of an epigenetic profile classifier that is associated with survival in head and neck cancer. Cancer Res 72, 2728–2737, 10.1158/0008-5472.CAN-11-4121-T (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Alekseyenko A. V. et al. Causal graph-based analysis of genome-wide association data in rheumatoid arthritis. Biology Direct 6, 25 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Kong J. et al. Integrative, multimodal analysis of glioblastoma using TCGA molecular data, pathology images, and clinical outcomes. IEEE Trans Biomed Eng 58, 3469–3474, 10.1109/TBME.2011.2169256 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Taylor B. S. et al. Integrative genomic profiling of human prostate cancer. Cancer cell 18, 11–22, 10.1016/j.ccr.2010.05.026 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Curtis C. et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature 486, 346–352, 10.1038/nature10983 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Daemen A. et al. A kernel-based integration of genome-wide data for clinical decision support. Genome Med 1, 39; 10.1186/gm39 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gevaert O., De Smet F., Timmerman D., Moreau Y. & De Moor B. Predicting the prognosis of breast cancer by integrating clinical and microarray data with Bayesian networks. Bioinformatics 22, e184–190, 10.1093/bioinformatics/btl230 (2006). [DOI] [PubMed] [Google Scholar]
  11. Daemen A., Gevaert O. & De Moor B. Integration of clinical and microarray data with kernel methods. Conference proceedings: … Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference 2007, 5411–5415, 10.1109/IEMBS.2007.4353566 (2007). [DOI] [PubMed] [Google Scholar]
  12. Li L. et al. Integration of clinical information and gene expression profiles for prediction of chemo-response for ovarian cancer. Conference proceedings: … Annual International Conference of the IEEE Engineering in Medicine and Biology Society. IEEE Engineering in Medicine and Biology Society. Conference 5, 4818–4821, 10.1109/IEMBS.2005.1615550 (2005). [DOI] [PubMed] [Google Scholar]
  13. Troyanskaya O. G. Putting microarrays in a context: integrated analysis of diverse biological data. Brief. Bioinform. 6, 34–43 (2005). [DOI] [PubMed] [Google Scholar]
  14. Pittman J. et al. Integrated modeling of clinical and gene expression information for personalized prediction of disease outcomes. Proc. Natl. Acad. Sci. U.S.A. 101, 8431–8436 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Aliferis C. F., Statnikov A. & Tsamardinos I. Challenges in the analysis of mass-throughput data: a technical commentary from the statistical machine learning perspective. Cancer Informatics 2, 133–162 (2006). [PMC free article] [PubMed] [Google Scholar]
  16. West M. et al. Predicting the clinical status of human breast cancer by using gene expression profiles. Proceedings of the National Academy of Sciences of the United States of America 98, 11462–11467, 10.1073/pnas.201162998 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Huang E. et al. Gene expression predictors of breast cancer outcomes. Lancet 361, 1590–1596, 10.1016/S0140-6736(03)13308-9 (2003). [DOI] [PubMed] [Google Scholar]
  18. Chang H. Y. et al. Robustness, scalability, and integration of a wound-response gene expression signature in predicting breast cancer survival. Proceedings of the National Academy of Sciences of the United States of America 102, 3738–3743, 10.1073/pnas.0409462102 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Knudson A. G. Jr Mutation and cancer: statistical study of retinoblastoma. Proc Natl Acad Sci U S A 68, 820–823 (1971). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Nordling C. O. A new theory on cancer-inducing mechanism. Br J Cancer 7, 68–72 (1953). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Stephens P. J. et al. Massive genomic rearrangement acquired in a single catastrophic event during cancer development. Cell 144, 27–40, 10.1016/j.cell.2010.11.055 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hastie T., Tibshirani R. & Friedman J. H. The elements of statistical learning: data mining, inference, and prediction. (Springer, 2001). [Google Scholar]
  23. Scarselli F. & Chung Tsoi A. Universal approximation using feedforward neural networks: A survey of some existing methods, and some new results. Neural Networks 11, 15–37 (1998). [DOI] [PubMed] [Google Scholar]
  24. Hammer B. & Gersmann K. A Note on the Universal Approximation Capability of Support Vector Machines. Neural Processing Letters 17, 43–53 (2003). [Google Scholar]
  25. Busso C. et al. Analysis of emotion recognition using facial expressions, speech and multimodal information. Proceedings of the 6th international conference on Multimodal interfaces 205–211, 10.1145/1027933.1027968 (2004). [Google Scholar]
  26. Picone M. et al. Enabling heterogeneous data integration and biomedical event prediction through ICT: the test case of cancer reoccurrence. Advances in experimental medicine and biology 696, 367–375, 10.1007/978-1-4419-7046-6_37 (2011). [DOI] [PubMed] [Google Scholar]
  27. Lanckriet G. R., Deng M., Cristianini N., Jordan M. I. & Noble W. S. Kernel-based data fusion and its application to protein function prediction in yeast. Pac Symp Biocomput 300–311 (2004). [DOI] [PubMed] [Google Scholar]
  28. Vapnik V. N. Statistical learning theory. (Wiley, 1998). [DOI] [PubMed] [Google Scholar]
  29. Guyon I. Kernel ridge regression tutorial. Technical report, http://clopinet.com/isabelle/Projects/ETH/KernelRidge.pdf (2005, accessed on 10/10/2013).
  30. Guyon I. et al. Feature selection with the CLOP package. Technical report, http://clopinet.com/isabelle/Projects/ETH/TM-fextract-class.pdf (2006, accessed on 10/10/2013).
  31. Genkin A., Lewis D. D. & Madigan D. Large-scale Bayesian logistic regression for text categorization. Technometrics 49, 291–304 (2007). [Google Scholar]
  32. Genkin A., Lewis D. D. & Madigan D. Large-scale Bayesian logistic regression for text categorization. Technical Report DIMACS (2004). [Google Scholar]
  33. Breiman L. Random forests. Machine Learning 45, 5–32 (2001). [Google Scholar]
  34. Guyon I., Weston J., Barnhill S. & Vapnik V. Gene selection for cancer classification using support vector machines. Machine Learn 46, 389–422 (2002). [Google Scholar]
  35. Braga-Neto U. M. & Dougherty E. R. Is cross-validation valid for small-sample microarray classification? Bioinformatics 20, 374–380 (2004). [DOI] [PubMed] [Google Scholar]
  36. Statnikov A., Tsamardinos I., Dosbayev Y. & Aliferis C. F. GEMS: a system for automated cancer diagnosis and biomarker discovery from microarray gene expression data. Int. J. Med. Inform. 74, 491–503 (2005). [DOI] [PubMed] [Google Scholar]
  37. Scheffer T. Error estimation and model selection, Ph.D. Thesis, Technischen Universität Berlin, School of Computer Science, (1999). [Google Scholar]
  38. Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence (IJCAI) 2, 1137–1145 (1995). [Google Scholar]
  39. Fawcett T. ROC Graphs: Notes and Practical Considerations for Researchers. Technical Report, HPL-2003-4, HP Laboratories (2003). [Google Scholar]
  40. Ling C. X., Huang J. & Zhang H. AUC: a statistically consistent and more discriminating measure than accuracy. Proceedings of the Eighteenth International Joint Conference of Artificial Intelligence (IJCAI) (2003). [Google Scholar]
  41. Ling C. X., Huang J. & Zhang H. AUC: a better measure than accuracy in comparing learning algorithms. Proceedings of the Sixteenth Canadian Conference on AI (2003). [Google Scholar]
  42. Menke J. & Martinez T. R. Using permutations instead of student's t distribution for p-values in paired-difference algorithm comparisons. Proceedings of 2004 IEEE International Joint Conference on Neural Networks 2, 1331–1335 (2004). [Google Scholar]
  43. DeLong E. R., DeLong D. M. & Clarke-Pearson D. L. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44, 837–845 (1988). [PubMed] [Google Scholar]
  44. Lee A. J. U-statistics: theory and practice. (M. Dekker, 1990). [Google Scholar]
  45. Benjamini Y. & Hochberg Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society. Series B (Methodological) 57, 289–300 (1995). [Google Scholar]
  46. Benjamini Y. & Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Ann. Statist 29, 1165–1188 (2001). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep04411-s1.pdf (1.1MB, pdf)
Supplementary Information

Supplementary File 1

srep04411-s2.xls (179KB, xls)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES