IDENTIFICATION OF ADDITIONAL PROTEINS IN DIFFERENTIAL PROTEOMICS USING PROTEIN INTERACTION NETWORKS

Abstract

In this study, we developed a novel computational approach based on protein-protein interaction (PPI) networks to identify a list of proteins that might have remained undetected in differential proteomic profiling experiments. We tested our computational approach on two sets of human smooth muscle cell (SMC) protein extracts which were affected differently by DNase I treatment. Differential proteomic analysis by saturation DIGE resulted in the identification of 41 human proteins. The application of our approach to these 41 input proteins consisted of four steps: 1) Compilation of a human PPI network from public databases, 2) Calculation of interaction scores based on functional similarity, 3) Determination of a set of candidate proteins that are needed to efficiently and confidently connect the 41 input proteins, and 4) Ranking of the resulting 25 candidate proteins. Two of the three highest-ranked proteins, beta-arrestin 1 and beta-arrestin 2, were experimentally tested, revealing that their abundance levels in human SMC samples were indeed affected by DNase I treatment. These proteins had not been detected during the experimental proteomic analysis. Our study suggests that our computational approach may represent a simple, universal, and cost-effective means to identify additional proteins that remain elusive for current 2D gel-based proteomic profiling techniques.

1. INTRODUCTION

Proteins and their abundance or state changes are of key importance in many fundamental cellular processes, such as growth, differentiation, and response to environmental stimuli. The study of proteins is therefore essential for the understanding of such cellular processes. However, there appear to be large gaps in our comprehensive understanding of protein function. According to a recent estimate, 75% of reported protein research in 2009 focused on those 10% of known proteins that were already known when the human genome was mapped [1]. Indeed, a considerable number of human proteins have not been tied to specific cellular functions. As of March 6, 2012, the human UniProtKB-GOA [2] contained less than 16,000 human proteins with human-curated Gene Ontology annotations. Proteomic technologies that help implicate new proteins in cellular processes are therefore of critical importance.

Although proteomic technologies have greatly evolved during the past decade [3], they still confront challenges, mainly sensitivity of detection. Among gel-based strategies, two-dimensional gel electrophoresis (2-DE) [4] combined with MS for protein identification, is commonly used for the separation and quantification of thousands of proteins from complex samples, like eukaryotic cells [5]. Despite its potential and high resolving power, 2-DE is subject to technical limitations, in particular the detection of proteins with extreme molecular weight, extreme pI, high hydrophobicity, or low abundance [6]. To increase sensitivity, the DIGE saturation dyes [7] were developed, requiring the use of only five μg of protein sample to perform a 2D-gel as we have recently shown [8]. Gel-free strategies are commonly based on the use of liquid chromatography coupled to tandem mass spectrometry (LC-MS/MS). This approach is also subject to technical limitations, rendering the detection of proteins over the whole dynamic range of protein concentrations very challenging [9, 10]. In summary, current experimental techniques for proteomic detection and quantification, suffer from specific biases and limitations in terms of proteome coverage.

Recent computational approaches downstream of the experimental analysis place a set of identified, or differentially regulated proteins into an interpretation context with other proteins, for example in interaction networks [11]. The bioinformatic Steiner tree approach [12] starts with a set of given, experimentally determined, genes in a regulatory process. It connects the given genes into one or several regulatory subnetworks (Steiner trees) by adding protein interactions and additional genes (Steiner nodes), according to aggregate measures of reliability of protein interactions.

Scott et al. [12] applied this approach to a set of differentially regulated genes from S. cerevisiae transcriptome data. They showed that the approach can identify compact subnetworks that are consistent with prior knowledge about regulatory subnetworks, and argue that the newly identified subnetworks represent plausible hypotheses for downstream analysis. Huang and Fraenkel [13] extended the approach by including data from phosphoproteomic experiments and published a web server-based tool called SteinerNet [14] that allows users to apply a generalization of the Steiner tree approach to custom interactomes and proteins of interest. In both cases, the resulting hypotheses were demonstrated to be useful for the downstream analysis of the data in different ways, but no direct hypotheses about the relevance of the newly identified proteins and their interaction were evaluated.

Other network-based computational approaches use different principles to infer additional proteins. The MSNet approach by Ramakrishnan et al. [15] aims to identify additional proteins in shotgun proteomics. Candidates are those – commonly unreported – proteins for which only marginal evidence exists, e.g. proteins for which only a single peptide has been determined experimentally. A mathematical diffusion model propagates additional likelihood from high-confidence proteins along the edges of a “probabilistic functional gene network”. MSNet then selects those candidate proteins that can accumulate a sufficiently high additional likelihood from their local network neighborhood. When applied to global profiling experiments, the approach was shown to significantly increase the number of identifications at a given false discovery rate. The enrichment approach by Li et al. [16] uses protein-protein interaction networks to identify additional proteins that have only weak support in MS/MS data, but are members of a group of densely interacting confidently identified proteins.

All the above computational Steiner approaches aim to identify the members of functional context, but direct evidence for the actual presence of these additional proteins has been missing., With this study, we present direct experimental evidence for the presence of additional proteins inferred by a computational Steiner tree approach.

2. MATERIALS AND METHODS

2.1. Overview

We used a Steiner tree-based computational approach to identify additional proteins in proteomic experiments and evaluated its utility on a dataset generated from the comparison between unaffected and affected human smooth muscle cell (SMC) protein extracts after DNase I treatment. Figure 1 provides an illustration of the workflow. Detailed information on SMC protein extraction and 2D-DIGE analysis is provided as supplemental data.

Figure 1. Workflow.

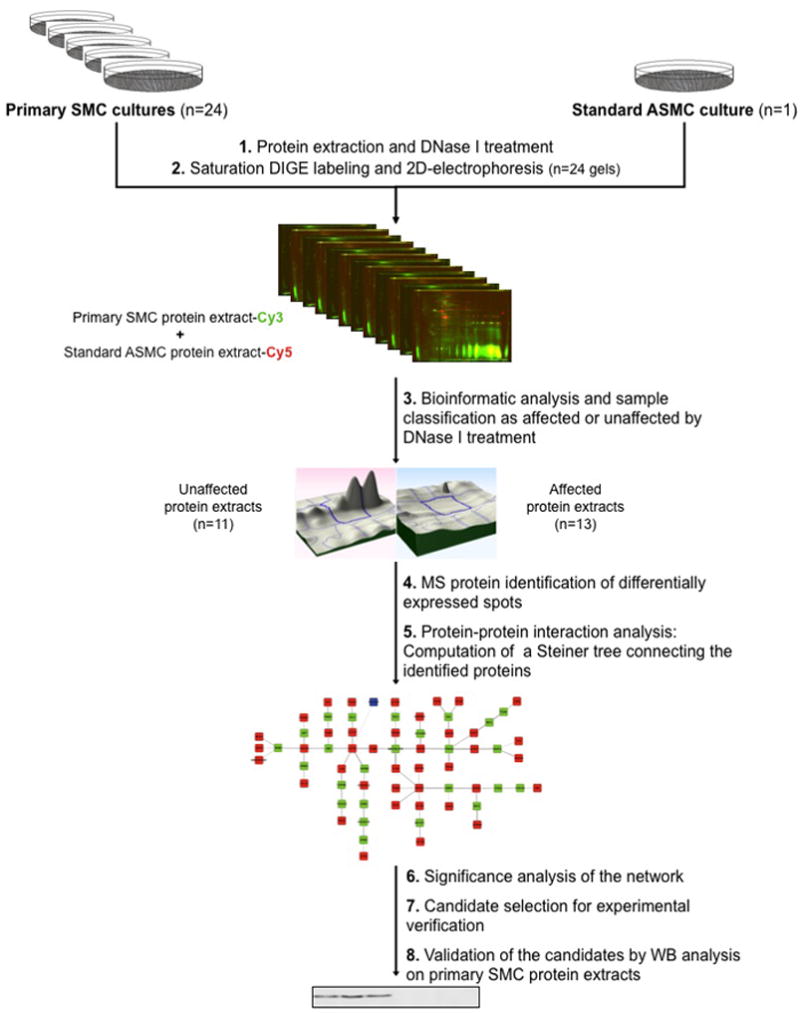
Twenty-four primary human SMC and one ASMC cultures were performed and the corresponding protein extracts were treated with DNase I (1). Then, using saturation DIGE labeling, 24 2D-gels were performed with the 24 human SMC protein extracts and the ASMC protein extract as standard (2). Bioinformatic image analysis of the gels allowed the classification of protein extracts as unaffected or affected by DNase I treatment (3). Differential spots were identified by MALDI-TOF MS (4), and the set of identified proteins was subjected to a Steiner tree-based computational approach in order to predict a network containing further proteins potentially affected by DNase I treatment (5). After statistical evaluation of the network (6), two Steiner node proteins were selected (7) and their profile was validated as significantly differring by Western Blot (8).

2.2. Steiner tree approach

The Steiner tree approach presented here builds a protein-protein interaction (PPI) network between proteins that differ between profiles, thereby identifying proteins missed in the experiment. It consists of the following four steps (Fig. 2).

Figure 2. Steiner-tree approach.

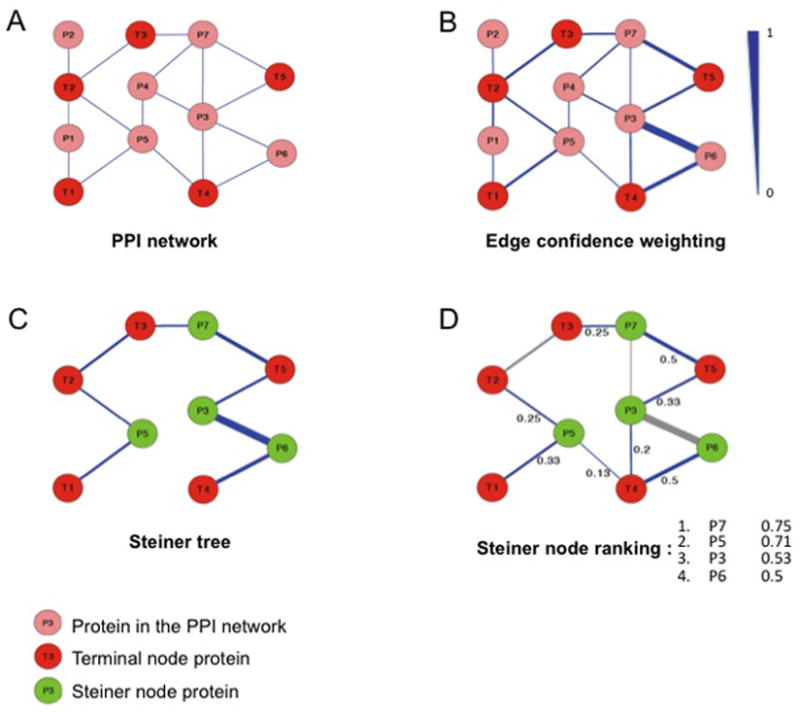
A: Initial protein-protein interaction network including input proteins (terminal nodes marked in red). B: Edge confidence score, based on functional similarity (GO biological process) of connected proteins (scale: 0 to 1). C: Determination of the Steiner nodes (in green) connecting all input proteins with a minimal overall sum of edge costs. Edge cost is defined as the inverse of interaction confidence. D: Ranking of Steiner node proteins according to summed confidence scores of edges directly connecting them to terminal nodes.

2.2.1. Compilation of a human protein-protein interaction network

A network of human protein-protein interactions was built by merging the two databases IntAct [17] and BIND [18]. IntAct data was retrieved in the form of a PSIMITAB-formatted file on March 29, 2010 from the IntAct website (http://www.ebi.ac.uk/intact). To acquire the BIND data, the identifier search interface supplied by the Biomolecular Object Network Database (BOND) webpage (http://bond.unleashedinformatics.com) was used to extract all interactions between human proteins (requiring the taxon id 9606 for both interactors). The search results were retrieved on March 29, 2010 and stored in “GI pair” format. The two networks were merged by matching protein UniProt IDs. This led to a consolidated protein-protein interaction network containing 21.022 proteins and 51.975 interactions.

2.2.2. Computation of edge confidence scores

Confidence scores were assigned to all edges of the compiled PPI network according to the functional similarity of interacting proteins. The functional similarity of two proteins was quantified using the rfunsimBP score [19]. rfunsimBP scores the similarity of two sets of Gene Ontology (GO) biological process annotations by taking into account all pair-wise semantic similarities of terms from the two annotation sets. Its output is a similarity score in the interval [0,1], with higher scores indicating higher functional similarity. The GO annotations were retrieved from the UniProtKB-GOA project [2] and the resulting score was transformed into edge costs by taking the inverse (cost=1/rfunsimBP). The resulting values were restricted to a maximum of 10 to avoid excessively large costs for interactions between functionally distinct proteins.

2.2.3. Determination of Steiner nodes

The merged PPI network, costs of the edges, as well as the list of input proteins was imported into the graph tool library GOBLIN version 2.8 [http://www.math.uni-augsburg.de/~fremuth/goblin.html] (see supplementary material for source code). An algorithm supplied by the GOBLIN library, which is based on the heuristic described in Mehlhorn et al. [20] was applied to compute a Steiner tree connecting the proteins detected in the 2D-DIGE analysis. The aim of Mehlhorn’s heuristic is to identify a tree that is able to connect all given ‘terminal nodes’ (i.e. the input set of proteins differing between proteome profiles) with a minimal sum of costs along its edges. The difference to the well-known minimum spanning tree approach initially described by Kruskal [21] is that a Steiner tree can include additional nonterminal nodes of the full network, so-called ‘Steiner nodes’, in the solution. Cytoscape v2.7 [22] was used to visualize the resulting Steiner tree.

To assess the statistical significance of the obtained Steiner tree solution, we performed a simulation study in which the Steiner tree heuristic described above was executed 10,000 times on the human PPI network using as input a set of 41 target proteins randomly selected from the full PPI network. The 41 random target proteins were selected to have a similar distribution of node degrees when compared to the 41 original target proteins. In each run, we recorded the number of Steiner nodes that were used to connect the 41 terminal nodes, along with the sum of the Steiner tree edge costs. For both measures, we fitted a Normal distribution to the data and computed a p-value for the probability to obtain, by chance, a network at least as small as the one determined on the experimental data.

2.2.4. Candidate selection for experimental verification

To find candidates for the experimental verification of our in-silico results, we ranked the Steiner node proteins, based on the “augmented network” induced by the selection of all Steiner and terminal nodes and the full set of edges connecting these nodes in the compiled human PPI network. The score used for ranking the Steiner nodes was computed as the sum of the functional similarity scores of all edges that connect a given Steiner node to any of the terminal nodes. A similar ranking of the terminal node proteins, in this case summing up the scores of all edges linking a given terminal node to any other terminal node, was also performed.

2.3. Western blot analysis

Fifteen μL of 95% Laemmli buffer (2% SDS, 25% glycerol, 62.5 mM Tris HCl, 0.01% Bromophenol blue)/5% beta-mercaptoethanol were added to the volume corresponding to 50 μg of each SMC protein extract (10 unaffected and 11 affected), and incubated at 95°C for 10 min. Denaturized samples were separated by 10% acrylamide SDS-PAGE and proteins were electrotransferred onto a 0.45 μm Hybond nitrocellulose membrane (GE Healthcare). Transferred proteins were incubated at 4°C, overnight with primary antibodies, (monoclonal rat anti human beta-arrestin 1 (1:150 v/v, R&D Systems, UK) and polyclonal goat anti human beta-arrestin 2 (1:500 v/v, Abcam, UK)), that were diluted in 5% w/v non-fat dry milk in TBS-Tween.

Incubation with secondary antibodies (donkey anti goat (Abcam) and ECL rabbit IgG-HRP (GE Healthcare)), diluted 1:5000 v/v in 5% w/v non-fat dry milk in TBS-Tween, was performed at room temperature for 1.5 h. Then, the specific proteins were detected using ECL Plus western blotting detection reagent (GE Healthcare) followed by membrane scanning with an Ettan DIGE Imager scanner (GE Healthcare) at excitation/emission wavelengths of 480 nm/530 nm to yield images with a pixel size of 100 μm. Finally, Quantity One software (Biorad, UK) was used for the acquisition of intensity values of detected proteins from blot images.

2.4. Application of MSNet to the 2D-DIGE dataset

We applied the MSNet method published by Ramakrishnan et al. [15] to our 2D-DIGE dataset, consisting of the weighted PPI network and the set of proteins identified with different abundances between the proteome profiles of the SMC protein extracts. Since MSNet needs a protein identification probability for each protein in the network as input, we assigned a probability of 1.0 to all 41 identified proteins. Lacking identification probabilities scores for the remaining proteins in our weighted PPI network, we assigned them a low probability of 0.1.

We used the REST-based Web API supplied by the MSNet method to upload the necessary data and tried a range of different input parameter values. In detail, we used 10, 20, 40 or 60 network reshufflings for estimation of FDRs (default value for human data: 10) and set the parameter weighing the relative contribution of the network information versus the determined MS/MS-based score to either of the values 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 or 15 (default value: 10). For each parameter combination we retrieved a list of proteins with their associated MSNet identification scores, as well as score cutoffs corresponding to different network shuffling based significance levels represented as q values (data downloaded on September 15, 2011).

2.5. Application of SteinerNet to the 2D-DIGE dataset

The SteinerNet method attempts to solve a generalized version of the Steiner tree problem, called prize-collecting Steiner tree (PCST). In this problem formulation, each terminal node is assigned a negative cost (prize) contribution to the overall score, and solutions to the PCST include also networks that only connect a subset of the terminal nodes.

To compare the results of our method to the SteinerNet web service, we reformatted the PPI network and the list of terminal nodes to match the input specifications of SteinerNet as stated on their web page (http://fraenkel.mit.edu/steinernet/quickstart.html#Inputs). As protein interaction confidence, we used the functional similarity (rfunsimBP) of the interacting proteins. We increased each score of less than 0.1 to 0.1 to reflect the maximal edge cost of 10.0 used in our approach. As recommended on their Web page, the numerical prize score for all terminal node proteins was set to 1.0. The input parameter β that controls the trade-off between including terminal nodes and excluding edges, was left at its default value of 4.0.

Upon completion of the calculations, SteinerNet outputs the resulting Steiner tree as well as an augmented network, created from all found Steiner and terminal nodes along with all interactions in the full PPI network that connect any two of those nodes. We used the same candidate ranking scheme as described in section 2.2.4 to prioritize the Steiner nodes found by SteinerNet.

3. RESULTS

In the present study, we have used a computational Steiner tree-based approach and evaluated it on the proteomic profile modifications between two sets of human SMC protein extracts that were affected differently by DNase I treatment.

3.1. Morphology of human SMC

Twenty-four primary human SMC cultures were prepared and all SMC primary cultures showed a hill-and-valley pattern that was maintained throughout all subcultures (Suppl. Fig. 1A). ASMC (passage 9) were used as standard for the DIGE labeling strategy and showed an elongated, spindle-shaped morphology (Suppl. Fig. 1B).

3.2. Differential protein profiles between affected and unaffected SMC protein extracts

The proteomic profile of 13 SMC cultures appeared to be affected by DNase I treatment during protein extraction (Suppl. Fig. 2), missing four intense spots that were present in the proteomic profile of unaffected SMC protein extracts (Detailed insert in Suppl. Fig. 2).

Bioinformatic analysis between 2D-DIGE images of 11 unaffected and 13 affected SMC protein extracts resulted in 569 polypeptide spots differentially profiled (p-value <0.05). Of these, 408 polypeptide spots presented a fold-change equal or higher than 2. After manual validation that required a q-value <0.05, 135 spots were selected as differentially profiled (Suppl. Table 1). Of these, 62 had increased and 73 decreased abundance in 2D-DIGE gels of unaffected compared to affected SMC protein extracts (Suppl. Fig. 3).

MALDI MS led to the identification of 78.5% of selected spots, i.e. 41 different human proteins from 100 spots (Suppl. Table 2), and 7 spots corresponded to bovine DNase I (Suppl. Table 3), three of which were used for the classification of protein extracts. The 41 identified human proteins were classified into biological processes, according to Gene Ontology annotations registered in SwissProt. Interestingly, more than half of the proteins whose abundance differed between unaffected and affected SMC protein extracts could be classified into two classes: proteins involved in apoptosis, and proteins involved in cell motion and actin cytoskeleton reorganization.

3.3. Proteins detected by the Steiner tree approach

To discover new proteins whose profile might systematically differ between unaffected and affected SMC protein extract, we applied a Steiner tree approach (Fig. 2). Of the 42 terminal node proteins (bovine DNase I and 41 human proteins) supplied to the Steiner tree algorithm, one (adenylyl cyclase associated protein 1) could not be connected to the rest of the network. For the construction of a network connecting the remaining 41 proteins (Fig. 3), 25 Steiner node proteins were selected by our algorithm. Both terminal and Steiner node proteins were ranked according to their number and confidence of interactions with other terminal nodes of the network using a functional similarity score (for details on the score used for ranking see Materials and Methods, Section 2.2.4 and Table 1). Interestingly, in the PPI network, DNase I interacted solely with one protein: actin, cytoplasmic 1, which is the terminal node protein with the highest number of interactions in the Steiner network (Table 1).

Figure 3. Computed Steiner tree.

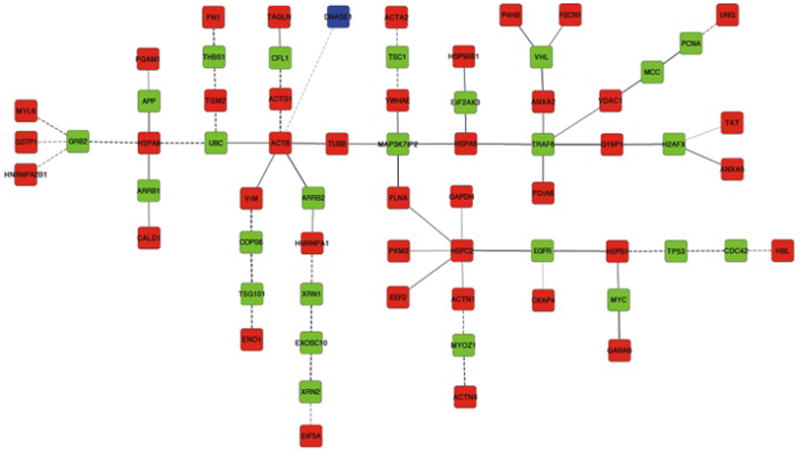
Terminal nodes corresponding to human proteins are represented in red, DNase I in blue. Steiner node proteins are represented in green. Edge gray levels indicate confidence scores. Interactions tested in human samples are represented by solid lines and interactions tested only in other organisms are shown as dashed lines.

Table 1.

Proteins included in the Steiner tree solution

SwissProt Accession number	Protein name	Gene name	Total interactions	Terminal interactions	Score*
Steiner node proteins
P62993	Growth factor receptor-bound protein 2	GRB2	23	19	7.55
P32121	Beta arrestin 2	ARRB2	17	14	6.131
P49407	Beta arrestin 1	ARRB1	18	14	5.436
Q9Y4K3	TNF receptor-associated factor 6	TRAF6	15	10	4.705
P16104	Histone H2A.x	H2AFX	16	12	4.387
P00533	Epidermal growth factor receptor	EGFR	10	8	3.756
Q9NYJ8	TGF-beta-activated kinase 1 and MAP3K7-binding protein 2	MAP3K7IP2	8	6	2.968
P62988	Ubiquitin	UBC	10	3	2.267
P23528	Cofilin 1	CFL1	7	3	2.045
P40337	Von Hippel-Lindau disease tumor suppressor	VHL	6	5	1.958
P05067	Amyloid beta A4 protein	APP	4	4	1.818
P01106	Myc proto-oncogene protein	MYC	4	3	1.614
P07996	Thrombospondin-1	THBS1	2	2	1.542
Q9NZJ5	Eukaryotic translation initiation factor 2-alpha kinase 3	EIF2AK3	2	2	1.27
Q9NP98	Myozenin 1	MYOZ1	2	2	1.255
Q92574	Hamartin	TSC1	3	3	1.228
P23508	Colorectal mutant cancer protein	MCC	8	4	1.052
Q7L5N1	COP9 signalosome complex subunit 6	COPS6	3	1	0.997
Q99816	Tumor susceptibility gene 101 protein	TSG101	3	1	0.757
P04637	Cellular tumon antigen p53	TP53	3	1	0.657
Q8IZH2	5′-3′ Exoribonuclease 1	XRN1	3	1	0.583
P12004	Proliferating cell nuclear antigen	PCNA	3	1	0.426
P60953	Cell division control protein 42 homolog	CDC42	3	1	0.415
Q9H0D6	5′-3′ Exoribonuclease 2	XRN2	2	1	0.379
Q01780	Exosome component 10	EXOSC10	2	0	0
Terminal node proteins
P60709	Actin, cytoplasmic 1	ACTB	19	13	3.992
P08238	Heat shock protein HSP 90beta	HSPC2	10	7	2.334
P63261	Actin, cytoplasmic 2	ACTG1	6	2	1.268
P07437	Tubulin beta chain	TUBB	7	1	0.655
P08670	Vimentin	VIM	4	1	0.5
P21796	Voltage dependent anion selelctive channel protein 1	VDAC1	5	3	0.484
P13639	Elongation factor 2	EEF2	3	1	0.43
P21333	Filamin A	FLNA	5	1	0.425
P04406	Glyceraldehyde-3-phosphate dehydrogenase	GAPDH	4	2	0.358
P11142	Heat shock protein cognate 71kDa protein	HSPA8	9	1	0.349
P12814	Alpha actinin 1	ACTN1	3	1	0.311
P14618	Pyruvate kinase isozymes M1/M2	PKM2	5	1	0.294
P06733	Alpha-enolase	ENO1	4	1	0.257
Q16658	Fascin	FSCN1	4	1	0.129
P24855	Deoxyribonuclease I	DNASE1	1	1	0.127
P09651	Chain A, UP1, heterogeneous nuclear ribonucleoprotein A1	HNRNPA1	6	1	0.1
Q14697	Neutral alpha glucosidase AB	GANAB	5	1	0.1
P07355	Annexin A2	ANXA2	8	1	0.1
P60660	Light myosin polypeptide -6	MYL6	5	1	0.1
P22626	Heterogeneous nuclear ribonucleoproteins A2/B1	HNRNPA2B1	2	1	0.1
Q05682	Caldesmon	CALD1	1	0	0
P02751	Fibronectin	FN1	2	0	0
P13051	Uracyl DNA glycosylase	UNG	1	0	0
P09382	Galectin 1	HBL	1	0	0
Q01995	Transgledin	TAGLN	1	0	0
P29401	Transketolase	TKT	3	0	0
Q15084	Protein disulfide isomerase A6	PDIA6	2	0	0
P08758	Annexin A5	ANXA5	1	0	0
P21980	Protein glutamine gamma glutamyltransferase 2	TGM2	2	0	0
P14314	Glucosidase 2 subunit beta	G19P1	2	0	0
Q07065	Cytoskeleton associated protein 4	CKAP4	2	0	0
P62736	Actin, aortic smooth muscle	ACTA2	1	0	0
P18669	Phosphoglycerate mutase 1	PGAM1	1	0	0
P07237	Protein disulfide isomerase	P4HB	4	0	0
P63241	Eukaryotic translation initiation factor 5A-1	EIF5A	1	0	0
P14625	Endoplasmin	HSP90B1	2	0	0
P62258	14-3-3 protein epsilon	YWHAE	7	0	0
P04792	Heat shock protein beta 1	HSPB1	4	0	0
P11021	Glucose regulated protein 78kDa	HSPA5	7	0	0
O43707	Alpha-actinin 4	ACTN4	2	0	0
P09211	Glutathione S-transferase P	GSTP1	1	0	0

^*The ranking score is computed as the sum of rfunsimBP scores of all edges connecting a given protein to any terminal node protein

3.4. Statistical significance of the Steiner tree solution

To determine whether an input of 41 randomly selected – and thus largely functionally unrelated – proteins would be likely to result in a Steiner network such as then one observed in our results, we performed 10,000 simulation runs and recorded for each simulation the number of Steiner nodes used to connect the 41 terminal nodes, along with the sum of the Steiner tree edge costs. The two resulting distributions are approximately Normal and clearly show that the network obtained from the proteins differing in abundance between proteome profiles was much smaller than expected when using randomly selected proteins with a comparable number of connections in the PPI network (Suppl. Fig. 4). In fact, none of the 10,000 simulations yielded a network with scores as low as the ones obtained from the experimental data with respect to either of the measures. The corresponding p-values indicated statistical signficance for both the number of Steiner nodes (3.6*10e-5) and the sum of edge costs (2.3*10e-4), suggesting overall close relatedness of the input proteins in the PPI network, corroborating the hypothesis that the proteins whose abundance differed between profiles were indeed affected by the DNase I treatment.

3.5. Biological validation of two predicted proteins

To biologically validate some of the proteins the Steiner tree approach predicted to be affected by the DNase I treatment, we examined the second and third protein in the candidate list, beta-arrestin 1 and beta-arrestin 2 (Table 1), as these proteins also showed an interaction with actin, cytoplasmic 1. Moreover, both beta-arrestins together interacted with 17 of the 41 terminal node proteins (Fig. 4A).

Figure 4. Protein-protein interactions and experimental profile of beta-arrestins.

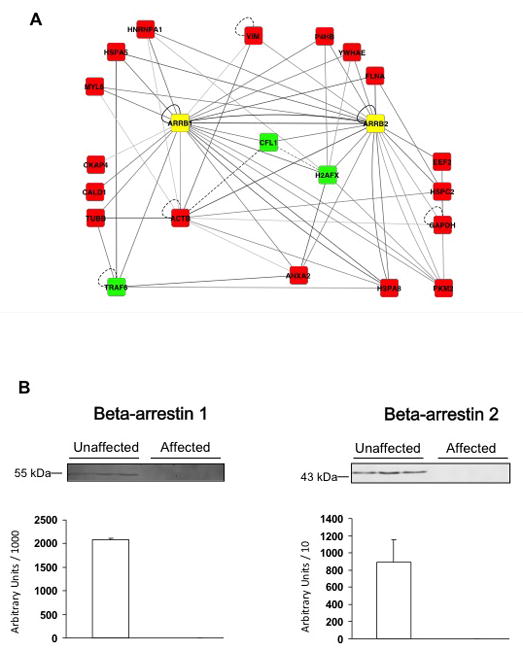
A: The network shows all interactions between the two beta-arrestins and the set of terminal and steiner node proteins. Terminal node proteins are represented in red, Steiner node proteins in green, and beta-arrestins (ARRB1 and ARRB2) in yellow. Edge gray levels indicate confidence scores. Interactions tested in human samples are represented by solid lines and interactions tested only in other organisms are shown as dashed lines. B: Beta-arrestin 1 and beta-arrestin 2 were quantified by Western blot analysis of 50 μg of each protein from extracts of unaffected (n=10) and affected (n=11) SMC. Western blots from three representative samples for each group and a histogram representing total amounts over all samples are shown.

Quantification of beta-arrestin 1 and beta-arrestin 2 was performed on unaffected (n=10) and affected (n=11) SMC protein extracts by Western blot (Fig. 4B). The results clearly showed that protein abundance of both beta-arrestins were higher in unaffected compared to affected samples.

3.6. MSNet results on the 2D-DIGE dataset

In order to evaluate whether the MSNet method [25] would be able to identify the same proteins predicted in the present study, we applied MSNet to our 2D-DIGE dataset, e.g. the weighted PPI network and the set of 41 experimentally identified proteins In the input for the MSNet method, we set a high identification probability to proteins found in the 2D-DIGE dataset and a basal low probability to all other proteins in the network, thus allowing the method to identify any protein reachable from the set of experimentally detected proteins.

Using a range of different input parameter settings (see Materials and Methods, section 2.4), MSNet was unable to predict the two beta-arrestins validated by Western blots at a reasonable q value cutoff. Regardless of the supplied input parameters, the MSNet probability score for the two beta-arrestins never exceeded 0.12. Selecting a prediction score cutoff low enough to identify the beta-arrestins led on average to the prediction of 2,356 out of the roughly 21,000 proteins in the network, which is also reflected by the low significance level estimated at a q value of 0.3.

3.7. SteinerNet results on the 2D-DIGE dataset

Using a generalization of the Steiner tree problem, the web server SteinerNet [14] also computes Steiner trees given a PPI network and a set of terminal node proteins (cf. Materials and Methods, section 2.5). Running SteinerNet on our scored PPI network and the 41 experimentally identified proteins resulted in a list of 74 Steiner proteins (Suppl. Table 4) that connected all 41 input proteins with a total cost of 174.7 (compared to 25 Steiner proteins connecting all inputs with total cost of 140.5 in our solution). Since SteinerNet attempts to solve a generalization of the Steiner tree problem and finds a solution that is also valid for the regular Steiner tree problem (all terminal nodes are connected), the higher cost of its solution relative to our implementation can only be attributed to the different heuristic it uses. The list of 74 Steiner proteins found by SteinerNet overlapped the list of proteins found by our approach, but was considerably longer. While 18 of the 25 proteins identified by our method were also contained in the SteinerNet result, some high-ranking proteins were missed (e.g. beta-arrestin-2 and EGFR). At the same time, the SteinerNet solution introduced few high-scoring new candidates. Only one protein, TRAF2, was not found by our method and ranked in the top ten, when the two result lists were combined. The average score of the top ten candidates in the SteinerNet list was 3.53, while our method achieved an average score of 4.12 within its top ten candidates. These results indicate that our method not only found a better solution of the Steiner tree problem, but also produced a protein candidate ranking in which high-ranking proteins had more interactions with – and were functionally more similar to – the input proteins.

4. DISCUSSION

The aim of the present study was to probe the potential of the computational Steiner tree approach to identify novel proteins that are not detected by a differential proteomics approach (saturation DIGE analysis). To our knowledge, this is the first experimental validation of this approach, in its first reported application to only a single proteomic dataset, and to samples of a complexity higher than yeast cell lysate. The present paper presents clear evidence that the combined experimental-computational approach gives access to proteins that were not found by 2D DIGE analysis alone.

4.1. The Steiner tree approach is a straightforward and widely applicable method to implicate additional proteins in differential proteomics

The Steiner tree approach, in its different variations, is a computational procedure that requires, besides an experimentally determined set of proteins, only access to public databases on protein function, protein interactions, and relatively mild computational means. Our study shows that it can be successfully applied even to complex human samples. In the future, protein interaction and functional knowledge databases can be expected to become more complete and reliable, and the computational means will only improve as well. This suggests that the Steiner tree approach represents an inexpensive, widely applicable technique that can be routinely applied to implicate additional, potentially undetected proteins in differential proteomics experiments, such as 2D gel electrophoresis or even LC-MS/MS.

A few recent studies have previously proposed Steiner tree techniques to integrate experimental evidence into functional subnetworks, but our study suggests a simpler, more direct, and experimentally testable use of the technique. We applied it here to a single proteomic dataset using only public interactome and GO annotation data, whereas previous applications [12, 13] require additional quantitative data like phosphoproteomic, ChIP-chip and transcriptomic measurements. Previous work focused on elucidating regulatory subnetworks or pathways potentially implicated in the process under study, rendering the downstream validation and use of the results less obvious. The simple and straightforward protein detection and ranking scheme presented here allows direct experimental testing of the predicted proteins. Moreover, the previously published methods were tailored to data obtained in Saccharomyces cerevisiae, which is to be attributed to the wealth of knowledge and high-throughput experimental results collected for this model organism. By applying our method successfully to a set of experimentally detected human proteins, we were able to show that the human interactome now approaches a level of completeness that enables the application of such graph-based prediction methods.

A key difference to the MSNet method is that a diffusion model tends to select additional proteins whenever they are close in the network to many input proteins. A Steiner tree represents a maximally sparse connecting structure between input proteins, which can be justified using an obvious parsimony argument. We deem the former approach more suitable for protein identification in global profiling experiments, whereas the Steiner tree approach, which assumes that the differentially regulated proteins tend to form a connected subnetwork, may be most suitable for data from differential proteomics. The fact that we were not able to predict the two additional proteins identified by our method using the MSNet method supports the idea that the two approaches may indeed have different application domains: The Steiner tree approach may be more suitable for “network-local” datasets typical for differential proteomics, whereas diffusion-based approaches may be better in the case of global datasets. The enrichment approach by Li et al. [16] can also be viewed as complementary to the Steiner approach, as it aims at complementing (typically already strongly connected) sets of input proteins by additional proteins in the same biological complex.

Although we could only test two of the 25 predicted proteins due to the limited amount of protein extract gathered from the SMC samples, the fact that we were able to clearly confirm those two proteins (beta-arrestins) experimentally still appears significant, given that the approach uses no knowledge that could have specifically favored the detection of these proteins. An explanation for the success of our prediction strategy may lie in the fact that it favors proteins that are interacting with many of the experimentally detected proteins in the PPI network. It can thus be understood as an extension of the ‘guilt-by-association’ rule, which is commonly used in protein function classification and prediction of disease-causing genes [23, 24].

4.2. Sensitivity of saturation DIGE versus the Steiner tree approach

The effect of DNase I on the novel proteins added by the Steiner tree approach was assessed by measuring levels of abundance of two confidently predicted Steiner node proteins, beta-arrestin 1 and beta-arrestin 2. These proteins showed such a strong differential abundance in SMC protein extracts that beta-arrestin 1 and beta-arrestin 2 were not at all detected in unaffected samples (Fig. 4B).

While the beta-arrestins were detected by the Steiner tree approach, their differential profile passed unnoticed by the experimental proteomic approach. Their biochemical properties (Suppl. Fig. 5) do not correspond to known biases or specific limitations of saturation DIGE technology. We verified that the bioinformatic analysis of DIGE images carried out by the SameSpots software should be able to detect and quantify differences in abundance levels of a magnitude as observed in the Western blots for the beta-arrestins. We also verified that the expected Mr and pI of the two beta-arrestins after DIGE labeling did not correspond to any of the spots that failed protein identification by MALDI-TOF MS. We therefore suspect that the beta-arrestins remained undetected in the experimental proteomic approach due to their low abundance in the SMC extracts. We note that, also for LC-MS/MS-based approaches, each beta arrestin would have likely generated only a single peak, as these proteins were undetectable even by Western blot in one set of SMC extracts – and would therefore not have been detected with different abundance levels by most standard data analysis approaches.

However, our and any other Steiner tree-based methods suffer from other biases and limitations. One of them could be called “region bias”. As the Steiner tree approach depends on connecting previously detected proteins in an experiment, it is unable to penetrate into regions of the protein-protein interaction network in which no proteins have been detected experimentally. Conversely, the uneven quality and coverage in current protein interaction databases [25] can cause biases against, or entirely prevent, the detection of certain proteins, for instance, those that have not yet been tested for interactions, which may also imply a slight bias against low abundance [26]. Similarly, as the edge weights of our method are biased towards including interactions with similar GO annotations, it is biased against unannotated proteins. Finally, other interactions than protein-protein interactions may be involved in the network propagation of molecular changes, and may have to be included in computational methods such as the one presented here.

We therefore consider the Steiner tree approach not an endpoint, but – akin to other bioinformatics methods – rather a tool for the generation and prioritization of hypotheses that can be experimentally validated by low- and medium-throughput experimental methods. The reason for the apparent effectiveness of the Steiner method may lie in the independence of the above biases relative to the biases of the experimental methods, a principle that may be key for the discovery of other large-scale data integration approaches as well.

4.3. Conclusions

When applied to proteins found by 2D-DIGE analysis, the computational Steiner tree approach we present here identified additional proteins that were subsequently validated using Western blots. The biochemical properties of the additional proteins did not correspond to the specific limitations of the 2D-DIGE platform, suggesting that the Steiner tree approach may be a simple, cost-effective, and generic computational tool that can also be useful on other platforms, such as LC-MS/MS used for differential proteomics experiments.

While network-based approaches are not free of their own limitations, their potential to predict significant numbers of additional proteins suggests that they might also be followed by highly sensitive, targeted, medium-throughput MS techniques like SRM. In the future, such strategies will be able to draw on increasingly complete and accurate interaction networks. Network-based approaches might therefore prove to be important new tools to extend the reach of purely experimental methods.

ABBREVIATIONS

ASMC

aortic smooth muscle cell

BIND

biomolecular interaction network database

BOND

biomolecular object network database

Cy

cyanine

DNase

deoxyribonuclease

GO

gene ontology

LIFT

laser induced fragmentation technique

PFF

peptide fragmentation fingerprint

PPI

protein-protein interaction

RNase

ribonuclease

SMC

smooth muscle cell

TCEP

tris (2-carboxyethyl) phosphine)