Abstract
Here we report a web server, the DelPhi web server, which utilizes DelPhi program to calculate electrostatic energies and the corresponding electrostatic potential and ionic distributions, and dielectric map. The server provides extra services to fix structural defects, as missing atoms in the structural file and allows for generation of missing hydrogen atoms. The hydrogen placement and the corresponding DelPhi calculations can be done with user selected force field parameters being either Charmm22, Amber98 or OPLS. Upon completion of the calculations, the user is given option to download fixed and protonated structural file, together with the parameter and Delphi output files for further analysis. Utilizing Jmol viewer, the user can see the corresponding structural file, to manipulate it and to change the presentation. In addition, if the potential map is requested to be calculated, the potential can be mapped onto the molecule surface. The DelPhi web server is available from http://compbio.clemson.edu/delphi_webserver.
Keywords: DelPhi, electrostatics, proteins, continuum models, electrostatic potential, Finite-Difference Poisson-Boltzmann solver
1. Introduction
Electrostatic force has profound role in molecular biology [1–4]. However, computing electrostatic properties of biological objects has always posed challenging and significant problems to the biomedical computational community [5, 6]. The main reason for this difficulty is that biological macromolecules are made of thousands/millions of atoms, with different size and partial charge. More importantly, these molecules perform their function in a water phase. Since the individual positions and orientations of the water molecules are not know a priori, modeling the water phase is not trivial.
The importance of electrostatic interactions and energies is illustrated by the fact that proteins, DNAs, and RNAs are made of charged atoms and frequently the entire molecule(s) carry significant net charge as well. Since all atoms have charge, along with the small (angstrom scale) distances that are prevalent in biological systems, the magnitude of electrostatic interactions is typically very large and frequently overpasses other energy components [7–9]. Also, many biological phenomena are predominantly electrostatic in origin as is salt-dependence of binding [10–13] and folding [14], pH-dependence[15, 16], and pKa shifts in proteins [17, 18] and RNAs [19]. Moreover, electrostatics is the only long range force that is present within biological systems. All of these factors illuminate the importance of electrostatics in biology, which ultimately leads to the necessity of determining accurate electrostatic energy of biological systems and objects within these systems.
A major difficulty that is posed within the area of electrostatic calculations is modeling the solvent surrounding the biological macromolecules. Two general approaches [20, 21] are currently being used, explicit [22, 23] and implicit models [24–27], although hybrid approaches were introduced as well [28–31]. Without focusing on the differences (both advantages and disadvantages) of these methods (interested readers are referred to excellent papers [20, 24, 32–35]), we briefly outline a particular resource, DelPhi [36, 37], version 5, which is based on the continuum approach and solves the Poisson-Boltzmann equation via the Finite-Difference algorithm [38]. The biological entities (proteins, DNAs, RNAs, lipid membranes and other small molecules), are treated at an atomistic level of detail and considered a low dielectric cavity region surrounded by a water phase modeled as a continuum media with a high dielectric constant. The mobile ions in the water phase are treated as non-interacting particles and their effect is calculated through the Boltzmann law. The corresponding equations are solved on a grid and the electrostatic components of a variety of energies are calculated [37, 39]. While being user-friendly, the usage of DelPhi (as a stand-alone software package) still requires the user to have a local computer, to be able to protonate the 3D structure of interest, and perhaps fix structural defects if they are present. Selection of the input parameters and output quantities can also be problematic for some inexperienced users. All of these factors motivated us to create a Delphi web server which is aimed to provide easy access to performing electrostatic calculations in biological systems without prior knowledge and without having a computational infrastructure in place.
With the development of modern internet connection technology, a large amount of web server based methods within computational biology have been on the rise [40–46]. These listed servers provide the biomedical community with tools for sequence alignment [47–51], structure alignment and prediction [52–55], estimation of the folding energy change upon mutations [56, 57], and many others [44, 53, 58, 59]. However, with the pronounced exception of the APBS server [43], the community was not offered a web-based tool for calculating electrostatic potential and energy of biological macromolecules. Here, we report such a web-based resource, which is built around the DelPhi program [25, 36]. The Delphi web server is intended to provide an easily accessible, user friendly method for calculating electrostatic parameters and energies of systems made of biological macromolecules and objects. It allows the usage of four different force field parameters, offers fixing structural errors, and builds up hydrogen atoms with the corresponding 3D structure of the molecule(s). Our newly developed DelPhi web server gives any user the capability of performing extensive electrostatic calculations with automated, fast runs, coupled with support and data analysis. The user receives a package of their results along with the needed parameter and PDB files in both human-readable and technical formats. By providing this free and easily accessible service, the field of biological electrostatic calculations can be performed with ease and minimal, if any, complications. The 3D structure of the biological macromolecule selected by the user is visualized and the user is given options to choose different presentations and to map the calculated potential map onto molecular surface.
2. DelPhi web server algorithm and architecture
2.1 Overview of the methodology of computing electrostatic energies and potential with DelPhi
In order for a successful completion of a DelPhi run, at minimum four files are needed. The input files that are needed for the web server are as follows: the users PDB file, a DelPhi format specific parameter file, and the charge and size files with force field parameters. The PDB file must be in the conventional PDB format, however, it must contain all hydrogen atoms, along with any missing atoms to assure correct partial charges assignment. The online web server that is presented in this paper provides the user with the option to utilize additional software for these extra functions. The software that is provided in conjunction with the DelPhi web server are packages called “profix” [60] (a software module within the JACKAL package, http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software:Jackal_General_Description), which predicts and places any missing atoms/residues, and the TINKER Molecular Dynamics Software [61, 62] for inserting all missing hydrogen atoms.
It is necessary for DelPhi to have a force field’s charge and size parameters for each atom. These parameter files are provided within the web server application, but the user also has the ability to upload his or her own. The provided files that are available for use within the web server are Amber98 [63], Charmm22 [64], OPLS [65–67], and PARSE [68, 69] force field parameters. The user should use caution with using their own charge/size files, however, since these files must match with what was used for the predicting methods and/or the molecular dynamics software that was used.
The core of the DelPhi application’s parameter files is the DelPhi format file. This parameter file specifies all of the needed values/parameters that are used within the DelPhi algorithm. These minimum specifiers are as follows: grid scale, percentage fill of grid by molecule, interior and exterior dielectric constants, probe radius, salt concentration, boundary conditions, and a convergence criterion. These values can be chosen from a default list (provided if the user is unsure or new to choosing these values) or can be manually entered for his or her specific run. DelPhi also has various energies that can be outputted which are also specified within this file. The available energies that can be calculated are: coulombic, solvation, and grid energies. DelPhi builds molecular surface according to the Lee and Richard’s model. Detailed description of all parameters and functions available in DelPhi can be found in DelPhi manual (http://compbio.clemson.edu/delphi.html).
2.2 Architecture of DelPhi web server
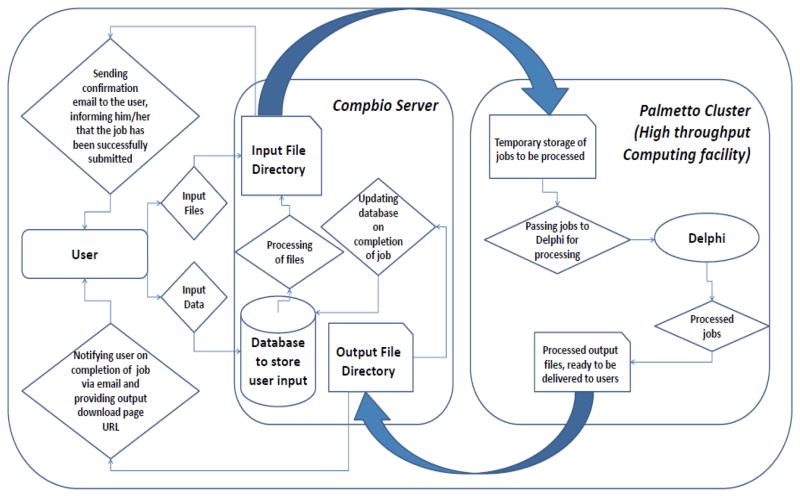
The web server follows a client-server architecture built on PHP[70] and HTML[71]. Various Perl[72] scripts are present to maximize utilization of the web server’s resources by the client. The main work-flow of the server can be broadly classified into two parts based on its visibility to the end users, namely (a) the client facing server, and (b) the high performance computational server. The overall web server work-flow is shown in Figure 1. On the end-user facing server side, users fill up details as text input and file uploads. The input text and files get stored on Compbio server, subsequent processing is done on it and the files along with relevant data are then passed to the Palmetto Cluster (http://citi.clemson.edu/training_palm) for the energy calculation. Meanwhile, a confirmation email is sent to the user informing him/her on successful submission of their job. Once the files are on the Palmetto cluster, scripts will pass the jobs on queue for processing on the cluster on a periodic basis. When a job is processed, another script, also running at a certain time-interval, will take those files along with the output, and pass it back to Compbio server. Processed jobs, upon reaching Compbio server, will be processed by another script (again, running at a specific time-interval), moved to a different directory wherefrom users will be able to access and download them. Simultaneously, users will be notified via email of a successful completion of their jobs and relevant output download link will be provided to them. Below we describe these components separately.
Figure 1.
Architecture of Delphi web-server (http://compbio.clemson.edu/delphi_webserver/).
2.3 The client facing server
It is responsible for handling user data storage, user uploaded file storage, notification of successful completion of submission of request, notification upon completion of job and finally displaying the result. User input related data was stored using MySQL[73] for fast and efficient retrieval as well as reliable storage. The overall architecture of the application is general (with regards to application modification), robust, and allows users to have a high level of flexibility in regard of input and output options.
When the end user is interacting with the server, the user fills up pertinent details as text input as well as uploading various files. As for text input, the user needs to provide the following details (a) which portion of the PDB file the user wishes to have Delphi running the calculations for (ATOM and/or HETATM), (b) whether to run profix and TINKER, and (c) choice of Delphi parameters (which can be from a default set, provided by us, or manually given).
Also, the user needs to upload his/her PDB file and choose from a list of default charge and size force field parameters (Amber98, Charmm22, OPLS, and Parse) or, for added flexibility, the user has the option to upload their own charge and size files. The user is given an option to request linear or non-linear PB equation to be solved.
Finally, the user is given the option for choosing output based on the different types of energies to be calculated (for the time being, this feature is limited to Coulombic, Solvation and Grid Energies). Also, for the visualization purpose of output, the user can choose from a potential or dielectric constant map.
Once all the inputs are fed into the system correctly, an email is dynamically sent to the user confirming the order and providing him/her with the request reference number which is used for identifying each request uniquely.
2.4 High-performance computing (HPC) server
This server gets all inputs necessary for a successful Delphi run. Cron jobs take the inputs per request, adds it to the queue of the jobs to be processed on the Palmetto high-performance computing facility (http://citi.clemson.edu/training_palm). Each node has 4GB RAM capable of handling Delphi runs up to approximately grid size of 500. Once the jobs are processed, another cron job runs to collect the results of Delphi run along with other necessary files. There is no limitation of the length of the execution time.
2.5 Downloadable files, results and visualization
Upon completion of the calculations, the user receives email notification that the job is finished along with ID number and a link. Clicking on the link, the user is directed to the DelPhi web server download and visualization page. On this page, the user are given options to download the results, protonated and fixed PDB files and parameter files used in this particular job. In addition, the page utilized Jmol which is a 3D Java viewer for chemical structure and users can render and manipulate the structure of molecules with great flexibility (Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/). If the user had requested potential map to be calculated, then the potential map in “cube” format is also available for download and for visualization. By clicking on the potential map file, the user initiates procedure which results in mapping the potential onto molecular surface of the corresponding biological macromolecule.
3. Tests of DelPhi accuracy
The core of the DelPhi web server is the DelPhi program, which provides numerical solution of PB equation and delivers the corresponding electrostatic energies. In this section we benchmark DelPhi calculated energies against analytical solutions and test DelPhi energies for convergence, if analytical solution is not available. Following the work of Guowei Wei and co-workers [74, 75], the results will be discussed in terms of accuracy order as well.
3.1 Testing the accuracy of the calculated energies against analytical solution
In this section we will consider simple systems for which analytical solution for the electrostatic component of the energy is available. Although such systems are typically made of objects with regular shapes, from point of view of the grid algorithm, they are equally difficult to model as irregularly shaped biomolecules.
3.1.1. Electrostatic component of the solvation (Born) energy of a sphere
Consider an atom (sphere) in a solvent, then using the Born formula, the electrostatic component of solvation energy is given by [76]:
| (1) |
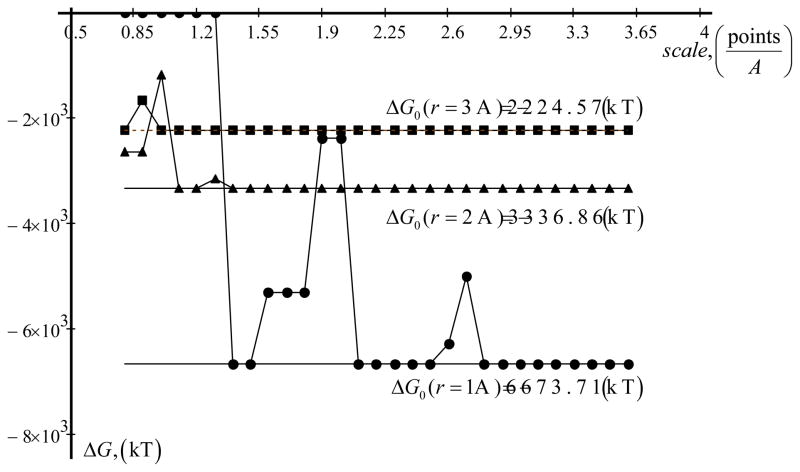
where Q and r is charge and radius of the atom, εint - is interior dielectric constant. The solvent dielectric constant is εext. The numerical calculations from Delphi are shown on Fig. 2. Three different cases were calculated, corresponding to three different radii (Fig. 2). In all cases, the increase of the scale (grid resolution) makes DelPhi energies closer to the corresponding analytical solutions. After scale larger than 3 grids/A, in all cases, the energies calculated with DelPhi match exactly the analytical solutions. As to be expected, the solvation energy of larger spheres (larger radius) is easier to calculate.
Figure 2.
Solvation energy. Q = 10·e, where e is elementary charge. εint = 4, εext= 80. Analytical value ΔG0 is calculated with eq. (1).
3.1.2. Spherical cavity immersed in high dielectric medium
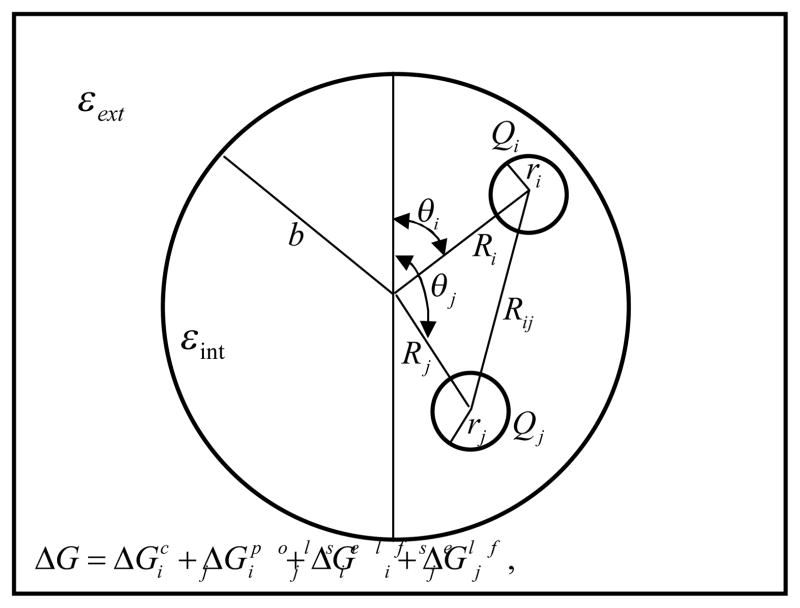
Following previously published work of Honig and co-workers [1], let’s consider a spherical protein within a high dielectric medium (Fig. 3) without ions. Within the sphere there are two charges, shown as Qi and Qj in Fig. 3. The total electrostatics energy of the molecule is [1]:
Figure 3.
A spherical protein with interior dielectric constant εint within a high dielectric medium with εext. Charge Qi has a radius ri and located at the point 12 (Ri, θi). Distance between charges is Rij. b is the radius of spherical region.
where is the pairwise coulomb interaction energy, is the pairwise polarization interaction energy and is the total self-energy. The formulas for the corresponding energy terms are taken from Ref. [1] and are provided below:
| (3) |
| (4) |
| (5) |
Where
| (6) |
and Pn (cos (θi – θj)) are Legendre polynomials.
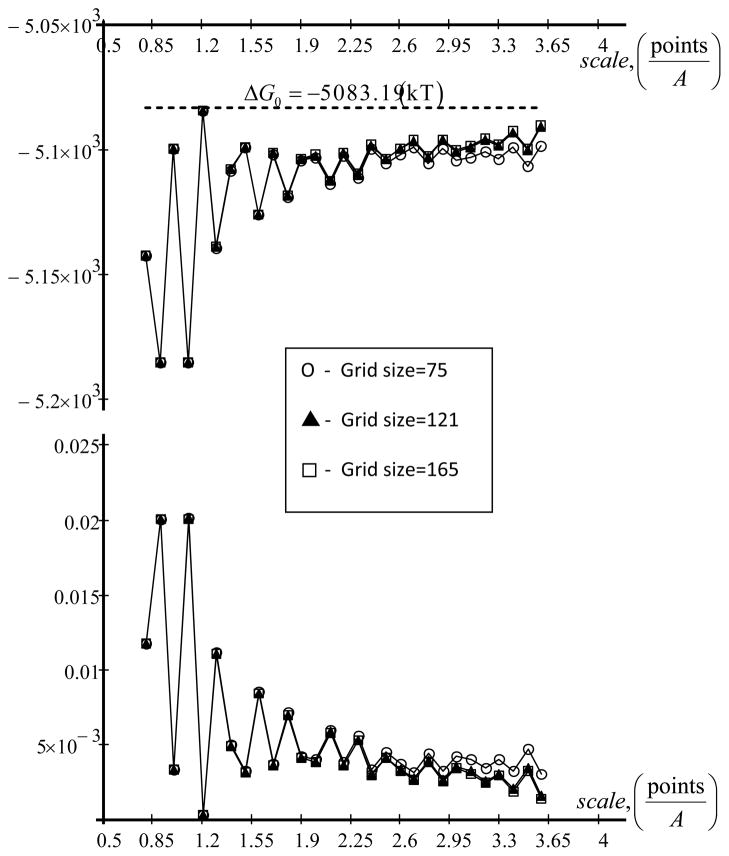
The results calculated with DelPhi for two charges in the spherical region are shown in Fig. 4 and compared with the corresponding analytical solution. Similar observation as above can be made: as the scale increases (the grid resolution) the numerical solutions quickly approaches the analytical one. The results are practically independent on grid size and at scale about 4 grids/A, the relative error is less than 0.5%. The accuracy orders are 0.44 and 1.36, respectively, for mesh size h=0.25 and h=0.125, respectively. For accuracy order details for other PB solvers, see Refs. [74, 75].
Figure 4.
Top - dependence of total energy of two charges ΔG in a spherical protein in water from scale (grid size fixed) is shown. Bottom -the relative error. The parameters taken in to the calculations are as follow: Q1 = Q1 = 10·e. , θ1 = π/4, θ2 = 3π/4, b=10A and r=1A. ΔG0 = −5083.19(kT) is analytical solution according [1].
3.1.3. Electrostatic component of solvation energy of a sphere approaching semi-infinite dielectric region
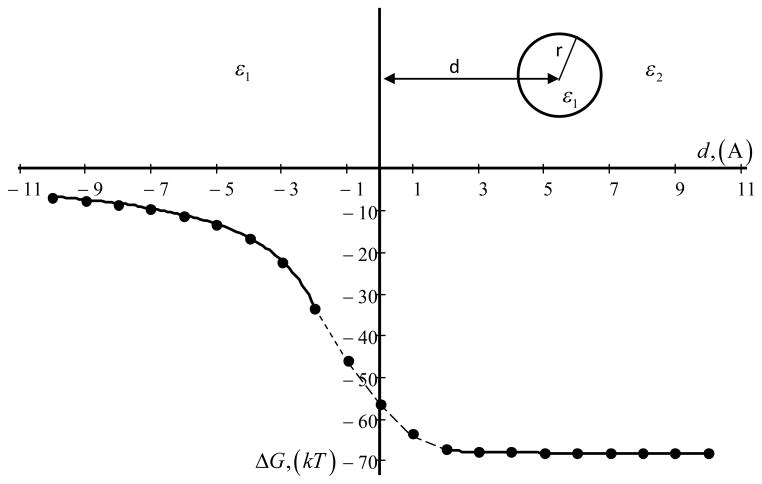
Consider 3D case such that the space d < 0 is occupied by homogeneous dielectric medium with low dielectric constant, ε1, while the region d > 0 is taken by high dielectric homogeneous medium of ε2 (Fig. 5). A sphere with a low dielectric constant ε1 is initially positioned in region with high dielectric constant and stepwise moves into the region of low dielectric constant (Fig. 5).
Figure 5.
Total energy of a spherical shell of charge as a function of it position relative to a planar dielectric boundary. ε2 = 80, ε1 = 2, r = 2A. Solid line is an analytical result (7) and (8), points are result from Delphi. Of course equations (7) and (8) are not valid for overlapping area in the region −r < d < r.
In the space d > 0 (right side in Fig. 5) the total energy ΔG is the sum a solvation energy (1), (the first term in (7)) and polarization interaction with boundary (the second term in (7)) (see [1]).
| (7) |
When d < 0 (left side in Fig. 5) the total energy ΔG is only a polarization energy.
| (8) |
The results from DelPhi calculations are shown with filled dots in Fig. 5, while the analytical solution (if available) is given by a solid line. It can be seen that numerical solutions exactly match expected values.
3.2 Testing DelPhi energies for convergence
In this section we will calculate the total electrostatic energy of real biological macromolecules. Obviously in such cases, the analytical solution is not available. However, we will investigate the sensitivity of the calculated energies with respect to scale (the grid resolution).
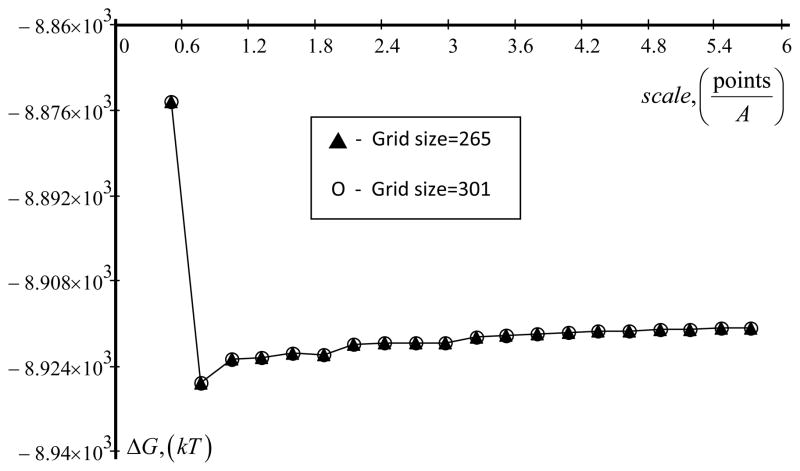
3.2.1. Protein of typical size (barstar)
Barstar is a protein made of 90 amino acids and represent a typical case of a medium protein. The 3D structure is experimentally available, PDB ID 1A19 [77]. The structure was submitted to DelPhi web server and the protons were added with TINKER.
Figure 6 shows the results from numerical calculations carried out with DelPhi web server at different scales and two grid sizes. One can see that the grid size, being large in this case, does not affect the results. Increasing of the scale makes the output energies almost independent of the scale and at scale > 3.5 grids/A the calculated energies are practically constant. The convergence order is 0.94 at mesh size 0.5, taking as a reference the energy obtained at h=0.25.
Figure 6.
Dependence of total energy of real protein (PDB ID 1A19)ΔG from scale (grid size fixed) is shown. Parameters are: internal dielectric permeability (indi) is 4, external dielectric permeability (exdi) is 80 and a radius of probe molecule (prbrad) is 1.4. Force field parameters is Parse set.
3.2.2. The largest protein in PDB database
By performing a search on Protein Data Base (PDB) [78], we identified the largest protein in terms of longest polypeptide chain. It is a crystal structure of mammalian fatty acid synthase (ID 2VZ8) with contains 29969 atoms (1962 amino acids). Fatty acids are aliphatic acids fundamental to energy production and storage, cellular structure and as intermediates in the biosynthesis of hormones and other biologically important molecules.
Figure 7 shows the calculated total electrostatic energy of fatty acid synthase. At low grid resolution (small scale) the results fluctuate with the change of the scale, but after reaching scale of about 1.7 grids/A, the curve flattens out and the calculated energy is almost scale independent.
Figure 7.
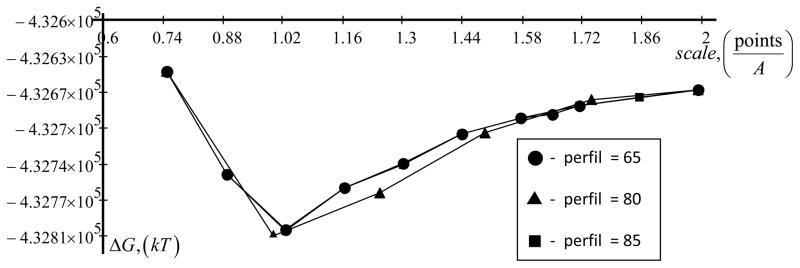
Dependence of total energy of largest protein (PDB ID 2VZ8)ΔG as a function of scale is shown. A percentage of the object longest linear dimension to the lattice linear dimension size (perfil) is 65, 80 and 85. Parameters are: internal dielectric permeability (indi) is 2, external dielectric permeability (exdi) is 80 and a radius of probe molecule (prbrad) is 1.4. Force field parameters are Charmm22.
4. Availability
The web server is available from URL (http://compbio.clemson.edu/delphi_webserver). It was tested on various web browsers as Opera 11.50, Chrome 12.0, Firefox 3.6+, Safari 5.0, Internet Explorer 8.0+ and the following operating systems: Windows XP, Windows Vista, Windows 7, CentOS 5, Ubuntu 10.10.
Acknowledgments
The authors thank Barry Honig for the continuous support and encouragement. The work was supported by a grant from the Institute of General Medical Sciences, National Institutes of Health, award number 1R01GM093937-01.
References
- 1.Gilson MK, Rashin A, Fine R, Honig B. On the calculation of electrostatic interactions in proteins. J Mol Biol. 1985;184(3):503–16. doi: 10.1016/0022-2836(85)90297-9. [DOI] [PubMed] [Google Scholar]
- 2.Honig B, Nicholls A. Classical electrostatics in biology and chemistry. Science. 1995;268(5214):1144–9. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 3.Russell ST, Warshel A. Calculations of electrostatic energies in proteins. The energetics of ionized groups in bovine pancreatic trypsin inhibitor. J Mol Biol. 1985;185(2):389–404. doi: 10.1016/0022-2836(85)90411-5. [DOI] [PubMed] [Google Scholar]
- 4.Zhang Z, Witham S, Alexov E. On the role of electrostatics in protein-protein interactions. Phys Biol. 2011;8(3):035001. doi: 10.1088/1478-3975/8/3/035001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Harvey SC. Treatment of electrostatic effects in macromolecular modeling. Proteins. 1989;5(1):78–92. doi: 10.1002/prot.340050109. [DOI] [PubMed] [Google Scholar]
- 6.Lebard DN, Matyushov DV. Protein-water electrostatics and principles of bioenergetics. Phys Chem Chem Phys. 2010;12(47):15335–48. doi: 10.1039/c0cp01004a. [DOI] [PubMed] [Google Scholar]
- 7.Guest WC, Cashman NR, Plotkin SS. Electrostatics in the stability and misfolding of the prion protein: salt bridges, self energy, and solvation. Biochem Cell Biol. 2010;88(2):371–81. doi: 10.1139/o09-180. [DOI] [PubMed] [Google Scholar]
- 8.Laederach A, Shcherbakova I, Jonikas MA, Altman RB, Brenowitz M. Distinct contribution of electrostatics, initial conformational ensemble, and macromolecular stability in RNA folding. Proc Natl Acad Sci U S A. 2007;104(17):7045–50. doi: 10.1073/pnas.0608765104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Avbelj F, Fele L. Role of main-chain electrostatics, hydrophobic effect and side-chain conformational entropy in determining the secondary structure of proteins. J Mol Biol. 1998;279(3):665–84. doi: 10.1006/jmbi.1998.1792. [DOI] [PubMed] [Google Scholar]
- 10.Bertonati C, Honig B, Alexov E. Poisson-Boltzmann calculations of nonspecific salt effects on protein-protein binding free energies. Biophysical Journal. 2007;92(6):1891–1899. doi: 10.1529/biophysj.106.092122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jensen JH. Calculating pH and salt dependence of protein-protein binding. Curr Pharm Biotechnol. 2008;9(2):96–102. doi: 10.2174/138920108783955146. [DOI] [PubMed] [Google Scholar]
- 12.Spencer DS, Xu K, Logan TM, Zhou HX. Effects of pH, salt, and macromolecular crowding on the stability of FK506-binding protein: an integrated experimental and theoretical study. J Mol Biol. 2005;351(1):219–32. doi: 10.1016/j.jmb.2005.05.029. [DOI] [PubMed] [Google Scholar]
- 13.Talley K, Kundrotas P, Alexov E. Modeling salt dependence of protein-protein association: Linear vs non-linear Poisson-Boltzmann equation. Communications in Computational Physics. 2008;3(5):1071–1086. [Google Scholar]
- 14.Yang AS, Honig B. On the pH dependence of protein stability. J Mol Biol. 1993;231(2):459–74. doi: 10.1006/jmbi.1993.1294. [DOI] [PubMed] [Google Scholar]
- 15.Mitra RC, Zhang Z, Alexov E. In silico modeling of pH-optimum of protein-protein binding. Proteins-Structure Function and Bioinformatics. 2011;79(3):925–936. doi: 10.1002/prot.22931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alexov E. Numerical calculations of thepH of maximal protein stability. The effect of the sequence composition and three-dimensional structure. Eur J Biochem. 2004;271(1):173–85. doi: 10.1046/j.1432-1033.2003.03917.x. [DOI] [PubMed] [Google Scholar]
- 17.Yang AS, Gunner MR, Sampogna R, Sharp K, Honig B. On the calculation of pKas in proteins. Proteins. 1993;15(3):252–65. doi: 10.1002/prot.340150304. [DOI] [PubMed] [Google Scholar]
- 18.Georgescu RE, Alexov EG, Gunner MR. Combining conformational flexibility and continuum electrostatics for calculating pK(a)s in proteins. Biophysical Journal. 2002;83(4):1731–1748. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tang CL, Alexov E, Pyle AM, Honig B. Calculation of pK(a)s in RNA: On the structural origins and functional roles of protonated nucleotides. Journal of Molecular Biology. 2007;366(5):1475–1496. doi: 10.1016/j.jmb.2006.12.001. [DOI] [PubMed] [Google Scholar]
- 20.Ma B, Nussinov R. Explicit and implicit water simulations of a beta-hairpin peptide. Proteins. 1999;37(1):73–87. doi: 10.1002/(sici)1097-0134(19991001)37:1<73::aid-prot8>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 21.Zhou R. Free energy landscape of protein folding in water: explicit vs. implicit solvent. Proteins. 2003;53(2):148–61. doi: 10.1002/prot.10483. [DOI] [PubMed] [Google Scholar]
- 22.Druchok M, Vlachy V, Dill KA. Explicit-water molecular dynamics study of a short-chain 3,3 ionene in solutions with sodium halides. J Chem Phys. 2009;130(13):134903. doi: 10.1063/1.3078268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kony DB, Damm W, Stoll S, van Gunsteren WF, Hunenberger PH. Explicit-solvent molecular dynamics simulations of the polysaccharide schizophyllan in water. Biophys J. 2007;93(2):442–55. doi: 10.1529/biophysj.106.086116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baker NA. Poisson-Boltzmann methods for biomolecular electrostatics. Methods Enzymol. 2004;383:94–118. doi: 10.1016/S0076-6879(04)83005-2. [DOI] [PubMed] [Google Scholar]
- 25.Gilson MK, Honig B. Calculation of the total electrostatic energy of a macromolecular system: solvation energies, binding energies, and conformational analysis. Proteins. 1988;4(1):7–18. doi: 10.1002/prot.340040104. [DOI] [PubMed] [Google Scholar]
- 26.Lee MC, Yang R, Duan Y. Comparison between Generalized-Born and Poisson-Boltzmann methods in physics-based scoring functions for protein structure prediction. J Mol Model. 2005;12(1):101–10. doi: 10.1007/s00894-005-0013-y. [DOI] [PubMed] [Google Scholar]
- 27.Grochowski P, Trylska J. Continuum molecular electrostatics, salt effects, and counterion binding--a review of the Poisson-Boltzmann theory and its modifications. Biopolymers. 2008;89(2):93–113. doi: 10.1002/bip.20877. [DOI] [PubMed] [Google Scholar]
- 28.Fogolari F, Zuccato P, Esposito G, Viglino P. Biomolecular electrostatics with the linearized Poisson-Boltzmann equation. Biophys J. 1999;76(1 Pt 1):1–16. doi: 10.1016/S0006-3495(99)77173-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brancato G, Rega N, Barone V. A hybrid explicit/implicit solvation method for first-principle molecular dynamics simulations. J Chem Phys. 2008;128(14):144501. doi: 10.1063/1.2897759. [DOI] [PubMed] [Google Scholar]
- 30.Kelly CP, Cramer CJ, Truhlar DG. Adding explicit solvent molecules to continuum solvent calculations for the calculation of aqueous acid dissociation constants. J Phys Chem A. 2006;110(7):2493–9. doi: 10.1021/jp055336f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lieske SF, Yang B, Eldefrawi ME, MacKerell AD, Jr, Wright J. (−)-3 beta-Substituted ecgonine methyl esters as inhibitors for cocaine binding and dopamine uptake. J Med Chem. 1998;41(6):864–76. doi: 10.1021/jm970025h. [DOI] [PubMed] [Google Scholar]
- 32.Spaeth JR, I, Kevrekidis G, Panagiotopoulos AZ. A comparison of implicit-and explicit-solvent simulations of self-assembly in block copolymer and solute systems. J Chem Phys. 2011;134(16):164902. doi: 10.1063/1.3580293. [DOI] [PubMed] [Google Scholar]
- 33.Tan C, Yang L, Luo R. How well does Poisson-Boltzmann implicit solvent agree with explicit solvent? A quantitative analysis. J Phys Chem B. 2006;110(37):18680–7. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 34.Rod TH, Rydberg P, Ryde U. Implicit versus explicit solvent in free energy calculations of enzyme catalysis: Methyl transfer catalyzed by catechol O-methyltransferase. J Chem Phys. 2006;124(17):174503. doi: 10.1063/1.2186635. [DOI] [PubMed] [Google Scholar]
- 35.Pham TT, Schiller UD, Prakash JR, Dunweg B. Implicit and explicit solvent models for the simulation of a single polymer chain in solution: Lattice Boltzmann versus Brownian dynamics. J Chem Phys. 2009;131(16):164114. doi: 10.1063/1.3251771. [DOI] [PubMed] [Google Scholar]
- 36.Rocchia W, Sridharan S, Nicholls A, Alexov E, Chiabrera A, Honig B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. Journal of Computational Chemistry. 2002;23(1):128–137. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 37.Rocchia W, Alexov E, Honig B. Extending the applicability of the nonlinear Poisson-Boltzmann equation: Multiple dielectric constants and multivalent ions. Journal of Physical Chemistry B. 2001;105(28):6507–6514. [Google Scholar]
- 38.Warwicker J, Watson HC. Calculation of the electric potential in the active site cleft due to alpha-helix dipoles. J Mol Biol. 1982;157(4):671–9. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]
- 39.Sharp KA, Honig B. Electrostatic interactions in macromolecules: theory and applications. Annu Rev Biophys Biophys Chem. 1990;19:301–32. doi: 10.1146/annurev.bb.19.060190.001505. [DOI] [PubMed] [Google Scholar]
- 40.Rodriguez-Soca Y, Munteanu CR, Dorado J, Pazos A, Prado-Prado FJ, Gonzalez-Diaz H. Trypano-PPI: a web server for prediction of unique targets in trypanosome proteome by using electrostatic parameters of protein-protein interactions. J Proteome Res. 2010;9(2):1182–90. doi: 10.1021/pr900827b. [DOI] [PubMed] [Google Scholar]
- 41.Richter S, Wenzel A, Stein M, Gabdoulline RR, Wade RC. web PIPSA: a web server for the comparison of protein interaction properties. Nucleic Acids Res. 2008;36(Web Server issue):W276–80. doi: 10.1093/nar/gkn181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Shazman S, Celniker G, Haber O, Glaser F, Mandel-Gutfreund Y. Patch Finder Plus (PFplus): a web server for extracting and displaying positive electrostatic patches on protein surfaces. Nucleic Acids Res. 2007;35(Web Server issue):W526–30. doi: 10.1093/nar/gkm401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Unni S, Huang Y, Hanson RM, Tobias M, Krishnan S, Li WW, Nielsen JE, Baker NA. Web servers and services for electrostatics calculations with APBS and PDB2PQR. J Comput Chem. 2011;32(7):1488–91. doi: 10.1002/jcc.21720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Miteva MA, Tuffery P, Villoutreix BO. PCE: web tools to compute protein continuum electrostatics. Nucleic Acids Res. 2005;33(Web Server issue):W372–5. doi: 10.1093/nar/gki365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Jo S, Vargyas M, Vasko-Szedlar J, Roux B, Im W. PBEQ-Solver for online visualization of electrostatic potential of biomolecules. Nucleic Acids Res. 2008;36(Web Server issue):W270–5. doi: 10.1093/nar/gkn314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kinoshita K, Murakami Y, Nakamura H. eF-seek: prediction of the functional sites of proteins by searching for similar electrostatic potential and molecular surface shape. Nucleic Acids Res. 2007;35(Web Server issue):W398–402. doi: 10.1093/nar/gkm351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Altschul SF, Gertz EM, Agarwala R, Schaffer AA, Yu YK. PSI-BLAST pseudocounts and the minimum description length principle. Nucleic Acids Res. 2009;37(3):815–24. doi: 10.1093/nar/gkn981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Altschul SF, Koonin EV. Iterated profile searches with PSI-BLAST--a tool for discovery in protein databases. Trends Biochem Sci. 1998;23(11):444–7. doi: 10.1016/s0968-0004(98)01298-5. [DOI] [PubMed] [Google Scholar]
- 49.Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25(17):3389–402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lee MM, Chan MK, Bundschuh R. SIB-BLAST: a web server for improved delineation of true and false positives in PSI-BLAST searches. Nucleic Acids Res. 2009;37(Web Server issue):W53–6. doi: 10.1093/nar/gkp301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li Y, Chia N, Lauria M, Bundschuh R. A performance enhanced PSI-BLAST based on hybrid alignment. Bioinformatics. 2011;27(1):31–7. doi: 10.1093/bioinformatics/btq621. [DOI] [PubMed] [Google Scholar]
- 52.Norel R, Petrey D, Honig B. PUDGE: a flexible, interactive server for protein structure prediction. Nucleic Acids Res. 2010;38(Web Server issue):W550–4. doi: 10.1093/nar/gkq475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.MacCallum RM, Kelley LA, Sternberg MJ. SAWTED: structure assignment with text description--enhanced detection of remote homologues with automated SWISS-PROT annotation comparisons. Bioinformatics. 2000;16(2):125–9. doi: 10.1093/bioinformatics/16.2.125. [DOI] [PubMed] [Google Scholar]
- 54.Roy A, Kucukural A, Zhang Y. I-TASSER: a unified platform for automated protein structure and function prediction. Nat Protoc. 2010;5(4):725–38. doi: 10.1038/nprot.2010.5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang Y. I-TASSER: fully automated protein structure prediction in CASP8. Proteins. 2009;77(Suppl 9):100–13. doi: 10.1002/prot.22588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Schymkowitz J, Borg J, Stricher F, Nys R, Rousseau F, Serrano L. The FoldX web server: an online force field. Nucleic Acids Res. 2005;33(Web Server issue):W382–8. doi: 10.1093/nar/gki387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Dehouck Y, Kwasigroch JM, Gilis D, Rooman M. PoPMuSiC 2.1: a web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinformatics. 2011;12(1):151. doi: 10.1186/1471-2105-12-151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Liu IH, Lo YS, Yang JM. PAComplex: a web server to infer peptide antigen families and binding models from TCR-pMHC complexes. Nucleic Acids Res. 2011 doi: 10.1093/nar/gkr434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Macindoe G, Mavridis L, Venkatraman V, Devignes MD, Ritchie DW. HexServer: an FFT-based protein docking server powered by graphics processors. Nucleic Acids Res. 2010;38(Web Server issue):W445–9. doi: 10.1093/nar/gkq311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Petrey D, Xiang Z, Tang CL, Xie L, Gimpelev M, Mitros T, Soto CS, Goldsmith-Fischman S, Kernytsky A, Schlessinger A, Koh IY, Alexov E, Honig B. Using multiple structure alignments, fast model building, and energetic analysis in fold recognition and homology modeling. Proteins. 2003;53(Suppl 6):430–5. doi: 10.1002/prot.10550. [DOI] [PubMed] [Google Scholar]
- 61.Ren P, Ponder JW. Tinker polarizable atomic multipole force field for proteins. Abstracts of Papers of the American Chemical Society. 2002;224:U473–U473. [Google Scholar]
- 62.Ren PY, Ponder JW. Polarizable atomic multipole water model for molecular mechanics simulation. Journal of Physical Chemistry B. 2003;107(24):5933–5947. [Google Scholar]
- 63.Ponder JW, Case DA. Force fields for protein simulations. Adv Protein Chem. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 64.Brooks BR, Brooks CL, 3rd, Mackerell AD, Jr, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S, Caflisch A, Caves L, Cui Q, Dinner AR, Feig M, Fischer S, Gao J, Hodoscek M, Im W, Kuczera K, Lazaridis T, Ma J, Ovchinnikov V, Paci E, Pastor RW, Post CB, Pu JZ, Schaefer M, Tidor B, Venable RM, Woodcock HL, Wu X, Yang W, York DM, Karplus M. CHARMM: the biomolecular simulation program. J Comput Chem. 2009;30(10):1545–614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kahn K, Bruice TC. Parameterization of OPLS-AA force field for the conformational analysis of macrocyclic polyketides. Journal of Computational Chemistry. 2002;23(10):977–96. doi: 10.1002/jcc.10051. [DOI] [PubMed] [Google Scholar]
- 66.Kony D, Damm W, Stoll S, Van Gunsteren WF. An improved OPLS-AA force field for carbohydrates. Journal of Computational Chemistry. 2002;23(15):1416–29. doi: 10.1002/jcc.10139. [DOI] [PubMed] [Google Scholar]
- 67.Xu Z, Luo HH, Tieleman DP. Modifying the OPLS-AA force field to improve hydration free energies for several amino acid side chains using new atomic charges and an off-plane charge model for aromatic residues. Journal of Computational Chemistry. 2007;28(3):689–97. doi: 10.1002/jcc.20560. [DOI] [PubMed] [Google Scholar]
- 68.Sitkoff D, Lockhart DJ, Sharp KA, Honig B. Calculation of electrostatic effects at the amino terminus of an alpha helix. Biophys J. 1994;67(6):2251–60. doi: 10.1016/S0006-3495(94)80709-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Sitkoff D, Sharp KA, Honig B. Correlating solvation free energies and surface tensions of hydrocarbon solutes. Biophys Chem. 1994;51(2–3):397–403. doi: 10.1016/0301-4622(94)00062-x. discussion 404–9. [DOI] [PubMed] [Google Scholar]
- 70.Preprocessor, P.H. Available from: http://www.php.net.
- 71.Language, H.H.M.-u. Available from: http://www.w3.org/TR/html401/
- 72.Perl. Available from: http://www.perl.org/
- 73.database, M.T.w.s.m.p.o.-s. Available from: http://www.mysql.com/
- 74.Chen DA, Chen Z, Chen CJ, Geng WH, Wei GW. Software News and Update MIBPB: A Software Package for Electrostatic Analysis. Journal of Computational Chemistry. 2011;32(4):756–770. doi: 10.1002/jcc.21646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Geng WH, Yu SN, Wei GW. Treatment of charge singularities in implicit solvent models. Journal of Chemical Physics. 2007;127(11) doi: 10.1063/1.2768064. [DOI] [PubMed] [Google Scholar]
- 76.Kim JI, Duschner H, Born HJ, Hashimoto T. Preferential Solvation of Single Ions -Determination of Standard Free-Energies of Transfer for U-(+4), Uo2-(+2), Ucl6-(−2) and Uo2cl4-(−2) Ions from Water to Mixed Aqueous-Ethanol Solvents. Zeitschrift Fur Physikalische Chemie-Frankfurt. 1976;103(1–4):15–30. [Google Scholar]
- 77.Ratnaparkhi GS, Ramachandran S, Udgaonkar JB, Varadarajan R. Discrepancies between the NMR and X-ray structures of uncomplexed barstar: analysis suggests that packing densities of protein structures determined by NMR are unreliable. Biochemistry. 1998;37(19):6958–66. doi: 10.1021/bi972857n. [DOI] [PubMed] [Google Scholar]
- 78.Kouranov A, Xie L, de la Cruz J, Chen L, Westbrook J, Bourne PE, Berman HM. The RCSB PDB information portal for structural genomics. Nucleic Acids Res. 2006;34(Database issue):D302–5. doi: 10.1093/nar/gkj120. [DOI] [PMC free article] [PubMed] [Google Scholar]