This work presents a machine learning–based method for transcriptome analysis via comparison of gene coexpression networks, which outperforms traditional statistical tests at identifying stress-related genes. Analysis of an Arabidopsis stress expression data set led to the prediction of candidate stress-related genes showing expression and network changes in response to multiple abiotic stresses.
Abstract
Machine learning (ML) is an intelligent data mining technique that builds a prediction model based on the learning of prior knowledge to recognize patterns in large-scale data sets. We present an ML-based methodology for transcriptome analysis via comparison of gene coexpression networks, implemented as an R package called machine learning–based differential network analysis (mlDNA) and apply this method to reanalyze a set of abiotic stress expression data in Arabidopsis thaliana. The mlDNA first used a ML-based filtering process to remove nonexpressed, constitutively expressed, or non-stress-responsive “noninformative” genes prior to network construction, through learning the patterns of 32 expression characteristics of known stress-related genes. The retained “informative” genes were subsequently analyzed by ML-based network comparison to predict candidate stress-related genes showing expression and network differences between control and stress networks, based on 33 network topological characteristics. Comparative evaluation of the network-centric and gene-centric analytic methods showed that mlDNA substantially outperformed traditional statistical testing–based differential expression analysis at identifying stress-related genes, with markedly improved prediction accuracy. To experimentally validate the mlDNA predictions, we selected 89 candidates out of the 1784 predicted salt stress–related genes with available SALK T-DNA mutagenesis lines for phenotypic screening and identified two previously unreported genes, mutants of which showed salt-sensitive phenotypes.
INTRODUCTION
Cellular activities and biological functions are executed through complex physical and regulatory interactions of genes that resemble a network (Barabási and Oltvai, 2004; Long et al., 2008; Urano et al., 2010). Transcriptome profiling technologies, including microarray and high-throughput sequencing platforms, have made it possible to infer functional associations based on the concordant expression patterns of genes to direct subsequent biological experiments (Bansal et al., 2007; Moreno-Risueno et al., 2010; Less et al., 2011; Friedel et al., 2012). The traditional workflow of analyzing transcriptomic data focuses on assessing the changes in expression of each individual gene, which is called differential expression (DE) analysis. DE analysis uses hypothesis testing, such as the t test, F-test, or ANOVA, to deduce the statistical significance of an observed expression change, which is primarily based on comparing between-sample (condition) variation and within-sample (replicate) variation (Cui and Churchill, 2003). Although DE analysis may narrow down an entire gene set to a short list of candidate genes, the extent to which biologically important genes related to the biological questions under examination can be identified remains an open question (de la Fuente, 2010). This concern is raised because of the intricate nature of gene expression and the technical considerations of the aforementioned statistical tests. Transcriptomes in actual cells can be highly dynamic, reflecting the greatly varied transcriptional activity, transcript abundance, and mRNA stability of different genes in different types of cells, tissues, and pathways. Genes that have different functions can also have distinct expression patterns in response to different environmental stimuli or experimental conditions (Windram et al., 2012; Rasmussen et al., 2013). Technical factors such as the sample size, quality and number of replicates, form of data distribution, approach of false discovery rate (FDR) control for multiple testing, and arbitrary selection of a single P-value cutoff may also cause significant fluctuations in the results (Cui and Churchill, 2003; de la Fuente, 2010; Rapaport et al., 2013). Additionally, traditional statistics-based DE analysis methods based on an assumed distribution do not incorporate the estimates of the test performance (e.g., true positive rate [TPR] and false positive rate [FPR]) on the results.
The utilization of network theory and related methodologies to analyze various forms of large-scale data has become an essential part of systems biology (Albert, 2007; Lee et al., 2010; Ferrier et al., 2011; Hwang et al., 2011; Bassel et al., 2012; Li et al., 2012; Kleessen et al., 2013; Van Landeghem et al., 2013). Among the network analytical techniques that have recently been applied in biology, differential network (DN) analysis has shown robustness, which is evident in its ability to identify the DNA damage response genes in yeast (Bandyopadhyay et al., 2010; Califano, 2011), body weight–related genes in mice (Fuller et al., 2007; Gill et al., 2010), T cell differentiation-related genes in human (Elo et al., 2007), and human disease-relevant genes (Hudson et al., 2009; Amar et al., 2013). In contrast with DE analysis, which is a gene-centric analytic approach that assesses expression changes in individual genes, DN analysis is a network-centric analytic approach that focuses on detecting the changes in a gene’s associations with other genes via a comparison of two or more networks that were constructed under different experimental conditions (de la Fuente, 2010; Hudson et al., 2012; Ideker and Krogan, 2012). DN analysis has been validated to be complementary to traditional DE analysis and is especially effective in detecting biologically important genes that have less dramatic expression changes for certain experiments (Elo et al., 2007; Hudson et al., 2009; Southworth et al., 2009; de la Fuente, 2010). Currently, many methods and software systems have been developed for network inference based on gene expression data, but many technical issues have not been solved (Usadel et al., 2009; De Smet and Marchal, 2010; Marbach et al., 2012). In the gene coexpression network (GCN), the connection of two genes is usually established based on the correlation coefficient of their expression profiles, which does not necessarily indicate a direct physical or regulatory interaction but is instead a reflection of a potential functional association between the two genes (Horvath and Dong, 2008; López-Kleine et al., 2013). Thus, how to distill millions of edges in a GCN (even in a small network constructed from a thousand genes) and select biologically significant associations has been regarded as a critical step (Usadel et al., 2009; Friedel et al., 2012; Alipanahi and Frey, 2013). Moreover, most DN analysis studies examine only one network characteristic (Carter et al., 2004; Elo et al., 2007; Liu et al., 2010; Yu et al., 2011), such as the “degree,” which represents the number of connections of a gene to its directly connected genes; however, whether one characteristic is sufficient to identify all of the genes of interest remains to be evaluated.
Machine learning (ML) is a branch of artificial intelligence technology that has been widely applied in engineering, computer science, and informatics. In essence, ML approaches encompass a suite of computational algorithms for building prediction models, so-called intelligent systems, to learn interesting patterns automatically from existing data sets and to bring about self-improvement of the system performance for accurately predicting novel knowledge from a new data set (Mjolsness and DeCoste, 2001). Specifically, an ML-based intelligent system takes an input feature matrix, which includes characteristic values of designated positive and negative samples, and self-trains the prediction models in the system via learning the patterns in the feature matrix to ultimately address classification problems with respect to a data set. Several analytical transcriptome studies have employed an ML strategy, such as the clustering of gene expression patterns (Pirooznia et al., 2008) and the classification of human diseases and cancers (Piao et al., 2012). However, the application of ML in large-scale network inference, and especially in DN analysis, is still rarely performed (Krouk et al., 2010; Bassel et al., 2011).
In this study, we present a computational system for network-centric transcriptome analysis for identifying biologically important genes, essentially employing ML techniques for large-scale GCN inference and DN analysis. With this ML system, we revisited 12 microarray data sets from a stress-responsive gene expression atlas for seedling root and shoot tissues of Arabidopsis thaliana, under conditions of salt, cold, drought, heat, wound, and genotoxic stresses (Kilian et al., 2007). The positive samples for training the ML-based prediction models were composed of known stress-related genes collected from the DRASTIC and TAIR databases. The ML system first took 32 expression-based characteristics to preselect “informative” genes whose expression profiles provide sufficient information for GCN construction. This ML-based gene filtering process effectively eliminated “noninformative” genes that may generate biologically irrelevant correlations and greatly reduced the network complexity. For ML-based DN analysis, 33 network-based characteristics were considered to predict candidate stress-related genes based on detecting the topological changes between the control and stress networks. This system was implemented as an R package, machine learning–based differential network analysis (mlDNA), which is available for public use.
RESULTS AND DISCUSSION
Arabidopsis Stress Expression Data Sets and Positive Samples
To develop the ML-based system for DN analysis, we obtained the Affymetrix microarray data from the AtGenExpress database (http://www.weigelworld.org/resources/microarray/AtGenExpress), profiled under salt, cold, drought, wound, heat, and genotoxic stresses in seedling root and shoot tissues of Arabidopsis by Kilian et al. (2007). Each stress experiment included six time points, namely, 0.5, 1, 3, 6, 12, and 24 h after stress treatment (stress), and a series of the same time points under normal conditions (control). Expression levels of the 22,591 Arabidopsis genes on the microarrays across the 84 samples were normalized using the GC robust multiarray average method. Detailed information on the experimental procedure of the stress treatments and microarray data processing is documented by Kilian et al. (2007).
Positive sample sets composed of known stress-related genes for training the ML prediction models were compiled from two resources: TAIR 10 (http://www.Arabidopsis.org) and DRASTIC (Database Resource for the Analysis of Signal Transduction in Cells; http://www.drastic.org.uk) databases. Stress-related genes from TAIR were retrieved based on a keyword search. For example, the query of “salt” in TAIR returned 789 genomic loci, which encoded genes that were annotated in the gene ontology (GO) category of “response to salt stress,” with a total of 305 publications related to those genes. Stress-related genes in DRASTIC were primarily recorded based on the literature and have been categorized based on stress types. The six positive sample sets contained 895, 433, 394, 357, 46, and 42 nonredundant genes that were mostly experimentally validated to be related to salt, cold, drought, wound, heat, and genotoxic stresses, respectively (details provided in Supplemental Data Set 1).
ML-Based Preselection of “Informative” Genes for GCN Construction
Constructing a whole-genome GCN, including all of the 22,591 genes (nodes), will generate over 255 million correlations (edges) between any pair of genes, among which the majority of the edges will not represent biologically meaningful associations(Alipanahi and Frey, 2013). Thus, selection of a subset of genes based on DE analysis or genes annotated with biological functions of interest has typically been used for inferring a simplified network (Iancu et al., 2012; Rasmussen et al., 2013). In our system, we devised an ML-based gene filtering process to preselect genes that can be used for GCN construction, through learning the patterns of 32 expression characteristics of known stress-related genes. The filtering process classified “unlabeled” samples (genes not in the positive sample set) into two groups: “noninformative” genes and “informative” genes. The “noninformative” genes were mostly nonexpressed, constitutively expressed, or non-stress-responsive genes, whose expression profiles did not provide sufficient information to infer meaningful associations with other genes. By contrast, “informative” genes showing a certain extent of expression abundance and expression changes were able to be used by correlation analysis for GCN construction. Specifically, this filtering process learned the patterns of 32 expression characteristics from the known stress-related genes in the positive sample set and used a random forest (RF) classifier with the positive sample-only learning (PSOL) algorithm to classify “noninformative” genes and “informative” genes in the “unlabeled” samples (Wang et al., 2006) (see Methods; Supplemental Figure 1).The RF classifier has been applied to solve various classification and prediction problems in biology, including microRNA precursor identification (Jiang et al., 2007), polyadenylation site prediction (Kalkatawi et al., 2012), and expression-based cancer classification (Díaz-Uriarte and Alvarez de Andres, 2006); these studies showed that the RF classifier had comparable or even higher performance than other commonly used ML algorithms, such as the support vector machine. The RF algorithm builds thousands of decision trees with bootstrapped positive and negative samples and randomly selected characteristics in the input feature matrix (Breiman, 2001). This strategy can robustly reduce the influence from noise (the mislabeled positive or negative samples) and outliers (extremely high or low feature values) (Touw et al., 2013). The feature matrix submitted to the RF classifier included 12 characteristics of absolute expression values of a gene at six time points in control and stress situations, 12 characteristics of within-condition expression variations of a gene measured as z-scores at six time points in control and stress situations, six characteristics of between-condition expression changes of a gene measured as fold changes at six time points involving stress versus the control, and two characteristics of the coefficient of variation (CV) in stress and control situations (see Methods). Then, the PSOL-based RF classifier was run for a number of times to gradually remove “noninformative” genes from the “unlabeled” sample set.
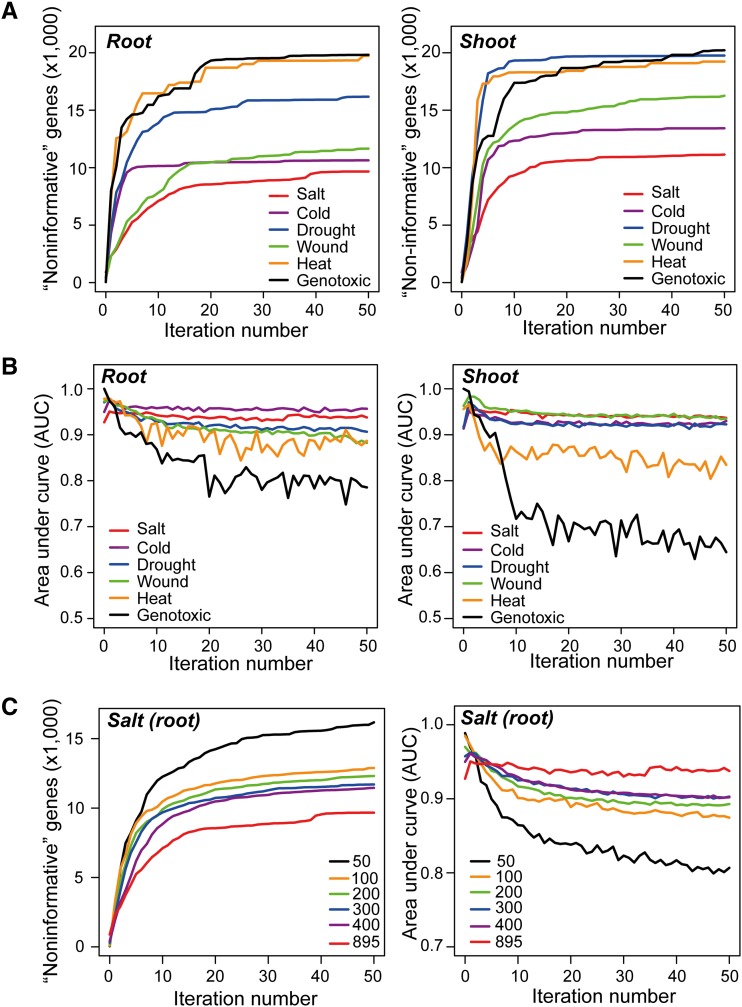
For the first iteration, an initial negative sample set with the same size as the positive sample set for a stress was constructed, which contained genes that were selected from “unlabeled” samples with the maximal Euclidean distance to known stress-related genes in the positive sample set. After each iteration, the prediction accuracy of the RF classifier was assessed to reveal the differences between positive and negative samples in expression changes with the 5-fold cross-validation method based on the values of the area under the curve (AUC) generated from a receiver operating characteristic (ROC) analysis (see Methods). With the increase in the number of iterations, the negative sample set was gradually expanded by the addition of newly detected negative samples from the “unlabeled” samples. The process was stopped after the 50th iteration, at which point the negative sample set has reached saturation (i.e., no new negative samples will be extracted from the “unlabeled” samples). The effectiveness of the ML-based gene filtering process is illustrated in Figure 1. As the “drought (root)” sample shows, the initial negative sample set used by the RF classifier contained 397 genes, with the maximum Euclidean distance being the 397 known drought stress-related genes in the positive sample set. After the 10th iteration, the negative sample set expanded from 397 to 14,790 genes (Figure 1A). Correspondingly, the AUC values of “drought (root)” decreased slightly from 0.97 to 0.90 because the genes in the positive sample set might not all be responsive to drought in the root tissue within 24 h (Figure 1B). From the 10th to 50th iteration, the size of the negative sample set and the corresponding AUC values became relatively stable, indicating that the negative sample set reached saturation after approximately the 10th iteration of running the PSOL-based RF classifier. This ML-based gene filtering process for drought, salt, cold, and wound stress reached saturation after the 10th to 15th iterations (i.e., the negative sample size and AUC values became stable), whereas the mean AUC values for heat and genotoxic stresses continuously decreased with increasing iterations (Figures 1A and 1B). We suspected that this finding was likely due to the relatively small size of the positive sample sets of the heat (46 genes) and genotoxic (42 genes) stresses. To evaluate the smallest number of stress-related genes in the positive sample set that is required for PSOL-based RF classification, we randomly selected 50, 100, 200, 300, and 400 genes and used all 895 genes from known salt stress–related gene set to perform the ML-based gene filtering process. Whereas the positive sample sizes of 100 to 400 genes showed slightly lower AUC values than the AUC values of the 895 genes, the AUC value dropped significantly when using 50 genes as the positive sample set (Figure 1C). This result indicated that there was indeed a dependence of the performance of the RF classifier on the size of the positive sample set; however, a size of more than 100 genes in the positive sample set should be sufficient for the ML-based gene filtering process.
Figure 1.
ML-Based Classification of “Informative” and “Noninformative” Genes.
(A) Numbers of “noninformative” genes (y axis) in root and shoot tissues at different iterations (x axis) when using the PSOL-based RF classification model.
(B) AUC scores using the PSOL-based RF classification model to classify positive samples (known stress-related genes) and negative samples (“noninformative” genes) in root and shoot tissues at different iteration times.
(C) Influence of the size of the positive samples on the PSOL-based RF classification model.
Distinct Expression Characteristics of “Informative” and “Noninformative” Genes
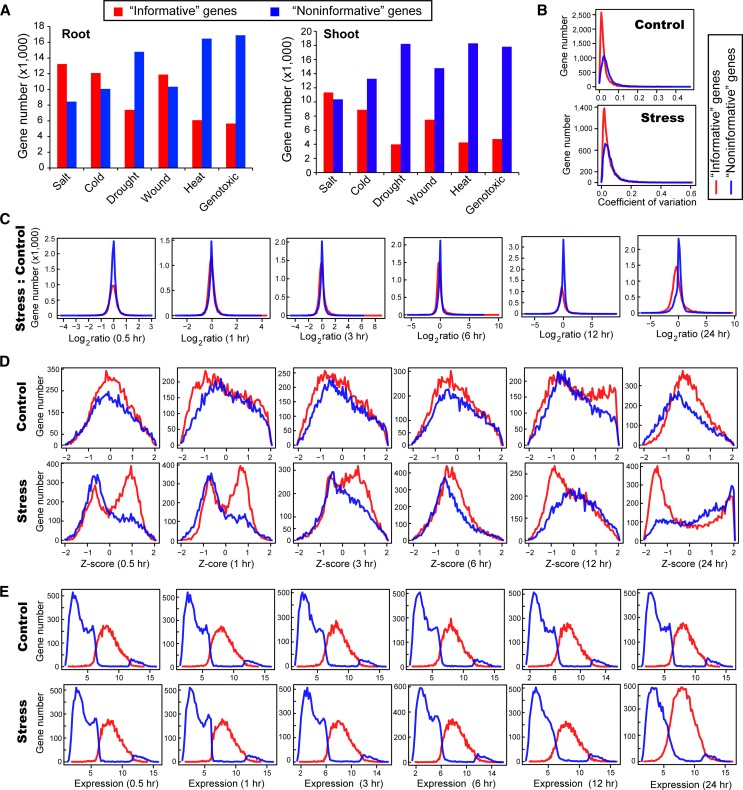
The number of “informative” and “noninformative” genes varied greatly across the 12 stress expression data sets, which reflected different response patterns of the transcriptomes under different stresses and in different tissues (Figure 2A; Supplemental Data Set 2). Under salt stress, 13,244 and 11,331 “informative” genes were identified in roots and shoots, respectively, which is consistent with the transcriptome in roots possibly being able to respond earlier and more dramatically than the transcriptome in shoots (Jia et al., 2002; Kilian et al., 2007). Under drought stress, there were fewer “informative” genes than under salt stress, 7407 and 3391 genes in roots and shoots within 24 h, respectively, which is consistent with the experimental design: In salt treatment, the plants were grown under high salinity (150 mM NaCl); in drought treatment, the plants were first stressed by 15-min dry air stream until 10% loss of fresh weight and then transferred to the climate chamber under normal condition (Kilian et al., 2007). The heat and genotoxic stress data sets contained the smallest number of stress-related candidate genes, most likely because a smaller proportion of genes in the genome were influenced by heat and genotoxic stresses than by salt, drought, cold, or wound stress (Kilian et al., 2007).
Figure 2.
Different Expression Characteristics of “Informative” and “Noninformative” Genes.
(A) Number of “informative” and “noninformative” genes under the six studied stress conditions and two tissues.
(B) Distributions of the CV of “informative” and “noninformative” genes in the cold (root) experiment.
(C) Distributions of the fold change of “informative” and “noninformative” genes in the cold (root) experiment.
(D) Distributions of the z-scores of “informative” and “noninformative” genes at the six time points in the cold (root) experiment.
(E) Distributions of the expression levels of “informative” and “noninformative” genes at the six time points in the cold (root) experiment.
To validate whether the 32 expression characteristics provided sufficient discriminatory power for the RF classifier to distinguish “informative” and “noninformative” genes, we compared the distributions of these characteristics in the cold (root) sample. The CV distributions of “informative” and “noninformative” genes were mostly overlapping, which indicates that CV is most likely the least effective factor for the classification (Figure 2B). The fold-change distributions of “informative” and “noninformative” genes were also mostly overlapping, which indicates that the ratio of gene expression of stress versus control might not be sufficient to differentiate the two groups of genes (Figure 2C). By contrast, the z-score, as a measure of the within-condition variation, appeared to be much more effective for RF classification than fold-change and CV, which was reflected by the clearly separated peaks of “informative” and “noninformative” genes (Figure 2D). Moreover, the z-scores of “informative” genes had two peaks, with the minor peak corresponding to the single peak of the “noninformative” genes in the stress and control samples. We speculate that this minor peak might represent the genes whose expression changes were due to normal developmental activity, such as the genes involved in biological rhythm, whereas the major peak of “informative” genes might represent actual stress-induced expression changes. Another interesting pattern was the shift of the z-score from positive values to negative values, which occurred at 6 h and indicates that many cold-responsive genes were likely upregulated before 6 h and then downregulated afterward. Last, the distributions of absolute expression values indicated that most “noninformative” genes were nonexpressed or low-expressed genes, according to the two clearly separated peaks of “informative” and “noninformative” genes (Figure 2E).
Among the 10,067 “noninformative” genes in the cold (root) sample, 82% were not statistically determined as differentially expressed (t test, P-value cutoff = 0.05) and 60% (98%) generated at least one correlation value above 0.95 (0.90) with other genes (Supplemental Data Set 2). This result indicates that “noninformative” genes with low expression and/or unchanged expression patterns mostly share similar expression profiles with each other, that can generate biologically meaningless associations with high correlation values, interfering in the construction of a meaningful GCN.
Network Characteristics for ML
The ML-based gene filtering process screened ∼4000 to 14,000 “informative” genes in the 12 stress experiments (Supplemental Data Set 2) whose expression changes were attributed to either normal physiological activity within 24 h or a stress-induced transcriptional response. To perform DN analysis, we first constructed a control network and a stress network using the known stress-related genes and “informative” genes for each time-series experiment of a stress condition. The edges in the two networks can be statistically established using multiple correlation and noncorrelation methods, with preference given to the Gini correlation coefficient (GCC) (Schechtman and Yitzhaki, 1999; Yitzhaki, 2003). We previously demonstrated the robustness of applying the GCC to infer regulatory relationships between genes and transcription factors (TFs) in plants (Ma and Wang, 2012). The GCC is a statistical algorithm that reciprocally uses the rank and value of two variables to compute the correlation (see Methods), which provides the advantages of being independent of the distribution form, being less influenced by outlier data points, being independent of the sample sizes, and having a higher sensitivity for detecting transient regulatory relationships than the traditional value-only Pearson correlation and rank-only Spearman correlation (Ma and Wang, 2012). The significance level of the GCC of a pair of genes was estimated with the permutation test method by shuffling the gene expression, and the pairs that had a P value ≤ 0.01 were connected as edges in the networks (see Methods).
To use the ML strategy to identify candidate stress-related genes that were subject to biologically meaningful changes in terms of their connections with other genes in networks, the system also required a feature matrix to build and train the prediction model. The feature matrix included 10 network characteristics of genes in the control (c) and stress (s) networks and their differences (d) between the two networks, which resulted in a total of 30 (10 × 3) characteristics (see Methods). Among them, 21 characteristics (7 × 3) described the “centrality” property of genes in the networks, including “degree,” “positive connectivity,” “negative connectivity,” “closeness,” “eccentricity,” “eigenvector,” and “PageRank.” Some of the “centrality” properties have been previously used in network analysis in biology, for example, the “degree,” which is also known as “connectivity,” indicates the number of edges of a node in direct connections to other nodes in a network (Fuller et al., 2007). Connectivity can be further divided into positive and negative connectivity based on the positive and negative value of the two genes’ correlation (Gustin et al., 2008). The distribution of the positive and negative connectivity could reflect different response patterns of gene expression changes under different stresses (Supplemental Figure 2). This arrangement further supports our rationale for applying an ML-based strategy based on the nature of the studied stresses and tissues, rather than using uniform statistical testing criteria. The eigenvector is another centrality measurement that is widely used in social network analysis and that describes a node’s centrality by taking its neighboring nodes’ centralities into account (Bonacich, 2007). This network characteristic helps to identify the low-degree nodes that directly connect to high-degree nodes. Thus, nodes with high eigenvector scores usually suggest that this type of node could have the role of bridging neighboring subnetwork modules that contain a group of highly connected nodes. The PageRank, a variant of the eigenvector, has been applied by the Google internet search engine to search web pages that are highly related to the user’s query (Page et al., 1999).
The feature matrix also includes nine more network characteristics (3 × 3) that describe a gene’s relationships with known stress-related genes (denoted as “knodes”), including “dist2knodes,” “closeness2knodes,” and “eccentricity2knodes” (see Methods). The “dist2knodes” measures the total length of the shortest paths from a given gene to known stress-related genes based on the assumption that stress-responsive genes should be closer to known stress-related genes than nonresponsive genes in the network. The“closeness2knodes” and “eccentricity2knodes” were variants of “closeness” and “eccentricity” that were modified to describe the closeness and eccentricity of a gene to known stress-related genes in the network. Two additional noncentrality characteristics, “average of specific connections (ASC)” and “corDistance,” were also included in the feature matrix to denote the difference in the edges of a gene connected to other genes in control and stress networks. The ASC is a measure of a gene’s connections that exist only in one network but are absent in the other network (Choi et al., 2005). The “corDistance” uses Euclidean distances to denote the changes in the correlation strengths of a given gene between its connected genes in the two compared networks (Liu et al., 2010). Finally, we included one expression characteristic, “expDistance,” to enhance the discrimination of the stress-responsive genes from the nonresponsive genes because stress-related genes should more or less demonstrate a certain extent of expression change. The “expDistance” measures the global gene expression change in response to a stress by calculating the Euclidean distance between expression values of the six time points in control and stress. The detailed definition of the characteristics in the network feature matrix for ML and the corresponding formulas to calculate these quantities are described in the Methods.
Multiple Features versus a Single Feature for DN Analysis
Previous DN analytical studies usually considered a single network feature to identify genes that show important changes in two networks (Choi et al., 2005; Elo et al., 2007; Fuller et al., 2007; Yu et al., 2011). However, whether a single feature is sufficient to detect all of the genes of interest remains unevaluated, considering that genes with different functional roles might have different connection patterns with other genes in a network. For example, a low-degree gene might have a high eigenvector feature score, which could serve as a bridging node to connect multiple modules that contain high-degree genes; genes that have the same connectivity might have a different proportion of positive and negative connectivity (Supplemental Figure 2). Our mlDNA system provides an avenue to synthetically consider a combination of 33 characteristics of network changes, relationship changes, and expression changes to improve the accuracy of predicting stress-related genes.
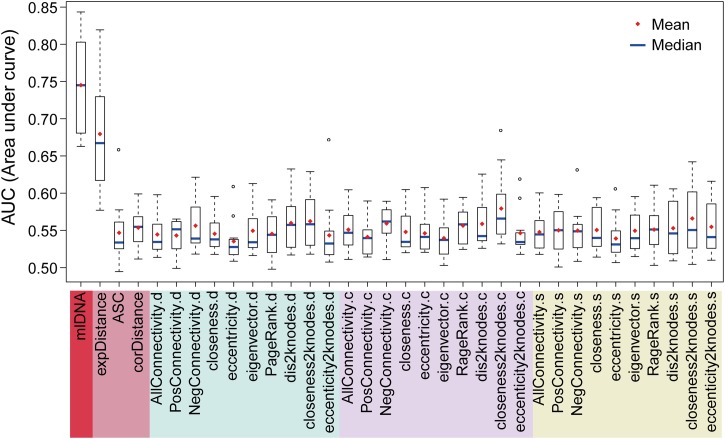
To evaluate the prediction performance of the network features for identifying candidate stress-related genes, we performed ROC analysis on the prediction results that were generated from the individual features and mlDNA (Figure 3). The known stress-related genes were regarded as positive samples, and “informative” genes for the corresponding stress were used as control samples. We then applied the 5-fold cross-validation method to train and test the RF classifier for preventing the overestimation of prediction performance (see Methods). The performance of the RF classifier in 5-fold cross-validation was visualized with five ROC curves, which are two-dimensional plots of the TPR (the fraction of detected true positives from positive samples) versus the FPR (the fraction of newly predicted stress-related genes from control samples) at different prediction score cutoffs. The five AUC values were averaged to evaluate the overall performances of the RF classifier. The testing data sets in 5-fold cross-validation were also applied to test the effectiveness of using a single feature in the ROC analysis for each of the 12 stress samples. Genes in the testing data sets were directly scored with the corresponding feature values. Because genes in the testing data sets can be prioritized based on their prediction scores, a higher AUC value indicated that the prediction model can rank known stress-related genes more closely to the top; thus, the prediction model was more powerful to identify candidate stress-related genes.
Figure 3.
Evaluation of Using a Single Feature and a Combination of 33 Features in Predicting Candidate Stress-Related Genes.
For each stress (tissue) experiment, the prediction accuracy of using a single feature and an RF-based classification model (mlDNA) while using a feature matrix that included 33 network characteristics was assessed using a 5-fold cross-validation to calculate an AUC value. A box plot was drawn to display the distribution of the 12 AUC values from the 12 stress (tissue) samples. The higher the average/median AUC values were, the more accurate the identification of candidate stress-related genes.
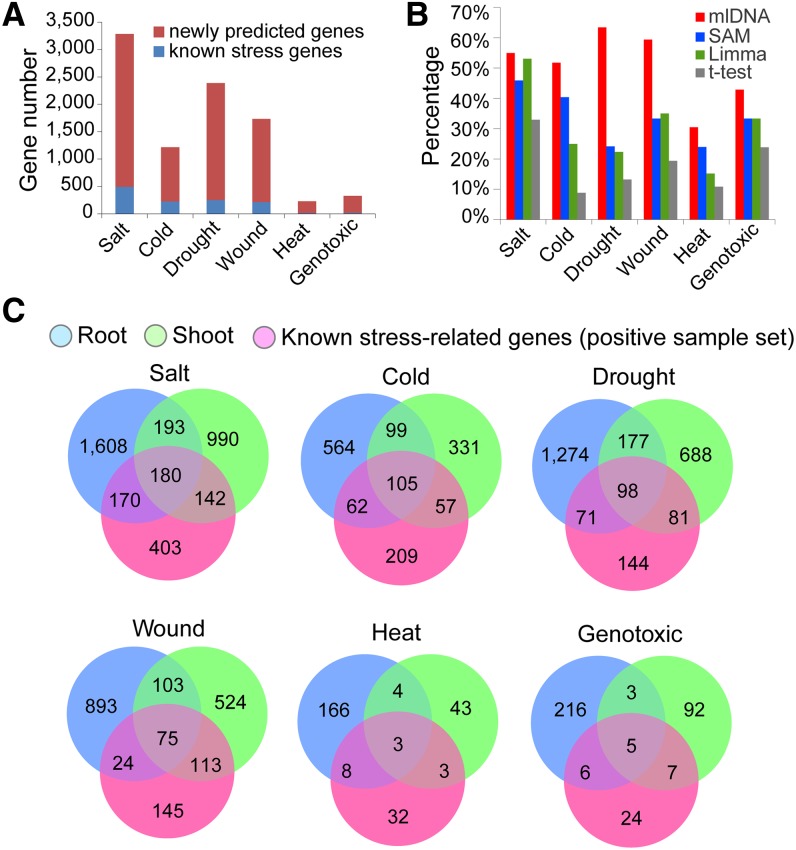
Network features varied in their power to discriminate positive samples from negative samples. On average, the AUC values of the 32 network features ranged from 0.5 to 0.6. We observed that the “closeness2knodes” feature showed relatively better performance than the other network features, which indicates that the unknown stress-related genes may be functionally associated with the known stress-related genes (Figure 3). The expression feature “expDistance” showed an average AUC value of 0.66, which indicates that the expression change was still the primary characteristic of stress-related genes. These results also indicate that the use of a single network characteristic is insufficient to effectively identify candidate stress-related genes, reflected by the relatively low AUC values. By sharp contrast, mlDNA generated substantially higher AUC values that ranged from 0.67 to 0.84, which indicates that the 32 network characteristics plus the complementary expression characteristic showed the best performance in predicting the stress-related genes (Figure 3).
mlDNA Outperformed Traditional DE Analysis at Detecting Candidate Stress-Related Genes
We further compared the prediction performance of mlDNA and three traditional DE analysis methods, including the t test in R/Bioconductor package GeneSelector (Boulesteix and Slawski, 2009), linear models for microarray analysis (Limma) (Smyth, 2004), and significance analysis of microarrays (SAM) (Tusher et al., 2001), using the ROC analysis and 5-fold cross-validation. In the ROC analysis, the positive sample set for each stress condition included the known stress-related genes, and the “informative” set of genes of each corresponding stress was used as the control. The accuracy of predictions by mlDNA and the three DE methods was assessed by the 5-fold cross-validation (see Methods). Because the unsupervised DE methods do not require a training process, DE methods were tested directly on the same testing data sets as those used for mlDNA for a fair comparison. The prediction score of each gene in the testing data sets was represented by the -log10(P value), where the P value was the significance level derived from the DE method.
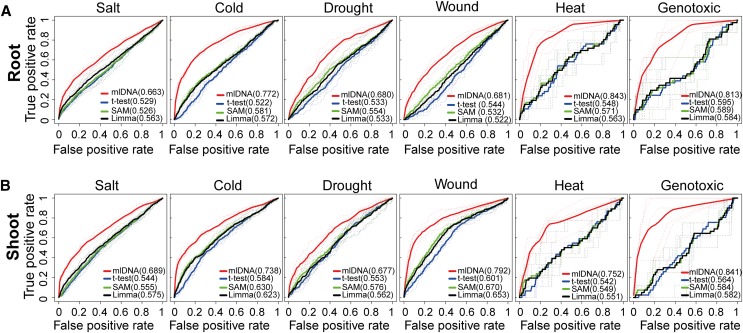
The ROC curves of the four tested methods were plotted for each stress separately in the root and shoot tissues (Figure 4). In all of the experiments, the mean AUC values of mlDNA were substantially higher than all three of the DE methods, with an average of 0.75 of the 12 samples. By contrast, the average AUC values of the 12 samples for the t test, Limma, and SAM were 0.56, 0.57, and 0.58, respectively. The AUC values of the salt and drought stresses were below 0.7, which is lower than for other stresses. We reasoned that the positive samples for these two stresses could contain salt and drought stress–related genes documented from other tissues or responding to stress after 24 h. By contrast, the AUC values of mlDNA for heat and genotoxic stresses were above 0.8, which likely can be attributed to the relatively small sizes of the positive sample set, which most likely contained most of the heat and genotoxic stress-related genes that were easily detected by mlDNA. Overall, the comparative evaluation showed that the network-centric mlDNA method markedly outperformed all three of the traditional gene-centric DE methods in all of the tissues and stress conditions in terms of identifying stress-related genes.
Figure 4.
Comparative Evaluation of mlDNA and Three DE Analysis Methods.
For each stress (tissue) experiment, the ROC curves were plotted to illustrate the prediction accuracy of mlDNA and three DE analysis methods, including the t test, SAM, and Limma. The dashed curves denote the curves from the testing data set in each round of 5-fold cross-validation. The solid curves represent the average curve from the five times that validations were performed. The numbers in parentheses represent the average AUC values on testing data sets generated from the 5-fold cross-validation for each prediction method.
The Candidate Stress-Related Genes Predicted by mlDNA
Subsequently, we applied mlDNA to identify candidate stress-related genes from the 12
stress expression data sets. We used the F-score method to determine an optimal score
for the RF classifier to predict candidate
stress-related genes, which is an algorithm commonly used in ML to assess the
prediction accuracy of a binary (two-class) classification model based on the
expected proportions of true positives (TPs), true negatives (TNs), false positives
(FPs), and false negatives (FNs) in the prediction results (Abeel et al., 2009). The F-score is defined as a weighted
average of “precision = TP/(TP+FP)” and “recall =
TP/(TP+FN),” which is computed by the formula: 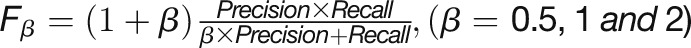 , where β
is a weight to control the preference toward “recall” or
“precision” of the classification model. Our analysis used the
, where β
is a weight to control the preference toward “recall” or
“precision” of the classification model. Our analysis used the
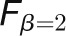 measure, which gives a higher preference to “recall” over
“precision” (Lexa et al.,
2011). This approach was based on the consideration that
“precision” was difficult to measure because the positive samples could
include an unknown fraction of stress-related genes that might not respond in shoots
and roots within 24 h, and the control samples could also include an unknown fraction
of genes that respond to stress with different degrees of intensity. Thus, the higher
preference of “recall” could facilitate identifying unknown
stress-related genes, as many as possible. The optimal score for the RF classifier running in each stress data set
was selected based on the prediction score showing the maximum F-score to indicate
the expected prediction accuracy of the results (Supplemental Figure 3).
measure, which gives a higher preference to “recall” over
“precision” (Lexa et al.,
2011). This approach was based on the consideration that
“precision” was difficult to measure because the positive samples could
include an unknown fraction of stress-related genes that might not respond in shoots
and roots within 24 h, and the control samples could also include an unknown fraction
of genes that respond to stress with different degrees of intensity. Thus, the higher
preference of “recall” could facilitate identifying unknown
stress-related genes, as many as possible. The optimal score for the RF classifier running in each stress data set
was selected based on the prediction score showing the maximum F-score to indicate
the expected prediction accuracy of the results (Supplemental Figure 3).
mlDNA identified 3283 (salt), 1218 (cold), 2389 (drought), 1732 (wound), 227 (heat), and 329 (genotoxic) candidate stress-related genes in shoots and roots, among which the majority were new (Figure 5A; Supplemental Data Set 3). We compared the known stress-related genes detected by mlDNA with the results of the SAM, Limma, and t test (Figure 5B). Under salt stress, the known stress-related genes that were detected by mlDNA and the DE methods were similar, most likely because salt stress–related genes usually respond with more dramatic expression changes than the genes that respond to other stresses. Under cold, drought, and wound stress conditions, substantially more known stress-related genes were detected by mlDNA than by SAM, Limma, and t test, which indicates that mlDNA was more effective at detecting genes that showed slight expression changes that were missed by DE analysis. We computed the significance level (P value) of DE for the mlDNA-predicted candidate stress-related genes using the three DE methods including the t test, Limma, and SAM. We found that, on average, 60% of the candidates were statistically determined as differentially expressed by any of the three methods using P value = 0.05 as cutoff (Supplemental Figure 4). However, genes failing to pass the cutoff may still be transcriptionally responsive to stress and even have important stress-related function. For example, we compared the mlDNA-predicted salt-related and cold-related genes with the genes associated with a strong phenotypic response in their T-DNA mutation lines documented in a recent large-scale phenotype screening work (Luhua et al., 2013) and found 16 salt-related genes (AT5G41080, AT2G32210, AT1G02660, AT1G76600, AT1G55040, AT2G47710, AT3G14060, AT3G26470,AT3G60520, AT2G15560, AT3G29370, AT5G06130, AT2G34600, AT5G57340, AT3G46960, and AT1G18900) and 13 cold-related genes (AT2G32210, AT5G51570, AT2G40000, AT1G79660, AT5G62920, AT4G31730, AT1G78070, AT2G25250, AT1G16730, AT1G18850, AT4G34630, AT1G30200, and AT1G56230) that did not pass the statistical cutoff by either the t test, Limma, or SAM. In addition, there were 83 stress-related genes experimentally supported by the large-scale phenotypic screening work (Luhua et al., 2013), of which 19 were known stress-related genes in the positive sample set, and 64 were newly predicted by mlDNA (Supplemental Data Set 4). For all six types of stress, we found that the majority of stress-related genes were tissue specific, with 75 to 85% of the genes usually specific to either roots or shoots (Figure 5C).
Figure 5.
Statistics of the Candidate Stress-Related Genes Predicted by mlDNA.
(A) Numbers of the candidate stress-related genes (known and newly predicted stress-related genes) for the six stresses.
(B) Percentages of known stress-related genes included in the prediction results of mlDNA and the DE analysis methods t test, SAM, and Limma using P value = 0.01 as the cutoff.
(C) Venn diagrams of the candidate stress-related genes in roots and shoots and the known stress-related genes in the positive sample sets.
Phenotypic Screen of Selected Candidate Stress-Related Genes
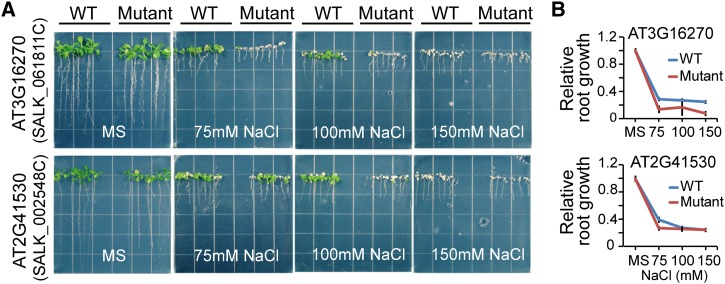
The mlDNA predictions provided a list of candidate stress-related genes that are worthy of experimental validation to further verify their functional roles in stress-related pathways using phenotypic screening methods. We performed a phenotypic screen of a selection of 89 candidate salt-related genes having a corresponding homozygous T-DNA knockout SALK line (ordered from the ABRC; Alonso et al., 2003). The wild-type (Columbia-0 [Col-0]) and mutant Arabidopsis seeds were sown on agar-solidified half-strength Murashige and Skoog (MS) medium supplemented with 5 g/L Suc for germination and early growth. Five days after germination, the seedlings were transferred to the same MS medium supplemented with 0, 75, 100, and 150 mM NaCl for vertical growth. Although most mutant lines showed no salt-related phenotypic response, a small fraction showed minor or major phenotypic changes including lethality. Two of the mutant lines, containing T-DNA insertions in AT3G16270 and AT2G41530, exhibited strong salt-related phenotypic changes (Figure 6A). AT3G16270 encodes a VHS (for Vps27, Hrs, and STAM) domain-containing protein that is involved in intracellular protein transport. AT2G41530 encodes a protein with S-formylglutathione hydrolase activity. Compared with the wild type, the mutant of AT3G16270, SALK_061811C (insertion in intron), exhibited a marked reduction in root length on all concentrations of NaCl (Figure 6B). A similar result was observed for the knockout mutant, SALK_002548C (insertion in intron), in AT2G41530 but only at 75 mM NaCl (Figures 6A and 6B).
Figure 6.
Salt Stress–Responsive Phenotypes of Two Candidate Stress-Related Genes.
(A) The wild-type Col-0 and two mutant lines were grown in MS medium with or without 75, 100, or 150 mM NaCl.
(B) Relative root length of wild-type and mutant plants.
Functional Enrichment of Candidate Stress-Related Genes
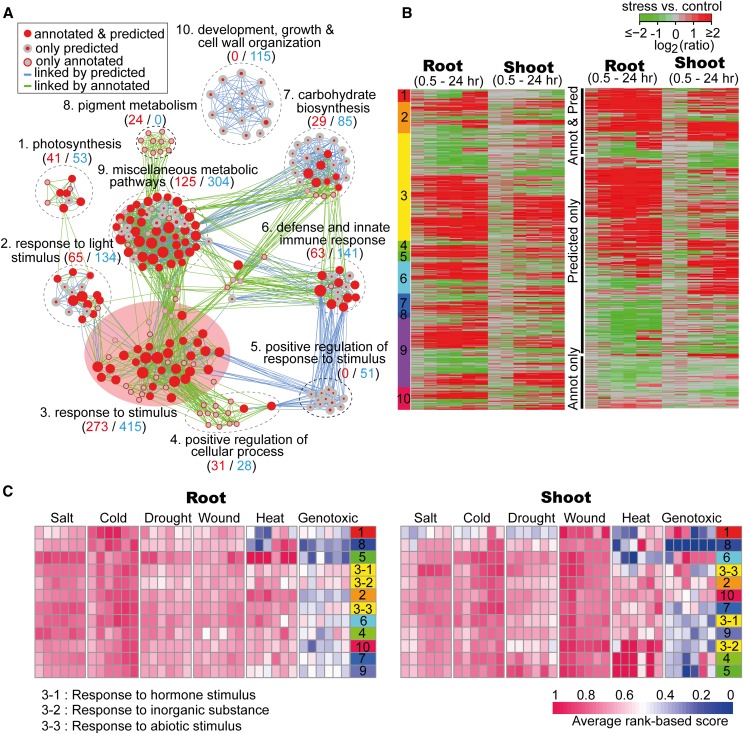
To computationally validate the mlDNA prediction results, we further performed GO enrichment analysis to compare the GO categories of mlDNA-predicted and known stress-related genes, as exemplified by the salt stress samples in Figure 7. The GO categories that were significantly enriched with known and predicted salt stress–related genes were separately identified using the hypergeometric test followed by the Benjamini and Hochberg (1995) FDR correction with the Cytoscape plug-in BiNGO (Maere et al., 2005). The enriched GO categories with FDR-adjusted P value ≤ 0.05 were loaded into the Enrichment Map (EM), a plug-in in Cytoscape for visualizing GO categories as a network (Merico et al., 2010). The EM clusters the GO categories with parent-daughter relationships into modules and connects the GO modules by genes shared between GO categories. Thus, the visualized network structure succinctly reflects the functional relationships of the biological pathways that are enriched with genes of interest, and at the same time, solves the redundancy issue caused by genes shared by multiple GO categories (Merico et al., 2010).
Figure 7.
Gene Set Enrichment Analysis of Known Salt Stress–Related Genes and Candidate Salt Stress–Related Genes.
(A) GO modules enriched with known salt stress–related genes and candidate salt stress–related genes visualized by the EM plug-in in Cytoscape.
(B) Expression heat map of salt stress–related genes in the root and shoot tissues. Left: Expression heat map of genes in the ten GO modules numbered according to the functional annotations of the GO modules in (A). Right: Genes that were classified into three groups, namely, predicted known stress-related genes in the positive sample set, genes only predicted by mlDNA, and known stress-related genes that were not included in the mlDNA prediction results.
(C) Regulation patterns of biological pathways inferred from the GO modules. The modules were numbered according to the functional annotation in (A).
A total of 1061 salt stress–related genes exhibited significant enrichment in the GO categories clustered into 10 clearly separated modules by the EM (Supplemental Data Set 5). The largest module contained the GO category of “response to stimulus” and its daughter categories, including a total of 273 known salt stress–related genes and 415 candidate stress-related genes (Figure 7A). Three daughter categories under “response to stimulus” were “response to hormone stimulus,” “response to inorganic substance,” and “response to abiotic stress” (Supplemental Figure 5). Lower-level GO categories under “response to hormone stimulus” included genes that function in hormone-mediated signal transduction, such as those responsive to abscisic acid, gibberellic acid, auxin, and ethylene, which are known to play important roles in stress signaling pathways (Zhu, 2002; He et al., 2005; Mahajan and Tuteja, 2005; Jiang and Deyholos, 2006; Cao et al., 2007). The “response to abiotic stress” category contained a large fraction of genes that were specifically responsive to “salt stress,” “water deprivation,” “desiccation,” and “hyperosmotic salinity.” Genes in “response to inorganic substance” mostly encode proteins that bind with metal ions, such as calcium and cadmium. Out of the 67 genes in the “response to cadmium ions,” 20 have been documented as related to salt stress, such as CONSTITUTIVELY ACTIVATED CELL DEATH1, OXIDASE1, MAPK/ERK KINASE KINASE1, and seven TF-encoding genes that belong to the MYB family. The second largest module included 125 known salt stress–related genes and 304 candidate stress-related genes dispersed in numerous biosynthetic and metabolic pathways of small molecules and organic substances, such as the phytohormones abscisic acid, jasmonic acid, salicylic acid, ethylene, and auxin, and organic oxoacid compounds, such as genes for synthesizing vitamin and fatty acid belonging to reactive oxygen species (Figure 7A). Other modules contain fewer salt stress–related genes dispersed in the GO categories of “defense and innate immune response,” “photosynthesis,” “positive regulation of response,” “carbohydrate biosynthesis,” etc. Among these modules, “positive regulation of response to stimulus” and “developmental growth and cell wall organization” modules contained 51 and 115 genes, respectively, that were only predicted by mlDNA. These genes might not be directly involved in the primary response to salt stress but, for example, could be associated with physiological functions secondarily influenced by stress.
Furthermore, most salt stress–related genes showed obvious expression changes with a distinct response time in root and shoot tissues after treatment. In roots, most responsive genes were upregulated as early as 0.5 and 1 h, whereas responsive genes in shoots usually exhibited expression changes after 3 h (Figure7B). Moreover, genes in certain functional categories also showed different response times. For example, genes in the “responsive to stimulus” category showed earlier and more dramatic expression changes compared with other categories, whereas genes in photosynthesis and light stimulus–related genes showed expression changes after 12 h. In addition, we also found that the majority (78%) of known salt stress–related genes included in the mlDNA prediction results were upregulated, whereas genes that were only predicted by mlDNA showed not only upregulation patterns but also downregulation patterns. Finally, known stress-related genes that were not predicted by mlDNA showed slight expression changes (Figure 7B). In brief, the GO enrichment analysis of the candidate salt stress–related genes predicted by mlDNA agreed with the general functional characteristics of genes that were responsive to salt stress, providing further support for the accuracy of the mlDNA prediction.
Different Responsive Activities of Biological Pathways
The gene set enrichment analysis revealed that stress-induced gene regulation
patterns were varied among certain GO modules
in different tissues and under different stresses, in terms of the expression time
and regulation trend (i.e., upregulation and downregulation). We further analyzed
these regulation activities at the pathway level based on the GO modules clustered by the EM algorithm (Merico et al.,
2010). We assumed that the global regulation activity of a GO module could be reflected by the expression
changes of all of the genes in a module. Thus, we quantified the activity of a module
based on the sum of the rank of the expression changes of all of the genes in this
module using the average rank-based score (AS) algorithm, formulated
as 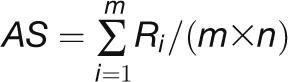 (Yang et al., 2011), where m
and n are the numbers of genes in the analyzed GO module and the genes in the genome included on the
microarray, respectively. Ri is the rank of the
expression change (|log2 (ratio)|) of gene i in the
genome. The AS score falls into a range of 0 to 1, in which the
higher the AS score is, the larger the regulation activity of a
GO module and the more drastically changed
the gene expression patterns. Because the AS score is a normalized
value with the total gene number in the module and the genes in the genome as a
background, this rank-based statistic is robust for directly comparing the activities
of modules with different gene numbers under different experimental conditions (Yang et al., 2011).
(Yang et al., 2011), where m
and n are the numbers of genes in the analyzed GO module and the genes in the genome included on the
microarray, respectively. Ri is the rank of the
expression change (|log2 (ratio)|) of gene i in the
genome. The AS score falls into a range of 0 to 1, in which the
higher the AS score is, the larger the regulation activity of a
GO module and the more drastically changed
the gene expression patterns. Because the AS score is a normalized
value with the total gene number in the module and the genes in the genome as a
background, this rank-based statistic is robust for directly comparing the activities
of modules with different gene numbers under different experimental conditions (Yang et al., 2011).
Each time point was assigned an AS score that is associated with a GO module to indicate its regulation activity at the specific time after stress treatment. In the salt (root) sample, modules 4 (“positive regulation of cellular process”), 5 (“positive regulation to response to stimulus”), 6 (“defense and innate immune response”), and one subcategory of module 3 (“response to abiotic stimulus”) showed a relatively high activity (AS > 0.74) as early as 0.5 h after salt treatment (Figure7C). In the salt (shoot) sample at 0.5 h, GO modules with the top four highest activity were “development, growth, and cell wall organization (module 10, AS = 0.69),” “carbohydrate biosynthesis (module 7, AS = 0.68),” “response to hormone stimulus (module 3, AS = 0.67),” and “positive regulation of cellular process (module 4, AS = 0.66).” Additionally, almost all of the modules showed increased activity after 3 h, which indicates a later response time in shoots than in roots. Moreover, 68% (49/72) of the AS scores were lower in shoots than in roots during stress responses from 0.5 to 24 h, which indicates that the regulation activity in root tissue is higher than in shoot tissue. This pattern agrees with the observation that the roots are first to sense the high salinity signal(s), which are subsequently transmitted to the shoots in a delayed manner (Jia et al., 2002).
While under cold stress, modules 1 (“photosynthesis”) and 8 (“pigment metabolism”) in roots and one subcategory of module 3 (“response to hormone stimulus”) in shoots had an AS score that was higher than 0.80 at the time point of 0.5 h which indicates that certain stress-related genes responded immediately after the cold treatment in both of the tissues (Figure 7C). In addition to cold stress, the module activity in both roots and shoots tended to be increased during the 24-h time period. By contrast, the module activity under wound and drought stresses in shoots tended to be decreased after 3 h of treatment. Moreover, 90% (65/72) of the AS scores were higher in shoots than those in roots during wound stress responses from 0.5 to 24 h, which is consistent with the fact that the shoots, rather than the roots, were directly wounded in the stress experiment (Kilian et al., 2007). In the heat (root and shoot) samples, the activity of GO modules 1 (“photosynthesis”) and 8 (“pigment metabolism”) were increased after 6 h of treatment, which indicates that certain stress-related genes that responded late after the heat treatment are highly activated at multiple time points. Under genotoxic (shoot) stress, decreased activity was observed in GO modules 1 (“photosynthesis”) and 3 (“response to abiotic stimulus”) after 6 h of treatment.
Genes Shared Between Multiple Stresses
In plants, certain stress-responsive genes are functionally shared by different types
of stresses, which could serve as “convergent points” of signal
transduction, transcriptional regulation, or other stress-related pathways (Fujita et al., 2006; Baena-González and Sheen, 2008). Based on the prediction
results of mlDNA, we deduced the “convergence degree” between each pair
of the six tested stresses based on the fractions of stress-related genes that were
shared between two stresses, using the same algorithm in the EM that calculates an “overlap coefficient” to
denote the convergence (Merico et al.,
2010). The “overlap coefficient” is a ratio value that ranges
from 1 (absolute convergence) to 0 (no convergence) and is computed as
 ,
where
,
where  and
and  represent the number of stress-related genes in stress A and B, respectively. The
salt, cold, and drought stresses showed the highest convergence with each other in
both the root and shoot tissues, whereas wound showed secondarily high convergence
with these three stresses (Figure 8A).
Moreover, heat showed a relatively high convergence only with salt, and genotoxic
stress showed the lowest convergence compared with any of the other stresses (Figure 8A).
represent the number of stress-related genes in stress A and B, respectively. The
salt, cold, and drought stresses showed the highest convergence with each other in
both the root and shoot tissues, whereas wound showed secondarily high convergence
with these three stresses (Figure 8A).
Moreover, heat showed a relatively high convergence only with salt, and genotoxic
stress showed the lowest convergence compared with any of the other stresses (Figure 8A).
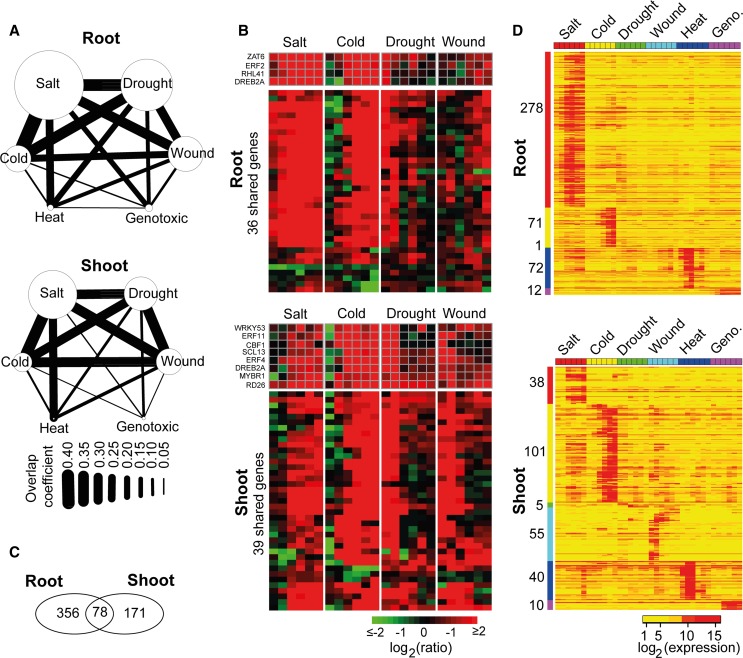
Figure 8.
Stress-Shared and Stress-Specific Gene Expression.
(A) “Convergence degree” between the six stresses in roots and shoots.
(B) Expression heat map of 36 (root) and 39 (shoot) shared genes commonly identified in salt, cold, drought, and wound stresses.
(C) Venn diagram of stress-specific expressed genes in roots and shoots.
(D) Expression heat map of stress-specific expressed genes in roots and shoots. Geno., genotoxic.
We found only four genes that were shared by salt, cold, drought, wound, and heat, without any shared genes found in genotoxic stress: HEAT SHOCK PROTEIN70, MULTIPROTEIN BRIDGING FACTOR1C (MBF1C), BETA-GALACTOSIDASE4, and EARLY-RESPONSIVE TO DEHYDRATION7. It has been reported that the constitutive expression of MBF1C in Arabidopsis enhances tolerance to salt, drought, and heat stresses (Suzuki et al., 2005).The salt, cold, drought, and wound stresses shared with 36 and 39 genes in roots and shoots, respectively, including 11 TF-encoding genes, among which DEHYDRATION-RESPONSIVE ELEMENT BINDING PROTEIN2A (DREB2A) was the only TF found in both the root and shoot tissues (Figure 8B; Supplemental Data Set 6). DREB2A has been demonstrated to play important roles in improving the stress tolerance of plants by specifically interacting with cis-acting dehydration-responsive element/C-repeat in the promoter region of various abiotic stress–responsive genes (Sakuma et al., 2006; Lata and Prasad, 2011). Most of these shared genes were upregulated after stress treatments, but the response times were different according to the stress and tissue types. In roots, the shared genes were upregulated at 0.5 and 3 h after salt and cold stress treatment, respectively. In the drought (shoot and root) samples, shared genes were upregulated at 0.5 and 1 h and then recovered to the normal level of expression after 3 h. This response pattern in drought is likely attributed to the experimental design: The plants were stressed by 15 min of dry air stream until there was a 10% loss in the fresh weight followed by normal growth in the climate chamber (Kilian et al., 2007). Hence, positive regulation of the a set of genes was immediately activated by the 15-min dry-air treatment, and when the plants were returned to normal conditions, the expression level of these genes declined to normal status. A similar pattern of regulation was also observed in wound (shoot) samples (Figure 8B), which was also likely due to the experimental design for wound treatment: The leaves of the plants were punctured by a pin-tool with 16 needles, and then shoot and root tissues were harvested for expression profiling (Kilian et al., 2007). In the wound (root) sample, a set of genes were not upregulated at 0.5, 1, and 3 h but were slightly upregulated from 6 to 24 h. Thus, because the root tissue was not directly wounded (Kilian et al., 2007), stress signals from the wounded shoot tissue may have required a few hours to be transmitted to the roots.
Stress-Specific Expressed Genes
Subsequently, we identified stress-specific expressed genes in roots and shoots that might be used as expression signatures for individual stress conditions. “Stress-specific expressed genes” refers to the genes that were transcriptionally activated to be highly expressed under only one stress condition but were not expressed or were minimally expressed under the other five stress conditions. We used a relatively stringent criterion to define “stress specificity” by measuring the difference in the maximum expression value of a gene under one stress condition against its maximum expression value under the other five stress conditions (see Methods). Overall, we identified 605 stress-specific expressed genes, including 356 genes in roots, 171 genes in shoots, and 78 that were shared by both tissues (Figure 8C; Supplemental Data Set 7). Whereas roots contained the highest number of salt-specific genes (278 genes), which were mostly activated after 0.5 or 1 h, shoots contained the most cold-specific genes (101 genes), which were mostly activated after 3 or 6 h (Figure 8D). This pattern was consistent with roots and shoots being the tissues that first sense the change in the salinity and temperature, respectively. We detected 55 wound-specific genes in shoots but none in roots, most likely because the wounding experiment was applied to the leaves of the plants without directly affecting the root tissue (Kilian et al., 2007). Under salt, cold, and genotoxic stress conditions, once the stress-specific genes had been transcriptionally activated at early time points, the high expression status of these genes was retained through the 24-h period. By contrast, the stress-specific genes for wound and heat showed the opposite trend: They were immediately activated at 0.5, 1, and 3 h, followed by recovering to nonexpression or a low-level expression status. This trend might also be explained by the experimental method for heat stress: The plants were treated for 3 h under 38°C heat stress in an incubator, followed by a 3-h recovery at 25°C (Kilian et al., 2007). This arrangement was likely the reason for the termination of the transcription activity of heat-specific genes as soon as the plants were returned to the normal growth temperature. We found only five drought-specific genes, one of which encodes a drought-induced TF, EFR53, that belongs to the AP2/EFR family.
Implementation of mlDNA
The workflow of the mlDNA was implemented as an R package (http://cran.r-project.org/web/packages/mlDNA; with a tutorial available at http://www.cmbb.arizona.edu/mlDNA/). The primary functional modules of mlDNA include a ML-based gene filtering process to classify “noninformative” and “informative” genes, large-scale GCN construction based on the GCC algorithm, and ML-based DN analysis to identify candidate stress-related genes. For GCN construction, mlDNA also provides four additional correlation methods (i.e., the Pearson product-moment correlation coefficient, Spearman's rank correlation coefficient, the Kendall tau rank correlation coefficient, and Tukey’s biweight correlation [Hardin et al., 2007]) and two noncorrelation methods (i.e., the mutual information and maximal information coefficient [Reshef et al., 2011]). For the DN analysis, gene expression matrices (genes in rows and samples in columns) under two different biological conditions are required for mlDNA. To perform ML analysis, the user provides a list of genes of interest as a positive sample set, which may be compiled based on GO annotation or other user-collected resources. The mlDNA package has integrated the 32 expression and 33 network characteristics used in this study into one function, which allows users to perform PSOL-based gene filtering and DN analysis. Users are also allowed to edit the feature matrix or provide a customized feature matrix for ML. By default, the mlDNA package constructs a prediction model using the RF classification model. Two other ML algorithms, the support vector machine and neural network, are also included via calling the R packages “e1071” and “nnet.” We also integrated the cross-validation algorithm and ROC analysis into mlDNA to allow users to evaluate the performance of the prediction models. To facilitate the downstream bioinformatic analysis of mlDNA predictions, we also implemented the algorithms for calculating the activity of biological pathways, estimating the “convergence degree” between different conditions (e.g., stresses) and detecting condition-specific expressed genes in the R package mlDNA.
METHODS
5-Fold Cross-Validation and ROC Curve Analysis
Cross-validation is an evaluation method that is widely used in ML for assessing the performance of a ML-based binary (two-class) classification model. In a 5-fold cross-validation algorithm, positive and negative samples are randomly partitioned into five groups that have an approximately equal number of genes, and each group is successively used for testing the performance of the ML system trained with the other four groups of positive and negative samples. For each cross-validation, the prediction accuracy of the ML-based RF classification model was assessed using ROC curve analysis. The ROC curve is a two-dimensional plot of the FPR (x axis) versus the TPR (y axis) at all possible thresholds. The value of the area under the ROC curve (AUC) was used to quantitatively score the prediction accuracy of the RF model. The AUC value ranges from 0 to 1, and a higher AUC value indicates better prediction accuracy for the RF model. After five groups have been successively used as the testing set, the five sets of (FPR and TPR) pairs were imported into the R package ROCR to visualize the ROC curves. The mean value of five AUCs was then computed as the overall performance of the ML system.
Computation of Expression Characteristics
Z-score measures the within-condition expression variations of a gene. Under
condition C(control [C0] or stress
[C1]), the z-score of gene i at time point
j is defined as: 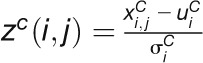 , where
, where
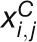 is
the log-transformed expression value of gene i at time point
j,
is
the log-transformed expression value of gene i at time point
j, 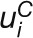 and
and 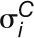 are the mean and sd of gene expression values across
six time points under the condition C, respectively. CV measures the stability of expression values
of a gene under a condition. The CV of gene
i under condition C is calculated with the
following formula:
are the mean and sd of gene expression values across
six time points under the condition C, respectively. CV measures the stability of expression values
of a gene under a condition. The CV of gene
i under condition C is calculated with the
following formula: 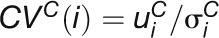 Fold change measures the ratio of the gene’s expression
values between control and stress conditions. The fold-change of gene
i at time point j is defined as:
Fold change measures the ratio of the gene’s expression
values between control and stress conditions. The fold-change of gene
i at time point j is defined as:
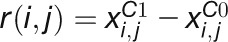 .
.
ML-Based Gene Filtering Using the PSOL Algorithm
The PSOL is developed for an ML-based binary classification system without prespecified negative samples. This approach has been previously applied to predict genomic loci encoding functional noncoding RNAs (Wang et al., 2006). In the ML process, the positive samples were the known stress-related genes, and genes not included in the positive sample set were called “unlabeled” samples (Supplemental Figure 1). The PSOL algorithm first selected a set of negative samples from “unlabeled” sample set based on the maximal Euclidean distances to known stress-related genes and then expanded negative samples iteratively using the RF classifier until the designated iteration number was reached. The genes retained in “unlabeled” samples were classified as “informative” genes. After each iteration, the prediction accuracy of the RF classifier was tested with the positive samples (i.e., known stress-related genes) and negative samples (i.e., “noninformative” genes) using the 5-fold cross-validation method and the AUC value generated from the ROC analysis. In general, a higher AUC value indicates that the expression characteristics of “noninformative” genes are quite different from those of known stress-related genes. The RF classifier with the best performance obtained from the 5-fold cross-validation was used to score known stress-related genes and genes in the “unlabeled” samples. “Noninformative” genes were extracted from the “unlabeled” samples with a user-adjustable threshold to ensure that a large fraction of known stress-related genes (98%) can be correctly identified.
Gene Coexpression Network Construction
The ML-based gene filtering process
identified “informative” genes for each stress data set. The GCN for a time-series stress experiment was then
constructed based on the concordant expression patterns of known stress-related genes
and “informative” genes inferred by the GCC algorithm (Ma and Wang,
2012). For a given gene pair (X, Y), the
GCC algorithm produces two correlation
values (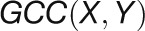 and
and 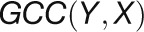 ) by
reciprocally using the value information of one gene and the rank information of the
other gene with the following formula:
) by
reciprocally using the value information of one gene and the rank information of the
other gene with the following formula: 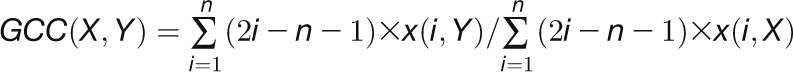 , and
, and
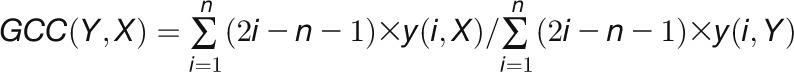 ,
where n is the number of time points.
,
where n is the number of time points.
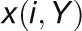 and
and 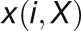 are
the ith value of gene expression profile
X sorted in an increasing order based on the expression values of
gene Y and X, respectively.
are
the ith value of gene expression profile
X sorted in an increasing order based on the expression values of
gene Y and X, respectively.
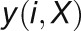 and
and 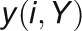 are
defined similarly to
are
defined similarly to 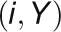 and
and 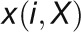 , respectively. The correlation value with the maximum absolute
value was chosen as the final GCC
correlation (Ma and Wang, 2012). For a
stress expression data set, we first calculated the GCCs for all possible pairs of
genes used for network construction and then estimated the significance level (P
value) of each GCC using the permutation
method to generate the background distribution of the correlations by permuting the
expression levels of these genes. Two genes were linked in the constructed network if
the P value of their correlation was ≤ 0.01.
, respectively. The correlation value with the maximum absolute
value was chosen as the final GCC
correlation (Ma and Wang, 2012). For a
stress expression data set, we first calculated the GCCs for all possible pairs of
genes used for network construction and then estimated the significance level (P
value) of each GCC using the permutation
method to generate the background distribution of the correlations by permuting the
expression levels of these genes. Two genes were linked in the constructed network if
the P value of their correlation was ≤ 0.01.
Computation of Gene Network Characteristics
Centrality Features
“Connectivity,” which is also known as “degree,”
measures the number of other genes that are directly connected to a gene in a
network (Horvath and Dong, 2008):
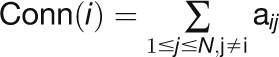 , where the GCN can
be represented by a symmetric adjacency matrix
, where the GCN can
be represented by a symmetric adjacency matrix 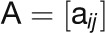 that is inferred from the
correlation matrix
that is inferred from the
correlation matrix 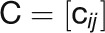 , for
, for 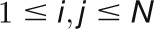 and N is the
total number of genes in the network. Here,
and N is the
total number of genes in the network. Here, 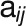 is a value between 0 and 1,
where 0 indicates that the correlation between genes i and
j(
is a value between 0 and 1,
where 0 indicates that the correlation between genes i and
j(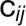 ) is not statistically significant and these genes are not
connected in the network, and 1 represents the fact that the correlation between
genes i and j is statistically significant and
these two genes are considered to be connected in the network.
) is not statistically significant and these genes are not
connected in the network, and 1 represents the fact that the correlation between
genes i and j is statistically significant and
these two genes are considered to be connected in the network.
“PosConnectivity” measures the number of connections that have positive correlation coefficients in a network (Gustin et al., 2008), which is defined as:
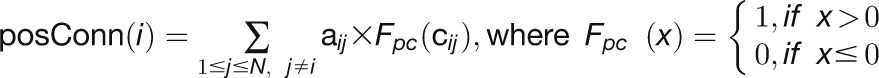 |
“NegConnectivity” measures the number of connections that have negative correlation coefficients in a network (Gustin et al., 2008), which is defined as:
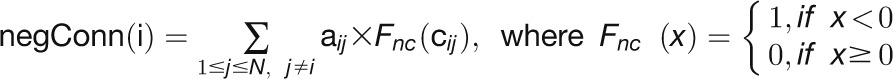 |
“Closeness” measures how close a gene is to
other genes in the network (Freeman,
1978): 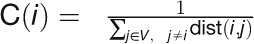 , where
, where 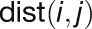 represents the minimal distance
of gene i to gene j in the network and is
calculated with the R package igraph. V denotes the set of genes
in the whole network.
represents the minimal distance
of gene i to gene j in the network and is
calculated with the R package igraph. V denotes the set of genes
in the whole network.
“Eccentricity” describes how easily accessible a gene is from other
genes (Hage and Harary, 1995), which is
defined as: 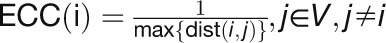 .
.
“Eigenvector” measures the importance of the nodes in the whole
network, especially favoring the nodes that are connected to important neighbors
(Bonacich, 2007). For gene
i, the eigenvector centrality score is proportional to the sum
of the scores of its directly connected genes and is calculated with the following
formula: 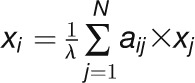 , where
, where 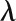 is a constant that satisfies
the equation
is a constant that satisfies
the equation 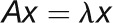 .
.
“PageRank” is a variant of the eigenvector and was previously used
by the Google Web search engine to search for important Web pages (Page et al., 1999). For gene
i, the PageRank centrality score is defined as:
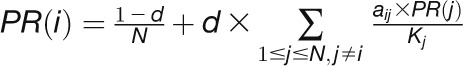 , where d is the damping factor, which is
usually set at 0.85 (Page et al.,
1999).
, where d is the damping factor, which is
usually set at 0.85 (Page et al.,
1999).
Network Characteristics of a Gene That Is Directly Connected to Known Stress-Related Genes
“Dist2knodes” measures the distance of one gene to all of the known
stress-related genes in the network: 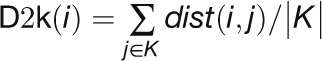 , where K
denotes the set of known stress-related genes.
, where K
denotes the set of known stress-related genes.
“Closeness2knodes” estimates the importance of genes that can
communicate quickly with known stress-related genes:
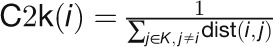 .
.
“Eccentricity2knodes” calculates how easily accessible a gene is
from the known stress-related genes: 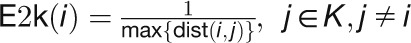 .
.
Network Difference
For each gene, network differences were first measured for differences in the
centrality feature values in stress and control networks and then characterized
with two additional features: “ASC” and “corDistance.” “ASC” is the mean number of connections that
specifically exist in either the control or stress network (Choi et al., 2005): 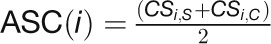 , where
, where
 and
and  denote the number of specific
connections in the stress and control network, respectively.
denote the number of specific
connections in the stress and control network, respectively.
“corDistance” measures the change in the correlation strengths of a
gene between its connected genes in the stress and control networks (Liu et al., 2010):
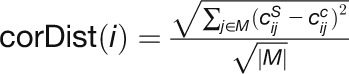 , where
, where 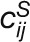 and
and
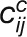 represent the correlation between gene i
and j in the stress and control conditions, respectively.
M denotes the set of connected genes for gene
i in the two compared networks. |M| is the
number of genes in the gene set M.
represent the correlation between gene i
and j in the stress and control conditions, respectively.
M denotes the set of connected genes for gene
i in the two compared networks. |M| is the
number of genes in the gene set M.
Expression Difference
“expDistance” is the Euclidean distance between two expression
profiles of one gene in the control and stress samples:
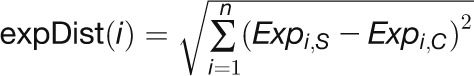 , where
, where 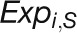 and
and
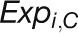 represent the log2-transformed expression values
of a gene at time point i in the stress and control samples,
respectively.
represent the log2-transformed expression values
of a gene at time point i in the stress and control samples,
respectively.
Stress Specificity Score
The stress specificity of a gene for stress condition S is defined
as: 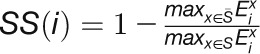 ,
where
,
where 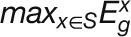 and
and 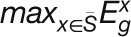 represent the maximum expression values of gene i under one stress S
and under other stresses, respectively. Thus, the higher the stress specificity score
of a gene is for a stress, the more likely the gene is to be specifically expressed
under this stress. We set a stress specificity threshold of 0.75 for detecting
stress-specific expressed genes in this study.
represent the maximum expression values of gene i under one stress S
and under other stresses, respectively. Thus, the higher the stress specificity score
of a gene is for a stress, the more likely the gene is to be specifically expressed
under this stress. We set a stress specificity threshold of 0.75 for detecting
stress-specific expressed genes in this study.
Phenotypic Screen of Candidate Stress-Related Genes under Salt Treatment
The Arabidopsis thaliana Col-0 ecotype was used as the wild-type control. We selected 89 candidate stress-related genes, based on the availability of homozygous lines, for phenotypic screening using SALK T-DNA insertion lines obtained from the ABRC (Alonso et al., 2003). We first conducted a preliminary screen using 100 mM NaCl as salt treatment. The wild-type and mutant seeds were sterilized for 10 min in a solution containing 12% sodium hypochlorite and 0.1% Triton X-100 and then rinsed with sterile water five times. The seeds were then cold treated in water for 3 d at 4°C in the dark. Subsequently, the seeds were plated on half-strength MS medium (supplemented with 0.5% [w/v] Suc and 0.3% Phytagel agar; Sigma-Aldrich) to allow for germination and growth for 5 d. Two mutant lines showing a strong phenotypic response, SALK_061811C for AT3G16270 and SALK_002548C for AT2G41530, were tested on different salt concentrations, 75, 100, and 150 mM NaCl, to further confirm their phenotypes. The wild-type and mutant seedlings were photographed and their root lengths were measured at 10 d after transfer.
Accession Numbers
The Affymetrix microarray data set reanalyzed in this article can be downloaded from the AtGenExpress database (http://www.weigelworld.org/resources/microarray/AtGenExpress). The design information of SALK lines for AT3G16270 and AT2G41530 can be found in the TAIR database under accession numbers SALK_061811C and SALK_002548C, respectively. The accession number of all analyzed genes is given in Supplemental Data Set 2.
Supplemental Data
The following materials are available in the online version of this article.
Supplemental Figure 1. Workflow of the Gene Filtering Process Based on the ML-Based RandomForest Classification Model Using the Positive Sample-Only Learning Algorithm.
Supplemental Figure 2. Comparison of the Distributions of Two Network Characteristics, Positive and Negative Connectivity, of Known Stress-Related Genes and “Informative” Genes in Control and Stress Networks to Illustrate Network Changes in the Two Networks.
Supplemental Figure 3. Determination of the Prediction Threshold of the RF Classification Model Using the F-Score Algorithm.
Supplemental Figure 4. The Percentages of Differentially Expressed Genes in mlDNA-Predicted Stress-Related Candidate Genes.
Supplemental Figure 5. Number of Salt Stress–Related Genes in the GO Category “Response to Stimulus” and Its Three Daughter GO Categories.
The following materials have been deposited in the DRYAD repository under accession number http://dx.doi.org/10.5061/dryad.41b9g.
Supplemental Data Set 1. Known Stress-Related Genes Collected from the TAIR and DRASTIC Databases, Their Expression Changes in the Stress Microarray Data Sets, and the Statistical Results of Their Gene Ontology Annotations.
Supplemental Data Set 2. “Informative” Genes Obtained from PSOL-Based ML Analysis for Gene Coexpression Network Construction under Six Studied Stresses in Two Tissues.
Supplemental Data Set 3. Candidate Stress-Related Genes Predicted by mlDNA.
Supplemental Data Set 4. List of the Candidate Stress-Related Genes Evidenced by a High-Throughput Phenotypic Screening Experiment.
Supplemental Data Set 5. Detailed Information for Gene Ontology Modules Enriched with Salt Stress–Related Genes.
Supplemental Data Set 6. List of Stress-Shared Genes.
Supplemental Data Set 7. List of Stress-Specific Genes.
Supplementary Material
Acknowledgments
This work was supported by U.S. National Science Foundation Grant DBI-1261830 (to X.W.). K.A.F. acknowledges the ABRC for seeds used in this research.
AUTHOR CONTRIBUTIONS
C.M. and X.W. designed the research, analyzed the data, and wrote the article. M.X. and K.A.F. performed the phenotypic screening experiment.
Glossary
- DE
differential expression
- FDR
false discovery rate
- TPR
true positive rate
- FPR
false positive rate
- DN
differential network
- GCN
gene coexpression network
- ML
machine learning
- mlDNA
machine learning–based differential network analysis
- GO
gene ontology
- RF
random forest
- PSOL
positive sample-only learning
- CV
coefficient of variation
- AUC
area under the curve
- ROC
receiver operating characteristic
- GCC
Gini correlation coefficient
- TF
transcription factor
- ASC
average of specific connection
- SAM
significance analysis of microarrays (
- Col-0
Columbia-0
- MS
Murashige and Skoog
- EM
Enrichment Map
Footnotes
Online version contains Web-only data.
References
- Abeel T., Van de Peer Y., Saeys Y. (2009). Toward a gold standard for promoter prediction evaluation. Bioinformatics 25: i313–i320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert R. (2007). Network inference, analysis, and modeling in systems biology. Plant Cell 19: 3327–3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alipanahi B., Frey B.J. (2013). Network cleanup. Nat. Biotechnol. 31: 714–715. [DOI] [PubMed] [Google Scholar]
- Alonso J.M., et al. (2003). Genome-wide insertional mutagenesis of Arabidopsis thaliana. Science 301: 653–657. [DOI] [PubMed] [Google Scholar]
- Amar D., Safer H., Shamir R. (2013). Dissection of regulatory networks that are altered in disease via differential co-expression. PLOS Comput. Biol. 9: e1002955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baena-González E., Sheen J. (2008). Convergent energy and stress signaling. Trends Plant Sci. 13: 474–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandyopadhyay S., et al. (2010). Rewiring of genetic networks in response to DNA damage. Science 330: 1385–1389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bansal M., Belcastro V., Ambesi-Impiombato A., di Bernardo D. (2007). How to infer gene networks from expression profiles. Mol. Syst. Biol. 3: 78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási A.L., Oltvai Z.N. (2004). Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 5: 101–113. [DOI] [PubMed] [Google Scholar]
- Bassel G.W., Gaudinier A., Brady S.M., Hennig L., Rhee S.Y., De Smet I. (2012). Systems analysis of plant functional, transcriptional, physical interaction, and metabolic networks. Plant Cell 24: 3859–3875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassel G.W., Glaab E., Marquez J., Holdsworth M.J., Bacardit J. (2011). Functional network construction in Arabidopsis using rule-based machine learning on large-scale data sets. Plant Cell 23: 3101–3116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. (1995). Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57: 289–300. [Google Scholar]
- Bonacich P. (2007). Some unique properties of eigenvector centrality. Soc. Networks 29: 555–564. [Google Scholar]
- Boulesteix A.L., Slawski M. (2009). Stability and aggregation of ranked gene lists. Brief. Bioinform. 10: 556–568. [DOI] [PubMed] [Google Scholar]
- Breiman L. (2001). Random forests. Mach. Learn. 45: 5–32. [Google Scholar]
- Califano A. (2011). Rewiring makes the difference. Mol. Syst. Biol. 7: 463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao W.H., Liu J., He X.J., Mu R.L., Zhou H.L., Chen S.Y., Zhang J.S. (2007). Modulation of ethylene responses affects plant salt-stress responses. Plant Physiol. 143: 707–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter S.L., Brechbühler C.M., Griffin M., Bond A.T. (2004). Gene co-expression network topology provides a framework for molecular characterization of cellular state. Bioinformatics 20: 2242–2250. [DOI] [PubMed] [Google Scholar]
- Choi J.K., Yu U., Yoo O.J., Kim S. (2005). Differential coexpression analysis using microarray data and its application to human cancer. Bioinformatics 21: 4348–4355. [DOI] [PubMed] [Google Scholar]
- Cui X., Churchill G.A. (2003). Statistical tests for differential expression in cDNA microarray experiments. Genome Biol. 4: 210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de la Fuente A. (2010). From ‘differential expression’ to ‘differential networking’ - Identification of dysfunctional regulatory networks in diseases. Trends Genet. 26: 326–333. [DOI] [PubMed] [Google Scholar]
- De Smet R., Marchal K. (2010). Advantages and limitations of current network inference methods. Nat. Rev. Microbiol. 8: 717–729. [DOI] [PubMed] [Google Scholar]
- Díaz-Uriarte R., Alvarez de Andrés S. (2006). Gene selection and classification of microarray data using random forest. BMC Bioinformatics 7: 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elo L.L., Järvenpää H., Oresic M., Lahesmaa R., Aittokallio T. (2007). Systematic construction of gene coexpression networks with applications to human T helper cell differentiation process. Bioinformatics 23: 2096–2103. [DOI] [PubMed] [Google Scholar]
- Ferrier T., Matus J.T., Jin J., Riechmann J.L. (2011). Arabidopsis paves the way: Genomic and network analyses in crops. Curr. Opin. Biotechnol. 22: 260–270. [DOI] [PubMed] [Google Scholar]
- Freeman L.C. (1978). Centrality in social networks: Concept clarification. Soc. Networks 1: 215–239. [Google Scholar]
- Friedel S., Usadel B., von Wirén N., Sreenivasulu N. (2012). Reverse engineering: A key component of systems biology to unravel global abiotic stress cross-talk. Front. Plant Sci. 3: 294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujita M., Fujita Y., Noutoshi Y., Takahashi F., Narusaka Y., Yamaguchi-Shinozaki K., Shinozaki K. (2006). Crosstalk between abiotic and biotic stress responses: A current view from the points of convergence in the stress signaling networks. Curr. Opin. Plant Biol. 9: 436–442. [DOI] [PubMed] [Google Scholar]
- Fuller T.F., Ghazalpour A., Aten J.E., Drake T.A., Lusis A.J., Horvath S. (2007). Weighted gene coexpression network analysis strategies applied to mouse weight. Mamm. Genome 18: 463–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill R., Datta S., Datta S. (2010). A statistical framework for differential network analysis from microarray data. BMC Bioinformatics 11: 95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gustin M.P., Paultre C.Z., Randon J., Bricca G., Cerutti C. (2008). Functional meta-analysis of double connectivity in gene coexpression networks in mammals. Physiol. Genomics 34: 34–41. [DOI] [PubMed] [Google Scholar]
- Hage P., Harary F. (1995). Eccentricity and centrality in networks. Soc. Networks 17: 57–63. [Google Scholar]
- Hardin J., Mitani A., Hicks L., VanKoten B. (2007). A robust measure of correlation between two genes on a microarray. BMC Bioinformatics 8: 220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X.J., Mu R.L., Cao W.H., Zhang Z.G., Zhang J.S., Chen S.Y. (2005). AtNAC2, a transcription factor downstream of ethylene and auxin signaling pathways, is involved in salt stress response and lateral root development. Plant J. 44: 903–916. [DOI] [PubMed] [Google Scholar]
- Horvath S., Dong J. (2008). Geometric interpretation of gene coexpression network analysis. PLOS Comput. Biol. 4: e1000117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson N.J., Dalrymple B.P., Reverter A. (2012). Beyond differential expression: The quest for causal mutations and effector molecules. BMC Genomics 13: 356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson N.J., Reverter A., Dalrymple B.P. (2009). A differential wiring analysis of expression data correctly identifies the gene containing the causal mutation. PLOS Comput. Biol. 5: e1000382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang S., Rhee S.Y., Marcotte E.M., Lee I. (2011). Systematic prediction of gene function in Arabidopsis thaliana using a probabilistic functional gene network. Nat. Protoc. 6: 1429–1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iancu O.D., Kawane S., Bottomly D., Searles R., Hitzemann R., McWeeney S. (2012). Utilizing RNA-Seq data for de novo coexpression network inference. Bioinformatics 28: 1592–1597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T., Krogan N.J. (2012). Differential network biology. Mol. Syst. Biol. 8: 565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jia W., Wang Y., Zhang S., Zhang J. (2002). Salt-stress-induced ABA accumulation is more sensitively triggered in roots than in shoots. J. Exp. Bot. 53: 2201–2206. [DOI] [PubMed] [Google Scholar]
- Jiang P., Wu H., Wang W., Ma W., Sun X., Lu Z. (2007). MiPred: Classification of real and pseudo microRNA precursors using random forest prediction model with combined features. Nucleic Acids Res. 35: W339–W344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y., Deyholos M.K. (2006). Comprehensive transcriptional profiling of NaCl-stressed Arabidopsis roots reveals novel classes of responsive genes. BMC Plant Biol. 6: 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalkatawi M., Rangkuti F., Schramm M., Jankovic B.R., Kamau A., Chowdhary R., Archer J.A., Bajic V.B. (2012). Dragon PolyA Spotter: Predictor of poly(A) motifs within human genomic DNA sequences. Bioinformatics 28: 127–129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilian J., Whitehead D., Horak J., Wanke D., Weinl S., Batistic O., D’Angelo C., Bornberg-Bauer E., Kudla J., Harter K. (2007). The AtGenExpress global stress expression data set: Protocols, evaluation and model data analysis of UV-B light, drought and cold stress responses. Plant J. 50: 347–363. [DOI] [PubMed] [Google Scholar]
- Kleessen S., Klie S., Nikoloski Z. (2013). Data integration through proximity-based networks provides biological principles of organization across scales. Plant Cell 25: 1917–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krouk G., Mirowski P., LeCun Y., Shasha D.E., Coruzzi G.M. (2010). Predictive network modeling of the high-resolution dynamic plant transcriptome in response to nitrate. Genome Biol. 11: R123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lata C., Prasad M. (2011). Role of DREBs in regulation of abiotic stress responses in plants. J. Exp. Bot. 62: 4731–4748. [DOI] [PubMed] [Google Scholar]
- Lee I., Ambaru B., Thakkar P., Marcotte E.M., Rhee S.Y. (2010). Rational association of genes with traits using a genome-scale gene network for Arabidopsis thaliana. Nat. Biotechnol. 28: 149–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Less H., Angelovici R., Tzin V., Galili G. (2011). Coordinated gene networks regulating Arabidopsis plant metabolism in response to various stresses and nutritional cues. Plant Cell 23: 1264–1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lexa M., Martínek T., Burgetová I., Kopeček D., Brázdová M. (2011). A dynamic programming algorithm for identification of triplex-forming sequences. Bioinformatics 27: 2510–2517. [DOI] [PubMed] [Google Scholar]
- Li S., Pandey S., Gookin T.E., Zhao Z., Wilson L., Assmann S.M. (2012). Gene-sharing networks reveal organizing principles of transcriptomes in Arabidopsis and other multicellular organisms. Plant Cell 24: 1362–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu B.H., Yu H., Tu K., Li C., Li Y.X., Li Y.Y. (2010). DCGL: An R package for identifying differentially coexpressed genes and links from gene expression microarray data. Bioinformatics 26: 2637–2638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long T.A., Brady S.M., Benfey P.N. (2008). Systems approaches to identifying gene regulatory networks in plants. Annu. Rev. Cell Dev. Biol. 24: 81–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Kleine L., Leal L., López C. (2013). Biostatistical approaches for the reconstruction of gene co-expression networks based on transcriptomic data. Brief Funct. Genomics 12: 457–467. [DOI] [PubMed] [Google Scholar]
- Luhua S., et al. (2013). Linking genes of unknown function with abiotic stress responses by high-throughput phenotype screening. Physiol. Plant. 148: 322–333. [DOI] [PubMed] [Google Scholar]
- Ma C., Wang X. (2012). Application of the Gini correlation coefficient to infer regulatory relationships in transcriptome analysis. Plant Physiol. 160: 192–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maere S., Heymans K., Kuiper M. (2005). BiNGO: A Cytoscape plugin to assess overrepresentation of gene ontology categories in biological networks. Bioinformatics 21: 3448–3449. [DOI] [PubMed] [Google Scholar]
- Mahajan S., Tuteja N. (2005). Cold, salinity and drought stresses: An overview. Arch. Biochem. Biophys. 444: 139–158. [DOI] [PubMed] [Google Scholar]
- Marbach D., et al. DREAM5 Consortium (2012). Wisdom of crowds for robust gene network inference. Nat. Methods 9: 796–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merico D., Isserlin R., Stueker O., Emili A., Bader G.D. (2010). Enrichment map: a network-based method for gene-set enrichment visualization and interpretation. PLoS ONE 5: e13984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mjolsness E., DeCoste D. (2001). Machine learning for science: State of the art and future prospects. Science 293: 2051–2055. [DOI] [PubMed] [Google Scholar]
- Moreno-Risueno M.A., Busch W., Benfey P.N. (2010). Omics meet networks - Using systems approaches to infer regulatory networks in plants. Curr. Opin. Plant Biol. 13: 126–131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Page, L., Brin, S., Motwani, R., and Winograd, T. (1999). The PageRank Citation Ranking: Bring Order to the Web. (Stanford, CA:Stanford InfoLab). [Google Scholar]
- Piao Y., Piao M., Park K., Ryu K.H. (2012). An ensemble correlation-based gene selection algorithm for cancer classification with gene expression data. Bioinformatics 28: 3306–3315. [DOI] [PubMed] [Google Scholar]
- Pirooznia M., Yang J.Y., Yang M.Q., Deng Y. (2008). A comparative study of different machine learning methods on microarray gene expression data. BMC Genomics 9 (suppl. 1): S13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapaport F., Khanin R., Liang Y., Pirun M., Krek A., Zumbo P., Mason C.E., Socci N.D., Betel D. (2013). Comprehensive evaluation of differential gene expression analysis methods for RNA-seq data. Genome Biol. 14: R95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen S., Barah P., Suarez-Rodriguez M.C., Bressendorff S., Friis P., Costantino P., Bones A.M., Nielsen H.B., Mundy J. (2013). Transcriptome responses to combinations of stresses in Arabidopsis. Plant Physiol. 161: 1783–1794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reshef D.N., Reshef Y.A., Finucane H.K., Grossman S.R., McVean G., Turnbaugh P.J., Lander E.S., Mitzenmacher M., Sabeti P.C. (2011). Detecting novel associations in large data sets. Science 334: 1518–1524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakuma Y., Maruyama K., Osakabe Y., Qin F., Seki M., Shinozaki K., Yamaguchi-Shinozaki K. (2006). Functional analysis of an Arabidopsis transcription factor, DREB2A, involved in drought-responsive gene expression. Plant Cell 18: 1292–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schechtman E., Yitzhaki S. (1999). On the proper bounds of the Gini correlation. Econ. Lett. 63: 6. [Google Scholar]
- Smyth G.K. (2004). Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol. 3: e3. [DOI] [PubMed] [Google Scholar]
- Southworth L.K., Owen A.B., Kim S.K. (2009). Aging mice show a decreasing correlation of gene expression within genetic modules. PLoS Genet. 5: e1000776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki N., Rizhsky L., Liang H., Shuman J., Shulaev V., Mittler R. (2005). Enhanced tolerance to environmental stress in transgenic plants expressing the transcriptional coactivator multiprotein bridging factor 1c. Plant Physiol. 139: 1313–1322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Touw W.G., Bayjanov J.R., Overmars L., Backus L., Boekhorst J., Wels M., van Hijum S.A. (2013). Data mining in the Life Sciences with Random Forest: A walk in the park or lost in the jungle? Brief. Bioinform. 14: 315–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tusher V.G., Tibshirani R., Chu G. (2001). Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl. Acad. Sci. USA 98: 5116–5121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Urano K., Kurihara Y., Seki M., Shinozaki K. (2010). ‘Omics’ analyses of regulatory networks in plant abiotic stress responses. Curr. Opin. Plant Biol. 13: 132–138. [DOI] [PubMed] [Google Scholar]
- Usadel B., Obayashi T., Mutwil M., Giorgi F.M., Bassel G.W., Tanimoto M., Chow A., Steinhauser D., Persson S., Provart N.J. (2009). Co-expression tools for plant biology: Opportunities for hypothesis generation and caveats. Plant Cell Environ. 32: 1633–1651. [DOI] [PubMed] [Google Scholar]
- Van Landeghem S., De Bodt S., Drebert Z.J., Inzé D., Van de Peer Y. (2013). The potential of text mining in data integration and network biology for plant research: A case study on Arabidopsis. Plant Cell 25: 794–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C., Ding C., Meraz R.F., Holbrook S.R. (2006). PSoL: A positive sample only learning algorithm for finding non-coding RNA genes. Bioinformatics 22: 2590–2596. [DOI] [PubMed] [Google Scholar]
- Windram O., et al. (2012). Arabidopsis defense against Botrytis cinerea: Chronology and regulation deciphered by high-resolution temporal transcriptomic analysis. Plant Cell 24: 3530–3557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang H., Cheng C., Zhang W. (2011). Average rank-based score to measure deregulation of molecular pathway gene sets. PLoS ONE 6: e27579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yitzhaki S. (2003). Gini's mean difference: A superior measure of variability for non-normal distributions. METRON LXI: 285–316. [Google Scholar]
- Yu H., Liu B.H., Ye Z.Q., Li C., Li Y.X., Li Y.Y. (2011). Link-based quantitative methods to identify differentially coexpressed genes and gene pairs. BMC Bioinformatics 12: 315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J.K. (2002). Salt and drought stress signal transduction in plants. Annu. Rev. Plant Biol. 53: 247–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.