The statistical power of epidemiological studies analyzing the relationship between exposure to ionizing radiation and cancer, with special reference to childhood leukemia and natural background radiation

Abstract

Little M.P., Wakeford R., Lubin J.H. and Kendall G.M., The statistical power of epidemiological studies analyzing the relationship between exposure to ionizing radiation and cancer, with special reference to childhood leukemia and natural background radiation. Radiat. Res. The etiology of childhood leukemia remains generally unknown, although risk models based on the Japanese A-bomb survivors imply that the dose accumulated from protracted exposure to low-level natural background ionizing radiation materially raises the risk of leukemia in children. In this paper a novel Monte Carlo score-test methodology is used to assess the statistical power of cohort, ecological and case-control study designs, using the linear low-dose part of the BEIR V model derived from the Japanese data. With 10 (or 20) years of follow-up of childhood leukemias in Great Britain, giving about 4600 (or 9200) cases, under an individual-based cohort design there is 67.9% (or 90.9%) chance of detecting an excess (at 5% significance level, 1-sided test); little difference is made by extreme heterogeneity in risk. For an ecological design these figures reduce to 57.9% (or 83.2%). Case-control studies with five controls per case achieve much of the power of a cohort design, 61.1% (or 86.0%). However, participation bias may seriously affect studies that require individual consent, and area-based studies are subject to severe interpretational problems. For this reason register-based studies, in particular those that make use of predicted doses that avoid the need for interviews, have considerable advantages. We argue that previous studies have been underpowered (all have power <80%), and some are also subject to unquantifiable biases and confounding. Sufficiently large studies should be capable of detecting the predicted risk attributable to natural background radiation.

The etiology of most childhood leukemias remains unknown, but exposure to moderate and high levels of ionizing radiation is an established risk factor. Risk models based on the Japanese atomic bomb survivors imply that low-level exposure to radiation appreciably increases the risk of childhood leukemia (1;2). Natural background radiation accounts for the greatest radiation exposure of the average member of the Great Britain (GB, i.e. England, Wales and Scotland) population and this has prompted interest in a possible link between radiation from natural sources and childhood leukemia. For example, in GB the mean annual effective dose from terrestrial gamma and cosmogenic radiation is estimated to be 0.68 mSv (3), and in the USA this figure is only slightly lower, 0.54 mSv (4). Wakeford et al. (5) showed that using risk models based on the latest Japanese atomic bomb survivor data (1;2) about one-fifth of the cases of childhood leukemia in GB might be attributable to natural background radiation, raising the possibility that such excess risk may be detectable in an epidemiological study.

Epidemiological studies investigating the role of natural background radiation in the etiology of childhood leukemia have been undertaken (2). Some studies (e.g., (6;7)) have reported a positive association between exposure to naturally-occurring radon and childhood leukemia; but in GB, various large studies (8–11) did not provide convincing evidence of a positive association with either background gamma radiation or radon. The purpose of this paper is to explore what may be the main reason for the failure to detect an effect – a lack of statistical power consequent on an insufficient number of cases. Other possible reasons are also considered in the Discussion.

In this paper we derive formulae for statistical power based on score tests for cohort, geographical correlation (“ecological”) and case-control study designs somewhat similar to those considered by Lubin and Gail (12), differing principally in that we assume a conditional likelihood and a linear relative risk, or odds ratio, function of exposure. We demonstrate that heterogeneity in the excess relative risk has minimal effect on the statistical power, and estimate the statistical power required to investigate realistically the relationship between childhood leukemia and natural background radiation. We consider both individual-based cohort studies and geographical correlation studies based on incidence and exposure averaged over areal units; formally, these two types of study are identical, but as we show the power of ecological studies is somewhat less than cohort studies because of the narrower dose distribution.

MATERIALS AND METHODS

Doses to red bone marrow

The main sources of exposure to natural background radiation are terrestrial gamma rays, cosmic rays, radionuclides in food and isotopes of the radioactive gas radon (13). The components of red bone marrow (RBM) dose that can be estimated on an individual basis in epidemiological studies account for about half the total such dose from natural radiation sources (Table A1). In epidemiological studies, measurements of gamma rays will generally have included the directly ionizing component of cosmic rays and in this paper we use the term “gamma” in this sense. A GB National Survey (3;14) provided evidence of indoor exposures to: (a) terrestrial gamma rays plus the directly ionizing component of cosmic rays; and (b) radon-222. Using methods described by Kendall et al. (15), these measurements were converted to annual doses to RBM and used to estimate deciles of the distribution of RBM dose from these components, separately or jointly (Tables A2–A3). We also derive the deciles of exposure distribution for English county districts and comparable administrative divisions elsewhere in GB. These typically contain a population of about 100,000, so that the variability of mean dose rates will be somewhat less than for individuals (Tables A2–A3).

Data on childhood leukemia

Annual numbers of registered incident cases of childhood leukemia by sex and year of age, diagnosed during 1991–2000 while resident in GB, and the derived incidence rates were obtained from the National Registry of Childhood Tumours (Table A4). This registry is thought to be substantially complete (16;17). All simulations are conditional on a given number of cases in each stratum (which is generally determined by age), as given by the age distribution implicit in Table A4.

Statistical methods

The methods used to calculate statistical power are given in Appendix B. Table 1 presents results for cohort, GB county district-based ecological and case-control studies, showing the percentage of normalized score simulations that are greater than the various assumed nominal values given in the leftmost column. These were calculated using the deciles of dose distribution given in Appendix A. To assess the distribution of the score statistic 100,000 simulations from the assumed distribution are used. From equations (B4) and (B5) in Appendix B the normalised score assuming a single stratum with 10 years of UK cases can be shown to have mean 2.325. Since this has variance 1 the Monte Carlo error for N samples will be $1/\sqrt{N}$, which for N = 100,000 is 0.0032, which we judge to be acceptably small. We assume a standard two-year minimum latent period for leukemia (1;2;18;19). For simplicity we employ the BEIR V leukemia risk model throughout, which is a pure excess relative risk (ERR) model (18). The more recent BEIR VII leukemia model (1) is a combination of additive and multiplicative models, and is less attractive for evaluating power in a case-control study, in which we make use of the near equivalence of odds ratio and relative risk. Since we are only concerned with expression of leukemia risk in childhood, and both models are based on the Japanese atomic bomb survivor mortality data (20;21), there should be minimal difference between them, driven mainly by the change in dosimetry system from DS86 to DS02 (21). The BEIR V leukemia excess relative risk (ERR) model (18) assumes a linear-quadratic dose-response, so that the leukemia risk in childhood in group i with underlying leukemia risk p_i and dose D_i is given by p_i[1 + θ[1 + βD_i]D_i]. At low doses the dose response curve is approximately linear with a slope (on the relative risk scale) of θ = ERR = 32.1 Sv⁻¹.

Table 1.

Distribution of Normalized Score Statistic (Based on 100,000 Monte Carlo Samples) for Hypothetical GB Childhood Leukemia Studies (Assuming that a 10-year Follow-up Results in 2593 Registrations Among Boys and 1983 Amongst Girls, and Assuming the BEIR V (18) Risk Coefficient (ERR = 32.15 Sv⁻¹))

Nominal score statistic	Percentile of standard normal distribution	Percent of simulations with score > nominal value
		Cohort study (individual)		Geographical correlation study (county district)		Case-control study (1 control per case)		Case-control study (5 controls per case)
		10-year follow-up	20-year follow-up	10-year follow-up	20-year follow-up	10-year follow-up	20-year follow-up	10-year follow-up	20-year follow-up
1.28	90.00	79.51	95.50	71.17	90.74	58.67	79.92	74.23	92.65
1.64	95.00	67.91	90.88	57.92	83.18	44.29	68.44	61.13	86.01
1.96	97.50	55.99	84.62	45.37	74.13	32.40	56.60	48.62	77.78
2.33	99.00	41.62	74.45	31.49	61.14	20.54	42.14	34.25	65.40
2.58	99.50	32.07	65.90	23.15	51.43	14.14	32.71	25.65	55.97
2.81	99.75	24.24	57.17	16.73	42.36	9.66	24.92	18.82	46.64
3.09	99.90	16.35	46.10	10.67	31.64	5.71	16.79	12.24	35.75
3.29	99.95	11.87	38.16	7.49	24.88	3.74	12.25	8.72	28.49
3.48	99.98	8.56	31.12	5.24	19.25	2.45	8.73	6.03	22.49
3.72	99.99	5.45	23.24	3.17	13.48	1.34	5.57	3.73	16.07

In Figure 1 we also assess the power for a population with heterogeneous risk. For illustrative purposes, we assume, somewhat arbitrarily, that the cohort is split into three: the first stratum, with 50% of the cases, is assumed to have the BEIR V ERR = 32.15 Sv⁻¹, and the other two strata, each with 25% of the cases, have ERR = 1.9 × 32.15 Sv⁻¹ = 61.08 Sv⁻¹ and 0.1 × 32.15 Sv⁻¹ = 3.21 Sv⁻¹, respectively. The risk coefficient multipliers 1.9 and 0.1 are ad hoc selections reflecting the range of values of ERR coefficients for childhood leukemia, which spans at least an order of magnitude, as highlighted by a recent review (22). Therefore, the “average” ERR is approximately the same as that of BEIR V, but with a substantial fraction having an ERR that is smaller or larger, reflecting an appreciable variation in the background risk of leukemia within the cohort.

Figure 1.

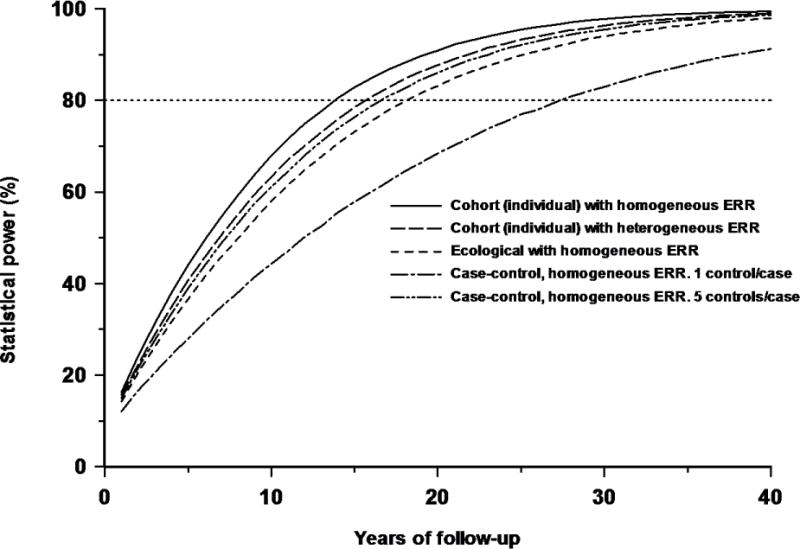
Influence of heterogeneity of excess relative risk (ERR) in a cohort on the power of a study to detect an increasing trend of risk with dose, and comparison with power of a geographical correlation study and a case-control study with one or five controls per case and the same excess odds ratio (EOR), all as a function of years of follow-up in a GB population. Five curves are presented: for a cohort with assumed homogeneous ERR of 32.15 Sv⁻¹, for a cohort with assumed heterogeneous ERR (see text), for an ecological (geographical correlation) study based on county district averages with a homogeneous ERR of 32.15 Sv⁻¹, and for a case-control study (with one or five controls per case) with the same (homogenous) EOR. The power illustrated is to detect a statistically significant (1-sided p=0.05) increasing trend of risk with dose, assuming distributions for RBM doses as in Table A2, and case distribution per year in the GB as in Table A4.

The BEIR V leukemia risk model applies only to radiation doses received after birth and not to doses received in utero. In order to accommodate risk from exposure in utero, we assume the intrauterine dose generates an excess risk throughout childhood with the same ERR coefficient. There is evidence that diagnostic X-ray exposure in utero induces a leukemia risk that is compatible with that produced by exposure in early childhood (23;24), although this evidence remains controversial (25), with some maintaining that there is no evidence of excess risk associated with in utero exposure (26). In Table 2 we explore the sensitivity of results to this assumption using calculations in which the in utero dose has no effect upon leukemia incidence; the Table shows the percentage of normalized score simulations that are greater than the various assumed nominal values given in the leftmost column. We also explore the effect of assuming that only radon or gamma radiation contributes to the induction of leukemia.

Table 2.

Distribution of Normalized Score Statistic (Based on 100,000 Monte Carlo Samples) for Hypothetical GB Childhood Leukemia Case-Control Study (5 Controls per Case) With Variant Assumptions (Radon Dose Only, Gamma Dose Only, No Contribution from In Utero Dose) (Assuming that a 10-year Follow-up Results in 2593 Registrations Among Boys and 1983 Amongst Girls, and Assuming the BEIR V (18) Risk Coefficient (ERR = 32.15 Sv⁻¹))

Nominal score statistic	Percentile of standard normal distribution	Percent of simulations with score > nominal value
		Radon dose only		Gamma dose only		No in utero dose
		10-year follow-up	20-year follow-up	10-year follow-up	20-year follow-up	10-year follow-up	20-year follow-up
1.28	90.00	37.81	53.53	65.03	85.91	70.43	90.19
1.64	95.00	25.04	39.17	50.85	76.18	56.84	82.24
1.96	97.50	16.21	28.05	38.28	65.43	44.14	72.91
2.33	99.00	8.88	17.11	25.34	51.25	30.47	59.60
2.58	99.50	5.49	11.71	18.09	41.43	22.22	49.74
2.81	99.75	3.42	7.83	12.75	32.63	16.03	40.57
3.09	99.90	1.79	4.44	7.76	23.23	10.16	30.03
3.29	99.95	1.08	2.86	5.27	17.57	7.07	23.57
3.48	99.98	0.67	1.83	3.57	13.15	4.83	18.19
3.72	99.99	0.35	1.02	2.01	8.74	2.93	12.61

We use separate strata for each calendar year of age and sex.

RESULTS

Table 1 shows that with a 10 year (or 20 year) follow-up of all GB childhood leukemias, after which there are 4576 (or 9152) registrations, there is 67.9% (or 90.9%) chance of detecting an excess score at the 1-sided 5% significance level for an individual-based cohort study, 57.9% (or 83.2%) for an area-based (county district) design, and 61.1% (or 86.0%) for a case-control study with five controls per case. Case-control studies with five controls per case achieve much of the statistical power of a cohort design (and are more powerful than area-based designs), 61.1% (or 86.0%), although the power is reduced with only a single control per case, 44.3% (or 68.4%) (Table 1, Figure 1). There is minimal improvement in power for more than five controls per case (Figure 2), e.g., with 10 and 20 controls per case the power with 20 years of follow-up is 88.6% and 89.9%, respectively. Figure 1 shows that the effects of heterogeneity in risk serve to slightly degrade the power of the individual-based cohort study, so that at 10 years (or 20 years) of follow-up there is 63.2% (or 87.7%) chance of detecting the excess.

Figure 2.

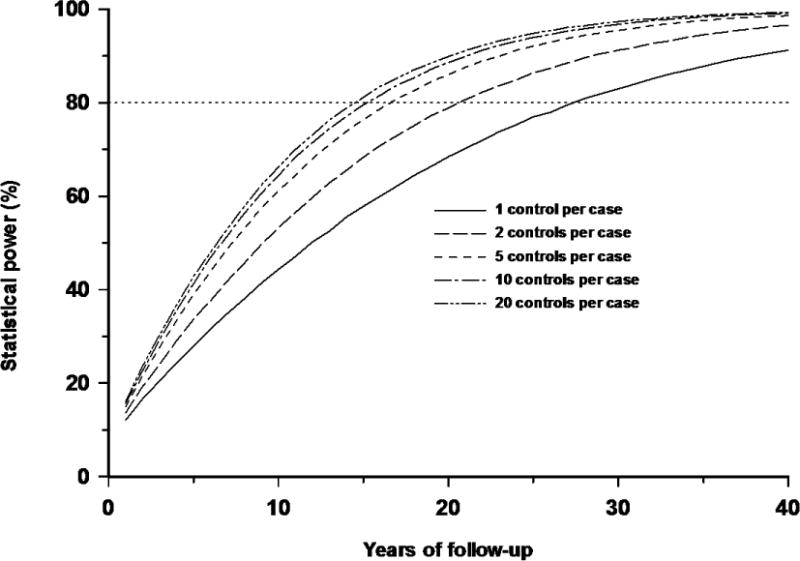
Influence of numbers of controls per case in a case-control study, all as a function of years of follow-up in a GB population. All five scenarios (1, 2, 5, 10, 20 controls per case) assume homogeneous EOR of 32.15 Sv⁻¹, and a distributions for RBM doses as in Table A2, and case distribution per year in GB as in Table A4.

Another way of considering this issue is to examine the year of follow-up when 80% power is achieved. Figures 1–2 show that with 1, 2, 5, 10 and 20 controls per case, 80% power (for a 1-sided 5% test) is achieved with approximately 28, 21, 17, 16 and 15 years of follow-up respectively; these time points correspond to studies that include ≈12800, 9600,7800, 7300 and 6900 cases, respectively. Likewise, an individual-based cohort study achieves 80% power with 14 years of follow-up, with about 6400 cases, whereas an area-based design only achieves this power with 19 years of follow-up, and 8700 cases.

Similar power is achieved if only gamma radiation is assumed to contribute to leukemia risk, with 50.9% power at 10 years and 76.2% at 20 years of follow-up for a case-control study with 5 controls per case; for radon alone the power is much less, 25.0% at 10 years and 39.2% at 20 years of follow-up (Table 2). Omission of in utero dose only minimally affects statistical power, resulting in 56.8% power at 10 years and 82.2% at 20 years of follow-up (Table 2).

Power is markedly affected by the assumed level of risk. As can be seen from Figure 3, if the BEIR V ERR coefficient is increased by a factor of 2 (or 4) then with a single control per case 80% power is achieved (for a 1-sided 5% test) within 10 (or 5) years of follow-up (corresponding to about 4580 (or 2290) cases), and with five controls per case within 6 (or 3) years of follow-up (corresponding to about 2750 (or 1370) cases). Conversely, if the ERR is decreased by a factor of 2 (or 4) then even after 40 years of follow-up (corresponding to about 18300 cases) the statistical power is only 50.6% (or 22.2%) with a single control per case, and 68.5% (or 30.0%) with five controls per case.

Figure 3.

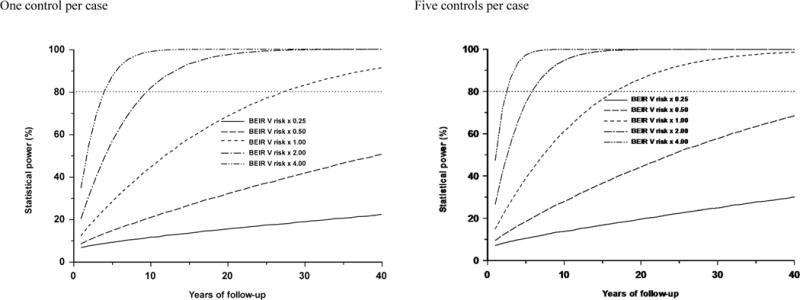
Influence of size of excess relative risk coefficient on power in a case-control study, all as a function of years of follow-up in a GB population. All five pairs of scenarios (BEIR V × 0.25 (EOR=8.04 Sv⁻¹), BEIR V × 0.50 (EOR=16.07 Sv⁻¹), BEIR V × 1.00 (EOR=32.15 Sv^{− 1}), BEIR V × 2.0 (EOR=64.29 Sv⁻¹), BEIR V × 4.0 (EOR=128.59 Sv⁻¹)) assume one or five controls per case, and a distributions for RBM doses as in Table A2, and case distribution per year in GB as in Table A4.

DISCUSSION

In this paper we have assessed the practical effect on the statistical power of differences in design for studies of childhood leukemia and exposure to natural background ionizing radiation. We have also demonstrated that even under fairly extreme heterogeneity in excess relative risk, little difference is made to the statistical power (Figure 1). Case-control studies with five controls per case achieve much of the power of an individual-based cohort design, and are more powerful than geographical correlation studies (Figure 2). The minimal gain in power with more than five controls per case is known in other contexts (27;28). With one or five controls per case it is estimated that to achieve 80% power for a 1-sided 5% test would require 28 or 17 years of childhood leukemia cases in GB, respectively. The childhood population in GB over the period 1991–2000 averaged about 9.3 million, which implies that of the order of 130 million person-years of follow-up would be required for an individual-based cohort study to have 80% power.

Calculations based on the case numbers occurring within the catchment area of the 17 registries included in the US Surveillance, Epidemiology and End Results (SEER) program (29) and the likely US (terrestrial gamma and cosmogenic) dose distribution (4) suggest, apparently paradoxically, that there is only slightly more power available per year of follow-up in the USA than in GB. Although the 17 SEER registries have about twice the number of childhood leukemia cases per year compared with GB, the mean dose (for the US as a whole) is somewhat less – for example, the UK mean annual effective dose from terrestrial gamma and cosmogenic radiation is estimated to be 0.68 mSv (SD (over counties) 0.09), as discussed by Kendall et al. (3) which compares with the mean for the USA of 0.54 mSv (SD (over states) 0.10) (4). This highlights what should be clear from the results of Appendix B (see the remarks immediately after (B.6) and (B.19)), namely that statistical power is much more affected by differences in mean dose than by the number of cases.

In epidemiological studies there may be differences between exposed and unexposed groups in some unmeasured factor(s) that affect the risk of childhood leukemia, and that may be correlated with exposure, i.e., confounding. For a high-exposure study with a large expected effect, such variations are fairly inconsequential. However, for a low-exposure study with small expected effect the magnitude of such confounding may well obscure the expected radiation effect. Assessment of the pattern of results in low-exposure studies may sometimes provide indications of artefactual findings. For example, Puskin (30), in an ecological study, investigated cancer mortality and estimates of mean radon exposure in US counties, and showed that smoking-related cancers exhibited strongly negative correlations with radon daughter exposure, while non-smoking related cancer was uncorrelated, suggesting that smoking confounds the radon dose-response for some smoking-related cancers. Various methods have been proposed for assessing the possible effects of such unmeasured confounding factors (31;32). Unmeasured confounding variables may play a role in the negative findings in some previous studies of leukemia and natural background radiation (8–10). Confounding factors, in particular lifestyle factors, can be most easily addressed in case-control studies, since few population registries ascertain this type of information. There are not many known substantial risk factors for childhood leukemia apart from ionizing radiation (unlike many cancers in adulthood), so that at least for this endpoint it is not so important to adjust for such variables, although confounding by unknown major risk factors must remain a possibility.

The United Kingdom Childhood Cancer Study (UKCCS), which included radiation measurements on about 2200 cases of childhood cancer of all types (of which about a third are leukemia) and around twice as many controls (9;10) has, by the results of our paper, little power to detect trends with dose – our calculations suggest that it would require at least 9600 leukemia cases to have 80% power of detecting a positive trend at the 1-sided 5% level.

Case-control studies may be affected by participation bias when individual measurements of radiation exposure are required. For example, 87% of cases of childhood cancer eligible for inclusion in the UKCCS were interviewed, but only 64% of eligible controls (9). Radon measurements were then made in the homes of 58% of interviewed cases, but of only 49% of interviewed controls (9). Thus, radon measurements were actually made in the homes of 50% of eligible cases, but only 31% of eligible controls, leaving considerable scope for bias. Moreover, the UKCCS found strong and socioeconomic-related participation bias with, for example, the non-interviewed first-choice controls showing a skew towards the more deprived groups, with 25% of those refusing to be interviewed coming from the most deprived seventh (where 15% would be expected) (33). The participation bias that potentially affects the UKCCS (9) and other case-control studies could equally affect cohort studies. For this reason register-based studies, in particular those that make use of model-based predicted doses that avoid the need for measurements in individual homes, have considerable advantages. For example, the Danish case-control study of radon exposure and childhood leukemia of Raaschou-Nielsen et al. (7) estimated individual doses from radon using national registry data on house and soil type and a model based upon a previous program of radon measurements. In principle, a similar algorithm for predicting gamma (and cosmic ray) dose rates in houses could be developed, or map data could be used.

The area-based study of Richardson et al. (8), with 6691 cases of childhood leukemia, is also somewhat underpowered according to the above calculations –8700 cases are required for 80% power. As a geographical correlation study it is free of the participation bias which apparently affected the UKCCS. However, such studies are vulnerable to bias and confounding, such as that resulting from unmeasured (within area) correlations between risk factors and radiation dose (34;35); this bias occurred in ecological studies of radon and lung cancer, where statistically significant negative correlations are observed (36;37).

The Danish case-control study of radon exposure and childhood leukemia of Raaschou-Nielsen et al. (7), with only 1503 leukemia cases and 2306 controls, appears underpowered. Assuming an age-sex distribution of cases as in GB and that radon doses are 2–3 times those in GB (7) implies that the study should have power for a 1-sided 5% test in the range 21–33%. Cases and controls were drawn from national registries (which contained residential history) so participation bias was avoided. The radon exposures were estimated using a model based on geographical region, soil type and house characteristics, which again avoided potential participation bias. Raaschou-Nielsen et al. reported that cumulative radon exposure was associated with risk for acute lymphoblastic leukemia, with a magnitude greater than would be expected from conventional risk estimates, but not for other types of childhood cancers. The errors associated with the radon concentration predictions were thought to be largely Berksonian (38), so that appreciable bias in the trend estimate would not be expected; but since the model was developed empirically, the use of estimated parameters can introduce classical error, which can induce bias in the regression. For an under-powered study, if any risk estimate is statistically significant, its magnitude is in all likelihood a substantial overestimate of the “true” risk (39). This may partially explain the apparently strong trend with radon exposure in the Danish study (7), although it is likely that once statistical uncertainties are taken into account the association is compatible with the predictions of conventional risk models. The strengths of this type of record-based case-control study (potentially large numbers of cases and freedom from participation bias) would in principle also apply to an analogous study of gamma rays. However, the use of estimated doses rather than those measured directly in the homes in question will inevitably lead to increased uncertainty. Uncertainty in dose estimates is not taken into account in our calculations, but its impact in assessing trends of dose response is likely to be substantial. In general the effect of uncertainties in dose is to widen confidence intervals for regression parameters and thereby lower the power of a study (40). It is implicit in the form of risk models used and the preponderance of cases under the age of 5 years that doses in early life are much more important than doses later in childhood. For this reason it is less important to know the place of residence at the time of diagnosis than the place of birth. This is a critical consideration for ecological studies, and implies that these should be organized in terms of area of birth rather than area of diagnosis of the case. Migration is another issue that would affect ecological studies if analyzed in terms of residence at time of diagnosis than at birth, and as people move house on average every five to seven years it would be expected to appreciably dilute the observed risk.

For simplicity the BEIR V leukemia risk model has been used, for the reasons stated in the Methods section. This model expresses the radiation-induced risk purely in terms of the ERR of leukemia. As discussed by Wakeford et al. (5) a significant source of uncertainty in the estimation of the childhood leukemia risk arises from the assumption of the nature of the transfer of the radiation-induced risk between populations when the baseline risk of childhood leukemia differs, as it does between the Japanese atomic bomb survivors and British children in the late 20^th century – the rate of incidence of childhood leukemia in GB during the 1990s was ~2½ times greater than that in Japan during the 1950s. Transfer of the Japanese atomic bomb survivors ERR, which is implicit in the BEIR V risk model, leads to a greater predicted number of radiation-induced cases of leukemia among British children than if the excess absolute risk (EAR), or some mixture of the ERR and EAR, is transferred. Wakeford et al. (5) argued that transfer of the ERR, or of the 70% ERR/30% EAR mixture adopted by the BEIR VII Committee, is better supported by the epidemiological evidence, but that this evidence is limited (22). Transfer of EAR to a GB population would be approximately equivalent to use of the BEIR V model with the risk coefficient reduced by a factor of ~2½, and the results of figure 3 imply that in this case 80% power would not be achieved even with 40 years of follow-up, when using five controls per case. The BEIR V leukemia model (18) does not assume any variation in relative risk for those exposed in childhood up to 15 years after exposure. More recent risk models would certainly predict such variation (1;2), but it is unlikely that such variation of risk over this time period would much affect the calculations presented here.

Our main results are for studies in which doses from gamma rays and radon have been combined. In principle, this approach provides higher and more variable doses which should result in improved power, but at the cost of becoming dependent on the reliability of the calculated doses. However, our results indicate that little improvement is obtained by combining gamma and radon doses over gamma alone. This suggests that the simpler approach, of considering the components separately, is to be preferred. It is highly probable that the risks from gamma rays and from radon are proportional to the measured quantity (dose rate and radon concentration, respectively) and that the analysis can be carried out in terms of these quantities, as has usually been done.

Studies of childhood leukemia and gamma rays have greater power than studies of radon of a similar size. The preponderance of studies of radon and childhood leukemia in the literature may be a consequence of the greater availability of detailed data on radon exposures compared to gamma rays, and possibly also to the positive findings of studies of residential radon exposure and lung cancer.

We emphasize studies of childhood leukemia in relation to natural background radiation exposure in part because of the elevated radiosensitivity of this endpoint at this age; this results in such studies having generally greater statistical power than similar studies of cancer in adulthood. “Childhood” is usually taken to refer to disease diagnosed at the ages 0–14 years. For example, this age range is the basis of case ascertainment employed by the UK National Registry of Childhood Tumours (NRCT) (41), UKCCS (9) and the Childhood Leukemia International Consortium (CLIC) (42); however, a larger age range, up to at least age 18 years, is used in the International Childhood Cancer Cohort Consortium (I4C) (43). There is some degree of arbitrariness in the precise age range to be used, and the issue of latency clearly complicates what should be the natural age range to consider.

The UK NRCT (41) has virtually complete ascertainment of cases of childhood cancer in GB over the last several decades. These data together with matched controls selected from national birth registers and doses estimated from national radon and gamma maps could provide the basis for a study similar to that of Raaschou-Nielsen et al. (7), and indeed such a study is underway. In principle, a similar study might be undertaken with other large databases, in particular the CLIC and I4C studies (42;43). The focus of the present paper is largely methodological, and the USA and GB are used illustratively mainly because of the good quality national cancer registers there. Nevertheless, studies could be undertaken in many other developed countries, and are most likely to be informative in areas with good quality cancer registries and having particularly high (and variable) natural background radiation exposure.

5. Conclusions

In summary, for a GB population, the number of years of accumulated childhood leukemia cases to achieve 80% power for a 1-sided 5% test would be:

• For a cohort study: 14 years (6400 cases)

• For a case/control study (5 controls per case): 17 years (7800 cases)

• For a case/control study (1 control per case): 28 years (12800 cases)

• For an ecological study: 19 years (8700 cases)

These estimates assume that doses from radon and gamma rays (including the directly ionizing component of cosmic rays) are combined. For studies using gamma rays alone the required numbers of cases would be somewhat larger and for radon alone much larger. In addition, participation bias may seriously affect studies which require individual consent, while geographical correlation studies suffer from severe interpretational problems. We argue that most previous studies have been underpowered and that most were subject to unquantifiable biases and confounding. Experience suggests that studies requiring individual consent are subject to (possibly large) participation bias and are likely to be extremely expensive if an adequate number of cases is to be included. Record-based studies avoid these problems, though they are not entirely free of difficulty (e.g., in that doses have to be estimated rather than measured). Nonetheless, our results show that large studies should be capable of detecting the predicted risk of childhood leukemia from natural background radiation and potentially provide important evidence on the risk of childhood leukemia following low-level irradiation, a subject that continues to be debated.