Using Matched Molecular Series as a Predictive Tool To Optimize Biological Activity

Abstract

A matched molecular series is the general form of a matched molecular pair and refers to a set of two or more molecules with the same scaffold but different R groups at the same position. We describe Matsy, a knowledge-based method that uses matched series to predict R groups likely to improve activity given an observed activity order for some R groups. We compare the Matsy predictions based on activity data from ChEMBLdb to the recommendations of the Topliss tree and carry out a large scale retrospective test to measure performance. We show that the basis for predictive success is preferred orders in matched series and that this preference is stronger for longer series. The Matsy algorithm allows medicinal chemists to integrate activity trends from diverse medicinal chemistry programs and apply them to problems of interest as a Topliss-like recommendation or as a hypothesis generator to aid compound design.

Introduction

Matched molecular pair analysis (MMPA) has proven to be a powerful tool to rationalize and predict many aspects of structure–activity relationships (SARs) within a series of analogues.¹⁻³ MMPA is based upon the concept of a matched (molecular) pair which in the simplest case is defined as two molecules with the same scaffold but which have different substituents at a particular position (R groups). The power of MMPA is derived from the hypothesis that changes in property values are easier to predict than absolute values. Furthermore, as the property change is associated with a single structural change, the origin of the property change is clearly defined.

MMPA has successfully been used for the prediction of physicochemical properties such as log P and solubility.⁴ It has also has been used to find bioisosteres, R group or molecular scaffold replacements that retain biological activity across a wide range of targets.^5,6 However, as a guide to improving biological activity, MMPA has had limited success as a general method. Hajduk and Sauer⁷ analyzed SAR data for 84 000 compounds from lead optimization programs against 30 protein targets at Abbott Laboratories and found that the potency changes associated with most R group transformations were (nearly) normally distributed around zero. For the specific case of the “magic methyl”, Jorgensen⁸ also found a normal distribution of potency changes for H → Me centered around zero.

The difficulty in applying MMPA to predicting biological activity is that such an analysis involves averaging data from diverse binding sites with different SAR characteristics, hence the distributions observed by Hajduk and Sauer. This is in contrast to using MMPA for physicochemical properties which depend on molecular interactions with bulk solvent rather than on the specific nature of the protein environment around the bound ligand. Indeed several physicochemical properties may be predicted reasonably well using group or atomic contribution approaches (e.g., log P ⁹), and so it is not surprising that the change in property value caused by an R group replacement can be calculated.

Several approaches have been adopted to address this deficiency of MMPA by restricting the analysis to those matched pairs having the same context (in some way) as the scaffold or target of interest. The simplest approach is to use only matched pairs obtained from the same assay for the same target. Where sufficient data are available, for example, for common off-targets, or where the activity correlates strongly with a physicochemical descriptor, this approach may work well; for example, inhibition of the hERG potassium channel correlates strongly with log D.¹⁰ Papadatos et al.¹¹ and Warner et al.¹² (“WizePairZ”) have gone further and included context in the form of the atom environment around the R group attachment position. The 3D matched pair approach of Posy et al.¹³ used 3D protein–ligand structures to restrict predictions to those matched pairs where the R group is in the same location in the binding site. For many targets an alternative approach is required, as sufficient matched pair data for a particular target does not exist. In addition matched pair data from targets with similar binding sites may also yield useful predictions. The VAMMPIRE database of Weber et al.¹⁴ uses 3D protein–ligand structures to characterize the amino acid environment of a particular matched pair under the assumption that if the environment is the same, then the same matched pair transformation will always have the same effect on binding affinity.

Here we describe a method that uses matched molecular series to predict R groups that improve binding affinity. The concept of matched series was introduced in 2011 by Wawer and Bajorath¹⁵ (“matching molecular series”) as a generalization of matched pairs; where matched pairs involve exactly two molecules (i.e., N = 2) with the same scaffold but different R groups, a matched series may contain two or more molecules (i.e., N ≥ 2; see Figure 1). Matched series have been extensively investigated by Bajorath and co-workers in the context of SAR transfer,¹⁶⁻¹⁹ mechanism hopping,²⁰ and the visualization of SAR networks¹⁵ and SAR matrices.²¹ With the SAR transfer approach, one searches a database to find matched series where the corresponding activities are highly correlated with a query matched series. When found, any additional R groups in the database match that have improved activities are considered likely to improve activity also in the query series. Mills et al.²² have used the same concept (“series with well-matched SARs”) to predict compounds with improved potency by finding matching series in the Pfizer database. The SAR transfer methods described by Mills and Bajorath work well for longer matched series (about N > 6, although they might work well for shorter series if using a focused data set) if a match to the series can be found with high activity correlation. However, in general, either no such match can be found (particularly for publicly available data) or the series length is too short for a specific match.

Figure 1.

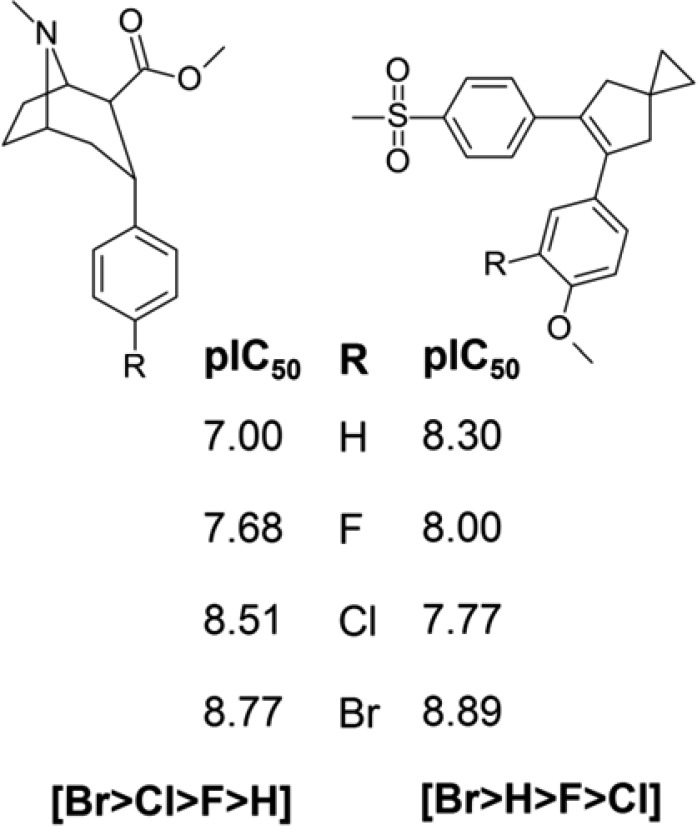
Activity data for two examples of the same matched series [H, F, Cl, Br]. The example on the left from Carroll et al.³² (binding to dopamine transporter) has the most preferred order [Br > Cl > F > H], while that on the right from Chavette et al.³³ (inhibition of COX-2) has the least preferred order [Br > H > F > Cl].

Our algorithm (“Matsy” from “MATched SEries”) uses a statistical approach to predict the R groups most likely to improve activity given an observed activity order for a matched series. A similar statistical approach has been used previously for matched pair data (Leach et al.,⁴ for example) and for triplets (Mills et al.²² describe the use of a third R group to add context to a matched pair). We identify the basis for predictive success as preferences for particular orders in matched series and show that the longer the matched series, the more successful it will be at predicting activity. The method is validated using a retrospective test that places a lower bound on expected prospective performance. We compare the data-driven predictions of the Matsy algorithm with those of the rationally designed Topliss tree²³ to show how the algorithm could be used in practice to guide a medicinal chemistry project. The results presented here describe a practical method to exploit SAR data from historical medicinal chemistry projects to yield concrete prospective guidance for new projects.

Results

Preferred Order of Matched Series

The predictive method proposed, Matsy, relies on the hypothesis that a particular matched series tends to have a preferred activity order, for example, that not all six possible orders of [Br, Cl, F] are equally frequent (see Methods for details of this notation). Although a rather straightforward idea, we have been unable to find any quantitative analysis of this question in the literature. Let us consider two examples of R group substituents that frequently occur in medicinal chemistry projects: a set of halides and a set of alkanes of increasing length.

Table 1 shows the details of the halide set. There are 15 588 instances of ordered matched series for [H, F] in the data set, 3849 of [H, F, Cl], and 982 of [H, F, Cl, Br]. Table 1 also shows the values for the enrichment defined as the ratio of the observed frequency to that expected by chance, assuming all N! orders of the series are equally likely.

Table 1. Preferred Activity Order for Halide Matched Series.

series	enrichment	p (corrected)a	observations
F > H	1.06	0.000 (0.000)	8250
H > F	0.94	0.000 (0.000)	7338
Cl > F > H	1.85	0.000 (0.000)	1185
H > F > Cl	1.08	0.038 (0.189)	690
F > Cl > H	0.88	0.001 (0.005)	566
Cl > H > F	0.79	0.000 (0.000)	504
F > H > Cl	0.78	0.000 (0.000)	503
H > Cl > F	0.63	0.000 (0.000)	401
Br > Cl > F > H	5.62	0.000 (0.000)	230
Cl > Br > F > H	2.79	0.000 (0.000)	114
H > F > Cl > Br	1.69	0.000 (0.001)	69
F > Cl > Br > H	1.47	0.004 (0.090)	60
Br > Cl > H > F	1.39	0.013 (0.302)	57
Cl > Br > H > F	0.88	0.473 (10.873)	36
F > Cl > H > Br	0.86	0.380 (8.738)	35
Cl > F > Br > H	0.83	0.299 (6.880)	34
Br > H > Cl > F	0.81	0.231 (5.304)	33
H > Br > Cl > F	0.76	0.128 (2.954)	31
H > F > Br > Cl	0.73	0.093 (2.132)	30
Br > F > Cl > H	0.68	0.038 (0.865)	28
F > Br > Cl > H	0.66	0.025 (0.574)	27
F > H > Cl > Br	0.61	0.008 (0.191)	25
Cl > F > H > Br	0.56	0.003 (0.069)	23
Cl > H > F > Br	0.49	0.000 (0.009)	20
H > Br > F > Cl	0.49	0.000 (0.009)	20
Cl > H > Br > F	0.46	0.000 (0.004)	19
Br > F > H > Cl	0.44	0.000 (0.002)	18
H > Cl > Br > F	0.44	0.000 (0.002)	18
F > H > Br > Cl	0.42	0.000 (0.001)	17
H > Cl > F > Br	0.37	0.000 (0.000)	15
F > Br > H > Cl	0.34	0.000 (0.000)	14
Br > H > F > Cl	0.22	0.000 (0.000)	9

^aThe p-value measured the likelihood of the observed enrichment occurring by chance. This was measured using a two-tailed binomial test. The p-value was corrected for multiple testing using the Bonferroni correction. This is a conservative correction that involves multiplying the original p-value by the degrees of freedom. Here there were N! – 1 degrees of freedom, and so the values for N = 4 were corrected by multipling by 23. Values are considered to be significant if the corrected p-value is ≤0.05.

For the series of length 2 (the matched pairs) the maximum enrichment observed (1.06) is not very large. However, on moving to longer series, there is a large increase in the maximum enrichment from 1.06 to 1.85 to 5.62. The most frequent order for the quartet is [Br > Cl > F > H], where the order of activity corresponds to increasing molecular weight. The second most frequent order is a slight variation that may correspond to situations where the Br is too large to fit the binding site. The third most frequent order is the exact opposite of the most frequent, with the R groups decreasing in activity with increasing molecular weight. The frequency table also highlights orders that are unfavored or occur less frequently than expected by chance. For example, the least frequent order is [Br > H > F > Cl]. Examples of the most frequent and least frequent orders are shown in Figure 1.

The data for the alkanes are shown in Table 2. There are 6349 instances of ordered matched series for [C, CC] in the data set, 1166 of [C, CC, CCC], and 404 of [C, CC, CCC, CCCC]. Again, on moving to longer matched series, the maximum enrichment increases from 1.00 to 1.79 to 5.64.

Table 2. Preferred Activity Order for Alkane Matched Series.

series	enrichment	p (corrected)	observations
CC > C	1.00	0.744 (0.744)	3188
C > CC	1.00	0.744 (0.744)	3161
CCC > CC > C	1.79	0.000 (0.000)	348
C > CC > CCC	1.32	0.000 (0.000)	256
CC > CCC > C	1.04	0.556 (2.778)	202
CC > C > CCC	0.96	0.582 (2.912)	187
C > CCC > CC	0.57	0.000 (0.000)	111
CCC > C > CC	0.32	0.000 (0.000)	62
CCCC > CCC > CC > C	5.64	0.000 (0.000)	95
CCC > CCCC > CC > C	3.15	0.000 (0.000)	53
CC > C > CCC > CCCC	1.54	0.033 (0.755)	26
CC > CCC > CCCC > C	1.49	0.046 (1.064)	25
C > CC > CCC > CCCC	1.49	0.046 (1.064)	25
CCC > CC > CCCC > C	1.49	0.046 (1.064)	25
CC > CCC > C > CCCC	1.37	0.133 (3.066)	23
CC > C > CCCC > CCC	0.83	0.617 (14.193)	14
CCC > CC > C > CCCC	0.83	0.617 (14.193)	14
CCCC > CC > CCC > C	0.77	0.453 (10.420)	13
CC > CCCC > CCC > C	0.59	0.104 (2.387)	10
C > CCC > CCCC > CC	0.53	0.060 (1.379)	9
CCCC > CCC > C > CC	0.53	0.060 (1.379)	9
C > CCC > CC > CCCC	0.53	0.060 (1.379)	9
CC > CCCC > C > CCC	0.42	0.012 (0.274)	7
C > CCCC > CC > CCC	0.42	0.012 (0.274)	7
C > CCCC > CCC > CC	0.36	0.004 (0.089)	6
CCCC > C > CCC > CC	0.36	0.004 (0.089)	6
C > CC > CCCC > CCC	0.36	0.004 (0.089)	6
CCC > C > CC > CCCC	0.30	0.001 (0.025)	5
CCC > CCCC > C > CC	0.30	0.001 (0.025)	5
CCCC > CC > C > CCC	0.24	0.000 (0.009)	4
CCC > C > CCCC > CC	0.24	0.000 (0.009)	4
CCCC > C > CC > CCC	0.24	0.000 (0.009)	4

These two examples illustrate the general observation that longer matched series are more likely to exhibit preferred orders while matched pairs exhibit only a small preference if any. Indeed it is striking that while [CCCC > CCC > CC > C] occurs 5.64 more than expected by chance, the [C, CC] matched pair shows almost no preferred order. At the matched pair level, the signals from all of the preferred orders from longer matched series cancel each other out.

Matsy Algorithm: Prediction of Substituents That Will Improve Activity

Let us consider the question “If we have observed that [H > F > Cl], would Br be likely to increase the activity further?” Using just the data in Table 1 , there are 69 observations of [H > F > Cl > Br], 30 of [H > F > Br > Cl], 20 of [H > Br > F > Cl], and 9 of [Br > H > F > Cl]. In other words, out of 128 observations of [H > F > Cl] in combination with Br, in only 9 cases (7%) did Br increase the activity. In addition, the fact that the enrichment for [Br > H > F > Cl] is very low (at 0.22) indicates that this is not a likely order.

The actual question we wish to answer is “Given an observed order for a matched series, what substituent is likely to improve the activity?” The prediction method we propose follows from the previous example, and we refer to this algorithm as the Matsy algorithm.

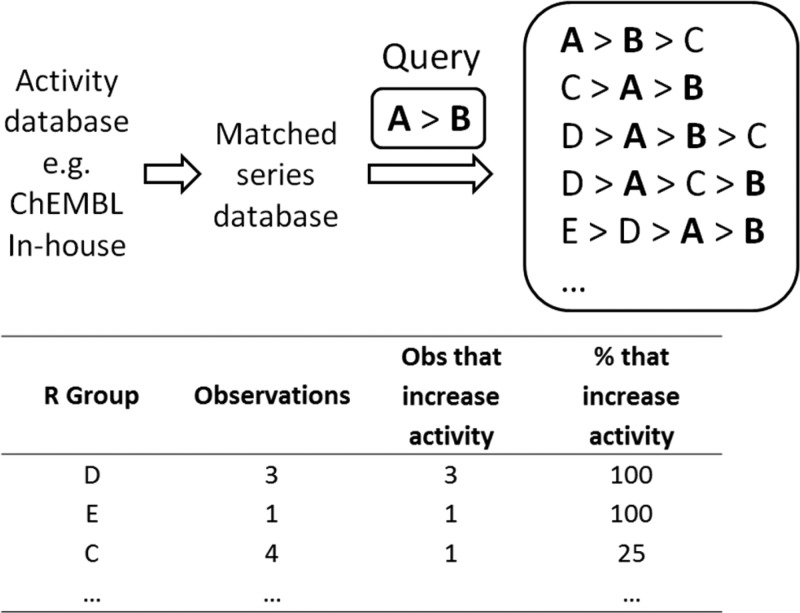
Let us suppose that we have synthesized and measured the activity of two analogues in a matched series, that is, [A, B], and their observed activity order is [A > B]. We wish to make a prediction for what substituent R will increase the activity further, i.e., such that [R > A > B]. For each potential substituent R, the database is searched for all instances of the matched series [R, A, B] with [A > B]. The percentage of cases where [R > A > B] is true is then calculated. The substituent R associated with the highest percentage is then considered the most likely to increase activity. This procedure is illustrated in Figure 2. A cutoff is typically applied as described in the Methods.

Figure 2.

Overview of the Matsy algorithm. Given a database of matched series and a query matched series, the algorithm identifies R groups likely to improve activity.

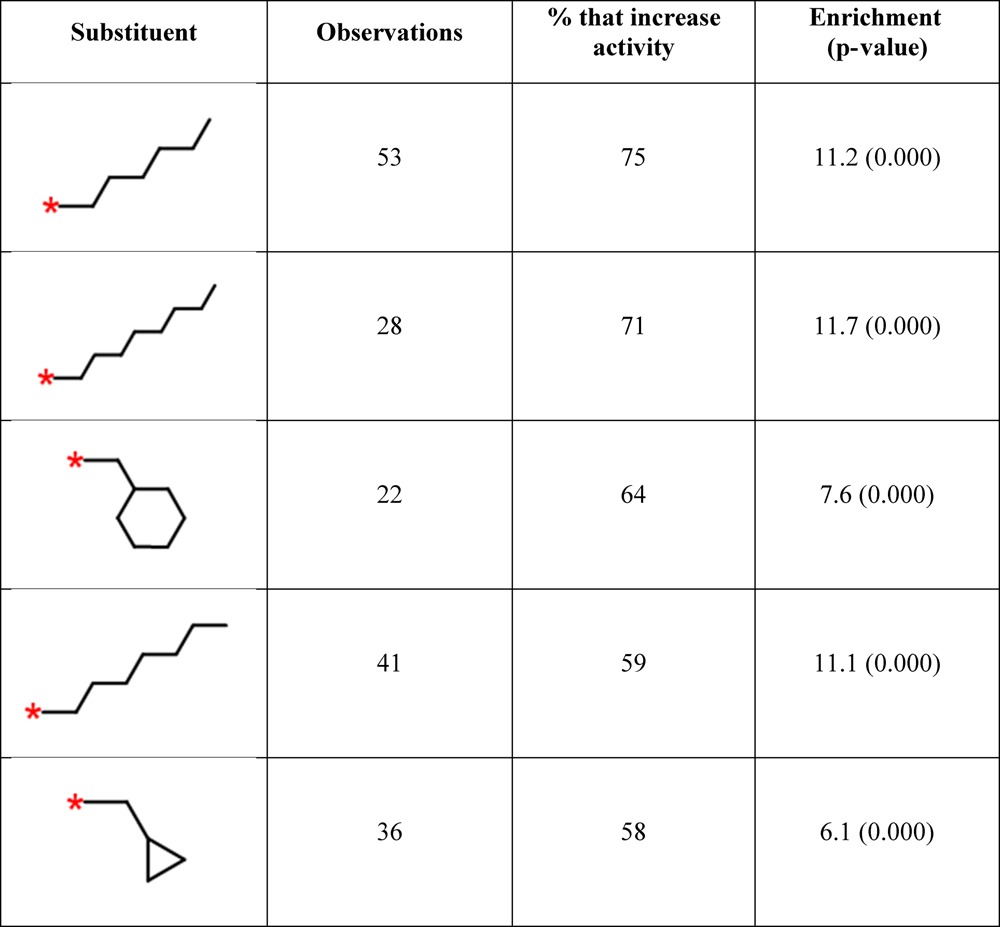
Table 3 shows the top five predictions for [CCC > CC > C] using a cutoff of 20. Not surprisingly, the method predicts that longer or more bulky alkanes will increase the activity further. The top prediction is a hexyl chain which was observed 53 times in combination with [CCC > CC > C]; in 40 of those cases (75%) it was associated with increased activity. The targets associated with these 40 cases are diverse and include 22 GPCRs (muscarinic acetylcholine, glucagon, endothelin, and angiotensin receptors), 5 oxidoreductases (cytochrome P450 and cyclooxygenase), 3 acyltransferases, and 3 hydrolases. Futher details of the 40 targets and scaffolds are included in the Supporting Information. The scaffolds are diverse, even where the same target is involved multiple times (as for the muscarinic acetylcholine receptor), although duplicates do exist.

Table 3. Top Five Predictions for Substituents That Will Improve Activity for the Query [CCC > CC > C].

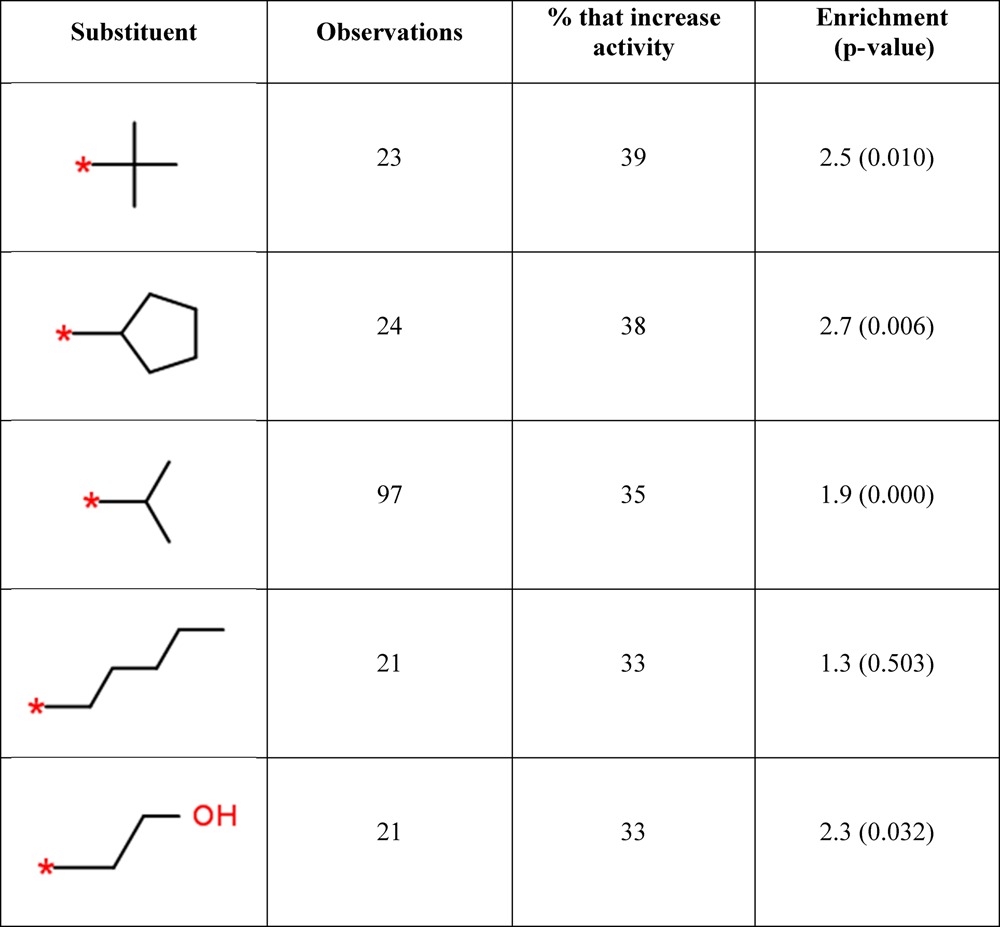
When the order of the ethyl and propyl is swapped to give [CC > CCC > C], the predictions change accordingly (Table 4). While longer alkyl groups are still featured, the knowledge-based predictions now highly rank the less bulky isopropyl and tert-butyl groups. The top prediction of tert-butyl was observed to increase the activity 9 times (39%) out of 23 observations in combination with the query. While the absolute percentage values are much lower than in Table 3, by digging down into the underlying data and assessing it by comparison to the actual target or compound of interest, a decision can be made whether to proceed with making the tert-butyl analogue or not. In this case the nine targets include three proteases (HIV-1 protease and cathepsin K), two kinases (serine/threonine protein kinase ATR and CDK2), and a single GPCR (melanin-concentrating hormone receptor).

Table 4. Top Five Predictions for Substituents That Will Improve Activity for the Query [CC > CCC > C].

Comparison with the Topliss Tree

The idea behind the Matsy algorithm is that general trends in activity exist across different targets and scaffolds and that these trends can be used to make predictions. In one of the best known applications of this idea, Topliss²³ described a decision tree approach to guide a medicinal chemist to the most potent analogue by rational analysis of the activity order observed so far. The Matsy algorithm may be considered the data-driven equivalent to the Topliss tree based on observed trends in the data, and it is interesting to compare the predictions from Matsy with the guidance provided by Topliss.

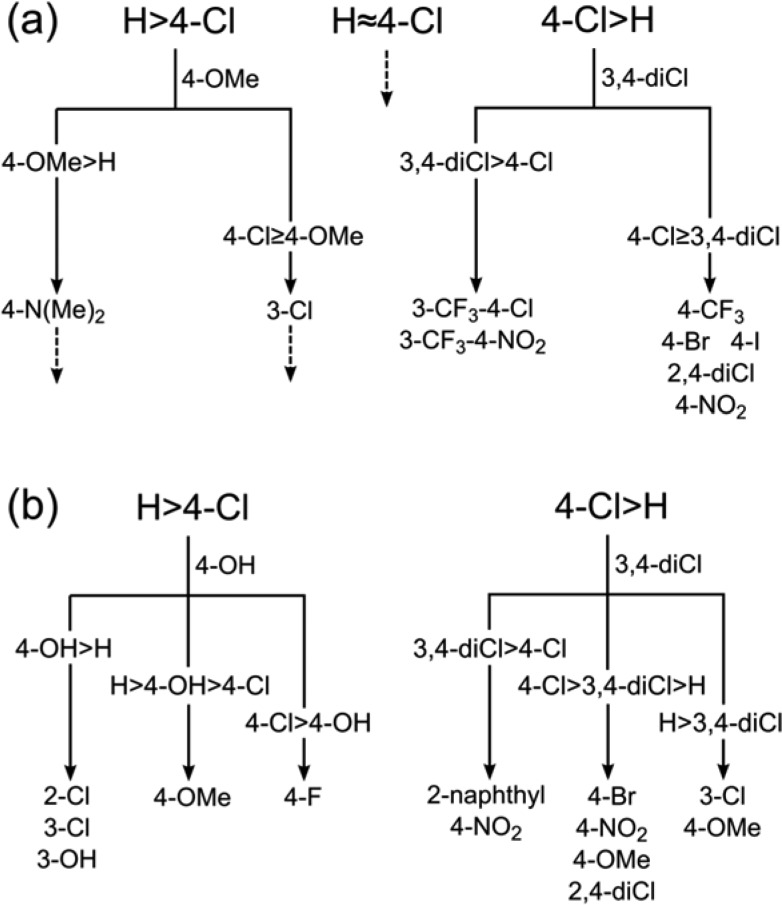
Topliss described a decision tree for a substituted phenyl ring, a subset of which is reproduced in Figure 3a. Given that [4-Cl > H], Topliss recommends 3,4-diCl. This is also the top prediction by Matsy (54% of 326 observations, using a cutoff of 100). If this group is indeed more potent, then Topliss recommends 3-CF₃-4-Cl or 3-CF₃-4-NO₂ whereas Matsy recommends 2-naphthyl to replace the phenyl (30% of 50, cutoff of 20) or 4-NO₂ (28% of 40). However it is worth noting that if the cutoff is reduced to 10, then the Matsy recommendation is also 3-CF₃-4-Cl (36% of 11). For the situation where 3,4-diCl does not improve the activity beyond Cl, i.e., [4-Cl > 3,4-diCl > H], Topliss recommends 4-CF₃, 4-Br, or 4-I. The top Matsy recommendations are 4-Br (53% of 34, cutoff of 20), 4-NO₂ (33% of 27), 4-OMe (27% of 60), and 2,4-diCl (19% of 26). Apart from the 4-OMe, the others all appear on that branch of the Topliss tree.

Figure 3.

(a) Decision tree described by Topliss²³ for a substituted phenyl ring. The abbreviations used follow Topliss (e.g., 4-Cl means 4-chlorophenyl). Only the portion of the Topliss tree discussed in the text is shown (the dotted lines indicate further branches). (b) Matsy predictions for a substituted phenyl ring given either [H > 4-Cl] or [4-Cl > H]. The 2-naphthyl replaces the phenyl ring (rather than being a substituent).

On the left-hand branch of the tree, there is less agreement. Given that [H > 4-Cl], Topliss recommends 4-OMe while Matsy recommends 4-OH (45% of 134, cutoff of 100). In fact, the 4-OMe is the 20th recommendation (26% of 668) and that particular order is not considered to be enriched (enrichment of 0.78 based on 1356 observations). If it turns out to be more active than the phenyl, i.e., [4-OMe > H > 4-Cl], then Topliss recommends 4-N(Me)₂ whereas Matsy is even more insistent on 4-OH (65% of 31, cutoff of 20). If instead it turns out to be less active than 4-Cl, i.e., [H > 4-Cl > 4-OMe], Topliss recommends 3-Cl which is the fourth recommendation of Matsy (39% of 84, cutoff of 20) after 2-F (48% of 46), cyclohexyl (45% of 31), and 4-OH (31% of 39).

Figure 3b summarizes the “Matsy trees” for [H > 4-Cl] and [4-Cl > H], showing the results if the Matsy predictions are followed at the first branch rather than the Topliss recommendations.

Case Study: Sunitinib

Sunitinib is a receptor tyrosine kinase inhibitor used to treat renal cell carcinoma and gastrointestinal stromal tumor. The ChEMBL assay CHEMBL768949 (Sun et al.²⁴) contains the matched series [F > Cl > Br > H] for IC₅₀ values of the structure shown in Figure 4a against PDGF-Rβ (platelet-derived growth factor receptor β); the fluorine analogue is sunitinib. If the fluorine is removed and the remaining members are used as a query (i.e., [Cl > Br > H]), then the Matsy predictions based on the kinase data set (see Methods) are methyl (24% of 36 observations), methoxy (22% of 37 observations), fluorine (17% of 47 observations after removing the self-prediction), and CF₃ (5% of 22 observations).

Figure 4.

Scaffolds (a, b) and R groups (c) from the sunitinib case study.

Although improving potency is only one aspect of the multiobjective problem that is developing a drug, it is interesting to see whether Matsy can predict R groups that would improve the binding affinity further. Given [F > Cl > Br > H] as a query and again using just the kinase data, Matsy finds the eight R groups shown in Figure 4c. Each of these R groups was observed 5 times in combination with the query, and in all of the 5 cases each showed improved binding affinity over sunitinib. However, on inspection the primary sources of the data are two assays against CDK1 and CDK2 in the same paper (Bramson et al.²⁵) involving the scaffold shown in Figure 4b; the other three observations are duplicate reports in more recent literature. Although the evidence for these R groups turns out to be based simply on a single paper, the similarity of the scaffolds may indicate a potential for SAR transfer.

Retrospective Test of the Matsy Algorithm

To assess the predictive ability of ordered matched series, we took matched series with known activities, removed the most active R group (the reference), and checked whether it occurred in the top five Matsy predictions (see Methods for details). Note that not being able to find the known R group in the top five does not necessarily mean that the predictive method failed. There may be one or more true actives in the five predictions, and this would be a positive outcome. However, since we can only assess the method on the basis of the known data, the measure of success will be the percentage of cases where the reference appears in the top five. This value is a lower bound on the true measure of success and will be used to compare performance of different data sets.

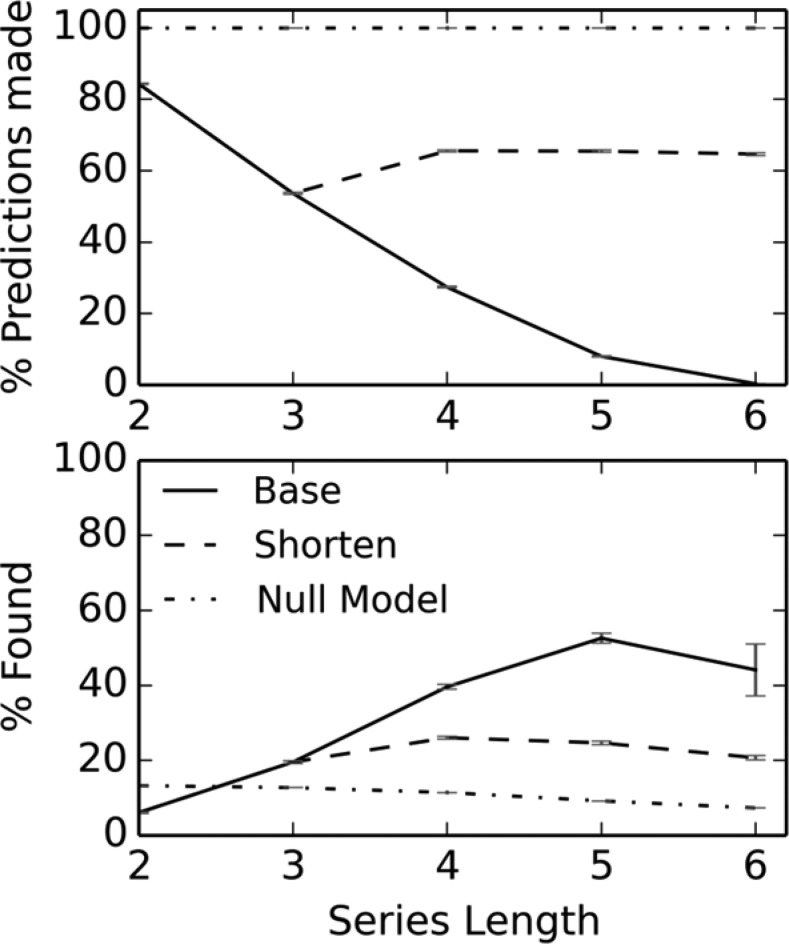
The average results from the 100 repetitions (see Methods) are shown in Figure 5, while Table 5 shows in more detail the corresponding values for the first of the 100 repetitions. Figure 6 shows the predicted rank of the reference substituent (where the reference substituent was listed in the predictions) for the data described in Table 5.

Figure 5.

Retrospective test results for the Matsy algorithm. The results denoted as “base” are those obtained using the entire matched series as present in the test set, while “shorten” indicates the results obtained if the series is shortened when no prediction is originally found (see text for details). The “null model” uses the most common substituents.

Table 5. Retrospective Test Results for Series of Different Lengths.

series length	test set size	predictions	number in top five	% found predicteda	% found overallb
2	41789	35251 (84%)	2124	6	5
3	37313	19982 (54%)	3926	20	11
4	29807	7942 (27%)	3180	40	11
5	20792	1682 (8%)	891	53	4
6	14655	52 (0%)	25	48	0

^aThe percentage of series where predictions were made, where the reference R group appeared in the top five predictions.

^bThe percentage of all test series, where the reference R group appeared in the top five predictions.

Figure 6.

Rank of the reference substituent in the Matsy predictions (if present).

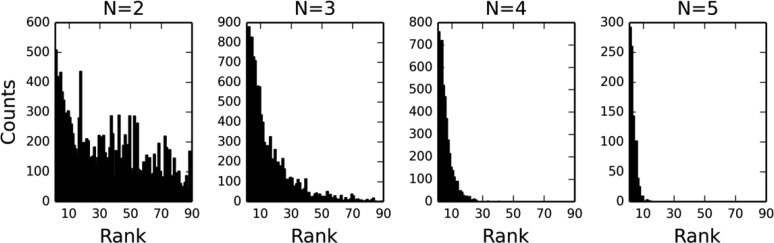
As shown in Figure 5, for those cases where predictions were made, the quality of predictions increases with increasing length: from 6.1% for matched pair data through 19.6% for N = 3, 39.6% for N = 4, and 52.6% for N = 5 (the value of 44.2% for N = 6 is on the basis of only a small number of results and has large error bars). However, at the same time, the percentage of series for which predictions could be made decreases rapidly with increasingly series length: 84.3% for N = 2, 53.7% for N = 3, 27.4% for N = 4, 8.0% for N = 5, and 0.4% for N = 6. No prediction is made where there is no match to the query series in the database or where there are insufficient observations to have confidence. These situations may arise in particular for longer series because of the smaller number of such series in the data set as well as the increasing number of ways in which N items may be ordered.

One approach to handling cases where no predictions are made is to successively remove the least common substituent until either some predictions are made or the series is too short. Here we define too short as series of length 3. In other words, a series of length 5 might be shortened first to 4 and then to 3 to find predictions but it will not be shortened further. The results are shown as the dashed line in Figure 5. Predictions are now made for 53–66% of the series, but as expected, the percentage success is reduced compared to the original test as the more accurate results for longer series are combined with less accurate results for shorter subseries.

To put these results in context, we compared the performance of the Matsy algorithm to that of a very simple prediction method: What if we use the five most frequent substituents in the training set series (that do not occur in the query) as the predictions? The five most frequent substituents were hydrogen, methyl, phenyl, chloro, and methoxy. Figure 5 shows the results compared to the Matsy algorithm; this trivial prediction method does surprising well because of the fact that the five most frequent substituents comprise 32.5% of the training data, and so just by chance they will often occur at the top of any matched series. In fact, the Matsy predictions for N = 2 are beaten by this simple method.

The median numbers of predictions for the data in Table 5 are 72 for N = 2, 16 for N = 3, 8 for N = 4, 4 for N = 5, and 2 for N = 6. It may be argued that the relatively poor performance of matched pairs is solely due to the fact that while a larger number of predictions are typically generated for matched pairs, only the top five are considered in this test. Figure 7 gives a more complete picture of the performance by considering the top X predictions where X is from 1 to 100 (and not just X = 5). For example, this shows that while 40% are found in the top five for N = 4 (Figure 7 and Table 5), to get equivalent performance when using matched pairs, one needs to consider the top 65 and even then the null model would perform slightly better (41%).

Figure 7.

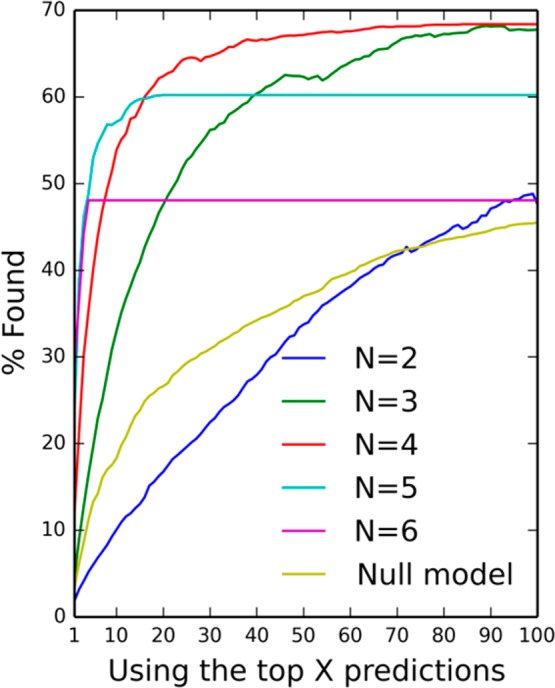
Effect on performance of searching for the reference R group in the top X predictions, where X is from 1 to 100. The “null model” uses the most common substituents. The curve for N = 6 levels off at X = 4 as the reference R group (if present) never appears beyond the top 4; similarly the N = 5 curve levels off at X=20 and N = 4 at 84.

It is also worth considering the performance when no cutoff is used. For the predictions summarized in Table 5, if we consider the test to pass when the reference R group appears anywhere in the predictions, then the success rates are 62% for N = 2, 62% for N = 3, 61% for N = 4, 58% for N = 5, and 48% for N = 6. That is, almost equivalent performance is found for N = 5 and its four predictions (on average) as for N = 2 with 18 times the number of predictions.

Further tests were carried out to investigate whether using a focused subset of the data would perform better, that is, whether kinase data are better at predicting kinases (as done for the sunitinib case study earlier) and similarly for GPCR data. These tests are described in the Supporting Information. Although the amount of data available is much less, it appears that for shorter series at least the focused subset performs better.

Correlation with Physicochemical Properties

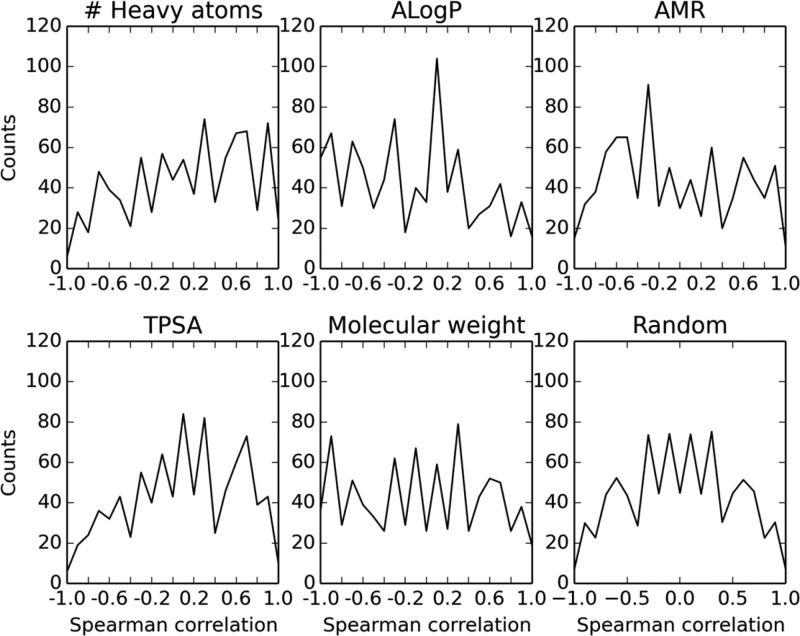
Increased binding affinity as measured by pIC₅₀ may correlate trivially with a physicochemical property such as molecular weight or log P. To check whether the predictive success of Matsy is solely linked to such correlations, we took the 891 series of length 5 listed in Table 5 as correctly predicted and calculated the Spearman correlation versus a number of common descriptors, namely, predicted log P, molar refractivity (MR), molecular weight, total polar surface area (TPSA), and heavy-atom count. Descriptor values were calculated using the RDKit.²⁶

The results are shown in Figure 8. For example, the data for log P indicate that 16 series are perfectly correlated with log P while 55 have perfect anticorrelation. Some weak trends may be observed: increased activity is associated with more heavy atoms, lower log P and MR, and greater TPSA. It is clear, however, that the activity order observed is not explained by any one descriptor.

Figure 8.

Spearman correlations between the activity order of 891 matched series of length 5 and their calculated descriptor values. The graph labeled “random” indicates the frequencies of different correlations for 891 random series (created using 100 000 random series and then scaled).

Discussion

The Matsy algorithm is an extension of the SAR transfer methods developed by Mills and Bajorath. Whereas those methods make predictions based on a single match to an ordered series in a database, our approach combines the results from multiple matches to come up with R groups most likely to improve activity. In the limit of a single match in the database the Matsy predictions are identical to those made using SAR transfer, although in practice a minimum cutoff of five observations (or more if possible; see Methods) is recommended when using the Matsy algorithm so that the calculated likelihoods are reliable.

The basis of the Matsy algorithm is that particular matched series have preferred orders. For example, if each of the 24 orders of [hexyl, C, CC, CCC] were equally likely, then the hexyl would not rank particularly highly in Table 3. The reason that it does is that the order [hexyl > CCC > CC > C] is enriched. An alternative and equally valid way of looking at this is that instead of basing our prediction on all of the matched pairs [hexyl, CCC], we have used the information that [CCC > CC > C] is true to filter the matched pairs to just those that are most relevant. To illustrate this, the entire data set shows that [hexyl > CCC] is true in 65% of cases, compared to 75% when [CCC > CC > C]. As discussed in the Introduction, this can be seen as another example of annotating matched pairs using context; in this case the context is the presence of an observed activity order for a query matched series. Knowing the relative activities of two (or more) R groups tells us more information than just considering an R group on its own. Some matched pairs studies have touched on this idea. Mills et al.²² refer to “local SAR” and Hajduk and Sauer⁷ to “compound triplets”. However, we believe that matched series provide a simpler and more elegant approach to the handling of activity orders between more than two R groups at the same scaffold position.

Note that the observed frequencies in preferred orders may be affected by sampling bias. For example, with reference to the data in Table 2, if we assume that the shorter carbon chains would have been synthesized and analyzed first, then the butyl analogue would not have been synthesized unless it was expected to improve the activity. Therefore, except for those cases where the four analogues were synthesized prior to any measurement of activity, there will be an increased frequency in the database for those orders involving butyl at the more active end of the series of four.

The origin of the preferred orders of particular series has not been investigated in the current study beyond ruling out a general link to simple physicochemical descriptors. Topliss²⁷ related the possible potency orders of five substituted phenyl rings to the Hansch π and σ parameters and steric effects. Mills et al.²² describe the identification of “well-matched SARs” as a purely empirical approach that could work because the binding pockets are similar or because of similar steric and conformational constraints. Weber et al.¹⁴ in their 3D method assume that potency changes relating to a particular matched pair transformation must depend on the protein atoms around that location and are able to rationalize a published SAR relationship for COX-2 on the basis of matched pairs from similar environments in factor Xa and thrombin.

The Matsy algorithm may be considered a formalism of aspects of how a medicinal chemist works in practice. Observing a particular trend, a chemist considers what to make next on the basis of chemical intuition, experience with related compounds or targets, and ease of synthesis. The structures suggested by Matsy preserve the core features of molecules while recommending small modifications, a process very much in line with the type of functional group replacement that is common in lead optimization projects. This is in contrast to recommendations from fingerprint-based similarity comparisons where the structural similarity is not always straightforward to rationalize and near-neighbors may look unnatural to a medicinal chemist.

The algorithm may also be seen as a way to package existing SAR data from multiple medicinal chemistry projects and make it available as a tool to help decision-making in other projects. One can view it as a recommender system²⁸ (“I see that the observed activity order in your project is [C > CC > CCC]; 30% of matched series that displayed this activity order had improved activity with chlorine.”) or as a tool for hypothesis generation or simply as a way to navigate and explore existing SAR information. It is a completely knowledge-based method, and all predictions can be linked back to the underlying data, the targets and structures from which the predictions are derived. There is no black box, fingerprint calculation, or complex machine-learning model. All of the information used to make the prediction is available and can be inspected. This means that in practice one can look beyond the stated statistical preference of a particular substituent and assess whether the supplied prediction is likely to apply in a particular case. The results are also dynamic, with predictions being updated as new data are incorporated into the underlying data set.

Being a knowledge-based method also comes with certain disadvantages, as it is not possible to extrapolate beyond the underlying training set. For example, there may be little or no data for unusual or uncommon substituents. As shown in the evaluation, a more serious problem is that even where substituents are common, a particular matched series may not be. For longer matched series this is particularly true (see Figure 5), a situation that can only be improved by using larger databases of assay data; in this respect it is worth mentioning the approach of MedChemica³ who pools matched pair data from several pharmaceutical companies for mutual gain. To handle the situation in practice, the approach described earlier is useful where the least common substituent in a matched series is successively removed until a prediction can be made.

Here we have focused on improving binding affinities. However, the Matsy algorithm can be used equally well to predict R groups that decrease binding affinity to an antitarget given a particular matched series. In practice, selectivity between very similar binding sites may be difficult to achieve if it relies on subtle differences that are unique to one or the other, as the predictive method relies on matches in the underlying database.

All of the work described here used publicly available activity data abstracted from the literature by the ChEMBL group. If this were to be applied to in-house pharmaceutical data, it is expected that equivalent or better results would be obtained because there would be a large number of results from a smaller number of assays. Furthermore, given the systematic approach of medicinal chemists in pharmaceutical companies toward the synthesis and testing of structural series, the quantity of matched series data available in-house is also expected to be larger.

Conclusions

We have developed an algorithm, Matsy, for predicting R groups that improve biological activity given an observed activity order for other R groups. This is similar to the decision tree approach described by Topliss except that predictions are linked to observed data rather than a proposed rationale.

The basis of the method is preferred activity orders in matched series. We show that there is little enrichment of particular orders in matched pair data (in agreement with previous work) but that as one moves to longer matched series, the maximum enrichment increases significantly and it is possible to identify transformations that increase activity. By measuring performance in a retrospective test, we show that longer series are more predictive and that these predictions are not simply driven by correlations to physicochemical properties. In short, the concept of matched molecular series is much more effective than matched molecular pairs at capturing and predicting trends in biological activity.

Our algorithm provides a straightforward way for medicinal chemists to apply matched series information from previous medicinal chemistry projects to their project, whether as an absolute guide, a hypothesis generator, or simply a way of querying existing activity data.

Methods

Ordered Matched Series

A matched (molecular) series is a straightforward extension of the concept of a matched pair to encompass more than just a pair of molecules. Specifically, here we consider a matched series to be a set of two or more molecules all of whose structures can be interconverted by replacement of terminal groups at the same point. A matched series of length 2 is synonymous with the term matched pair.

Rather than consider a specific set of molecular structures, it is useful to consider generic matched series as characterized by just the structural replacements, e.g., the matched series [F, Cl, Br]. This represents not just the specific three molecules that comprise a matched series but all other sets of three structures that just differ by halide replacement at the same position.

In general, a matched series describes a set of molecules without any implicit ordering. An ordered matched series is one where the set of molecules is ordered with respect to some experimental property, for example, binding affinity to a protein. For example, the ordered matched series [F > Cl > Br] may indicate a set of halides where the fluorine analogue has the best binding affinity to a particular target, followed by the chlorine analogue and then the bromide.

Data Set of Matched Series from ChEMBLdb

All analyses presented use pIC₅₀ data derived from the IC₅₀ values in ChEMBLdb 16.²⁹ The assays with which these data are associated are grouped into three types: “B” for binding data, “F” for functional assays, and “A” for ADMET. Only data from assays marked as type “B” were included. In total, this came to 188 801 assays and 2 165 644 data points. For certain analyses, a subset of these data relating to kinases or GPCRs was used. Information on which targets are kinases and GPCRs is available from ChEMBL as part of the Kinase SARfari and GPCR SARfari interfaces. The kinase data set includes 24 288 assays and 144 036 data points, while the GPCR data set includes 31 693 assays and 282 731 data points.

All matched series in these data were calculated using the method of Hussain and Rea³⁰ using in-house Python code and the OEChem toolkit.³¹ The fragmentation scheme used involved a single cut at each acyclic single bond in turn if either end of the bond was involved in a ring or if the bond was between a non-sp²-hybridized carbon atom and a non-carbon atom. Scaffolds were required to have 5 or more heavy atoms, while R groups were required to have 12 or fewer heavy atoms.

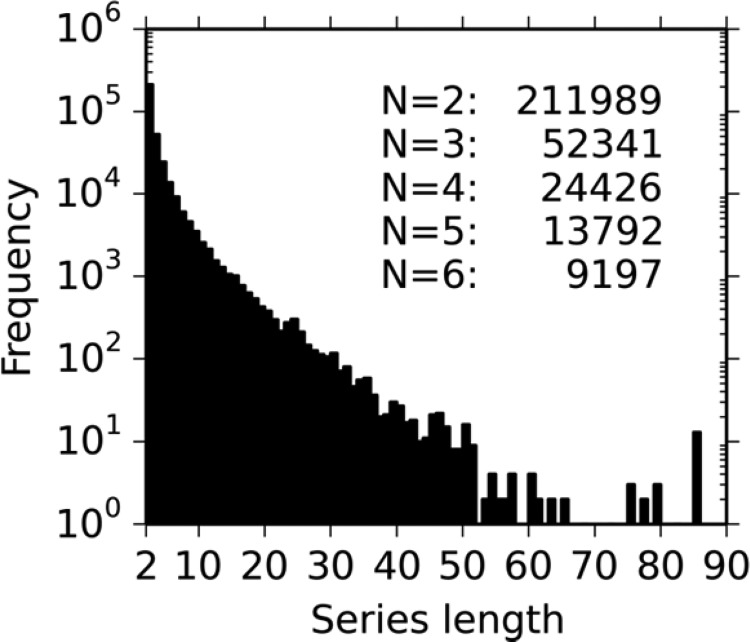
Figure 9 gives an overview of the distribution of the matched series of different lengths. Note that although there were only 9197 matched series of length 6, there are many more matched series of length 6 embedded in series that are longer. The five most common R groups in the matched series data set are hydrogen, methyl, phenyl, chloro, and methoxy.

Figure 9.

Histogram showing the frequency of matched series of different lengths. Note that the y axis uses a log scale.

IC₅₀ values in ChEMBLdb may be marked as “NA” (not active) or include qualifiers such as “>1000”. As all of our analyses rely simply on the order of values, “NA” values were rank-ordered at the bottom of any series. For values with qualifiers, the qualifier was simply removed.

Use of Cutoffs for Matsy Predictions

To avoid spurious results when using Matsy such as 100% improvement based on a single or low number of observations as for D and E in Figure 2, it is useful to implement a cutoff for the number of observations required. We have found that a value of 20 observations provides a useful initial cutoff. If no predictions initially pass the cutoff, then this is reduced to 10 and finally 5. After this there are two approaches: either no prediction is made or else members of the series are removed until a prediction is made for a subseries. Since inability to predict is due to insufficient data, the R group removed was chosen to maximize the number of observations of the remaining ordered matched series; typically this is the least common R group.

Training and Test Data for Retrospective Test

The training and test data were chosen to simulate prospective prediction. The training set was all data in our ChEMBLdb-derived pIC₅₀ data set from before 2012, while the pIC₅₀ data from 2012 or later were used as source data to generate the test set.

First of all, series of length 5 or shorter were discarded from the source data. To avoid trivial predictions due to duplicates, we discarded any series in the test set that had the same scaffold as any series in the training set. To generate the test set for series of length N (where N was from 2 to 6), 10 subsets of length N were selected from each series in the source data. The 10 subsets were chosen at random without replacement from all possible subsets. Series in the test set where the activity values were not ordered (for example, two “NA” values) were discarded. Generation of the test set was repeated 100 times with different random seeds in order to estimate the variance.

For each series in the test set, the R group with the highest activity was removed. The Matsy algorithm was then used to predict substituents that improve activity based on the remaining R groups.

Glossary

Abbreviations Used

Matsy

an algorithm that uses matched series to propose R groups that improve activity

MMPA

matched molecular pair analysis

MR

molecular refractivity

Supporting Information Available

A comparison of how common frequent R groups are in matched series of different lengths, retrospective test results when using focused GPCR or kinase subsets of the data, enrichment values for predictions related to the Topliss tree, and scaffolds and targets for the Matsy prediction of n-hexyl for [CCC > CC > C]. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare the following competing financial interest(s): NextMove Software Ltd. has developed a commercial product based on the Matsy algorithm described in this paper.