The effects of local prevalence and explicit expectations on search termination times

Abstract

In visual search tasks, the relative proportions of target-present and -absent trials have important effects on behavior. Miss error rates rise as target prevalence decreases (Wolfe, Horowitz, & Kenner, Nature 435, 439–440, 2005). At the same time, search termination times on target-absent trials become shorter (Wolfe & Van Wert, Current Biology 20, 121–124, 2010). These effects must depend on some implicit or explicit knowledge of the current prevalence. What is the nature of that knowledge? In Experiment 1, we conducted visual search tasks at three levels of prevalence (6%, 50%, and 94%) and analyzed performance as a function of “local prevalence,” the prevalence over the last n trials. The results replicated the usual effects of overall prevalence but revealed only weak or absent effects of local prevalence. In Experiment 2, the overall prevalence in a block of trials was 20%, 50%, or 80%. However, a 100%-valid cue informed observers of the prevalence on the next trial. These explicit cues had a modest effect on target-absent RTs, but explicit expectation could not explain the full prevalence effect. We conclude that observers predict prevalence on the basis of an assessment of a relatively long prior history. Each trial contributes a small amount to that assessment, and this can be modulated but not overruled by explicit instruction.

One may search for various objects in a variety of scenes. For example, one may look for a friend in a lecture hall or for a traffic signal when riding in a car. Even though visual searches play an important role in daily life, we sometimes fail to find a target. If targets appear rarely, we miss them more frequently (Wolfe, Horowitz, & Kenner, 2005). This phenomenon is termed the “prevalence effect” (Gur et al., 2004). Wolfe et al. (2005) demonstrated that hit rates were far lower at 1% target prevalence than at 50% prevalence when observers searched for an object amid a noisy background, roughly simulating an X-ray baggage screening task with nonexpert viewers. This prevalence effect has been replicated (Rich et al., 2008; Wolfe et al., 2007; Wolfe & Van Wert, 2010) and debated (Fleck & Mitroff, 2007). In addition to modulating error rates, prevalence alters search termination times on target-absent trials. Reaction times (RTs) on target-absent trials decline as the target prevalence declines. When targets are very rare, observers tend to terminate unsuccessful searches much more rapidly than they do when targets are more common. In contrast, RTs on target-present trials are minimally affected by target prevalence. The prevalence effect may be of importance, since low prevalence is characteristic of tasks such as airport security, medical screening (Gur et al., 2004), or a predator’s search for prey (Bond & Kamil, 1998; Olendorf et al., 2006).

Given that prevalence alters search behavior, it follows that observers must have an estimate of the prevalence that applies to the current trial. Where does that estimate come from? It could be based on the perceived prevalence over some previous sets of trials. Thus, if the last 10 trials have yielded 5 target-present and 5 target-absent trials, the observer might guess that the current prevalence is about 50%. Alternatively, the observer could respond to explicit information about the current trial. Even if the last 10 trials have been 5 target-present and 5 target-absent trials, the observer might change his behavior if told that the probability of a target on the current trial is 90% or 10%. We will call this an “expectation” effect. Under normal circumstances, these factors are confounded. The local prevalence (e.g., the last 10 trials) is related to the global prevalence (the prevalence for the entire block of trials), and the expectation for the next trial is based on what the observer has been told about the block of trials and/or what that observer has figured out from the history of preceding trials. In this article, we will attempt to disentangle these effects.

In visual search studies, Maljkovic and Nakayama (1994) were among the first to explicitly distinguish between expectation effects and estimates based on the recent history of previous trials. In their experiment, observers were asked to direct their attention to a singleton item. It could be red amongst green items or green amongst red items. On some blocks, the color of targets varied randomly from trial to trial. In those cases, the observers could not predict what color would come next. In other blocks, the target color alternated from one trial to the next, allowing observers to predict what color would come next. RTs were significantly shorter when the target color was repeated, as compared to when it was not. The influence of approximately the last seven trials could be detected in the RT for the current trial. In contrast, RTs were not affected by the predictability of the color. The sure knowledge that the next trial was a green target trial did not change performance. Consequently, Maljkovic and Nakayama concluded that RT facilitation was influenced by past repetition, not future expectation.

As has been noted, the conditions for repetition and expectation effects tend to happen together (e.g., if prevalence is low, you will get more repetitions of target-absent trials), so they could be easily confounded. For example, Kristjánsson, Wang, and Nakayama (2002) required observers to perform conjunction searches for two types of potential targets (red–vertical or a green–horizontal targets among red–horizontal and green–vertical distractors). The observers performed better when the type of target remained the same throughout the whole block rather than varying randomly (see also Egeth, 1977; Wolfe, Butcher, Lee, & Hyle, 2003). Obviously, in a design of this sort, blocked conditions are associated with more repetitions and a clear expectation for target type.

Wolfe and Van Wert (2010) dissociated local prevalence from global prevalence by varying prevalence in a sinusoidal fashion from 1.0 to 0 over 500 trials, and then back again to 1.0 in the next 500 trials. The authors calculated target prevalence, error rates, target-absent RTs, and criterion values over blocks of 50 trials. Each prevalence occurred twice, once as prevalence was falling and once as it was rising. The error rates, target-absent RTs, and criterion values clearly tracked the change in target prevalence. However, equivalent prevalence values produced different results in the falling and rising phases of the experiment. The error rates, target-absent RTs, and criterion values lagged behind the current prevalence. It was possible to use this lag to roughly estimate the number of trials that were contributing to the observer’s estimate of the prevailing prevalence. Wolfe and Van Wert concluded that “it appears that observers compute prevalence over about four dozen trials.”

Can the effects of prevalence be influenced by explicit future expectations, or only by past repetitions? Wolfe and Van Wert’s (2010) study was not equipped to look at this factor, since prevalence changed in a predictable manner, confounding prevailing prevalence and explicit expectations about prevalence. Lau and Huang (2010) addressed this question by giving their observers different instructions on different trials (see also Reed, Ryan, McEntee, Evanoff, & Brennan, 2011). In their Experiments 1 and 2, observers were told that one color background meant high (50%) prevalence of a target, while another color meant low (10%) prevalence. On some blocks this was true. On other blocks, the color cue was unrelated to the constant target prevalence. Although target-absent RTs were affected by the probabilistic cues, miss rates were governed by the actual prevalence and were not influenced by the cues. In Experiments 3 and 4 of Lau and Huang (2010), the cues were always valid. Even though target-absent RTs were affected by the cue, again, the effect of prevalence on miss rates was linked to the overall prevalence and not to a future expectation provided by the cue. There are three reasons to think that this might not be the end of the story. First, Lau and Huang focused on error rates rather than RTs. Wolfe and Van Wert argued that error rates and RTs were influenced separately by prevalence. Thus, it is possible that there could be a significant effect on RTs, even if there was no effect on errors. Second, the largest effect on RTs for Wolfe and VanWert occurred when prevalence was very high. Lau and Huang only explored the low-to-middle range of prevalence. Third, Wolfe and VanWert’s experiment permitted only a rather crude estimate of the number of trials required to estimate prevalence. Here we looked for evidence of more fine-grained effects.

In the present study, our primary focus was on search termination times on target-absent trials, in an attempt to clarify the roles of local prevalence and explicit expectations. In Experiment 1, we used three target prevalence conditions in a simulated luggage search task (6%, 50%, and 94%). We found, at best, only small effects of local prevalence, not enough to explain the overall prevalence effect. In Experiment 2, we used reliable cues about the target probability on the upcoming trial to dissociate the prevailing local and global prevalences from explicit expectations. We found that there were reliable cue effects, though as with local prevalence, the effects of expectation were not enough to account for the prevalence effect. These results led us to the conclusion that the prevailing estimate of prevalence is built up quite slowly over a rather large number of trials.

Experiment 1

Method

Stimuli: making luggage

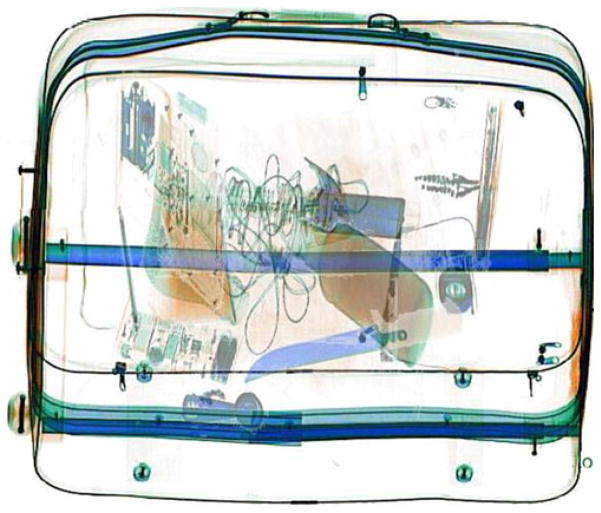
We used stimuli like those developed by Wolfe et al. (2007) and Wolfe and Van Wert (2010). This laboratory version of luggage screening made use of jpeg X-ray images supplied by the Department of Homeland Security’s Transportation Security Laboratory. The image set included empty bags and images of objects that could be found in those bags. Targets were drawn from a set of 100 images of guns and 100 images of knives. Bags were created with MATLAB using the Psychophysics Toolbox (Brainard, 1997). Each bag was loaded with 18 randomly chosen objects. Objects were drawn to scale, so a hair dryer would be bigger than a nail clipper. Selection of objects was random from the set, so some bags contained unusual collections of objects. The bag images varied in height from 9.5 to 20 deg at a 57-cm viewing distance, and in width from 16 to 21.5 deg. Clothing appeared in X-ray images as an orange haze. Eight pieces of clothing were added to each bag to produce this effect, but these were not counted as “items” in the bag. Figure 1 shows a sample bag. In the standard color scheme, blue indicates metal, orange shows organic material, and green shows material of intermediate density.

Fig. 1.

An example of the luggage-like stimuli used in these experiments

Observers

In Experiment 1, 15 novice observers who had never seen the stimuli were tested in all conditions (ages 19–27 years, mean age = 22.3 years, SD = 2.0; 6 women, 9 men). By self-report, the observers had no history of eye or muscle disorders. None were colorblind (Ishihara plates), and all had visual acuity no worse than 20/25 with correction. Informed consent was obtained from observers, and each was paid 1,000 yen/h for his or her time.

Procedure

On each trial, a fixation cross was presented for 1,000 ms. Then a bag stimulus was presented until the observers responded. Observers pressed one key for target presence and another if they felt that there was no target. Observers received accurate feedback. The target, if present, was outlined on the screen after a response was made. Correct “present” responses were rewarded with the written comment “Good for you. You found the target. Take a look and then press a key to continue.” The message after a miss error “You missed the target. Take a look and then press a key to continue.” Messages after target-absent trials indicated whether the response was correct or incorrect. Observers made another keypress to move to the next trial.

Observers were given 50 practice trials at 50% prevalence and then tested in three blocks having 6%, 50%, or 94% prevalence. There were 300 trials per block. Block order was counterbalanced across observers. The computer enforced breaks every 50 trials; therefore, 300 trials in each block were divided into six sessions composed of 50 trials each. Observers could get up and leave the testing room during breaks, but this was not required.

Data analysis

RTs over 5,000 ms and under 200 ms were removed from the analysis. In Experiment 1, we did not inform observers about target prevalence. Therefore, we treated the first 50 trials of each block as practice trials that allowed observers to learn the prevailing target prevalence.

Results

Eliminating RT outliers resulted in the removal of 0.14% of trials. The pattern of errors was the same with and without the data from those trials. Removing these outlier RTs decreased the variability in the RT analysis.

Subjective prevalence

After a block of trials, observers were asked to give an explicit estimate of the prevalence. The average subjective prevalence was 7% (SEM = 0.8) in the 6% prevalence condition, 55% (SEM = 3.0) in the 50% prevalence condition, and 92% (SEM = 0.7) in the 94% prevalence condition. These results showed that observers acquired an accurate and explicitly accessible estimate of target prevalence in each condition.

Replication of the prevalence effect

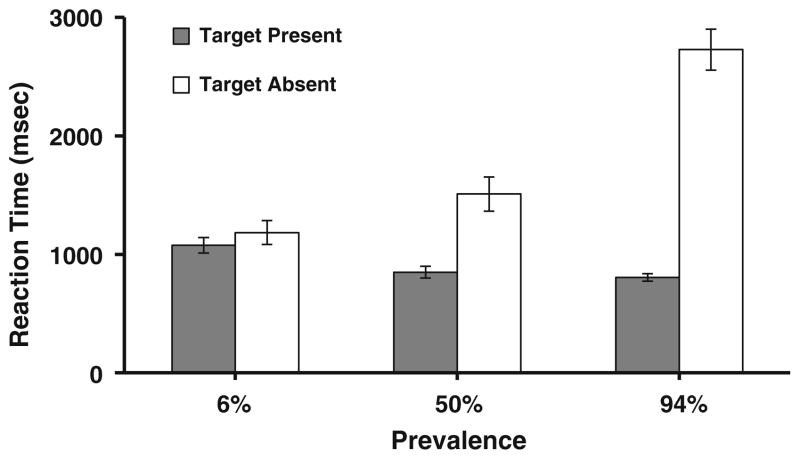
Figure 2 shows that target prevalence influenced search termination time in our study. As reported in the previous works, search termination time increased from an average of 1,184 ms at 6% prevalence to 1,510 ms at 50% prevalence, and it was an average of 2,728 ms at 94% prevalence. The main effect of prevalence was statistically significant [F(2, 28) = 61.32, p < .001]. Subsequent Bonferroni-corrected comparisons indicated that there were significant differences among the three conditions (all ps < .05). The target-present RTs were reliably slower at low prevalence [F(2, 28) = 23.50, p < .001]. Subsequent Bonferroni-corrected comparisons indicated that RTs at 6% prevalence were longer than those at both 50% prevalence and 94% prevalence (p < .05), and that there was no difference between the 50% prevalence and 94% prevalence conditions. There was a more modest effect of prevalence on target-present RTs. These results showed clear evidence that Experiment 1 produced a typical prevalence effect on search termination times.

Fig. 2.

Average reaction times for target-present and -absent trials in Experiment 1. Error bars represent ±1 SEM

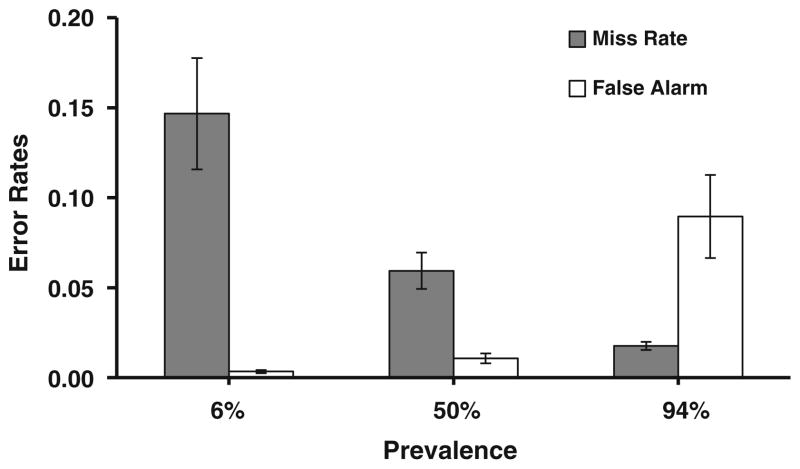
Prevalence had the usual effects on the error rates. The miss rates are shown in Fig. 3 as a function of prevalence. Miss rates decreased from an average of .15 at 6% prevalence, to .06 at 50% prevalence, to .02 at 94% prevalence. We used a nonparametric Friedman test because the number of 100%-correct cells rendered the distribution of errors clearly non-Gaussian (miss errors, Friedman statistic = 19.6, p < .001; false alarms, Friedman = 14.3, p < .01). Wilcoxon tests (Bonferroni corrected) indicated significant differences among the three conditions in miss rates (p < .05). False alarms were higher at 94% prevalence than at either 6% prevalence or 50% prevalence (p < .05), and there was no difference between the 6% and 50% prevalence conditions. The trade-off between miss and false alarm errors also showed that, as has been reported elsewhere (Healy & Kubovy, 1981; Wolfe et al., 2007), the main effect of prevalence was on criterion and not on sensitivity (d′). The d’s were 3.6 at 6% and 3.6 at 94% [F(2, 28) = 1.26, p = .30], while criterion changed from .6 at 6% to –.3 at 94% [F(2, 28) = 54.01, p < .001]. Subsequent Bonferroni-corrected comparisons indicated significant differences among the three conditions (all ps < .05).

Fig. 3.

Error rates for Experiment 1. Error bars represent ±1 SEM

As Fig. 2 shows, there were very large effects of prevalence on target-absent RTs, with smaller effects, as has been reported elsewhere (Godwin, Menneer, Cave, & Donnelly, 2010), in the opposite direction on target-present RTs.

Local prevalence effect on RTs

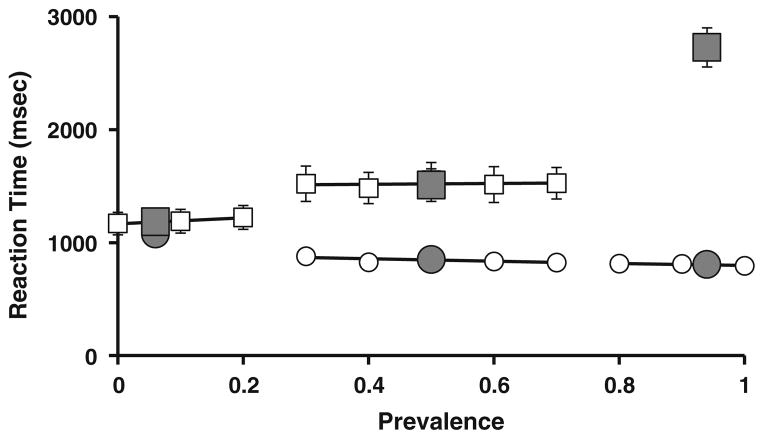
As noted, Wolfe and Van Wert (2010) changed prevalence slowly over the course of 1,000 trials and found that RTs changed with the prevailing prevalence. They could roughly estimate that prevailing prevalence was computed over about 40–50 trials. The structure of the present experiment allowed us to look for more local effects within an experimental design that varied overall prevalence. Though the prevalence over a block might be 6%, 50%, or 94%, the local prevalence would vary. Thus, if one looks, for example, at just the previous 10 trials, the local prevalence could be 0%, 10%, 20%,… or 100%, depending on the number of target-present trials in the group of 10. Of course, at 94% prevalence, 0% or 20% local prevalence will occur very rarely, and at 6% prevalence, there will not be many higher values of local prevalence. Nevertheless, there will still be substantial variation in local prevalence over trials.

Figure 4 shows the results of such an analysis. Large symbols reproduce the mean RT data from Fig. 2. Smaller figures show the RTs as a function of the local prevalence. Data are plotted for those conditions that produced at least 150 trials, accumulated across all 15 observers. Thus, at 6% global prevalence, there are 150 trials at 0%, 10%, and 20% prevalence. Runs of 10 trials with, say, 5 target-present trials occur at very low rates at 6% prevalence. Lines are regression lines through the local-prevalence RT values for each global prevalence. The target-absent trials are the RTs of interest. The slopes of the local-prevalence lines are very shallow. Indeed, the effects of local prevalence on RT are not statistically reliable [50% global prevalence, F(4, 56) = 0.31, p = .87; 6% global prevalence, F(2, 28) = 0.97, p = .39]. The results are qualitatively similar for local prevalence computed for windows of 20, 7, or 5 trials (all ps > .05).

Fig. 4.

Reaction time (RT) spreads as a function of global and local prevalence in Experiment 1. Large symbols reproduce the RT data from Fig. 2; the squares are target-absent trials, the circles target-present trials. Smaller figures and regression lines show RTs as a function of local prevalence. Data are plotted only for those conditions producing at least 150 trials across 15 observers. Error bars represent ±1 SEM

Discussion

Apparently, observers are not highly responsive to local variation in prevalence. There are three possibilities. (1) Perhaps the effect of prevalence builds up slowly, and this experiment simply lacked the power to see the effects that occurred over 5 or 10, or even 20, trials. Wolfe and Van Wert (2010) estimated that performance was based on prevalence over 40–50 trials. The design of Experiment 1 was able to look at shorter runs of trials. Once the run length became longer, the range of local prevalence did not vary much from the global prevalence, making this experimental design uninformative. (2) Alternatively, perhaps there is no effect of prevalence until observers have a quite large sample of trials. Perhaps it appears ballistically after that large number of trials have been evaluated. Finally, (3) maybe prevalence effects on RTs occur only when observers have gathered enough information to explicitly predict the prevalence of the next trial. Experiment 2 will show that there is some evidence for a role of explicit information.

Experiment 1b

However, Proposition (1) above also seems to be true. In order to look for subtle effects of local prevalence, we analyzed data collected for a different experiment (dubbed 1b here).

Method

A group of 20 observers between the ages of 18 and 55 searched for a “T” among “L”s for 600 trials at 50% prevalence. By self-report, they had no history of eye or muscle disorders. None were colorblind (Ishihara plates), and all had visual acuity no worse than 20/25 with correction. Informed consent was obtained from all observers, and each was paid $10/h for his or her time.

Observers searched for a black “T” among black “L”s presented on a white background. All items could be presented in any of four 90-deg rotations. Letter’s subtended approximately 2 deg. Set sizes were 5, 10, 15, and 20 items. On each trial, a fixation cross was presented. Then a stimulus was presented until observers responded. Observers pressed one key for target presence and another if they felt that no target was present. Observers received accuracy feedback after each trial.

Results

Eliminating outliers (RTs > 3,000 ms) resulted in the removal of 0.075% of trials. The error rates were 4.1% miss and 1.5% false alarm errors.

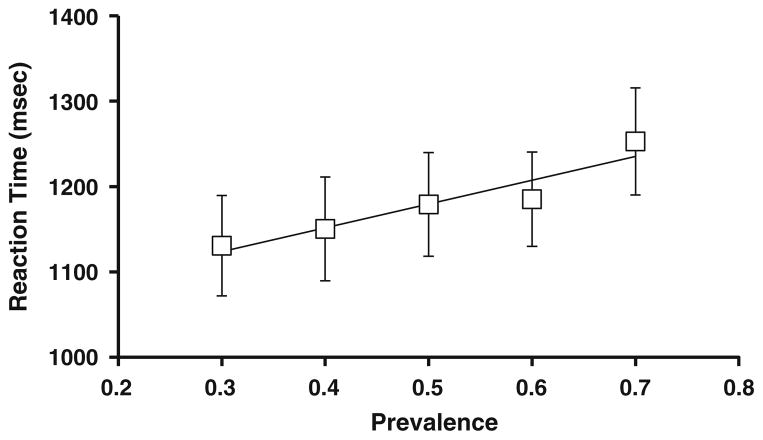
In what may be a mere coincidence, the slope of the RT × prevalence function for these data (2.8 ms per percent prevalence; see Fig. 5) is identical to the slope for the 50% global prevalence data, shown in Fig. 4. However, the greater number of subjects and trials rendered the local prevalence effect significant in this case [F(4, 76) = 4.65, p = .002]. Subsequent Bonferroni-corrected comparisons indicated that RTs were longer for 70% prevalence than for 30% prevalence (p < .05), and that there were no differences among the other conditions. We conclude, therefore, that observers can respond to local prevalence. The effect of each trial is small and, as a consequence, it takes many trials, perhaps the four dozen or so suggested by Wolfe and Van Wert (2010), before prevalence reaches its full effect. This might seem to suggest an analysis in which we look for an effect of not-so-local prevalence over a range of 40 or 50 trials. As noted above, the difficulty with this analysis is that the range of local prevalence over 50 trials is very limited. At 50% global prevalence, for example, the great bulk of local-prevalence values lie between 45% and 55%, a range too small to see a prevalence effect on RTs.

Fig. 5.

The effects of local prevalence on RTs for a T-versus-L search (Exp. 1b). Data are plotted only for those conditions producing at least 300 trials across 20 observers. Error bars represent ±1 SEM

Experiment 2: The role of explicit information about prevalence

Experiment 1 showed that local prevalence effects are, at best, quite small. However, a second type of a local effect could be larger. If the observer has explicit and credible information about the target probability on the upcoming trial, perhaps that clear expectation about the future could have more of an impact than the estimate of the recent past. Lau and Huang (2010) argued against such an effect, but as noted, they may not have looked for the effect in the place where it was most likely to appear. In Experiment 2, we created situations in which the prevailing prevalence history was different from this future expectation. In this experiment, high- and low-prevalence trials were randomly mixed in a block. Of course, the mixture created an overall prevalence for the block. Those overall target prevalence rates were 20%, 50%, and 80%. One of two levels of prevalence expectation was indicated by a cue before each trial (see Table 1). This design allowed us to compare the magnitudes of the effects of block prevalence and cued prevalence expectation.

Table 1.

Marginal probabilities and conjunctive probabilities for the conditions of Experiment 2

	Cue		Total
	50%	Extreme
20% Overall Prevalence
Present	.16	.04	.20
Absent	.16	.64	.80
Total	.32	.68	1.0
Prevalence	.50	.06
50% Overall Prevalence
Present	.16	.34	.50
Absent	.16	.34	.50
Total	.32	.68	1.0
Prevalence	.50	.50
80% Overall Prevalence
Present	.16	.64	.80
Absent	.16	.04	.20
Total	.32	.68	1.0
Prevalence	.50	.94

Method

Stimuli

The stimuli used were the same as in Experiment 1.

Observers

In Experiment 2, 15 observers with no previous experience of the stimuli were tested in all conditions (ages 18–23 years, mean age = 20.1 years, SD = 1.6; 2 women, 13 men).

Procedure

In Experiment 2, the procedure was the almost same as in Experiment 1, but fixation cues appeared on each trial, informing the observer about the prevalence on the next trial. Table 1 shows the marginal probabilities and the conjunctive probabilities for each condition in this experiment. Observers were given 50 practice trials at 50% prevalence and were then tested for 300 experimental trials in each of the 20%, 50%, and 80% overall prevalence conditions. In each overall prevalence condition, there were 96 “50%-cue” trials (32%) and 204 “extreme-cue” trials (68%). In the 20% prevalence condition, target prevalence was 50% when the 50% cue appeared, but was 6% when the extreme cue appeared. In the 80% prevalence condition, target prevalence was 50% when the 50% cue appeared but was 94% when the extreme cue appeared. In the 50% prevalence condition, both cues were associated with 50% prevalence. In Experiment 2, we used two kinds of fixation cue (“+” and “*”). For each observer, these were randomly assigned as the 50% cue and the extreme cue. Therefore, observers needed to learn the relationship of the cue to the probability of a target on that trial. The first 50 trials of each block were practice trials that allowed the observers to learn the global prevalence and the cue values.

Results

Eliminating outliers resulted in the removal of 1% of trials. The pattern of errors was the same with and without the data from those trials. Removing these outlier RTs decreased the variability in the RT analysis.

Subjective prevalence

Since observers would need to learn the probabilities associated with the cues, it was important to determine whether, in fact, they did learn these probabilities. We asked observers to estimate the subjective prevalence associated with each cue. In the 20% prevalence condition, they reported that the subjective prevalences were 46% (SEM = 4.5) for the 50%-cue trials (objective prevalence = 50%) and 13% (SEM = 1.8) for the extreme (6%) cue. In the 80% prevalence condition, they reported that the subjective prevalences were 47% (SEM = 5.8) for the 50%-cue trials (50%) and 88% (SEM = 1.2) for the extreme (94%) cue. In the 50% prevalence condition, they reported that the subjective prevalences were 43% (SEM = 4.8) for the 50%-cue trials (50%) and 58% (SEM = 4.1) for the extreme-cue trials (50%). These results showed that observers acquired a broadly accurate impression of target prevalence in all conditions.

Replication of the global prevalence effect

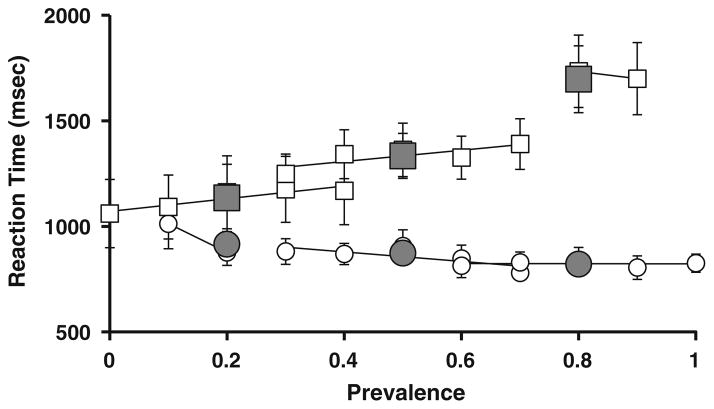
Experiment 2 can be treated as a replication of Experiment 1. This is shown in Fig. 6. There was a strong overall prevalence effect on target-absent RTs [F(2, 28) = 10.81, p < .001]. Subsequent Bonferroni-corrected comparisons indicated that RTs were longer with 80% overall prevalence than with either 20% or 50% prevalence (p < .05) and that there was no difference between the 20% and 50% prevalence conditions. There was no overall prevalence effect on target-present trials [F(2, 28) = 2.45, p = .10]. We restricted the analysis of local prevalence to those local prevalence values that generated at least 150 total trials over the 15 observers. The local prevalence effect was significant in the 20% overall prevalence condition [F(4, 56) = 3.64, p = .01]. Subsequent Bonferroni-corrected comparisons indicated a significant difference only between 10% local prevalence and 30% local prevalence (p < .05). The local prevalence effects were not significant at 50% overall prevalence [F(4, 56) = 1.73, p = .15] or 80% overall prevalence [t(14) = 0.55, p = .59]. This pattern of results is similar to that seen in Experiment 1. Local effects of prevalence are either weakly present or so weak as to be statistically unreliable, again consistent with the idea that larger numbers of trials are used to derive the estimate of prevalence that drives search behavior.

Fig. 6.

Local and global prevalence effects in Experiment 2. The upper data points (squares) show target-absent trials. Circles are target-present trials. Open squares and circles show RTs as a function of local prevalence averaged over 10 preceding trials. Filled squares and circles show average target-absent RTs for each prevalence block. Data are plotted only for those conditions producing at least 150 trials across 15 observers. Error bars represent ±1 SEM

Replication of the cueing effect on miss rates

The error rates are shown in Fig. 7 as a function of prevalence and cue condition. The basic prevalence effect on errors was replicated, with overall miss errors declining as prevalence rises and false alarm errors rise. These effects were statistically significant. We used a nonparametric Fried-man test because the number of 100% correct cells rendered the distribution of errors clearly non-Gaussian. (miss errors, Friedman statistic = 15.6, p < .001; false alarms, Friedman = 13.6, p < .01). Wilcoxon tests (Bonferroni corrected) indicated significant differences among the three conditions in terms of miss rates (all ps < .05). False alarms were higher in the 80% prevalence than in either the 20% prevalence or the 50% prevalence condition (p < .05), and there was no difference between 20% prevalence and 50% prevalence. The only effect of cue that appears to be reliable is a difference between 1% and 2.4% false alarm errors at 20% prevalence (Wilcoxon signed rank: p = .048). This effect, while tiny, is in the predicted direction: Higher expected prevalence (50%) produces more false alarm errors than does lower expected prevalence (6%). No other comparisons approach significance (all ps > .2).

Fig. 7.

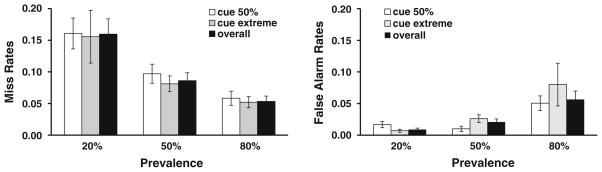
Error rates for Experiment 2 as a function of prevalence and cue condition. Error bars represent ±1 SEM

Expectation effect on RTs

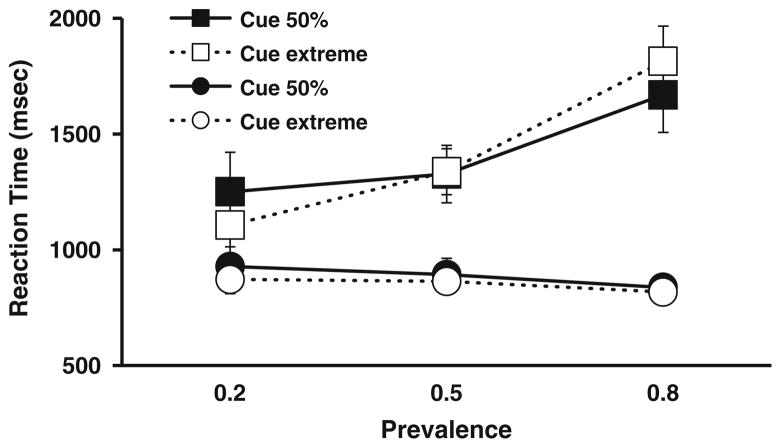
The main question of interest in Experiment 2 was whether a cue that reliably tells the observer about the probability of a target on the next trial influences the search termination time on that trial. Figure 8 shows the RT data as a function of cue types. If the prevalence effect were entirely driven by the expected prevalence, then 50%-cue RTs should be the same in all prevalence conditions, since that cue reliably indicated 50% prevalence on the next trial in all cases. Clearly, that hypothesis can be rejected. There is a significant effect of overall prevalence on 50%-cue target-absent RTs [F(2, 28) = 6.12, p = .006]. Subsequent Bonferroni-corrected comparisons indicated that RTs were longer at 80% prevalence than at 50% prevalence (p < .05) and that no differences appeared between 20% prevalence and 50% prevalence and between 20% prevalence and 80% prevalence. However, we can also reject the hypothesis that the cues had no effect. If there were no effect of the cues, the 50%-cue and extreme-cue RTs should be the same. This hypothesis can also be rejected. At 20% overall prevalence, a 6% cue produced reliably shorter RTs than did a 50% cue [t(14) = 4.53, p < .001], and at 80% prevalence, a 94% cue produced reliable longer RTs than did a 50% cue [t(14) = 2.78, p = .015]. Fortunately, there was no effect at 50% overall prevalence, since both cues denoted 50% prevalence on the next trial [t(14) = 0.35, p = .73]. There were no significant effects of cues on target-present trials [all t(14)s < 1.5, all ps > .15].

Fig. 8.

RTs as a function of cue types. Squares show target-absent RTs, and circles show target-present RTs. Error bars represent ±1 SEM

Thus, the results of Experiment 2 replicated those of Experiment 1. In addition, they showed that search termination RTs could be influenced by information about future prevalence. However, the effect was only modest in size. Explicit expectation was certainly not the primary source of the prevalence effect seen in other experiments.

General discussion

In two experiments, we again replicated significant prevalence effects on errors and RTs. Obviously, observers must have information about prevalence that drives these effects. In a standard search experiment, the plausible sources of information are highly correlated with each other. When prevalence is fixed, the explicit expectation of the prevalence on the next trial is essentially same as the history of prevalence over some preceding set of trials. Here we could begin to tease apart the effects of different sources of information, and we could reject some hypotheses.

Is the prevalence effect based primarily on the expected prevalence?

Their results allowed Lau and Huang (2010) to reject this hypothesis. Indeed, they found no reliable effects of expected prevalence. Our Experiment 2 results, likewise, did not support that hypothesis.

Is the prevalence effect entirely unaltered by expected prevalence?

The results of our Experiment 2 did not support this hypothesis, as well. Expected prevalence produced reliable effects on target-absent RTs. There was only a hint of an effect on error rates. Wolfe and Van Wert (2010) proposed that prevalence effects on errors and RTs should be partially dissociable, because prevalence affected two internal decision criteria. One criterion governs decisions about individual items during search (“Is this attended item a target?”). The other is specifically related to quitting times on target-absent trials. Both of these will influence error rates. The quitting criterion will be the primary source of prevalence effects on target-absent RTs. Thus, if explicit expectations had a greater influence on the quitting criterion than on the target/nontarget criterion, we might expect to see larger expectation effects on target-absent RTs than on error rates.

Is the prevalence effect based primarily on the local prevalence over the last few trials?

The results of both Expriments 1 and 2 allow us to reject this hypothesis. We presented an analysis of local prevalence defined by a 10-trial window. However, RTs were not strongly related to the local prevalence over any small window of trials. Only in the 20% prevalence condition of Experiment 2 did local prevalence over a 10-trial window reach statistical significance, and one might worry whether a single significant outcome is actually significant, in the broader sense of that term.

Is the prevalence effect entirely unrelated to local prevalence over the last few trials?

Finally, we can reject this hypothesis, too. Experiment 1b showed that with enough statistical power, the weak effects of local prevalence are statistically reliable.

Taken together with the results of Wolfe and VanWert (2010), the present results are consistent with the view that the effects of prevalence build up incrementally over many instances of a search. The estimate of four dozen given by Wolfe and VanWert might be correct, but it would take a very large study to pin this number down accurately, even if a fixed number of trials were used to derive the current estimate of prevalence. It seems more plausible that a given target-present or target-absent trial has its greatest impact on the next trials and that its impact then fades over time. Again, measuring such a function would be extremely laborious. It is probably adequate to say that several dozen trials go into the prevailing estimate of prevalence and that explicit information about future prevalence can modify but cannot completely dominate this prevailing estimate.