BAYESIAN DATA AUGMENTATION DOSE FINDING WITH CONTINUAL REASSESSMENT METHOD AND DELAYED TOXICITY

Abstract

A major practical impediment when implementing adaptive dose-finding designs is that the toxicity outcome used by the decision rules may not be observed shortly after the initiation of the treatment. To address this issue, we propose the data augmentation continual re-assessment method (DA-CRM) for dose finding. By naturally treating the unobserved toxicities as missing data, we show that such missing data are nonignorable in the sense that the missingness depends on the unobserved outcomes. The Bayesian data augmentation approach is used to sample both the missing data and model parameters from their posterior full conditional distributions. We evaluate the performance of the DA-CRM through extensive simulation studies, and also compare it with other existing methods. The results show that the proposed design satisfactorily resolves the issues related to late-onset toxicities and possesses desirable operating characteristics: treating patients more safely, and also selecting the maximum tolerated dose with a higher probability. The new DA-CRM is illustrated with two phase I cancer clinical trials.

1. Introduction

The continual reassessment method (CRM) proposed by O’Quigley, Pepe and Fisher (1990) is an influential phase I clinical trial design for finding the maximum tolerated dose (MTD) of a new drug. The CRM assumes a single-parameter working dose–toxicity model and continuously updates the estimates of the toxicity probabilities of the considered doses to guide dose escalation. Under some regularity conditions, the MTD identified by the CRM generally converges to the true MTD, even when the working model is misspecified (Shen and O’Quigley, 1996). A variety of extensions of the CRM have been proposed to improve its practical implementation and operating characteristics (Goodman, Zahurak and Piantadosi, 1995; Møller, 1995; Heyd and Carlin, 1999; Leung and Wang, 2002; and O’Quigley and Paoletti, 2003; Garrett-Mayer, 2006; Iasonos and O’Quigley, 2011; among others). Recently, several robust versions of the CRM have been proposed by using the Bayesian model averaging and posterior maximization (Yin and Yuan, 2009; and Daimon, Zohar and O’Quigley, 2011), so that the method is insensitive to the prior specification of the dose–toxicity model.

In real applications, to achieve its best performance, the CRM requires that the toxicity outcome be observed quickly such that, by the time of the next dose assignment, the toxicity outcomes of the currently treated patients have been completely observed. However, late-onset toxicities are common in phase I clinical trials, especially in oncology areas. For example, in radiotherapy trials, dose-limiting toxicities (DLTs) often occur long after the treatment is finished (Coia, Myerson and Tepper, 1995). Desai et al. (2007) reported a phase I study to determine the MTD of oxaliplatin for combination with gemcitabine and the concurrent radiation therapy in pancreatic cancer. In that trial, on average, a new patient arrived every two weeks, whereas it took nine weeks to assess the toxicity outcomes of the patients after the treatment is initiated. Consequently, at the moment of dose assignment for a newly arriving patient, the patients under treatment might not have yet completed the full assessment period and thus their toxicity outcomes might not be available for making the decision of dose assignment. Late-onset toxicity has been becoming a more critical issue in the emerging era of the development of novel molecularly targeted agents, because many of these agents tend to induce late-onset toxicities. A recent review paper in the Journal of Clinical Oncology found that among a total of 445 patients involved in 36 trials, 57% of the grade 3 and 4 toxicities were late-onset and, as a result, particular attention has been called upon to the issue of late-onset toxicity (Postel-Vinay et al., 2011).

Our research is motivated by one of the collaborative projects, which involves the combination of chemo- and radiation therapy. The trial aims to determine the MTD of a chemo-treatment while the radiation therapy is delivered as a simultaneous integrated boost in patients with locally advanced esophageal cancer. The DLT is defined as CTCAE 3.0 (Common Terminology Criteria for Adverse Events version 3.0) grade 3 or 4 esophagitis, and the target toxicity rate is 30%. In this trial, six dose levels are investigated and toxicity is expected to be late-onset. The accrual rate is approximately 3 patients per month, but it generally takes 3 months to fully assess toxicity for each patient. By the time of dose assignment for a newly enrolled patient, some patients who have not experienced toxicity thus far may experience toxicity later during the remaining follow-up. It is worth noting that whether we view toxicity as late-onset or not is relative to the patient accrual rate. If patients enter the trial at a fast rate and toxicity evaluation cannot keep up with the speed of enrollment, this situation is considered as late-onset toxicity. On the other hand, if the patient accrual is very slow, e.g., one patient every three months, and toxicity evaluation also requires a follow-up of three months, then the trial conduct may not cause any missing data problem. For broader applications besides this chemo-radiation trial and to gain more insight into the missing data issue, we explore several options to design such late-onset toxicity trials, including the CRM and some other possibilities discussed below.

Operatively, the CRM does not require that toxicity must be immediately observable, and the update of posterior estimates and dose assignment can be based on the currently observed toxicity data while ignoring the missing data. However, such observed data represent a biased sample of the population because patients who would experience toxicity are more likely to be included in the sample than those who do not experience toxicity. In other words, the observed data contain an excessively higher percentage of toxicity than the complete data. Consequently, the estimates based on only the observed data tend to overestimate the toxicity probabilities, and lead to overly conservative dose escalation. Alternatively, Cheung and Chappell (2000) proposed the time-to-event CRM (TITE-CRM), in which subjects who have not experienced toxicity thus far are weighted by their follow-up times. Based on similar weighting methods, Braun (2006) studied both early- and late-onset toxicities in phase I trials; Mauguen, Le Deley and Zohar (2011) investigated the EWOC design with incomplete toxicity data; and Wages, Conaway and O’Quigley (2013) proposed a dose-finding method for drug-combination trials. Yuan and Yin (2011) proposed an expectation-maximization (EM) CRM approach to handling late-onset toxicity.

In the Bayesian paradigm, we propose a data augmentation approach to resolving the late-onset toxicity problem based upon the missing data methodology (Little and Rubin, 2002; and Daniels and Hogan, 2008). By treating the unobserved toxicity outcomes as missing data, we naturally integrate the missing data technique and theory into the CRM framework. In particular, we establish that the missing data due to late-onset toxicities are nonignorable. We propose the Bayesian data augmentation CRM (DA-CRM) to iteratively impute the missing data and sample from the posterior distribution of the model parameters based on the imputed likelihood.

The remainder of the article is organized as follows. In Section 2, we briefly review the original CRM methodology, and propose the DA-CRM based on Bayesian data augmentation to address the missing data issue caused by late-onset toxicity. In Section 3.1, we present simulation studies to compare the operating characteristics of the new design with other available methods, and in Section 3.2 we conduct a sensitivity analysis to further investigate the properties of the DA-CRM. We illustrate the proposed DA-CRM design with two cancer clinical trials in Section 4, and conclude with a brief discussion in Section 5.

2. Dose-Finding Methods

2.1. Continual Reassessment Method

In a phase I dose-finding trial, patients enter the study sequentially and are followed for a fixed period of time (0, T) to assess the toxicity of the drug. During this evaluation window (0, T), we measure a binary toxicity outcome for each subject i,

$$Y_i=\{\begin{array}{cc}1\hfill & \text{if a drug-related toxicity is observed in}(0,T)\hfill \\ 0\hfill & \text{if no drug-related toxicity is observed in}(0,T).\hfill \end{array}$$

Typically, the length of the assessment period T is chosen so that if a drug-related toxicity occurs, it would occur within (0, T). Depending on the nature of the disease and the treatment agent, the assessment period T may vary from days to months.

Suppose that a set of J doses of a new drug are under investigation, the CRM assumes a working dose–toxicity curve, such as

$${\pi }_d={\alpha }_d^{\text{exp}(a)},d=1,\dots ,J,$$

where π_d is the true toxicity probability at dose level d, α_d is the prespecified probability constant, satisfying a monotonic dose–toxicity order α₁ < ⋯ < α_J, and a is an unknown parameter. We continuously update this dose–toxicity curve by re-estimating a based on the observed toxicity outcomes in the trial.

Suppose that n patients have entered the trial, and let y_i and d_i denote the binary toxicity outcome and the received dose level for the ith subject, respectively. The likelihood function based on the toxicity outcomes y = {y_i, i = 1, …, n} is given by

$$L(\mathit{y}|a)=\prod _{i=1}^n{\left\{{\alpha }_{d_i}^{\text{exp}(a)}\right\}}^{y_i}{\{1-{\alpha }_{d_i}^{\text{exp}(a)}\}}^{1-y_i}.$$

Assuming a prior distribution f(a) for a, e.g., f(a) is a normal distribution with mean 0 and variance σ², a ~ N(0, σ²), then the posterior distribution of a is given by

$$f(a|\mathit{y})=\frac{L(\mathit{y}|a)f(a)}{\int L(\mathit{y}|a)f(a)\mathrm{d}a},$$ (2.1)

and the posterior means of the dose toxicity probabilities are given by

$${\mathrm{\pi ̂}}_d=\int {\alpha }_d^{\text{exp}(a)}f(a|\mathit{y})\mathrm{d}a,d=1,\dots ,J.$$

Based on the updated estimates of the toxicity probabilities, the CRM as-signs a new cohort of patients to dose level d* which has an estimated toxicity probability closest to the prespecified target φ; that is,

$$d^{*}={\text{argmin}}_{d\in (1,\dots ,J)}|{\mathrm{\pi ̂}}_d-\varphi |.$$

The trial continues until the exhaustion of the total sample size, and then the dose with an estimated toxicity probability closest to φ is selected as the MTD.

2.2. Nonignorable Missing Data

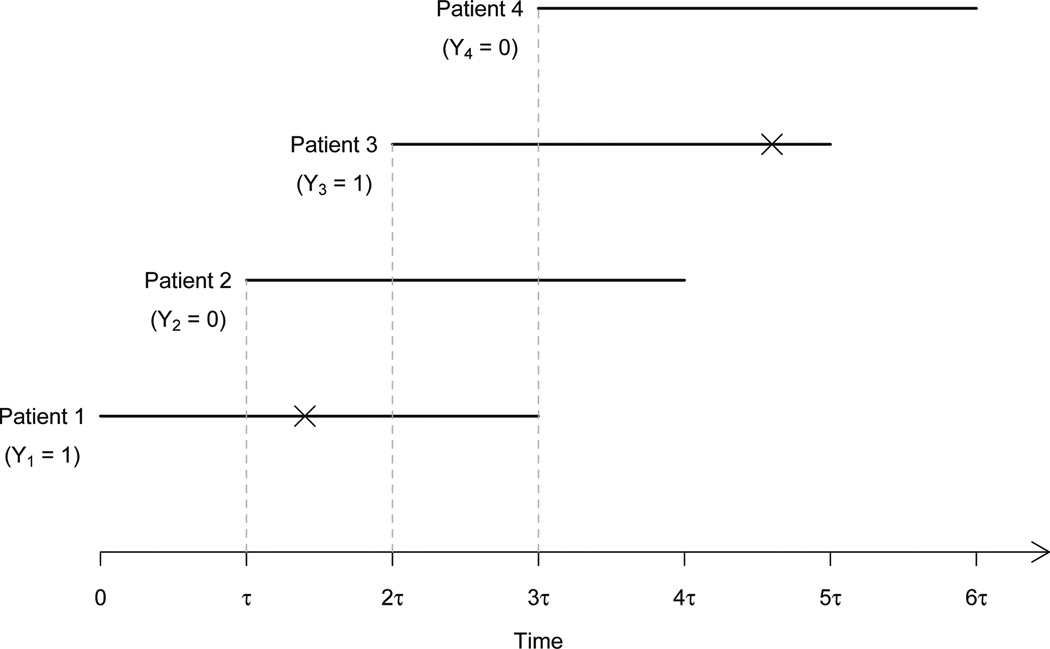
One of the practical limitations of the CRM is that the DLT needs to be ascertainable quickly after the initiation of the treatment. Figure 1 illustrates the situation where the patient inter-arrival time τ is shorter than the assessment period T. By the time a dose is to be assigned to a newly accrued patient (say patient 4 at time 3τ), some of the patients who have entered the trial (i.e., patients 2 and 3) may have been partially followed and their toxicity outcomes are still not available. More precisely, for the ith subject, let t_i denote the time to toxicity. For subjects who do not experience toxicity during the trial, we set t_i = ∞. At the moment of decision making for dose assignment, let u_i (0 ≤ u_i ≤ T) denote the actual follow-up time for subject i, and let M_i(u_i) be the missing data indicator for Y_i. Then it follows that

$$M_i(u_i)=\{\begin{array}{ccc}1\hfill & \text{if}\hfill & t_i>u_i\text{and}{u}_i<T,\hfill \\ 0\hfill & \text{if}\hfill & t_i\le u_i\text{or}{u}_i=T.\hfill \end{array}$$ (2.2)

That is, the toxicity outcome is missing with M_i(u_i) = 1 for patients who have not yet experienced toxicity (t_i > u_i) and have not been fully followed up to T (u_i < T); and the toxicity outcome is observed with M_i(u_i) = 0 when patients either have experienced toxicity (t_i ≤ u_i) or have completed the entire follow-up (u_i = T) without experiencing toxicity. For notational simplicity, we suppress u_i and take M_i ≡ M_i(u_i). Due to patients’ staggered entry, it is reasonable to assume that u_i is independent of t_i, i.e., the time of dose assignment (or the arrival of a new patient) is independent of the time to toxicity.

Fig 1.

Illustration of missing toxicity outcomes under fast accrual. For each patient, the horizontal line segment represents the follow-up, on which toxicity is indicated by cross. At time τ, the toxicity outcome of patient 1 is missing (i.e., Y₁ is missing); at time 2τ, the toxicity outcome of patient 2 is missing (i.e., Y₁ = 1, but Y₂ is missing); and at time 3τ, the toxicity outcomes of both patients 2 and 3 are missing (i.e., Y₁ = 1, but Y₂ and Y₃ are missing).

Under the missing data mechanism (2.2), the induced missing data are nonignorable or informative because the probability of missingness of Y_i depends on the underlying time to toxicity, and thus implicitly depends on the value of Y_i itself. More specifically, the data from patients who would not experience toxicity (Y_i = 0) in the assessment period are more likely to be missing than data from patients who would experience toxicity (Y_i = 1). The next theorem provides a new insight to the issue of late-onset toxicity.

Theorem 1. Under the missing data mechanism (2.2), the missing data induced by late-onset toxicity are nonignorable with Pr(M_i = 1|Y_i = 0) > Pr(M_i = 1|Y_i = 1).

The proof of the theorem is briefly sketched in the Appendix. In general, the missing data are more likely to occur for those patients who would not experience toxicity in (0, T). This phenomenon is also illustrated in Figure 1. Patient 2 who will not experience toxicity during the assessment period is more likely to have a missing toxicity outcome at the decision-making times 2τ and 3τ than patient 1 who has experienced toxicity between time τ and 2τ. Compared with other missing data mechanisms, such as missing completely at random or missing at random, nonignorable missing data are the most difficult to deal with (Little and Rubin, 2002), which bring a new challenge to clinical trial designs. Because the missing data are nonignorable, the naive approach by simply discarding the missing data and making dose-escalation decisions solely based on the observed toxicity data is problematic. The observed data represent a biased sample of the complete data and contain more toxicity observations than they should be because the responses for patients who would experience toxicity are more likely to be observed. As a result, approaches based only on the observed toxicity data typically overestimate the toxicity probabilities and thus lead to overly conservative dose escalation.

During the trial conduct, the amount of missing data depends on the ratio of the assessment period T and the interarrival time τ, denoted as the A/I ratio = T/τ. The larger the value of the A/I ratio, the greater the amount of missing data that would be produced, because there would be more patients who may not have completed the toxicity assessment when a new cohort arrives.

2.3. DA-CRM Using Bayesian Data Augmentation

An intuitive approach to dealing with the unobserved toxicity outcomes is to impute the missing data so that the standard complete-data method can be applied. One way to achieve this goal is to use data augmentation (DA) proposed by Tanner and Wong (1987). The DA iterates between two steps: the imputation (I) step, in which the missing data are imputed, and the posterior (P) step, in which the posterior samples of unknown parameters are simulated based on the imputed data. As the CRM is originally formulated in the Bayesian framework (O’Quigley et al., 1990), the DA provides a natural and coherent way to address the missing data issue due to late-onset toxicity. Note that the missing data we consider here is a special case of nonignorable missing data with a known missing data mechanism as defined by (2.2). Therefore, the nonidentification problem that often plagues the nonignorable missing data can be circumvented as follows.

In order to obtain consistent estimates, we need to model the nonignorable missing data mechanism in (2.2). Toward this goal, we specify a flexible piecewise exponential model for the time to toxicity for patients who would experience DLTs, which concerns the conditional distribution of t_i given Y_i = 1. Specifically, we consider a partition of the follow-up period [0, T] into K disjoint intervals [0, h₁), [h₁, h₂), …, [h_K−1 , h_K ≡ T], and assume a constant hazard λ_k in the kth interval. Define the observed time x_i = min(u_i, t_i) and δ_ik = 1 if the ith subject experiences toxicity in the kth interval; and δ_ik = 0 otherwise. Let λ = {λ₁, …, λ_K}; when the toxicity data y = {y₁, …, y_n} are completely observed, the likelihood function of λ based on n enrolled subjects is given by

$$L(\mathit{y}|\mathit{\lambda })=\prod _{i=1}^n\prod _{k=1}^K{\lambda }_k^{{\delta }_{ik}}\text{exp}\{-y_i{\lambda }_k{s}_{ik}\},$$

where s_ik = h_k − h_k−1 if x_i > h_k; s_ik = x_i − h_k−1 if x_i ∈ [h_k−1, h_k); and otherwise s_ik = 0. Similar to the TITE-CRM, we assume that the time-to-DLT distribution is invariant to the dose level, conditioning on that the patient will experience toxicity (Y_i = 1). This assumption is helpful to pool information across different doses and obtain more reliable estimates. The sensitivity analysis in Section 3.2 shows that our method is not sensitive to the violation of this assumption.

In the Bayesian paradigm, we assign each component of λ an independent gamma prior distribution with the shape parameter ζ_k and the rate parameter ξ_k, denoted as Ga(ζ_k, ξ_k). When there is some prior knowledge available regarding the shape of the hazard for the time to toxicity, the hyperparameters ζ_k and ξ_k can be calibrated to match the prior information. Here we focus on the common case in which the prior information is vague and we aim to develop a default and automatic prior distribution for general use. Specifically, we assume that a priori toxicity occurs uniformly throughout the assessment period (0, T), which represents a neutral prior opinion between early-onset and late-onset toxicity. Under this assumption, the hazard at the middle of the kth partition is λ̃_k = K/{T(K − k + 0.5)}. Thus, we assign λ_k a gamma prior distribution,

$$f({\lambda }_k)=Ga({\mathrm{\lambda ̃}}_k/C,1/C),$$

where C is a constant determining the size of the variance with respect to the mean, as the mean for this prior distribution is λ̃_k and the variance is Cλ̃_k. Based on our simulations, we found that C = 2 yields a reasonably vague prior and equips the design with good operating characteristics.

Based on the time-to-toxicity model as above, the DA algorithm can be implemented as follows. At the I step of the DA, we “impute” the missing data by drawing posterior samples from their full conditional distributions. Let y = (y_obs, y_mis), where y_obs and y_mis denote the observed and missing toxicity data, respectively; and let 𝒟_obs = (y_obs, M) denote the observed data with missing indicators M = {M_i, i = 1, …, n}. As the missing data are informative, the observed data used for inference not only include the observed toxicity outcomes y_obs, but also the missing data indicators M. Inference that ignores M (such as the CRM) would lead to biased estimates. It can be shown that, conditional on the observed data 𝒟_obs and model parameters (a, λ), the full conditional distribution of y_i ∈ y_mis is given by

$$y_i|({𝒟}_{\text{obs}},a,\mathit{\lambda })~\text{Bernoulli}(\frac{{\alpha }_{d_i}^{\text{exp}(a)}\text{exp}(-{\mathrm{\Sigma }}_{k=1}^K{\lambda }_k{s}_{ik})}{1-{\alpha }_{d_i}^{\text{exp}(a)}+{\alpha }_{d_i}^{\text{exp}(a)}\text{exp}(-{\mathrm{\Sigma }}_{k=1}^K{\lambda }_k{s}_{ik})}).$$

At the P step of the DA, given the imputed data y, we sequentially sample the unknown model parameters from their full conditional distributions as follows:

1. Sample a from f(a|y) given by (2.1), where y is the “complete” data after filling in the missing outcomes.

2. Sample λ_k, k = 1, …, K, from

   $${\lambda }_k|\mathit{y}~Ga({\mathrm{\lambda ̃}}_k/C+\sum _{i=1}^n{\delta }_{ik},1/C+\sum _{i=1}^n{y}_i{s}_{ik}).$$

The DA procedure iteratively draws a sequence of samples of the missing data and model parameters through the imputation (I) step and posterior (P) step until the Markov chain converges. The posterior samples of a can then be used to make inference on π_d to direct dose finding.

2.4. Dose-finding Algorithm

Let φ denote the physician-specified toxicity target, and assume that patients are treated in cohorts, for example, with a cohort size of three. For safety, we restrict dose escalation or de-escalation by one dose level of change at a time. The dose-finding algorithm for the DA-CRM is described as follows.

1. Patients in the first cohort are treated at the lowest dose level.

2. At the current dose level d^curr, based on the cumulated data, we obtain the posterior means for the toxicity probabilities, π̂_d (d = 1, …, J). We then find dose level d* that has a toxicity probability closest to φ, i.e.,

   $$d^{*}={\text{argmin}}_{d\in (1,\dots ,J)}|{\mathrm{\pi ̂}}_d-\varphi |.$$

   • If d^curr > d*, we de-escalate the dose level to d^curr − 1;
   • if d^curr < d*, we escalate the dose level to d^curr + 1;
   • otherwise, the dose stays at the same level as d^curr for the next cohort of patients.

3. Once the maximum sample size is reached, the dose that has the toxicity probability closest to φ is selected as the MTD.

In addition, we also impose an early stopping rule for safety: if Pr(π₁ > φ|𝒟_obs) > 0.96, the trial will be terminated. That is, if the lowest dose is still overly toxic, the trial should be stopped early.

3. Numerical Studies

3.1. Simulations

To examine the operating characteristics of the DA-CRM design, we conducted extensive simulation studies. We considered six dose levels and assumed that toxicity monotonically increased with respect to the dose. The target toxicity probability was 30% and a maximum number of 12 cohorts were treated sequentially in a cohort size of three. The sample size was chosen to match the maximum sample size required by the conventional “3+3” design. The toxicity assessment period was T = 3 months and the accrual rate was 6 patients per month. That is, the interarrival time between every two consecutive cohorts was τ = 0.5 month with the A/I ratio = 6.

We considered four toxicity scenarios in which the MTD was located at different dose levels. Due to the limitation of space, we show only scenarios 1 and 2 in Table 1, and the other scenarios are provided in Table S1 of the Supplementary Materials. Under each scenario, we simulated times to toxicity based on Weibull, log-logistic, and uniform distributions, respectively. For Weibull and log-logistic distributions, we controlled that 70% toxicity events would occur in the latter half of the assessment period (T/2, T). Specifically, at each dose level, the scale and shape parameters of the Weibull distribution were chosen such that

1. the cumulative distribution function at the end of the follow-up time T would be the toxicity probability of that dose; and

2. among all the toxicities that occurred in (0, T), 70% of them would occur in (T/2, T), the latter half of the assessment period.

Because the toxicity probability varies across different dose levels, the scale and shape parameters of the Weibull distribution need to be carefully chosen for different dose levels, and similarly for the scale and location parameters of the log-logistic distribution. For the uniform distribution, we simulated the time to toxicity independently for each dose level and controlled the cumulative distribution function at the end of the follow-up time T matching the toxicity probability of each dose. In the proposed DA-CRM, we used K = 9 partitions to construct the piecewise exponential time-to-toxicity model. We compared the DA-CRM with the CRM_obs, which determined the dose assignment based on only the observed toxicity data as suggested by O’Quigley et al. (1990), and the TITE-CRM with the adaptive weighting scheme proposed by Cheung and Chappell (2000). As a benchmark for comparison, we also implemented the complete-data version of the CRM (denoted by CRM_comp), assuming that all of the toxicity outcomes in the trial were completely observed prior to each dose assignment. The CRM_comp required repeatedly suspending the accrual prior to each dose assignment to wait that all of the toxicity outcomes in the trial were completely observed. Although the CRM_comp is not feasible in practice when toxicities are late-onset, it provides an optimal upper bound to evaluate the performances of other designs. Actually, when all toxicity outcomes are observable (i.e., no missing data), the DA-CRM and TITE-CRM are equivalent to the complete-data CRM_comp. For all methods, we set the probability constants in the CRM (α₁, …, α₆) = (0.08, 0.12, 0.20, 0.30, 0.40, 0.50), and used a normal prior distribution N(0, 2) for parameter a. Under each scenario, we simulated 5,000 trials.

Table 1.

Simulation study comparing the complete-data CRM (CRM_comp), the CRM based on the observed toxicity data only (CRM_obs), time-to-event CRM (TITE-CRM) and the proposed data augmentation CRM (DA-CRM) with the sample size 36, the cohort size 3, and the A/I ratio = 6.

Time to toxicity	Design	Recommendation percentage at dose level							NMTD+	Duration (months)
		1	2	3	4	5	6	None
Scenario 1	Pr(toxicity)	0.1	0.15	0.3	0.45	0.6	0.7
	CRMcomp	0.6	13.8	61.9	22.9	0.6	0.0	0.2	9.0	36.4
	# patients	4.8	7.2	14.9	7.6	1.3	0.1
Weibull	CRMobs	0.4	7.5	48.4	27.4	2.4	0.1	13.7	4.0	8.2
	# patients	7.5	8.3	13.2	3.0	0.9	0.1
	TITE-CRM	3.4	23.1	55.9	16.5	0.6	0.0	0.5	15.5	9.0
	# patients	5.1	6.3	9.0	8.1	4.9	2.5
	DA-CRM	0.9	14.7	56.4	25.1	1.5	0.0	1.2	10.4	8.9
	# patients	9.4	7.6	8.3	6.0	3.0	1.3
Log-logistic	CRMobs	0.3	7.8	48.2	27.4	2.7	0.1	13.6	4.0	8.2
	# patients	7.4	8.4	13.2	3.0	0.9	0.1
	TITE-CRM	3.6	22.6	56.3	16.5	0.6	0.0	0.4	15.4	9.0
	# patients	5.1	6.4	9.1	8.2	4.8	2.4
	DA-CRM	0.9	13.9	58.1	23.8	1.9	0.0	1.3	10.3	8.9
	# patients	9.5	7.6	8.2	6.0	3.0	1.3
Uniform	CRMobs	0.1	4.7	38.0	30.5	2.9	0.1	23.6	2.8	7.5
	# patients	8.6	8.2	10.9	2.3	0.5	0.0
	TITE-CRM	2.1	20.4	56.6	19.1	1.4	0.0	0.4	13.0	9.0
	# patients	6.3	7.0	9.7	8.0	3.7	1.3
	DA-CRM	0.6	11.2	56.9	27.6	1.7	0.0	1.9	8.7	8.9
	# patients	10.8	7.6	8.5	5.7	2.2	0.7
Scenario 2	Pr(toxicity)	0.08	0.1	0.2	0.3	0.45	0.6
	CRMcomp	0.0	1.4	23	55.9	18.8	0.8	0.1	6.6	36.4
	# patients	4.1	4.1	9.0	12.2	5.5	1.0
Weibull	CRMobs	0.0	1.0	18.9	48.5	22.2	1.8	7.6	2.9	8.5
	# patients	5.7	6.7	13.8	5.2	2.3	0.7
	TITE-CRM	0.1	2.6	29.2	52.4	14.9	0.8	0.1	11.2	9.0
	# patients	4.2	4.7	7.1	8.8	6.8	4.4
	DA-CRM	0.0	1.5	24.4	54.0	17.7	1.4	1.1	7.3	8.9
	# patients	8.4	6.3	7.0	6.7	4.5	2.8
Log-logistic	CRMobs	0.0	0.9	19.0	48.5	22.0	1.9	7.7	2.9	8.5
	# patients	5.7	6.7	13.8	5.1	2.3	0.7
	TITE-CRM	0.1	2.6	29.0	52.3	15.1	0.8	0.1	11.1	9.0
	# patients	4.1	4.7	7.2	8.8	6.8	4.3
	DA-CRM	0.0	1.4	23.3	54.0	18.7	1.6	1.0	7.5	8.9
	# patients	8.3	6.2	6.9	6.8	4.6	2.9
Uniform	CRMobs	0.0	0.7	14.9	45.3	23.3	2.3	13.5	2.0	8.1
	# patients	6.9	7.1	12.3	4.5	1.7	0.4
	TITE-CRM	0.1	2.2	26.9	54.4	15.4	0.9	0.1	9.6	9.0
	# patients	4.9	5.0	7.6	8.8	6.2	3.3
	DA-CRM	0.0	1.3	23.7	54.0	18.8	1.1	1.2	6.2	8.9
	# patients	9.3	6.3	7.1	6.8	4.2	2.0

Following each scenario in Tables 1 and S1, the first row is the true toxicity probabilities; rows 2 and 3 show the dose selection probability (with the percentage of inconclusive trials denoted by “None”) and the average number of patients treated at each dose based on the complete-data design CRM_comp, respectively; the remaining rows provide the corresponding summary statistics for the CRM_obs, TITE-CRM and DA-CRM under various settings of late-onset toxicity and time-to-toxicity distributions. The CRM_comp does not depend on the distributions of the times to toxicity because the design assumes that all toxicity outcomes are completely observed before each dose assignment.

When evaluating the trial designs with late-onset toxicities, one of the most important measures of the design performance is patient safety because the main issue of the late-onset toxicities is that ignoring them will lead to overly aggressive dose escalation and thus treating too many patients at excessively toxic doses, i.e., the doses higher than the MTD. As a measure of safety, in Tables 1 and S1, we also report the number of patients treated at doses above the MTD (denoted as N_MTD+) averaged across 5,000 simulated trials.

In scenario 1, the MTD (shown in boldface) is at dose level 3, and the complete-data design CRM_comp yielded an optimal selection probability of 61.9%. The selection probability of the MTD using the DA-CRM was slightly lower than this optimal value, but higher than that of using the CRM_obs. For instance, when the time to toxicity followed the log-logistic distribution, the selection probability using the DA-CRM was 58.1%, whereas that of the CRM_obs was 48.2%. The CRM_obs appeared to be overly conservative and led to a high percentage (about 13.6%) of inconclusive trials. This was because the CRM_obs estimated the toxicity probabilities based solely on the observed toxicity data, which is a biased sample of the complete data with an excessively number of toxicities. Therefore, the CRM_obs tended to overestimate the toxicity probabilities, resulting in conservative dose escalations and high percentages of early termination of the trial. The TITE-CRM yielded similar selection percentages as the DA-CRM, but the DA-CRM was much safer: the number of patients treated above the MTD (i.e., N_MTD+) using the DA-CRM was notably smaller than that of the TITE-CRM and close to that of the complete-data design. For example, when the time to toxicity followed the Weibull distribution, N_MTD+ was 9.0 and 10.4 using the complete-data design and the DA-CRM, respectively, while that based on the TITE-CRM was 15.5. As the CRM_obs is overly conservative, N_MTD+ = 4.0 is the smallest under the CRM_obs.

In scenario 2, the MTD is the fourth dose, and in scenario 3 (see Table S1), the MTD is the second. Compared to the TITE-CRM, the DA-CRM yielded comparable MTD-selection probabilities but appeared to be safer, which reduced N_MTD+ by more than 30% in both scenarios. For example, in scenario 2, when the time to toxicity followed the Weibull distribution, N_MTD+ using the DA-CRM was 7.3, approximately 35% less than that using the TITE-CRM (N_MTD+ = 11.2). A similar extent of decreasing in N_MTD+ was observed in scenario 3 when using the DA-CRM. The CRM_obs again led to a high percentage of inconclusive trials (particularly under the uniform distribution), and a relatively low selection percentage of the MTD due to the overestimation of the toxicity probabilities. For Scenario 4 in Table S1, in which the fifth dose is the MTD, the CRM_obs yielded a similar selection percentage as the TITE-CRM and DA-CRM.

We further investigated the performance of the designs under a smaller sample size of 27 patients treated in a cohort size of 3, and 21 patients treated in a cohort size of 1. The pattern of the results is generally similar to those described above (see Tables S2 and S3 in the Supplementary Materials). We also examined the operating characteristics of the DA-CRM under a lower A/I ratio of 3 with the cohort interarrival time τ = 1 month (see Table S4 in the Supplementary Materials). In this case, the accrual rate was relatively slower and thus late-onset toxicities became of less concern since the majority of toxicity outcomes would be observed at the moment of dose assignment. As expected, the performances of the CRM_obs, TITE-CRM, and DA-CRM were rather comparable across different scenarios and time-toxicity distributions. Actually, when the A/I ratio is less than or equal to 1 (i.e., no late-onset toxicities and no missing data), the CRM_obs, TITE-CRM, and DA-CRM are exactly the same.

These results suggest that, when the A/I ratio is low (e.g., when the disease under study is rare and thus the accrual rate is slow), the CRM_obs has little bias and is still a good design option for phase I clinical trials. However, when the accrual is fast, for example, in multi-center clinical trials for some common type of cancer (e.g., breast or lung cancer), the A/I ratio can be high (particularly when radiotherapies or some targeted agents are used), and using the proposed DA-CRM can lead to better operating characteristics.

3.2. Sensitivity Analysis

We investigated the robustness of the proposed DA-CRM design when (1) the underlying times to toxicity were heterogeneous across the doses, by simulating the times to toxicity from a Weibull distribution at dose levels of 1, 3 and 5, and from a log-logistic distribution at dose levels of 2, 4 and 6; (2) the number of partitions used in the piecewise exponential model for the times to toxicity was K = 5 and 12; and (3) the prior distribution for a was N(0, 0.57), the “least-informative” prior proposed by Lee and Cheung (2011). The results show that the performance of the DA-CRM (e.g., the selection percentages and N_MTD+) was very similar across different conditions (see Table S5 in the Supplementary Materials), which suggests the robustness of the proposed design.

4. Applications

4.1. Pancreatic cancer trial

Muler et al. (2004) described a phase I trial to determine the MTD of cisplatin that could be added to the full-dose gemcitabine and radiation therapy in patients with pancreatic cancer. The protocol treatment was consisted of two 28-day cycles of chemotherapy, with radiation given during the first cycle of chemotherapy. Radiation and gemcitabine doses were held constant, while four dose levels of cisplatin (20, 30, 40 and 50 mg/m²) were investigated in the trial. The DLTs were defined as CTCAE 2.0 grade 4 thrombocytopenia, grade 4 neutropenia lasting more than 7 days, or grade 3 toxicity in other organ systems. Patients were required to be followed for nine weeks in order to fully assess their toxicity outcomes. The goal of the trial was to determine the dose of cisplatin associated with a target DLT rate of 20%.

As shown in Table 2, one challenge of designing this trial is that the accrual was fast, compared to the 9-week assessment period for DLTs (i.e., the toxicity was late-onset). In the DA-CRM design, we took α =(0.1, 0.15, 0.2, 0.25) as the prior estimates of the toxicity probabilities for the four dose levels of cisplatin, and used 30 mg/m² as the starting dose of the trial. For patient safety, we required that at least two patients must have fully completed their toxicity assessment at the lower dose before the dose can be escalated to the next higher level.

Table 2.

Dates, doses and DLTs for eighteen evaluable patients enrolled in the pancreatic cancer trial.

Patient No.	Day on study*	Day off study*	Dose (mg/m2)	DLT	Patient No.	Day on study*	Day off study*	Dose (mg/m2)	DLT
1	0	67	30	No	10	224	291	50	No
2	43	98	30	No	11	280	303	50	Yes
3	50	116	30	No	12	301	347	50	Yes
4	56	108	30	No	13	322	382	50	No
5	70	133	40	No	14	329	389	50	No
6	147	217	40	No	15	343	372	50	Yes
7	161	224	40	No	16	364	423	40	No
8	182	238	40	No	17	371	408	50	Yes
9	224	284	50	No	18	455	528	30	No

^*days since the initiation of the study.

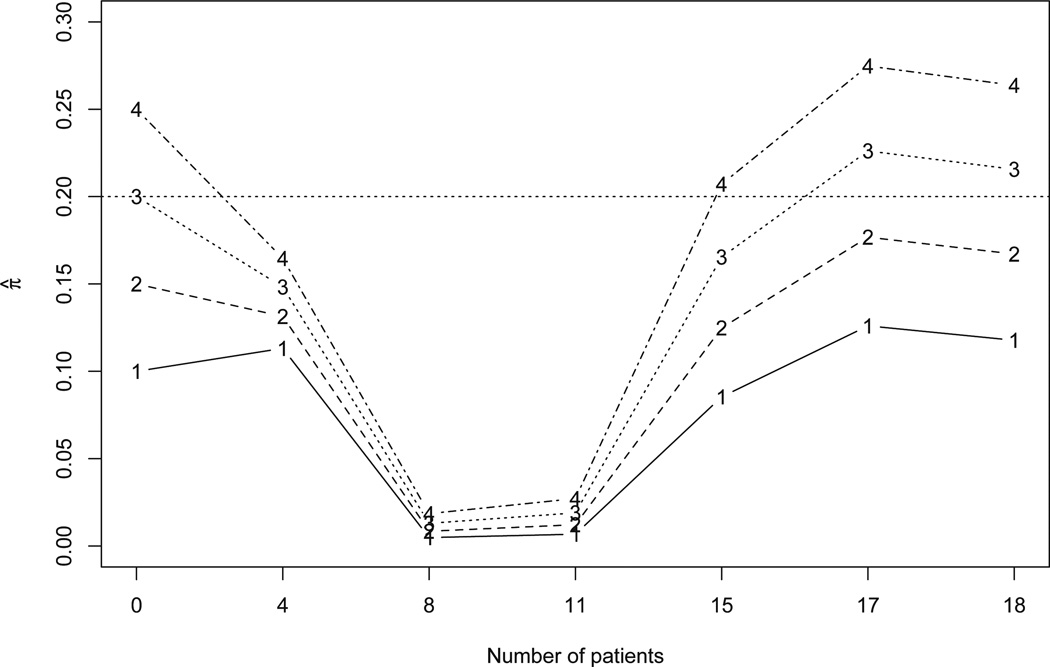
Figure 2 summarizes how the posterior estimates of the toxicity probabilities of four doses were updated as more patients were enrolled during the trial conduct. The first four patients were assigned to the dose of 30 mg/m². Based on the days from the initiation of the trial, when patient 5 arrived on day 70, patient 1 had completed the follow-up, while patients 2, 3 and 4 had finished only 43%, 32% and 22% of their follow-ups, without experiencing any DLTs. The estimates of toxicity probabilities of four doses were π̂ =(0.113, 0.131, 0.148, 0.165). We escalated the dose and subsequently treated patients 5 to 8 at the dose of 40 mg/m². Patient 2 died after 63 days on therapy, but was judged to be secondary to the hypercoaguable state associated with pancreatic cancer. Therefore, that death was classified as unrelated to therapy (i.e., not a DLT).

Fig 2.

Estimates of the toxicity probabilities of four doses with the cumulative number of patients in the pancreatic cancer trial. Numbers 1–4 in the figure indicate the four dose levels.

Upon the arrival of patient 9 on day 224, patients 1 to 7 had completed their toxicity assessment and none of them had experienced DLT. These data yielded the updated toxicity estimates π̂ =(0.005, 0.008, 0.013, 0.019), suggesting that the doses of 30 mg/m² and 40 mg/m² were safe. As a result, we further escalated the dose and assigned patients 9 to 11 to 50 mg/m². On day 301 when patient 12 was accrued, patients 1 to 10 had completed their toxicity assessment without experiencing DLT, yielding the updated estimates of the toxicity probabilities π̂ =(0.007, 0.012, 0.019, 0.027). Consequently, patients 12 to 15 were also treated at 50 mg/m².

After patient 12 experienced a DLT (i.e., duodenal ulcer) on day 347, the estimates of the toxicity probabilities began to increase, i.e., π̂=(0.085, 0.125, 0.165, 0.207), but not sufficiently to trigger dose de-escalation. According to the dose-finding algorithm, the incoming patients 16 and 17 should be treated at 50 mg/m². However, because the investigators were concerned about a potential DLT in patient 15, only patient 17 was treated at 50 mg/m², while patient 16 was treated at a lower dose 40 mg/m².

By the time that patient 18, the last enrolled patient, arrived on day 455, 4 out of 8 patients previously treated at 50 mg/m² had experienced DLTs (i.e., one duodenal ulcer, one diarrhea resulting in dehydration, and two grade 3 anorexia and nausea leading to a two-level decline in performance status). This significantly increased π̂ to (0.126, 0.177, 0.228, 0.275). Therefore, patient 18 was assigned to a lower dose 30 mg/m². At the end of the trial, the estimates of the toxicity probabilities were π̂ =(0.118, 0.167, 0.215, 0.264) and thus the dose 40 mg/m² was selected as the MTD because its estimated toxicity probability was closest to the target of 0.2.

4.2. Esophageal cancer trial

In the esophageal cancer clinical trial described in Section 1, the target toxicity probability was 30% and a total of 30 patients were treated sequentially in cohorts of size 3. Six doses were investigated and the trial started by treating the first cohort at dose level 1. Under the DA-CRM design, the posterior estimates of the dose toxicity probabilities were updated only when the first patient of each new cohort (i.e., patient 4, 7, 10, 13, 16 …) was enrolled.

The three patients in cohort 1 were enrolled at days 3, 6 and 18, respectively (see Table S6 in the Supplementary Materials). On day 28 when patient 4 (i.e., the first patient of cohort 2) was enrolled, the three patients in cohort 1 had finished only 28%, 24% and 11% of their 3-month follow-ups without experiencing toxicity (i.e., DLT). The estimates of the toxicity probabilities of six dose levels were π̂ =(0.172, 0.185, 0.209, 0.236, 0.264, 0.294). We escalated the dose and treated patient 4, and subsequently patients 5 and 6, at dose level 2.

When patient 7 (the first patient of cohort 3) arrived on day 57, we again updated the estimates of the toxicity probabilities and obtained π̂ =(0.315, 0.336, 0.369, 0.407, 0.445, 0.486). Although at that moment, we still had not observed any DLTs yet, the values of π̂ increased compared with the previous estimates of π. This is because on day 57, more patients (i.e., patients 1 to 6) were under treatment and none of them had finished their 3-month follow-ups yet. There was greater uncertainty regarding the toxicity probabilities of the doses and it was preferable to be conservative. Our algorithm automatically took into account such uncertainty and de-escalated the dose back to the first level for treating cohort 3.

One day 91 when the first patient of cohort 4 (i.e., patient 10) was accrued, patients 1, 2 and 3 were very close to completing their 3-month follow-ups without experiencing toxicity, indicating that the first dose level was safe and dose escalation was needed. The proposed algorithm timely reflected this data information and escalated the dose to level 2. The dose was further escalated to levels 3 and 4 for treating cohorts 5 and 6, respectively, as no DLT was observed. By the time when patient 19 arrived, the toxicity outcomes of all patients treated in the trial had been observed. In particular, all three patients (i.e., patients 16–18) treated at dose level 4 had experienced DLTs. Our algorithm de-escalated the dose to level 3 to treat cohort 7. Thereafter, there were always at least 18 toxicity outcomes (from patients 1–18) fully observed, thus π̂ became rather stable and consistently indicated that dose 3 was the MTD. The last 3 cohorts were all treated at dose level 3 and, at the end of the trial, dose 3 was selected as the MTD with the estimated toxicity probability of 0.259.

Figure 3 displays the estimate of the unknown parameter α during the trial conduct. At the beginning of the trial, there was quite variability for the estimate of α due to sparse data, while the estimate became stabilized after six cohorts of patients were enrolled. Correspondingly, Table 3 summarizes the estimates of the toxicity probabilities π for the six doses at each decision-making time.

Fig 3.

Estimate of the unknown parameter α with cumulative cohorts in the esophageal cancer trial.

Table 3.

Estimates of the toxicity probabilities of six doses with the cumulative number of cohorts in the esophageal cancer trial.

Dose level	Cumulative number of cohorts
	1	2	3	4	5	6	7	8	9	10
1	0.172	0.315	0.028	0.021	0.080	0.175	0.186	0.171	0.189	0.125
2	0.185	0.336	0.035	0.026	0.114	0.228	0.240	0.223	0.243	0.172
3	0.209	0.369	0.050	0.037	0.181	0.320	0.333	0.314	0.337	0.259
4	0.236	0.407	0.071	0.053	0.268	0.422	0.435	0.415	0.440	0.361
5	0.264	0.445	0.096	0.071	0.359	0.515	0.528	0.509	0.532	0.458
6	0.294	0.486	0.128	0.093	0.454	0.603	0.615	0.598	0.619	0.553

5. Conclusions

We have proposed the DA-CRM design to address the issues associated with late-onset toxicities in phase I dose-finding trials. In the new design, unobserved toxicity outcomes are naturally treated as missing data. We established that such missing data are nonignorable and linked the missing data mechanism with the time to toxicity based on a flexible piecewise exponential model. Simulation studies showed that the DA-CRM outperforms other available methods, particularly when toxicities need a long follow-up time to be assessed. The selection percentage of the DA-CRM is often close to the optimal value, and much fewer patients would be treated at overly toxic doses.

This paper has focused on the single-agent dose finding using the CRM, but the proposed methodology provides a general and systematic approach to transforming the late-onset toxicity problem into a standard complete-data problem by imputing the missing toxicity outcomes. The proposed method can serve as a universal adaptor to extend existing trial designs to accommodate more complicated dose-finding problems with late-onset toxicity. For example, by incorporating the data augmentation procedure into the partial-order CRM (Wages, Conaway and O’Quigley, 2011), we can address the late-onset toxicity for drug-combination trials or dose finding with group heterogeneity. It is also worth emphasizing that although we have focused on the late-onset toxicity, the proposed method can also be used to handle other kinds of late-onset outcomes, such as delayed efficacy responses in phase I/II or phase II trials, as well as response-adaptive randomization designs.

APPENDIX A: PROOF OF THEOREM 1

Considering that each subject is fully followed up to T, if t_i > T, then Y_i = 0; and if t_i ≤ T, then Y_i = 1. We demonstrate the nonignorable missingness for the missing data caused by late-onset toxicity as follows. For a subject who will not experience toxicity, the probability that his/her toxicity outcome will be missing is given by

$$\mathrm{P}\mathrm{r}(M_i=1|Y_i=0)=\mathrm{P}\mathrm{r}(t_i>u_i,u_i<T|Y_i=0)=\mathrm{P}\mathrm{r}(u_i<T|Y_i=0)\mathrm{P}\mathrm{r}(t_i>u_i|u_i<T,Y_i=0)=\mathrm{P}\mathrm{r}(u_i<T|t_i>T)\mathrm{P}\mathrm{r}(t_i>u_i|u_i<T,t_i>T)=\mathrm{P}\mathrm{r}(u_i<T),$$

where the last equality follows because t_i and u_i are independent, and Pr(t_i > u_i|u_i < T, t_i > T) = 1. Similarly, for a subject who will experience toxicity, the probability that his/her toxicity outcome will be missing is given by

$$\mathrm{P}\mathrm{r}(M_i=1|Y_i=1)=\mathrm{P}\mathrm{r}(t_i>u_i,u_i<T|Y_i=1)=\mathrm{P}\mathrm{r}(u_i<T|Y_i=1)\mathrm{P}\mathrm{r}(t_i>u_i|u_i<T,Y_i=1)=\mathrm{P}\mathrm{r}(u_i<T|t_i\le T)\mathrm{P}\mathrm{r}(t_i>u_i|u_i<T,t_i\le T)=\mathrm{P}\mathrm{r}(u_i<T)\mathrm{P}\mathrm{r}(t_i>u_i|u_i<T,t_i\le T).$$

Because of Pr(t_i > u_i|u_i < T, t_i T) < 1, it follows that

$$\mathrm{P}\mathrm{r}(M_i=1|Y_i=0)>\mathrm{P}\mathrm{r}(M_i=1|Y_i=1).$$

Therefore, the missing data are more likely to occur for those patients who will not experience toxicity in (0, T).