Mathematical and computational models of drug transport in tumours

Abstract

The ability to predict how far a drug will penetrate into the tumour microenvironment within its pharmacokinetic (PK) lifespan would provide valuable information about therapeutic response. As the PK profile is directly related to the route and schedule of drug administration, an in silico tool that can predict the drug administration schedule that results in optimal drug delivery to tumours would streamline clinical trial design. This paper investigates the application of mathematical and computational modelling techniques to help improve our understanding of the fundamental mechanisms underlying drug delivery, and compares the performance of a simple model with more complex approaches. Three models of drug transport are developed, all based on the same drug binding model and parametrized by bespoke in vitro experiments. Their predictions, compared for a ‘tumour cord’ geometry, are qualitatively and quantitatively similar. We assess the effect of varying the PK profile of the supplied drug, and the binding affinity of the drug to tumour cells, on the concentration of drug reaching cells and the accumulated exposure of cells to drug at arbitrary distances from a supplying blood vessel. This is a contribution towards developing a useful drug transport modelling tool for informing strategies for the treatment of tumour cells which are ‘pharmacokinetically resistant’ to chemotherapeutic strategies.

1. Introduction

A characteristic feature of solid tumours is the presence of a poorly organized and dysfunctional vasculature. The blood vessels that develop in response to angiogenic stimuli are structurally and functionally different from those of normal tissues, leading to poorly perfused areas of the tumour [1]. This results in the establishment of a microenvironment that can have profound effects on tumour biology and response to chemotherapy. The tumour microenvironment is characterized by gradients of oxygen tension, nutrient status, catabolite concentrations, extracellular pH, cell proliferation rates and a multitude of biochemical changes that enable cells to adapt to these hostile conditions [2], unless conditions become so extreme that tumour cells cannot survive and regions of necrosis occur. Where delivery of cancer drugs to cells within the tumour microenvironment is impaired, these cells are ‘pharmacokinetically resistant’; this form of resistance, distinct from cellular resistance, is increasingly recognized as a barrier to effective treatment [3]. In this paper, we use the generic term ‘chemotherapy’ to cover both conventional cytotoxic drugs and novel ‘targeted’ therapies, because the challenges of drug delivery apply to both.

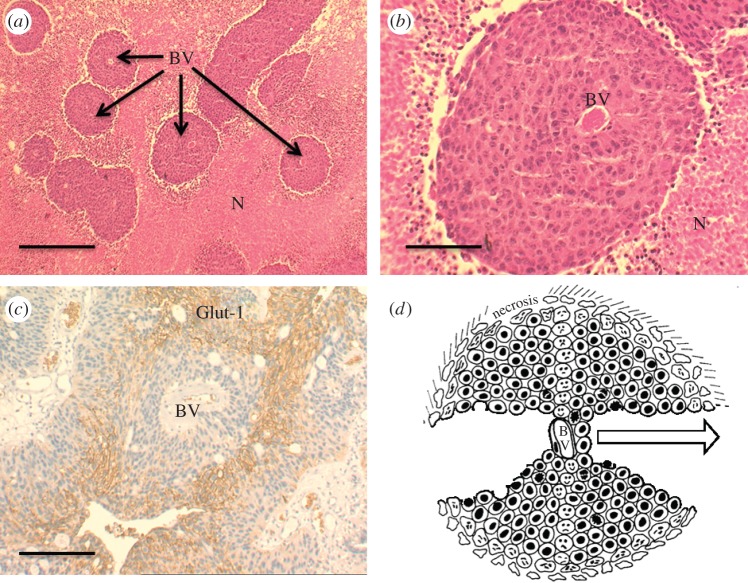
The variations in microenvironment in vivo are extremely complex, and depend on distance from a supporting blood vessel. Important insights can, however, be gained from a much simpler representation, that of a ‘tumour cord’, where a ‘collar’ of cells surrounds a supporting blood vessel, with cells at a distance from the vessel comprising regions of necrosis (figure 1). This model forms the biological platform for the studies described within this paper, which focuses on predicting the ability of drugs to penetrate through several layers of cells from a central blood vessel, and reach more distant cells. This ability of drug to reach cells some distance from the vessel is key to the effectiveness of chemotherapy, for both cytotoxics and targeted drugs, because these cells are typically resistant to current cytotoxic treatment, mainly owing to inadequate drug penetration.

Figure 1.

HCT116 human colorectal tumour xenografts. (a) Histological sections at low magnification showing blood vessels (BV) surrounded by cords of viable cells and necrotic areas (N) further distanced from the vessels. (b) Higher magnification of a blood vessel and surrounding viable area. (c) Section through a clinical sample of a transitional cell carcinoma of the bladder immunostained for Glut-1, a glucose transporter which is upregulated under hypoxic conditions. Glut-1-positive staining, visible as darker, denser regions (brown membrane staining), can be seen distal from the supporting blood vessel (BV). (d) Schematic of the tumour cord where the central blood vessel (BV) is surrounded by viable cells, but as distance from the BV increases (as indicated by the arrow) the microenvironment becomes more extreme, leading to regions of necrosis. Cells that reside some distance away from the BV are ‘pharmacokinetically resistant’ to chemotherapy as drugs cannot effectively penetrate through multi-cellular layers. The solid scale bars represent 500 μm (a,c) and 100 μm (b). (Online version in colour.)

The interplay between cellular factors and drug transport is complex, but drug delivery can be broken down into three stages: drug delivery to a tumour is determined by the supply of drug via the blood vessels in tumours; the flux or movement of drug through the tumour mass; and sequestration, which includes binding to cellular or extracellular components and metabolism of the drug [3]. The impact of each stage on drug delivery will vary depending upon the pharmacology of individual drugs and the biological properties of individual cancers (e.g. differential expression of targets or drug-metabolizing enzymes).

It is recognized from the outset that the models describing these processes represent considerable simplifications of complex biology and geometry [4], which may be better described by a more sophisticated computational framework [5]. However, we believe simpler mathematical models play an important role in developing more complex schemes by providing what might be described as ‘semi-quantitative’ understanding of the biological transport mechanisms, and offering a simple approach to assessing the relative merits of different protocols. Changing drug administration protocols varies the concentration and exposure time of drugs within the central blood vessel (both in practice and in our tumour cord models), and these models allow us to investigate how these factors influence drug delivery. To test a range of scheduling options in purely experimental animal tumour models is expensive and conflicts with the aim of reducing, refining and replacing (the 3Rs) animal experiments that is currently promoted by institutions such as the Medical Research Council. In silico modelling offers the promise of being able to test multiple experimental scenarios and streamline the search for drug treatment regimens that optimize drug delivery to tumour cells throughout the tumour microenvironment.

There exists a plethora of models describing the transport of drugs in tissue, ranging from compartmental models that account for exchange of drug within spatially distinct intracellular compartments [6–9] to continuum models describing the transport over macroscopic tissue scales [10–14]. If modelling is to have greater predictive impact on the development of new therapeutic agents, then it is important that the relative merits and limitations of these different descriptions are clearly understood.

The key questions this paper seeks to address are ‘Does each of these models give similar results for the variation in drug concentration in the tumour cord?’ and ‘How do the administration schedule and cell response affect drug delivery?’ Where differences do appear, we will seek to explain the reasons for them and the consequences for the choice of modelling approach. Three approaches to modelling the spatio-temporal evolution of drug concentrations in a tumour cord are compared, each of which is representative of a class of models: (i) a multi-dimensional cell-centre model that defines a network of nodes (each node corresponding to a computational cell which is identifiable with a biological cell), in which drug transport is defined locally between nodes and their nearest neighbours; (ii) a compartmental model, which makes use of the concentric-layer structure of tumour cords; and (iii) a continuum model that assumes Fickian diffusion in the cylindrical geometry of the cord. The first of these approaches is amenable to multi-scale modelling [5,15], because each node may be characterized by a bespoke microenvironment consisting of, for example, a cell cycle and molecular pathways. The remaining models are tailored to the tumour cord geometry, so are less flexible but much simpler (and faster) computationally.

In §2, after outlining the underlying binding model, which is parametrized by experimental data for the cytotoxic drug doxorubicin, a description of each spatio-temporal model is given, emphasizing the relationship between the three discrete transport models. In §3, the model predictions are compared for two scenarios: in the first, each model is tested using a single set of model parameters (and hence a single homogeneous biological environment) estimated from bespoke in vitro experimental data, allowing us to investigate the influence that the choice of mathematical approach to drug transport has on the predictions (with the same binding model). The second scenario explores the effect on the model predictions of varying the pharmacokinetic (PK) profile and model parameters representing the drug's binding affinity, a biological characteristic which can, to some degree, be controlled by the administration of other drugs. The results are then discussed in §4 in relation to the choice of modelling approach.

2. Models

Three distinct modelling approaches are considered, each of which represents drug delivery from a central blood vessel to a surrounding tumour cord. Each model assumes axial uniformity—the dependence of the drug concentration on the distance from the central vessel does not vary along the vessel, to reduce the complexity (as in reference [16]). A genuinely multi-dimensional model is developed in §2.2, followed by two simplified, one-dimensional models (§§2.3 and 2.4) in which radial symmetry is assumed.

The interaction of the chemotherapeutic agent with the microenvironment is restricted to drug binding only. This binding model, which is common to all three approaches, is discussed in §1. The in vitro experiments used to parametrize the model were conducted over relatively short time-scales and contained no elimination mechanism for the drug: explicit modelling of decay or elimination (other than clearance via the supplying vessel) is left to future work.

2.1. Binding model

The interaction of the chemotherapeutic agent with the microenvironment of cells is described by a three-compartment model, composed of extracellular space (volume V₁) with a concentration C₁ of free drug and intracellular space (volume V₂) with concentrations C₂ and C₃ corresponding to free and bound drug, respectively (where, in this model, the term bound includes both DNA-intercalated drug and drug bound to the cell in other ways). The binding is described by a simple kinetic model: drug binds reversibly to sites within the cell.

Applying the principle of mass action leads to three coupled ordinary differential equations which describe the system,

2.1

2.2

2.3

in which k₁ is the rate constant for the transmembrane transport of drug, a is the area of the interface between the extracellular and intracellular spaces (the surface area of the cell), k₂ and k₋₂ are the drug association and dissociation rates, respectively, and C₀ is the concentration of binding sites within the cell. It is assumed that mixing in each compartment is instantaneous—that is, intracellular and extracellular diffusion are assumed to be fast on the scale of an individual cell. This model is illustrated by the two-dimensional schematic in figure 2. Note that the model presented in (2.1)–(2.3) is an extension of those in [12] and [17], in which drug binding is non-saturable and non-reversible. It would be straightforward to modify the binding model in this way, or to account for Michaelis–Menten-type transport should this be required, as in [8,18,19], for example.

Figure 2.

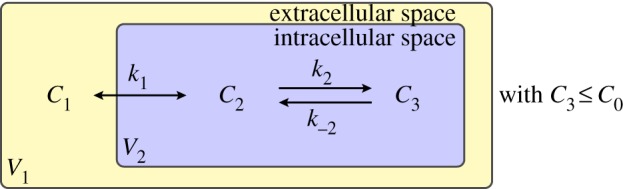
A three-compartment model of drug distribution in tissue. C₁ represents the extracellular drug concentration, C₂ the free intracellular drug concentration and C₃ the bound intracellular drug concentration. (Online version in colour.)

Values for the kinetic rate constants for the binding process are derived from a bespoke experimental binding assay. Doxorubicin binding to DLD-1, a colorectal adenocarcinoma cell line, was studied by incubating 10⁶ tumour cells suspended in tissue culture medium (37°C) with a range of doxorubicin concentrations (0–100 μM). At evenly distributed times between 0 and 2 h, a fixed volume of the culture was removed, and cells pelleted by centrifugation. Free doxorubicin in the supernatant was extracted and measured by a sensitive and specific high-performance liquid chromatography technique [20]. Binding was calculated by comparison with cell-free doxorubicin solutions incubated in parallel. The data from these experiments are included in the electronic supplementary material. DLD-1 was also the cell line used to estimate the transport rate, k₀, taken from [6].

Two sets of experiments were performed, providing both steady-state and time-dependent data. A chi-squared minimization, described in the electronic supplementary material, was then performed to provide estimates for the parameters k₁, k₂, k₋₂ and C₀, given in table 1.

Table 1.

Summary of model parameter values for baseline studies. In the final column, ‘experiment’ refers to the fitting to experimental data described in §2.1 and the electronic supplementary material, and ‘histology’ indicates estimation from histological tissue images, such as those illustrated in figure 1 or at www.virtualpathology.leeds.ac.uk, or from the cited references. The parameter k₀ has been estimated based on the value of r₁ (transport rate between cell layers) in the multi-layer model of [6]. The parameter k_v has been chosen to give slower transport across the vessel wall than across the cell membrane, though in the disordered, leaky tumour vasculature this is likely to be highly variable. Note that the volume fractions used in §2 are defined by 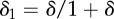and 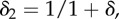where they are combined with the relevant compartmental volumes, V_i. We chose these to match the volumes of biological cells, though this is not necessary.

variable	value	description	source of estimate
l	1.6 × 10−5 m	vessel radius	histology [21]
L	2.0 × 10−4 m	cord radius (vessel + approx. nine cells)	histology [22,23]
r	∼1.0 × 10−5 m	cell radius	histology [24]
δ	0.0625	extracellular–intracellular volume ratio parameter	histology [6,25]
α	∼1.94028 × 105 m−1	membrane surface–tissue volume ratio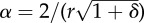
k0	2.5 × 10−6 m s−1	permeability between cells	[6]
k1	1.0 × 10−6 m s−1	permeability across cell membrane	experiment
k2	0.90 × 10−6 μM−1 s−1	drug association rate	experiment
k−2	14.0 × 10−5 s−1	drug dissociation rate	experiment
kv	1.25 × 10−7 m s−1	permeability across vessel wall	estimated
D	5.0 × 10−11 m2 s−1	interstitial diffusion rate	D = 2k0r
C0	2.6 × 103 μM	binding site concentration	experiment

2.2. Multi-dimensional cell-centre model

The most general approach considered here is a multidimensional model in which each biological cell in the cord is represented as a computational node (cell centre) characterized by geometrical and biological information: position, cell radius, binding rates and concentration of binding sites. Each of these nodes in isolation acts in accordance with the three-compartment binding model illustrated in figure 2, providing the potential to insert a bespoke model of the microenvironment for each node/cell. The binding model is augmented by a description of the spatial transport of the drug, described locally by defining transport terms between nodes and their nearest neighbours.

A representative geometry of a slice through the tumour cord is illustrated in figure 3 (cf. figure 1b). We assume uniformity in the axial direction—variations along the vessel are assumed negligible—so only two-dimensional cord cross sections are considered in this paper. The terms volume and area are used as though the model were fully three dimensional but, for the sake of simplicity, the factor of the cord length is omitted from all of the analysis, because it cancels.

Figure 3.

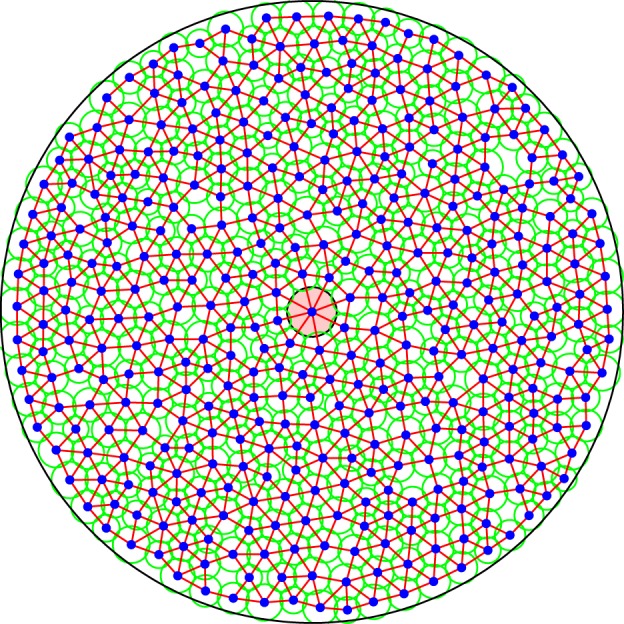
A representative tumour cord geometry for the two-dimensional cell-centre model in which the computational nodes (cell centres) surround a central vessel. The radius associated with each node is illustrated by the surrounding circle and the connectivity is designated by the connecting lines. (Online version in colour.)

Each computational node (see figure 3) is assigned associated interstitial and intracellular volumes, δ₁V_i and δ₂V_i, respectively, where δ₁ and δ₂ are volume fractions, parametrized by δ in table 1 (see the electronic supplementary material for full details) and three concentrations: interstitial, intracellular free and intracellular bound drug denoted by 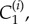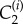and 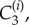respectively. The transport between nodes is assumed to be proportional to the concentration difference and the interface area, A_ij, between connected nodes.

Under these assumptions, the spatial variation represented by introducing distinct computational nodes can be included in the model by adapting equations (2.1)–(2.3) to include terms for transport between nodes and having a separate set of equations for each node, i.e.

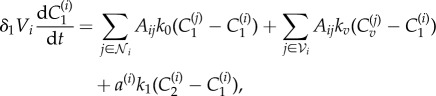2.4

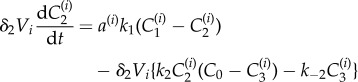2.5

2.6

Here, A_ij is the area of the interface between nodes i and j (see the electronic supplementary material) and a⁽ⁱ⁾ is the area of the interface between the intra- and extracellular space surrounding node i. 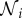and are sets of indices of, respectively, the nodes and blood vessels neighbouring node i: all simulations presented in this paper have been carried out with a single central vessel. C_v(t) is a predefined PK profile in the blood vessel and determines the flux of drug through the vessel wall. At the outer boundary, this model automatically implies zero flux of drug, because there are no connections to nodes outside the cord geometry. This models a situation in which the tumour cord is surrounded by similar cords, providing a symmetry boundary condition.

It is assumed, in this model, that the transport of drug is limited to the interstitium—drug is only exchanged between neighbouring nodes via the compartments representing extracellular space. Internalization and binding terms in equations (2.4)–(2.6) are analogous to those for the binding model. The additional rate parameter in this model is the spatial transport coefficient k₀, which has the units of permeability and is estimated in table 1 according to data provided in [6].

2.3. Radially symmetric compartment model

A simpler way to augment the binding model with a spatial component is to exploit the shell-like nature of tumour cords, the geometrical property that cells are broadly arranged in concentric circles around a central blood vessel (see figures 1 and 4a). It is again assumed that variations along the vessel are negligible.

Figure 4.

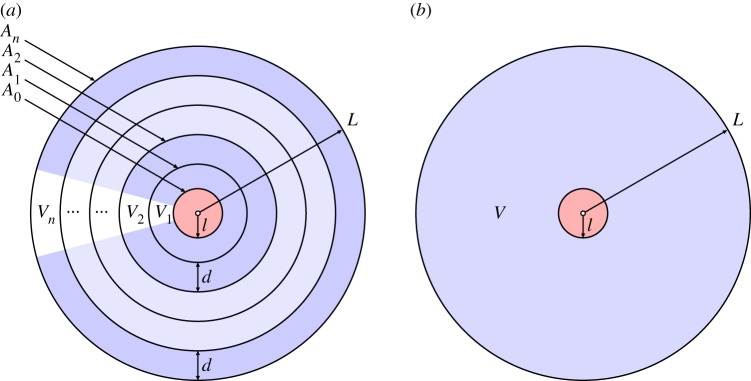
Schematics of the two radially symmetric models: (a) the shell-like arrangement for the compartmental model and (b) the continuum model, for the tumour cord. (Online version in colour.)

We now assume that the rate of transport of drug between neighbouring shells is proportional to the shared interface area (denoted by A_i for the interface between shells i and i + 1) and the difference in concentration across the interface. Under these assumptions, the spatial variation in the radial direction can be included by adapting equations (2.1)–(2.3) to give

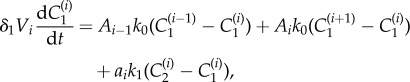2.7

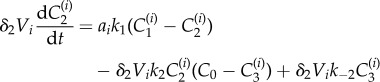2.8

2.9

for i = 1, … , n, where n is the number of shells, and a_i is the cellular surface area within the ith shell. In this work, n = 9 is chosen so that each shell can be identified with a layer of biological cells. The superscript corresponds to the shell number, and this index increases with distance from the blood supply (see figure 4a). The boundary conditions are imposed at the vessel wall by setting 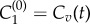to be a predefined PK profile in the blood vessel and replacing k₀ by k_v at this interface. A no-flux boundary condition is imposed at the outer boundary of the cord by setting A_n = 0 (equivalent to replacing k₀ by zero at this interface).

The volumes V_i of the shells are readily determined from the geometry: assuming a shell thickness d and a vessel radius l, the volume (again omitting the factor of the vessel length owing to the assumed uniformity along the vessel) of the ith shell is

2.10

The factors δ₁ and δ₂ are defined as in the cell-centre model, so that δ₁V_i and δ₂V_i are, respectively, the extracellular and intracellular volumes in the ith layer. The interface area between shells i and i + 1 is

2.11

Note the similarity between compartmental and cell-centre equations. In fact, equations (2.7)–(2.9) can be viewed as a special case of equations (2.4)–(2.6), in which nodes are replaced by shells, and the concentrations within each shell represent the averages over the conglomerate of biological cells it contains.

2.4. Radially symmetric continuum model

The final model, the geometry of which is illustrated in figure 4b, is derived by disregarding the cellular structure of the tumour cord and assuming that transport of molecules occurs by isotropic Fickian diffusion in a continuum. A model for the tumour cord is then readily obtained as the system of partial differential equations (PDEs) [10,12]

2.12

2.13

2.14

where the factors δ₁ and δ₂ are defined as before, and D is a diffusion coefficient related to the permeability k₀. The precise nature of this relationship can be derived by noting that

2.15

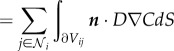2.16

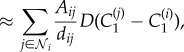2.17

in which n represents the unit normal pointing outwards from volume V_i. Note that the direction of n varies over the surface of V_i. Hence, the relationship between transport coefficients of discrete and continuum models is

2.18

where d is a length parameter, taken here to be the average cell diameter, 20 μm. The parameter α in equations (2.12) and (2.13) is easily derived from equations (2.7) or (2.8) and represents the ratio of the cellular surface area within a region to that region's volume, α = a/V (table 1).

Given these definitions, integrating equations (2.12)–(2.14) over a cell or shell returns the equations of the multi-dimensional cell-centre and radially symmetric compartmental models, respectively. The boundary conditions imposed are the same as for the other two models. The flux of free drug across the vessel wall is assumed to be proportional to the difference in concentration between vessel and interstitium, so [15]

2.19

that is, the normal flux at the vessel wall is proportional to k_v, the vessel permeability and the difference in free drug concentration across the vessel wall (C_v being the drug concentration in the blood, determined by the prescribed PK profile). A no-flux condition is imposed at the outer boundary

2.20

The respective unit normal vectors, at the vessel and the outer boundary, pointing out of the intervening tissue, are denoted by n₁ and n₂.

A spectral method [26,27] is used in this work for the spatial discretization of equations (2.12)–(2.14). Note that, because radial symmetry is assumed, the Laplacian term in equation (2.12) is actually of the form

2.21

2.5. Pharmacokinetic profiles

The clinical pharmacokinetics of doxorubicin are well characterized in the literature [28]. Doxorubicin concentrations are known to decay in a tri-exponential manner following intravenous (IV) bolus or infusion and typical parameters are available in the literature (e.g. [29], in which doxorubicin is administered as an IV bolus, not infusion).

The first PK profile considered here is based on the data provided by Robert et al. [29], in which C_v(t) is assumed to decay as a tri-exponential (see also [8]), i.e.

2.22

for t ≥ τ, where τ is the infusion time, D₀ is the dose and parameters A, B, C, α, β and γ are estimated by taking averages of the values given in table 2 of reference [29]. This gives (to three significant figures)

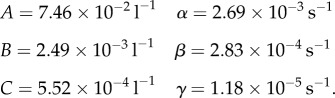The rapid initial infusion of the drug is modelled by taking

2.23

for t < τ, which lifts the concentration to the appropriate value at t = τ. The duration of the perfusion for the total dose injected, τ = 180 s, was also taken from [29], and the total dose D₀ = 1.19827×10² μmol was calculated to give an ‘area under the curve’ of

2.24

which is typical of what one might find in a patient [30,31]. The AUC is an important parameter, because the area under the plasma drug concentration–time curve (AUC) is considered to reflect the actual tumour (cellular) exposure to drug after administration of a drug dose, and to correlate with toxicity—though it is more difficult to correlate with clinical efficacy [32].

Two further PK profiles, both constructed to give the same AUC, are also simulated, to investigate their influence on the drug distribution.

• — A mono-exponential profile, 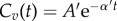with A′ = 50 μM and α′ = 0.005 s⁻¹.

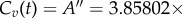
• — A uniform (steady-state) profile, up to t = 72 h (and zero afterwards), representing prolonged infusion. This takes the form of a rectangular pulse.

3. Results

3.1. Model comparison

The first set of numerical results are generated to address the key question ‘Does each of these models give similar results for the variation in drug concentration in the tumour cord for similar parameters?’ In order to assess this, we compare the predictions for a set of parameter values, shown in table 1, common to all three models. These simulations are carried out for the tri-exponential (IV bolus) PK profile described in §2.5.

All numerical experiments were carried out on the same computational domain, comprising a single circular blood vessel of radius 16 μm at the centre of a circular cord of tumour cells of radius 200 μm. The vessel radius approximates the average radius of arterioles and venules rather than larger vessels. For the radially symmetric compartmental model, the region between the vessel and outer boundary was divided into nine shells of equal width (approximately the diameter of a biological cell). The two-dimensional cell-centre results were generated using 60 separate configurations, to assess the effect that small random variations in the distribution of the node positions and radii have on the drug distribution. Each configuration is derived from a different randomly generated set of node positions and radii (see §2.2) and contains approximately 400 nodes, the number required to fill the domain with cells of the given radius.

The nature of the binding model means that the node spacing does not have to match the biological cell size, because each compartment contains both intracellular and extracellular concentrations. However, future developments may treat the cells as separate entities, immersed in interstitial fluid, so this is a useful length scale at which to investigate the model. The impact on the results of changing the spacing is similar to that of changing the resolution in an approximation to a continuum model. Increasing the spacing will effectively increase the rate of diffusion, because the model assumes that, at each time step, any drug that passes into a compartment instantaneously equidistributes its concentration throughout that compartment. We have conducted numerical experiments with different cell sizes and, although there are small quantitative differences, we have found no evidence that the qualitative behaviour might be changed.

In order to visualize the two-dimensional simulation results, both mean values and standard deviations are plotted, after clustering the nodes from all 60 configurations into 20 bins, according to their distance from the blood vessel. The mean distance is plotted against the mean concentration for each of these bins, and the standard deviations of both variables are illustrated by horizontal (distance) and vertical (concentration) bars. The compartmental model is illustrated using solid dots plotted at the centres of the cylindrical shells, and the continuum model is represented by a solid line.

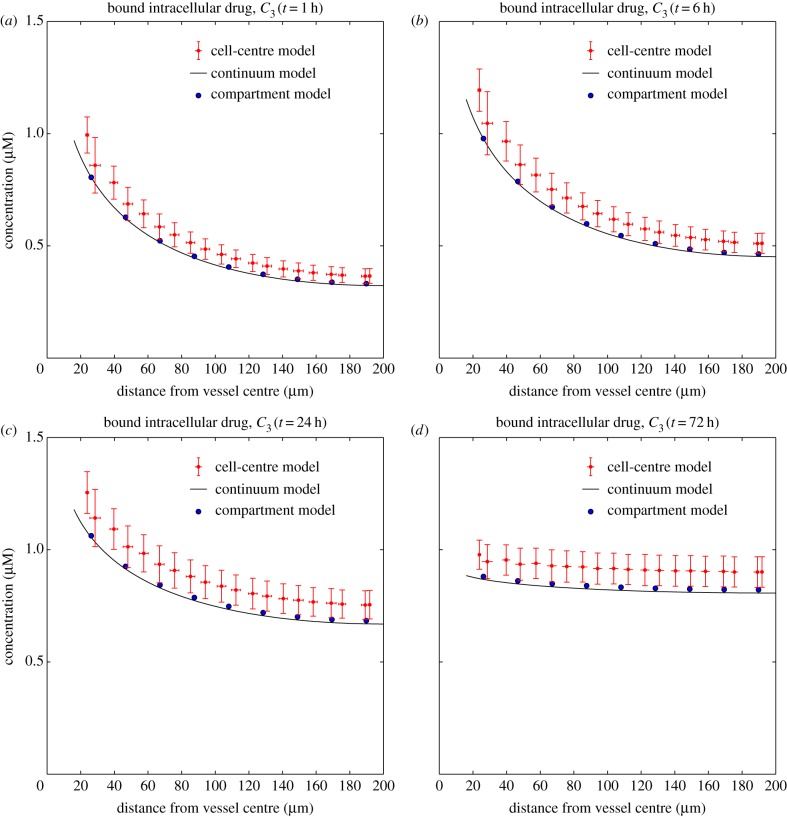
Figure 5 shows snapshots of the concentration profiles, as a function of distance from the source of the drug, for C₃ after 1, 6, 24 and 72 h, generated using the tri-exponential PK profile from §2.5 and the parameter values shown in table 1. Note that the results for C₁ and C₂ (in the electronic supplementary material) are almost indistinguishable. This similarity is common to all the tests we have run and consistent with very rapid transport of drug across the cell membrane.

Figure 5.

Dependence of the concentrations of bound drug, C₃, on distance from the drug supply at times t = 1 h (a), t = 6 h (b), t = 24 h (c) and t = 72 h (d). The solid line represents the continuum model, the large solid dots represent the compartmental model and the smaller dots with vertical and horizontal bars represent the cell-centre model. The tri-exponential (IV bolus) PK profile has been used as input. (Online version in colour.)

3.2. Comparing pharmacokinetic profiles

Section 2.5 described three distinct PK profiles, one representing administration by an IV bolus with a tri-exponential decay (characteristic of doxorubicin), a simplified, mono-exponential, approximation to this decay profile and a uniform profile representing infusion of the drug. All profiles had the same AUC, because this is a standard measure of cellular toxicity.

Because the numerical results presented in §3.1 showed similar results for all three models of the tumour cord, the simplest—the compartmental model described in §2.3—was chosen to illustrate how the distribution of the drug is influenced by the PK profile of the supplied drug, C_v(t). The model parameters used are those given in table 1. The other models have been run with the same parameters, but the data are not shown because they contain no significant differences.

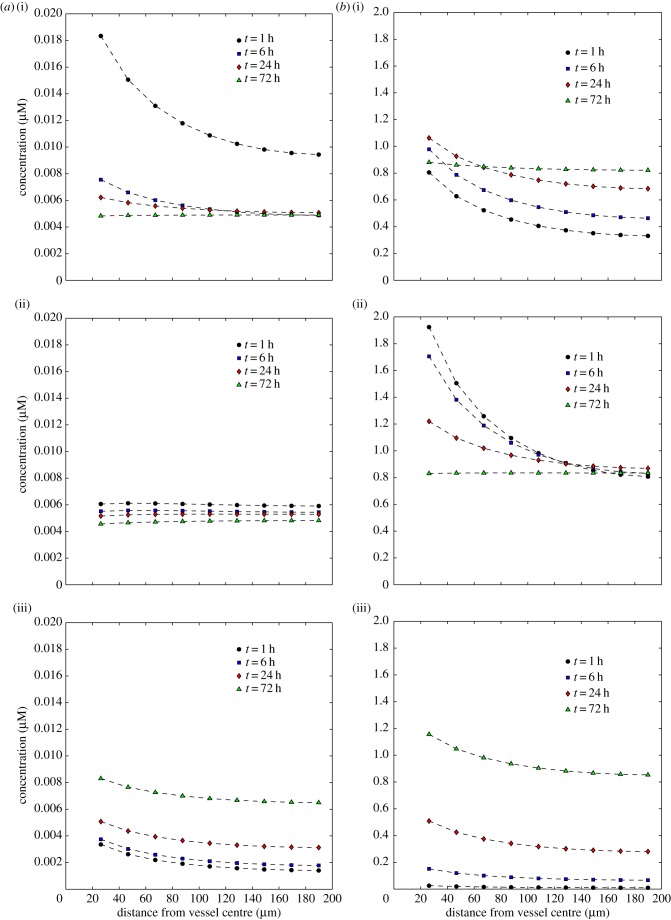
Figure 6 shows the evolution of the extracellular and bound drug distributions, C₁ and C₃, as a function of distance from the drug source for each of the three PK profiles described in §2.5. The time variation of the concentrations of both free and bound drug in a given cell layer generally follows that of the PK profile in the vessel, though there is a time-lag which increases the further away from the vessel a cell layer is. For both exponential profiles, the concentration increases initially to a peak value (particularly rapidly for the mono-exponential profile), then decreases monotonically, but for the uniform profile, it increases monotonically for the duration of the experiment.

Figure 6.

Dependence of the concentrations of extracellular drug, C₁ (a), and bound drug, C₃ (b), on distance from the drug supply for three PK profiles: tri-exponential/IV bolus (i), mono-exponential/simplified IV bolus (ii), uniform/infusion (iii). Each graph shows profiles at times t = 1, t = 6, t = 24 and t = 72 h. (Online version in colour.)

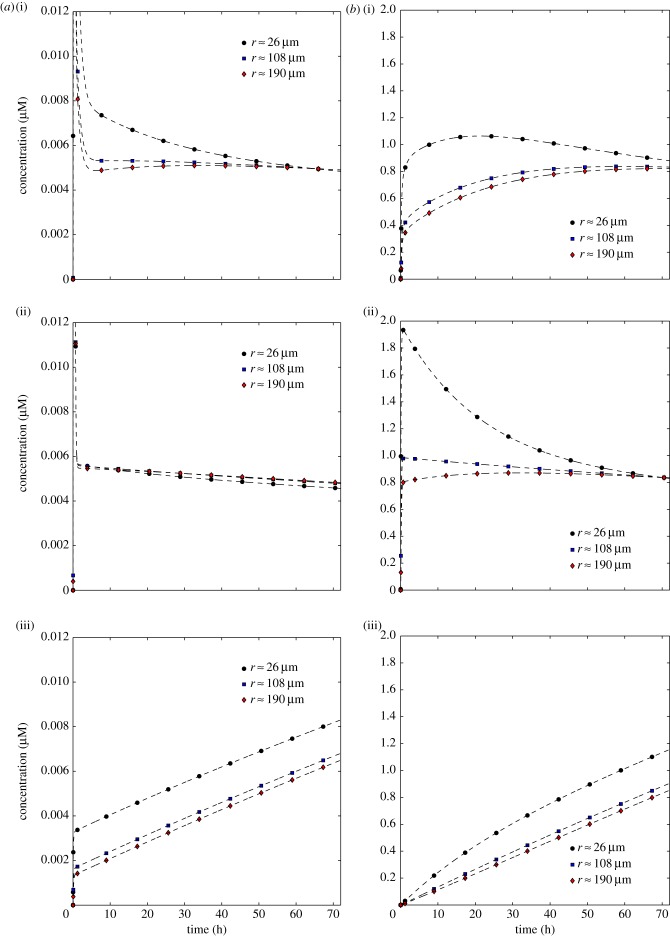
This is confirmed by examining the temporal variation of the concentrations at specific points in the domain. Figure 7 shows this at the centres of the first (innermost), fifth (middle) and ninth (outermost) shells of the compartmental model. Note that the extracellular drug concentrations at very early times (less than 1 h) extend far beyond the maximum value on the vertical axis of the graph for the IV bolus profiles: the true maximum values are given in table 2. These peaks become less extreme further away from the vessel.

Figure 7.

Dependence of the concentrations of extracellular drug, C₁ (a), and bound drug, C₃ (b), on time for three PK profiles: tri-exponential/IV bolus (i), mono-exponential/simplified IV bolus (ii), uniform/infusion (iii). Each graph shows profiles at the centres of the first, fifth and ninth of the model's shells (distances 26, 108 and 190 μm from the centre of the vessel). (Online version in colour.)

Table 2.

Maximum concentrations of free extracellular and bound intracellular drug, to 3 significant figures, and the experiment times at which they occur, to the nearest second (for three distances from the centre of the blood vessel and all three PK profiles).

layer index	1	5	9
distance from vessel centre (μm)	26	108	190
tri-exponential/IV bolus
maximum C1 (μM)	0.382	0.140	0.112
time of maximum C1 (h:m:s)	00:03:56	00:08:21	00:10:01
maximum C3 (μM)	1.06	0.838	0.822
time of maximum C3 (h:m:s)	21:18:33	59:48:33	70:23:33
mono-exponential/IV bolus
maximum C1 (μM)	1.80	0.523	0.406
time of maximum C1 (h:m:s)	00:01:15	00:04:25	00:06:14
maximum C3 (μM)	1.93	0.983	0.872
time of maximum C3 (h:m:s)	00:41:02	01:02:28	31:45:39
uniform/infusion
maximum C1 (μM)	0.00830	0.00681	0.00650
time of maximum C1 (h:m:s)	72:00:00	72:00:00	72:00:00
maximum C3 (μM)	1.16	0.904	0.853
time of maximum C3 (h:m:s)	72:00:00	72:00:00	72:00:00

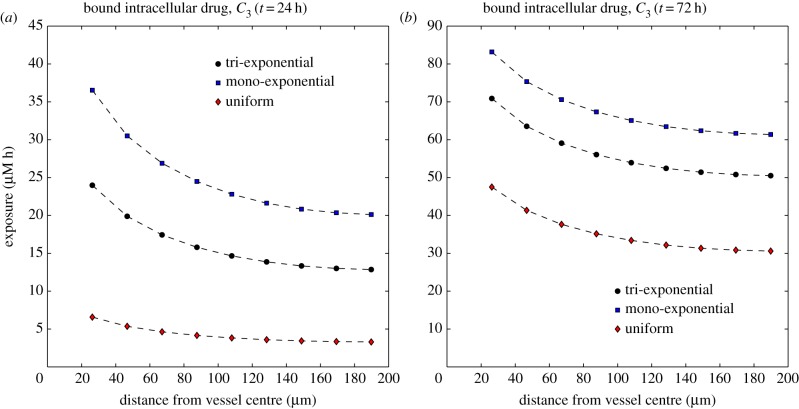
Figure 8 shows the variation of the exposure of the cells to the bound drug (AUC, given by 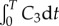) as a function of distance from the blood vessel, after T = 24 h and T = 72 h. Early in the simulations, the exponential profiles give a far higher exposure than the uniform profile, but as time progresses, the differences between the profiles reduce. However, results at later times should be interpreted carefully, because elimination of drug is not included in the model, and the only drug clearance is due to the drug returning to the vessel. This effect will be addressed in future models, through the inclusion of elimination mechanisms such as cellular metabolism, sequestration/binding to the extracellular matrix and drug efflux. Drug clearance owing to lymphatics may be considered for larger tumour volumes, though functional lymphatic vessels are not thought to be prevalent in tumours [3].

Figure 8.

Dependence of the exposure to bound drug 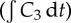on distance from the supply of drug at t = 24 h (a) and t = 72 h (b) for three PK profiles: tri-exponential/IV bolus, mono-exponential/simplified IV bolus, uniform/infusion. (Online version in colour.)

3.3. Comparing binding affinities

The final set of numerical experiments investigates the effect that changing the binding affinity of the intracellular drug, parameters k₂ and k₋₂ in our model, has on the exposure of the cells to bound drug. This attempts to address one aspect of the question ‘How does the administration schedule and cell response affect drug delivery?’ As in §3.2, the compartmental model (§2.3) was used to produce the numerical results presented here. No significant differences were seen when the same tests were carried out with the other models (data not shown).

The qualitative changes caused by adjusting k₂ and k₋₂ depended most significantly on the ratio k₋₂/k₂, so only results for different values of k₂ (the association rate) are shown in figure 9. All other parameters take the values shown in table 1.

Figure 9.

Dependence of the exposure to bound drug on distance from the supply of drug at t = 72 h for three different binding affinities where the association rate constant only varies over the range: k₂ = 4 × 10⁻⁷, k₂ = 4 × 10⁻⁶ and k₂ = 4 × 10⁻⁵ μM⁻¹ s⁻¹. The tri-exponential/IV bolus PK profile was used as input. (Online version in colour.)

4. Discussion

In §2, three different approaches to modelling the delivery of drug from a blood vessel to a surrounding tumour cord were presented. One of these, a discrete cell-centre model which identifies computational nodes with individual biological cells, is genuinely multi-dimensional and could be applied to more complex geometries than the one investigated here, such as those modelled using a finite-element discretization of a reaction–diffusion system in [33]. The remaining two (a discrete, compartment-based, model and a continuum, PDE-based, model) are tailored to the specific problem of drug delivery from a single vessel to a homogeneous tumour cord, assuming radial symmetry. All were built on a binding model involving extracellular drug and free and bound intracellular drug, which extends those of [12] and [17] by allowing drug binding to be saturable and reversible.

The two radially symmetric models are much simpler and therefore computationally much faster than the multi-dimensional model, but this leads to the question ‘Does each of these models give similar results for the variation in drug concentration in the tumour cord?’ Figure 5 shows a representative comparison of the bound drug variations of the three models for a PK profile derived from in vivo data for an IV bolus. The concentrations predicted by the three models differ by less than 15% throughout the simulation. In fact, the plotted standard deviations for the multi-dimensional cell-centre model show that the variation between the randomly generated two-dimensional configurations (particularly when there is a steep gradient in the drug concentration close to the central vessel) is typically larger than the difference between the average multi-dimensional results and the radially symmetric results. This observation is supported by further simulations, some of which are shown in the electronic supplementary material. In all cases, the qualitative features of the concentration profiles are similar, whichever model is used.

In figure 5, the two radially symmetric models agree more closely with each other than with the multi-dimensional model. This is not generally the case for all parameter sets. We note that the discrete models would be expected to converge to the continuum model asymptotically if the sizes of the ‘cells’ were allowed to tend to zero, though this is not biologically realistic, because continuum models of this type are designed for use at much larger length scales. By contrast, although the discrete models operate on realistic cell sizes, in doing so, they implicitly assume that diffusion/mixing within a cell happens instantaneously.

We have conducted a range of numerical simulations for the tumour cord geometry, with different parameters, without finding any systematic differences between the results which might suggest that one model is consistently more accurate than the others. All three models give qualitatively and quantitatively similar results, and we do not yet have experimental data to enable us to assess whether one model is better or worse than another. The multi-dimensional model is, computationally, more expensive and therefore inefficient for the radially symmetric tests considered here, but we include it because it would be used for more complex geometries and heterogeneous tissue. Continuum models are very commonly used, but are based on the assumption that the differential equation is valid at every point in space. The radially symmetric, compartment-based, model only assumes that the differential equation is valid in an integral-averaged sense (and is, in effect, a finite volume discretization of the continuum model [34], an integration of the continuum model over volumes chosen to be on the scale of the biological cells), leading to a very natural framework for simulating mass balance processes. The compartmental model is limited to radially symmetric problems (cords, multicell spheroids), but this is a common constraint imposed in computational modelling for (i) efficiency of computation and (ii) direct comparison with mathematical analysis, which is often limited to such quasi-one-dimensional geometries.

We have conducted a range of numerical simulations for the tumour-cord geometry, with different parameters, without finding any systematic differences between the results which might suggest that one model is consistently more accurate than the others. All three models give qualitatively and quantitatively similar results, and we do not yet have experimental data to enable us to assess whether one model is better or worse than another. The multidimensional model is, computationally, more expensive and therefore inefficient for the radially symmetric tests considered here, but we include it, because it would be used for more complex geometries and heterogeneous tissue. Continuum models are very commonly used, but are based on the assumption that the differential equation is valid at every point in space. The radially symmetric, compartment-based, model only assumes that the differential equation is valid in an integral-averaged sense (and is, in effect, a finite volume discretization of the continuum model [34], an integration of the continuum model over volumes chosen to be on the scale of the biological cells), leading to a very natural framework for simulating mass balance processes. The compartmental model is limited to radially symmetric problems (cords, multicell spheroids), but this is a common constraint imposed in computational modelling for (i) efficiency of computation and (ii) direct comparison with mathematical analysis, which is often limited to such quasi-one-dimensional geometries.

We therefore choose to use the radially symmetric, compartment-based model to investigate further the effect of varying the supplied PK profile and the behaviour of the underlying binding model, and note that the similarity of the results provides some validation of the more complex approaches. This gives us confidence that they could be used reliably in the more complex scenarios for which they are designed. A more comprehensive validation would involve comparison with measurements of drug distribution from an in vitro tumour cord model system. Simple modifications to the model geometry would also allow validation against experimental data for multi-cell spheroids. In both cases, knowledge of heterogeneity in the system could be readily incorporated in the multi-dimensional approach described in §2.2.

Drug delivery to tumours is dependent upon a number of factors, the principal ones being the dose and schedule of administration, delivery of the drug via the blood vessels, the flux or distribution of drug through avascular tissue and consumption of drug by the cells or the extracellular matrix [3]. For example, increasing the diffusion rate, k₀, tends to make the distribution of the drug more homogeneous ([35] and the electronic supplementary material), because the drug can be transported further before it is bound. However, in this paper, we focus on other factors.

In §3.2, three different delivery profiles were compared, all of which provide the same overall dose. Figures 6 and 7 show significant differences between the distribution of drug in the tissue at any given point in time. When the PK profile in the blood vessel represents an IV bolus, a sharp peak in free drug concentration occurs in the first hour as the drug diffuses rapidly into the surrounding tissue and is transported into the cells. The profiles at t = 1 h in figure 6 are similar in shape to the experimentally measured gradients in [23]. The concentration of free drug then drops steeply as it is bound until an approximate equilibrium is reached. This is followed by a slower decrease once the concentration of drug in the vessel drops below that of the free drug in the tissue, and the net flux is of drug returning to the vessel. Because the binding process acts more slowly than the initial influx of drug, the concentration of bound drug changes less rapidly and only cells close to the vessel experience an initial peak in concentration (most extreme for the mono-exponential PK profile). As a consequence, early in the simulation, when the concentration in the vessel is high and changing rapidly, the drug concentration close to the vessel is much higher than in cells further away, because drug has not had sufficient time to reach and bind to cells at a relatively large distance from the vessel. Later, the drug concentration in the vessel is still decreasing, but slowly enough, relative to the rates at which it is transported through the tissue and binds to the cells, for the drug distribution in the tissue to remain uniform throughout.

When the PK profile represents infusion over a longer period, the concentrations in the tissue steadily increase during the period of infusion, after an initial rapid increase in free drug concentrations. The spatial distribution of the concentration is quite even, though slightly higher close to the vessel, because the concentration of supplied drug is not varying in time.

Given the large differences in concentration profiles, it might be expected that the exposure to bound drug also depends critically on the supplied PK profile. The results shown in figure 8 suggest that, for the model of binding proposed in §2.1, all of the PK profiles give a similar spatial distribution of exposure to bound drug. After 72 h, infusion gives a significantly lower exposure than IV bolus (40–50% lower than the mono-exponential profile), but this difference is less significant than after 24 h and continues to reduce over longer time scales. However, our binding model contains no explicit elimination or decay term: drug can only leave the system through free drug returning to the vessel when the concentration in the vessel is below that in the adjacent tissue. A more sophisticated binding model could account for this and include a representation of the cell cycle, which will have an influence over longer time scales. These would need to be included before investigating the dependence of exposure on PK profiles over longer time scales.

In order to assess how the binding affects the delivery of the drug, a final set of numerical simulations investigated the influence of binding affinity. Figure 9 shows that the exposure of the cells to bound drug depends strongly on the ratio of the intracellular drug association and dissociation rates (β = k₋₂/k₂). For the original parameter set (table 1) β ≈ 16 μM, for which the exposure of the cells to bound drug was fairly uniformly distributed between the blood vessel and the outer boundary of the domain (200 μm from the centre of the vessel), decreasing only slightly with distance from the vessel. When β is increased—the net affinity for the drug is reduced—the spatial distribution remains uniform, but the exposure of each layer of cells is reduced. When β is decreased, the exposure of the cells close to the vessel increases, but the exposure further away from the vessel actually starts to decrease. If k₂ is increased further than shown in figure 9, then this behaviour becomes more pronounced, to the point where almost no drug gets beyond 100 μm from the supply, because it is all consumed by the cells close to the vessel. This ‘binding site barrier’ [35,36] is reduced in tissue which allows more rapid interstitial drug diffusion (see numerical results in the electronic supplementary material).

This suggests that, for this model of binding, there is an optimal binding affinity which allows optimal exposure to doxorubicin: if the binding is too weak, then none of the cells gains enough exposure; if it is too strong, then the cells distant from the vessel are pharmacokinetically resistant, because the closer cells consume the drug. If true, then this might have implications for the use of additional agents which can alter the binding behaviour of doxorubicin, e.g. by occupying binding sites, to adjust drug penetration. It also suggests that variations in the tumour microenvironment could influence the effectiveness of the drug.

The model presented in this paper has been tailored to simulate a tumour cord geometry, and the parameters have been estimated based on the binding of doxorubicin to colorectal adenocarcinoma cells (DLD-1). However, it is sufficiently general to be applied to other drugs and other cell lines if the appropriate data are available. This may require the design of new binding models.

There is no sufficient evidence to suggest that any of the three models of drug transport proposed in this paper is better than the others, so the simplest was chosen to investigate the influence of the delivery profile and the cell biology. However, the comparison has validated the more flexible multidimensional model, which therefore provides a framework that can be used to gain insights into progressively more complex situations in which the influence of the characteristics of the tumour microenvironment on the PK delivery of the drug and the effects of spatial heterogeneity can be investigated.

It is important to emphasize that all models are approximations to reality and the models described here are clearly significant simplifications of complex biology and geometry. The value of models in biology and medicine lies in their role in the iterative development of a quantitative, logical, predictive framework, placing them at the heart of ‘model-building’; the need to write down equations describing the biological mechanisms demands assumptions and yields predictions which can be tested and measurements which have to be made. This, in turn, leads to improved models and initiates a further cycle of experimentation and model building. We also believe that these models have the ability to demonstrate, at least semi-quantitatively, the relative efficacy of some aspects of therapeutic protocols.

Funding statement

This work was funded by Yorkshire Cancer Research Project grant no. B208, with additional support from the Leeds Cancer Research UK Centre.