Orthogonal resonators for pulse in vivo electron paramagnetic imaging at 250 MHz

Abstract

A 250 MHz bimodal resonator with a 19 mm internal diameter for in vivo pulse electron paramagnetic resonance (EPR) imaging is presented. Two separate coaxial cylindrical resonators inserted one into another were used for excitation and detection. The Alderman-Grant excitation resonator (AGR) showed the highest efficiency among all the excitation resonators tested. The magnetic field of AGR is confined to the volume of the detection resonator, which results in highly efficient use of the radio frequency power. A slotted inner single loop single gap resonator (SLSG LGR), coaxial to the AGR, was used for signal detection. The resulting bimodal resonator (AG/LGR) has two mutually orthogonal magnetic field modes; one of them has the magnetic field in the axial direction. The resonator built in our laboratory achieved 40dB isolation over 20 MHz bandwidth with quality factors of detection and excitation resonators of 36 and 11 respectively. Considerable improvement of the B₁ homogeneity and EPR image quality in comparison with reflection loop-gap resonator of similar size and volume was observed.

1. Introduction

Rapid development of low frequency (250 MHz – 1 GHz) electron paramagnetic resonance (EPR) in vivo imaging [1] of physiologic parameters such as oxygen [2, 3], pH and redox potential [4, 5] has stimulated continuous adaptation of EPR instrumentation for different aspects of acquisition methodologies. EPR imagers operating at the lower edge of the frequency range are primarily designed for imaging of large parts of animal anatomy and typically use resonators fully enclosing the sample.

Resonators serve multiple functions. First of all, they confine the magnetic field to the sample location. The conversion of the applied radio frequency (RF) power into the RF magnetic field B₁ is characterized by parameter Λ, the resonator efficiency and is measured in G/√W. Resonators with larger Λ require less power to generate the same B₁ and, reciprocally, detect higher signals from the same spin system. Resonator efficiency depends on its geometry, which is characterized by the filling factor η. η is the ratio of the volume integrals of B₁² over the useful volume (sample) and over all space. Energy efficient resonators have high η or, in other terms, most of magnetic field is localized at sample's position. The electrical parameter characterizing a resonance circuit is the quality factor, Q = ν₀/Δν_FWHH, the ratio of resonator base frequency and the half-power bandwidth. Λ is proportional to the square root of Q.

Beside its primary function of production of the B₁ field and detection of the excited magnetization, the resonator as an integral part of the radio frequency bridge is important for isolation of sensitive receiver from the excitation power. This can be a direct isolation provided by bimodal resonators or indirect contribution through the absorption of excitation power like in the case of reflection mode resonators used in combination with a transmit receive (T/R) switch. Finally, resonators are characterized by a number of other parameters such as field homogeneity and convenience of use. Different designs of resonator exhibit different combinations of these features and thus have different applications.

Loop-gap resonators (LGR) were introduced to EPR by Froncisz and Hyde [6, 7] and found wide use in low frequency imagers [8]. LGRs have very high η, moderately high quality factors and are transparent to modulation field necessary for continuous wave (CW) experiments. LGRs are robust and simple in construction. These resonators were used in reflection mode in combination with T/R switches, typically, circulator-based [9]. In CW operation the isolation of well-matched circulator-resonator system is defined by a maximum isolation provided by the circulator, ~20 dB at 250 MHz. This isolation is adequate to keep receiver in the linear operating region at powers below −10 dBm. Excitation power requirements for Rapid Scan [10] acquisition method are higher than that for CW by one to two orders of magnitude. These levels of excitation power necessitate better receiver isolation. A bimodal resonator with detection wire-loop-gap resonator and Helmholtz pair excitation resonator was described elsewhere [11]. This resonator demonstrated ~45 dB of isolation and allowed the 250 MHz spectrometer to operate at excitation power of up to 20 dBm. The very light structure of the wire loops renders this resonator transparent for the externally applied ramping magnetic field at frequencies of tenths to hundreds of kHz. The drawback of application of Helmholtz pair for excitation was the considerable reduction of the excitation resonator efficiency due to the excitation of much larger volume than that used by the receiver resonator.

Pulse EPR imagers demanded another three to four orders increase in excitation power that reached 50–60 dBm levels [12, 13]. Such high levels of power even for relatively small samples of ~10cm³ are dictated by the necessity to generate tens of nanosecond long pulses with high B₁. Generation and handling of this level of power is challenging. Therefore, excitation resonators with the highest efficiency are desirable.

For pulse measurements the imaging protocol dictates the excitation and acquisition bandwidths and hence the resonator Q. The original high Q of resonator is lowered for imaging using resistive damping or over-coupling [12]. Under circumstances of given Q and resonator volume V, it is instrumental to introduce resonator efficiency independent of Q and V, a normalized efficiency,

$${\Lambda }_{\mathit{norm}}=\Lambda \frac{\sqrt{V}}{\sqrt{Q}}.$$ [1]

For a given Q and resonator volume, the normalized efficiency allows the comparison between different resonator concepts and is approximately equal for resonators with similar design. In our experience, other resonator components such as shields or matching circuits contribute to less than 15% of Λ_norm. Between all the 250 MHz resonators of different Q and volumes tested in our laboratory, the single loop single gap LGR had the highest Λ_norm of ~0.24 Gcm^3/2/√W. In comparison, the Λ_norm of Helmholtz pair resonators was considerably lower, about 0.08 Gcm^3/2/√W.

In pulse operational mode the overall isolation of a T/R switch and reflection resonator is limited. Independently of the direct leakage of RF power from power amplifier to receiver, the overall isolation can not be made better than ~10 dB over the bandwidth of the resonator, due to resonator ringing. Upon application of RF pulse, the power in resonator will not dissipate immediately. The resonator will `ring' and this ringing will be routed to the receiver. The initial amplitude of ringing is comparable to the incident power of the pulse and thus harmful to detector. As mentioned above, the protection of the receiver is typically performed at the expense of inability to detect during excitation. Although, the resulting voltage on receiver can be reduced using destructive interference with separately synthesized waveform with the phase opposite to that of ringing this protection method is rarely used due to its technical complexity. It also results in artifacts and lowering of the EPR signal to noise ratio. Therefore, the only practical solution for high isolation is a system where excitation and detection resonant modes are spatially isolated, a bimodal resonator.

The specifications for a bimodal resonator for pulse in vivo applications include:

• High isolation between excitation and detection resonators

• Λ_norm of detection resonator close to that of the best single mode resonators

• High Λ_norm of excitation resonator; confinement of the excitation resonator magnetic field to the active volume of detection resonator

• Low inductance of excitation and detection resonators for electrical stability

• Open structure for easy animal access

The bimodal Rapid Scan resonator [11] described above is suitable for pulse operation. However, for imagers with limited power budget, the Helmhotz pair excitation that has low Λ_norm and low (~0.25) fraction of volume occupied by sample relative to the active volume of resonator might be not optimal. Rinard and coworkers demonstrated another bimodal resonator comprising of two LGRs intersecting at right angle [14]. This resonator was made of thick solid copper blocks and had solid copper shield. It provided very high isolation of 60 dB. However, complex geometry of the structure resulted in a lower normalized efficiency of both resonators relative to standalone LGR. We estimate the normalized efficiency of 0.16 Gcm^3/2/√W and 0.18 Gcm^3/2/√W for excitation and detection resonators, respectively. Only a fraction of the excitation resonator volume (low η) was used, which further reduced the excitation resonator efficiency. In the original design, these issues were compensated with very high quality factors.

In this work we present a resonator design for in vivo pulse EPR imaging with high efficiency, good isolation, high B₁ uniformity and convenient access.

2. Description of Resonator

The bimodal 250 MHz Alderman-Grant/Loop-gap resonator (AG/LGR) presented in this work contains two independent resonators of cylindrical shape, housed coaxially one inside another (Figure 1A). A coaxial cylindrical RF shield opened on face sides surrounds the resonators. The inner resonator is the signal detection single loop single gap resonator (SLSG LGR), slotted for B₁ penetration from the outer resonator. Signal is excited by the outer Alderman-Grant resonator. Mechanical support attached to shield holds inner resonator while AGR is rotated freely around the axles.

FIGURE 1.

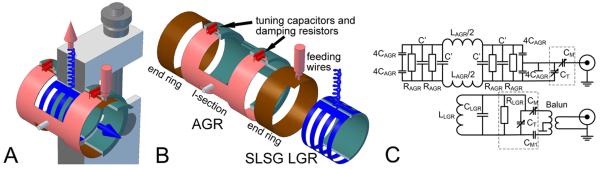
Alderman-Grant/Loop-Gap resonator. A. Assembled view; B. Exploded view without support structure. Nonconductive elements are cut by vertical plane for better visualization. C. Equivalent electrical scheme of resonator with tune and match elements. AGR elements: L_AGR/2 is the inductance of an I-section, 4C_AGR is the capacitance formed between end rings and I-section wings; C' is the added capacitance between I-section wings and R_AGR – is the resistance of 4 damping resistors installed between I-section wings. The effective resonating capacitance of AGR is C_AGR+C'. This does not include capacitances of the tuning and matching elements. SLSG LGR: L_LGR is the inductance of the loop, C_LGR is the resonating capacitance and R_LGR is resistance of the damping resistor. C_T and C_M are the tuning and matching capacitors, respectively. Elements located on the tune and match boards are surrounded by dashed line rectangles.

The conductive surfaces of SLSG LGR were built using the type 1245 copper tape (35.6 microns thick, 3M, MN) with pressure-sensitive conductive adhesive on one side. At 250 MHz, the 35.6 microns constitute about nine copper skin depths. The resonator was built on a hollow cylinder support with 21 mm OD and 19 mm ID, 15 mm in length machined from polycarbonate plastic solid rod. For the proper penetration of the RF field of the outer resonator to the inner volume, 3/7 of the loop surface has been removed by cuts made in the plane orthogonal to the resonator's axis (Figure 1A). These cuts did not affect resonator performance and marginally increased its inductance by ~5 %. This efficiently created four 2.25 mm wide loops separated by 2 mm. To ensure field homogeneity in the gap area, the ends of the LGR loop were separated only by a narrow 0.25 mm gap. This gap had a negligible capacitance and an external capacitor was used to resonate the structure (not shown in the Figure 1A). It was found that mounting of any components in close proximity to the loop reduced the local B₁ homogeneity. On the other hand distant location of the resonant capacitor reduced the Q. We experimentally arrived to the optimum distance of ~20 mm above the SLSG LGR surface. The electric scheme of the SLSG LGR is given in Figure 1C. The design of slotted SLSG LGR resembles that of the parallel loop resonator (PLR) [15]: however it has very different performance characteristics. The PLR consists of multiple parallel wire loops, inductance of which increases the overall resonator inductance more than twice in comparison to the slotted LGR. The inductance of a 25.4 mm diameter and 25.4 mm long PLR given in [15] is 49 nH while the slotted SLSG LGR of identical dimensions with 5 slots of 2mm in width, fabricated and tested by us, has an inductance of only 25 nH. As it was mentioned in introduction, low inductance is one of the design criteria that reduces the effect of stray capacitance and enhances the overall resonator stability.

The LGR was connected to the tune and match circuit board made of G-10-FR4 copper clad. This board located inside the RF shield was elevated above the resonator surface by ~20 mm, mounted on top of the resonator support and connected using twisted wires shown in the Figure 1A. The matching circuit had a standard design including a matching and a fine frequency tuning capacitor, which was chosen to have a small fraction of resonating capacitor, sufficient to adjust frequency in desired range of about 15 MHz centered around 250 MHz. The resonator and the circuit board were interconnected by a PTFE 24 AWG twisted pair transmission line (3 full twists over 20 mm length). The tune and match circuit board is coupled to the RF line by a balun (TP101-PIN, M/A-COM Technology Solutions Inc., MA) located on the outer side of RF shield.

The SLSG LGR detects magnetic field oriented parallel to the resonator axis (blue arrow in Figure 1A). Different resonators capable of creating magnetic field orthogonal to this direction were applied previously. Saddle coils are commonly used in MRI [16]. For EPR Hyde and coworkers suggested use of an additional LGR in “coaxial juxtaposition” [17]. Two resonant modes produced in this case were mutually orthogonal and provided more than 35 dB of isolation at 4 GHz. The designs of Rinard and coworkers used additional LGR intersecting at right angle [14] and Helmholtz pair [11]. Our design employs an Alderman-Grant resonator (AGR).

The AGR was introduced in NMR to solve the problem of sample heating due to the electric field losses [18, 19]. This became possible due to negligible electric fields in the active volume of resonator. Later it was found that the same design is an excellent match for MRI of large objects and significant efforts were spent on AGR design elucidation [20–22]. AGR was also applied for proton-electron double resonance imaging as an EPR coil [23]. Three factors make AGR an excellent choice for an excitation coil. First of all AGR has a cylindrical shape with magnetic field orthogonal to the cylinder axis (pink arrow in Figure 1A). The magnetic field of the resonator is confined to the space occupied by inner resonator. Finally, most of the resonator electric fields is confined to the end ring capacitors and do not extend to a sample. Additionally, very low inductance of the resonator elements results in lower working voltages and easy scaling of AGR both to larger volumes and higher frequencies. The Λnorm of the critically coupled AGRs of different dimensions tested in our laboratory at 250 MHz was about 0.19 Gcm^3/2/√W. This is twice better than that of Helmholtz pair resonators that can accommodate the receiver of the same size and is approaching the efficiency of LGR (0.24 Gcm^3/2/√W).

The AGR was built using type 1245 copper tape (3M, St. Paul, MN) on a hollow cylindrical support consisting of 3 parts, inner cylinder and two outer I-shaped clamps. The cylindrical part has 25.4 mm OD and 23 mm ID; 40 mm in length. The ring conductors are pasted onto the outer surface of the cylinder. The I-shaped conducting sections were pasted onto inner surface of the I-shaped clamps. The end-ring supported cylinder was machined to precision to allow 76 microns (0.003 inch) thick Teflon (PTFE) sheet in between of end rings and I-shaped clamps. This formed the main resonant capacitor. The end-ring and I-sections sandwich was held together by eight screws (not shown in the Figure). The areas of the support not covered by conducting surfaces were machined out for easier access to the inner volume.

The electrical equivalent circuit of the bimodal resonator is shown in Fig. 1C. The end rings form the major resonant capacitance with very small inductive contribution and most of the AGR resonator inductance, L_AGR, is due to the central part of I-sections. The design parameters of AGR were calculated according to Refs [20, 21].

RF power is applied between end ring and one of the I-sections, the feeding coaxial RF cable is shown at the top of Figs. 1A and 1B. Even though electrical ground is connected only to one of the end rings, due to the resonator symmetry the other floating end ring is also at ground potential and thus the regions encompassed by the end rings are free from electric field. The unloaded quality factor of the resonator in the absence of damping resistors was ~100. Four resistors, R_AGR, are symmetrically placed across the I-sections to damp the resonator Q to the desired value. The assembled resonator showed two resonant modes: main at 250 MHz and another one associated with end rings at 316 MHz.

Both AGR and SLSG LGR are mutually interchangeable in a sense that any of them can serve as a detection or excitation resonator and assume inner or outer position. If the AGR has to be used as an inner resonator, its I-sections need to be slotted for B₁ penetration. In the presented design we maximized the detected signal and installed the resonator with the higher efficiency, SLSG LGR, as the detection resonator. Since smaller volume resonators have higher efficiency (Eq. 1), the SLSG LGR that has a better Λ was installed in the inner position, as a receiving resonator.

3. Materials and Methods

Spin probe

The spin probe used for the EPR imaging was the trityl OX063 radical methyl-tris[8-carboxy-2,2,6,6-tetrakis[2-hydroxyethyl]benzo[1,2-d:4,5-d']bis[1,3]dithiol-4-yl]-trisodium salt, molecular weight = 1,427 from GE Healthcare (Little Chalfont, Buckinghamshire, UK) and partially deuterated OX063 radical synthesized in the Center for EPR Imaging In Vivo Physiology.

Imager

A versatile pulse 250 MHz imager was used to produce the images [12].

Rabi nutation imaging for B₁ characterization

For B₁ mapping, a trityl phantom with deoxygenated 2 mM deuterated OX063 was installed in the resonator. The phantom had 19 mm diameter, 8 cm length and filled with trityl solution without head space. The two pulse imaging echo sequence used was: t_α – τ – τ_π – τ – echo; with t_α a pulse with variable flip angle. The duration of the π-pulse, t_π, was determined prior to imaging. 6 dB smaller RF power was applied for a t_α pulse; with t_α flip angle close to π/2. The delay between pulses, τ was measured between the mid-times of RF pulses. A number of images with different t_α was taken. The imaging methodology is similar to the one used for relaxation mapping [12]. The image voxel intensity is proportional to sin(α), where α is the flipping angle of t_α pulse [24] at this voxel position. The B₁ image was obtained by fitting voxel amplitude dependence on t_α with sin(γB₁t_α) function, where γ is the gyromagnetic ratio of the electron, 1.7608×10¹¹ r/s⁻¹T⁻¹.

Phantom imaging

Phantom containing 0.1 mM solution of OX063 in saline was fabricated from Wheaton vial, flat-bottomed borosilicate glass cylinders with 9.5 mm inner diameter and 45 mm length. The vial was flame sealed upon deoxygenation. 10 minutes long image acquisition included 208 projections and 53 baselines with 1.5 G/cm gradient modulus.

Animal imaging

A female C3H type mouse (Harlan Sprague Dawley Inc., Indianapolis, IN) with human mammary tumor cells, MCA4 F6m (M. D. Anderson Hospital, Houston, TX), implanted and grown subcutaneously in the mid-distal hind leg was used. To prevent motion during imaging, the animal was immobilized using a soft elastic vinyl polysiloxane dental mold material (GC America Inc., Alsip, IL) and anesthetized with 1–2% isoflurane. Respiration frequency and depth during imaging were monitored continuously. A 24 gauge angiocatheter was used to cannulate the mouse tail vein for i.v. injection of the 80 mM solution of partially deuterated OX063. A digital needle probe thermometer (Physitemp, Clifton, NJ) monitored skin temperature, which was maintained at ~37° C using adjustable opposed heating lamps. Animal experiments were performed according to the US Public Health Service “Policy on Humane Care and Use of Laboratory Animals” and the protocols were approved by the University of Chicago Institutional Animal Care and Use Committee (ACUP No. 71697). The University of Chicago Animal Resources Center is an AAALAC approved animal care facility. 10 minutes long image acquisition included 208 projections and 53 baselines with 0.75 G/cm gradient modulus. Oxygen concentration was obtained using R1 imaging protocol [25].

4. Results

The parameters of AG/LGR are summarized in Table 1. The AG/LGR fabricated in our laboratory showed 40 dB of isolation as determined from the network analyzer trace S21 parameter (Figure 2A). A 38.5 dB dynamic isolation was observed during application of broadband 55 ns 500 W 250 MHz pulses. The isolation was measured as a ratio of maximum power applied to AGR and maximum power received from SLSG LGR. Figures 2B and 2C present the distribution of B₁ in AG/LGR obtained using Rabi nutation [24] imaging. An interesting feature of AGR is high homogeneity of B₁ in the vertical (YX) plane. In the horizontal plane (YZ) the distribution is similar to the one found in loop-gap resonators. The larger dimensions of excitation resonator result in better field uniformity in axial (Y) direction in comparison to stand-alone LGR. One can expect that insertion of detection resonator into AGR may reduce AGR efficiency. The electrical surfaces of the inner resonator shield the magnetic field and slightly affect B₁ homogeneity. Figure 2C shows that insertion of SLSG LGR inside AG is indeed attenuated B₁ by up to 20 %, but did not affect B₁ homogeneity significantly. This is due to the multiple cuts made in the conducting surface of SLSG LGR. The efficiency of SLSG LGR also reduced upon insertion in to the excitation resonator by 12 % since AGR also acts as a shield located in the close proximity to the resonator.

TABLE 1.

Dimensions and electrical parameters of resonators

	SLSG LGR	AGR
Inner diameter	19 mm	23 mm
Outer diameter	21 mm	25.4 mm
Length	15 mm	22 mm active region 40 mm with end rings
I-shaped conductor central part	-	12 mm
Fraction of volume occupied by sample*	0.82	0.46
L	21 nH**	19 nH***
C	10pF	4C = 87.63pF***
C'	N/A	3 pF
R	2.9 kΩ	1 kΩ
λ	0.3G/√W (Q=36)****	0.12G/√W (Q=11)*

^*fraction is calculated as a ratio of the sample volume of AG/LGR to the volume with strong B₁ in a resonator;

^**measured parameter;

^***calculated parameter;

^****measured in assembled AG/LGR, while AGR was terminated by 50 Ω load

FIGURE 2.

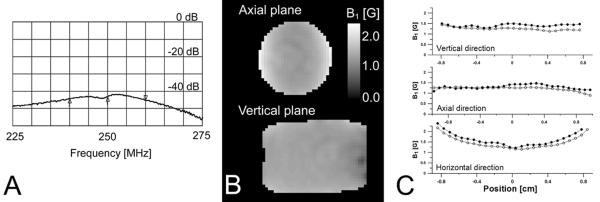
Parameters of AG/LGR. A. Isolation. Markers show 20 MHz frequency range and the center frequency. B. B₁ maps of AG/LGR as measured by Rabi nutation imaging. C. B₁ along three directions passing the geometric center of a resonator. Solid circles mark B₁ of the standalone AGR, while open circles mark AG/LGR.

Below we compare performance of AG/LGR with the standard (not slotted) reflection mode LGR (STLGR) used in our laboratory for pulse EPR imaging. The design of this resonator is identical to the design of the SLSG LGR with the exception of slotting, which is absent in STLGR. For comparison we adjusted resonator bandwidths to be equal. The sample volume of the AG/LGR and STLGR compared in this study is a cylinder of 19 mm diameter and 15 mm length. Although the AG/LGR showed much better performance in the fringe fields along axial direction and the length of active volume is de facto 20% longer, we will ignore this difference.

Imaging applications require similar excitation and detection bandwidths to accommodate the bandwidth of the signal from the object, which is a function of object extent and the gradient strength. The method for measurement of the imaging bandwidth was suggested in [12]. The bandwidth is measured by tracking EPR signal amplitude as a function of frequency offset from the resonance. Frequency of the signal is altered by magnetic field offset. Bandwidth is defined as a full width at half signal power. For comparison of the resonators we equalized this imaging bandwidth to 5.3 MHz rather than equalizing the resonator's Q. For the AG/LGR the Q of excitation resonator was set to 11, while detection Q was adjusted to 36. The Q of STLGR was set to 17.

Setting different Q values for detection and excitation resonators in a bimodal resonator improves the overall resonator performance. Signal amplitude is proportional to √Q, however higher Q reduces the imaging bandwidth. There are two components in this reduction. The first component is due to the reduction of the detected signal amplitude at particular frequency offset due to the limited resonator bandwidth. The second component is reduction of generated EPR signal due to lowered turning angle from RF pulses. The intensity of electron spin echo used in our imaging sequences is proportional to sin(α)sin(β/2)², where α and β are the turning angles of the first and the second RF pulses [24]. In a resonator these angles will be frequency dependent, lower at larger offsets from the resonance frequency, higher around resonance frequency. In the AG/LGR, choosing lower Q for the excitation resonator minimizes the second signal reduction component. This, in turn, allows increasing Q of the detection resonator and thus EPR signal, while preserving the overall imaging bandwidth. In the case of the AG/LGR, the Q of the SLSG LGR was increased from 17 to 36, providing a nearly 46% increase in signal.

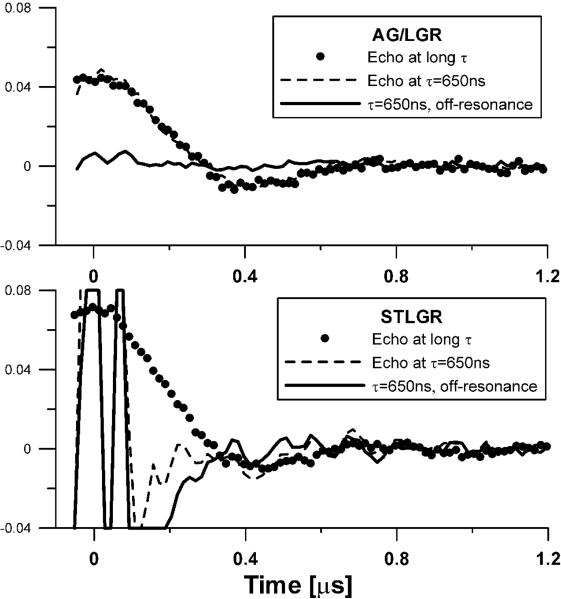
The choice of a phantom affects the dead time definition. Resonators with larger baseline instability show better performance with stronger signals. We chose a phantom with intensity of approximately half of that observed in an animal during imaging. Figure 3 shows on-resonance traces and the baselines obtained on 0.1 mM OX063d24 phantom under 1.4 G/cm static gradient, a condition similar to the one met during imaging. Zero time corresponds to the maximum of the echo. The AG/LGR shows very minor baseline, while baseline in STLGR exceeds the EPR signal by an order of magnitude (clipped at times below 0.2 μs). The “echo at long τ” trace represents an undistorted shape of the signal. It is obtained at with τ, large enough that the echo shape is not affected by the dead time. The dead times of both resonators were ~550 ns. For STLGR the signal from 0 to 0.2 μs can be recovered by baseline subtraction. The dead times of AG/LGR and STLGR are the same because AG/LGR has a detection resonator with twice higher Q. For the applications that require shorter dead times the choice of lower detection Q for AG/LGR may be more optimal.

FIGURE 3.

Two pulse spin echo (t_π/2–τ–t_π–τ– echo) traces of partially deuterated 0.1mM OX063 trityl phantom in: Top - AG/LGR; and Bottom - 19 mm id STLGR. 650 ns delay between pulses, τ, was used. Zero time corresponds to the echo maximum. 1.4 G/cm gradient was applied. The trace obtained at τ = 650 ns and the off-resonance field contains only instrument related baseline. The `Echo at long τ' trace was obtained with τ, large enough that the echo shape is not affected by the dead time. This trace is then scaled to match the amplitude of the trace with τ=650 ns.

Figure 4 shows slices of the T₁ images obtained from 0.1 mM trityl phantom using AG/LGR and STLGR and T₁ distributions. The relaxation measurements are used for in vivo oxymetry and their precision is of high importance. One of the ways to characterize this precision is by calculation of standard deviation for all voxels in the homogeneous phantom. Larger standard deviation means lower precision and vice versa. Table 2 compares standard deviations obtained from images acquired using AG/LGR and STLGR. One can see that correction of the baseline is crucial for image reconstruction from the data obtained using STLGR. In contrast, for AGR this procedure is not necessary and deteriorates the imaging precision. One can see that for identical protocol STLGR shows somewhat better performance. This is expected as the efficiency and hence SNR of standalone resonator is slightly higher. However, the elimination of baseline correction allows increasing SNR by approximately √2 which results in much better imaging accuracy using AG/LGR.

FIGURE 4.

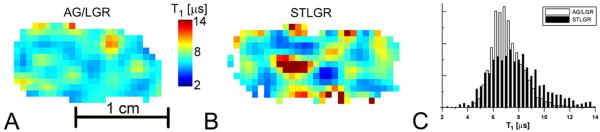
A and B: slices of T₁ images of 0.1mM OX063 trityl phantom obtained using AG/LGR and STLGR. STLGR image is reconstructed with baseline correction. C. T₁ frequency histogram of all voxels in the images. AG/LGR image is reconstructed without baseline correction.

TABLE 2.

The T₁ standard deviation in the image of deoxygenated 0.1 mM homogeneous phantom obtained with and without baseline correction.

	With correction [μs]	Without correction [μs]
STLGR	2.16	N/A*
AG/LGR	2.6	1.3

^*not measured due to severe image artifacts

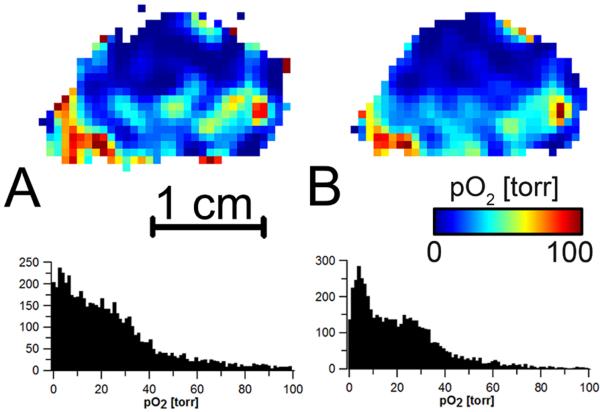
The AG/LGR demontrated high stability and good performance with a live animal. Interstingly, the insertion of a mouse into relatively high Q resonator did not affect the resonator tuning and isolation. Figure 5 demonstrates a mouse oxygen image slices obtained using AG/LGR. The histograms of all voxels in the three dimensional image are given on the right side of each image. The same data are reconstructed with and without baseline correction. Similar to the phantom study the baseline correction for the AG/LGR is not only unnessesary but deteriorates the image. This can be seen from the broadenning of image histograms and additional noise. It should be noticed that elimination of baseline acquisition from the imaging protocol decreases the imaging time by 25%.

FIGURE 5.

A selected slice from three dimensional oxygen images in a mouse leg bearing tumor obtained using AG/LGR. Images are reconstructed from the same dataset A. with baseline correction; and B without baseline correction. The histograms below each slice show the distribution of oxygen in the volume of the images.

5. Discussion

The data presented here demonstrate high performance characteristics of the AG/LGR. The resonator shows better performance in comparison with reflection type STLGR. Although the efficiency of detection resonator is still ~20% lower than that of STLGR other advantages more than compensate.

A number of approaches for further improvement of STLGR performance can be considered. Using two independent resonators for excitation and detection allows adjusting their parameters independently. As it was shown above, different Q for excitation and detection resonators enhanced image SNR. Different matching of the resonators should be considered. In our imagers we coupled resonators critically. In our experience, the signal artifacts due to the standing waves produced by an over-coupled resonator, overwhelm the signal enhancement achieved in this mode. For a bimodal resonator, the excitation resonator can be kept critically coupled, while the detection resonator can be over-coupled. This coupling scheme ensures best delivery of the RF power to resonator and detection of the highest possible signal. Additionally, independent resonators for excitation and detection allow use of Q spoiling for dead time reduction as described by Rinard and cowokers [14].

6. Conclusion

The AG/LGR resonator appears to be an excellent choice for in vivo pulse EPR imaging applications. It demonstrates all the advantages of bimodal resonators, such as isolation of receiver from high power, reduced dead time and excellent baseline stability. Application of the AGR for excitation resulted in lower power requirements in comparison with other bimodal resonators. Additionally, the AG/LGR has lower electric field losses, which reduces sample heating and makes acquisition less dependent on sample motion. The use of an LGR on the detection side ensures high SNR. The AG/LGR assembly is very compact, relatively easy to build and can be used virtually in any imager. Finally, the low inductances of the excitation and detection resonators allow scaling of an AG/LGR to larger volumes and higher frequencies.

Highlights

• Novel design of a bimodal resonator for 250 MHz in vivo imaging

• This design improves signal to noise ratio per unit of time of in vivo images

• Alderman-Grant resonator is an optimal choice for excitation coil in bimodal resonator design

• Alderman-Grant resonator generates very low E-field in a sample which is important for in vivo imaging