High-throughput particle separation and concentration using spiral inertial filtration

Abstract

A spiral inertial filtration (SIFT) device that is capable of high-throughput (1 ml/min), high-purity particle separation while concentrating recovered target particles by more than an order of magnitude is reported. This device is able to remove large fractions of sample fluid from a microchannel without disruption of concentrated particle streams by taking advantage of particle focusing in inertial spiral microfluidics, which is achieved by balancing inertial lift forces and Dean drag forces. To enable the calculation of channel geometries in the SIFT microsystem for specific concentration factors, an equivalent circuit model was developed and experimentally validated. Large particle concentration factors were then achieved by maintaining either the average fluid velocity or the Dean number throughout the entire length of the channel during the incremental removal of sample fluid. The SIFT device was able to separate MCF7 cells spiked into whole blood from the non-target white blood cells (WBC) with a recovery of nearly 100% while removing 93% of the sample volume, which resulted in a concentration enhancement of the MCF7 cancer cells by a factor of 14.

INTRODUCTION

High throughput particle separation and concentration are critical for applications in the chemical, environmental, and biomedical fields. In particular, a number of cellular and sub-cellular purification and enrichment applications are used to enable the quantitative study and diagnosis of disease. Commercial products are available for cell separation, whole blood fractionation, and subcellular fractionation using density gradients. However, these techniques have poor separation resolution and are inappropriate for recovering rare cells. Commercially available fluorescence-activated cell sorting (FACS) systems enable automated cell separation and counting, but cannot process large sample volumes and are also inappropriate for recovering rare cells.

Many microfluidic techniques have emerged for sorting, concentrating, or purifying particles and cells.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10} Recent research into microfluidic devices has enabled applications that include microorganism recovery from environmental and biological samples,¹¹ white blood cell (WBC) counting for immune deficiency diagnosis,¹² and circulating tumor cell (CTC) counting for cancer metastasis diagnosis and prognosis.^{13, 14} Most of these techniques, with rare exception, operate in the range of 1–100 μl/min, but a significantly higher throughput is needed for applications that require processing large volumes of fluid to obtain usable quantities of a target species, such as rare cell concentration. Methods designed for rare cell recovery must therefore be capable of significantly reducing the total fluid volume, from ml to 100 μl or less, to enable downstream microfluidic steps while preserving the rare targeted particles.

Recently, the need for high-throughput separation has been addressed by inertial-migration-based particle separation strategies, which are capable of achieving greater than 1 ml/min throughput.¹⁵ When inertial migration of particles occurs, an inertial lift force acts to drive the particles to discrete equilibrium positions along the channel periphery.^{16, 17} This was first shown by Segre and Silberberg¹⁸ at the centimeter-scale and later by others for microscale applications.^{11, 19, 20, 21, 22, 23, 24, 25, 26, 27} The inertial lift force, F_L, is the net force of a shear-induced inertial lift force that arises due to the parabolic flow profile and acts towards the microchannel wall and a wall induced inertial lift force that acts towards the microchannel center. The net lift force can be expressed as^{28, 29}

$$F_L=\frac{4\rho {U_f}^2{a_p}^2{C}_L}{D_h},$$ (1)

where ρ is the density of the fluid, U_f is the average fluid velocity, a_P is the particle diameter, C_L is the non-dimensional lift coefficient that is a function of position in the channel and the channel Reynolds number, Re_c. The hydraulic diameter, D_h, is determined from

$$D_h=\frac{2wh}{w+h},$$ (2)

where w and h are the channel width and height, respectively. The channel Reynolds number, Re_c, is expressed as

$${\text{Re}}_{\mathrm{c}}=\frac{\rho U_f{D}_h}{\mu },$$ (3)

where μ is the fluid dynamic viscosity.

The use of curvilinear geometries such as arc,^{30, 31, 32, 33, 34, 35} asymmetric serpentine,^{36, 37, 38} and spiral^{29, 39, 40, 41, 42, 43, 44, 45, 46, 47} channels introduces a third force, the Dean force, F_D, due to the formation of secondary flows, known as Dean vortices. The strength of these secondary flows is described by the dimensionless Dean number (De)^{48, 49}

$$De=\frac{\rho U_f{D}_h}{\mu }\sqrt{\frac{D_h}{2R}},$$ (4)

where R is the radius of curvature of the curvilinear channel. The Dean vortices are counter-rotating and act to laterally displace particles across the channel by imposing a drag force. The magnitude of the Dean force, F_D, is approximated by assuming a stokes drag force²⁹

$$F_D=3\pi \mu a_P{U}_D,$$ (5)

where U_D is the average Dean velocity and scales as U_D = 1.8 × 10⁻⁴De^1.63.⁵⁰

The Dean force acts in combination with the net lift forces to alter the equilibrium positions of focused particles to two vertically aligned positions located at the same distance from inner wall of the channel (Figure 1a).⁴⁵ The lift force goes as F_L∝a_p⁴ and the Dean force goes as F_D∝a_p, where a_p is the particle diameter.²⁹ The equilibrium position is thus particle-size-dependent. It is worth noting that for neutrally buoyant particles centrifugal forces are negligible compared to F_L and F_D and are thus ignored.⁵¹

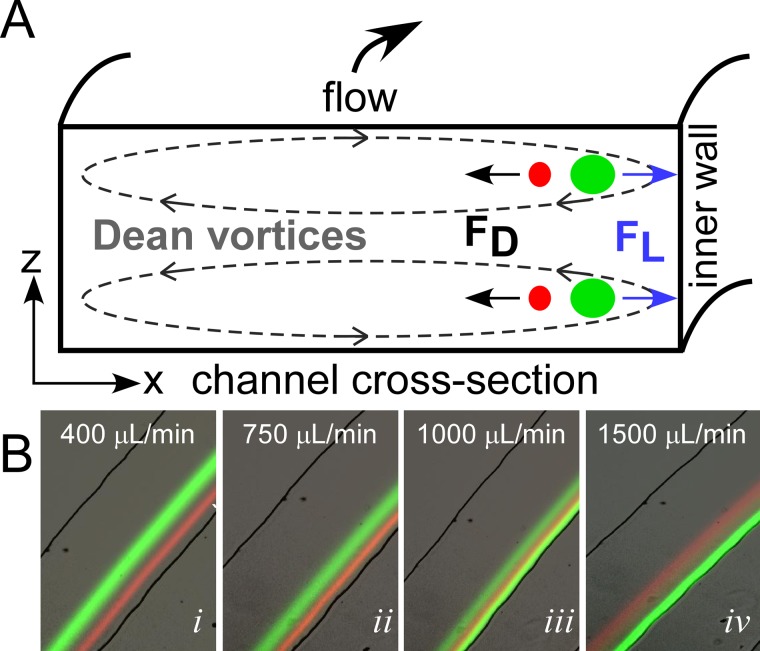
Figure 1.

(A) Schematic of a microfluidic channel cross-section, illustrating the principle of inertial spiral microfluidics. The main flow (into the page) follows a curvilinear path leading to the development of secondary flows, known as Dean vortices (dashed lines). Dispersed particles experience a combination of lift forces (F_L) and Dean forces (F_D), which result in differential migration of the particles to unique equilibrium positions near the inner wall. (B) Illustration of the transition from switched focusing mode to traditional focusing mode with increasing flow rate for two particles, 15 μm (green) and 8 μm (red).

Traditionally, spiral inertial microfluidics are operated such that the larger particles focus near the inner wall with the smaller particles focusing near the channel center (traditional focusing mode). Xiang et al.⁵² recently illustrated that the focusing position of different sized particles could be controlled by changing the flow rate. They developed a five-stage process model to describe the transition between these modes.⁵² At lower flow rates, the lift force, F_L, dominates and particles gradually migrate to equilibrium positions near the inner wall. With increasing flow rate, the particles under the dominant F_L migrate further inward towards the inner wall. Increasing the flow rate further leads to a transition from F_L dominated to F_D and the particles begin migrating away from the inner wall. At much higher flow rates, the particle streams defocus due to the Dean mixing effect.⁴⁸ Since the focusing position of the different sized particles has different dependencies on flow rate (due to the differences in the forces, F_L and F_D, acting on the particles), conditions can be found for focusing in either the traditional mode or in a switched focusing mode where the larger particles instead focus near the channel center and the smaller particles aligned near the inner wall. Figure 1b illustrates this transition between switch focusing mode (Figure 1) at low flow rates and traditional focusing (Figure 1) at higher flow rates.

Spiral inertial microfluidic devices have been successfully used in a wide range of applications including particle^{29, 40, 42, 45} and cell^{40, 53, 54} separations, cell synchronization,⁴¹ circulating tumor cell isolation,^{55, 56} and electroporation.⁴⁶ These devices typically utilize a branched outlet to collect the concentrated, focused particle, or cell streams. Ultimately, for any geometry, the concentration factor is limited by the width of the branched outlet channel through which a separated and purified particle stream is collected. The concentration factor is defined as the concentration of particles collected at each outlet over the inlet particle concentration. Devices with branched outlets of up to eight channels have been shown,⁴⁰ yielding a theoretical maximum concentration factor of 8× (i.e., 87.5% removal of the inlet fluid). However, using only branched outlets, further increases to greater than 10× (90% fluid removal) are challenging.

For example, 93% removal corresponds to a 14× concentration factor, which would require collecting all particles in the particle stream into an outlet 1/14 the width of the main channel. For a 250 μm main channel, the width of the branched outlet would be ∼18 μm. In practice, focused particle streams have a width greater than the diameter of the particles. The particles are assumed to be focused when the full-width of the particle stream at half max is two times the particle width.⁴² If we aim to recover 95% of the particles, then (assuming the particle stream has a normal distribution) the width of the particle stream is 3.4 times the diameter of the particle. For a 15 μm particle, this corresponds to ∼50 μm, which is too wide to be collected in a single outlet channel, leading to particle loss and a decrease in particle recovery. Of course, the width of the main channel could be expanded (which is commonly done) to increase the widths of the outlets. However, the expansion is accompanied by a corresponding increase in the width of the fluid streamlines, and thus the width of the particle stream.

To increase the concentration factor of spiral inertial microfluidics while relaxing the requirements for narrow outlets or precisely controlled outlet resistances, we developed a new approach known as Spiral Inertial FilTration (SIFT). This technique utilizes the focusing behavior of inertial microfluidics in a spiral geometry to create a large particle-free region from which a large fraction of fluid can be “skimmed” through waste channels. Traditional skimming techniques rely on the natural formation of small particle-free regions near channel walls^{57, 58, 59, 60, 61} (Figure 2a) or geometrical features⁶² (Figure 2b). The major drawback of this strategy is that the performance drops at increased flow rates. In SIFT, particles are instead focused near the inner wall, creating a large particle-free region at the outer wall (Figure 2c); this particle-free region exists for both the typical operation and the switched mode. By utilizing side channels that extend away from the outer wall, fluid can be removed from this particle-free region, thus increasing the concentration of the particles in the microfluidic channel. In addition, due to the focusing nature of spiral inertial microfluidics, the particle streams are minimally disrupted by removing large amounts of fluid. Leveraging this concept, the SIFT system utilizes waste channels extending from the outer edge of the outer-most ring of the spiral to generate a large concentration factor, as shown in Figure 3.

Figure 2.

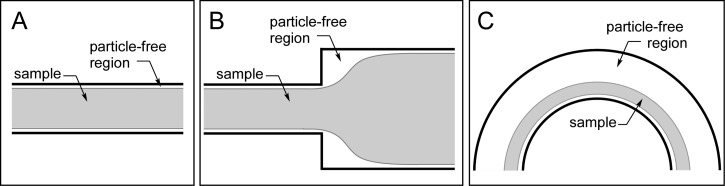
Schematics illustrating the creation of particle-free regions in (A) straight channels, (B) expansions, and (C) curvilinear channels.

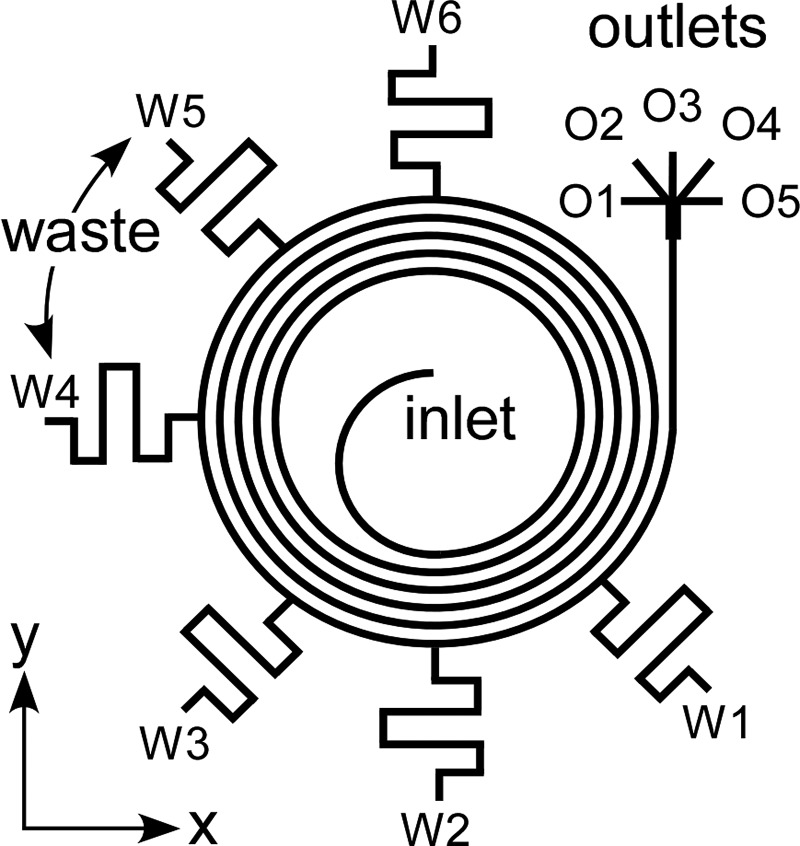
Figure 3.

Schematic of the SIFT device. Fluid is removed from six waste channels labeled W1–W6 starting closest to the outlet. Concentrated particle streams are collected through one of five outlets (labeled O1–O5).

Increasing particle concentration and purity by removing fluid through microfluidic waste channels has been previously reported for similar designs. In one approach, posts^{63, 64} or dams⁶⁵ located at the outer wall were used to filter particles. Fluid and smaller particles were able to pass through the post or dam filters and were removed, while larger particles were retained. Unlike in SIFT, these devices were operated at low flow rates (<100 μl/min) in order to minimize the inertial effects and the secondary Dean flows. As a result, centrifugal forces dominated and pushed particles to the outside wall of the curvilinear channels. Another design took advantage of centrifugal forces to push blood cells against the outer wall and remove plasma from a waste channel on the inner wall.³⁰ Flow rates up to 120 μl/min were achieved. In a third approach, inertial lift forces focused targeted cells away from the walls, creating a target-free region where waste channels removed fluid and non-targeted cells;^{66, 67} this design achieved >500 μl/min. These devices focused on enriching targeted cells relative to high-concentration, non-targeted species, and were not aiming to achieve high concentration factors.

In this work, we demonstrate that the SIFT design concept presented in Figure 3 is capable of recovering a targeted cell (or particle) with nearly 100% recovery and concentrating the targeted species by more than an order of magnitude while operating at a sample processing rate of ∼1 ml/min. We start by developing the equations needed to design a SIFT device for specific fluid removal. We then validate the design equations by demonstrating removal of a desired fraction of the sample fluid (without removing targeted particles) by controlling the channel geometries. The experimental results demonstrate that the amount of fluid removed from the sample is limited by changes in particle position and particle stream width caused by decreases in the linear velocity in the channel, U_f, and the Dean number, De, as fluid is removed. To overcome the limitation on larger fluid removal rates, we demonstrate a method to correct the channel geometry to maintain U_f or De following fluid removal.

Finally, separation and recovery of MCF7 cancer cells spiked into blood is demonstrated using a SIFT device with 6 waste channels and 5 outlets (Figure 3). Using this design, we demonstrate nearly 100% recovery of the cells while removing 93% of the inlet fluid, which leads to a 14× concentration increase.

MATERIALS AND METHODS

Device fabrication

To evaluate the design methodology, a series of SIFT microfluidic devices with a single waste channel (at the W2 position in Figure 3) were fabricated. These devices consisted of a 7-loop Archimedean spiral (inner radius of 0.5 cm) with a single inlet, a waste channel, and a bifurcating outlet. The spiral channel was 250 μm × 50 μm (w × h) and had a 250 μm gap between successive loops. The number of loops was chosen so that the channel length was sufficient to ensure that the particles would be completely focused¹⁵ prior to fluid removal from the waste channel. The widths of the waste channels were set between 40 and 250 μm to remove a certain fraction of fluid: 5%, 10%, 20%, or 50%. As discussed below (Sec. 3E), the flow removed by a waste channel depends on its fluidic resistance, which is proportional to the channel length divided by its width. The soft lithography technique that we used achieved widths within 2–5 μm of the designed widths; therefore, to distinguish devices designed to remove different amounts of fluid, the waste channel widths needed to differ by more than 5 μm. Ensuring this tolerance necessitated a channel length of 19 mm, which was fit compactly next to the spiral using a meander path.

Subsequently, to demonstrate a concentration increase of greater than an order of magnitude for separated and recovered particles, a device with a series of 6 waste channels was fabricated. This device was similar to the single waste channel devices except that it consisted of a 6-loop Archimedean spiral, six waste channels, and five branched outlets (Figure 3). Each of the waste channels was 35 μm wide, 50 μm high, and 19 mm long.

The devices were fabricated using standard soft lithography. A 10:1 mixture of polydimethylsiloxane (PDMS) prepolymer and curing agent (Sylgard 184, Dow Corning) was cast over a silicon master mold and cured at 50 °C for 2 h. The master mold was formed by spin coating photoresist (Shipley 1813) onto a silicon wafer to a thickness of 3 μm, pre-baking for 1 min at 95 °C, and exposing to 365 nm UV for 13 s. The photoresist was developed for 75 s in Microposit developer CD-30 (Shipley). The wafer was then etched at a rate of ∼2 μm/min with deep reactive ion etching (DRIE) using the photoresist as the mask. The resist was stripped using Remover PG (MicroChem Corp.). To aid in the release of the cured PDMS, the silicon mold was silanized with trichloro(1H, 1H, 2H, 2H-perfluorooctyl)silane (Sigma Aldrich) using vapor deposition. Inlets and outlets were punched into the PDMS substrate, and it was sonicated in isopropanol for 90 min to remove PDMS debris and dust. The PDMS substrate was placed on an 85 °C hotplate for 2 h to remove the isopropanol and was then irreversibly bonded to glass using O₂ plasma (13 s at 0.75 Torr and 50 mW). Tygon tubing (0.02 in. I.D., 0.06 in. O.D.) was inserted into the inlet and outlets of the bonded devices.

Fluid removal quantification

To determine the amount of fluid removed by the waste channels, deionized (DI) H₂O was pumped into the devices at particular flow rates using a syringe pump (New Era Pump Systems, Inc.). To ensure that the flow rate had stabilized, each rate was held for 5 min. Fluid was then collected from the waste channels and the outlets for 5 min and the fluid was weighed to determine the volume collected. This was repeated three times for each flow rate for a single device. The fraction of fluid removed by a waste channel was calculated as the volume of fluid collected at a given waste channel over the total volume of fluid collected.

Particle focusing

Fluorescent polystyrene particles 15 μm in diameter (14% coefficient of variation (CV), density of 1.05 g/cm³) (ThermoFisher Scientific), and 8 μm (18% CV, density of 1.05 g/cm³) (ThermoFisher Scientific) dispersed in DI H₂O at a concentration of 0.003% by weight were injected into the SIFT devices using the syringe pump. Images of the focused particles were taken using an inverted fluorescence microscope (Olympus Corporation, model IX51) equipped with a 12-bit digital CCD camera (Hamamatsu Photonics, model ORCA-03G). Three-second exposures were used to create visible particle traces. A sequence of 15 images was overlaid to create a composite image. To visualize the channel walls, a bright field image was taken, the image was inverted (converted to a negative) using ImageJ (U.S. National Institutes of Health), and the image was overlaid onto the particle focusing composite to create the final image.

Cell separation and concentration

MCF7 cells were cultured in Dulbecco's modified eagle medium (DMEM) with 4 mM L-glutamine, 4.5 g/l glucose and reduced sodium pyruvate supplemented with 5 μl/ml penicillin/streptomycin, 1% non-essential amino-acids, and 10% fetal bovine serum (FBS) in tissue-culture-treated T25 flasks in a 37 °C incubator with 5% CO₂. Cells were subcultured every 5–7 days by trypsinization with 0.25%/0.02% trypsin/EDTA.

To allow for visualization of the cells during experiments, the live stain Calcein AM was used. MCF7 cells were collected and suspended in 1× phosphate-buffered saline (PBS) with 4 μM Calcein AM and incubated for 30 min. The cells were spun down at 150 × g for 2 min and washed with fresh PBS to remove free Calcein AM that had not been taken up by the cells.

Blood was collected into K₂ EDTA coated tubes from healthy volunteers in accordance with the Institutional Review Board at the University of Maryland, College Park and stored on ice. A sample of 4 ml of blood was mixed at a ratio of 1:4 with 1x RBC lysis buffer (eBioscience, Inc.) and incubated at room temperature for 5 min. This resulted in lysis of ∼60% of the RBCs. The mixture was then centrifuged at 150 × g for 5 min, the supernatant was removed, and the pelleted cells were suspended into 20 ml of 1× PBS. MCF7 cells were then added at a concentration of 3 × 10⁵ cells/ml. For experiments in which the WBCs were stained, LavaCell (Active Motif) was added to the blood sample according to the manufacturer's protocol prior to the addition of the MCF7 cells.

The sample was injected into the multi-waste-channel SIFT device (Figure 3) at a flow rate of 750 μl/min. The flow was allowed to equilibrate for 5 min. Fluid was collected from the waste channels and the outlets into vials for 5 min. MCF7 cells in each vial were counted using a hemocytometer (INCYTO). The separation was repeated three times.

RESULTS AND DISCUSSION

Spiral inertial filtration design principle

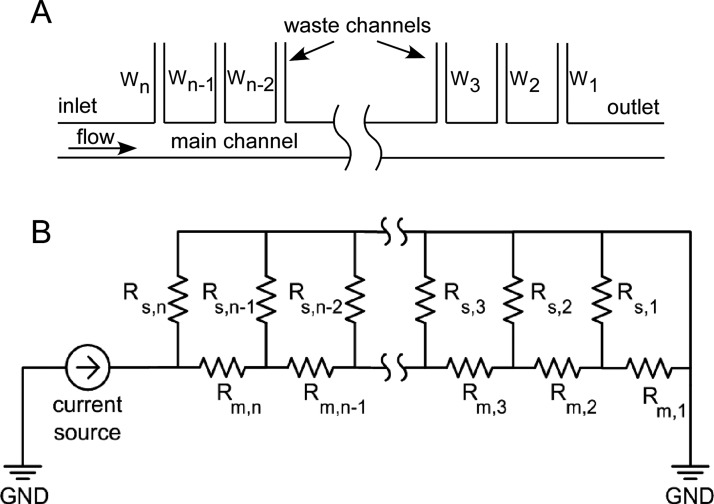
An equivalent circuit analog^{57, 68} (Figure 4) was used to design for the removal of specific volumes of fluid from the SIFT devices. The volumetric flow rate (Q) was determined using

$$\Delta P=Q{R}_H,$$ (6)

where ΔP is the pressure drop and R_H is the fluidic resistance. The flow removed by any given waste channel is specified by the ratio of fluidic resistances of the waste channel and the main channel. A schematic of the equivalent electrical circuit is shown in Figure 4. The flow rate at the inlet of the device is described as a current source, and all outlets are terminated at ground, as they have the same pressure. For a volumetric flow ratio, r_Q,j, of the main channel (Q_m,j) to a side waste channel at the jth node (Q_s,j), the resistance relationship between the main and waste channels satisfies

$$R_{s,j}=r_{Q,j}\left(R_{m,j}+\frac{R_{s,j-1}}{1+r_{Q,j-1}}\right),$$ (7)

where R_s,j and R_m,j are the resistances of the waste channel and main channel at the jth node, respectively, R_s,j−1 is the resistance of the waste channel at the previous node, and r_Q,j−1 is the volumetric flow ratio at the previous node. This holds for j = 2, 3, 4,…, n − 1, n. For j = 1, the resistance is simply R_s,1 = r_Q,1R_m,1. Equation 7 illustrates that once r_Q,j is specified, the resistance of the waste channel, R_s,j, at any node is determined only by the resistance in the main channel, R_m,j, the resistance of the previous waste channel, R_s,j−1, and the flow ratio of the previous waste channel, r_Q,j−1.

Figure 4.

The equivalent circuit analog used to design the SIFT devices: (A) schematic of the fluidic network and (B) the equivalent circuit. The subscripts “m” and “s” represent the main channels and side channels.

Once the resistances of the main channel and the waste channels are obtained, the channel dimensions can be calculated. For w > h or w ≈ h (see the supplementary material),⁶⁹ the hydraulic resistance of a square duct is given by⁷⁰

$$R_H=\frac{12\mu L}{w{h}^3}{\left(1-\frac{192h}{{\pi }^{5}w}{\displaystyle \sum _{n=1,3,5,\mathrm{...}}^{\infty }\frac{\tanh \left(\frac{n\pi w}{2h}\right)}{n^5}}\right)}^{-1},$$ (8)

where μ is the fluid dynamic viscosity, and w, h, and L are the width, height, and length of the channel. If w > h, Eq. 8 simplifies to⁷⁰

$$R_H\approx \frac{12\hspace{0.17em}\mu L}{w{h}^3(1-0.63\frac{h}{w})}.$$ (9)

Assuming constant L and h, Eq. 9 illustrates that the fluidic resistance of a waste channel can be controlled by changing its width. The width is given by

$$w\approx \frac{12\hspace{0.17em}\mu L}{h^3{R}_H}+0.63h.$$ (10)

Equation 10 is only valid for the case of w > h. However, when attempting to remove only a small fraction of fluid, a thin channel may be required, and thus the width may be less than the height. For this case, the full Eq. 8 should be solved to determine the width, which requires a numerical solver.

To design the system for a targeted performance, the waste channel width is set in order to remove a targeted fraction of the sample fluid. The fraction of fluid removed through a waste channel, x_s,j, is related to r_Q,j through

$$x_{s,j}=\frac{1}{1+r_{Q,j}},$$ (11)

where the fraction of the flow remaining in the main channel, x_m,j, is given by

$$x_{m,j}=\frac{r_{Q,j}}{1+r_{Q,j}}.$$ (12)

By simply specifying the ratio of volumetric flow between the main channel and a waste channel (r_Q,j), a spiral inertial filtration device can be designed for the removal of a specific fraction of the inlet fluid.

Validation of design equations

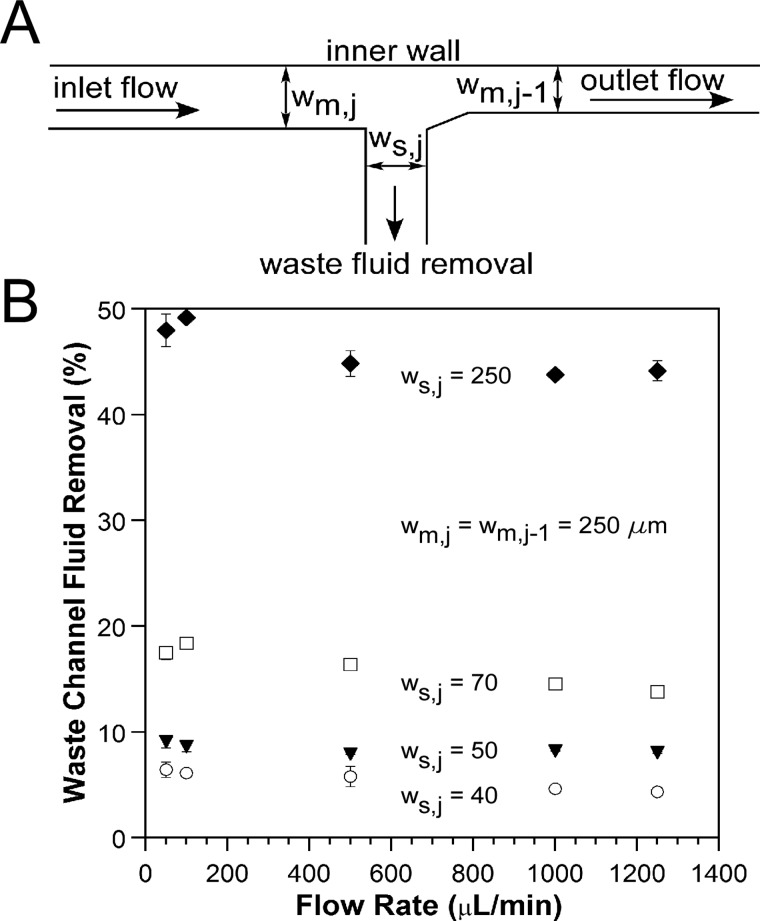
The fraction of fluid removed from a SIFT device can be controlled by designing for a specific flow ratio, r_Q,j, at each waste channel, which is achieved by properly balancing the fluidic resistances. To verify the design equations derived above, devices designed for removal of 5%, 10%, 20%, and 50% of the inlet fluid through a single waste channel were fabricated and tested. The waste channel was located at the W2 position (Figure 3). A schematic of the waste channel is shown in Figure 5a. As described above, the width of the waste channel, w_s,j, was set to control the amount of fluid removed from the main channel. The main channel width prior to the waste channel, w_m,j, and the main channel width after the waste channel, w_m,j−1, were both 250 μm.

Figure 5.

(A) Schematic illustrating the dimensions of a device with a single waste channel located at the W2 position (Figure 3). (B) Percentage of fluid actually removed from devices designed for the removal of 5% (○), 10% (▼), 20% (◻), and 50% (♦) of the inlet fluid. The widths in μm are listed for each of the devices. The widths of the main channel before the waste channel, w_m,j, and after the waste channel, w_m,j−1, are both 250 μm.

Figure 5b shows the percentage of fluid removed through the waste channel as a function of inlet volumetric flow rate (see supplementary material SM_Figure 1 for the same figure as a function of De and Re_c).⁶⁹ Error bars indicate the standard deviation across three experiments for a single device. To measure variation due to fabrication, two conditions were tested with duplicate devices: 20% fluid removal at 50 μl/min and 10% fluid removal at 1000 μl/min. The 20% results agreed to within 1.5%, and the 10% results were within 0.5%.

At low flow rates, the fraction of fluid removed matched closely with the designed fluid removal. For 50 μl/min (De = 0.39 and Re_c = 5.6), the fraction of fluid removed for the 5%, 10%, 20%, and 50% fluid removal devices was 6.4% ± 0.7%, 9.1% ± 0.6%, 17.5% ± 0.6%, and 48.5% ± 1.5%, respectively. With increasing flow rate, the measured fluid removal fraction decreased, flattening at 1000 μl/min (De = 7.9 and Re_c = 111.1) to 4.6% ± 0.1%, 8.2% ± 0.1%, 14.5% ± 0.3%, and 43.8% ± 0.3% for the 5%, 10%, 20%, and 50% fluid removal device. According to Eq. 7, the fluid removal rate should be independent of flow rate. We attribute this flow rate dependence to the elasticity of the PDMS. It is known that deformation of PDMS microchannels occurs under pressure-driven flow, causing changes in the channel height and width.^{71, 72} Our design equations did not account for this behavior. As a result, for the flow rates at which we want to operate (>750 μl/min), the fluid removal rates were different than what we designed. The widths of the waste channels could be adjusted to account for PDMS deformation, or other materials can be used that do not expand under pressure, such as thermal plastics.

Equation 10 was used to design these devices even though for the 5% removal w is less than h, so this approximation was not valid. For that 5% device, the difference in widths calculated by solving Eqs. 8, 10 is 5 μm. Given the fabrication tolerances (see above), a 5 μm difference in the widths was deemed to be acceptable. As shown in Figure 5b, this did not add substantial error to the 5% fluid removal device (see the supplementary material for a more detailed explanation).⁶⁹

Effect of fluid removal on particle focusing

Figure 5 showed that one can design for specific fluid removal rates; however, it is important to determine the impact of the fluid removal on the concentration and position of focused particle streams. To test this, we injected 15 μm fluorescent particles at two flow rates (100 μl/min and 1250 μl/min) into devices containing a single waste channel of varying width. These flow rates were used to illustrate the effect of low (100 μl/min, De = 0.79, and Re_c = 11.1) and high (1250 μl/min, De = 9.87, and Re_c = 138.9) flow rate on particle focusing. At low fluid removal rates (5%), there was little effect on the focused particle stream (Figures 6i, 6ii) because the De and Re_c do not significantly change. For 100 μl/min (De = 0.79 and Re_c = 11.1), the De and Re_c decrease to 0.75 and 10.6, respectively; and for 1250 μl/min (De = 9.87 and Re_c = 138.9), they decrease to 9.38 and 131.9 following the waste channel (see supplementary material SM_Table I for a complete list of De and Re_c both prior to and following the waste channel).⁶⁹ With increasing flow rate (i.e., increasing De and Re_c), the particle stream moved from an equilibrium position near the center (Figure 6i) to a new equilibrium position closer to the inner wall (Figure 6ii). This behavior was expected and was recently illustrated.^{42, 52}

Figure 6.

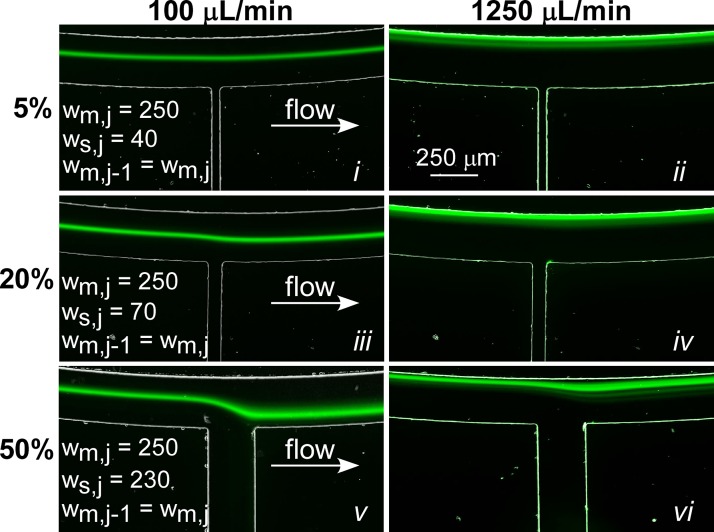
Representative fluorescent images of 15 μm particles focused in a SIFT device containing a single waste channel. Results are shown for three devices designed for 5% (i) and (ii), 20% (iii) and (iv), and 50% (v) and (vi) fluid removal at two flow rates (100 μl/min and 1250 μl/min). The channel dimensions (μm) are given for ease of comparison. A table with De and Re_c prior to and following fluid removal for each device can be found in the supplementary material.⁶⁹

At a fluid removal rate of 20% (Figures 6iii, 6iv), there was a noticeable change of ∼17 μm in the position of the focused particle stream as it went past the waste channel. As fluid is removed, the average velocity in the channel U_f, along with De and Re_c, decreases. For 100 μl/min (Figure 6iii), U_f decreased from 0.13 m/s to 0.11 m/s. De and Re_c decreased from 0.79 to 0.63 and 11.1 to 8.9, respectively. This was accompanied by an increase in the width of the particle steam and a shift in the particle position. Previous reports have shown that the width of particle streams in a spiral channel increases with decreases in U_f.⁴² Since De and Re_c govern the focusing behavior, a change in these values will lead to changes not only in the particle stream width but will also cause the particles to migrate to a new focusing position. In addition, distortions in the fluid streamlines caused by the large fluid removal rates, drawing the particle stream toward the waste channel, likely contribute to the change in focusing behavior. At the higher flow rate (Figure 6iv), the change in focusing position is not as apparent because the impact of the waste channel on the particle stream decreased due to the particles occupying streamlines closer to the inner wall, which are less affected by the waste channel (Figure 6iv). In addition, as the streamlines are distorted, the width of the streamlines increases, causing a further increase in the width of the particle stream.

At 50% fluid removal (Figures 6v, 6vi), the shift in particle position and increase in particle stream width were exacerbated. At a flow rate of 100 μl/min (Figure 6v), the distortion of the particle stream (∼100 μm) caused some of the particles to be drawn out of the waste channel (faint particles traces not easily visible in the figure). Following fluid removal, the De and Re_c decrease from 0.79 and 11.1 to 0.39 and 5.6, respectively. Even at high flow rates (Figure 6vi), the particle stream was affected by the fluid removal. Following the waste channel, the particle stream partially recovered because of the focusing nature of the spiral geometry; however, the large decrease in De and Re_c to 4.9 and 69.4, respectively, resulted in a wider particle stream that did not refocus to the original focusing position, instead focusing closer to the center of the channel. In practice, this limits the amount of fluid that can be removed from one waste channel (without adversely affecting the results) to ∼20%. At higher fluid removal rates, losses in recovery will occur.

Channel width correction

To achieve high fluid removal rates without dispersing the particles as they pass the waste channels, the focusing parameters must be maintained. The important parameters to consider are De, Re_c, and the particle Reynolds number, Re_p. Re_p is defined as³⁷

$${\mathit{\text{Re}}}_{\mathit{p}}={\mathit{\text{Re}}}_{\mathit{c}}\frac{a_p^2}{D_h^2},$$ (13)

where a_p is the particle diameter. Maintaining these parameters is most easily accomplished by changing the width of the main channel following the waste channel. However, De, Re_c, and Re_p have different dependences on the channel width and cannot be simultaneously corrected. Instead of correcting each individually, we chose to correct for changes in U_f. Since De, Re_c, and Re_p are all dependent on U_f, correcting for flow velocity offered a compromise between each of the parameters where each parameter would vary by less than 20% following the waste channel; whereas, correcting for each individually would have led to larger variations of the other parameters (supplementary material SM_Table I).⁶⁹ For comparison, we also investigated correcting for De.

To maintain De, the width of the main channel following the waste channel, w_m,j−1, was calculated using

$$\frac{w_{m,j-1}+h}{w_{m,j-1}^{1/3}}={\left(\frac{2x_{m,j}{Q}_{m,j-1}\rho h^{1/2}}{\mu R^{1/2}De}\right)}^{2/3},$$ (14)

which was obtained by taking Eq. 2 and substituting in Eq. 4 and U_f,m,j−1 = x_m,jQ_m,j−1(w·h)⁻¹ (see the supplementary material for design equations to correct for Re_c and Re_p).⁶⁹

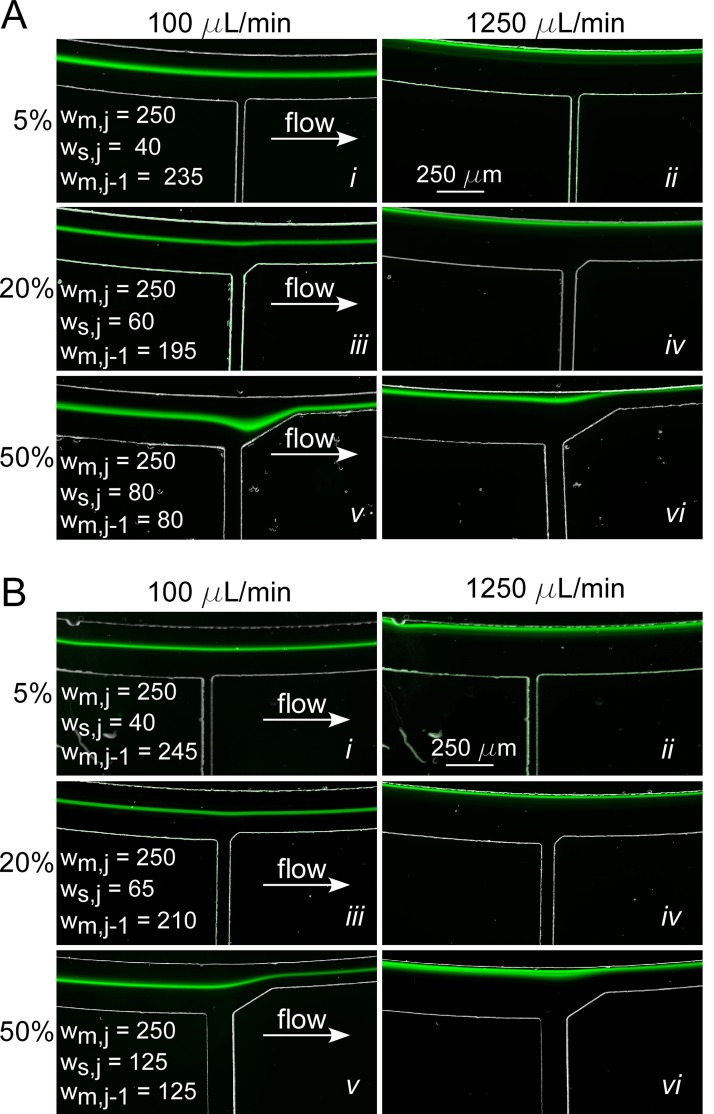
Devices with a single waste channel and corrected channel widths for three removal rates were fabricated to experimentally confirm the prediction of Eq. 14 on maintaining De. To ensure targeted fluid removal, the width of the side channels was corrected to account for the increased fluidic resistance due to the decreased main channel width. The downstream corners of the waste channels were filleted to allow for a gradual change to the corrected width. Fluorescent particles of 15 μm diameter at a concentration of 0.003% were injected into the three devices. Figure 7a shows the particle stream at fluid removal rates of 5%, 20%, and 50% at 100 μl/min and 1250 μl/min. As expected for a low fluid removal rate, at 5%, there was no noticeable impact on the position or width of the particle stream due to the presence of the waste channel (Figures 7 and 7). For low fluid removal rates, it is unnecessary to correct w_m,j−1 because De does not change significantly enough to impact particle focusing.

Figure 7.

Representative particle focusing results for SIFT devices with the main channel widths corrected to maintain (A) Dean number, De, and (B) average fluid velocity, U_f, following fluid removal from a single waste channel. Results for devices with fluid removal rates of 5%, 20%, and 50% at low and high flow rates (100 μl/min and 1250 μl/min) are shown. The waste channel was located at the W2 position (Figure 3). The channel widths in μm are listed for ease of comparison.

At 20% removal, the influence of the waste channel was effectively minimized by the width correction (compare Figures 7 and 7 with Figures 6iii, 6iv). For a flow rate of 1250 μl/min, the waste channel had no impact on the particle stream (Figure 7). The De was maintained and Re_c decreased from 138.9 to 136.1 and Re_p increased from 4.5 to 4.8. At 100 μl/min, the particles maintained an almost fixed position relative to the inner wall (Figure 7), unlike the case without De correction, in which they shifted towards the waste channel. In fact, there was a minute shift (13 μm) in Figure 7 toward the inner wall as a result of the change in w_m,j−1. This occurs because changing w_m,j−1 to correct for De results in a different channel aspect ratio (w/h) following the waste channel. It has been shown that particle stream width and position depend on the aspect ratio; at a smaller aspect ratio, particles occupy an equilibrium position closer to the inner wall.

For 50% fluid removal, there was a sizeable distortion in the particle stream at 100 μl/min (Figure 7). However, unlike for the uncorrected devices, particles did not exit the waste channel; and following the waste channel, the particle stream refocused to a new equilibrium position. Again, the change in position of the focused stream can be explained by the change in aspect ratio: to correct for 50% fluid removal, w_m,j−1 was decreased from 250 μm to 80 μm, a change in the aspect ratio from 5 to 1.6. The normalized particle position, defined as the distance from the inner wall over the total channel width, prior to the waste channel was 0.42, and after the waste channel it was 0.7. Unlike for the 20% fluid removal (Figure 7) case, the resulting shift in focusing position was towards the outer half of the channel. This behavior was unexpected, and the underlying physics is not yet known, but we suspect that the initial particle position before the sudden large change in channel width plays a role along with changes in the Re_c and Re_p. There was a small increase in the Re_c from 11.1 to 12.8 and large increase in Re_p from 0.36 to 0.76. Such shifts could limit the amount of fluid removed using this strategy at the low flow rate of 100 μl/min. If a second waste channel removing a sizeable fraction of fluid were located further downstream, it is likely that the particle stream would be drawn out of the second waste channel. For 100 μl/min, this limits the fluid removal to ∼50%, far short of the >90% desired. However, for 1250 μl/min, the particle stream fully recovered after the waste channel even though Re_c increased from 138.9 to 160.3 and Re_p increased from 4.5 to 9.5. Unlike at 100 μl/min, at 1250 μl/min, the particle stream was not directly affected by the sudden change in channel width because the initial focusing position was near the inner wall. Again, the change in the aspect ratio had a noticeable effect on the particle stream, which, as expected, moved closer to the inner wall. At this speed, further removing fluid through downstream waste channels is possible, allowing both higher fluid removal and greater particle concentration factors to be achieved simultaneously, a significant benefit of this design.

One of the major limitations of adjusting channel width to maintain De is that as fluid is removed from sequential waste channels (Figure 3) and w_m,j−1 is adjusted after each one, eventually the channel becomes too narrow to continue. Martel and Toner⁴² showed that as the aspect ratio (w/h) approaches unity, particle confinement, defined as the ratio of the channel width to the particle stream width, decreases. If the particle streams occupy a larger fraction of the channel, particles of different sizes come into close proximity or even overlap, making separation difficult.

We next tested the approach of correcting the width to maintain the fluid velocity, U_f, to determine if this provides an advantage as compared to correction for De since all of the focusing parameters (De, Re_c, and Re_p) will be better maintained. In this case, the new width depends only on the fraction of fluid remaining in the main channel, x_m,j−1, and the width of the previous main channel, w_m,j

$$w_{m,j-1}=x_{m,j-1}{w}_{m,j}.$$ (15)

Figure 7b shows the results of focusing 15 μm fluorescent particles in devices designed to maintain U_f. The waste channel had little to no effect on the particle stream for 5% (Figures 7 and 7) and 20% (Figures 7 and 7) removals. The results were similar to those obtained for maintaining De (Figure 7a) because w_m,j−1 corrected for De and U_f for 5% and 20% removal differed by only 4% and 7%, respectively. For 50% fluid removal, the w_m,j−1 was 36% larger for the U_f correction than for the De correction; at the 100 μl/min flow rate, the particle stream recovered in both cases but to different equilibrium positions. In this case, changes in Re_c, Re_p, and De were minimized compared to the De correction: Re_c decreased from 11.1 to 9.5, Re_p increased from 0.36 to 0.42, and De decreased from 0.79 to 0.63. At 1250 μl/min, the values before and after the side channel were nearly indistinguishable.

Figure 7 shows that correcting for either De or U_f eliminated particle loss through the waste channel and improved focusing after the waste channel. However, there are advantages to the U_f correction. For low flow rates (100 μl/min), U_f correction prevented particle stream dispersion at the waste channel (Figure 7b). It maintained its trajectory at a normalized particle position of 0.45 and minimized changes in the focusing parameters. In addition, since the corrected width for U_f is wider than for De, more fluid can be removed from sequential waste channels without negatively affecting particle focusing and separation.

Cell sorting and concentration in the SIFT microsystem

To achieve fluid removal rates larger than an order of magnitude, a SIFT device containing six waste channels and five outlets was designed and tested for the separation and concentration of MCF7 cells spiked into whole blood. For W3–W6, r_Q was 5; and for W1 and W2, r_Q was 10. In this case, more waste fluid is removed during the first four waste channels, where the particle-free region is larger, and less fluid is removed from waste channels five and six where, due to the decrease in channel width, the particle-free region is smaller. The five outlets, each having an r_Q of 4, were used to further increase the amount of fluid separated from the recovered particles. Table TABLE I. lists the r_Q and the calculated fraction of fluid removed from the waste channels, x_s,j,calc.

TABLE I.

List of parameters and dimensions for the multi-waste-channel spiral inertial filtration device shown in Figure 3 (the standard deviation of five trials is indicated by ±).

Channel	rQ	xs,j,calc	xs,j,rev	xs,j,exp	wm,j−1,rev (μm)	ws,j,calc (μm)	ws,j,rev (μm)
Inlet	…	…	…	…	250	…	…
W6	5	0.17	0.13	0.14 ± 0.010	210	41	35
W5	5	0.17	0.13	0.18 ± 0.016	175	40	35
W4	5	0.17	0.13	0.15 ± 0.006	145	40	35
W3	5	0.17	0.13	0.16 ± 0.005	120	40	35
W2	10	0.09	0.11	0.15 ± 0.003	110	32	35
W1	10	0.09	0.08	0.12 ± 0.003	100	37	35
O1	4	0.20	0.20	0.19 ± 0.010	…	75	75
O2	4	0.20	0.20	0.21 ± 0.012	…	75	75
O3	4	0.20	0.20	0.19 ± 0.029	…	75	75
O4	4	0.20	0.20	0.20 ± 0.006	…	75	75
O5	4	0.20	0.20	0.20 ± 0.008	…	75	75

The waste channel width, w_s,j,calc, to achieve these r_Q was calculated. To be able to use Eq. 10, the w_s,j,calc must be greater than h (50 μm); if not, the error from using the approximation was >10 μm. To achieve the desired fluid removal, w_s,j,calc would be < h (50 μm), and so the full Eq. 8 was solved to calculate w_s,j,calc (see the supplementary material for a discussion on using Eq. 8 for w > h and w ≈ h).⁶⁹ The w_s,j,calc are listed in Table TABLE I.. With the exception of W2, they were within 4 μm of each other; and as mentioned previously, fabrication tolerances were 2–5 μm. The waste channels were therefore all (including W2) made 35 μm wide (w_s,j,rev), where “rev” indicates revised parameters. This value was conservative to ensure that fabrication variations or expansion of the PDMS microchannels would still result in channels that yielded the desired fluid removal. Based on the success shown in Figure 7b, the width of the main channel following channels W3–W6, w_m,j−1,calc, was adjusted to maintain U_f. Using a 35 μm width for each of the waste channels and the w_m,j−1,calc, the fraction of fluid to be removed from the waste channels, x_s,j,rev, was determined (Table TABLE I.).

The fractions of fluid collected experimentally from each waste channel and outlet, x_s,j,exp, are given in the 5th column of Table TABLE I.. The experimental values, x_s,j,exp, closely matched x_s,j,rev, differing by less than 5% in all cases.

To demonstrate the high-purity separation and high concentration factor of sorted species, the multi-waste channel SIFT device was used to separate and concentrate MCF7 cells spiked into blood. To separate the MCF7 cells (>20 μm) from blood cells using the geometry presented here, it is best to utilize the SIFT device in the switched mode of operation. Under these conditions, the larger MCF7 cells focus near the channel center with the smaller WBC near the inner wall. One advantage of operating in switched focusing mode is that it occurs at lower flow rates compared to the traditional focusing regime.⁵² The ability to operate at lower flow rates helps to minimize lysing of target species. (Note: the SIFT device with the geometry presented here can also be operated under traditional focusing mode to sort and concentration smaller particles. See the supplementary material for particle separation and concentration results under traditional focusing conditions).⁶⁹

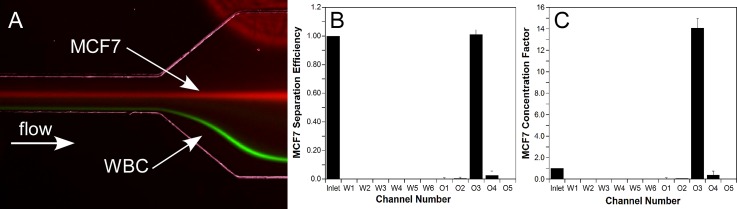
Figure 8 shows the results of the separation experiment. The MCF7 cells are focused into a single stream and completely separated from the WBCs (Figure 8a). The channel was expanded to allow for the two streams to be separated into different outlets, with the MCF7 cells flowing through the center outlet (O3). Because of the channel width correction, the cell streams were not impacted by the waste channels. Even at the expansion, where 63% of the inlet fluid had been removed, there was no noticeable impact on the streams (Figure 8a). A recovery of 101.1% ± 3.3% was measured for the MCF7 cells (the recovery greater than 100% is attributed to errors associated with particle counting using a hemocytometer). One potential concern with the SIFT device is that target species could be lost out of the waste channels; however, this does not occur, as indicated by our 100% recovery, even with the target species focusing near the channel center. Using this device we achieved a concentration factor of 14.1 ± 0.92 (>93% of the inlet fluid removed).

Figure 8.

(A) Representative fluorescent images showing the separation of MCF7 cells (red) from WBC (green). (B) MCF7 separation efficiency calculated as the number of particles collected at each outlet over the number input into the device. (C) MCF7 concentration factor (concentration at each outlet over the inlet concentration). Errors bars are standard deviations from three experimental runs.

Other groups have demonstrated the separation of cancer cells from WBCs. Sun et al.⁷³ and Warkiani et al.⁷⁴ operated under conditions that gave rise to the traditional focusing mode and were able to achieve recoveries greater than 80%. Sun et al.⁵⁵ also performed a separation of cancer cells from blood while operating under switched focusing mode. However, in these reports, the objective of the work was to demonstrate the separation of cancer cells from WBCs and not to maximize concentration factors. Since they were not actively removing waste fluid, as is the case with our SIFT device, Sun et al. and Warkiani et al.⁷⁴ only showed concentration factors of ∼3 (trifurcating outlet) and ∼2 (bifurcating outlet), respectively, 4.5× lower than we achieved in this report.

CONCLUSIONS

Techniques that can quickly process large sample volumes while achieving efficient recovery and enrichment of rare particles are necessary for lab-on-a-chip (LOC) applications that require a large volume reduction in order to enable subsequent microfluidic processing steps. Spiral inertial microfluidic devices are capable of high-throughput particle separation. However, the maximum concentration factors achieved in these devices is limited. In this work, a SIFT device capable of achieving concentration factors exceeding 13× (removal of 93% of the inlet fluid, recovery of 95%–100%) at ∼1 ml/min was presented. Utilizing the focusing effect of spiral inertial microfluidics, waste fluid was “skimmed” from the channel through a series of waste side channels, relaxing the need for narrow outlet channels. The amount of fluid removed was accurately controlled by designing a device with the fluidic resistances precisely balanced between the main flow channel and the waste channels. By ensuring that the fluid velocity in the main channel was maintained following each fluid removal, we were able to remove large fractions of the inlet fluid without disrupting the focused particle streams. We achieved essentially 100% recovery, 100% separation efficiency, and 14× concentration for MCF7 cells spiked into whole blood using the SIFT device.