Allosteric activation transitions in enzymes and biomolecular motors: insights from atomistic and coarse-grained simulations

I. INTRODUCTION

For several decades, numerous experimental and computational studies have clearly illustrated that protein molecules exhibit motions that span a broad range of length and time scales. It is thus natural to ask what subset(s) of these motions are particularly important to the biological function of proteins. For enzymes, whose main biological function is to accelerate chemical transformations, the task becomes identifying motions that are intimately coupled to the chemical reaction. In addition to the fundamental importance, investigations along this line are also of practical significance since engineering necessary motions or flexibility into artificial enzymes is believed to be a key step to enhancing their catalytic proficiency to the level of natural enzymes. Despite progress made in the field of rational protein/enzyme engineering,^1–3 most design studies rely on a framework that involves optimization of active site in static structures. This is at least one important reason why computationally designed enzymes (e.g., abzymes⁴) are often substantially inferior in activity to naturally evolved enzymes. Therefore, although there is a growing awareness of the role of motions in catalysis, additional insight from integrated experimental and theoretic approaches is urgently needed before enzymes can be well designed de novo.

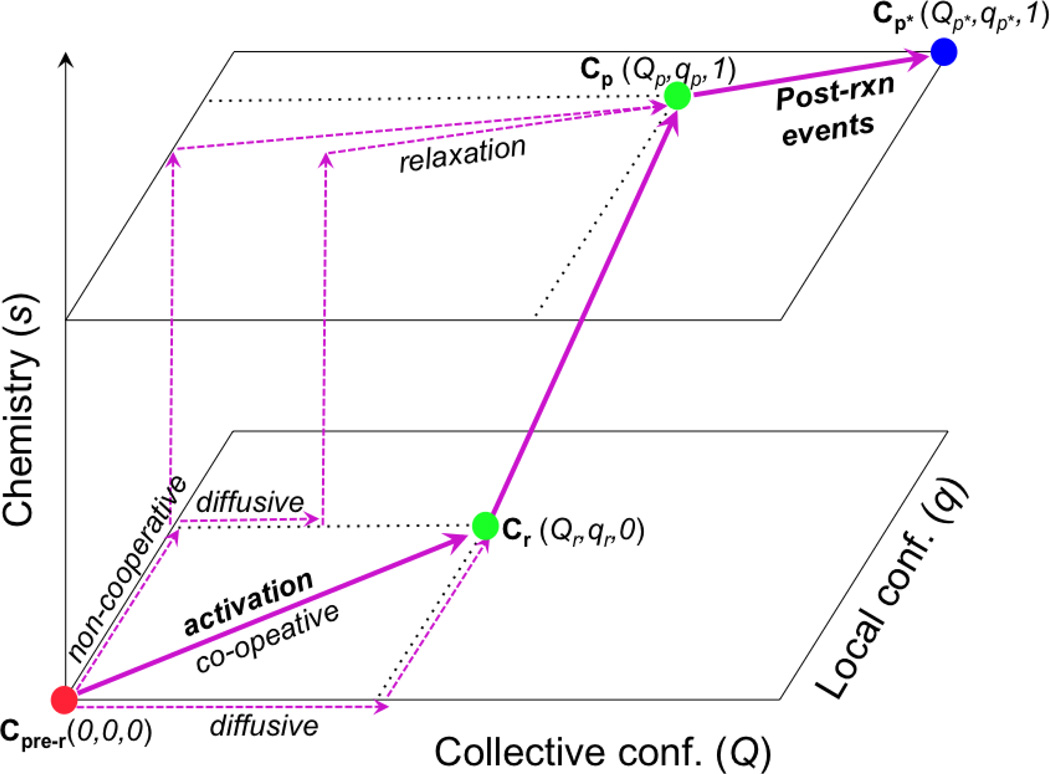
To help define the question more precisely, we note that, as illustrated schematically in Fig.1, the chemical step in an enzyme is generally sandwiched between conformational change events that are kinetically distinct steps. In a “simple” enzyme, the transition prior to the chemical step corresponds to the closure of the active site upon substrate binding, and the conformational transition following the chemical step corresponds to opening of the active site for product release; in more complex enzymes such as molecular motors (see below), these transitions before and after the chemical step are more complex in nature and coupled to the binding/association of other protein partners, such as actin or microtubule. All three steps, including the chemical step itself, may involve structural transitions that span multiple scales, as Fig.1 attempts to highlight using two abstract conformational coordinates, Q and q. Therefore, by asking “what motions are intimately coupled to chemistry in an enzyme”, one may study any one of these three steps⁵; in this context, it is worth recalling that the rate-limiting event for a catalytic cycle does not have to be the chemical transformation itself.

Figure 1.

A schematic sketch that illustrates the coupling between multi-scale structural changes (both collective and local conformational transitions) and chemistry in enzymes. The filled circles indicate kinetic states with different conformational (Q, q) and chemical (s) coordinates; the thick arrows indicate the dominant pathways that feature highly co-operative conformational transitions, while the dashed arrows indicate hypothetic pathways that are less co-operative and presumably have less flux. The “activation” process that goes from a pre-reactive conformation (C_pre−r) to a reactive conformation (C_r) may correspond to an open/close transition of an enzyme active site (e.g., in adenlyate kinase) or the recovery stroke of myosin (see below); this “activation” process is the focus of this article. The chemical step may also involve structural transitions of multiple scales, as discussed in other studies. Finally, the C_p → C_p* transition corresponds to structural changes following the chemical step in the catalytic cycle, such as opening of the active site for product release or the power stroke of myosin due to actin binding and release of inorganic phosphate.

Since efficient chemical reactivities are the defining feature of enzymes, it’s not surprising that much attention has been given to the elucidation of motions that are directly involved in the chemical step; in part, this is because most enzyme catalyzed chemical reactions are fairly local in nature, thus the idea that they are coupled to much larger scale motions is intriguing. Along this line, both experimental and theoretical studies have made great progress in the past decade, especially in the context of proton/hydride transfer reactions (collectively referred to as H-transfer below) in several enzyme systems^6–9. As reviewed by other chapters in this special issue, the motions tightly coupled to such H-transfer reactions are mostly rather fast and localized vibrations (e.g., at frequency ~200 cm⁻¹) that modulate the barrier crossing transmission coefficient^10–12. By comparing the conformational ensembles for the reactant state and transition state from potential of mean force simulations, more collective motions have been suggested to determine the free energy barrier and therefore be “conducive” to H-transfer reactions^13,14; the causality relation between such motions and the H-transfer process, however, is not always straightforward to determine.

In our recent studies, we have been focusing on slow motions in enzymes that we term “activation” transitions in Fig.1. It is important to study these motions because they are required to bring catalytic motifs to proximity so that the chemical step can occur efficiently; since multiple structural rearrangements are involved, one question of interest is what rear-rangements are in fact most important to the activation of the subsequent chemical step, and another general question is what factor(s) control the couplings among the various structural rearrangements and the overall rate of the transition. Unlike the motions that occur during the chemical transformation, as discussed in the study of H-transfer reactions, the activation processes of interest correspond to transitions between well-defined kinetic states of the enzyme-substrate complex (e.g., C_pre−r → C_r in Fig.1) and therefore are mostly in the micro- to milli-second time scale. They can be studied directly with various experimental approaches, which provide important information for and the opportunity to test theoretical analyses.

To study specific examples, we have chosen biomolecular motors and signaling proteins in our studies. Our choice is motivated by the consideration that a tight mechanochemical coupling (i.e., coordination between chemistry and conformational transitions) in these systems is likely essential to their biological function (i.e., high efficiency for energy/signal transduction^15,16), thus it is particular worthwhile to understand the mechanism through which the chemical step (e.g., phosphorylation or ATP hydrolysis) is coupled with the multitudes of conformational rearrangements. From a biomedical perspective, such research is also significant because many mutations that affect the mechanochemical coupling are involved in serious diseases. For example, mutations that perturb the coupling between the ATPase activity and the recovery stroke in the motor myosin (see below) are known to cause hypertrophic or dilated cardiomyopathies¹⁷. Similarly, mutations that modify the response of kinases to phosphorylation are implicated in various cancers^18,19.

Regarding another model system, we focus on the open/close transition in the enzyme adenylate kinase (AK). Kinetic analysis has established that the open/close transition is rate-limiting for several bacterial AKs,²⁰ and the relatively small size of AK makes it an ideal system for in-depth analyses regarding factors that control the rate of large-scale motions in enzymes^21–23. Indeed, the system has been studied by many computational approaches at both atomistic^24–30 and coarse-grained (CG) levels^31–37. Nevertheless, as we discuss below, the discrepancies that remain between different models highlight several fundamental issues regarding the mechanism of large-scale motions in proteins.

In the following, we first briefly discuss the computational methods used in our studies of slow activation transitions in enzymes; for another complementary review that focuses on other computational techniques for studying functional transitions in small signaling proteins and ion channels, see Ref.³⁸. Next, we discuss a few key results concerning the mechanochemical coupling in myosin and the open/close transition in AK from our recent work^39–45. Finally, we summarize the key conclusions and also comment on future directions of research.

II. COMPUTATIONAL METHODS

Two key objectives for a computational study of functional transitions are (i) to identify the factors that dictate the spatial scale and rate of the transition and (ii) to identify the functional impact of different components of the underlying motions. For the second objective, computational studies are particularly useful because one can construct in silico models that include only a subset of motions (which is difficult to accomplish with experiments) and then explicitly evaluate the functional consequence, such as by doing QM/MM calculations for the subsequent chemical step; this is illustrated below with the example of ATPase activation in the molecular motor myosin. To achieve the first objective, it is important to characterize the transition pathway(s), and arguably more importantly, the transition state ensemble for the transition of interest. Since the underlying motions of interest are in the micro- to milli-second regime, this is a challenge difficult to meet with straightforward atomistic simulations, although advances are being made in both computational hardwares^46,47 and/or sampling techniques (also see Sect.IV). With the standard computational facilities, the most practical strategies for large proteins remain atomistic simulations with carefully chosen biases and coarse-grained simulations.

In biased atomistic simulations, an additional biasing potential is used to drive the relevant conformational transition to occur during the time scale accessible to computations. The bias can be applied either as a restraint or a holomonic constraint, leading to biased (BMD⁴⁸) or targeted molecular dynamics (TMD^49,50), respectively; BMD is also similar to the steered molecular dynamics (SMD⁵¹). Due to the presence of the biases, the results of these simulations have to be interpreted with care, especially when the time scale of the simulation is much faster than the realistic time scale. An additional factor to consider is the coordinate being biased, which is often chosen based on intuition - such as relative RMSD (ΔRMSD), rotational angles between domains. The choice of the bias coordinate may have a non-trivial impact on the observed sequence of motions⁵². For example, a collective coordinate such as ΔRMSD is likely to encourage large-scale motions that greatly reduce the RMSD values over more local motions. Therefore, the causality of different motions from biased MD simulations should be interpreted with great care. At this point, these biased MD simulations are best thought as approximate means to identify transient interactions not readily detected from structures that correspond to the end states of the transition, and the kinetic relevance of these transient interactions is best tested with experimental studies. Better understanding the causality of different motions requires computing the underlying free energy landscape, which is only possible when the number of active degrees of freedom is relatively small⁵³, or sampling with more advanced techniques such as milestoning⁵⁴, thermal string methods⁵⁵ and multi-state Markov models^56,57 (see Sect.IV).

The complementary approach is to use coarse-grained (CG) models⁵⁸, which are computationally efficient and therefore can be used to sample the relevant slow motions without additional biases. Compared to CG models for lipids and DNA, however, generally reliable and transferrable CG models for proteins are not yet available⁵⁹. Thus most CG studies of protein conformational transitions employ structure based (or native-centric) models, also referred to as Go models. Different strategies have been proposed and applied to construct such models for more than one conformational state^60,61. The underlying assumption behind these structure-based CG models is that protein motions are largely dictated by the structural topology of the system rather than detailed energetics⁶². Despite the apparent success of such models in application to several protein and protein-RNA/DNA systems^58,63, establishing relevant experimental verifications of these models and their predictions remains an active area of research.

III. RESULTS AND DISCUSSION

In this section, we briefly review two systems that we have studied recently: myosin and adenylate kinase; they illustrate the value of atomistic and CG simulations in the analysis of slow functional transitions (activation) in proteins, respectively.

A. Myosin

Myosin is a family of molecular motors that play various essential roles such as cellular transportation and cell division⁶⁴. The one that we have analyzed is Myosin II, simply referred to as myosin below, is involved in muscle contraction. It is one of the best characterized motors at the kinetic and structural levels^65–67. The two kinetic/conformational states of relevance here are the “post-rigor” and “pre-powerstroke” states of the motor domain, which differ in both the nucleotide binding domain and the converter domain as well as the intervening structural motifs, such as the relay helix (Fig.2a); the two domains are separated by more than 40 Å and rotation of the converter is further propagated into the striking displacement of the lever arm that is most visible in single molecule studies of processive myosin motors. The transition between the two states, referred to as the “recovery stroke”, occurs on the 10 ms scale, and the hydrolysis of ATP is believed to occur only in the pre-powerstroke conformation. A thorough understanding of mechanochemical coupling in myosin, therefore, requires elucidating the detailed transition pathway between the “post-rigor” and “pre-powerstroke” states and establishing what subset(s) of motions during this recovery stroke are most important to the activation of the ATPase activity.

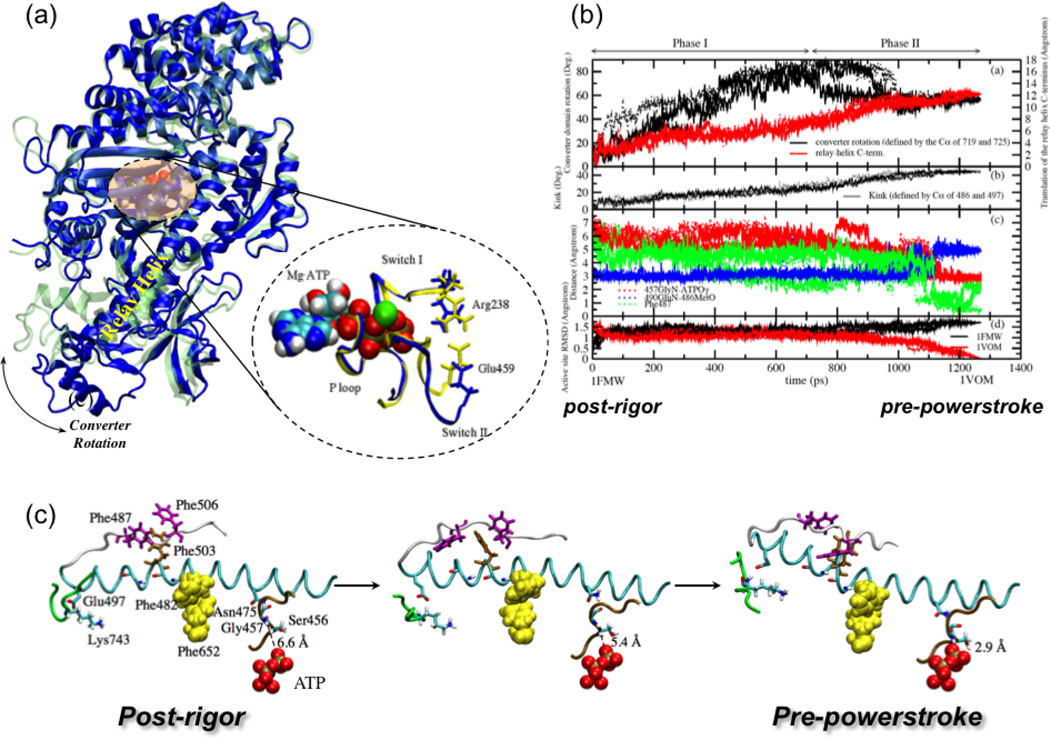
Figure 2).

The recovery stroke of myosin II, which is the conversion between the post-rigor and pre-powerstroke kinetic states. (a) Structural differences between two X-ray conformations (post-rigor⁷¹, in blue, and pre-powerstroke⁷², in green) of the Dictyostelium discoideum myosin motor domain. The most visible transition is the converter rotation, although there are also notable changes in the nucleotide binding site and the relay helix that connects the converter and the nucleotide binding site. With $\mathrm{A}\mathrm{D}\mathrm{P}·\mathrm{V}{\mathrm{O}}_4^{-}$ bound, the nucleotide binding site of the pre-powerstroke state has a closed configuration (in yellow); with ATP bound, the nucleotide binding site in the post-rigor state is open (in blue) due to displacement of the Switch II loop.(b) Variation of critical structural parameters along the three Targeted Molecular Dynamics (TMD) trajectories for illustrating the sequence of events along the approximation transition paths for the recovery stroke⁴⁰. (c) Three snapshots (at 0.0 ps, 630.0 ps, 1270.0 ps) from one of the three TMD simulations, in the same format as Fig.2 in Ref.⁶⁸ for comparison, to illustrate the proposed coupling between the small motion of SwII with the large translation of the relay helix C-terminus.

1. Approximate pathways for the recovery stroke

To probe the mechanism of the recovery stroke, several computational studies have been carried out. Fischer and co-workers⁶⁸ have calculated a minimum energy path (MEP) that connects the two conformational states, and the results pointed to a two-phase transition mechanism that initiates from a hydrogen-bond formation near the active site (between Gly457 and the γ-phosphate of ATP) and propagates sequentially through the relay helix to the converter domain. A set of hydrophobic interactions that form during the transition were proposed to stabilize the local unwinding of the relay helix, which ultimately leads to the translation/rotation of the C-terminal helix and converter. A recent set of milestoning calculations⁶⁹ based largely on the MEP pathway as the initial guess led to an estimated time-scale for the transition that is consistent with the experimental transition rate.

Using a rather different targeted molecular dynamics (TMD) approach and an implicit solvent model, we found that most rotation of the converter domain occurs in the first stage of the transition while structural changes in the relay helix and complete closure of the active site occurs at a later stage to stabilize the converter conformation via a series of hydrogen bonding interactions as well as hydrophobic contacts (Fig.2b).⁴⁰ For example, the “unwinding” of the relay helix happens much later in the TMD simulations compared to the MEP description. In contrast to the MEP results, which suggest that the kink and unwinding in the relay helix are induced by Switch II (SwII) closure via a single hydrogen-bonding interaction from Asn 475, the TMD simulations tend to suggest that the converter rotation, via strong polar interactions to the relay helix and the relay loop, induces the formation of the hydrophobic cluster halfway in the relay helix as well as some polar interactions (e.g. Asn483-Glu683) to produce the kink in the relay helix. The interactions between the Sw II and the relay helix stabilize, in return, the new conformation of the relay helix.

Since there are major approximations in all reported computational studies so far, it remains unclear which mechanism dominates in reality; the MEP study used a simpler potential function and does not include thermal fluctuations of the protein, while the TMD approach uses an approximate biasing coordinate (ΔRMSD) that may encourage collective motions (e.g., converter rotation) in the early stage of the transition. The encouraging aspect is that both TMD and MEP studies point to the importance of a consistent set of hydrophobic interactions (e.g., between Phe482, Phe487, Phe503, Phe506, and Phe652) and hydrogen bonding/salt bridge interactions (e.g., Glu497-Lys743) between the relay helix, active site and the converter domain (see Fig.2c); it is worth noting that mutations involving several of these corresponding residues in human cardiac myosin (e.g., Phe506, Glu497) are known to cause cardiac contractile dysfunctions. These discussions highlight both the value of these approximate computational techniques and the need for developing novel methods that allow a quantitative computational analysis of slow motions in biomolecules.

We have also carried out PMF calculations⁴² for the recovery stroke process with ATP as the ligand using the ΔRMSD reaction coordinate defined using the crystal structures of the “post-rigor” and “pre-powerstroke” states. Analysis of key geometrical properties in different windows found very similar trends as in the TMD simulations, indicating no major mechanistic change between the non-equilibrium TMD simulations and the umbrella sampling simulations that are closer to equilibrium (in total ~ 50 ns with an implicit solvent model). Overall, the calculated PMF is largely downhill in nature and reveals a rather broad basin around the pre-powerstroke state; this is qualitatively consistent with results from normal mode analysis as well as the experimental observation that the pre-powerstroke state has a significant degree of flexibility in the lever arm/converter. The downhill nature is qualitatively similar to the PMF results of a study using myosin II from a different organism and explicit solvent simulations⁷⁰, although the degree of exothermicity is significantly smaller in our result. The quantitative nature of these PMF results is unclear given the scale of the structural transition and various approximations inherent in this type of analysis. Nevertheless, the results suggest that the recovery stroke is largely diffusive in nature and doesn’t involve any major energetic bottleneck; this is qualitatively consistent with the observation from TMD/MEP simulations that multiple polar and hydrophobic interactions break and form continuously throughout the recovery stroke.

2. Coupling between conformational changes and ATP hydrolysis

To evaluate the functional impact of motions implicated in the recovery stroke, we have carried out QM/MM simulations for ATP hydrolysis using snapshots collected from MD simulations of not only the two relevant x-ray structures^71,72 but also a hybrid conformational state in which the active site in the post-rigor x-ray structure was closed in silico by displacing the commonly discussed SwII loop^66,67. This was meaningful to do because our PMF calculations³⁹ showed that SwII closure has a rather at free energy profile in the post-rigor state. The goal is to explicitly establish whether only structural changes in the immediate neighborhood of ATP are sufficient to activate the hydrolysis activity. This is only possible to do computationally and clearly illustrates the unique value of computational studies in establishing the functional relevance of specific motions.

Remarkably, QM/MM calculations⁴¹ found that ATP hydrolysis tends to have very high barriers even though the key residues directly in contact with the γ phosphate have the same average configuration as in the pre-powerstroke state (Fig.3a). Part of this is due to the difference in the key “nucleo-philic attack angle” (O^3β-P^γ-O^lytic), whose distribution peaks around 165° in the pre-powerstroke state but around 150° in both the post-rigor and the closed post-rigor conformations. Since the average nucleophillic attack angle in the transition state is ~169°, the free energy penalty associated with properly aligning the lytic water in both the post-rigor and the closed post-rigor conformations is on the order of 2–3 kcal/mol (Fig.3b). Although this is not a small contribution in kinetic terms (corresponds to 30–150 fold change in the rate constant at 300 K according to transition state theory), it is clear that the nucleophilic attack angle is not as dominating a factor as commonly suggested for dictating the hydrolysis activity^73,74.

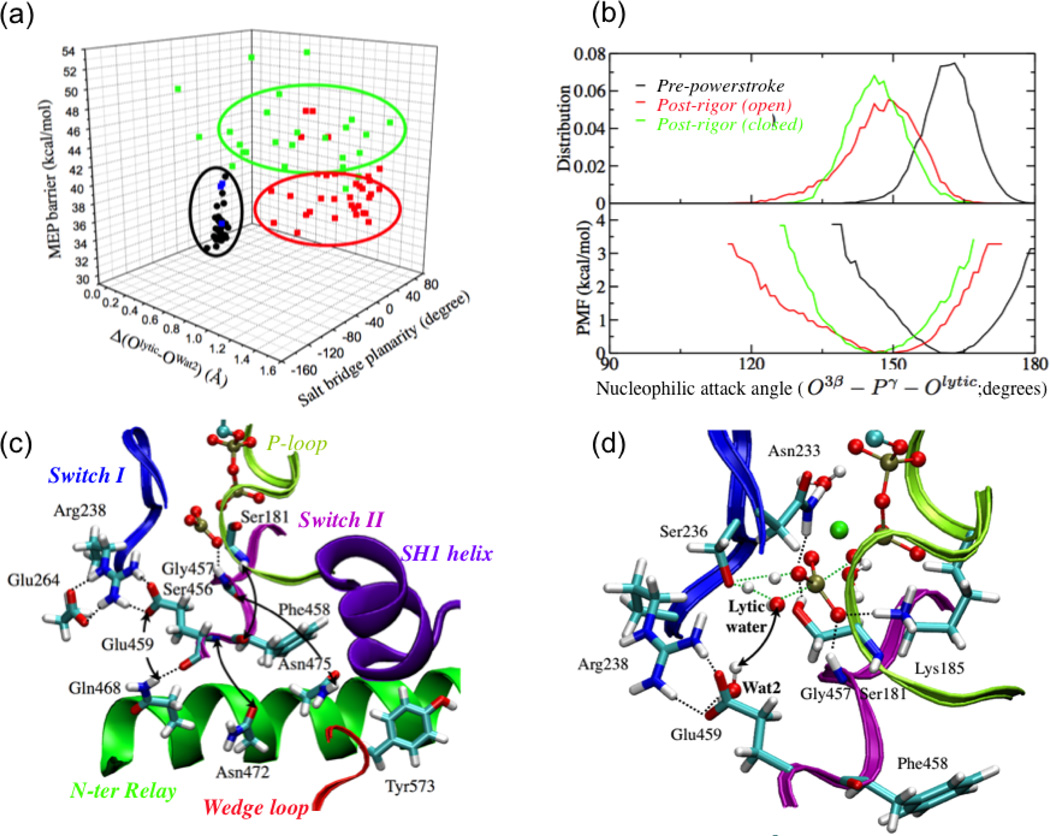
Figure 3).

The dependence of ATPase activity of the myosin on the structural state of the motor domain, i.e., the mechanochemical coupling in myosin. (a) Minimum energy path (MEP) barriers for the first step of ATP hydrolysis calculated starting from snapshots collected from equilibrium simulations of the pre-powerstroke state and a closed post-rigor structure (see text). The barriers are plotted against the Arg238-Glu459 salt bridge planarity and the differential distance between the lytic water and Wat2 (see panel d) in the reactant and transition state. The black dots indicate data for the pre-powerstroke state; the blue, green and red set indicate data from the closed post-rigor simulations with different behaviors of Wat2⁴¹. Note that the MEP barriers are systematically higher than the free energy barrier due to the lack of sampling specific local rearrangements; see Ref.⁴¹ for discussions. (b) Comparison of the distribution and corresponding PMF for the nucleophilic attack angle based on equilibrium simulation for the pre-powerstroke state and two post-rigor structures. (c) Key hydrogen-bonding interactions in the active site region of the closed post-rigor structure. The arrows indicate interactions that are broken when SwII is displaced to close the active site in the post-rigor state; i.e., rearrangements in the N-terminus of the relay helix and wedge loop are required to form the stable active site as in the pre-powerstroke state. (d) A representative active site structure for the ATP hydrolysis transition state with a twisted Arg238-Glu459 salt-bridge configuration. The notable feature is that Wat2 in the active site remains hydrogen bonded to Glu459 and therefore does not provide the critical stabilization for the transition state.

Further analysis found that the ATP hydrolysis barrier in the closed post-rigor conformation is higher because displacing SwII alone to close the active site in the post-rigor state leaves many crucial interactions unformed or even breaks existing interactions (Fig.3c). For example, although Gly457 forms a stable hydrogen bonding interaction with the γ phosphate of ATP upon SwII displacement, the interaction between Ser456 main chain and Asn475 in the relay helix is broken; the interaction between Gly457 and γ phosphate also becomes weaker in the later segment of the simulations. Similarly, although Glu459 forms a salt-bridge interaction with Arg238 when SwII is displaced, the interactions between the main chain of Glu459 and Asn472 in the relay helix are lost; instead, the carbonyl of Glu459 forms a hydrogen bond with the sidechain of Gln468. As a result, the extensive hydrogen-bonding network that involves Arg238, Glu459, Glu264 and Gln468 observed in the pre-powerstroke state is not present in the closed post-rigor state, which explains the higher rotational flexibility of Glu459 in the latter conformational state. Finally, since Tyr573 in the “wedge loop”⁷⁵ remains far from SwII in the closed post-rigor state, there is ample space for Phe458 to sample multiple rotameric states and its main chain interaction with Ser181 remains unformed, in contrast to the situation in the pre-powerstroke state. Although these additional structural flexibility seems fairly subtle, analysis indicates that they have a significant impact on the hydrolysis barrier. For example, as Glu459 rotates out of the salt-bridge plane, the second active-site water (Wat2) tightly associated with its sidechain forms a hydrogen-bonding interaction with the lytic water only in the reactant state but not the transition state of hydrolysis (Fig.3d). Accordingly, Wat2 makes an unfavorable contribution (~6 kcal/mol) to the hydrolysis barrier.

Therefore, the emerging picture is that the transition from the post-rigor state to a structurally stable closed active site (which apparently is critical to efficient ATP hydrolysis) relies on not only the displacement of SwII but also more extensive structural rearrangements in the nearby region. Without the latter, residues in the “second coordination shell” of the γ phosphate may adopt configurations that hamper the effective hydrolysis of ATP. In other words, structural transitions remote from the active site can play an active role in regulating the hydrolysis of ATP, rather than passively responding to structural changes in the active site; this is likely a general feature shared among biomolecules whose function relies on mechanochemical coupling between distant sites.

B. Adenylate kinase

In recent years, Adenylate Kinase (AK) has emerged as a prototypical system and its chemically rate-limiting open/closed (O/C) transition (Fig.4a) has been subjected to numerous experimental^{20–23,76,77} and computational^24–37 analyses; still, factors that dictate the O/C transition rate remain elusive. For example, dynamic importance sampling³⁰ has suggested that a few contacts in the LIDNMP interface region progressively ‘zip’ in the closing transition and thus determine the O/C rate. In addition, normal-mode analysis³⁵ and a mixed Go model^32,33 have suggested that a few residues must locally unfold or ‘crack’ to relieve strain associated with the LID and NMP domain motions; the two studies, however, pointed to different stressed regions. By contrast, recent experiments have suggested a different (but not exclusive) mechanism wherein functionally important dynamics are distributed among many residues. For example, swapping the entire LID and NMP domain sequences (but not just the CORE-LID hinges) between homologous mesophilic and thermophilic AKs interconverts catalytic properties (and, thus, presumably the O/C rate).²³

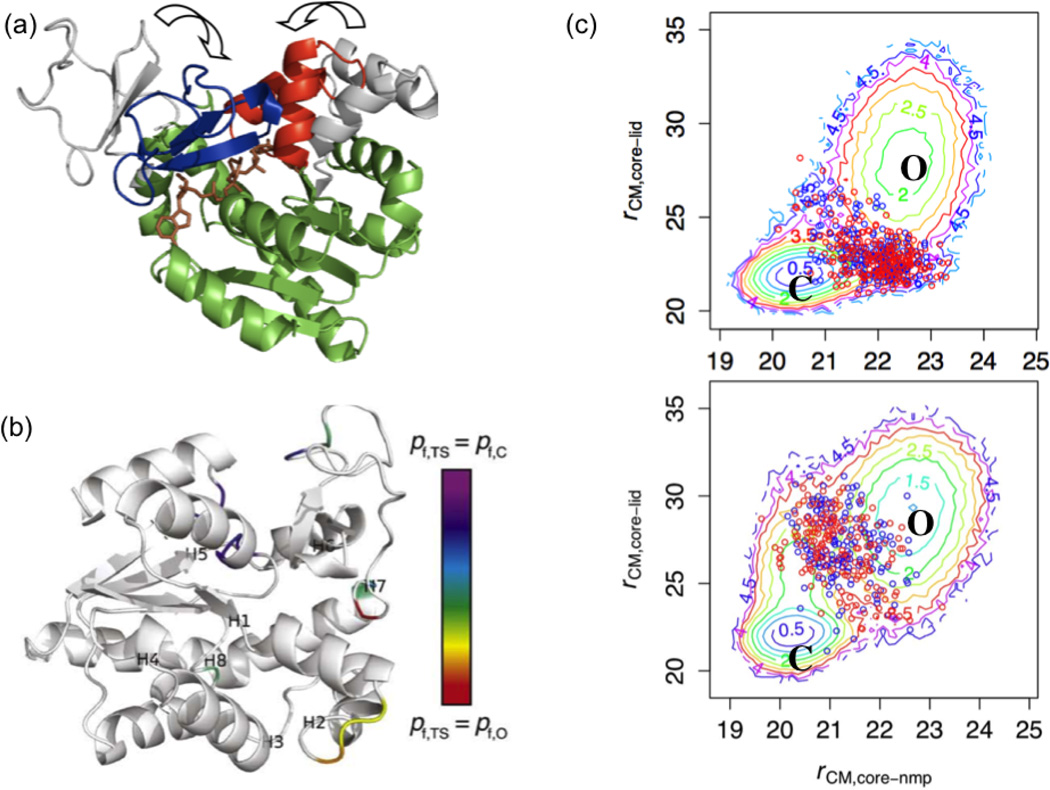
Figure 4).

Coarse-grained (CG) simulation results for the Open/Close (O/C) transition of E. coli adenylate kinase (AK). (a) Open (grey) and closed (colored) conformations are superimposed by the coordinates of the CORE domain (green). Blue: LID domain, red: NMP-binding domain; brown: bisubstrate analog AP₅A. (b) Fractional progress of folding in the TS ensemble relative to the O and C ensembles. For residues that differ substantially in flexibility (characterized by p_fold in Ref.⁴³), the flexibility in the TS ensemble is contoured on a rainbow scale from red (0) to purple (1); the results highlight that different regions contribute differently to the entropic barrier of the transition. Labels H1H8 indicate the respective central residues of the eight hinges identified in Ref.²². (c) Potentials of mean force that contrast the free energy landscape for NMP versus LID motions in ligated and apo simulations. The circles indicate the location of representative TS ensembles collected during the simulations.

Since the time scale of the transition is millisecond and the transition process is complex, atomistic simulations have been limited to the elucidation of the most salient features of the transition (e.g., intrinsic flexibility of the LID domain, local flexibility of hinges and the role of ligands in stabilizing the closed conformation) and coarse-grained models have been found valuable for probing the transition mechanism. In the following, we summarize results from our CG studies^43,44 and also initial efforts to validate the CG model using small angle X-ray scattering (SAXS) data⁴⁵.

1. CG models for the open/close transitions

We have carried out detailed analysis of the TS ensemble for the O/C transition using a double-well Go model with and without pseudo-contacts added to the closed potential to simulate ligand binding. By simultaneously characterizing the contributions of rigid-body (Cartesian), backbone dihedral, and contact breaking/formation motions to the TS structure and energetics, we were able to predict specific residues and contacts that influence the O/C transition rate. For example, we found that backbone fluctuations are reduced in the O/C transition in parts of all three domains. Among these “quenching” residues, most in the CORE domain, especially residues 11–13, are rigidified in the TS of the ligated simulation and thus slow the O/C transition by entropically raising the free energy of the TS relative to the native states, while residues 42–44 in the NMP domain are flexible in the TS and thus facilitate the O/C transition (Fig.4b). In contact space, in both unligated and ligated simulations, one nucleus of closed-state contacts includes parts of the NMP and CORE domains. These results allowed us to predict mutations that will perturb the opening and/or closing transition rates by changing the entropy of dihedrals and/or the enthalpy of contacts. Considering the approximate nature of the CG model, we note that the use of “enthalpy” and “entropy” factors here is qualitative and largely reflect whether inter-residue interactions or changes in thermal fluctuations make the dominant contribution.

Moreover, we observed that LID closure precedes NMP closure in the ligated simulation, consistent with other coarse-grained models of the AK transition³³. However, NMP-first closure is preferred in the unligated simulation (Fig.4c), which highlights that ligand binding can not only stabilize the closed conformation but also alter the kinetic pathway of closure. In this case, the driving factor for the pathway switch is likely enthalpic, since ligand binding adds many more contacts to the CORE-LID interface than to the CORE-NMP interface in the TS.

Another interesting observation from our study⁴³ is that “cracking”^32,33 was not necessarily involved in the O/C transition of AK. In the TS ensemble of our model, for all dihedral degrees of freedom, folding probability lies approximately within the interval set by the O and C states; i.e., no local unfolding unique to TS is implicated. This difference in results from previous CG studies^32,33 probably arises from differences between the dihedral potentials in our work and that of Whitford and co-workers³³; although the dihedral potential of Whitford et al. is specific to the O state, the dihedral potential in our model (that of Brooks and co-workers⁷⁸) is sequence specific but generic to the native structures. Since our CG model is also approximate in nature, our observations do not necessarily rule out the relevance of cracking in large structural transitions; our results suggest that such transitions do not have to invoke local unfolding and highlight the importance of carefully validating the CG model for the problem of interest (see below).

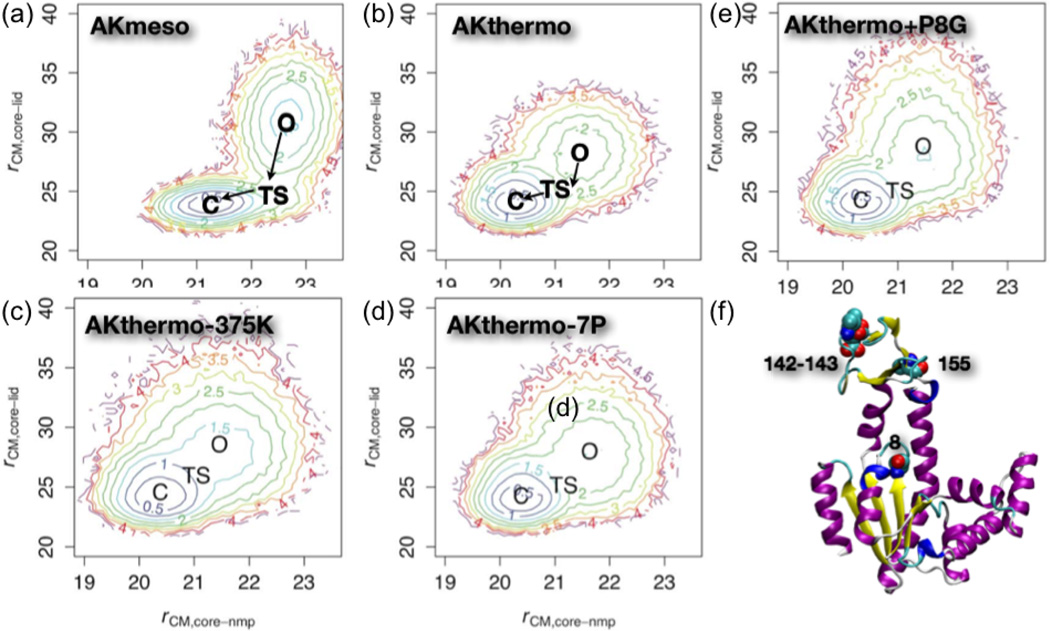
In a more recent study⁴⁴, we have applied the similar computational framework to comparatively analyze the structural transitions in the mesophilic (E. coli) and thermophilic (Aquifex aeolicus) AK enzymes (AKmeso, AKthermo). Experimentally, the latter was shown to have a lower opening rate than AKmeso at the room temperature; the closing rates were more similar^21,76. Computationally⁴⁴, the double-well Go model found that AKmeso and AKthermo share a LID-first closure pathway in the presence of ligand, although LID rigid-body flexibility is considerably less in the O ensemble of AKthermo than in that of AKmeso (Fig.4a,b). Backbone foldedness in O and/or transition state (TS) ensembles increases significantly relative to AKmeso in some interdomain backbone hinges and within LID. In contact space, the TS of AKthermo has fewer contacts at the CORE-LID interface but a stronger contact network surrounding the CORE-NMP interface than the TS of AKmeso. Consistent with the corresponding states hypothesis^79,80, increasing the simulation temperature of AKthermo increases LID rigid-body flexibility in the O ensemble (Fig.4c).

We have also attempted to use the CG framework to probe whether we can computationally interconvert the motional characteristics of AKthermo and AKmeso. Motivated by the discussions of Henzler-Wildman et al.²², we have also focused on the Pro residues unique to AKthermo. Although computational mutation of 7 prolines in AKthermo to their AKmeso counterparts produced the expected perturbations (Fig.4d), mutation of these sites, especially positions 8 and 155 (see Fig.4f), to glycine was required to achieve LID rigid-body flexibility and hinge flexibilities comparable to AKmeso (Fig.4e). Analysis of the impact of these mutations on rigid body motion, dihedral flexibility and inter domain contacts suggested that the contacts between CORE and CORE-LID connector helix 1 are likely the most important for modulating the global transition. Interestingly, other mutants spatially close to the P8 sites have been shown in recent experiments to have significant functional effects. For example, glycine mutants that destabilize the CORE-LID connector helices (I116G+L168G) increase ATP binding affinity by increasing the O to C equilibrium constant⁷⁷. On the other hand, mutating the 7 sites to proline in AKmeso reduces some hinges’ flexibilities, especially hinge 2, but does not reduce LID rigid-body flexibility, suggesting that these two types of motion are decoupled in AKmeso. Therefore, our results suggest that hinge flexibility and global functional motions alike are correlated with but not exclusively determined by the hinge residues.

2. Validation of the CG model with SAXS

Although the Go-based CG simulations are informative and can stimulate new experiments, it remains an fundamental challenge to validate a CG model for complex biomolecules. For example, parameters in our model were calibrated to make RMSD from the CG simulations of individual O and C states fit atomistic MD results²⁴. It is possible, however, that these ~50-ns atomistic simulations underestimate the true flexibility of the system at the biologically relevant us-ms timescale, as hinted … as hinted by H/D exchange data from a recent NMR study⁸¹. Establishing proper benchmarks for CG models and improving their robustness remains an active and fruitful area for theoretical research.

As a useful step in this direction, we have recently carried out a study⁴⁵ that combines CG simulations and SAXS, taking advantage of a recently developed algorithm for computing SAXS profiles using residue-level CG models for proteins⁸². We have several aims. First, to estimate global flexibility for AK, we compare experimental SAXS curves to those calculated from CG simulation ensembles of AK using different strengths of inter-residue interactions. Second, to identify possible population shifts, we fit SAXS curves measured in both the absence and the presence of ligand to linear combinations of predicted scattering from the O and C state simulations (i.e., I_comb = w_OI_O + w_CI_C). Specifically, we fit log[I_comb] to experiment using linear regression over the range 0.14 < q < 0.3. Finally, as discussed in Ref.⁴⁵ but not here, we have also calculated the correlation between predicted scattering and various structural metrics over large simulation ensembles; Suggesting that scattering is most sensitive to the CORE-LID distance. this provides a way to better interpret SAXS data at the structural level.

As discussed in our previous work⁴³, we calibrated the simulated flexibility of AK by varying the contact energy scale (S_con), by which we scale the Karanicolas/Brooks energies to compensate for extra backbone bond angle potential. For our O/C conformational transition simulations, we calibrated S_con to 2.5 so that the C simulation averaged about 2.0 Å Cα RMSD with respect to the closed crystal structure to reproduce prior atomistic simulations of AK. This significantly exceeded the S_con of 1.7 that was used in double-well Go simulations of smaller conformational transitions^61,83.

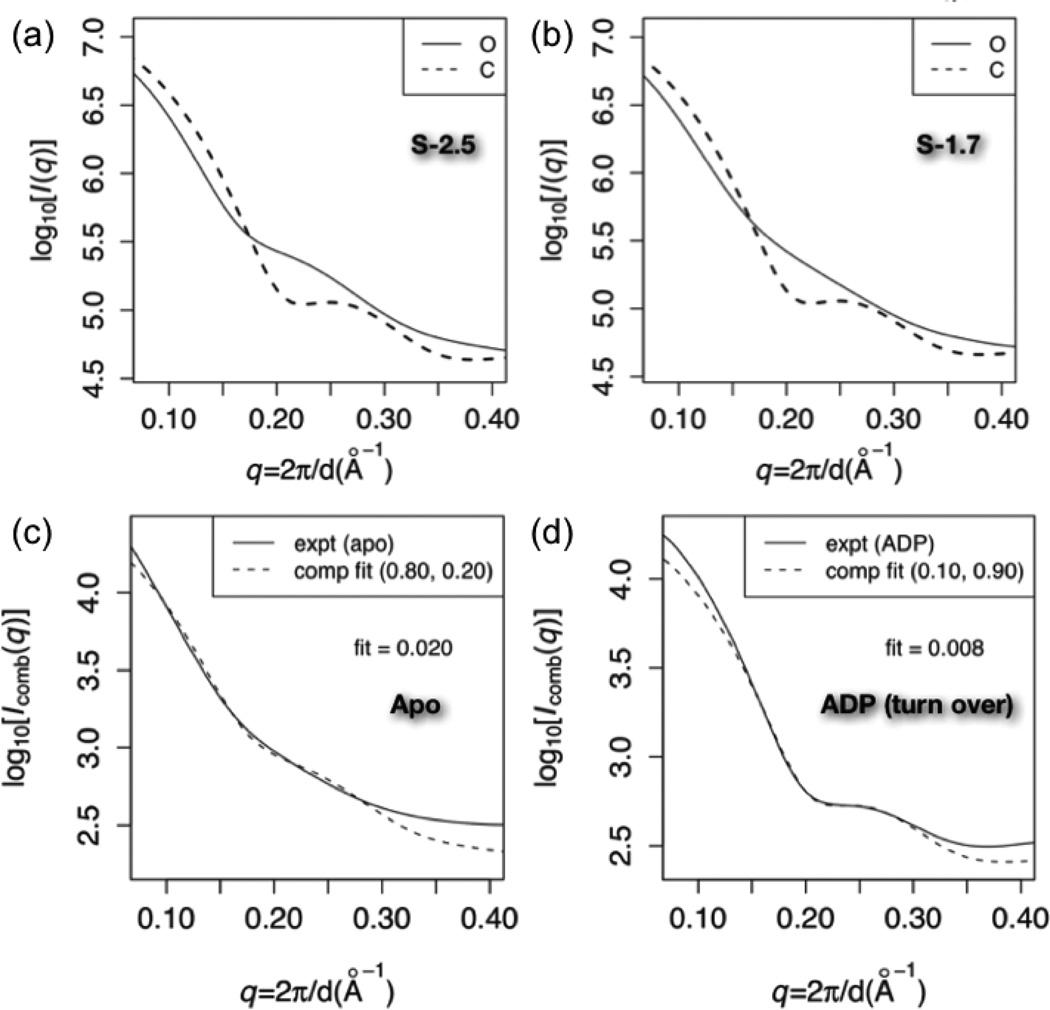
Fig.6a shows that with S_con = 2.5, the C simulation predicts a more curved SAXS profile than the O simulation, especially near q ~ 0.22Å⁻¹; this is consistent with C being more ordered than O as expected. With S_con = 1.9 (Fig.6b), the predicted O scattering profile is substantially less inflected near q ~ 0.22Å⁻¹ than at S_con = 2.5. Conversely, the predicted C curves are similar for ensembles generated using the two S_con values, both exhibiting a small dip near q ~ 0.22Å⁻¹.

Figure 6).

Experimental vs. predicted Small Angle X-ray Scattering (SAXS) profiles for various states of AK. Panels (a) and (b): predicted scattering at contact energy scales (S_con) of 2.5 and 1.9, respectively. The solid (dashed) line indicates the prediction from the O (C) simulation. For each calculation, predicted scattering (I(q)) is averaged over 1000 randomly selected structures from the corresponding simulation ensemble, and log₁₀[I_avg(q)] is plotted. (c): fits of log₁₀(I_comb) at S_con = 2.5 to the apo experimental data over 0.14 < q < 0.3. I_comb is the optimal linear combination of predicted O and C scattering to fit the data; the weights (w_O, w_C) are indicated in parentheses. “fit” in the panel indicates the root mean square deviation between experimental and fitted computational data over that q range. (d): fit of log₁₀(I_comb) at S_con = 1.9 to the ADP-bound experimental data. Note that the experimental data were collected for B. globisporus AK while all calculated ensembles were collected using the E. coli AK; SAXS patterns from E. coli and B. globisporus AKs correspond closely under conditions where data from both species are available (data not shown).

Fig.6c shows that the optimal fit over 0.14 < q < 0.3Å⁻¹ occurs for S_con = 1.9 with w_O = 90% for the apo condition; with S_con = 2.5, the predicted scattering is more strongly inflected at q ~ 0.22Å⁻¹ than the experimental data, while at S_con = 1.5, the predicted scattering curve is substantially shallower. This provides a measure of the impact of the strength of inter-residue interactions on the intrinsic flexibility of the system and the corresponding sharpness of features in the scattering pattern. We also note that the S_con = 2.5 O simulation produces a slightly better fit at low angles (q < 0.14) than the S_con = 1.9 O simulation. The relatively dominant population of the O state in the absence of any substrate makes biochemical sense, although it is worth noting that the single molecule FRET study suggested that the C state is dominant even in the absence of substrates.

Fig.6d shows the fit of I_comb at S_con = 1.9 to experimental data collected in the presence of substrate ADP (i.e., turning over condition). A 10% population of O attens the small dip predicted at q ~ 0.22Å⁻¹ (Fig.6b), producing a very small RMSD for the fit. The significant population shift going from the apo to the ADP condition is biochemically consistent with the conformational equilibrium required for catalytic cycling. By contrast to the apo experimental data, a broad range of S_con, especially between 1.7 and 2.1, produces good fit to the ADP data.

IV. CONCLUDING DISCUSSIONS AND FUTURE OUTLOOK

Enzyme catalysis is a multi-step process that involves complex interplay of chemistry and conformational motions that span many temporal and spatial scales. To identify motions that dictate the catalytic function of enzymes, it’s imperative to clearly define which step of the catalytic cycle is of interest (Fig.1). Depending on the specific process of interest, the appropriate resolution of the model may vary although one may argue that, ultimately, a complete atomistic model with predictive power is the “holy grail”.

A. Insights from myosin and AK studies regarding allosteric “activation transitions” in enzymes

In this article, using two specific examples, myosin and adenylate kinase (AK), we aim to illustrate how atomistic and CG models can be used to better understand the nature and functional impact of slow “activation motions” in enzymes (Fig.1). Specifically, we review our studies of the “recovery stroke” in myosin and the open/close (O/C) transition in AK. Both transitions occur in the millisecond time scale and are kinetically separable from the chemical step that involves bond breaking/formation in ATP. Therefore, these transitions can be studied by various experimental approaches, making it possible to compare computational and experimental results.

The processes that we have analyzed here are allosteric in nature in the sense that they implicate a large number of residues, many of which are far from the active site where substrate binding and chemical transformation occur; they include both domain-scale motions and more localized side chain rearrangements. It is such “multi-scale” nature that makes allosteric transitions both fascinating and challenging to study using computational approaches^84,85. The key challenge is to establish among all these multitudes of motions, what subset(s) of motions constitute the kinetic bottleneck and what rearrangements have the most significant impact on the subsequent chemical step. A closely related goal is to identify “hotspot” or “hub” residues/interactions that maintain the tight coupling between the multitudes of motions and therefore the long-range and co-operative (see below) features of allosteric transitions.

Several approaches have been proposed in the literature to identify “hotspot” residues in allosteric transitions, most notably perhaps being informatics based analysis based on either sequence (e.g., statistical coupling analysis^86,87) or structure⁸⁸ and various perturbative analyses based on normal mode models of proteins^89,90. In our analysis of myosin⁴⁰, we found significant overlap between predictions from statistical coupling analysis and hinge analysis based on low frequency normal modes⁹¹. Mutation of some of these residues was indeed known to lead to the decoupling phenotype in myosin (i.e., decoupling between ATPase and motility), supporting their role in mediating long-range couplings. These results and many recent studies^92–94 have highlighted the functional relevance of intrinsic structural flexibility of proteins, which is often well captured by a small set of low-frequency normal modes or motions prior to the allosteric activation⁹⁵. These observations support the view⁸⁴ that many allosteric proteins are constructed from semi-rigid domains or subdomains with hinges and/or semi-rigid subunits, which can move relative to each other, so that the “jigglings and wigglings” (Brownian motion, which is always present at physiological temperatures) can be harnessed through biasing of the free energy surface by ligand binding, modification, and release to propagate the resulting local changes over a long distance to affect activities elsewhere.

A more thorough analysis of “hotspot” residues and kinetic bottleneck of allosteric transitions, however, requires explicitly studying the transition pathway and the corresponding transition state ensemble. This is currently difficult to do with bias-free atomistic simulations for large proteins. As we have illustrated here using myosin and AK, biased atomistic simulations and CG simulations can provide valuable insights, although the results should be interpreted with care considering the approximations inherent in these models. Overall, these more detailed studies provide additional support to the “domain-hinge” view of allostery; on the other hand, they also help highlight additional complexities and various deviations from the somewhat simplistic picture of “domain motions mediated by hinges”⁹⁶.

In AK, for example, LID and NMP domain closures are clearly the dominant motions for the O/C processes, and significant closure motions have been observed in both experimental²⁰ and simulation studies^24–26 even in the absence of the substrates. Mutating the hinge residues such as the unique Pro residues in AKthermo into the corresponding ones in AKmeso indeed induce changes in the domain flexibilities toward AKmeso (especially LID), thus partially supporting the role of hinges in the O/C processes. On the other hand, at least in the simulation models⁴⁴, the reverse mutations in AKmeso don’t cause significant changes in the LID flexibility, suggesting that hinge flexibility and global transitions are partially decoupled in AKmeso. The limited significance of hinges in AK has also been hinted at by the experimental chimera studies of Bae et al.²³, who found that swapping the entire LID and NMP domain sequences (but not just the CORE-LID hinges) between AKthermo and AKmeso interconverts catalytic properties (and, thus, presumably the O/C rate). Thus the stability and internal flexibility of domains, in addition to the relative displacements of domains, may also contribute to the rate of large scale transitions. Along this line, the “cracking” hypothesis^32,33,96 argues that local unfolding/refolding could be an important part of allosteric transitions. Our CG studies of AK⁴³ didn’t find any compelling evidence for cracking, although more systematic studies are needed before solid conclusions can be drawn.

Regarding the role of subset(s) of motions in enzyme activation, our studies of recovery stroke in myosin that integrated QM/MM studies and classical MD simulations serve as a relevant example⁴¹. By constructing an in silico model based on classical simulation results and explicitly evaluating the ATP hydrolysis barrier as compared to those in various crystal structures, we were able to probe the roles of local and longer-range structural rearrangements in activating the ATPase activity in this prototypical molecular motor. Our results highlight that local changes important to chemistry require stabilization from more extensive structural changes; in this sense, more global structural transitions are needed to activate the chemistry in the active site. In fact, even in more “regular” enzymes that catalyze highly localized chemical transformations, such as hydride transfers, collective structural changes are believed to be important. This is also likely because otherwise active site features conducive to the chemical step are not stably maintained¹⁴.

It is important to emphasize that our results do not suggest that all global conformational changes are required to turn on efficient ATP hydrolysis. In many “decoupling mutants” of myosin^97,98, the ATPase activity is very close to being normal, indicating that the lack of converter/lever arm rotation does not significantly impair ATP hydrolysis. Therefore, a more likely scenario is a two-phase process (also schematically sketched in Fig.1): during the first phase, structural transitions near the N-terminus of the relay helix are coupled to the SwII displacement to establish a stable active site and to turn on the ATP hydrolysis; in the second “relaxation phase”, the rest of the conformational cascades propagate into the rotations of the converter and the lever arm. This two-phase description is reminiscent of coupled tertiary and quaternary structural changes for O₂-binding-induced allostery in hemoglobin, where it has been shown that tertiary structural changes induced by oxygen binding precede quaternary structural changes^99,100.

These discussions further highlight the importance of understanding factors that control the coupling between local and global structural changes. If the coupling is very tight such that the various structural rearrangements are highly co-operative, the population of the system in which only a subset(s) of the structural transitions have occurred is extremely low, then it’s less meaningful, at least for practical purposes, to ask what transitions have a more significant impact on the chemical step. In the context of biomolecular motors, ensuring that the transitions between different functional states are highly co-operative is likely essential to maintaining an efficient energy transduction^16,39, i.e., avoiding wasteful futile ATP hydrolysis that is not tightly coupled to large-scale structural transitions. Whether a high degree of co-operativity is observed in and critical to the function of “regular” enzymes remains to be carefully and systematically analyzed¹⁴. As to factors that control the degree of co-operativity, although “hotspot” residues discussed above are highly relevant, other considerations based on studies of protein folding/stability are expected to be useful as well, especially considering the argument that domain unfolding/refolding might contribute to large-scale transitions in proteins⁹⁶.

B. Future outlooks

In the following, we briefly comment on several directions that we believe are particularly worthy of further efforts from computational studies, or, more preferably, integrated computational and experimental investigations.

1. Kinetic bottlenecks and co-operativity for large-scale functional transitions

As emphasized repeatedly in the above discussions, it is important to understand factors that control the kinetics and the degree of co-operativity for large-scale motions in proteins. It is clear that functional transitions often involve both domain-scale motions and local structural rearrangements. Domain motions are more striking in scale while the local transitions more subtle, but the spatial magnitude of changes does not necessarily correlate with kinetic significance. As noted by many studies, large-scale structural transitions are correlated with low-frequency modes, which implies that biomolecules tend to have intrinsic structural flexibilities and the domain-scale motions are largely diffusive in nature; therefore, the kinetic bottleneck of a functional transition may, in fact, consist of key local structural changes that are thermally activated. Moreover, to ensure a high-degree of co-operativity, the diffusive domain motions need to be energetically coupled to local rearrangements. Thus it’s essential to characterize the underlying free energy landscape of multi-scale motions and the spatial-dependent diffusion properties.

At this moment with typical computational hardwares, characterizing the kinetic bottleneck and the underlying free energy landscape for large systems remains an outstanding challenge⁸⁵. Novel computational techniques and strategies such as transition interface/path sampling¹⁰¹, milestoning⁵⁴, the thermal string method⁵⁵ and multi-state Markov state models coupled with massively distributed computing^56,57 are promising avenues that have been applied to mainly the folding of small peptides/proteins. The milestoning approach has been applied to the recovery stroke of myosin⁶⁹, although more in-depth analysis would be useful regarding distinguishing different pathways and the role of key residues. The thermal string approach has also been applied to the transition of ligand (proton) gated ion channel¹⁰². Nevertheless, atomic simulations of these sorts remain rather computationally expensive, which makes it difficult to evaluate the convergence and statistical significance of the results. Therefore, at least in the near future, development of effective CG models for proteins remains an attractive and intellectually tantalizing direction^58,59. CG models can also be used as an approach to broadly sample possible transition pathways, which are then reversely mapped to atomistic scale and refined¹⁰³. Finally, novel approaches for characterizing and projecting multi-dimensional free energy surfaces have been developed but their application to large protein systems only start to appear^104,105.

2. Prediction of functional transitions at high resolution

For proteins that undergo large scale conformational transitions, it is not uncommon to have a high-resolution structure for only one of the many functional states (e.g., a molecular motor or kinase with a ATP analog as ligand). Therefore, an important challenge is to predict/construct reliable models for other functional states. Along this line, a productive avenue is to combine computational approaches with low-resolution experimental data for the functional state of interest; good examples include electron microscopy (EM), SAXS, FRET data and other spectroscopic data that provide geometrical constraints. For such a purpose, a judicious combination of physical based models (e.g., MD simulations) and structural informatics techniques (e.g., ROSETTA¹⁰⁶ or TASSER¹⁰⁷) is likely most productive in the near future. Notable examples have emerged in recent years, especially concerning using EM and SAXS as low-resolution structural constraints for macromolecular assemblies^108–110. Further pushing forward the resolution of such models remains a fascinating direction of research.

3. Connection between motions/dynamics and enzyme evolution

The discussions above have been limited to the function of a single protein/enzyme (complex) under in vitro condition. It is tempting to ask how do the dynamic properties of proteins/enzyme fit in the broader biological context, such as protein-protein interaction networks in the cell and protein evolution. For example, interesting discussions have been made regarding slow protein conformational fluctuations (i.e., dynamic disorder of protein activity) as an additional origin of stochasticity for protein interaction network¹¹¹; therefore, the time-scale of slow protein fluctuations might need to be tuned in the cellular context to be compatible with the sensitivity and robustness of the underlying protein network. Along this line, it is increasingly realized that the cellular environment is very different and effects such as molecular crowding has a major impact on the binding and dynamic properties as well as the stability of biomolecules¹¹². Although a significant fraction of the crowding effect can be understood based on “simple” physical arguments such as the excluded volume effect stabilizing more compact conformations relative to extended conformations, to what degree do slow motions of proteins differ (in terms both time scale and possibly mechanism) between the cellular and in vitro conditions remains to be systematically dissected.

As to the role of motions/dynamics in protein evolution, much considerations are given to the role of protein flexibility and evolvability, and the connection between specific motions and emergence/divergence of function only starts to be explored. As a fascinating example, Johnston et al.¹¹³ reported that a single mutation is able to switch a guanylate kinase enzyme (GK^enz) into spindle-binding protein (GK^dom). This mutation was shown to inhibit the GMP-induced GK domain closure, thus quenching the GK^enz activity, but allow protein binding and spindle orientation, the GK^dom function. Although this is an “artificial” example, it is conceivable that modulation of protein motions has played a role in the emergence/divergence of functions during evolution. By combining techniques such as ancestral sequence reconstruction¹¹⁴ with physical characterization of protein motions, we anticipate that much can be learned regarding how complex motions have been modulated through evolution to help shape the rich functional landscape of proteins in the cell.

Figure 5).

Potentials of mean force for the O/C transition in mesophilic AK (E. coli, AKmeso), thermophilic AK (Aquifex aeolicus, AKthermo) and various in silico mutants of AKthermo using the double-well Go CG model. AKthermo-375K indicates that the simulation is carried out at 375 K instead of 300 K (all other panels); AKthermo-7P indicates the AKthermo mutant in which all Pro residues unique to AKthermo are changed to the corresponding ones in AKmeso; AKthermo+P8G is the AKthermo mutant in which only Pro 8 (see position in the structure) is changed to a Gly. These results illustrate that AKmeso/AKthermo approximately satisfy the “corresponding state hypothesis”, and that Pro 8 is particularly important in controlling the flexibility of the LID domain in the O state.