Complex RNA Folding Kinetics Revealed by Single-Molecule FRET and Hidden Markov Models

Abstract

We have developed a hidden Markov model and optimization procedure for photon-based single-molecule FRET data, which takes into account the trace-dependent background intensities. This analysis technique reveals an unprecedented amount of detail in the folding kinetics of the Diels–Alderase ribozyme. We find a multitude of extended (low-FRET) and compact (high-FRET) states. Five states were consistently and independently identified in two FRET constructs and at three Mg²⁺ concentrations. Structures generally tend to become more compact upon addition of Mg²⁺. Some compact structures are observed to significantly depend on Mg²⁺ concentration, suggesting a tertiary fold stabilized by Mg²⁺ ions. One compact structure was observed to be Mg²⁺-independent, consistent with stabilization by tertiary Watson–Crick base pairing found in the folded Diels–Alderase structure. A hierarchy of time scales was discovered, including dynamics of 10 ms or faster, likely due to tertiary structure fluctuations, and slow dynamics on the seconds time scale, presumably associated with significant changes in secondary structure. The folding pathways proceed through a series of intermediate secondary structures. There exist both compact pathways and more complex ones, which display tertiary unfolding, then secondary refolding, and, subsequently, again tertiary refolding.

1. Introduction

RNA molecules are not merely simple carriers of genetic information but can assemble into complex tertiary structures and even catalyze reactions. In fact, the existence of catalytic RNA molecules (ribozymes) has led to the proposition of the RNA world hypothesis.¹ In modern cells, RNA molecules catalyze just two classes of chemical reactions: modifications of phosphodiester bonds (DNA and RNA cleavage, RNA splicing) and peptide bond formation.² Artificially designed ribozymes, however, are known to catalyze a wide range of chemical reactions.³

In some ribozymes, the slow opening and closing of tertiary structure (RNA breathing) is believed to be essential for product release.⁴ Therefore, catalysis may not be decoupled from RNA folding. This latter process is hierarchical, first proceeding on the secondary structure level via formation of fairly stable Watson–Crick base pairs. Subsequently, secondary structure elements fold into a compact, three-dimensional structure.

The folding of RNA into the native tertiary fold may proceed via a complex sequence of secondary structures.^2,5 The associated breaking of transiently formed (“misfolded”) base pairs often involves typical time scales of seconds or longer.^2,6 Any given secondary structure may be associated with a range of tertiary structures.⁷ Formation of compact tertiary structures may require the presence of counterions, particularly divalent cations such as Mg²⁺, which screen the intrinsic negative charges on the RNA phosphate groups and, thereby, stabilize certain tertiary motifs.⁷⁻⁹ Even small modifications of single nucleotides may result in different tertiary structures and hence different energy landscapes.^4,10,11 Indeed, RNA sequence, structure, and function interact in a complex, not yet fully understood fashion,² and the characterization of RNA folding kinetics, including the pathways of secondary and tertiary structure changes, remains an intricate problem.⁶

In this work, we have investigated the conformational equilibrium and the folding pathway of the 49mer single-stranded RNA ribozyme Diels–Alderase (DAse)¹² using a novel hidden Markov model (HMM) analysis of single-molecule FRET data. DAse catalyzes a Diels–Alder reaction,¹³ i.e., the [4 + 2] cycloaddition reaction between anthracene dienes and maleimide dienophiles. DAse is a true multiple-turnover catalyst and shows remarkable enantioselectivity (>95% enantiomeric excess).¹³ It has a well-defined folded structure, as revealed by X-ray crystallography. The folded state consists of three helices arranged around a pseudoknot region, in which the catalytic pocket of the ribozyme is located (Figure 1b). A continuous sequence of stacking interactions runs from the bottom of helix II to the top of helix III and has been termed the “spine” of the folded structure.¹⁴ The tertiary fold is held together by a pseudoknot, in which the 5′-G1-G2-A3-G4 segment bridges the unpaired strands of the asymmetric bulge (Figure 1a). The precise hydrogen-bond pattern in the pseudoknot region is known to be crucial both for thermal stability of the overall fold as well as for the shape of the catalytic pocket.^4,8,14,15 The crystallographic structure contains six Mg²⁺ cations.⁸ Recent experimental and computational evidence showed that cations specifically bind to certain sites that stabilize the tertiary fold, without interfering with the catalytic reaction.^4,15 Low Mg²⁺ concentrations were found to destabilize the folded conformation^4,9,15 and to dramatically decrease the catalytic activity of the ribozyme.¹³

Figure 1.

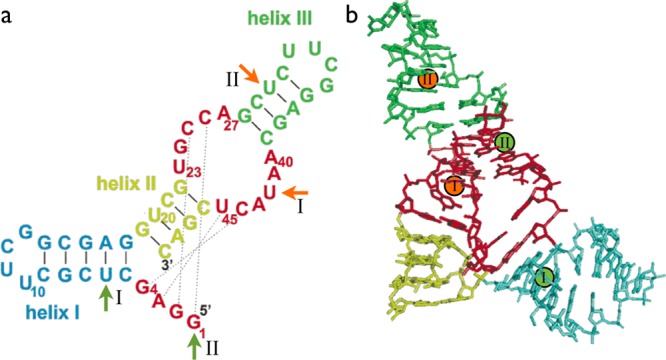
Diels–Alderase ribozyme. (a) Secondary and tertiary structure interactions in the folded state. Solid lines, secondary structure base pairs; dotted lines, tertiary structure base pairs. Attachment sites of the FRET labels are marked by green (donor dye Cy3 at U6 in construct I and at the 5′ end in construct II) and orange (acceptor dye Cy5 at U42 in construct I and at U30 in construct II) arrows. (b) Three-dimensional structure of the folded state. Color-coding of the secondary structure elements as in panel a. Attachment sites of the FRET labels are indicated by green (Cy3, donor) and red (Cy5, acceptor) spheres. (The figure has been adapted from Figure 1 in ref (9).)

Single-molecule Förster resonance energy transfer (smFRET) is a powerful tool to follow conformational fluctuations of biomolecules on length scales of a few nanometers in real time.¹⁶⁻²¹ smFRET measurements with surface-immobilized molecules revealed that DAse is highly dynamic and can exist in substantially different conformations, which were found to interconvert on time scales of hundreds of milliseconds.⁹ The concentration of Mg²⁺ influences the shape or population of the accessible conformational states, as indicated by the Mg²⁺ dependence of the FRET efficiency histograms and the apparent folding rates.⁹ Consistent with conformational fluctuations, a poor resolution of DAse spectra was found in subsequent NMR studies.⁴ The Mg²⁺-dependent FRET efficiency histograms revealed at least two conformational ensembles: (i) a high FRET state, attributed to the folded conformation, whose population increases with increasing Mg²⁺ concentration, and (ii) a distribution of intermediate FRET efficiencies, whose population decreases with increasing Mg²⁺ concentration. The intermediates were observed to spread out over a wide range of FRET efficiency values and, presumably, comprise multiple conformations with different secondary and tertiary structures.⁹

In practice, only two or three states with significantly different FRET efficiencies can be distinguished in a histogram-based analysis.^9,11 The emission intensity from an individual fluorophore is small. Consequently, stochastic fluctuations of the number of photons within a time bin (shot noise) significantly contribute to the widths of the FRET distributions and prevent the separation of states with similar mean FRET efficiencies.⁹ Of note, histogram analysis utilizes only FRET efficiency information. It completely neglects the time sequence of events in the single-molecule trajectories and, thus, discards a substantial part of the available information. In contrast, hidden Markov models²² can distinguish states in the data by using both the differences in FRET efficiency and the time sequence of events, and, thus, can decompose states with similar FRET efficiencies but different kinetic properties. Recent studies on single-molecule protein and RNA data sets²³⁻²⁶ have demonstrated the power of HMMs to resolve a multitude of states. HMM analysis has its intrinsic challenges, however, because (i) the results depend on the number of states used, (ii) the HMM optimization may get stuck in local minima, (iii) models with many states are difficult to validate, and (iv) the quality of the model depends crucially on the validity of the underlying likelihood function (i.e., the stochastic model of the measured process). Here, we present an HMM analysis scheme that addresses these problems.

At the core of this scheme is the idea that the number of states required to describe the kinetics in a hierarchical energy landscape is not fixed but depends on the time scales of interest (Figure 2).^27,28 Directly estimating HMMs with a few states often yields wrong kinetics,^29,30 as they tend to prefer models whose states have clearly different FRET efficiency. However, in real data, distinct and slowly interconverting conformations may have strongly overlapping FRET efficiency distributions, which are difficult to separate. Therefore, we construct an initial HMM with many states (corresponding to a fine discretization of conformational space). The initial number of states is determined by a validation scheme, which tests reproducibility and consistency of the model with the underlying data set. The initial states are subsequently coarse-grained on the basis of their kinetics.^31,32 This approach allows us to model (coarse) states even when they strongly overlap in their FRET efficiencies and have very irregular (e.g., non-Gaussian) FRET distributions. Our HMM uses a Poissonian likelihood function to model the physical process of photon emission.³³⁻³⁵ This approach is preferable over using Gaussian likelihood functions of the FRET efficiency.²³⁻²⁶ For a detailed discussion, see the Supporting Information. In addition, we have developed an approach to account for the trace-specific background noise.

Figure 2.

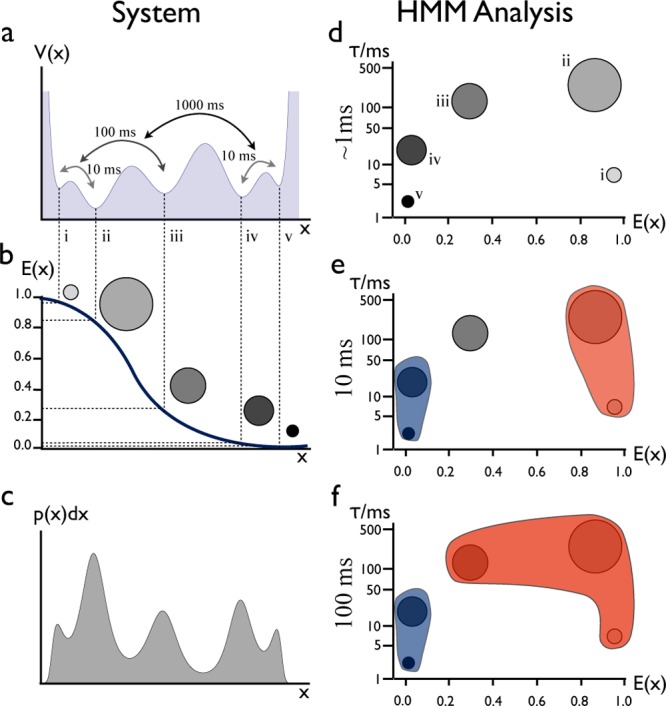
Conceptual illustration of a HMM-based FRET analysis. (a) Hierarchical free energy landscape with various minima (conformations) interconverting on different time scales. (b) A FRET efficiency versus distance curve, with the five conformations in panel a assigned to certain FRET efficiencies (distances). Conformations with suitably long lifetimes can be distinguished by HMM analysis of FRET traces but may have overlapping FRET efficiencies even when they are distinct. (c) Probability density function of finding the system at a certain value of the distance parameter. (d) The states found in the HMM analysis are depicted as disks located in a two-dimensional space of efficiency (abcissa) and lifetime (ordinate). (e, f) Some states kinetically merge on longer observation time scales indicated by the blue and red areas in panels e (τ = 10 ms) and f (τ = 100 ms). For example, state pairs (i, ii) and (iv, v) each merge into a single apparent state for times longer than 10 ms.

Independent HMM analyses were carried out on two differently labeled DAse constructs, referred to as constructs I and II. Altogether, four different data sets were analyzed (DAse construct I at Mg²⁺ concentrations of 0.0, 5.0, and 40.0 mM and DAse construct II at Mg²⁺ concentration 5.0 mM), yielding HMMs with seven to nine conformational states. These HMMs provide comprehensive models of the dynamics on millisecond time scales. We also determined relaxation times, identified the associated conformational transitions by an eigenvector/eigenvalue analysis of the transition matrix,³⁰ and computed the ensemble of RNA folding pathways.³⁶ On the basis of their kinetics, the original states were lumped together to effective five-state (on time scales of tens of milliseconds) and three- or four-state models (on time scales of hundreds of milliseconds). Most notably, we identified consistent, characteristic features of the kinetic network of DAse in all four data sets. To the best of our knowledge, these results represent the most detailed RNA folding models obtained from single-molecule measurements to date. They confirm the hierarchical nature of the RNA folding landscape. Furthermore, they reveal that the transition rates in this landscape change substantially as the Mg²⁺ concentration is varied, while the general topology of the landscape (position of minima, relative height of energy barriers) is not affected. At all Mg²⁺ concentrations, the observed kinetic processes can be attributed to either secondary or tertiary structure rearrangements.

2. Materials and Methods

2.1. Single-Molecule FRET Experiments and Data Processing

By using a combinatorial strategy, we had earlier synthesized a set of nine DAse FRET constructs with dyes attached at different nucleotide positions.⁹ Construct I was chosen for in-depth studies because it showed the most pronounced changes in its FRET histogram with varying Mg²⁺ concentration. Here we have also performed surface-immobilized measurements on a second variant, construct II, because (1) its FRET histogram was multimodal, suggesting that multiple states could be distinguished by the HMM, and (2) it was not too different from construct I and, therefore, could serve for validation (see below).

Single-molecule fluorescence time traces of surface-immobilized DAse were obtained for construct I (Cy3 at U6 and Cy5 at U42) at Mg²⁺ concentrations of 0, 5, and 40 mM and for construct II (Cy3 at the 5′ end and Cy5 at U30) at a Mg²⁺ concentration of 5 mM. Details on the data, the experimental procedures, and the effects of surface immobilization are included in the Supporting Information, Tables S1 and S2 and Figures S2 and S3. For each trace, the rates of the background noise, k_a,bg an k_d,bg, in the acceptor and donor channel, respectively, as well as the amount of spectral crosstalk, χ, from the donor into the acceptor channel were estimated, as described in the Supporting Information.

2.2. HMM Workflow

We have developed an HMM analysis and associated optimization algorithms for single-molecule FRET. The HMM analysis scheme has the following features:

• •The HMM works with discrete photon counts, which are assumed to obey Poissonian statistics (Figure S4, Supporting Information).
• •Background noise levels of measured photon traces are taken into account explicitly by employing an appropriate emission probability.
• •The reproducibility of the HMMs is tested.
• •The number of states of the HMM is maximized under a number of constraints, which ensures that the model reproduces physically and chemically relevant quantities.
• •The final HMM represents a fine discretization into states that, depending on the time scale, are lumped into larger states according to kinetic proximity.

A workflow diagram of the HMM analysis scheme is shown in Figure 3. The algorithms are described in full detail in the Supporting Information, and the salient characteristics of the workflow are discussed in the following sections.

Figure 3.

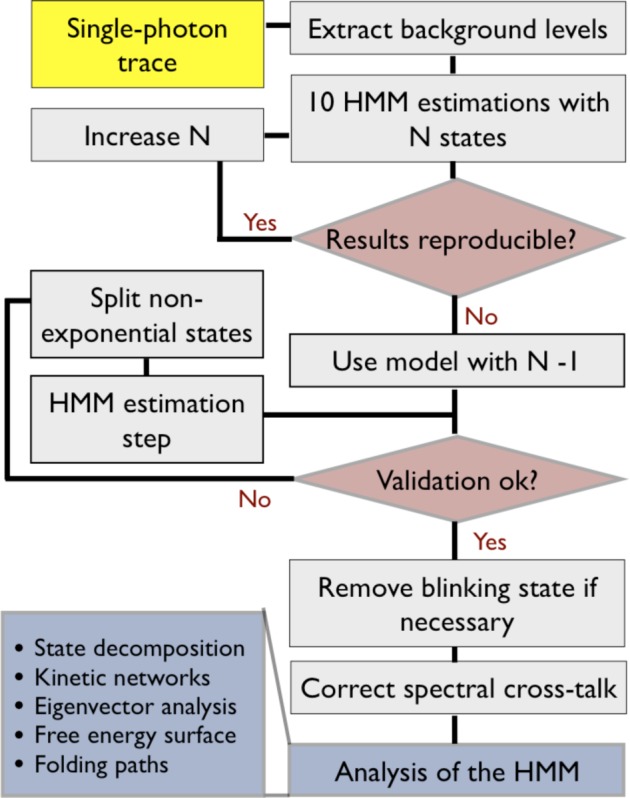
Workflow diagram used for our HMM analysis of single-molecule FRET data.

2.3. Illustration of a HMM

Figure 2 illustrates the type of information conveyed by HMM analyses. Consider the hypothetical energy landscape with five minima in panel a in Figure 2. Each minimum corresponds to a conformational state and is associated with a mean FRET efficiency, E_i (Figure 2b), and a fractional population in equilibrium, π_i (Figure 2c), where i denotes the number of the state. Using HMM analysis, these five states can be extracted from smFRET traces of a molecule diffusing in this free energy landscape. We represent the main characteristics of the states of the HMMs by scatter plots (Figure 2d): Each state is marked by a disc, the position of which encodes the mean FRET efficiency of the state and its lifetime, τ_i. The area of the disc is proportional to the stationary probability π_i of the state, as computed from the HMM.

The HMM transition matrix has eigenvalues corresponding to time scales of transitions and eigenvectors denoting states that interconvert on these time scales. This information induces kinetic clustering. Here, states i and ii interconvert on time scales of 10 ms (Figure 2a). Thus, when computing a FRET histogram with an averaging window much longer than 10 ms, these two states merge into a single apparent state. Likewise, states iv and v kinetically merge for time scales longer than 10 ms, as depicted by the red and blue regions in Figure 2e. States i and ii kinetically merge with state iii for time scales above 100 ms (Figure 2f). Complete equilibration occurs for times longer than 1 s.

In a high-dimensional energy landscape, kinetic merging may not necessarily involve only neighboring states along the FRET efficiency axis. In fact, high FRET efficiency states can merge kinetically with low FRET efficiency states even if there are states with intermediate FRET efficiencies in between.

2.4. Hidden Markov Models for Single-Molecule FRET

Hidden markov models (HMMs)²² are stochastic models, λ = (T, e), of the observed (measured) trace, O = (o₁, ..., o_N), with o_i = (n_a,i, n_d,i) containing the number of photons observed in the acceptor and donor channels at each time step i. In the construction of HMMs, it is assumed that the observation is generated by a hidden Markov chain with transition matrix T, whose states represent regions in the conformational space of the molecule. At every time step in the Markov chain, an additional stochastic process, 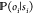, is invoked, which represents the measurement. The emission probability, 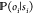, describes the conditional probability of observing the signal, o_i, given that the molecule is currently in conformation (hidden state) s_i. One typically chooses the same functional form of 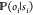for all hidden states but uses a parameter e_j to adapt it to a specific hidden state. The parameters e_j form a vector e and are part of the model λ. The HMM optimization problem maximizes the likelihood (i.e., the conditional probability of observing the measured trace O, given that the molecule is accurately described by the model λ = (T, e)):

1

over all values of (T, e) and all possible hidden paths. For a given number of states, N, the model λ consists of an N × N transition matrix, T, and of a vector of observation parameters e, of length N. HMM classes differ by the way that the hidden process and the measurement process are modeled and by the way that the corresponding parameters are optimized.

2.5. The Emission Probability for FRET Experiments Including Background Correction

It is crucial to choose an emission probability, 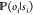, that models the measurement process as accurately as possible. The HMM scheme presented here works with discrete photon counts. The arrival times of the photons are assumed to obey Poissonian statistics, which is validated in Figure S4 (Supporting Information). The functional form of the emission probability is hence

2

Pois(k, n) is a Poisson distribution of variable n with rate coefficient k. The acceptor and donor photon count rates, k_a and k_d, are given as

3

where E_i is the apparent FRET efficiency of the current hidden state s_i and k_mol is the detection rate of photons emitted by the labeled molecule (through either the donor or the acceptor).³³⁻³⁵

A problem inherent in the experimental data is the presence of trace-dependent background noise, which may cause identical conformational states to display different apparent FRET efficiencies in different time traces. The trace specific background rates, k_a,bg and k_d,bg, can be estimated from the bleached phase of the measured photon traces. Given these rates, we derive a likelihood of observing (n_a, n_d) photons during a time step, Δt, in the acceptor and donor channels, respectively (see the Supporting Information). The emission probability has the functional form given in eq 2, but the photon count rates are now given as

4

We assume that background noise may vary from trace to trace but that all other measurement errors, including spectral cross-talk and differences in the quantum yield of the chromophores, depend on the conformational state but are identical for different traces. Then, e contains the apparent FRET efficiencies (without background noise) of the hidden states. These apparent FRET efficiencies can be corrected for spectral cross-talk a posteriori to obtain the true FRET efficiencies (see the Supporting Information).

2.6. HMM Optimization and Number of Hidden States

HMM optimization is done by using the expectation-maximization algorithm, which finds a local maximum of 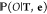from an initial guess of the parameters (T, e). To facilitate finding the global optimum, the HMMs presented here are obtained by first running 100 explorations that optimize random starting values of (T, e) for a few steps only. Subsequently, the parameter set with the largest likelihood is optimized to full convergence. Nonetheless, the HMM algorithm might find different local maxima for different initial parameters. Hence, for each Mg²⁺ concentration, we compute 10 HMMs in the described way to test for reproducibility. Two HMMs are accepted as identical if their log-likelihoods differ by less than 1.0. By a heuristic criterion, an HMM optimization is reproducible if identical maximum likelihood HMMs are found in at least 2 out of the 10 trials.

The number of states, N, is an input parameter for the HMM optimization algorithm. As argued in the Supporting Information, information-criteria-based choices of the number of states are inadequate for the present data. To determine the number of hidden states, we instead adopt a viewpoint for the construction of direct Markov models that is well established in the community:³⁰ Rather than finding the “ideal” number of states to statistically classify the data, we require the HMM to have sufficiently many states. Consequently, the resulting discretization of state space will be fine enough that the HMMs can reproduce the stationary and long-time kinetic behavior of the data. The resulting states can subsequently be grouped according to kinetic connectivity given by T, as described in refs (31 and 32) and illustrated in Figure 2. Following this approach, we build HMMs for a varying number of states, N = 2, 3, ..., and choose the largest number of states for which HMMs can be constructed reproducibly.

2.7. HMM Validation

Different tests were used to check whether the HMMs are consistent with the data set from which they were parametrized, and whether the hidden paths obtained from the HMMs are consistent with Markovian dynamics. The consistency of the HMM with the underlying data set was tested by comparing FRET efficiency histograms obtained from the data with histograms estimated from the HMMs. For this test, we used time windows between 10 and 100 ms. As previously discussed,³⁷ this approach tests both the stationary and kinetic properties of the model. The comparison was performed for background-corrected FRET efficiency distributions. The data-based distributions were obtained using the likelihood from eq 2, as described in the Supporting Information. The HMM-based distributions were obtained by sampling hidden trajectories of the time window length from an equilibrium distribution, and then generating artificial photon counts using Poisson statistics with the appropriate output rates (Figure 4a and Figures S6a, S7a, and S8a, Supporting Information). The Markovianity of individual states was tested by inspecting their lifetime distributions, which can be computed from the maximum-likelihood hidden paths, ŝ(t), of the HMM. A single exponential decay in these distributions is consistent with Markovian dynamics (Figure 4b). States that failed this test were split using a newly developed Bayesian model selection algorithm (Supporting Information). The overall Markovianity of the HMMs was tested using the implied time scales test³⁸ that is frequently used for simulation-based Markov state models. To this end, the relaxation time scales, t_i^HMM = −Δt/ln λ_i, were computed, where λ_i^HMM are the eigenvalues of the HMM transition matrix T. These are compared to the implied time scales of a Markov model T̂(τ) constructed from the maximum likelihood hidden paths, ŝ(t), for different lag times τ. If the overall dynamics is Markovian, these time scales should be independent of the lag time τ used to compute them, hence yielding constant functions in Figure 4c. As an additional test, they should agree with the HMM time scales, t_i. Figure S9 (Supporting Information) shows FRET traces colored according to the hidden states in the final model.

Figure 4.

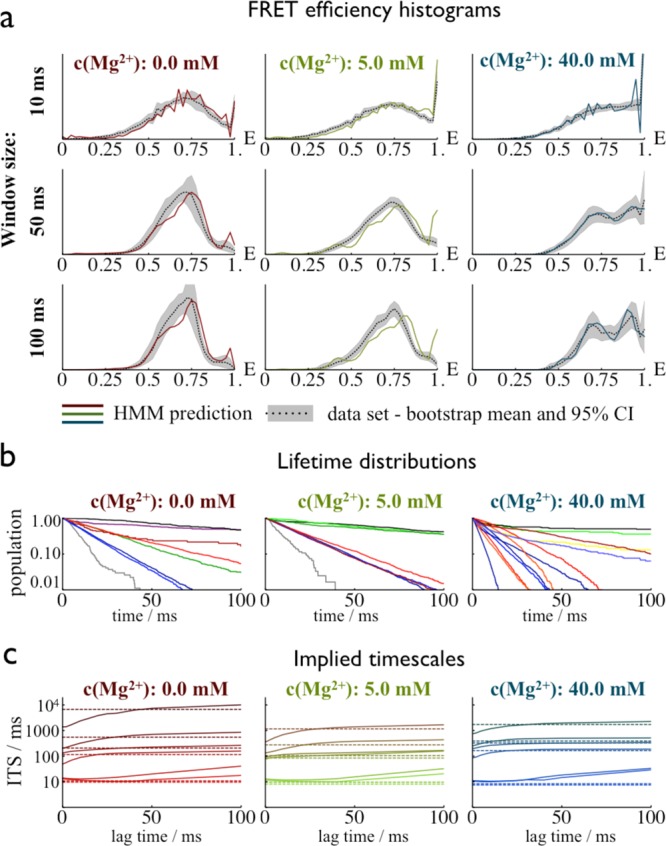
Validation of the hidden Markov models. (a) Dependence of the FRET efficiency histograms on the lengths of the time windows (10, 50, and 100 ms). Dashed colored lines, prediction from the hidden Markov model; gray areas/dotted black lines, estimation from the smFRET data set (bootstrapping mean/95% confidence interval). (b) Lifetime distributions of the individual states calculated from the maximum-likelihood paths. Line coloring corresponds to the coloring of the states in Figure 5. (c) Implied time scales, indicating that the long-time kinetics of the hidden paths is Markovian and converges to time scales similar to those found in the HMM. The divergence of the shortest time scales at larger lag times is expected and due to numerical problems.⁴⁸

3. Results and Discussion

3.1. FRET Efficiency Histograms

We analyzed three sets of smFRET traces of DAse construct I (chromophores attached to residues 6 and 42, see Figure 1), measured at different Mg²⁺ concentrations, 0.0, 5.0, and 40.0 mM. Background-corrected FRET efficiency distributions were calculated from these data sets by using the likelihood (eq 2) and a bootstrapping procedure to estimate the uncertainty in the data (dotted gray lines and gray areas in Figure 4a). These distributions exhibit features that have been described earlier.⁹ Two ensembles of states can be visually distinguished: a broad intermediate state in the FRET efficiency range 0.4–0.8 and a putative native state at efficiency values of 0.9–1.0. With increasing Mg²⁺ concentration, the populations shift to states with high FRET efficiency. In ref (9), it was already hypothesized that the broad ensemble at intermediate FRET efficiencies may consist of multiple conformational states with overlapping FRET efficiency distributions.

3.2. HMM Construction, Validation, and Refinement

HMMs were constructed for the smFRET data sets as described in the Materials and Methods section. The largest number of states for which HMMs could be reproducibly obtained was eight (0 mM Mg²⁺), eight (5 mM Mg²⁺), and seven (40 mM Mg²⁺) states, where we used the optimization protocol described in the Materials and Methods section. The eight-state models for 0 and 5 mM Mg²⁺ passed the validation test (Figure 4). A single, weakly populated state with FRET efficiency E ≈ 0, which was assigned to an acceptor blinking state, was removed from these models a posteriori. The seven-state model at 40 mM Mg²⁺ required an intermediate step, in which non-Markovian states were split and regrouped according to kinetic proximity, yielding a nine-state model. (See the Supporting Information for a detailed description of the protocol employed.)

To test whether the remaining nonexponentiality came from an actual non-Markovianity of the discrete state dynamics or just from spurious transitions generated from the estimation of the maximum likelihood, we conducted the implied time scale test as described in the Materials and Methods section. The results shown in Figure 4c demonstrate that the maximum likelihood hidden paths, ŝ(t), are non-Markovian in all models at short time scales but then converge to approximately constant time scale estimates at lag times of 10–30 ms. The time scales agree with the time scales estimated from the HMM transition matrix, indicating that the kinetics of all three HMMs are consistent with the data.

Note that the HMMs for the three different Mg²⁺ concentrations were constructed independently of each other. Therefore, when similar or consistent features are found across all three Mg²⁺ concentrations, this is a two-fold validation of an observation.

3.3. Conformational States

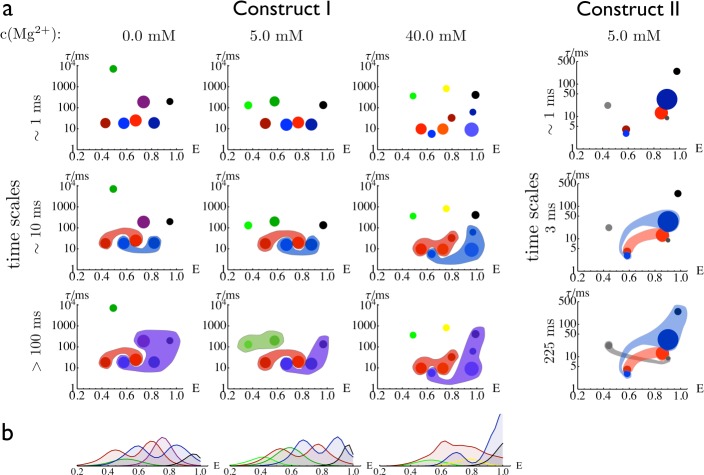
The scatter plots in Figure 5a (upper row) show the main characteristics of the (hidden) states of the HMMs: Each state is represented by a disc whose position indicates the mean FRET efficiency of the state and its lifetime τ_i = −Δt/ln T_ii, where Δt is the time step of the HMM transition matrix and T_ii are the diagonal elements of this matrix. The area of the disc is proportional to the stationary probability π_i of the state as computed from the HMM. The states that consistently appear in construct I at different Mg²⁺ concentrations are depicted in the same color (i.e., black, blue, red, and green states). The purple state at 0.0 mM Mg²⁺ could not be matched to any state at higher Mg²⁺ concentrations. Likewise, the yellow state only appears at 40.0 mM Mg²⁺.

Figure 5.

Conformational states and subensembles found by the HMM analysis of construct I and construct II. (a) First row: State parameters of the hidden Markov models which are for each state i: the FRET efficiency E_i (abcissa), the state lifetime τ_i (ordinate), and the equilibrium population π_i (disc size). Second and third rows: State decomposition for time scales of 10 and >100 ms. (b) FRET histograms of the subensembles of the states shown in the second row of panel a.

A feature found for all Mg²⁺ concentrations is the black high-FRET efficiency state. It has a relatively small stationary probability but a long lifetime at all Mg²⁺ conditions. The region of intermediate FRET efficiencies is populated mostly by short-lived states (blue, red), and a few long-lived states with low FRET efficiencies (green).

Remarkably, the states appearing at multiple Mg²⁺ concentrations show only rather subtle changes. There are two cooperative effects upon Mg²⁺ increase: (i) all states shift to slightly higher FRET efficiencies, indicating that Mg²⁺ causes these conformations to become more compact, (ii) the intermediate-efficiency purple state is depopulated with increasing Mg²⁺, while some substates with higher FRET efficiencies (light red state, which is split into an orange and a dark red state at 40 mM Mg²⁺, as well as the dark blue state) become more populated at high Mg²⁺ concentrations. The populations of the other red and blue states, as well as the black state, show surprisingly little dependence on the Mg²⁺ concentration, indicating that the associated conformations do not experience stabilization by Mg²⁺ ions.

To better understand the nature of the conformational states of the HMMs, we have investigated their kinetics. Detailed information is presented by the networks plotted in Figures S10–S13 (Supporting Information). Alternatively, an eigenvector/eigenvalue analysis of the transition matrix T allows conformational states interconverting faster than the time scale of interest to be grouped (Figures S10–S13, Supporting Information).^30,31 The second row of Figure 5a shows a striking feature found independently for the HMMs at all Mg²⁺ concentrations: At a few tens of milliseconds, the substates of the red subensemble as well as the substates of the blue subensemble interconvert. We note that these substates have very different FRET efficiencies. Consequently, kinetic proximitiy and proximity on the FRET axis are, in general, unrelated properties. This finding is emphasized by the FRET efficiency histograms of the corresponding subsembles in Figure 5b, which were constructed by partitioning the photon traces according to the associated hidden states. The blue and red subensembles are doubly peaked because they are composed of multiple hidden states. In addition, these subensembles overlap strongly, clearly showing why the present single-molecule FRET data were difficult to model kinetically, and emphasizing the usefulness of a detailed HMM analysis for dissecting them.

For all Mg²⁺ concentrations, the high-efficiency peak in the FRET histograms of the blue subensemble overlaps with the high-efficiency black state, indicating that the high-FRET-efficiency peak identified in ref (9) consists of two states, one of which rapidly interconverts with a state of intermediate FRET efficiency (blue) and is stabilized by Mg²⁺, and a long-lived high-efficiency state (black), which is insensitive to Mg²⁺. In Figure 5a, the third row shows that, on time scales of a few hundred ms, the long-lived state (black) interconverts with the blue subsemble. The mixing time for all subensembles is on the order of seconds (see Figure 6). These results indicate the presence of a hierarchical energy landscape, with different processes occurring on very different time scales, ranging from a few milliseconds to 1 s.

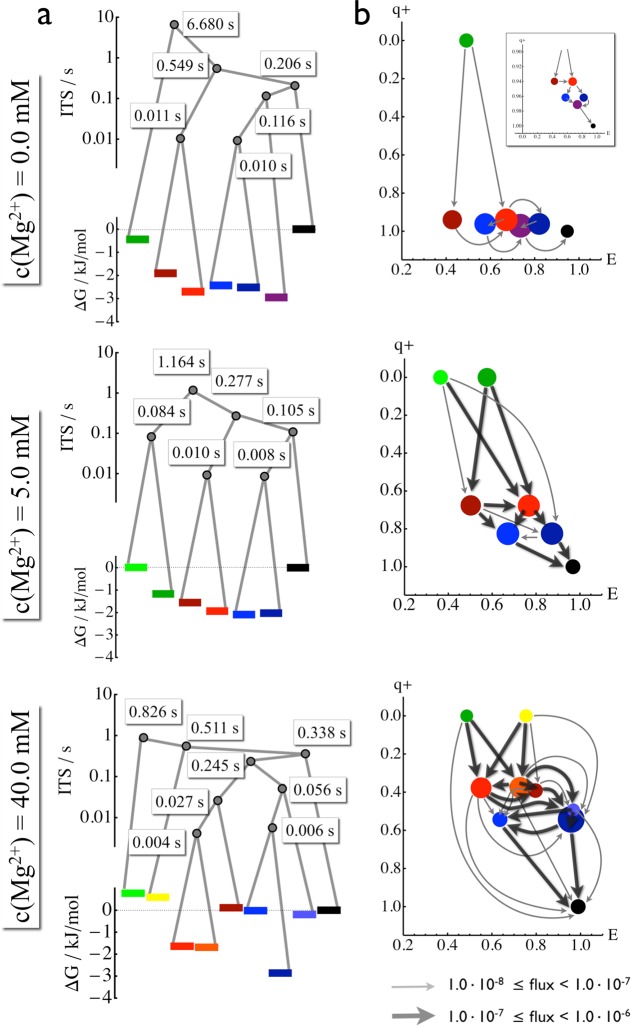
Figure 6.

Free energy landscape and folding pathways. States are indicated by bars or discs with the same colors used in Figure 5. (a) Free energy landscape and hierarchy of the kinetic processes. Bars indicate the free energy of states. Gray bullets indicate transition states facilitating that states or sets of states kinetically merge at longer time scales. The corresponding time scales are given in seconds. (b) The complete ensemble of folding pathways from the least compact states (green/yellow) to the most compact state (black). The states are positioned depending on their mean FRET efficiency (abcissa) and the probability of folding (committor, q⁺, ordinate). The thickness of an arrow is proportional to the probability that a green/yellow state will fold along this pathway.

On the basis of the processes depicted in Figure 5, we find fast interconversion between the “open” (E ≈ 0.5) and “closed” (E > 0.7) states within the blue and red subensembles, while the exchange dynamics between these subensembles happens much slower. We propose that the states within each subensemble (with a given color in Figure 5) have similar secondary structures yet different tertiary structures, interconverting rapidly without breaking large strands of Watson–Crick base pairs. This proposition is supported by the fact that, at high Mg²⁺ concentrations, the compact parts of the red and blue subensemble are stabilized. Different subensembles are proposed to correspond to different secondary structures because they are long-lived, suggesting that the stable Watson–Crick base pairs need to be broken in order to transit to another subensemble.

3.4. Kinetic Analysis

Figure 6 shows a detailed kinetic analysis and proposes the folding mechanism. The connectivity between different subensembles (and, thus, presumably different secondary structures) is similar at all Mg²⁺ concentrations. The high-efficiency (black) state is connected to the blue subensemble in the presence of Mg²⁺ (5 and 40 mM) directly and, at 0 mM Mg²⁺, via the purple intermediate. The blue subensemble is connected to the red subensemble. Finally, the green states are connected to the red subensemble. Figure 6a illustrates this connectivity, and the free energies of these conformations as well as the transition states (see the Materials and Methods section).

This connectivity suggests an ordering of subensembles from the least compact (lowest FRET efficiencies) to the most compact (highest FRET efficiencies) which can be found at all Mg²⁺ concentrations: (1) green, (2) red, (3) blue, and (4) black. The green states are long-lived but low-efficiency states. The fact that they have high lifetimes and FRET efficiencies that are much greater than zero suggests that they still have some secondary structure, although probably not the native one. They are therefore called “misfolded”.

This ordering suggests to study the transition pathways from the misfolded states (green) to the most compact state (black). Transition path theory^39,40 provides the basis for calculating the pathways between two subensembles. We use the protocol and equations described in ref (36) employing the implementation in the EMMA software.⁴¹ A transition pathway is defined as a series of transitions that lead from the misfolded to the native state without returning to the misfolded state. Figure 6b locates the states by their FRET efficiency, and by the committor value (vertical axis), i.e., the probability of the system, when being in this state, to move “forward” and fold toward the black state, rather than misfold back to the green state. The committor value q⁺ = 0.5 designates states in which the molecule is equally likely to go either way. These states effectively act as transition states in the folding pathway. Note that there is a continuous shift of these transition states with increasing Mg²⁺ concentration. At 0 mM Mg²⁺, the transition state lies between the green and red subensembles. Once a molecule has reached the red subensemble, it is likely to continue folding to the black state. With increasing Mg²⁺ concentration, the red and blue subensembles become more and more kinetic intermediates, and lie at committor values around 0.5 for 40 mM Mg²⁺.

Figure 6b shows the probability fluxes of transition pathways from misfolded states to the folded state. The size of the arrows indicates the probability flux, which is related to the folding rate. Without Mg²⁺, the folding rate k_AB is about 0.09 s^–1, and increases to 0.28 s^–1 for 5 mM and 0.17 s^–1 for 40 mM Mg²⁺. The strong increase in folding rate from 0 to 5 mM Mg²⁺ is mainly due to a lowering of the transition state energy, while the decrease in folding rate from 5 to 40 mM Mg²⁺ is mainly due to an increased stability of the dark blue intermediate state (compare Figure 6a and b). Moreover, it is apparent that addition of Mg²⁺ increases the number of accessible pathways, making the folding process more parallel. Two main mechanisms are observed at all Mg²⁺ concentrations: a compact folding mechanism, in which the green misfolded state refolds via the higher FRET efficiency substates of red and blue toward the black state, and an “close–open–close” mechanism, in which the green state folds via the open substates, or via successive closing, opening, and closing, i.e., involving tertiary unfolded states. Both types of pathways have similar weights, with some preference for close–open–close pathways at low Mg²⁺ concentrations and a slight preference for compact pathways at high Mg²⁺ concentrations.

3.5. Validation by a Second Construct

To further confirm our findings, we performed a fourth independent measurement on a DAse (construct II) with a different set of label positions. The changed label positions should mainly affect the FRET efficiencies of states. If they do not introduce major energetic conflicts, the state probabilities, time scales, and the kinetic connectivity should remain comparable.

Single-molecule FRET data were recorded, and an HMM was computed using the same approach as above. A seven-state model was found to pass the validation test (see Figure S14a and S14b, Supporting Information). Like construct I, construct II exhibits low-FRET, “open” states at efficiencies of 0.4–0.6 and high-FRET, “closed” states at efficiencies above 0.8. As for construct I, two pairs of rapidly interconverting states, each with a low- and a high-FRET state, were found. Additionally, a single stable state with high efficiency was also identified. Consequently, the red, blue, and black subensembles of construct II match the corresponding subensembles in construct I and, thus, can be identified in all experimental data with high confidence (see Figure 5a).

Moreover, the time scales found in constructs I and II are in qualitative agreement (see Figure S14c in the Supporting Information). Open and closed states of the red and blue subensembles interconvert at time scales of a few milliseconds (≤10 ms in construct I, 3 ms in construct II). At time scales of 100 ms to seconds, (i) the blue ensemble merges with the black state and (ii) the red and blue ensembles kinetically merge. At low Mg²⁺ concentrations, the blue–black interconversion is several 100 ms faster than the blue–red interconversion, while, at 40 mM Mg²⁺, the two processes happen at about the same time scales (Figure S14c, Supporting Information).

The gray states in construct II and the green/yellow states in construct I do not have clear corresponding states in the other construct. These states may be affected by the labeling. For example, the presence of a label in a particular position may prevent certain structures from forming. In the following discussion, we will thus concentrate on those states that can be safely matched across all data sets (red, blue, and black).

Note that, due to the reduced state lifetimes in construct II, the partitioning of the photon traces resulted in subtraces which were too short for a histogram analysis. Hence, the subensemble FRET histograms could not be generated (see Figure 5b).

4. Discussion

A kinetic pattern is found consistently for different Mg²⁺ ion concentrations and for different attachment points of the chromophores: (i) a long-lived, high-FRET-efficiency state (black), (ii) two ensembles of states (red, blue) comprising rapidly interconverting open and closed states, the ratio of which depends on Mg²⁺, and (iii) a linear connection between the three subensembles (red, blue, black). The long interconversion times along this linear connection suggest that these transitions involve breaking and reforming of Watson–Crick base pairs.

To investigate whether there are secondary structures consistent with this pattern, minimum energy secondary structures of the DAse were calculated using the Vienna RNA WebServer^5,42 (see the Supporting Information). The algorithm correctly identified the secondary structure of the known folded state (excluding the pseudoknot connectivity) as the lowest free-energy structure. Two alternative secondary structures with low free energies (ΔG < 1.4 kJ/mol above native, i.e., accessible at room temperature) were also identified. These structures (labeled 2 and 3) are shown along with the secondary structure of the folded state (labeled 1) in Figure 7. Although they are very close in energy and structurally very similar to each other, structures 2 and 3 differ from structure 1 in that helix II is broken and helix I is prolonged by two base pairs. All other secondary structures identified by the algorithm had estimated free energy differences of ΔG > 9.5 kJ/mol with respect to structure 1.

Figure 7.

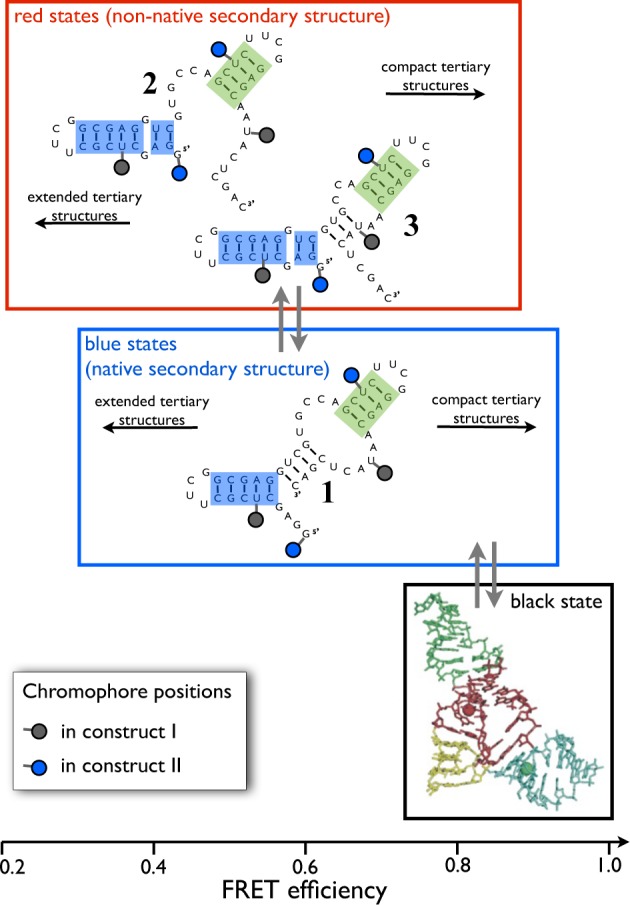
Proposed folding mechanism. Secondary structures were predicted by the Vienna RNA server.^5,42 The red set of states has a non-native secondary structure but includes both open (low-FRET) tertiary structures and compact (high-FRET) tertiary structures. The blue set of states has the native secondary structure but also includes both open and compact tertiary structures. Compact structures in the red and blue sets are stabilized by Mg²⁺. The black state has the native secondary and tertiary fold. In contrast to the compact blue state, it is additionally stabilized by the tertiary Watson–Crick pairs that form the pseudoknot.

In the absence of stabilizing tertiary interactions, secondary structures 1, 2, and 3 facilitate transitions between open and compact states, associated with large fluctuations in the donor–acceptor distance in both constructs. Therefore, they have properties matching those found for the blue and red subensembles in the HMM analysis. The black state displays exclusively high FRET efficiencies in all constructs under all conditions and is thus likely a compact state with a well-defined tertiary structure. Its long lifetime and the fact that its population does not vary strongly with the Mg²⁺ concentration suggest that it is stabilized by base-pairing rather than Mg²⁺ ions. Therefore, we propose that the black state represents the tertiary folded structure including the pseudoknot topology. The pseudoknot base pairs (G1–C26, G2–C25, A3–U45, G4–C44; see Figure 1) are consistent with stable interactions that do not depend on Mg²⁺. Their formation stabilizes an already compact structure with the correct secondary fold so as to acquire a well-defined tertiary structure. This proposal is supported by computer simulations which show that the active site of DAse is distorted if Mg²⁺ is removed (explaining the loss in catalytic activity) but the overall lambda-shaped tertiary structure stays intact.¹⁵

Since the blue subensemble acts as a precursor to the black tertiary folded structure (linearly connected folding path, Figure 6), it is only logical to match the blue state with the secondary structure of the folded state (structure 1). The native secondary structure still facilitates extended and compact states. Like the fully native black state, the high-efficiency blue states are compact and possess the correct native secondary structure, but in contrast to the black state, they lack the pseudoknot base pairs, which stabilize the native tertiary fold. Consistently, the probability of extended versus compact blue states depends on the concentration of Mg²⁺ ions that are required to stabilize the compact state in the absence of tertiary base pairs.

Consequently, the red ensemble contains structures 2 and/or 3, i.e., extended and compact states with non-native secondary structure. This assignment leads to a putative folding mechanism summarized in Figure 7.

The proposed assignment is consistent not only with the kinetic connectivity and the Mg²⁺-dependent equilibrium populations but also with the observed time scales. The fluctuation between open and compact conformations within the blue and red ensembles involves no or little secondary structure change, consistent with relatively short transition time scales (Figures 5 and 6). In contrast, a transition from the red to the blue subensemble involves rupture of Watson–Crick pairs, which is consistent with slower transition time scales of hundreds of milliseconds (Figures 5 and 6). Likewise, the change of tertiary base-pairing is consistent with long transition time scales between the blue and black states and the long lifetime of the black native state.

The kinetic model found here and our proposed folding mechanism exhibits a number of features consistent with previous findings or hypotheses for other RNA systems. In particular, secondary and tertiary structure formation has been proposed to be kinetically decoupled, such that secondary structure elements can exist without further stabilization by specific tertiary interactions.⁵³ For the Tetrahymena thermophila ribosome, metastable structures with a partially misfolded secondary structure have been described, lending credibility to the present assignment of the red subensemble to structures 2 and/or 3.⁴⁹⁻⁵¹ In addition, other RNAs have been proposed to fold via multiple parallel pathways.^49,50,52

To the best of our knowledge, we have presented the most detailed experimentally derived model of an RNA folding mechanism, providing a kinetic model connecting different secondary and tertiary stabilized structures, and showing how they are orchestrated during the folding pathways. The multitude of time scales found in the data provide direct evidence that the RNA folding landscape is hierarchical and that secondary and tertiary structure formation occur on different time scales. The techniques described here also facilitate detailed kinetic models to be derived for other macromolecular systems.

As yet, the field is still lacking an experiment that could simultaneously resolve kinetics and the structures of the individual states in detail. Unfortunately, computational approaches cannot step in here. With folding times on the order of seconds, the dynamics are as yet out of reach for direct molecular dynamics (MD) simulation. Over time, however, enhanced sampling strategies may help access these processes.⁴³ However, molecular modeling and MD simulation may be useful for exploring the local dynamics within individual states, and by using new biophysical techniques, the distribution of measurable FRET values can be computed and compared to the subensemble distributions shown in Figure 5b.^44,45 On the experimental side, using multicolor-FRET⁴⁶ or the systematic reconciliation of multiple dual-color-FRET experiments⁴⁷ may provide distance constraints to resolve the structures in more detail. Finally, the combination of FRET and site-specific fluorescence quenching may also be employed to disentangle the tertiary dynamics from secondary structure formation.

Supporting Information Available

Theoretical background on the likelihood function and the HMM. Estimation algorithms for the HMM. Theoretical background and algorithms for the HMM validation and refinement. Diels–Alderase measurement and analysis protocol. Statistics of the data set (Figure S2, Tables S1 and S2). Effects of the surface immobilization (Figure S3). Statistics of the photon arrival time (Figure S4). Validation of the HMMs (Figures S6–S8 and S14). Additional kinetic analyses (Figures S9–S13). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.