Local packing modulates diversity of iron pathways and cooperative behavior in eukaryotic and prokaryotic ferritins

Abstract

Ferritin-like molecules show a remarkable combination of the evolutionary conserved activity of iron uptake and release that engage different pores in the conserved ferritin shell. It was hypothesized that pore selection and iron traffic depend on dynamic allostery with no conformational changes in the backbone. In this study, we detect the allosteric networks in Pseudomonas aeruginosa bacterioferritin (BfrB), bacterial ferritin (FtnA), and bullfrog M and L ferritins (Ftns) by a network-weaving algorithm (NWA) that passes threads of an allosteric network through highly correlated residues using hierarchical clustering. The residue-residue correlations are calculated in the packing-on elastic network model that introduces atom packing into the common packing-off model. Applying NWA revealed that each of the molecules has an extended allosteric network mostly buried inside the ferritin shell. The structure of the networks is consistent with experimental observations of iron transport: The allosteric networks in BfrB and FtnA connect the ferroxidase center with the 4-fold pores and B-pores, leaving the 3-fold pores unengaged. In contrast, the allosteric network directly links the 3-fold pores with the 4-fold pores in M and L Ftns. The majority of the network residues are either on the inner surface or buried inside the subunit fold or at the subunit interfaces. We hypothesize that the ferritin structures evolved in a way to limit the influence of functionally unrelated events in the cytoplasm on the allosteric network to maintain stability of the translocation mechanisms. We showed that the residue-residue correlations and the resultant long-range cooperativity depend on the ferritin shell packing, which, in turn, depends on protein sequence composition. Switching from the packing-on to the packing-off model reduces correlations by 35%–38% so that no allosteric network can be found. The influence of the side-chain packing on the allosteric networks explains the diversity in mechanisms of iron traffic suggested by experimental approaches.

INTRODUCTION

The concept of regulatory intra-molecular networks is widely used to describe dynamics and allostery in biological machines.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} Such networks act by propagating energy and structure perturbation from one functional site (e.g., an effector binding site) to another, distal site (e.g., a substrate binding site). The networks are readily revealed when the constituting residues experience conformational changes that distinguish the active and inactive protein conformations.^{11, 12} However, many allosteric proteins do not show significant conformational changes, suggesting that allosteric behavior can arise out of changes in highly correlated molecular fluctuations.^{13, 14, 15, 16} Although, the understanding of allostery with and without a conformational change has accumulated, the prediction of allosteric networks remains a significant challenge. Effective network modeling is also highly sought for the development of a new class of drugs—allosteric inhibitors of protein-protein interactions.^{17, 18}

A variety of allosteric mechanisms observed among homologous proteins is a biological phenomenon attracting a great deal of interest to the corresponding protein families.¹⁹ The ferritin (Ftn) and bacterioferritin (Bfr) proteins of the ferritin-like superfamily constitute a prime example of a remarkable combination of evolutionary conserved iron uptake and release processes that are integrated with a variety in iron translocation mechanisms,^{20, 21, 22} which may depend on allostery with no changes in molecular architecture at the backbone level. Ferritin and ferritin-like molecules (Bfr and bacterial Ftn) are supramolecular assemblies built from 24 subunits into a nearly spherical architecture with a hollow core (Figure 1) where up to 4000 iron ions can be stored as a ferric mineral that is protected from indiscriminant cellular reducing agents. When iron is needed for metabolism, the ferric mineral is reduced and ferrous ion exits the interior cavity by traversing the ferritin shell. Details of the specific protein-protein interactions that are necessary to control the outflow of iron from the ferritin shell are just beginning to emerge.²³

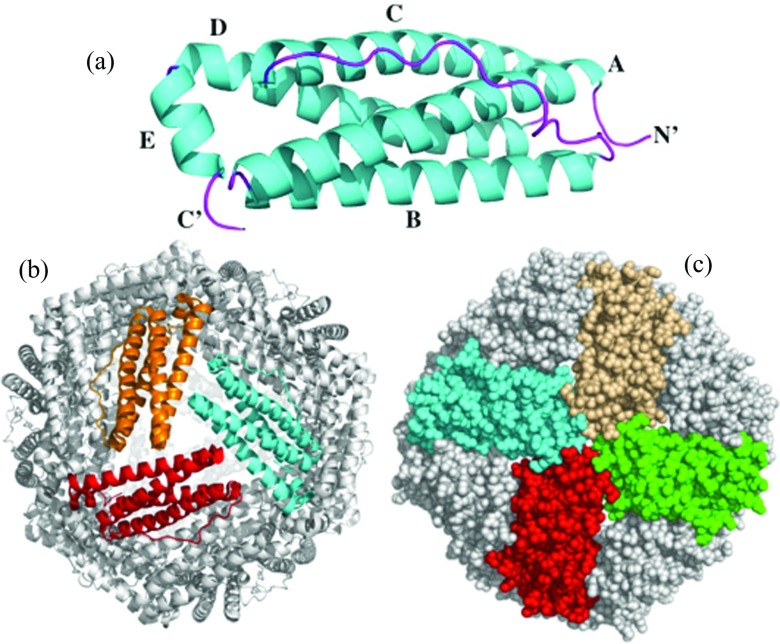
Figure 1.

Structural organization of Pa BfrB. (a) The subunit, (b) the 24-mer view down a 3-fold axis of symmetry, and (c) a 4-fold axis of symmetry. Sphere representation illustrates four B-bores surrounding a 4-fold pore.

It is thought that iron translocation across the ferritin shell requires cooperative motions of residues aligning the path. In the process of iron capture and storage, iron traverses from the ferritin exterior surface to the interior cavity via a ferroxidase center, where soluble Fe²⁺ is oxidized to Fe³⁺.²⁰ A ferroxidase center is located in the middle of each subunit in Bfrs and bacterial Ftn, and in the heavy (H) type and M-type subunits of eukaryotic Ftns. Release of iron from the ferritin cavity requires reduction of ferric iron in the interior ferritin cavity and egress of ferrous ions via pores in the protein shell. The processes of iron uptake and release are thought to include yet unknown import and export pathways of anions (hydroxide and phosphate ions) that balance the charge of a growing or shrinking ferric iron mineral.^{24, 25} In addition to the ferroxidase center, iron traffic in and out of Ftns and Bfrs is thought to proceed via different types of pores passing through the ferritin shell (Fig. 1). The B-pores located at the intersection of three subunits are observed in the structures of Bfrs and bacterial Ftns only, and 3- and 4-fold pores aligned with the 3- and 4-fold axes of symmetry in the structures (Fig. 1). The 3-fold pores are considered to be the main channels of iron traffic in eukaryotic ferritins,²¹ whereas the ferroxidase pores and the B-pores are the likely conduits for iron ions in prokaryotic Bfrs.^{22, 26} The existence of distinct iron pathways suggests sequence-based variability in the underlying allosteric networks within the ferritin family, impeding application of the evolutionary approaches to the conserved networks.^{3, 4, 5, 6} Despite the increasing number of Ftns and Bfrs crystallized recently, the structural basis of cooperative dynamics and its relationship to the ferritin sequence are still unclear.

Current structure-based approaches to allostery include ensemble-based approaches,^{1, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37} 3D graph-based models of molecular rigidity,^{8, 38} and elastic network models (ENMs).^{39, 40, 41, 42, 43, 44, 45, 46, 47, 48} Ensemble-based modeling requires generating large conformational ensembles via conventional or accelerated molecular dynamics or other sampling algorithms without solving explicit equations of motion. These methods have been used to successfully predict the allosteric networks, but are sensitive to the size of the systems and the time scale of the allosteric transitions.^{49, 50} The Pseudomonas aeruginosa bacterioferritin (Pa BfrB), Pseudomonas aeruginosa ferritin (Pa FtnA), and bullfrog M and L ferritins considered here are large macromolecules comprising between 3696 and 4224 residues (see Figure 1 and Tables S1 and S2 and Figure S1 in the supplementary material⁵¹). Elastic network models overcome the size limitation by reducing an all-atom representation of a protein to a coarse-grained one, represented by Cα atoms. The methods based on normal mode analysis (NMA) in ENMs have been used to detect allosteric coupling in proteins that show conformational change in the backbone only,^{40, 43, 45, 46, 47, 52} because by design a Cα-based model cannot address cooperative motions in the side chains. The Ftns and Bfrs have a highly conserved architecture. The largest backbone root-mean-square deviation (RMSD) between the molecules considered here is 1.9 Å (Table S1 in the supplementary material⁵¹). This suggests that if the shape-dependent modes are in charge of allostery in Ftns and Bfrs, then mammalian and bacterial ferritins, as well as bacterioferritins should show high similarity in cooperative motions and so in mechanisms of iron trafficking, when in fact there is significant body of experimental data suggesting the opposite.^{20, 21, 22} Consequently, we pursued a hypothesis that variations in local dynamics are responsible for the dissimilarities between the iron translocation mechanisms in Ftns and Bfrs. Local atom and residue fluctuations depend strongly on intra-protein packing,^{53, 54, 55} which is a major determinant of protein structure⁵⁶ not accounted for in common Cα-based ENMs. The importance of packing is also supported by the observation of rigid pathways coupling effector and catalytic sites⁸ and long-range correlations between the side-chain motions sampled on a fixed backbone.³³ Hence, sequence variations in the different ferritin-like molecules (eukaryotic Ftn, bacterial Ftn, and Bfr) result in dissimilar packing within the conserved ferritin shell architecture and therefore cause different local dynamics in different ferritins. Our goal is to find out how these local variations orchestrate a globally different allosteric behavior. In order to address these issues, we applied the packing-on and packing-off ENMs in conjunction with a novel network-weaving algorithm (NWA; see Materials and Methods) to detect and characterize allosteric networks in Pa BfrB, Pa FtnA, and bullfrog M and L Ftns via correlation analysis of residue fluctuations. The four types of Ftn chosen for the study are representatives of the large ferritin-like superfamily. The packing-on model⁵⁴ explicitly introduces the atom-packing factor into the original anisotropic network model, ANM,⁵⁷ and is derived by shifting the Cα-based nodes of ANM to the residue centers of mass. The packing-off model is derived by turning off the sensitivity to atom packing in the packing-on model. The network-weaving algorithm passes threads of an allosteric network through highly correlated residues (correlation ⩾0.5) in agglomerative manner using hierarchical clustering.

The results show that each type of ferritin-like molecule has an extended network of highly correlated residues, connecting distant pores and the ferroxidase center. Most of the network residues are found on the wall lining the inside cavity (inner surface), or are buried inside the subunits or at subunit interfaces. These observations suggest that ferritin structure could have evolved to limit the influence of functionally unrelated events in the cytoplasm on the allosteric network, in order to maintain stability of the iron translocation mechanisms. The allosteric networks are in agreement with current understanding of iron traffic: The networks in BfrB and FtnA connect the ferroxidase center with the 4-fold pores and B-pores, leaving the 3-fold pores unengaged. In contrast, the 3-fold pores connect directly to the 4-fold pores in both L and M Ftns. The allosteric network in M Ftn also includes one half of the ferroxidase center. Our data indicate that the residue-residue correlations and the resultant long-range cooperativity depend on the ferritin shell packing. Switching from the packing-on model to the packing-off model reduces residue-residue correlations below 0.41–0.43 so that no allosteric network can be found. These findings suggest that cooperative communication in the ferritin structures strongly depend on side-chain mobility, and indicate that the function of the ferritin-like molecules relies on dynamic allostery without a change in the backbone conformation.^{13, 14}

RESULTS

Bfr and Ftn structure

Ftns and Bfrs proteins consist of 24 subunits that form a spherical shell (Fig. 1). Despite significant variations in sequence similarity,^{20, 21, 58} the subunit structure – a four-helix bundle (A-D) plus a B-C loop and a C-terminal helix (E) – is highly conserved among the Ftn and Bfr proteins. Mammalian ferritins are formed from two types of subunits,^{59, 60} which have different masses and thus are called light (L) and heavy (H). An additional M type subunit is found in amphibian Ftns.⁶¹ Tables S1 and S2 and Figure S1 in the supplementary material⁵¹ show comparison of sequence and structure alignments of the subunits from Pa BfrB, Pa FtnA, and M and L Ftns.

Allosteric communication via networks of highly correlated residues

We have applied normal mode analysis in conjunction with the packing-on and packing-off models to calculate pairwise correlations between residue fluctuations and to analyze the distribution of highly correlated residues (correlation ≥ 0.5) in Pa BfrB, Pa FtnA, and M and L Ftns. The packing-on model⁵⁴ explicitly accounts for the number of interatomic interactions and so is sensitive to atom packing (Eq. 1 in Materials and Methods). The packing-off model (Eq. 2) is derived from Eq. 1 by switching off the sensitivity to molecular packing.

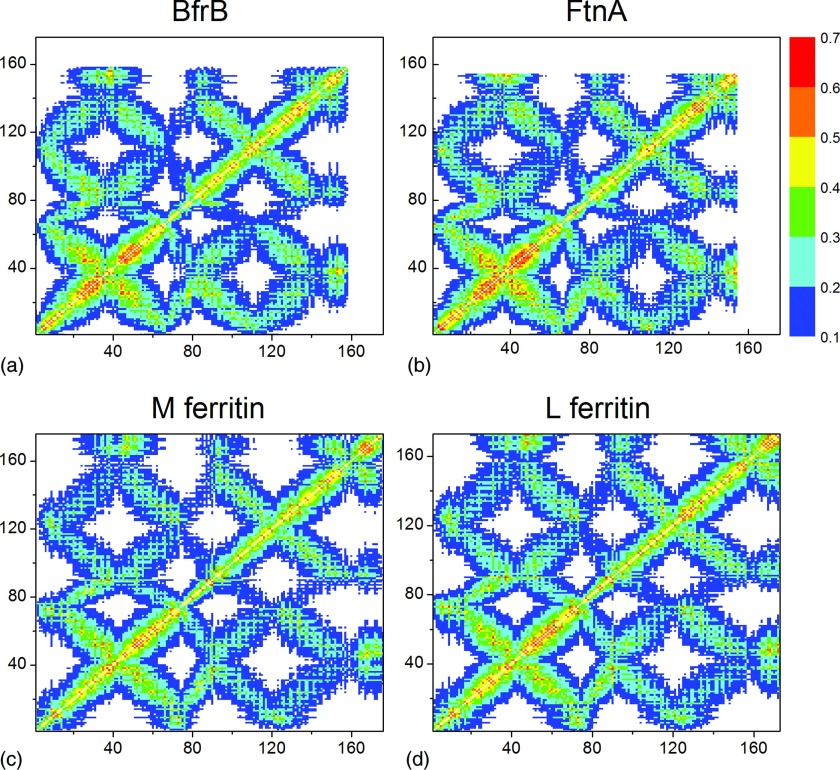
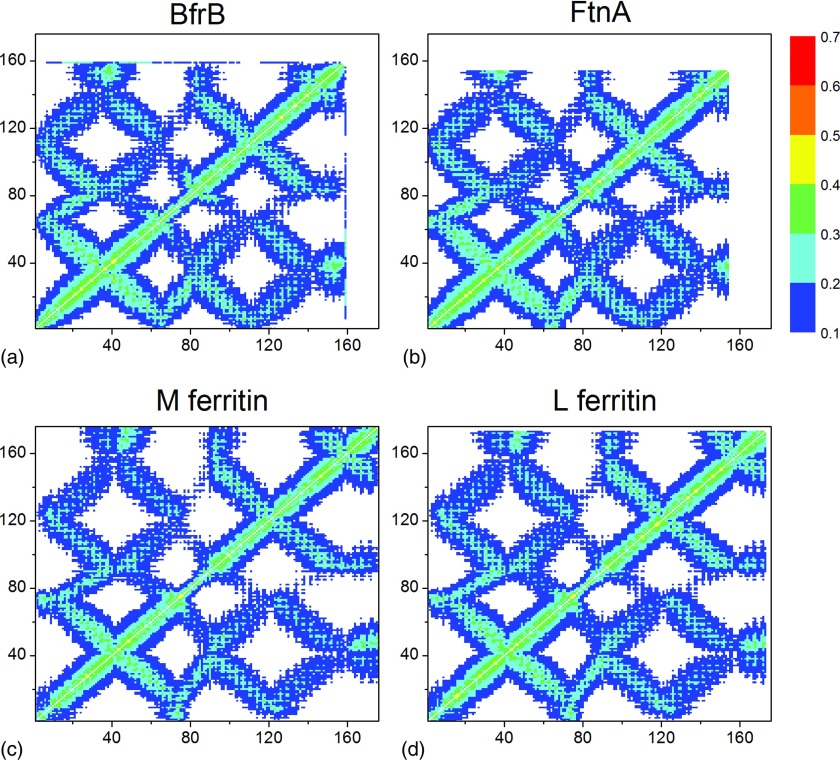
Figures 23 show correlation matrices for the four ferritins studied with the packing-on and packing-off models. A strong influence of the ferritin shell packing on the residue-residue correlations is evident: The packing-off model yielded significantly lower residue-residue correlations in comparison to the packing-on model. The maximum correlations decrease from 0.67 in the packing-on model to 0.41–0.43 in the packing-off model, which is equivalent to a 35%–38% reduction. This means that, surprisingly, in the packing-off model all four structures completely lose their cooperative character, which is made evident by the highly correlated residues in the packing-on model. The lowest negative correlation remained unchanged at the −0.1 level in both models. These findings strongly suggest that local packing and local structural features, characteristic of each of the Ftn-like structures studied, control and modulate long-range allosteric communication via correlation networks in the macromolecular ferritin structure.

Figure 2.

The intra-subunit correlations between the residue fluctuations in the packing-on model: (a) Pa BfrB, (b) Pa FtnA, (c) M Ftn, and (d) L Ftn.

Figure 3.

The intra-subunit correlations between the residue fluctuations in the packing-off model: (a) Pa BfrB, (b) Pa FtnA, (c) M Ftn, and (d) L Ftn.

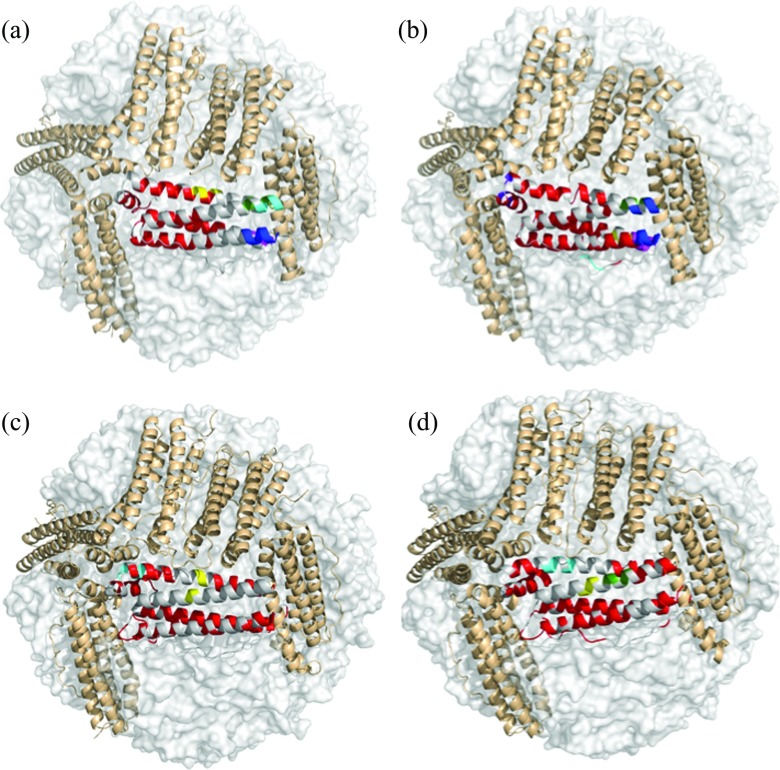
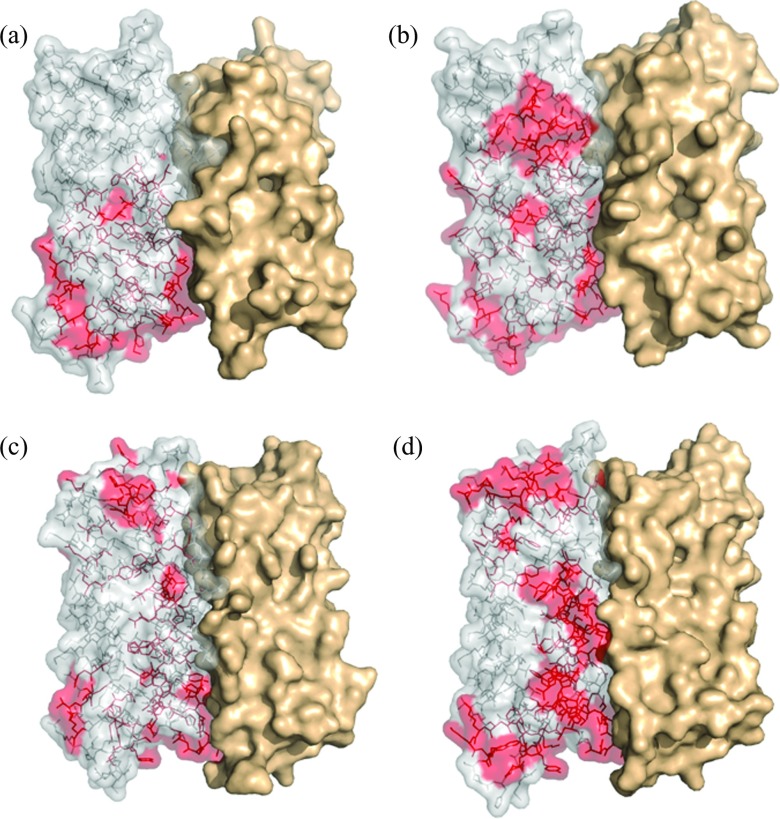
To detect the correlation networks, we developed a network-weaving algorithm that passes “threads” through highly correlated residues in each subunit in agglomerative manner using hierarchical clustering (Materials and Methods). The networks were defined as disjoint clusters of the intersecting “threads.” Applying NWA to the four-ferritin structures revealed that each molecule has a single extended network (red in Fig. 4 and Table S3 in the supplementary material⁵¹) and several distinct local networks (blue, yellow, cyan, green, and purple in Fig. 4 and Table S3 in the supplementary material⁵¹), which connect a small number of neighboring residues. The number of residues in the local networks is on average approximately an order of magnitude smaller than that in the extended network. The latter, herein termed the allosteric network, connects 36% of all residues in a BfrB subunit, 47% in a FtnA subunit, 39% in M Ftn, and 49% in L Ftn subunits (Table S4 in the supplementary material⁵¹). Note that the majority of residues in the allosteric network are either on the inner surface or buried inside the subunit fold or at the subunit interfaces (Fig. 5). In BfrB and M Ftn, the allosteric networks have the lowest solvent accessible surface area. The allosteric network in BfrB contributes minimally to the binding site of the bacterioferritin associated ferredoxin,²³ Bfd, which promotes heme-mediated electron transfer through the BfrB shell to reduce the core ferric mineral and facilitate iron mobilization. We found only four interatomic interactions between Bfd and BfrB residues Leu27 and Met31 at 3.9–5.5 Å distances. Both residues contribute less than 20 Ų to the BfrB-Bfd interface of 607 Ų. Hiding the allosteric network from Bfd and other interactions on the ferritin surface, and limiting the influence of stochastic changes in the cytoplasm obviously serve to improve the stability of communication via the hidden network. Interestingly, in L Ftn that lacks the ferroxidase center, the allosteric network has the largest access to the solvent.

Figure 4.

Networks of highly correlated residues. The networks are color-coded. The allosteric network is in red. The local networks are in yellow, blue, cyan, magenta, and purple. (a) BfrB. (b) FtnA. (c) M Ftn. (d) L Ftn.

Figure 5.

Allosteric networks. View of the solvent accessible surface area of a subunit dimer. The residues of the allosteric networks (red) are shown in one of the subunits. (a) BfrB. (b) FtnA. (c) M Ftn. (d) L Ftn.

The allosteric networks are more similar within the bacterial and eukaryotic species (Fig. 4 and Table S4 in the supplementary material⁵¹): In BfrB and FtnA the allosteric network connects all residues of the ferroxidase center with the ferroxidase pore, the B-pore and the 4-fold pore. Interestingly, these pores and the ferroxidase center are thought to be involved in iron traffic.^{23, 26, 62} The difference between the BfrB and FtnA allosteric networks is that in FtnA it extends over the A helix closer to the N-terminus, similar to the allosteric networks in the M and L Ftns. In contrast to M and L Ftns, BfrB and FtnA have two small correlation networks in the 3-fold pores, which do not communicate to either the ferroxidase center or the other pores. One of these networks lines the inner surface of the 3-fold pore. The other surrounds the 3-fold pore's opening in the cytoplasm and is relatively larger in FtnA than in BfrB. In contrast to BfrB, in FtnA this network includes residues from helix A. A layered structure of charge distribution in the BfrB 3-fold pore may contribute to the formation of these networks. A small network is also found in the 4-fold pores of FtnA and M Ftn. Interestingly; the longest BC loop, making the interface with Bfd, is not involved in the allosteric network in BfrB at all. In FtnA, this loop contributes only one residue, Arg70. In contrast to BfrB and FtnA, the BC loop contributes 3 and 7 residues to the allosteric networks in M and L Ftns, respectively.

In M Ftn, the allosteric network includes one half of the ferroxidase center only. In contrast to BfrB and FtnA, the allosteric network in L and M Ftns connects the 3-fold with the 4-fold pores. In M Ftn it traces the pathway suggested for iron uptake through the 3-fold pores⁶¹ and the mineral nucleation channel mapped by NMR experiments.⁶³ This, approximately 40-Å-long communication, benefits to a large extent from helices A and B, forming an interface in the subunit dimer. Note that the most exposed helix C does not contribute to the M Ftn allosteric network at all (Fig. 4 and Table S4 in the supplementary material⁵¹). In L Ftn, only three residues Leu114, His115, and Asp120 at the C-terminus of helix C together with the N-terminal residues of helix D extend the allosteric network inside the 3-fold pore. In BfrB and FtnA, only N-terminal residues of helix C contribute to the allosteric network. Majority of these residues are buried inside the subunit.

Residue fluctuations

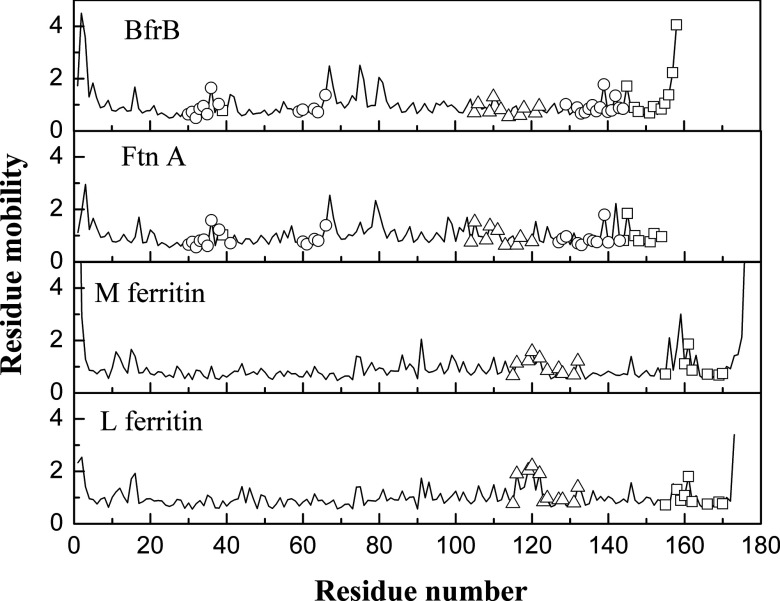
Comparing average residue fluctuations in different pores shows that the 4-fold pores are the most mobile ones in BfrB and FtnA (Fig. 6 and Table S5 in the supplementary material⁵¹). The opposite is found in L and M Ftns, where the 3-fold pores are characterized by the largest average mobility. In L Ftn, the residue fluctuations in the 3-fold pores significantly exceed those in the 4-fold pores. This stems from the high mobility of Ala116, Ala119, Asp120, and Ser122 that form a cup-like structure at the cytoplasmic 3-fold pore opening in L Ftn. In BfrB, the residue fluctuations in the 4-fold pores significantly exceed those in the 3-fold pores and B-pores.

Figure 6.

The residue fluctuations in a subunit of Pa BfrB, Pa FtnA, and M and L Ftns. Calculations were done in the packing-on model. The fluctuations in the B-pore, 3- and 4-fold pores are shown by circles, triangles, and squares.

Tables S6–S8 in the supplementary material⁵¹ show distribution of the top-30 highly fluctuating residues in each of the ferritin structures. Most of these residues are either glycines or other amino-acid residues that are significantly exposed at the termini or on the outer or inner surfaces of the ferritin shell. The increased mobility in the BfrB 4-fold pores can be explained by the high mobility of two last C-terminal residues (Fig. 6), which are disordered in the X-ray structure. If these are not taken into account, the average mobility drops to 1.0, i.e., to the average mobility in the BfrB structure. Even in this case, the average mobility in the 4-fold pore will be larger than the average mobility in the 3-fold pore and the B-pore by 9% and 18%, respectively.

The extended loop connecting helices B and C in BfrB has three highly mobile glycines that show three distinct peaks in the mobility in Fig. 5. Two of them – Gly67 and Gly80 – are at the N and C termini of the BC loop. The third Gly75 is in the middle of the loop. The B-C loop in FtnA shows only two peaks associated with the pair of terminal Gly residues. The third glycine is not conserved in FtnA. The relatively lower peaks in the B-C loop of M and L Ftns are at Gly75, Glu86, Gly91 and Gly74, Gly75, Ser81, Gly93 correspondingly.

DISCUSSION

The relation between side-chain mobility and allostery was first discussed in the context of the bullfrog L Ftn,⁵⁹ where a set of mutations in the middle of the subunit affecting helices A and B had a propagating effect on multiple residues, reaching the 3-fold and 4-fold pores. We found that, in agreement with Ref. 59, all the described residue substitutions belong to the allosteric network that extends between the 3-fold and 4-fold pores mainly over helices A and B. In the frog M Ftn, a 20-Å-long part of the Fe³⁺ pathway from the ferroxidase center to the central cavity was recently mapped by NMR experiments.⁶³ This pathway is consistent with the structure of the calculated allosteric network in M Ftn. Both approaches suggest that Fe³⁺ moves along a solvent-shielded channel, called the mineral nucleation channel, inside the four-helix bundle. The allosteric network connecting the 3-fold pores and the ferroxidase center in M Ftn possibly explains how residue substitutions in the 3-fold pore reduced ferroxidase activity in the distal ferroxidase center.⁶⁴ Communication of the same type was found in BfrB from Mycobacterium tuberculosis, where truncation of an extended C-terminus adjacent to the 4-fold pore E helix had a profound effect on the ferroxidase activity.⁶⁵

Differences in Ftn and Bfr sequences influence both packing inside the ferritin shell and charge distribution inside the pores, resulting in favorable, disfavorable, or neutral conditions for ion transport. Iron release from eukaryotic Ftns is thought to take place via 3-fold pores⁶⁴ that are lined up with negatively charged residues.⁶⁰ This concentration of negative charge may aid in the cationic transport. Electrostatic analysis⁶⁶ and MD simulations⁶⁷ in the human H Ftn support this hypothesis. On the other hand, the 3-fold pores in Bfrs have a layered structure of alternating positively and negatively charged residues, which itself has a less obvious influence on the cationic transport. In our study, this layered structure appears as two small networks disconnected from the allosteric network. Sulfate and phosphate ions were observed in the 3-fold pores of Pa BfrB and Pa FtnA,^{68, 69} and Dd Bfr,⁷⁰ suggesting that, in contrast to eukaryotic ferritins, these pores traffic anions in Bfrs and bacterial Ftns, including the phosphate, which is required for the formation of core mineral in nearly 1:1 ratio with iron.²⁵

The 4-fold pores in the eukaryotic Ftns have no charged or polar residues and are narrower than the 3-fold pores. In contrast to the eukaryotic Ftns, the 4-fold pores in Bfrs typically contain hydrophilic residues. K⁺ and Ba²⁺ were found in the 4-fold pores of Av and Pa Bfrs,^{68, 71} leading to the hypothesis that Fe²⁺ may traffic through these pores. On the other hand, the B-pores surrounding the 4-fold pores in Bfrs and bacterial Ftns (Fig. 1) may also facilitate iron trafficking. These pores are lined up with hydrophilic residues and have a relatively large number of negatively charged residues. Mg²⁺ and Na⁺ ions were found inside the B-pores of Ms Bfr⁶² and Pa BfrB²³ correspondingly. Recent MD simulations of Pa BfrB²⁶ showed that K⁺ ions can move in and out of the BfrB cavity via the ferroxidase pores and B-pores, but not via the 3-fold or 4-fold pores. We have showed that in contrast to the L and M Ftns, in Bfrs and bacterial Ftns, the allosteric network completely excludes the 3-fold pore from the communication grid, connecting the ferroxidase pore with the B-pore and the 4-fold pore only.

CONCLUSIONS

Normal mode analysis and the network-weaving algorithms were applied to study allosteric networks in four representatives of the ferritin-like superfamily. We found that long-range communication between the functionally related pores and the ferroxidase center is mediated by a single intra-subunit network of highly correlated residues, encompassing between 36% and 49% of all residues in the corresponding subunits. In Pa BfrB and Pa FtnA, this network connects the ferroxidase center with the 4-fold and B pores, leaving the 3-fold pores unengaged. In M and L Ftns, the allosteric network directly links the 4-fold pores with the 3-fold pores and also involves one half of the ferroxidase center in M Ftn. The structure of the allosteric networks is consistent with functional observations of iron transport and can guide biochemical experiments on ferritin mutants to decipher roles of the network residues in iron transport and allosteric communications. We showed that the allosteric networks are practically buried inside the ferritin shell. We hypothesize that the ferritin structures evolved in a way to limit the influence of functionally unrelated changes and interactions in the cytoplasm on the allosteric network to maintain stability of the translocation mechanisms. It is likely that the network protection is intrinsic to various biomolecules that evolved in a way to preserve dynamic allostery to function.^{5, 72} We showed that the allosteric networks strongly depend on the ferritin shell packing, which, in turn, depends on protein sequence composition. This relationship explains a remarkable diversity in mechanisms of iron uptake and release suggested by experimental approaches. Thus, our study unifies functional measurements of iron uptake and release with X-ray data and normal mode-dynamics in producing the first model of the long-range communication in ferritins and bacterioferritins.

MATERIALS AND METHODS

Packing-on and packing-off elastic network models

We applied a program Vibe⁵⁴ in conjunction with two ENMs (Eqs. 1, 2) to calculate fluctuations of the residue centers of mass and correlations between the residue fluctuations in each of the 24-mer molecules. The first model (Eq. 1), called the packing-on model,⁵⁴ introduces sensitivity to all-atom packing in the coarse-grained approach by means of the number of interatomic interactions in the inter-residue potential

$$U_{ik}\left({\vec{r}}_i-{\vec{r}}_k,\overrightarrow{R_{ik}^o}\right)=\frac{\alpha }{{\left(R_{ik}^o\right)}^2}{\left(\frac{\overrightarrow{R_{ik}^o}}{R_{ik}^o}\left({\vec{r}}_i-{\vec{r}}_k\right)\right)}^2{N}_{ik},$$ (1)

where N_ik is the number of interatomic interactions between residues i and k separated by less than 10 Å, $\overrightarrow{R_{ik}^o}$ is the radius vector between the centers of mass of residues i and k, ${\vec{r}}_{i,k}$ are the deviations of the residue centers of mass from its equilibrium position, and α characterizes the potential energy strength. The second model, called the packing-off model, is derived by substituting N_ik with δ = 1 or 0 into Eq. 1 and thereby switching off sensitivity to atom packing:

$$U_{ik}\left({\vec{r}}_i-{\vec{r}}_k,\overrightarrow{R_{ik}^o}\right)=\frac{\alpha }{{\left(R_{ik}^o\right)}^2}{\left(\frac{\overrightarrow{R_{ik}^o}}{R_{ik}^o}\left({\vec{r}}_i-{\vec{r}}_k\right)\right)}^2\delta ,$$ (2)

where δ equals to 1 if the distance between any two atoms from residues i and k ≤ 10 Å or to 0 if the distance between all of them >10 Å. Equation 2 has a form of a Tirion potential, which is commonly used in anisotropic elastic network models. Both models were used to derive normal modes in each of the molecules to calculate residue fluctuations

$$⟨{{\vec{r}}_k}^2⟩=T{k}_B\sum _{i=1}^{3N-6}\frac{G_{k_{x}i}^2+G_{k_{y}i}^2+G_{k_{z}i}^2}{M_i{\omega }_i^2}$$ (3)

and temperature-independent pairwise correlations between the residue fluctuations as

$$\begin{array}{ccc}\hfill C\left(p,k\right)& =& \frac{⟨{\vec{r}}_p{\vec{r}}_k⟩}{\sqrt{⟨{{\vec{r}}_p}^2⟩⟨{{\vec{r}}_k}^2⟩}}\hfill \\ & =& \frac{T{k}_B}{\sqrt{⟨{{\vec{r}}_p}^2⟩⟨{{\vec{r}}_k}^2⟩}}\sum _{i=1}^{3N-6}\frac{G_{pxi}{G}_{kxi}+G_{pyi}{G}_{kyi}+G_{pzi}{G}_{kzi}}{M_i{\omega }_i^2},\hfill \end{array}$$ (4)

where ⟨…⟩ denotes a Boltzmann average over the normal modes, G is a matrix of the normalized eigenvectors, M_i is the effective mass of the ith normal mode, and {ω_i} are protein eigenfrequencies.⁵⁴ Equation 3 was used to derive the residue mobility as ${\mathcal{R}}_i=⟨{{\vec{r}}_i}^2⟩/{⟨r^2⟩}_{av},$ where ${⟨r^2⟩}_{av}={\sum }_{i=1}^N⟨{{\vec{r}}_i}^2⟩/N$ is the average mean-square fluctuation in a protein. The average fluctuations and mobility in the pores were calculated as ${⟨r^2⟩}_{pore}={\sum }_{i=1}^{N_{pore}}⟨{{\vec{r}}_i}^2⟩/N_{pore}$ and ${\mathcal{R}}_{pore}={\sum }_{i=1}^{N_{pore}}{\mathcal{R}}_i/N_{pore}$ correspondingly. By their definition, the residues mobility and the residue-residue correlation (Eq. 4) are independent of the parameter α and temperature.

Network-weaving algorithm

We have developed a network-weaving algorithm that passes “threads” through highly correlated residues in each subunit. The networks were defined as disjoint clusters of intersecting pathways. The algorithm performs exhaustive scan to find all the pathways in the structure. The clustering procedure proceeds from the N-terminus to the C-terminus. Starting from the first N-terminal residue, we consider its correlation C(1, j) with all other residues. If C(1, j) ⩾ 0.5, then the residue j is assigned to the first network. Then we inspect correlations between each of the residues just assigned to this network and all other residues to add new residues that show correlations higher than 0.5. At the next step, we repeat the algorithm for all newly added residues. The first network grows till no residues can be assigned to it. The second network grows up from the lowest-number residue that was not covered by the first network. At this stage, correlations of this residue with the rest of the unassigned residues are inspected. The algorithm repeats until all residues will be assigned to the networks. The networks with less than three residues were discarded. This algorithm can be used for clustering anti-correlated residues too. In our case, none of the four ferritin-like molecules showed correlation lower than −0.1. A kindred method was developed to map allosteric networks through the covariance analysis of NMR chemical shifts.⁷³ An alternative approach to the detection of the allosteric networks uses the Girvan-Newman algorithm.⁷⁴ In general, the NWA algorithm can be used in conjunction with any type of ENMs. Particular attention should be paid to the choice of the correlation threshold. For the ferritin-like molecules, the size of the largest network experiences a sharp decrease from 95% to 7% of all residues in the corresponding subunits as the correlation threshold increases from 0.4 to 0.6. Our threshold is a middle point of this practically all-or-nothing transition.