Abstract
Shape is an intrinsic marker of cell cycle, an important factor for identifying a bioparticle, and also a useful indicator of cell state for disease diagnostics. Therefore, shape can be a specific marker in label-free particle and cell separation for various chemical and biological applications. We demonstrate in this work a continuous-flow electrical sorting of spherical and peanut-shaped particles of similar volumes in an asymmetric double-spiral microchannel. It exploits curvature-induced dielectrophoresis to focus particles to a tight stream in the first spiral without any sheath flow and subsequently displace them to shape-dependent flow paths in the second spiral without any external force. We also develop a numerical model to simulate and understand this shape-based particle sorting in spiral microchannels. The predicted particle trajectories agree qualitatively with the experimental observation.
INTRODUCTION
The separation and sorting of target particle or cell types from a complex mixture is essential to many chemical and biological applications. A variety of microfluidic methods have been demonstrated to sort particles and cells based on either external labeling (e.g., fluorescence-1 and magnetic-activated sorting2) or intrinsic properties (e.g., size and density).3, 4 The latter label-free separations are simpler and more desirable, which can take place in both a batch-wise5 and a continuous-flow process.6, 7, 8 Traditional batch separations include centrifugation,9 electrophoresis,10 field-flow fractionation (FFF),11 etc. Continuous-flow separation can be implemented by imposing an external force such as electrical,12 optical,13 magnetic,14 acoustic,15 and hydrodynamic16 forces. Channel topology-induced internal forces have also been utilized to sort particles and cells continuously, including insulator-based dielectrophoresis,17 deterministic lateral displacement,18 hydrodynamic filtration,19 hydrophoresis,20 inertial microfluidics,21 etc. In addition, viscoelasticity effects have been recently demonstrated for continuous particle and cell sorting.22 However, the majority of these sorting techniques can only separate particles and cells based on a single parameter, which has been primarily the size.3, 4, 5, 6, 7, 8 They often become inefficient in handling real chemical and biological samples due to the inherent deviation in particle and cell sizes. It is thus important and necessary to explore other potential passive markers for particle and cell sorting.
Shape is an important factor for identifying a bioparticle such as rod-like bacilli and spherical cocci.23 It has been found to play a dominant role in phagocytosis where macrophages internalize diverse targets including pathogens and airborne particles of various shapes.24 Shape is also a marker of cell cycle, e.g., the budding yeast undergoes dramatic changes in shape during cell division.25 Moreover, it can be an indicator of cell state that is useful information for disease diagnostics, for example, sickle-cell anemia26 and malaria27 are accompanied with the changes of red blood cells from biconcave shapes to other shapes. Therefore, shape can be a specific marker in label-free particle and cell sorting for applications like the removal of aggregates from synthesized particles for drug delivery, the isolation of pathogens from biological fluids for disease diagnostics, and the cell-cycle synchronization for understanding gene-expression profiles specific to cell stages, etc.
However, only till very recently has the particle and cell shape been exploited as a passive sorting marker. Beech et al.28 demonstrated a classification of morphologically altered red blood cells based on shape using deterministic lateral displacement.18 This technique requires the fabrication of a high-resolution cylindrical28 or I-shaped29 post array. Sugaya et al.30 implemented the separation of budded and single yeast cells with the hydrodynamic filtration technique,19 which requires the use of a highly complicated network of microchannels. Masaeli et al.31 performed a continuous sorting of rods with different aspect ratios and as well yeast cells at various stages based on the difference of equilibrium position in a long straight microchannel.32 Such an inertia-based sorting technique, which has also been demonstrated in curving33, 34 and contraction/expansion microchannels,35, 36 favors high flow rate and hence may become problematic in handling precious samples. Moreover, the device of Masaeli et al.31 requires a sophisticated design of the multiple outlet branches in order that the effluent positions of the differentially focused particles can be tuned without complicated physical actuation or valving. This complexity may impede the integration of inertial sorter into lab-on-a-chip devices. In addition, Valero et al.37 demonstrated a label-free synchronization of yeast cell division by balancing opposing dielectrophoretic forces at multiple frequencies. This only electric technique developed so far for shape-based cell sorting requires the integration of in-channel microelectrodes and a precise control of the buffer conductivity.
In this work, we demonstrate the use of our recently developed curvature-induced dielectrophoresis (C-iDEP)38, 39, 40 technique to continuously sort particles based on shape in an asymmetric double-spiral microchannel. This electric-field driven technique is essentially one type of insulator-based dielectrophoresis,41, 42, 43, 44 which has several advantages over traditional electrode-based dielectrophoresis45, 46, 47, 48, 49, 50, 51, 52 such as the ease of non-metal fabrication, the inert of insulating structure, etc.53, 54 We also develop a numerical model that considers the full interactions among the particles, electric field, and flow field to understand and simulate this shape-based particle separation.
EXPERIMENT
Fig. 1 shows a picture of the spiral microchannel used in our experiment, which was fabricated with poly(dimethylsiloxane) (PDMS) using the standard soft lithography technique. The channel is composed of two spirals that have three loops each and are asymmetric in structure. The first spiral is uniformly 50 μm wide and the second spiral has a constant width of 100 μm. A trifurcation is designed at the end of the second spiral in order to collect sorted particles into different reservoirs (labeled as outlets 1, 2, and 3 in Fig. 1). The channel is 25 μm deep everywhere and measures 39 mm in length. To demonstrate the shape-based sorting, 5 μm-diameter spherical polystyrene particles (Sigma Aldrich USA) and 3.5 μm-diameter/6 μm-length peanut-shaped polystyrene particles (Magsphere, Inc., Pasadena, CA) were mixed and re-suspended in 1 mM phosphate buffer to a final concentration of 106–107 particles/ml. A small amount of TWEEN 20 (0.1% by volume, Thermo Fisher Scientific) was added to the solution to suppress the particle-particle and particle-wall adhesions. The particle suspension was driven through the microchannel by pure DC electric fields that were supplied with a high-voltage power supply (Glassman PS/EL05P08LDM11). Particle motion was visualized using an inverted microscope (Nikon Eclipse TE2000U, Nikon Instruments, Lewisville, TX) equipped with a CCD camera (Nikon DS-Qi1Mc). The obtained digital images were processed using the Nikon imaging software (NIS-Elements AR 2.30).
Figure 1.
Picture of the microfluidic device (the spiral microchannel is filled with green food dye for clarity) used in the particle sorting experiment. The block arrows indicate the particle moving directions during the sorting process.
THEORY
Sorting mechanism
Fig. 2 shows the electric field lines (short arrows indicate the directions) and contour (represented by the background color, the darker the larger magnitude) in the most inner loop of the asymmetric double-spiral microchannel. The electric field reaches the maximum and minimum values at the inner and outer walls of each spiral, respectively, due to the variation in path length for electric current. Therefore, particles experience a transverse dielectrophoretic motion, UDEP, when they follow the electric field lines (equivalent to fluid streamlines for pure electrokinetic flows55) to move electrokinetically through the curving channel. Under the point-dipole approximation, UDEP of an ellipsoidal rigid particle is given by56, 57
| (1a) |
| (1b) |
| (1c) |
Figure 2.
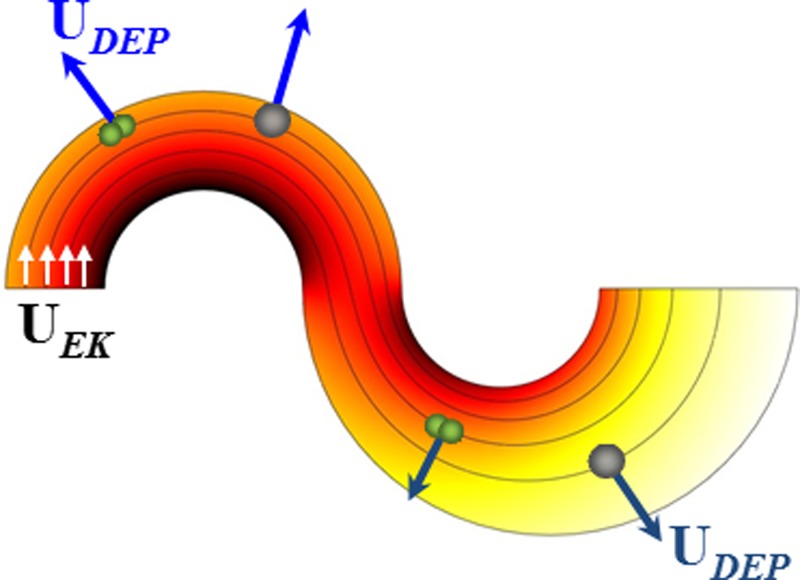
Illustration of the shape-based particle sorting mechanism in an asymmetric double-spiral microchannel. Particles are deflected by negative C-iDEP to align near the outer wall of the first spiral and then displaced by negative C-iDEP to shape-dependent flow paths in the second spiral. Also shown are the electric field lines (equivalent to fluid stream lines with short arrows indicating the directions) and contour (background color, the darker the larger magnitude).
In the above, μDEP is the dielectrophoretic particle mobility, E is the electric field vector with a magnitude of E, ℜ is the radius of curvature of an electric field line with n being its unit normal vector, dp is the equivalent diameter of a sphere having the same volume as the non-spherical particle, εm is the permittivity of the suspending medium, ηm is the dynamic viscosity of the medium, and fCM is the Clausius-Mossotti (CM) factor that is a function of the electric conductivities of the particle, σp, and the medium, σm, under pure DC electric fields.58 There are two particle shape dependent correction factors involved in UDEP: Ki in Eq. 1b accounts for the shape-dependence of the Stokes drag on a particle (note that Ki ≥ 1 where the equality applies to spherical particles because non-spherical particles have a larger surface area than spherical ones of equal volumes and hence experience a greater drag force);57Li in Eq. 1c is the shape related depolarization factor that affects the particle polarizability and reduces to 1/3 for spheres.59
As micron-sized non-metallic particles and biological cells appear poorly conducting in DC and low-frequency AC electric fields, they often experience negative DEP in typical buffer solutions.60 The resulting outward dielectrophoretic particle motion, UDEP (see the direction in Fig. 2), competes with the stream-wise electrokinetic particle motion, UEK,
| (2a) |
| (2b) |
where μEK is the so-called electrokinetic mobility due to a combination of medium electroosmosis and particle electrophoresis, s is the unit vector along the streamline, ζp is the zeta potential of the particle, ζw is the zeta potential of the microchannel wall, and Mi is the correction factor for the shape and size dependence of μEK which can be simply treated as unity in all cases unless particles closely fit the channel size.61 The resulting cross-stream particle deflection by C-iDEP can be expressed as62
| (3) |
where θ is the opening angle of the spiral channel in one direction. Apparently, this dielectrophoretic deflection increases with E and θ as well as the dielectrophoretic to electrokinetic mobility ratio,
| (4) |
The dependence of this mobility ratio on particle size (dp), shape (Ki, Li, and Mi), and surface charge (ζp) enables the continuous sorting of particles based on one or more of these intrinsic properties in an asymmetric double-spiral microchannel. Specifically, as shown in Fig. 2, negative C-iDEP deflects the particle mixture (illustrated are one spherical particle and one peanut-shaped particle of a similar volume) to a tight stream flowing near the outer wall of the first spiral. When this focused particle stream travels into the second spiral, particles still experience negative C-iDEP but with a reduced magnitude due to the increased width in the second spiral as compared to the first spiral (and hence a lower electric field magnitude/gradient in the second spiral). Therefore, particles are deflected towards the outer wall of the second spiral from nearly the same position while at a rate that is dependent on their mobility ratio, μDEP/μEK. The result is a split of the single stream into two sub-streams based on the difference in intrinsic particle properties. Such a continuous-flow particle sorting has been recently implemented based on size63 and surface charge62 by one of the authors' group.
Numerical modeling
To understand and predict the electrical sorting of particles based on shape by C-iDEP, we simulated the electrokinetic motions of spherical and peanut-shaped particles in the asymmetric double-spiral microchannel using an Arbitrary Lagrangian-Eulerian (ALE) method-based numerical model. This numerical method was developed by one of the authors' group64 and has been validated by comparing the predicted electrokinetic motions of spherical65, 66 and non-spherical67 particles with experiments in several structures of microchannels. It considers the dynamic particle-fluid-electric field interactions for moving particles in confined flows and computes the particle velocity (both translation and rotation) using hydrodynamic and Maxwell stress tensors.64 To save the computational time, our model considered only the particle transport in the horizontal plane (i.e., two-dimensional) of the most inner loop of the spiral microchannel. The exact dimensions of the microchannel and the particles in the experiment were used in the model. Other parameters are presented in Sec. 4.
RESULTS AND DISCUSSION
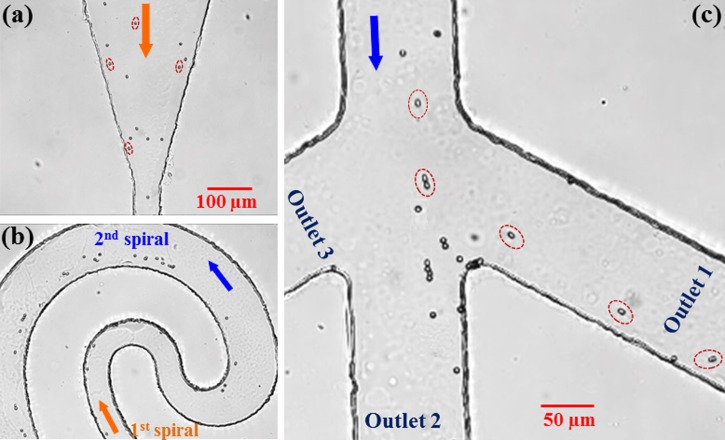
Fig. 3 demonstrates the electrical sorting of 5 μm-diameter spherical particles and 3.5 μm-diameter/6 μm-length peanut-shaped particles in the asymmetric double-spiral microchannel (see Fig. 1). The inlet reservoir was imposed with a 1000 V DC voltage, and the three outlet reservoirs were all grounded. Therefore, the average electric field in the channel was estimated to be around 250 V/cm. At the inlet of the microchannel, the spherical and peanut-shaped (some of them are highlighted for a better illustration) particles were uniformly mixed as seen from the snapshot image in Fig. 3a. They travelled at approximately the same speed in the straight section, indicating that they had a similar electrokinetic mobility, μEK. In the center region of the microchannel, these two shapes of particles lined the outer wall of the first spiral, which were then deflected away from the inner wall of the second spiral by negative C-iDEP as illustrated in Fig. 3b. The peanut-shaped particles appeared to experience a weaker DEP than the spherical ones and hence had a smaller mobility ratio, μDEP/μEK, of the two. Therefore, they were displaced at a lower rate and gradually separated from the stream of spherical particles. Finally at the channel trifurcation, the spherical and peanut-shaped particles were sorted into outlet 2 and outlet 1, respectively, as demonstrated in Fig. 3c, where the non-spherical particles have been individually highlighted for a better illustration.
Figure 3.
Snapshot images illustrating the continuous electrical sorting of 5 μm-diameter spherical particles and 3.5 μm-diameter/6 μm-length peanut-shaped particles in an asymmetric double-spiral microchannel by C-iDEP: (a) inlet, (b) center, and (c) trifurcation of the channel. The average DC electric field across the channel length is around 250 V/cm. Note that the peanut-shaped particles have been individually highlighted in (a) and (c) for a better illustration. The block arrows indicate the flow directions.
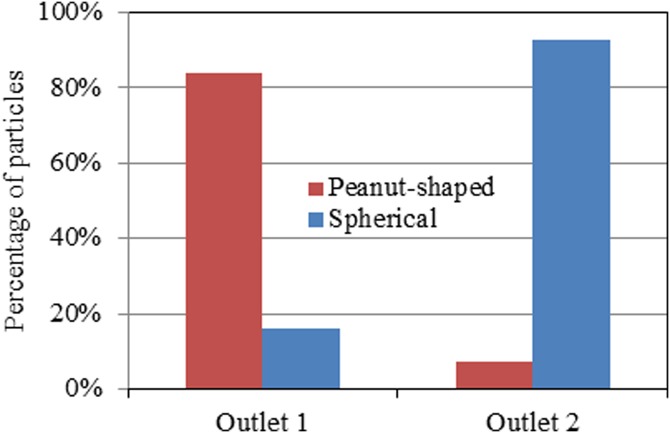
The flow throughput of this shape-based particle sorting was estimated to be 5 μl/h, which is relatively low for practical applications. It can be enhanced by increasing the applied electric field and the width/depth of the spirals. Alternatively, the throughput can be enhanced through a parallel operation of multiple double-spiral microchannels, which may be easily arranged in the radial direction of a circle for compactness. This is feasible as the C-iDEP sorter is all electric with easy connections and controls, which also facilitates its integration with other functional parts for building a real lab-on-a-chip device. We tested the sorting purity by manually counting the spherical and peanut-shaped particles in three independent videos. More than 300 particles were counted with at least 100 particles for each type. None of these particles were found to flow into outlet 3 [see the labeling in Figs. 13c]. The percentages of the spherical and peanut-shaped particles collected into outlet 1 and outlet 2, respectively, are presented in the column plot in Fig. 4. A better-than-80% sorting purity is achieved for the targeted particle type in each outlet (i.e., peanut-shaped particles in outlet 1 and spherical particles in outlet 2). This value can be further improved by imposing a small DC voltage bias upon one or two of the outlet reservoirs to finely tune the effluent positions of the sorted particles at the trifurcation.
Figure 4.
Purity test of the shape-based particle sorting by C-iDEP in terms of the percentages of spherical and peanut-shaped particles collected into outlet 1 and outlet 2 [see the labeling in Figs. 13c] of the spiral microchannel, respectively.
Fig. 5a displays the numerically predicted trajectories of spherical and peanut-shaped particles that start at similar initial positions in the spiral microchannel. Three particles (with one showing the shape) were picked for each type with initial positions being evenly distributed over the channel width at the entrance of the first spiral. The zeta potentials of the particles and the wall were set to −40 mV and −15 mV, respectively. These values were selected to match the experimentally measured electrokinetic mobility of 1.8 × 10−8 m2/V·s in a straight microchannel. The average electric field was set to 1200 V/cm in the model, which is about 5 times the value used in the experiment. This is viewed reasonable from Eq. 3 because only a half loop was considered in the model for each spiral that actually consists of three full loops in our experiment. All particles in Fig. 3a are fully deflected by negative C-iDEP to the outer wall of the first spiral, which is consistent with the experimental observation in Fig. 3b. In the second spiral, spherical particles are deflected by C-iDEP at a greater rate than the peanut-shaped particles, leading to a continuously increased displacement between the two particle streams. This explains qualitatively why the spherical and peanut-shaped particles are sorted into outlet 2 and outlet 1 of the spiral microchannel, respectively, in the experiment [see Fig. 3c]. Fig. 5b shows the predicted particle translation and rotation at the initial few time steps, where the long-axis of the peanut-shaped particle quickly aligns with the electric field. The distorted electric field lines and contour around a peanut-shaped particle are demonstrated in Fig. 5c, which explains why the particle rotates and transverse across the channel.
Figure 5.
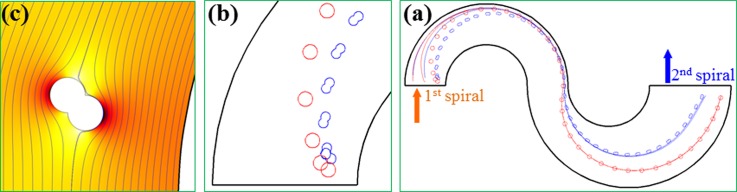
(a) The numerically predicted trajectories of spherical and peanut-shaped particles (three for each type with one showing the shape) moving electrokinetically through the most inner loop of an asymmetric double-spiral microchannel; (b) zoom-in view of the predicted translation and rotation of particles (one for each type) at the initial few time steps; (c) further zoom-in view of the distorted electric field lines and contour (the darker the larger magnitude) around a peanut-shaped particle. The block arrows in (a) indicate the flow directions.
It is important to point out that the 3.5 μm-diameter/6 μm-length peanut-shaped particle has an equal volume to a 4.5 μm-diameter spherical particle. Therefore, the size discrepancy, i.e., dp, in Eq. 4, between the peanut-shaped particle and the 5 μm-diameter spherical particle should also facilitate their sorting in the spiral microchannel by C-iDEP. This contribution is, however, estimated to be small as compared to that from the shape difference, which is confirmed through numerical modeling. We simulated the electrokinetic motion of a 4.5 μm-diameter spherical particle that starts from an initial position identical to that of a 5 μm-diameter spherical particle under the same working conditions. The predicted trajectories of these two particles (data not shown) were found to slightly deviate from each other in both spirals of the microchannel but are apparently displaced from that of the peanut-shaped particle. Following the protocol reported by Champion and Mitragotri,24 we are developing a setup to stretch polystyrene spheres to ellipsoidal shape with different aspect ratios while conserving the volume. These particles can be used to isolate the contribution of shape to separation from that of size difference.
CONCLUSIONS
We have demonstrated a microfluidic technique for continuous-flow electrical sorting of particles based on shape in an asymmetric double-spiral microchannel by C-iDEP. This technique is label-free and has the capability of separating particles and cells based on multiple intrinsic properties, e.g., size and shape simultaneously, as seen from Eq. 4. Other properties such as stiffness68, 69 are not considered in this work for rigid particles, which may be potential markers for the C-iDEP sorting of disease infected cells. We have also developed a numerical model to understand the shape-based particle sorting in the spiral microchannel, which predicts qualitatively the experimentally observed deflection behaviors of each type of particles in the two spirals. This model will be used to optimize the structure (e.g., Archimedean spiral or Fermat's spiral) and dimension (e.g., constant or varying width) of the spirals in our future work.
ACKNOWLEDGMENTS
This work was partially supported by NSF under Grants CBET-0853873 (X. Xuan) and DMS-1319078 (S. Qian), and by National Research Foundation of Korea under Grant 2011-0014246 (Joo).
References
- Fu A. Y., Spence C., Scherer A., Arnold F. H., and Quake S. R., Nat. Biotechnol. 17, 1109–1111 (1999). 10.1038/15095 [DOI] [PubMed] [Google Scholar]
- Adams J. D., Thévoz P., Shea H., Bruus H., and Soh H. T., Appl. Phys. Lett. 95, 254103 (2009). 10.1063/1.3275577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsutsui H. and Ho C. M., Mech. Res. Commun. 36, 92–103 (2009). 10.1016/j.mechrescom.2008.08.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gossett D. R., Weaver W. M., Mach A. J., Hur S. C., Tse H. T., Lee W., Amini H., and Di Carlo D., Anal. Bioanal. Chem. 397, 3249–3267 (2010). 10.1007/s00216-010-3721-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulrattanarak T., van der Sman R. G. M., Schroen C. G. P. H., and Boom R. M., Adv. Colloid Interface Sci. 142, 53–65 (2008). 10.1016/j.cis.2008.05.001 [DOI] [PubMed] [Google Scholar]
- Pamme N., Lab Chip 7, 1644–1659 (2007). 10.1039/b712784g [DOI] [PubMed] [Google Scholar]
- Lenshof A. and Laurell T., Chem. Soc. Rev. 39, 1203–1217 (2010). 10.1039/b915999c [DOI] [PubMed] [Google Scholar]
- Bhagat A. A., Bow H., Hou H. W., Tan S. J., Han J., and Lim C. T., Med. Biol. Eng. Comput. 48, 999–1014 (2010). 10.1007/s11517-010-0611-4 [DOI] [PubMed] [Google Scholar]
- Burger R. and Ducree J., Expert Rev. Mol. Diagn. 12, 407–421 (2012). 10.1586/erm.12.28 [DOI] [PubMed] [Google Scholar]
- Rodriguez M. A. and Armstrong D. W., J. Chromatogr. B: Anal Technol. Biomed. Life Sci. 800, 7–25 (2004). 10.1016/j.jchromb.2003.09.060 [DOI] [PubMed] [Google Scholar]
- Giddings J. C., Science 260, 1456–1465 (1993). 10.1126/science.8502990 [DOI] [PubMed] [Google Scholar]
- Gascoyne P. R. C. and Vykoukal J., Electrophoresis 23, 1973–1983 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S. B., Yoon S. Y., Sung H. J., and Kim S. S., Anal. Chem. 80, 2628–2630 (2008). 10.1021/ac8000918 [DOI] [PubMed] [Google Scholar]
- Liang L., Zhang C., and Xuan X., Appl. Phys. Lett. 102, 234101 (2013). 10.1063/1.4810874 [DOI] [Google Scholar]
- Adams J. T. and Soh H. T., Appl. Phys. Lett. 97, 064103 (2010). 10.1063/1.3467259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vig A. L. and Kristensen A., Appl. Phys. Lett. 93, 203507 (2008). 10.1063/1.3028652 [DOI] [Google Scholar]
- Srivastava S. K., Gencoglu A., and Minerick A. R., Anal. Bioanal. Chem. 399, 301–321 (2011). 10.1007/s00216-010-4222-6 [DOI] [PubMed] [Google Scholar]
- Huang L., Cox E. C., Austin R. H., and Sturm J. C., Science 304, 987–990 (2004). 10.1126/science.1094567 [DOI] [PubMed] [Google Scholar]
- Yamada M. and Seki M., Lab Chip 5, 1233–1239 (2005). 10.1039/b509386d [DOI] [PubMed] [Google Scholar]
- Choi S., Song S., Choi C., and Park J. K., Anal. Chem. 81, 1964–1968 (2009). 10.1021/ac8024575 [DOI] [PubMed] [Google Scholar]
- Di Carlo D., Lab Chip 9, 3038–3046 (2009). 10.1039/b912547g [DOI] [PubMed] [Google Scholar]
- Karimi A., Yazdi S., and Ardekani A. M., Biomicrofluidics 7, 021501 (2013). 10.1063/1.4799787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janca J., Halabalova V., and Rzicka J., J. Chromatogr. A 1217, 8062–8071 (2010). 10.1016/j.chroma.2010.10.082 [DOI] [PubMed] [Google Scholar]
- Champion J. A. and Mitragotri S., Proc. Natl. Acad. Sci. U.S.A. 103, 4930–4934 (2006). 10.1073/pnas.0600997103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin S., Cell Cycle 8, 3643–3647 (2009). 10.4161/cc.8.22.9891 [DOI] [PubMed] [Google Scholar]
- Ebert E. C., Nagar M., and Hagspiel K. D., Clin. Gastroenterol. Hepatol. 8, 483–489 (2010). 10.1016/j.cgh.2010.02.016 [DOI] [PubMed] [Google Scholar]
- Anstey N. M., Russell B., Yeo T. W., and Price R. N., Trends Parasitol. 25, 220–227 (2009). 10.1016/j.pt.2009.02.003 [DOI] [PubMed] [Google Scholar]
- Beech J. P., Holm S. H., Adolfsson K., and Tegenfeldt J. O., Lab Chip 12, 1048–1051 (2012). 10.1039/c2lc21083e [DOI] [PubMed] [Google Scholar]
- Zeming K. K., Ranjan S., and Zhang Y., Nat. Commun. 4, 1625 (2013). 10.1038/ncomms2653 [DOI] [PubMed] [Google Scholar]
- Sugaya S., Yamada M., and Seki M., Biomicrofluidics 5, 24103 (2011). 10.1063/1.3580757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masaeli M., Sollier E., Amini H., Mao W., Camacho K., Doshi N., Mitragotri S., Alexeev A., and Di Carlo D., Phys. Rev. X 2, 031017 (2012). 10.1103/PhysRevX.2.031017 [DOI] [Google Scholar]
- Hur S. C., Choi S. E., Kwon S., and Di Carlo D., Appl. Phys. Lett. 99, 044101 (2011). 10.1063/1.3608115 [DOI] [Google Scholar]
- Sun J., Liu C., Li M., Wang J., Xianyu Y., Hu G., and Jiang X., Biomicrofluidics 7, 011802 (2013). 10.1063/1.4774311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Zhou J., and Papautsky I., Biomicrofluidics 7, 044119 (2013). 10.1063/1.4818906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hur S. C., Mach A. J., and Di Carlo D., Biomicrofluidics 5, 022206 (2011). 10.1063/1.3576780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nivedita N. and Papautsky I., Biomicrofluidics 7, 054101 (2013). 10.1063/1.4819275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valero A., Braschler T., Rauch A., Demierre N., Barral Y., and Renaud P., Lab Chip 11, 1754–1760 (2011). 10.1039/c1lc00007a [DOI] [PubMed] [Google Scholar]
- Zhu J., Tzeng T., Hu G., and Xuan X., Microfluid. Nanofluid. 7, 751–756 (2009). 10.1007/s10404-009-0432-7 [DOI] [Google Scholar]
- Church C., Zhu J., Wang G., Tzeng T. J., and Xuan X., Biomicrofluidics 3, 044109 (2009). 10.1063/1.3267098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J., Canter R. C., Keten G., Vedantam P., Tzeng T., and Xuan X., Microfluid. Nanofluid. 11, 743–752 (2011). 10.1007/s10404-011-0839-9 [DOI] [Google Scholar]
- Lewpiriyawong N., Yang C., and Lam Y. C., Biomicrofluidics 2, 034105 (2008). 10.1063/1.2973661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jen C. P. and Chen W. F., Biomicrofluidics 5, 044105 (2011). 10.1063/1.3658644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regtmeier J., Eichhorn R., Viefhues M., Bogunovic L., and Anselmetti D., Electrophoresis 32, 2253–2273 (2011). 10.1002/elps.201100055 [DOI] [PubMed] [Google Scholar]
- Patel S., Showers D., Vedantam P., Tzeng T. R., Qian S., and Xuan X., Biomicrofluidics 6, 034102 (2012). 10.1063/1.4732800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng I. F., Chang H. C., Hou D., and Chang H. C., Biomicrofluidics 1, 021503 (2007). 10.1063/1.2723669 [DOI] [Google Scholar]
- Gagnon Z., Mazur J., and Chang H. C., Biomicrofluidics 3, 044108 (2009). 10.1063/1.3257857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valero A., Braschler T., Demierre N., and Renaud P., Biomicrofluidics 4, 022807 (2010). 10.1063/1.3430542 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuczenski R. S., Chang H. C., and Revzin A., Biomicrofluidics 5, 032005 (2011). 10.1063/1.3608135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velugotla S., Pells S., Mjoseng H. K., Duffy C. R. E., Smith S., De Sousa P., and Pethig R., Biomicrofluidics 6, 044113 (2012). 10.1063/1.4771316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alshareef M., Metrakos N., Perez E. J., Azer F., Yang F., Yang X., and Wang G., Biomicrofluidics 7, 011803 (2013). 10.1063/1.4774312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim S., Stemke–Hale K., Tsimberidou A. M., Noshari J., Anderson T. E., and Gascoyne P. R. C., Biomicrofluidics 7, 011807 (2013). 10.1063/1.4774304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pethig R., Biomicrofluidics 4, 022811 (2010). 10.1063/1.3456626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou C. F., Tegenfeldt J. O., Bakajin O., Chan S. S., Cox E. C., Darnton N., Duke T., and Austin R. H., Biophys. J. 83, 2170–2179 (2002). 10.1016/S0006-3495(02)73977-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapizco-Encinas B. H., Simmons B. A., Cummings E. B., and Fintschenko Y., Anal. Chem. 76, 1571–1579 (2004). 10.1021/ac034804j [DOI] [PubMed] [Google Scholar]
- Cummings E. B., Giffiths S. K., Nilson R. H., and Paul P. H., Anal. Chem. 72, 2526–2532 (2000). 10.1021/ac991165x [DOI] [PubMed] [Google Scholar]
- Zhu J. and Xuan X., J. Colloid. Interface Sci. 340, 285–290 (2009). 10.1016/j.jcis.2009.08.031 [DOI] [PubMed] [Google Scholar]
- Kirby B. J., Micro and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices (Cambridge University Press, New York, 2010). [Google Scholar]
- Hawkins B. G., Smith A. E., Syed Y. A., and Kirby B. J., Anal. Chem. 79, 7291–7300 (2007). 10.1021/ac0707277 [DOI] [PubMed] [Google Scholar]
- Jones T. B., Electromechanics of Particles (Cambridge University Press, New York City, NY, 1995). [Google Scholar]
- Jesús-Pérez N. M. and Lapizco-Encinas B. H., Electrophoresis 32, 2331–2357 (2011). 10.1002/elps.201100107 [DOI] [PubMed] [Google Scholar]
- Anderson J. L., Annu. Rev. Fluid Mech. 21, 61–99 (1989). 10.1146/annurev.fl.21.010189.000425 [DOI] [Google Scholar]
- Zhu J. and Xuan X., Biomicrofluidics 5, 024111 (2011). 10.1063/1.3599883 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J., Tzeng T. R., and Xuan X., Electrophoresis 31, 1382–1388 (2010). 10.1002/elps.200900736 [DOI] [PubMed] [Google Scholar]
- Qian S. and Ai Y., Electrokinetic Particle Transport in Micro/Nanofluidics: Direct Numerical Simulation Analysis (CRC Press, 2012). [Google Scholar]
- Ai Y., Joo S. W., Jiang Y., Xuan X., and Qian S., Electrophoresis 30, 2499–2506 (2009). 10.1002/elps.200800792 [DOI] [PubMed] [Google Scholar]
- Ai Y., Park S., Zhu J., Xuan X., Beskok A., and Qian S., Langmuir 26, 2937–2944 (2010). 10.1021/la902711x [DOI] [PubMed] [Google Scholar]
- Ai Y., Beskok A., Gauthier D. T., Joo S. W., and Qian S., Biomicrofluidics 3, 044110 (2009). 10.1063/1.3267095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geislinger T. M. and Franke T., Biomicrofluidics 7, 044120 (2013). 10.1063/1.4818907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G., Mao W., Byler R., Patel K., Henegar C., Alexeev A., and Sulchek T., PLoS One 8, e75901 (2013). 10.1371/journal.pone.0075901 [DOI] [PMC free article] [PubMed] [Google Scholar]