Conformational Properties of α- or β-(1→6)-Linked Oligosaccharides: Hamiltonian Replica Exchange MD Simulations and NMR Experiments

Abstract

Conformational sampling for a set of 10 α- or β-(1→6)-linked oligosaccharides has been studied using explicit solvent Hamiltonian replica exchange (HREX) simulations and NMR spectroscopy techniques. Validation of the force field and simulation methodology is done by comparing calculated transglycosidic J coupling constants and proton–proton distances with the corresponding NMR data. Initial calculations showed poor agreement, for example, with >3 Hz deviation of the calculated ³J(H5,H6R) values from the experimental data, prompting optimization of the ω torsion angle parameters associated with (1→6)-linkages. The resulting force field is in overall good agreement (i.e., within ∼0.5 Hz deviation) from experimental ³J(H5,H6R) values, although some small limitations are evident. Detailed hydrogen bonding analysis indicates that most of the compounds lack direct intramolecular H-bonds between the two monosaccharides; however, minor sampling of the O6···HO2′ hydrogen bond is present in three compounds. The results verify the role of the gauche effect between O5 and O6 atoms in gluco- and manno-configured pyranosides causing the ω torsion angle to sample an equilibrium between the gt and gg rotamers. Conversely, galacto-configured pyranosides sample a population distribution in equilibrium between gt and tg rotamers, while the gg rotamer populations are minor. Water radial distribution functions suggest decreased accessibility to the O6 atom in the (1→6)-linkage as compared to the O6′ atom in the nonreducing sugar. The role of bridging water molecules between two sugar moieties on the distributions of ω torsion angles in oligosaccharides is also explored.

Introduction

Oligosaccharides and polysaccharides play a variety of roles in biology and biochemistry along with proteins and lipids such as storage of energy, structural roles, chemical markers, and cell protectants, among others.^1,2 In biotechnology, they are important in biocompatible and biodegradable materials³⁻⁶ and carbohydrates may be a future source of renewable energy in terms of “biofuels”.⁷⁻⁹ The diverse and complex roles of carbohydrates may be attributed to their structural diversity including a variety of functional groups, numerous stereoisomers and diversity in length, branching pattern, sequence order, and type of linkages.¹⁰ To understand this class of molecules at a molecular level, knowledge of their three-dimensional structure and their conformational preferences in solution is essential.¹¹⁻¹³

Oligosaccharides are monosaccharide units linked together via α- or β-(1→X, where, X = 1, 2, ..., 6) glycosidic linkages. In addition to ring conformational preferences, the relative orientations of saccharide units are expressed in terms of the glycosidic linkage torsion angles ϕ (O5′–C1′–O6–C6) and ψ (C1′–O6–C6–C5). For (1→6)-linkages, the ω torsion angle (O6–C6–C5–O5) (Scheme 1a) provides additional flexibility over other glycosidic linkages which involve only two rotatable bonds, ϕ and ψ.¹⁴ Sampling of the ω torsion angle is described by means of the populations of the gauche–gauche (gg), gauche–trans (gt), and trans–gauche (tg) rotamers. The additional flexibility of the α- or β-(1→6)-linkages makes it more difficult to determine the preferential conformation in solution of oligosaccharides containing these linkages.¹⁵

Scheme 1. Schematic Representation of the manno-(1–3), gluco-(4–5), and galacto-(6–10)-Configured (1/2→6)-Linked Pyranosides Included in the Current Study.

Theoretical and experimental studies on the conformational preferences of the ring and rotational preferences of ω torsion angle have been carried out on monosaccharides, mainly gluco-, manno-, and galactopyranosides where ω is associated with a hydroxymethyl group.^14,16−27 In solution, ω in gluco- and manno-configured pyranosides shows a preference for gauche (gt and gg) orientations over the anti orientation (tg),^16,28,29 which is in contrast to the preference for the tg orientation shown in gas phase quantum mechanics (QM) calculations.³⁰⁻³² On the other hand, ω in galactopyranosides displays a high proportion of gt and tg over the gg rotamer in solution.³³⁻³⁵ Statistical analysis of X-ray structures of glucopyranoside derivatives³⁶ and mannopyranoside derivatives³⁷ yielded a rotamer population distribution of 40:60:0 (gt/gg/tg) and 40:55:5 (gt/gg/tg), respectively. Rotamer population distributions for ω in monosaccharides are mainly attributed to the gauche effect,^16,38−41 1,3-diaxial interactions,¹⁶ and solvent effects.⁴²⁻⁴⁶ In addition, NMR and circular dichroism (CD) data indicate that the rotamer populations of the hydroxymethyl group depend on the identity of the moiety attached at the C1 atom as well as the anomeric configuration in the residue.⁴⁷⁻⁵²

The variations in rotamer populations of ω influence the structure and function of oligosaccharides containing glycosidic (1→6)-linkages. However, the understanding of these rotamer preferences and their role in biology is still at an initial stage.⁵³⁻⁵⁶ Although conformational properties of carbohydrates are difficult to establish experimentally, several NMR and molecular dynamics (MD) simulation studies have addressed the rotational and conformational preferences in these disaccharides,⁵⁷⁻⁶⁵ as well as in larger structures.⁶⁶ In one such study, Salisburg et al.⁶⁷ have reported use of the GLYCAM force field⁶⁸ in studying conformational properties of two (1→6)-linked disaccharides (α-l-Fucp-(1→6)-β-d-GlcpNAc-OMe and α-d-Manp-(1→6)-β-d-Manp-OMe) using an implicit water representation. In another study, the OPLS-AA-SEI force field^18,69 was used to investigate the conformational preferences of the β-(1→6)-linkage present in β-gentiobiose using explicit solvent MD simulations and validated against data from NMR spectroscopy and X-ray crystallography.⁷⁰ Olsson et al.³⁷ reported conformational dynamics of β-d-GlcpNAc-(1→6)-α-d-Manp-OMe using a range of NMR experiments. The population distribution around (1→6)-linkages based on MD simulations employing the PARM22/SU01⁷¹ CHARMM-based force field was compared with experimental observation. Hünenberger and co-workers used the GROMOS force field for carbohydrates⁷² in combination with the local elevation umbrella sampling method to investigate conformational properties of the glucose-based (1→6)-linked disaccharides isomaltose and gentiobiose using explicit water MD simulations. Good agreement was found for ω conformational sampling in comparison to NMR spectroscopy and X-ray crystallography results.^73,74 While the above studies have yielded insights into the conformational properties of several disaccharides, concerns with respect to force field accuracy, diversity in the systems, and insufficient sampling of conformational space^{23,37,67,73−76} warrant further studies of these biologically interesting systems.⁷⁷

In this study, we investigate the performance of the CHARMM36 (C36) carbohydrate force field^25,78−83 for (1→6)-linkages, especially its ability to accurately treat gluco-, manno-, and galactopyranoside-based oligosaccharides. Initial results showed that the model poorly reproduces experimental data from NMR spectroscopy, motivating additional optimization of the ω dihedral parameters. New parameters for ω were subsequently optimized on the basis of QM data on model compounds that comprise two molecules of tetrahydropyran connected by a (1→6)-linkage. To overcome issues of convergence with respect to the sampling of conformational space, we employ Hamiltonian replica exchange (HREX) based simulations, using biasing potentials on the glycosidic torsions as previously performed in our laboratory as well as by others.⁸⁴⁻⁸⁶ The force field is validated by comparing transglycosidic J coupling constants and proton–proton distances from the simulations with NMR observations. Detailed molecular level analysis is performed to characterize the role of water in the conformational flexibility of the (1→6)-linked oligosaccharides.

Methods

NMR Spectroscopy

Oligosaccharides 1–10 (∼10 mg), available from previous studies,^{37,61,87−90} were lyophilized from D₂O prior to dissolution in 0.6 mL of D₂O. NMR experiments were performed at 298 K on a Bruker Avance III 700 MHz spectrometer equipped with a 5 mm TCI Z-gradient Cryoprobe, unless otherwise stated. Gradient pulses were of 1 ms length unless otherwise stated.

Homonuclear proton–proton coupling constants for all compounds and heteronuclear carbon–proton coupling constants for the site-specifically labeled compounds, viz., [6-¹³C]-3 and [1′,6-¹³C₂]-3, were obtained through iterative fitting of spin-simulated spectra to experimental 1D ¹H spectra using the PERCH NMR spin simulation software.⁹¹

Heteronuclear J_CH were determined using the constant time J-HMBC experiment reported by Meissner and Sørensen,⁹² with a low-pass J filter with τ₁ = 3.45, τ₂ = 3.13, and τ₃ = 2.78 ms being used to suppress one-bond ¹³C,¹H correlations. For ¹³C nuclei, inversion during the coupling evolution was achieved using an 80 kHz chirp pulse (0.5 ms, 20% smoothing), whereas, for refocusing during chemical shift evolution, an 80 kHz composite chirp pulse (2 ms, 20% smoothing) was used. Typically, three to four experiments were acquired for each compound with different coupling evolution delays (Δ) in the range 0.56–0.83 s. For compound 6, an additional experiment was performed with Δ set to 0.29 s, whereas, for compound 5, five experiments with Δ in the range 0.42–0.71 s were used. Three experiments for compound 10 were used in which Δ was set to 0.42, 0.56, and 0.63 s. Spectral widths were 2.5–5.0 and 60–80 ppm in the direct and indirect dimensions, respectively. The acquisition times were 0.6–2 s, and a delay of 1–1.4 s was used between transients. In the indirect dimension, 128–512 t₁ increments were used, averaging 4–32 transients per increment. For all cases, the maximum possible scaling factor (κ) was used, i.e., κ = Δ/t_1,max. Linear prediction to 256–1024 points, zero-filling to 4096 points, and multiplication by a squared 90° shifted sine-bell function were performed prior to Fourier transformation along the indirect dimension. Coupling constants were determined from the scaled peak separation in magnitude mode projections of the indirect dimension.

The HSQC-HECADE⁹³ experiment was used for the measurement of ²J(H5,C6) heteronuclear coupling constants in compounds 4, 5, 6, 9, and 10 and for ³J(C4,H6R) in 5. The ¹J_CH scaling factor was set to 0.4 for compounds 4, 5, 6, and 9 and to 0.3 for compound 10, and the isotropic mixing time was 60 ms. For compounds 4, 5, 6, and 9 the spectral width was 3 and 60 ppm in the direct and indirect dimension, respectively, and two transients were averaged for each of the 512 increments. The acquisition time in the direct dimension was 2 s. For compound 10, the number of increments was 1024 and the spectral widths were 5 and 70 ppm in the direct and indirect dimensions, respectively; for each increment, four transients were averaged using an acquisition time of 3 s. The direct dimension was zero-filled to a digital resolution of 0.1 Hz per point and multiplied with a 2 Hz exponential line-broadening function, while the indirect dimension was subjected to linear prediction and zero-filling to 8192 data points, and multiplied by a squared 90° shifted sine-bell function prior to Fourier transformation. Coupling constants were determined by comparing 1D projections for the different spin states.

¹H,¹H cross-relaxation rates in compounds 6 and 8 were determined on a Bruker Avance III 600 MHz spectrometer equipped with a 5 mm TXI Z-gradient probe using a 1D SPFGSE NOESY experiment.⁹⁴ Zero-quantum coherences were dephased⁹⁵ at the end of the mixing time by the simultaneous application of a 2 G·cm^–1 gradient pulse and a 20 kHz chirp pulse (10 ms, 20% smoothing). The 180° pulse at the center of the mixing time was flanked by 22 G·cm^–1 gradient pulses of opposite directions. Selective excitation was achieved by an r-SNOB shaped pulse⁹⁶ flanked by gradient pulses with the strength 8 G·cm^–1. The length of the selective pulse was 80 ms for H1′ in 6 and 8, 100 ms for H4 in 6, and 150 ms for H5 in 8. For each excitation, six mixing times between 50 and 500 ms were used and each experiment was performed three times in a random order. The spectral window of 10 ppm was sampled with 32k points, and the repetition time was 15 s. Prior to Fourier transformation, the FIDs were zero-filled to 256k points and multiplied by 0.3 Hz exponential line-broadening functions. Baseline correction and integration was performed using the same regions for all spectra having the same excitation. The integrals of relevant peaks were divided by that of the excited resonance,⁹⁷ before fitting of second order equations in which the linear terms correspond to the cross-relaxation rates (σ). Quadratic terms were excluded if an F-test yielded Pr(>F) = 0.01 or higher. For the excitation of H1′ in compound 6, the integrated region for H6S overlapped with that of H3′, H5′, and H6′R, and the region for H6R overlapped with H5 and H6′S. The estimated contributions from the intra-residue interactions were subtracted from the observed cross-relaxation rates, using the effective distances from the MD simulation.⁹⁸ Effective distances were calculated using the isolated spin-pair approximation. The value of σ_ref·r_ref⁶ was calculated for all available reference interactions using effective distances from the MD simulations, and the average of these, ⟨σ_ref·r_ref⁶⟩, was then used to calculate r_ij according to r_ij⁶ = ⟨σ_ref·r_ref⁶⟩/σ_ij for the interaction between protons i and j. For compound 6, the interactions of H1′ with H2′ and H4′ and of H4 with H1, H2, and H3 were used, giving ⟨σ_ref·r_ref⁶⟩ = 11.6 Å⁶·s^–1, and for compound 8, the interactions of H1′ with H2′, H3′, H4′, and H5′ and the H5–H1 interaction were used, giving ⟨σ_ref·r_ref⁶⟩ = 14.4 Å⁶·s^–1. From the T-ROESY cross-relaxation rates reported by Lycknert et al.⁸⁷ for compound 2, the value ⟨σ_ref·r_ref⁶⟩ = 23.5 Å⁶·s^–1 was determined.

Inaccuracies in the measurements as well as in the parametrization of Karplus-type equations contribute to uncertainties in the application of J coupling constants. The precision and accuracy are expected to be ∼0.1 and ∼0.3 Hz, respectively, for coupling constants determined using different types of NMR experiments, e.g., the J-HMBC experiment,⁹⁸⁻¹⁰⁰ compared with the estimated uncertainty of ∼0.5 Hz in the Karplus-type equations used. The main source of uncertainty is thus the parametrization of the Karplus-type equations, especially in the case that the molecule under study differs from the set of molecules used in the parametrization. The latter caveat applies to the relationships used for the ²J(H6R,H6S) and the transglycosidic ³J(C1′,H6R/S) and ³J(C6,H1′) coupling constants because these equations were parametrized for compounds bearing a hydrogen atom at O6 and for glycosidic linkages formed at a secondary carbon atom, respectively. The electronic environment can thus be expected to differ slightly, giving a systematic error in the calculated coupling constants.

The interpretation of NOESY cross-relaxation rates as proton–proton distances via the isolated spin-pair approximation is subject to the availability of suitable reference interactions.¹⁰¹ Additionally, for (1→6)-linked disaccharides, the rotational diffusion is expected to be slightly anisotropic, thereby introducing a dependence of the cross-relaxation rates on the orientation of the proton–proton interaction vectors. However, the effect on the determined effective distances under conditions similar to those used in this study has recently shown to be negligible.¹⁰²

Computational Details

QM calculations were performed with the Gaussian 03 software¹⁰³ using the MP2/cc-pVTZ//MP2/6-31G* model chemistry. Optimizations were performed to default tolerances. Empirical force field calculations were performed using the program CHARMM¹⁰⁴ with the CHARMM36 carbohydrate force field⁷⁸ and the CHARMM modified TIP3P water model.¹⁰⁵ Initial conformations of the model compounds were generated from the topology information present in the force field and were subjected to a 1000-step steepest descent (SD) energy minimization followed by an adopted basis Newton–Raphson (ABNR) energy minimization to a force gradient tolerance of 10^–6 kcal·mol^–1·Å^–2.^106,107 The energy minimized oligosaccharides were then immersed in a pre-equilibrated cubic water box of size 32 Å × 32 Å × 32 Å, which extends at least 10 Å beyond the non-hydrogen atoms of the oligosaccharides. Overlapping water molecules within 2.8 Å of non-hydrogen solute atoms were deleted. For all of the subsequent minimizations and MD simulations, periodic boundary conditions were employed using the CRYSTAL module implemented in the CHARMM program. The electrostatic interactions were treated via the particle-mesh Ewald method¹⁰⁸ with a real-space cutoff of 12 Å, and nonbonded interaction lists were updated heuristically out to 16 Å with a force switch smoothing function from 10 to 12 Å used for the Lennard-Jones interactions.¹⁰⁹ The system was heated during 100 ps from 100 to 298 K with 2.0 kcal·mol^–1·Å^–2 harmonic restraints on the non-hydrogen atoms of the solutes. This was followed by equilibration during 200 ps using the NVT ensemble with 1.0 kcal·mol^–1·Å^–2 harmonic restraints on the non-hydrogen atoms of the oligosaccharides. Subsequently, a 200 ps NPT simulation at 1 atm and 298 K was performed without restraints except for the SHAKE algorithm, which was used to constrain hydrogen atoms involved in covalent bonds.¹¹⁰ The center of mass (COM) of the solutes was restrained near the origin by using the MMFP module¹¹¹ in CHARMM using a harmonic restraint of 1.0 kcal·mol^–1·Å^–2.

The REPDSTR module of a modified version of CHARMM c37b2 was used to perform the HREX simulations.¹¹² The HREX simulations were started from the equilibrated coordinates and were carried out for 11 ns for each replica in the NPT ensemble using the system setup described above including the COM harmonic restraint. An exchange between neighboring replicas was attempted every 1000 MD steps, and the coordinates were saved every 1 ps. For all analyses, the trajectories obtained from the last 10 ns of the unperturbed replica (unbiased, ground state replica out of 8 replicas) were used.

Different HREX strategies and their applications to biological systems have been reported in the literature.^85,113−117 In the present study, a combination of the two-dimensional (2D) dihedral grid-based energy correction map (CMAP)¹¹⁸ and a Saxon–Woods potential¹¹⁹ as the biasing potential across the different replicas is used. CMAP biasing potentials (bpCMAP) are used corresponding to the ψ/ω dihedrals, while a Saxon–Woods potential is used to enhance conformational sampling about the ϕ dihedral angle. To arrive at the bpCMAPs, the underlying MM 2D free energy profiles were obtained by the following procedure. The conformational distribution of each disaccharide in vacuum was sampled using high temperature gas phase Langevin dynamics simulations at 500 K for 500 ns. 2D dihedral distributions for ψ/ω were computed from snapshots saved every 2 ps from the simulations. These 2D dihedral distributions were then converted to free energy profiles based on a Boltzmann probability distribution. The free energy surfaces were then used to generate the eight CMAPs for the eight replicas by scaling the free energy surface by a factor of −0.15n, where n was varied from 0 to 7. Thus, the first replica with 0% scaling represents a simulation with no perturbing potential and the subsequent replicas are under an influence of 15, 30, 45, 60, 75, 90, and 105% of the respective bpCMAPs. An example of a ψ/ω bpCMAP is presented in Figure S1 of the Supporting Information. For the ϕ dihedral, the Saxon–Woods potential utilized a scaled force constant term as the biasing potential across the replicas (eq 1).

1

where h = −0.15n kcal·mol^–1, with n going from 0 to 7 for replicas 1–8; P₁ = 0.1; P₂ = 0.3; and θ_ref = 60° (1, 4, 6, 8, and 10) and −75° (2, 3, 5, 7, and 9). θ_ref was set to the local minimum from a dihedral scan about ϕ in each system.

Calculation of J Coupling Constants

Sampling of the three conformational states of ω, i.e., gt (staggered conformation at 60°), gg (−60°), and tg (180°), can be determined from the homonuclear ³J(H5,H6R) and ³J(H5,H6S) coupling constants.^16,21 Different Karplus equations for these coupling constants have been proposed by Haasnoot et al.,¹²⁰ Imay and Osawa,¹²¹ and Stenutz et al.¹²² The modified Karplus equations proposed by Stenutz et al. for ³J(H5,H6R) and ³J(H5,H6S), eqs 2 and 3, respectively, were derived from combined experimental and computational density functional theory (DFT) studies.¹²² Continuing these efforts, Thibaudeau et al. proposed that the conformational distribution of the ω torsion angle can also be correlated with the ²J(H5,C6) and ²J(C4,C6) coupling constants, as given in eqs 4 and 5.¹²³

2

3

4

5

In this work, we used eqs 2 and 3 to calculate ³J(H5,H6R) and ³J(H5,H6S) coupling constants for the C5–C6 torsion angle in the reducing end residue as well as in the terminal residue.

Heteronuclear proton–carbon coupling constants, ³J(C6,H1′), which are related to ϕ (O5′–C1′–O6–C6) were analyzed using a Karplus equation developed by Widmalm et al., as shown in eq 6.¹²⁴

6

where ϕ_H = H1′–C1′–O6–C6. The phase shift, Δ, which is dependent on the stereochemistry of the linkage between the sugar residues, is −12° for α-d-hexopyranosides and β-l-hexopyranosides and +12° for β-d-hexopyranosides and α-l-hexopyranosides.

Heteronuclear proton–carbon coupling constants, ³J(C1′,H6R/S), were calculated from the simulations using eq 7.¹²⁴

7

where ψ_HR/S = C1′–O6–C6–H6R/S. The variable in-plane effect factor, κ, is 8, and ϕ_O5′ is the torsion angle involving the O5′ oxygen atom of the terminal residue. Coupling constants were calculated every 1 ps from the unperturbed replicas, amounting to 10 000 points (10 ns) from the HREX MD simulations. The calculated coupling constants are presented as averages and standard errors (SE) calculated by dividing the 10 ns of sampling into five 2 ns blocks and then calculating average values from each block, from which the average and standard error (n = 5) over the average values from the five blocks were obtained.

Results and Discussion

The conformational preferences of the α- or β-(1→6)-linked oligosaccharides, in terms of three dihedral angles, ϕ, ψ, and ω, were investigated using conformationally sensitive experimental parameters from NMR spectroscopy, as well as HREX aqueous MD simulations, using the herein optimized force field parameters, for disaccharides 1–9 and trisaccharide 10 (Scheme 1). Moreover, conformational preferences at ω′ (O6′–C6′–C5′–O5′) were analyzed for disaccharides 1–7. The compounds include gluco-, manno-, and galactopyranosides as O-methyl glycosides of the reducing end residue and gluco-, manno-, galacto-, and fucopyranosides at the nonreducing end, with α- or β-configurations at the anomeric carbons. Because of differences in stereoelectronic properties, differences in rotamer populations around ω are expected.^15,16

NMR Spectroscopic Data for Glycosidic (1→6)-Linkages

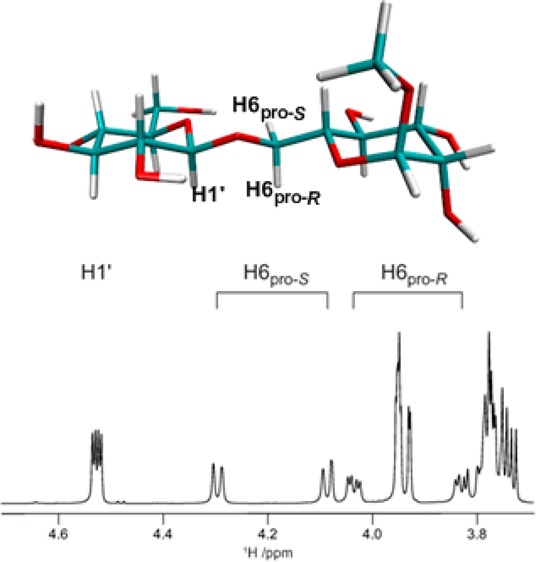
Homonuclear ¹H,¹H coupling constants were determined for all compounds by total line-shape analysis⁹¹ of experimentally determined 1D ¹H spectra. This gave values, shown in Table 1, for ³J(H5,H6R) and ³J(H5,H6S) which report on the conformational preferences at the ω torsion angle, as well as ²J(H6R,H6S) coupling constants (Table S1 in the Supporting Information), which are sensitive to both the ω and ψ torsion angles. Compound 3 was available also as the [6-¹³C] and [1′,6-¹³C₂] site-specifically labeled isotopologues, and thus, it was possible to determine the values for the ³J(H1′,C6), ³J(C1′,H6R), and ³J(C1′,H6S) coupling constants using the total line-shape analysis approach, as demonstrated in Figure 1. For samples at natural ¹³C abundance, the J-HMBC and HSQC-HECADE experiments were used for the determination of heteronuclear ¹³C,¹H long-range coupling constants, as shown for compound 5 in Figure 2. The resulting values are shown in Tables 2 and 3.

Table 1. ²J and ³J Coupling Constants (in Hz) for 1–9 Associated with ω (O5–C5–C6–O6) and ω′ (O5′–C5′–C6′–O6′) Obtained from Experiments and Calculated on the Basis of Dihedral Distributions from HREX MD Simulations (10 ns).

	ω (O5–C5–C6–O6)								ω′ (O5′–C5′–C6′–O6′)
	3J(H5,H6R)		3J(H5,H6S)		2J(H5,C6)		2J(C4,C6)		3J(H5,H6R)		3J(H5,H6S)
compound	expt.a	calc.a	expt.	calc.	expt.	calc.	expt.	calc.	expt.	calc.	expt.	calc.
1b	5.12	5.12 (0.89)c	1.96	1.81 (0.10)	–1.69d	–0.19 (0.64)	<0.5	0.12 (0.24)	5.98	6.69 (0.25)	2.20	2.27 (0.07)
2b	6.48	6.10 (0.98)	1.91	1.79 (0.06)	–2.15d	–1.11 (0.69)	<0.5	0.44 (0.26)	5.77	5.06 (0.89)	2.19	2.10 (0.07)
3	5.41	5.36 (0.60)	2.03	1.76 (0.04)	–1.29d	–0.44 (0.43)	<0.5	0.21 (0.16)	6.13	6.37 (0.43)	2.31	2.32 (0.12)
4	4.32	4.15 (0.90)	2.13	1.79 (0.09)	–1.0	–0.22 (0.68)	e	0.12 (0.25)	5.15	5.87 (0.54)	2.30	2.18 (0.11)
5	5.64	6.11 (0.60)	2.07	1.84 (0.07)	–1.7	–1.02 (0.43)		0.42 (0.16)	7.93	6.77 (0.15)	4.35	5.34 (0.20)
6	7.19	7.02 (0.66)	5.08	4.04 (0.34)	–5.8	–2.64 (0.36)		0.74 (0.16)	5.33	6.85 (0.57)	2.29	2.31 (0.11)
7	7.78	7.74 (0.36)	4.13	3.47 (0.59)		–3.09 (0.25)		0.96 (0.10)	5.82	5.56 (0.28)	2.20	2.27 (0.04)
8	7.35	6.32 (0.36)	4.97	4.45 (0.83)		–2.32 (0.18)		0.59 (0.08)
9	7.74	7.67 (0.38)	4.61	4.52 (0.72)	–5.4	–3.28 (0.07)		0.92 (0.09)
average SE		0.64		0.32		0.41		0.17		0.44		0.10

^aExpt., experimental; Calc., calculated.

^bExperimental values from ref (37).

^cStandard errors are presented in parentheses.

^dObtained by total line-shape analysis of site-specifically labeled ¹³C isotopologues.

^eNot determined.

Figure 1.

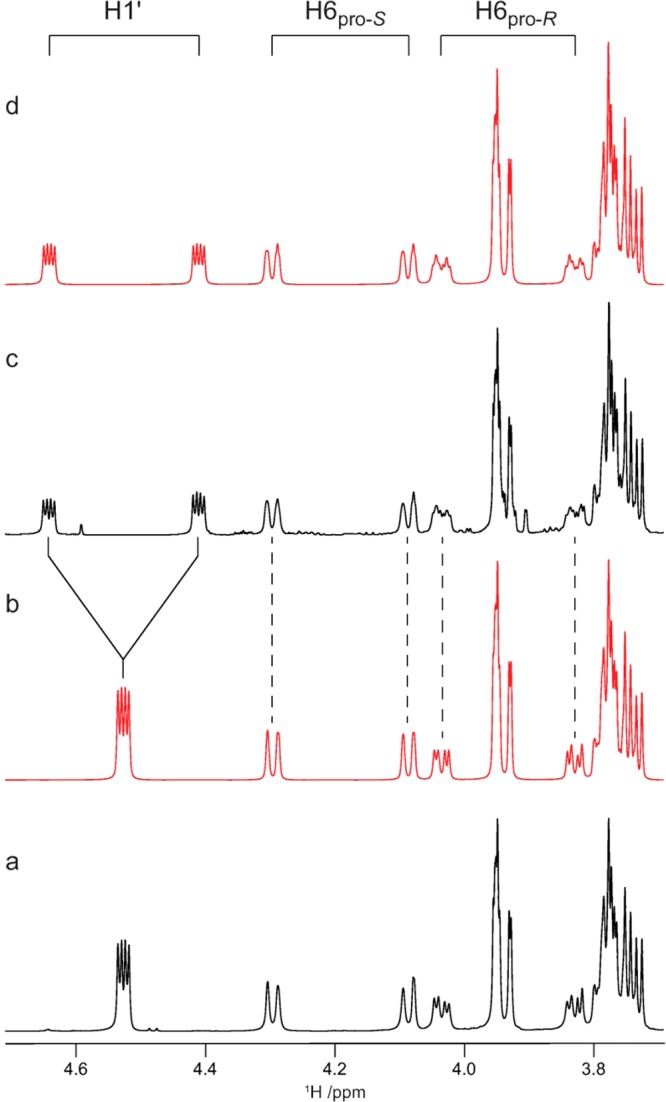
Selected region of 1D ¹H spectra for the site-specifically ¹³C labeled isotopologues of compound 3. Experimental (a) and spin-simulated (b) spectra for [6-¹³C]-3 and experimental (c) and spin-simulated (d) spectra for [1′,6-¹³C₂]-3.

Figure 2.

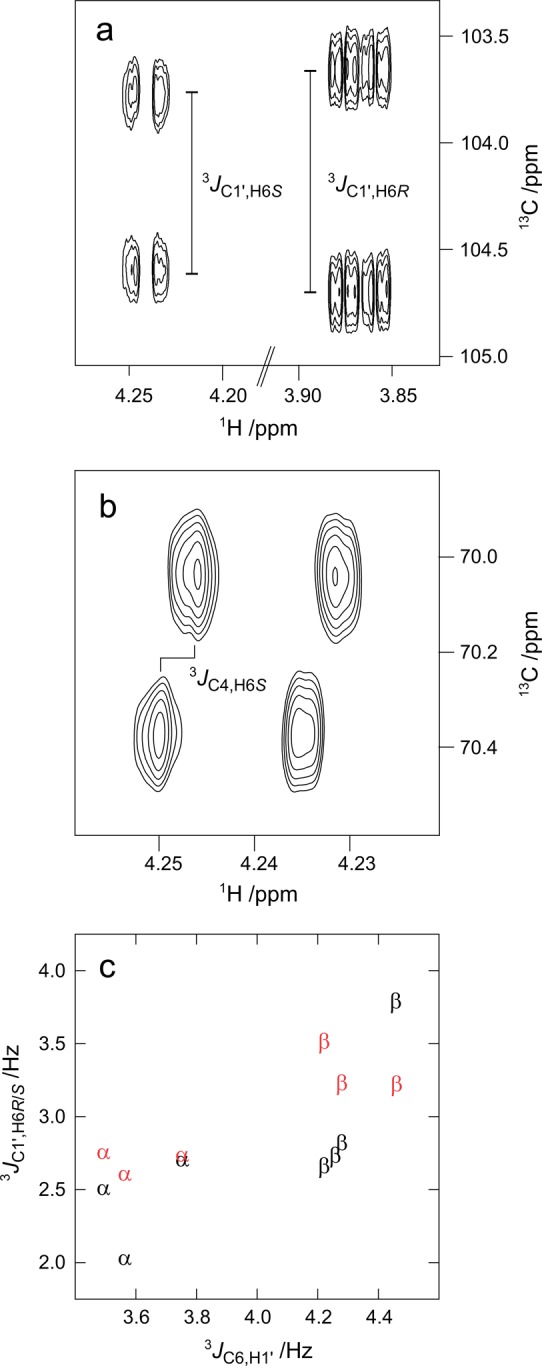
Examples of NMR spectra used in the determination of heteronuclear long-range coupling constants in compound 5: (a) determination of ³J(C1′,H6R) and ³J(C1′,H6S) using the J-HMBC experiment; (b) determination of ³J(C4,H6S) using the HSQC-HECADE experiment. (c) Correlation between the values for ³J(C1′,H6R) (red), ³J(C1′,H6S) (black), and ³J(C6,H1′) in compounds 1–8 labeled according to the stereochemistry at the anomeric carbon of the terminal residue.

Table 2. ³J Coupling Constants (in Hz) of 1–9 Associated with ϕ (O5′–C1′–O6–C6) Obtained from Experiments and Calculated on the Basis of Dihedral Distributions from HREX MD Simulations (10 ns).

	3J(C6,H1′)
compound	expt.a	calc.
1	3.36	3.16 (0.006)b
2	4.10c	3.34 (0.02)
3	4.26d	3.42 (0.08)
4	3.56	3.30 (0.02)
5	4.22	3.39 (0.03)
6	3.75	3.31 (0.03)
7	4.35	3.34 (0.01)
8	4.46	3.31 (0.01)
9	e	3.28 (0.02)
average SE		0.03

^aExpt., experimental; calc., calculated.

^bStandard errors are presented in parentheses.

^cExperimental value from ref (37).

^dFrom total line-shape analysis of [6-¹³C]-3 and [1′,6-¹³C₂]-3, the value was 3.89 and 3.91 Hz, respectively.

^eNot determined.

Table 3. ³J Coupling Constants (in Hz) of 1–9 Associated with ψ (C1′–O6–C6–C5) Obtained from Experiments and Calculated on the Basis of Dihedral Distributions from HREX MD Simulations (10 ns).

	3J(C1′,H6R)		3J(C1′,H6S)
compound	expt.a	calc.	expt.	calc.
1	2.75	2.74 (0.15)	2.50	2.08 (0.06)d
2	b	2.74 (0.14)		1.85 (0.08)
3	3.23c	2.13 (0.07)	2.82c	2.19 (0.08)
4	2.60	2.51 (0.19)	2.02	1.74 (0.02)
5	3.51	2.47 (0.10)	2.66	2.04 (0.05)
6	2.73	2.61 (0.18)	2.70	1.93 (0.09)
7		2.34 (0.05)	2.73	2.25 (0.08)
8	3.22	2.61 (0.07)	3.79	2.37 (0.02)
9	2.80	1.85 (0.03)	3.20	2.52 (0.07)
average SE		0.11		0.06

^aExpt., experimental; calc., calculated.

^bNot determined.

^cFrom total line-shape analysis of [1′,6-¹³C₂]-3, the values were 3.1 and 2.7 Hz for H6R and H6S, respectively.

^dStandard errors are presented in parentheses.

Using limiting values for ³J(H5,H6R) and ³J(H5,H6S),¹²² the relative populations of the three staggered rotamers gt, gg, and tg at the ω and ω′ torsion angles were determined (Table 4). The resulting populations are in agreement with previous studies in that, for manno- and glucopyranosides, there is an approximately equal population of the gt and gg rotamers and limited populations of tg, whereas, for galactopyranosides, the populations are gt > tg ≫ gg.¹²³ Generally, the population of the gt rotamer at the ω torsion angle was found to be higher in the β-d/α-l-linked compounds than in the α-d/β-l-linked compounds, in agreement with findings in a previous study of (1→6)-linked disaccharides.⁶¹ Thus, the population of gt is larger in the β-d-linked compounds 2, 3, and 5 than in the α-d-linked compounds 1 and 4. Similarly, the population of gt is larger in compounds 7 (β-d) and 9 (α-l) than in compounds 6 (α-d) and 8 (β-l).

Table 4. ω and ω′ Rotamer Distributions of Compounds 1–9 Using HREX MD (10 ns)^a.

	ω (O5–C5–C6–O6) population (%)						ω′ (O5′–C5′–C6′–O6′) population (%)
	gt		gg		tg		gt		gg		tg
compound	expt.b	calc.	expt.	calc.	expt.	calc.	expt.	calc.	expt.	calc.	expt.	calc.
1	45	44.6	49	54.4	6	1.0	54	63.3	38	31.2	8	5.5
2	60	57.0	35	41.9	5	1.1	51	45.6	41	50.0	8	4.4
3	48	48.1	46	51.7	6	0.2	55	60.5	36	33.0	9	6.5
4	35	35.3	57	64.5	8	0.3	44	54.6	47	40.3	9	5.1
5	50	56.8	43	42.8	7	0.4	66	55.1	3	1.9	31	43.0
6	55	59.3	7	15.0	38	25.7	46	61.7	45	32.0	9	6.3
7	65	70.5	7	9.6	28	19.9	52	51.0	40	42.6	8	6.4
8	57	50.5	6	19.6	37	29.9
9	63	64.7	4	4.7	33	30.6

^aDistributions are binned from 0 to 120° for gt, from −120 to 0° for gg, and from 120 to 180° and −120 to −180° for tg rotamers in the interval from −180 to 180°.

^bExpt., experimental; calc., calculated.

The coupling constant, ³J(H1′,C6), related to the ϕ torsion angle, was found to be around 4.3 Hz in the β-linked compounds and around 3.7 Hz in the α-linked compounds (Table 2, Figure 2c), indicating a slight difference in the conformational preferences depending on the anomeric configuration. Both of the ³J(C1′,H6R) and ³J(C1′,H6S) coupling constants (Table 3), related to the ψ torsion angle, were slightly larger in the β-linked compounds. For all disaccharides with α-d or β-d configuration at the terminal end residue (1–7), ³J(C1′,H6R) > ³J(C1′,H6S) where experimental data is available, whereas, for the two compounds with l-configuration at this residue (8 and 9), the reverse order was observed.

Parametrization and Computational Data of Glycosidic (1→6)-Linkages

The reported parameters for the glycosidic (1→6)-linkage in the CHARMM36 carbohydrate force field, which are represented by ϕ = O′_ring–C1′–O_link–C6, ψ = C1′–O_link–C6–C5, and ω = O_link–C6–C5–O_ring torsion angles, were developed on the basis of model compounds A and B for ϕ and C and D for ψ and ω (Scheme 2), in part due to the computational cost associated with the QM calculations needed to generate target data.⁷⁸ Optimization using A–D gave ψ/ω surfaces and O_link–C6–C5 angle geometries in good agreement with QM data. However, analysis of the population distribution around ω was not studied using explicit solvent MD simulations. This was undertaken in the present study, where our preliminary calculations using both standard MD and HREX simulations were unable to reproduce the correct ω conformational preferences for the molecules included in this study (Tables S2 and S3, Supporting Information). This motivated additional optimization of the ω torsion parameters.

Scheme 2. (a) Schematic Representation of Model Compounds; (b) Newman Projection of Ideal Staggered ω Rotamers about the C5–C6 Bond.

A–D are model compounds used previously, and E–H represent the new model compounds used for deriving dihedral parameters for the ω torsion angle.

To reparameterize the ω torsion angle, QM calculations were performed on model compounds that consist of two tetrahydropyran units connected by (1→6)-linkages. All of the four possible configurations at both of the C1′ and C5 sites were considered (E–H, Scheme 2). Full QM scans for all three torsion angles (ϕ, ψ, and ω) with the new model compounds would be computationally expensive; thus, a knowledge-based set of 192 conformations were optimized by constraining ϕ (O5′–C1′–O6–C6) to 60 or −60° and ψ (C1′–O6–C6–C5) to 180° while scanning ω (O6–C6–C5–O5) from −180 to 165° at an interval of 15°. During the optimization, we explored the possibility of both phase variation (i.e., phases allowed to assume any value) and non-phase variation (i.e., phase = 0 or 180°) with multiplicities of 1, 2, and 3. The results discussed below are based on parameters obtained through the non-phase-variation method, consistent with other dihedral parameters in the carbohydrate force field. Potential energy plots with parameters developed on the basis of phase variation and non-phase variation during dihedral fitting are given in Figures S2 and S3, respectively, in the Supporting Information. The optimization lead to satisfactory agreement with the QM data, while the enforcement of the phase to 0 or 180° required empirical adjustment of the dihedral parameter for the O6–C6–C5–C4 torsion angle. A somewhat decreased ability of the model to reproduce the QM data was required to balance the rotamer equilibrium between gt and gg in gluco- and mannopyranosides and between gt and tg in galactopyranosides. For example, the root-mean-square (RMS) energy difference over 192 conformations was 0.68 kcal·mol^–1 for the original C36 parameters, 1.01 kcal·mol^–1 for the phase restrained optimized parameters, and 1.02 kcal·mol^–1 for the parameters from phase variation. For illustrative purposes, ω sampling for compounds 1 and 2 from the HREX simulations using the original C36 and the new parameters are given in Figure S4 (Supporting Information). The original C36 parameters, despite being in better agreement with the gas phase QM data, were found to be biased toward gg conformational sampling in all compounds.

Conformational Analysis of ω Torsion Angles (O5–C5–C6–O6)

The results of four different types of J couplings that are dependent on ω, viz., ³J(H5,H6R), ³J(H5,H6S), ²J(H5,C6), and ²J(C4,C6) calculated from the HREX simulations, are presented in Table 1. In general, calculated ³J(H5,H6R) coupling constants are larger than ³J(H5,H6S) and agree very well with experimental observations. Disaccharides 1–5, having a manno- or gluco-configuration at the reducing end residue, show lower values for both of the ³J(H5,H6R) and ³J(H5,H6S) coupling constants than disaccharides 6–9 with a galacto-configuration in this residue, in the experimental measurements as well as from the simulations. The calculated ³J(H5,H6R) and ³J(H5,H6S) values generally agree within ∼0.5 Hz, although slightly larger deviations from the experimental values were observed in compounds 6–8.

The population distribution of ω (Table 4) shows that for 1–5 the gt and gg rotamers were significantly populated while the population of the tg rotamer was negligible. This is due to stabilization of the gg and gt rotamers in gluco- and mannopyranosides by the gauche effect between O5 and O6 as well as destabilization of the tg rotamer due to the 1,3-diaxial interaction between O4 and O6.²⁸ For 6–9, ω populates the gt and tg rotamers, whereas population of the gg rotamer is suppressed due to the 1,3-diaxial interaction between O4 and O6.²⁸ The larger values of the ³J(H5,H6R) and ³J(H5,H6S) coupling constants in 6–9 as compared with 1–5 are attributed to lower populations of the gg rotamers and higher populations of the tg rotamers in the former compounds. The minor discrepancies between calculated and experimental ³J values could be traced back to rotamer populations in 1–9. For instance, the larger deviation of the gt rotamer population found in 5 is clearly reflected in the discrepancy between calculated and experimental values for ³J(H5,H6R) for compound 5. In addition, the simulations slightly overestimate the gg populations and underestimate the tg populations for 6–8, resulting in underestimated values for the ³J(H5,H6S) coupling constants. However, excellent agreement between calculated and experimental rotamer distribution was obtained for 9.

The calculated ²J(C4,C6) coupling constants with values of ∼0.5 Hz and negative values for ²J(H5,C6) for all compounds are in qualitative agreement with the experimental values (Table 1). The simulations correctly predict larger magnitudes for the latter coupling constant in compounds with a galactose residue in the reducing end (6–9) than in the gluco- and manno-configured compounds 1–5. The values determined by NMR spectroscopy are −5.8 and −5.4 Hz for compounds 6 and 9, respectively, similar to the reported values for α-Galp-OMe and β-Galp-OMe, which are −5.2 and −5.5 Hz, respectively.¹²³ However, these values are lower than at the lowest point of the Karplus equation (−5.3 Hz), indicating that the relationship needs to be revised for compounds having a galacto-configuration. While the magnitude of the ²J(H6R,H6S) coupling constant is underestimated by at least 1 Hz for all compounds, the additional ³J(C4,H6R) and ³J(C4,H6S) coupling constants (see the Supporting Information, Table S1) are in good agreement with the experimental data. The results indicate that the CHARMM36 force field and the newly developed ω parameters satisfactorily reproduce the experimental trends in the rotamer distributions for all the studied compounds. While the new parameters yield a significant improvement over the original parameters, there is a slight overestimation of gg and underestimation of tg rotamer population for 6–8. This could be due to a small limitation in the current parameters.⁴² Additionally, the populations derived from NMR spectroscopy are expected to have some degree of uncertainty due to errors in the limiting coupling constant values for the three rotamers.¹²³ The calculated ³J(H5,H6R), ³J(H5,H6S), ²J(H5,C6), and ²J(C4,C6) coupling constants and the corresponding populations for compounds 1–9 obtained using the ω parameters derived with allowed phase variation are given in the Supporting Information, Tables S4 and S5, respectively.

Conformational Analysis of ω′ Torsion Angles (O5′–C5′–C6′–O6′)

The two ³J(H5,H6R) and ³J(H5,H6S) values related to the ω′ torsion angle in the nonreducing end residue of disaccharides 1–7 are given in Table 1. The calculated values are in good agreement with the experimental values. However, some minor discrepancies were observed, for instance, for 5 where the differences in experimental and calculated values for ³J(H5,H6R) and ³J(H5,H6S) are >1.0 Hz. Calculated values for the ²J(H5,C6) coupling constants are in agreement with the experimental values which are available for compounds 3, 4, and 6 (see the Supporting Information, Table S6). The previously published parameters for the hexopyranose monosaccharides have been reported to slightly overestimate the tg rotamer in galactopyranosides.²⁵ However, the overall performance of the parameters for the O5′–C5′–C6′–O6′ torsion is satisfactory in the CHARMM36 force field, as the model captures the trends from NMR spectroscopy and crystallography, i.e., a preferred equilibrium between gt and gg over tg in gluco- or mannopyranosides, whereas the favored equilibrium occurs between the gt and tg rotamers over the gg rotamer in galactopyranosides.^{123,125−127}

Free Energy Maps for α- or β-(1→6)-Linkage Dihedral Angles

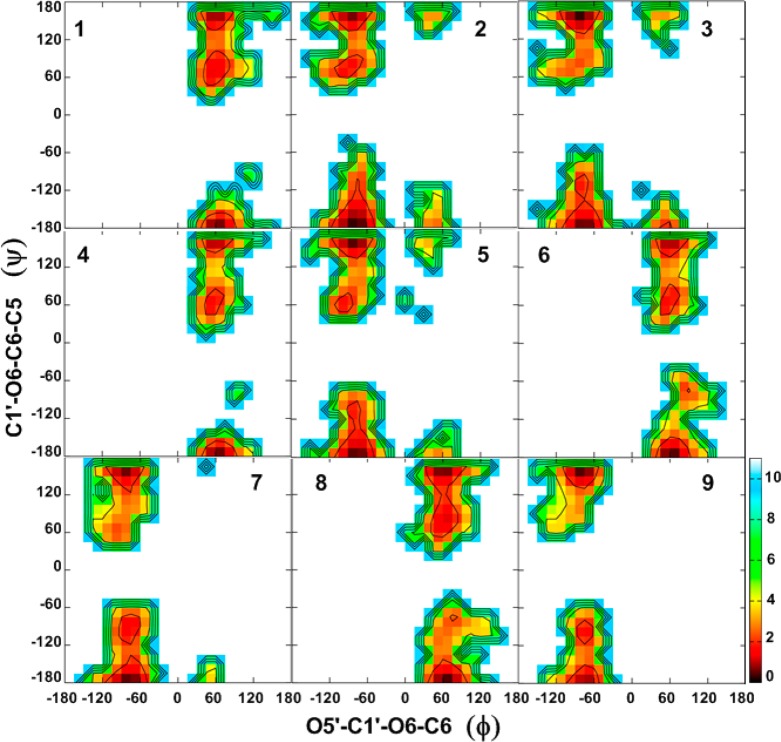
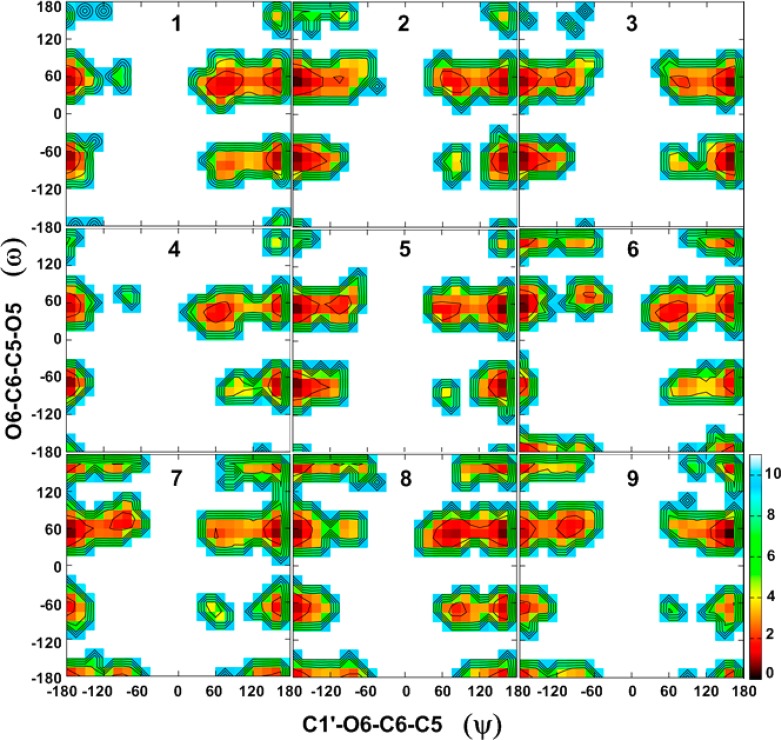
To obtain a detailed understanding of factors that govern specific conformational sampling around glycosidic linkages, 2D free energy maps for the dihedral angles ϕ/ψ and ψ/ω for 1–9 were calculated from the HREX simulations, and these are presented in Figures 3 and 4, respectively.

Figure 3.

Two-dimensional free energy surfaces for the ϕ (O5′–C1′–O6–C6) vs ψ (C1′–O6–C6–C5) dihedrals for 1–9, given in degrees, calculated from the HREX MD simulations. Free energies are calculated from the natural logarithm of the relative probability and are given in kcal·mol^–1.

Figure 4.

Two-dimensional free energy surfaces for the ψ (C1′–O6–C6–C5) vs ω (O6–C6–C5–O5) dihedrals for 1–9, given in degrees, calculated from the HREX MD simulations. Free energies are calculated from the natural logarithm of the relative probability and are given in kcal·mol^–1.

Combined analysis of both the ϕ/ψ and ψ/ω free energy maps provides clues regarding the global minimum conformations for 1–9 and other accessible conformations in the (1→6)-linkages. For all compounds, ϕ prefers an exoanomeric conformation with some transitions to higher energy conformations (anti-ϕ) (Figure 3, Table 5), as has previously been observed in a trisaccharide.¹²⁸ Slightly larger populations of the anti-ϕ conformations are observed for the β-linked gluco-configured disaccharides 2, 3, and 5 as compared to other disaccharides. For the α-d-/β-l-linked disaccharides 1, 4, 6, and 8, the ϕ torsion angle adopts values around 70°, while for the β-d-/α-l-linked disaccharides 2, 3, 5, 7, and 9 the values are around −70°. The preference for the exoanomeric conformation for ϕ was also confirmed by the calculated ³J(C6,H1′) coupling constants, which are in good agreement with the experimental values (Table 2). However, the experimental observation that this coupling constant is larger in β-linked than in α-linked disaccharides is not reproduced. For all compounds, the antiperiplanar conformation at the ψ torsion angle (i.e., 120° < ψ < 180° or −180° < ψ < −120°; ψ_180°) was preferred with populations ranging from 80 to 90% (Table 5). In addition, some sampling centered on 90° (0° < ψ < 120°; ψ_90°) or −90° (−120° < ψ < 0°; ψ_–90°) was observed. Although higher in energy in the present study, NMR and molecular modeling studies reported by Lycknert et al.⁸⁷ showed that conformations with ψ_–90° were present upon binding of β-d-GlcpNAc-(1→6)-α-d-Manp-OMe (2) with wheat germ agglutinin (WGA) lectin. The calculated ³J(C1′,H6R) and ³J(C1′,H6S) coupling constants are slightly underestimated as compared to the experimental values in most of the compounds (Table 3), indicating that the populations of the ψ_90° or ψ_–90° conformations are slightly larger than in the simulations. From the ψ/ω free energy maps shown in Figure 4, it is clear that all disaccharides show lower energy regions representing three rotamers of ω staggered around 60° (gt), −60° (gg), or 180° (tg). In 1–5, there is a preference for lower energy minima located around 60 and −60°, while minima at 180° have higher energy. Similarly, for 6–9, there is a preference for the two lower energy minima located around 60 and 180°, while minima at −60° are also being sampled.

Table 5. Populations (%) in Conformational Regions of the ϕ and ψ Torsion Angles Calculated for 1–9 from HREX MD (10 ns)^a.

compound	ϕexo	anti-ϕ	ψ180°	ψ90°	ψ–90°
1	99.7	0.3	81.9	18.1	0.0
2	97.7	2.3	89.5	7.7	2.8
3	96.2	3.8	92.7	3.2	4.1
4	99.9	0.1	89.8	10.2	0.0
5	98.6	1.4	89.1	6.4	4.5
6	99.8	0.2	86.4	9.9	3.7
7	99.6	0.4	87.0	3.1	9.9
8	99.6	0.4	81.0	15.2	3.8
9	99.8	0.2	90.2	1.2	8.6

^aFor ϕ_exo, an exoanomeric conformation was defined by the region 0° < ϕ < 120° for α-d-/β-l-anomeric compounds 1, 4, 6, and 8 and −120° < ϕ < 0° for β-d-/α-l-anomeric compounds 2, 3, 5, 7, and 9. For all compounds, the antiperiplanar ψ_180° conformation was defined by the regions 120° < ψ < 180° and −180° < ψ < −120°. The ψ_90° and ψ_–90° conformations were defined by the regions 0° < ψ < 120° and −120° < ψ < 0°, respectively, in the interval from −180 to 180°.

In general, ϕ/ψ and ψ/ω free energy maps for 1–9 qualitatively agree with the prior theoretical and experimental observations.^{37,60,64,74,129,130} For instance, Wormald et al.¹⁰ reported the crystallographic average of 64.7 ± 10.4°/–178.4° ± 10.0°/–60.3 ± 14.0° (gg rotamer) and 67.0 ± 10.5°/178.5 ± 13.7°/66.0 ± 13.8° (gt rotamer) for the ϕ/ψ/ω torsion angles in α-d-Manp-(1→6)-d-Manp. Detailed analysis of the ϕ/ψ and ψ/ω energy maps also provided conformational preferences of ω when ψ deviates from the antiperiplanar conformation. We observe that for all compounds (except for 8) there is a preference for the gt rotamer of ω when ψ adopts ψ_90° or ψ_–90° conformations, independent of the linkage configuration. For compound 8, with ψ_90°, there is a preference for gt at ω, while, with ψ_–90°, there is a preference for tg. 1D plots of probability distributions of ϕ, ψ, and ω for 1–9 are shown in Figure S5 of the Supporting Information.

To investigate the relationship between ring conformations and the glycosidic bond angle preferences, we performed ring pucker analysis for the 10 ns HREX aqueous simulations for all compounds. Two distinct formalisms, (i) reported by Cremer and Pople¹³¹ and (ii) described as the virtual α torsions by Rao,¹⁴ were used to analyze the ring puckering (see the Supporting Information, Tables S7 and S8, respectively). From analysis of the calculated total puckering amplitude Q values (∼0.60) and virtual α torsions (α1 = α2 = α3 ≈ −35° for d-sugars and α1 = α2 = α3 ≈ 35° for l-sugars), it is evident that the conformations of both rings in compounds 1–7 maintained the ⁴C₁ chair conformation (i.e., d-gluco-, d-manno-, and d-galactopyranosides), while the ¹C₄ inverted chair conformation was maintained in the β-l- and α-l-fucopyranoside rings in 8 and 9, respectively. These results are in agreement with recent experimental and theoretical studies which suggest preference for the ⁴C₁ chair conformation for gluco-, manno-, and galacto-based pyranosides.^132−134

Proton–Proton Distances

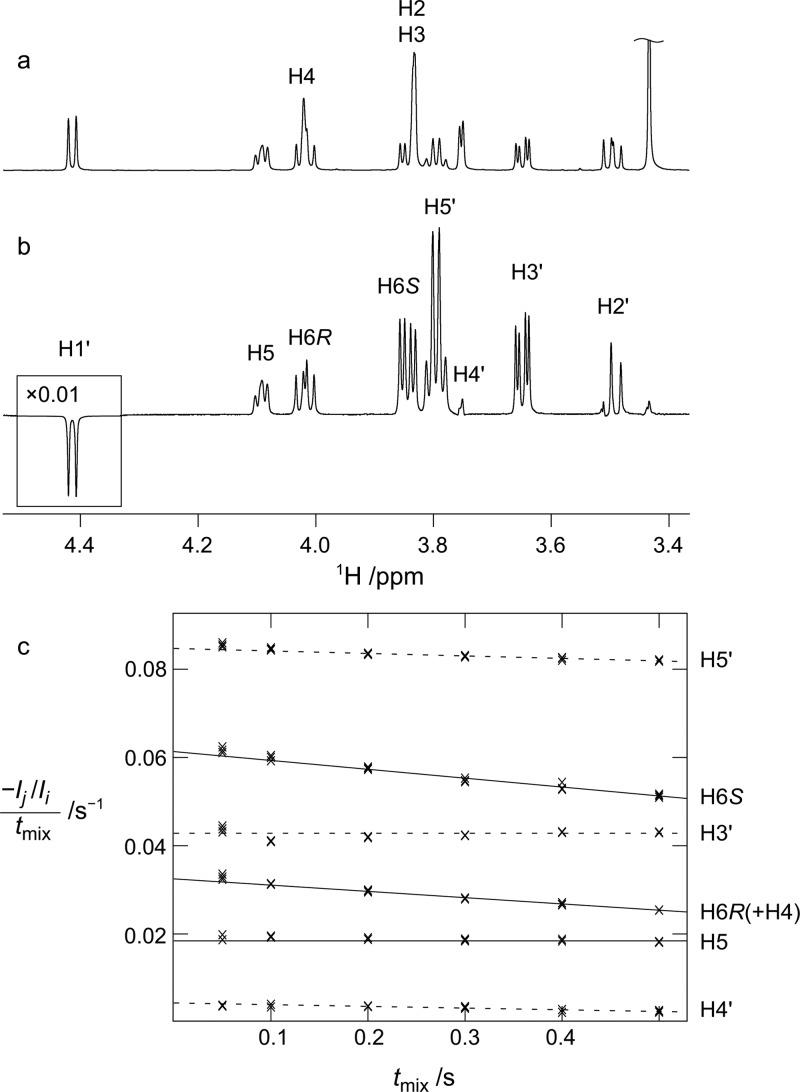
Proton–proton distances, r(H–H), calculated from NMR cross-relaxation rates and from HREX based explicit solvent MD simulations of compounds 2, 6, and 8 are given in Table 6. The cross-relaxation rates for compound 2 were available from a previous study.⁸⁷ In this study, we measured cross-relaxation rates, shown in Tables S9 and S10 in the Supporting Information, for compounds 6 and 8, representing disaccharides with a galacto-configuration in the reducing end residue. A sample spectrum as well as the peak integrals at different mixing times for compound 8 are shown in Figure 5. The effective interproton distances for relevant proton pairs were calculated over the MD trajectory as 1/r_eff = ⟨r_MD^–6⟩^1/6. There is good agreement between calculation and experiment for the rH1′–H6_pro-R values for 2 and for rH1′–H6_pro-S in 2, 6, and 8. Due to overlapping resonances, some proton–proton distances for 6 and 8 could not be measured. However, the sum of cross-relaxation rates obtained for rH1′–H5 and rH1′–H6_pro-R in 6 and for rH1′–H4 and rH1′–H6_pro-R in 8 are in very good agreement with the calculated values. The H1′–H4 distance in compound 6, as well as H4–H6_pro-S in compound 2, is overestimated in the new force field.

Table 6. Effective Proton–Proton Distances from HREX Explicit Solvent MD Simulations and NMR Experiments for Disaccharides 2, 6, and 8.

compd. 2			compd. 6			compd. 8
	reff (Å)			reff (Å)			reff (Å)
proton pair	MD	NMRa	proton pair	MD	NMR	proton pair	MD	NMR
			H1′–H2′(ref)	2.41	2.42	H1′–H2′(ref)	3.06	3.00
H1′–H3′(ref)	2.53	2.52				H1′–H3′(ref)	2.52	2.64
			H1′–H4′(ref)	4.07	4.05	H1′–H4′(ref)	4.02	3.88
H1′–H5′(ref)	2.32	2.33				H1′–H5′(ref)	2.32	2.35
H1′–H6pro-R	2.33	2.45	H1′–H6pro-R+H5b	2.59	2.50	H1′–H6pro-R+H4b	2.75	2.76
H1′–H6pro-S	2.73	2.69	H1′–H6pro-S	2.38	2.43	H1′–H6pro-S	2.36	2.48
H4–H6pro-S	3.18	2.85	H4–H6pro-S	2.71	2.61	H1′–H5c	3.04	3.03
H5–H6pro-S	2.48	2.22	H1′–H4c	4.51	4.07

^aCalculated using cross-relaxation rates from Lycknert et al.⁸⁷

^bOverlapping resonances, only sum of cross-relaxation rates obtained.

^cAverage of both excitations (H1′ → H4/H5 and H4/H5 → H1′).

Figure 5.

Cross-relaxation measurements in compound 8: (a) 1D ¹H spectrum and (b) 1D ¹H,¹H SPFGSE NOESY spectrum obtained with excitation at H1′ and a 500 ms cross-relaxation delay (t_mix). (c) Normalized peak integrals divided by t_mix for different values of t_mix (crosses) together with the fitted equations (lines). Intra- and inter-residual interactions are shown as dashed and full lines, respectively.

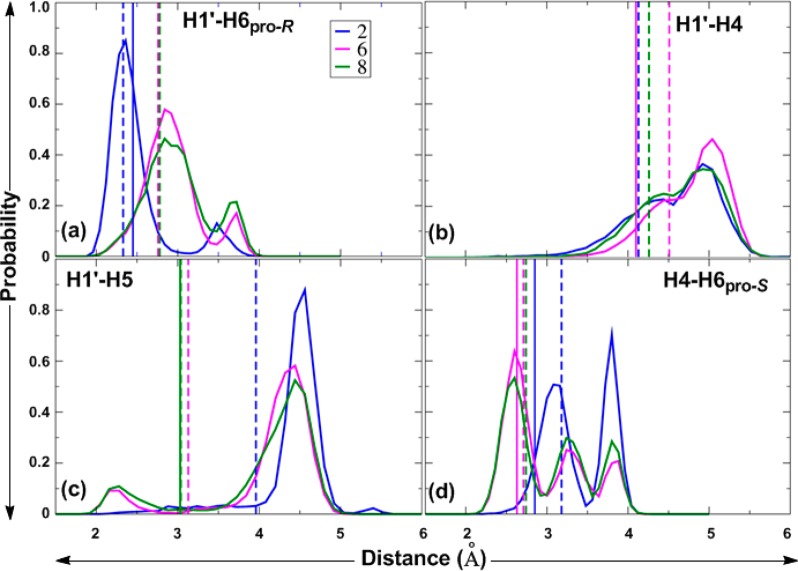
To obtain further insight into these discrepancies, probability distributions of the proton–proton distances, rH1′–H6_pro-R, rH1′–H4, rH1′–H5, and rH4–H6_pro-S, were calculated from HREX MD simulations of 2, 6, and 8 and are given in Figure 6.

Figure 6.

Proton–proton distance distributions for 2, 6, and 8 calculated from the HREX MD simulations. rH1′,H6_pro-R (a), rH1′,H4 (b), rH1′,H5 (c), and rH4,H6_pro-S (d) are given in Å. Solid spikes represent experimental effective distances, and dashed spikes represent effective distances from MD simulations.

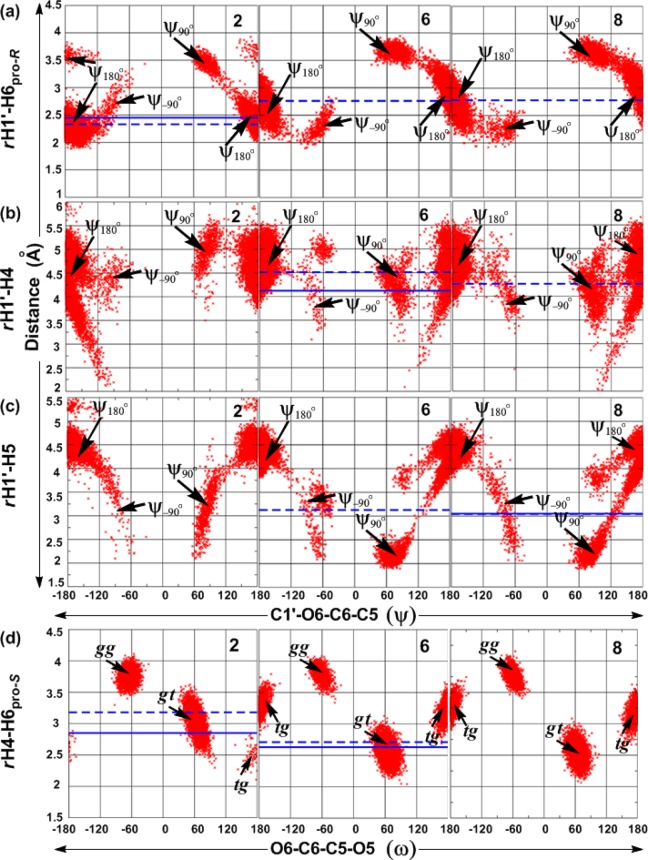
As shown in Figure 6a, the rH1′–H6_pro-R distribution has mainly two peaks for all three compounds. The effective rH1′–H6_pro-R distance is governed by ψ, as shown in plots of ψ versus rH1′–H6_pro-R for 2, 6, and 8 (Figure 7a). The ψ_180° population of the α-d-/β-l-(1→6)-linked compounds 6 and 8 has H1′–H6_pro-R distances mostly ranging from 2.5 to 3.5 Å, whereas, for the β-d-(1→6)-linked compound 2, these range from 2.0 to 3.2 Å (Figure 6a). The second peak in the range of >3.2 Å for 2 and of >3.5 Å for 6 and 8 corresponds to the H1′–H6_pro-R distance in the ψ_90° conformation. The slightly underestimated H1′–H6_pro-R distance in 2 may be due to underpopulation of the ψ_90° conformation. For 2, there is also a minor contribution from the anti-ϕ conformation with ψ_180°. Although 6 and 8 sampled minor populations with ψ_–90° (Table 5, Figure 7a), the third peak for H1′–H6_pro-R in the range 2.0–2.5 Å is not discernible in Figure 6a, as it overlaps with the contribution from ψ_180°. Only the sum of the cross-relaxation rates for the H1′–H6_pro-R and H1′–H5 (6) or H1′–H4 (8) interactions could be determined. Thus, it is not possible to determine the agreement between experiment and simulation for the individual interactions. However, the sums of the calculated effective distances are in excellent agreement with the experimental values.

Figure 7.

ψ vs rH1′–H6_pro-R (a), ψ vs rH1′–H4 (b), ψ vs rH1′–H5 (c), and ω vs rH4–H6_pro-S (d) for 2, 6, and 8 obtained from HREX MD simulations. Proton–proton distances are in Å and dihedral angles in deg. Solid blue lines represent experimental effective proton–proton distances, and dashed blue lines represent calculated effective proton–proton distances.

The rH1′–H4 distribution curves for 6 and 8 (Figure 6b) and the plot of ψ versus rH1′–H4 (Figure 7b) show two major peaks around 4.4 and 5.0 Å, representing sampling of all three ψ_180°, ψ_90°, and ψ_–90° conformations. However, rH1′–H4 is also dependent on the conformational preferences at ω, as shown in Table 7. The distribution curves for rH1′–H5 (Figure 6c) for 6 and 8 show two major peaks, one around 2.3 Å and a second around 4.3 Å. Plots of ψ versus rH1′–H5 (Figure 7c) show that the values of rH1′–H5 are around 2.3 Å in the ψ_90° conformation and that, in the ψ_180° conformation, the H1′–H5 distance is longer.

Table 7. Effective Proton–Proton Distances (Å) and the Population (%) for Each Conformational Region Calculated from Aqueous HREX MD Simulations for 6 and 8.

	compd. 6			compd. 8
ψ_ω	rH1′–H4	rH1′–H5	%PopMD	rH1′–H4	rH1′–H5	%PopMD
ψ180°_gt	4.88	4.11	48.2	4.78	3.99	37.5
ψ90°_gt	4.16	2.17	8.9	3.97	2.23	12.6
ψ–90°_gt	4.97	3.33	2.3	4.97	3.69	0.4
ψ180°_gg	5.01	4.53	14.1	5.02	4.54	17.4
ψ90°_gg	4.66	3.82	1.0	4.66	3.82	2.2
ψ–90°_gg	a		0.0	4.07	4.58	0.0
ψ180°_tg	4.12	4.39	24.1	4.05	4.39	26.1
ψ90°_tg	2.30	3.65	0.0	2.38	3.75	0.4
ψ–90°_tg	3.90	2.56	1.4	3.99	2.78	3.4

^aAbsent in the MD simulation.

To facilitate the understanding of the distribution of ψ and ω and the corresponding rH1′–H4 and rH1′–H5 distances, we calculated effective rH1′–H4 and rH1′–H5 distances for each of the different conformations of ψ and ω (Table 7). The populations of the conformations in the MD simulations are given in Table 7. For compound 6, the H1′–H4 distance from simulation, 4.51 Å, is slightly longer than the experimental value of 4.07 Å. This may be attributed to underpopulation of the two conformations in which this distance is short, namely, the ψ_90°_tg and ψ_–90°_tg conformations, having effective rH1′–H4 distances equal to 2.30 and 3.90 Å, respectively. In addition, overpopulation of the ψ_180°_gg conformation (14.1% in 6) with a long rH1′–H4 distance (5.01 Å) may have contributed to the overestimation of the rH1′–H4 in the simulations. In compound 8, the ψ_90°_gt and ψ_–90°_tg conformations, for which the effective rH1′–H5 distances are 2.23 and 2.78 Å, respectively, are likely adequately sampled, as deduced by the excellent agreement between the values from the simulation (3.04 Å) and from NMR spectroscopy (3.03 Å, Table 6).

The two or three peaks in the probability distribution curves of rH4–H6_pro-S for compounds 2, 6, and 8 (Figure 6d) represent the three different rotamers (gt, gg, and tg) of ω, as deduced from the plots of ω versus rH4–H6_pro-S (Figure 7d). The relationship between ω and the H4–H6_pro-S distance depends on the orientation of H4. For compound 2, which is a manno-configured pyranoside, H4 is axially oriented and the effective rH4–H6_pro-S distance is short, 2.51 Å, in the tg conformation of ω (Figure 7d). The experimental distance of 2.85 Å is consistent with small populations of the tg rotamer in 2. In the gt and gg rotamers, the effective distances are 3.01 and 3.75 Å, respectively. The overestimation of H4–H6_pro-S by approximately 0.3 Å is likely caused by the overpopulation of gg combined with the underpopulation of the tg conformation in compound 2. For the galacto-configured pyranosides in 6 and 8, with H4 being equatorially oriented, the H4–H6_pro-S distance is short, 2.54 and 2.51 Å, respectively, in the gt conformation and longer in the gg (3.77 and 3.76 Å, respectively) and tg conformations (3.22 and 3.20 Å, respectively). The slight overestimation of the H4–H6_pro-S distance by approximately 0.1 Å in compound 6 reflects the overpopulation of the gg rotamer at the expense of the tg rotamer, as compared with the experimental populations shown in Table 4.

Hydrogen-Bonding Analysis

Hydrogen bonding interactions were investigated to understand (i) to what extent intramolecular H-bonding is maintained in the aqueous phase and (ii) to what extent water-mediated intermolecular interactions play a role in determining distributions of ω in oligosaccharides. In addition to the type of sugar involved in the (1→6)-linkage, it is also important to investigate any role of anomeric differences in the water-mediated intermolecular H-bonding pattern and how these affect the conformational sampling. For this purpose, the intramolecular H-bonds in the disaccharides were analyzed in terms of intra-residue and inter-residue H-bonds. The H-bond occupancies from the HREX simulations of 1–9 are summarized in Table 8.

Table 8. Intra-Residue Hydrogen Bond Occupancies for 1–9 Obtained from HREX Simulations^a.

	O-methyl glycoside					terminal residue
compound	O2···HO3	O3···HO2	O4···HO3	O6···HO4	O2′···HO3′	O3′···HO2′	O4′···HO3′	O6′···HO4′	O5′···HO6′
1	0.21	0.12	0.05		0.19	0.11	0.05	0.01	0.19
2	0.20	0.12	0.06	0.00			0.04	0.01	0.16
3	0.20	0.11	0.06		0.07	0.10	0.05	0.01	0.15
4	0.07	0.10	0.04	0.01	0.08	0.10	0.05	0.01	0.18
5	0.07	0.10	0.05		0.07	0.09	0.22	0.01	0.06
6	0.07	0.10	0.24	0.11	0.07	0.11	0.06	0.02	0.16
7	0.06	0.11	0.24	0.09			0.04	0.01	0.13
8	0.06	0.12	0.25	0.15	0.01	0.10	0.27
9	0.06	0.12	0.21	0.04	0.06	0.10	0.26

^aHydrogen bonding occupancies based on a distance cutoff of 2.5 Å between the H-bond donors and acceptors.

Intra-residue H-bonds are characteristic of the residue type; for instance, 1, 2, and 3 with mannopyranoside as the reducing end residue favor the O2···HO3 and O3···HO2 intra-residue H-bonds, as well as the corresponding interactions in the terminal mannosyl residue in 1, while other intra-residue H-bonds were almost absent (Table 8). In 4 and 5, where glucopyranose is present as the reducing end residue and in 3, 4, and 6, where it is the nonreducing residue, the O3···HO2 intra-residue H-bond is present to approximately the same extent as for the mannopyranoses, whereas the occupancies of the O2···HO3 H-bonds are lower. The difference between manno- and glucopyranosides is attributed to the relative orientations of hydroxyls at positions C2 and C3 which are in axial–equatorial and equatorial–equatorial arrangements in the respective sugars. Moreover, for gluco- and mannopyranoside residues, the equatorial orientation of the hydroxyl at position C4 disfavors intra-residue H-bonds involving either of the O4 or HO4 atoms, as seen for compounds 1–5 (Table 8). Conversely, the axial orientation of the C4 hydroxyl in the galactopyranoside units found at the reducing end in 6–9 and at the nonreducing end in 5 leads to relatively higher occupancies for intra-residue H-bonds involving the C3 and C4 hydroxyl groups (O4···HO3, O6···HO4, and O4···HO6, Table 8). In contrast to the gluco- and mannopyranosides, where the C4 hydroxyl loses its intra-residue H-bonds in the presence of water, the galactopyranosides in 6–9 maintain the intraresidue H-bonds (O6···HO4 and O4···HO3) to a small extent.

In the absence of solvent, intra-residue H-bonding involving the C4 hydroxyl stabilizes the ω rotamer in which O4 and O6 are close to each other, that is, tg or gg in the case of an equatorial or axial hydroxyl at C4, respectively.^42,123 However, competing H-bonding with water diminishes the importance of these H-bonds in aqueous solution and consequently the repulsive interactions dominate, leading to the small populations typically observed for these rotamers.⁴²

Thus, although H-bonding between O6···HO4 is present to a large extent in the tg rotamer for compounds 1–5 with an equatorial C4 hydroxyl, the population of this rotamer is small in these compounds. Furthermore, the populations of the tg rotamer are similarly small in compounds 1–5, although compounds 1–3 have larger occupancies of the O6···HO4 H-bond in the tg rotamer than do compounds 4 and 5. Similarly, for compounds 6–9 having a galactose residue in the reducing end, O6···HO4 H-bonding is present to a large extent for the gg rotamer. However, the differences in the populations of the gg rotamer within this group do not correlate with the minor differences observed in the extent of O6···HO4 H-bonding in this rotamer. Thus, differences in the strength of the O6···HO4 H-bond are likely having a negligible influence on the rotameric distribution at the ω torsion angle in aqueous solutions in all of the studied compounds.

The distance probability distribution plots for the O6···HO4 distance in 1–9 (Figure 8) show that, for 1–5, this distance is >3 Å, while, for 6–9, there is a significant probability density below 2.5 Å (with lesser probability density for 9). This indicates that the O6···HO4 intrasugar H-bond can, to some extent, compete with the individual interactions with water.

Figure 8.

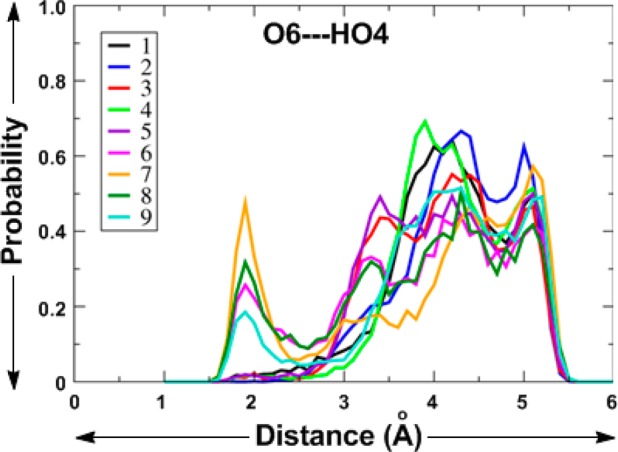
Distance probability distribution for the O6···HO4 distance in 1–9 obtained from HREX MD simulations.

Inter-residue H-bonding between the two monosaccharide units in 1–9 is absent in most of the disaccharides. This is consistent with the observation made by Perić-Hassler et al.⁷⁴ for two (1→6)-linked disaccharides, isomaltose and gentiobiose. However, H-bonding was observed in the present study between the linking oxygen, O6, and HO2′ in 4 (18.8%), 6 (14.2%), and 9 (19.7%), i.e., in all of the α-linked compounds except for compound 1 in which O2′ is axially oriented. Calculations of water radial distribution functions in 1–9 (Figure 9) show a decrease in water occupancy around the O6 atom (Figure 9a) compared to around the O6′ atom (Figure 9b). This is largely due to the increased steric hindrance in the former case compared to the hydroxymethyl O6′ atom. The decreased accessibility of water to the O6 atom is likely the reason for the inability of water to compete with the intramolecular O6–HO4 H-bond (vide supra).

Figure 9.

(a) Radial distribution functions for Ow (water oxygen) and O6. (b) Radial distribution functions for Ow and O6′. Note that O6′ is in the terminal end sugar and O6 participates in the (1→6)-glycosidic linkage.

Interestingly, there are pronounced differences in the region around 3 Å in the Ow–O6 RDFs, as shown in Figure 9a, with the β-linked compounds (2, 3, 5, 7, and 8) having higher densities than the α-linked compounds (1, 4, 6, and 9). This difference indicates that the O6 atom in a β-(1→6)-linkage is more exposed to the solvent than the corresponding atom in an α-(1→6)-linkage.

The role of bridging water molecules in the function and structural stability of carbohydrates has been extensively reported.^135,136 The probabilities of such bridging water molecules between the two residues which may have influenced the distributions of ω in gluco-, manno-, and galactopyranosides are summarized in Table 9. For compounds 1–5, with gluco- and mannopyranosides at the reducing end, both the gg and gt conformations allow water to simultaneously form an H-bond to one of the ring oxygens (O5 or O5′) and the linkage oxygen O6 atom (Figures 10a and b). Occasionally, there are cases where water simultaneously forms H-bonds to the ring oxygen of both monosaccharide units (Figure 10c), as has previously been observed in crystal structures.¹³⁷ Such water-mediated interactions between two monosaccharide units were not observed in the tg conformation in any of the compounds. For compounds 7–9, the gt rotamer is associated with the water-mediated O5···O6 (8 and 9) and O5′···O6 (7 and 8) interactions. Interestingly, the O5···O6 water-mediated interaction was absent for compounds 6 and 7 which have a d-configuration at the terminal end, in contrast to the two other compounds (8 and 9) with a galactose residue at the reducing end, which both have l-configured residues at the nonreducing end. The presence of the water-mediated O6···O5′ and O5···O5′ interactions was found to be higher for the β-linked compounds 2, 3, 5, 7, and 8 than for the other compounds which are α-linked and in which these interactions are virtually absent (Table 9). However, for 6, neither of the ring oxygens (O5 or O5′) was found to interact with the O6 atom via a water bridge. In 2, water-mediated O6···O=C (carbonyl oxygen) interactions may provide additional stabilization to the gt rotamer, as deduced by its greater population as compared to compound 3.

Table 9. Water Bridge Occupancies for 1–9 Obtained from HREX Simulations^a.

compound	O5···O6	O6···O5′	O5···O5′	O5···O2′	O5···HO2′	O6···O2′	HO4···O2′	O6···O=C
1	0.25		0.00
2	0.30	0.18	0.08					0.15
3	0.41	0.19	0.11	0.16		0.17	0.11
4	0.29		0.00	0.26	0.25	0.22
5	0.32	0.18	0.11	0.13		0.14	0.11
6			0.00			0.15
7		0.18	0.02					0.11
8	0.26	0.15	0.11			0.14
9	0.26		0.00	0.22	0.17	0.24

^aH-bond occupancies of >0.08 are shown. The BRIDge option in CHARMM was used for calculating the average number of water bridges formed between selected pairs of atoms.

Figure 10.

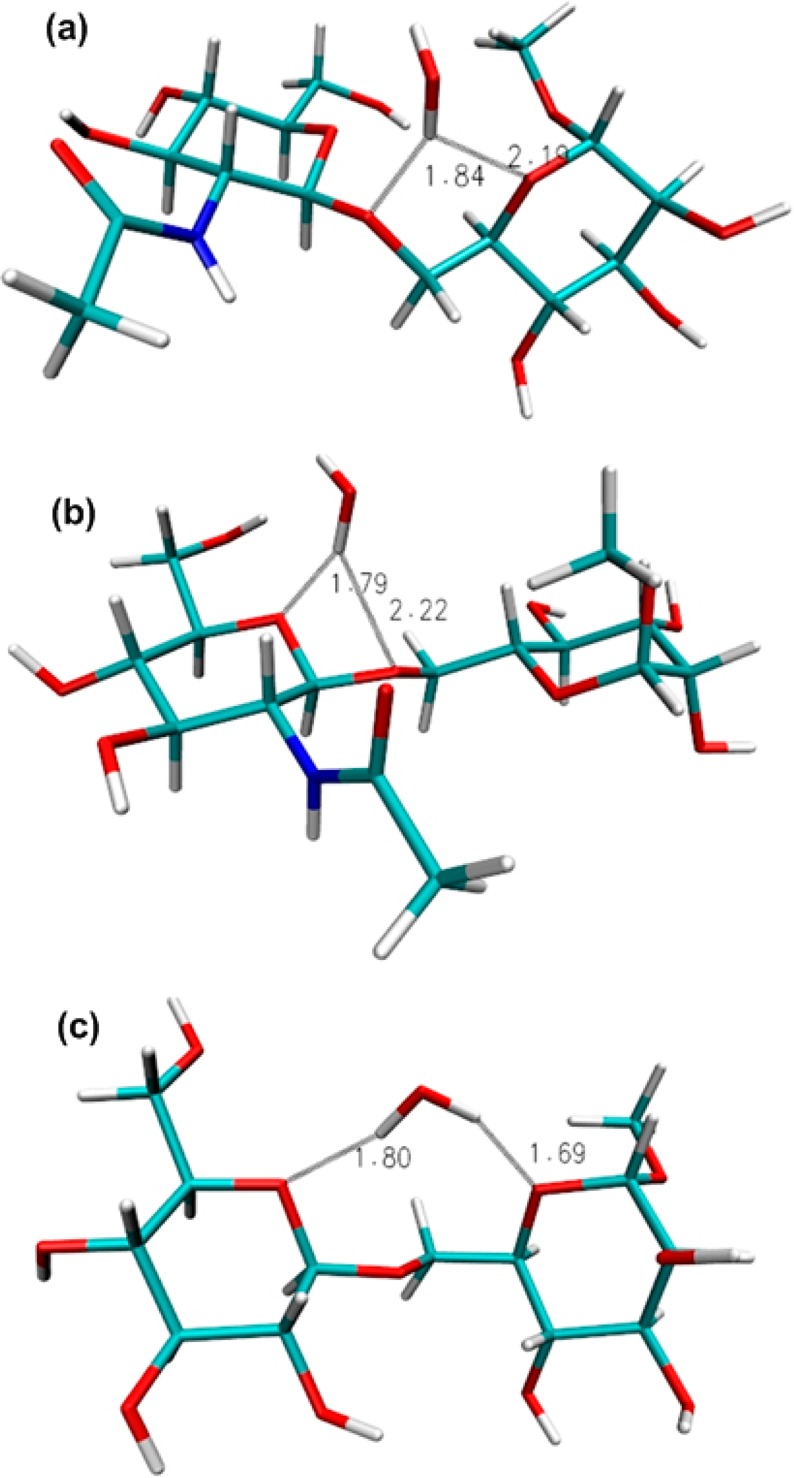
Representative snapshots from the HREX simulations of 2 and 3 showing bridging water molecules. (a) In 2, the gt conformation at ω allows water to simultaneously form an H-bond to ring oxygen O5 and linkage oxygen O6 atom, (b) in 2, the gt conformation allows a water bridge between the ring oxygen O5′ and the linkage oxygen O6 atom, and (c) in 3, the gg conformation allows a water bridge between the two ring oxygen atoms O5 and O5′.

Conformational Analysis of the ω Torsion Angle in the Trisaccharide α-Neu5Ac-(2→6)-β-d-Galp-(1→4)-β-d-Glcp-OEtN₃

Having confidence in the ability of the force field to reproduce conformational distributions around α- or β-(1→6)-linked gluco-, manno-, and galacto-configured disaccharides (1–9), we extended the HREX-MD simulation to the trisaccharide α-Neu5Ac-(2→6)-β-d-Galp-(1→4)-β-d-Glcp-OEtN₃ (10). It consists of an N-acetylated derivative of neuraminic acid (also known as sialic acid) linked to β-d-galactopyranoside by an α-(2→6)-linkage. N-Acetylneuraminic acid (Neu5Ac) is often a terminal unit in glycoproteins and glycolipids that play important roles in a variety of biochemical processes. A few NMR-based studies have been undertaken to determine the preferred conformation about α-Neu5Ac-(2→6)-linkages.^138−141

Analysis of the HREX simulation yielded calculated ³J(H5,H6R) and ³J(H5,H6S) values of 7.82 and 4.29 Hz, respectively, for compound 10. These are in good agreement with the experimental values, being 8.39 and 3.85 Hz, respectively. They are also similar to experimental values for the disaccharide α-Neu5Ac-(2→6)-β-d-Galp-OMe reported by Ohuri et al.,¹⁴² viz., 7.60 and 4.60 Hz for ³J(H5,H6R) and ³J(H5,H6S), respectively. The calculated value of −3.19 Hz for the ²J(H5,C6) coupling constant is underestimated compared to the experimental value (−5.4 Hz), as was observed also for compounds 5–9 (Table 1). The calculated population distribution for ω in 10 was 66:6:28 for the gt/gg/tg rotamers, in excellent agreement with the experimentally determined population distribution which was 73:2:25.

The ³J(C1′,H6R) and ³J(C1′,H6S) coupling constants calculated from the simulation were 2.58 and 1.65 Hz, respectively, in excellent agreement with the values from NMR spectroscopy, viz., 2.47 and 1.64 Hz, respectively. These values are smaller than the corresponding values for compounds 1–9, indicating that the conformational distribution with respect to the ψ torsion angle in 10 is different from that in compounds 1–9. Indeed, compared with conformational preferences of compounds 1–9, in the MD simulation of 10 the ψ torsion angle is considerably less flexible and the antiperiplanar conformation is present to 99%, while ψ_90° and ψ_–90° contribute only 1%. Interestingly, inter-residue H-bonding was observed between oxygen O3 of β-d-Glcp and HO7′ of α-Neu5Ac (19%), as shown in Figure 11, which occurs in an overall bended conformation in which the terminal residue and nonreducing end residue come close. A similar, folded conformation has previously been observed in the complex formed between α-Neu5Ac-(2→6)-β-d-Galp-(1→4)-d-Glcp and the HA70 hemagglutinin of botulinum toxin.¹⁴³ As for the other compounds having an equatorial linkage, i.e., the β-linked compounds 2, 3, 5, 7, and 8 (Table 9), for 10 the ring oxygen (O6′) interacts with the linkage O6 oxygen atom via a water bridge, being present to 24%. Furthermore, there were other water mediated interactions observed at the α-(2→6)-linkage, between O6···HO7′ (10%) as well as between O6 and the two oxygen atoms in the carboxylic acid group in the Neu5Ac residue (∼11% in each case).

Figure 11.

Molecular model of compound 10 showing H-bonding between O3 in the reducing end glucose residue and HO7′ in the terminal end Neu5Ac residue.

Conclusions

In the present study, the conformational dynamics of α- or β-(1→6)-linked gluco-, manno-, and galacto-configured oligosaccharides (1–10) have been explored using HREX-MD simulations and NMR spectroscopy. The three bonds that comprise the (1→6)-linkage showed the least flexibility for ϕ, which prefers the exoanomeric conformation, and intermediate flexibility for ψ, which prefers the antiperiplanar conformation (ψ_180°) with excursions to the ψ_90°/ψ_–90° conformations. The largest conformational fluctuations were observed for ω, with three main rotamers (gt, gg, and tg) being sampled. Discrepancies due to the force field were recognized by comparing with experimental J coupling constants and proton–proton distances, as well as with populations of the rotamers at the ω torsion angle (gt:gg:tg) deduced from NMR spectroscopy. This prompted us to further optimize the O6–C6–C5–O5 (ω torsion) and O6–C6–C5–C4 parameters, resulting in a revised force field which was shown to accurately predict the rotamer distributions in all of the studied compounds. However, a small limitation was observed in terms of a slight overestimation of gg rotamer populations for 2, 6, and 8, leading to a slight overestimation of the H4–H6_pro-S distances as compared to the experimental measurements for compounds 2 and 6. This could be due to either the current parameters or the TIP3P water model used during the simulations, as solvent plays a major role in the relative stabilities of the three ω rotamers. The slight overestimation of rH1′–H4 in 6 is likely caused by underpopulation of the ψ_90°_tg and ψ_–90°_tg conformations.

Direct intramolecular H-bonds between the two monosaccharide units were absent in most of the compounds, although O6···HO2′ H-bonding was observed in the α-(1→6)-linked compounds 4, 6, and 9. The diminished importance of intramolecular hydrogen bonding in aqueous solution results in an equilibrium between the gt and gg rotamers at the ω torsion angle for the gluco- and mannopyranoside-based disaccharides 1–5, as predicted by consideration of the gauche effect and the repulsive interactions between O4 and O6 in the tg conformer. Conversely, galactopyranoside-based oligosaccharides show population distributions in equilibrium between the gt and tg rotamers, as predicted by considering steric interactions disfavoring the gg rotamer and the decreased importance of the stabilizing O6···HO4 hydrogen bond in aqueous solutions. Water radial distribution functions, g(r), indicated that the accessibility for water to interact with O6, which is involved in the (1→6)-linkage, is reduced compared to the O6′ atom in the terminal residue, as expected due to steric effects.

In conclusion, the herein developed parameters for the ω torsion angle allow more accurate MD simulations to be performed for (1→6)-linked oligosaccharides. The CHARMM36 force field and the newly developed ω parameters reproduce the experimental trends in rotamer distributions for the disaccharides as well as the trisaccharide incorporated in this study. Although the new parameters show a significant improvement over the original parameters, there is a small limitation evident in terms of a slight overestimation of the gg populations and underestimation of the tg rotamer populations for galacto-configured residues. This could be caused by a small limitation in the current carbohydrate parameters or from the TIP3P water model, as solvent plays a major role in diminishing the importance of the O6···HO4 hydrogen bond as a stabilizing factor for the gg rotamer in galactopyranosides. It was also noted that the population distribution for ω in the (2→6)-linked galacto-configured trisaccharide did not show as much overpopulation of gg as in the galacto-configured disaccharides in the study. Furthermore, the small ³J(C1′,H6R/S) values with excellent agreement between experiment and simulation support the ψ torsion angle assuming an antiperiplanar conformation as its major conformational state at the (2→6)-linkage in trisaccharide 10.

Supporting Information Available

Additional ²J and ³J coupling constants associated with ω from experiments and HREX MD simulations using the new C36 parameters (Table S1); ²J and ³J coupling constants from original C36 parameters using standard MD (Table S2) and HREX MD (Table S3); ²J and ³J coupling constants (Table S4) and ω torsion population distributions (Table S5) calculated using ω parameters obtained from phase variation; additional ²J coupling constants associated with ω′ (Table S6); ring puckering calculations (Table S7 and S8); experimental cross-relaxation rates for compounds 6 (Table S8) and 8 (Table S9); examples of ψ/ω MM free energy surfaces; QM and MM energy scan for ω; comparative time series obtained for the ω torsion angle using the original C36 and new C36 ω parameters. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Author Contributions

^§ Equal contribution.

Funding Statement

National Institutes of Health, United States