Detection of candidate tumor driver genes using a fully integrated Bayesian approach

Abstract

DNA copy number alterations (CNAs), including amplifications and deletions, can result in significant changes in gene expression, and are closely related to the development and progression of many diseases, especially cancer. For example, CNA-associated expression changes in certain genes (called candidate tumor driver genes) can alter the expression levels of many downstream genes through transcription regulation, and cause cancer. Identification of such candidate tumor driver genes leads to discovery of novel therapeutic targets for personalized treatment of cancers. Several approaches have been developed for this purpose by using both copy number and gene expression data. In this study, we propose a Bayesian approach to identify candidate tumor driver genes, in which the copy number and gene expression data are modeled together, and the dependency between the two data types is modeled through conditional probabilities. The proposed joint modeling approach can identify CNA and differentially expressed (DE) genes simultaneously, leading to improved detection of candidate tumor driver genes and comprehensive understanding of underlying biological processes. The proposed method was evaluated in simulation studies, and then applied to a head and neck squamous cell carcinoma (HNSCC) dataset. Both simulation studies and data application show that the joint modeling approach can significantly improve the performance in identifying candidate tumor driver genes, when compared to other existing approaches.

1. Introduction

Copy number alteration (CNA) is a form of DNA structural change that leads to abnormal numbers of copies in specific DNA regions. CNA is closely associated with the development and progression of many human diseases, especially cancer [1, 2, 3]. CNA could directly affect mRNA expression during transcription (the process of generating mRNA from DNA). For example, genes in deletion regions have less or no copies of DNA, and therefore tend to have lower or no expression. On the other hand, genes in amplification regions have increased numbers of DNA copies, and may be over-expressed. As a result, the expression level of a gene is, in general, positively correlated with its copy number. For example, studies have shown that, in prostate epithelial cell lines, 51% of over-expressed genes were mapped to the chromosomal regions with DNA gain, and 42% of under-expressed genes were mapped to the chromosomal regions with DNA loss [4]. In breast tumor cell lines, 62% of highly amplified genes show moderately or highly elevated expression [5]. Similar evidence was later found in several other tumor types [6, 7].

In cancer research, driver genes are defined as genes whose structural or sequence mutations confer a selective advantage to the cancer cell [8]. Although they need not have CNAs or associated changes in gene expression, many driver genes that have such changes lead to oncogenesis. Studies have shown that the driver genes play essential roles in carcinogenesis, and could be potential targets for cancer therapies [9]. Therefore, it is of great interest to model the association between copy number and gene expression in order to identify candidate tumor driver genes [10], besides identifying genes with CNAs or expression changes alone. However, integrating these two types of data efficiently still remains a challenging problem, because the DNA copy numbers gain or loss may not be directly translated to the same quantity of expression changes in a complex genomic context. Simple and direct correlation analysis of the signal levels may not be effective.

CNA can be measured by comparative genomic hybridization (CGH) array platforms and, more recently, by genome-wide single-nucleotide polymorphism (SNP) array platforms. Several methods have been proposed to analyze copy number data, including recursively segmentation based methods, such as ‘Circular binary segmentation’ (CBS) [11], clustering based methods, such as ‘Cluster along chromosomes’ (CLAC) [12], neighborhood smoothing based methods, such as CGH-Explorer [13] and mixture model based methods [14]. Hidden Markov models (HMMs) have been successfully applied to study CNA [15]. Recently, Guha et al. [16] have developed a Bayesian HMM framework that models copy number data using a Bayesian hierarchical setup. The model draws statistical inference of the CNA status based on posterior probabilities, and does not rely on any tuning parameters. DeSantis et al. have further developed a latent class based HMM [17], which uses a supervised approach to improve statistical efficiency for analyzing copy number data.

To integrate copy number and gene expression data, conventional approaches analyze each type of data separately, and then take the overlapping genes. This is reasonable, but may lead to many false negatives. Several studies [18, 19] have demonstrated the feasibility and advantages of integrating genetic/epigenetic data with gene expression data. In addition, rigorous statistical methods [20, 21, 22, 23] have been developed to integrate different types of data sources. Specifically, to improve the detection of candidate tumor driver genes, several methods were proposed, and most of them take a two-step approach in which copy number and gene expression data are analyzed sequentially [24, 25, 26, 27, 28]. Recently, Schafer et al. [29] have proposed an equally directed abnormalities (edira) method, which uses a Wilcoxon test, combined with a modified correlation measure, to incorporate the dependency between copy number and gene expression data. Menezes et al. [30] introduced a gene set based integration method (SIM), which searches for associations between copy number and gene expression data, not only using individual genes, but also using gene sets. Wessel et al. [31] developed a nonparametric test (intCNGEan) to detect genes with copy number induced differential expression using a two-step approach. Choi et al. [32] proposed a double-layered mixture model (DLMM) to integrate copy number and gene expression data. DLMM directly models segmental patterns in CNA, and simultaneously evaluates the association between the two types of data. All of these approaches lead to improved detection of genes with copy number alterations that are functional in terms of their effect on gene expression, possibly enriching for tumor driver genes. In this study, we propose a novel Bayesian joint modeling approach to analyze copy number and gene expression data simultaneously, where the inherent biological connections between genetic and genomic changes are captured in one integrated model. For copy number data, we adapt an HMM in the spirit of Guha et al. [16] to model spatial patterns existing in CNAs. We further set up a conditional probability matrix to model the dependency of gene expression on CNA in an intuitive way. The copy number and gene expression data are then analyzed in parallel, so that they can borrow information from each other to improve the statistical efficiency. The method assigns high posterior probabilities of being a driver gene when consistent changes between tumor and normal samples in both gene expression and copy number are observed. Thus, the impact of CNA on gene expression can be naturally quantified by our model, which captures the probabilistic nature of the link between CNA and gene expression change, while providing an intuitive measure for biologists to understand the results. Both simulation studies and data application have shown that the proposed model can outperform the edira, SIM, intCNGEan and DLMM methods in detecting candidate tumor driver genes.

The outline of this article is as follows: Section 2 describes the integrated Bayesian model for copy number and gene expression data. Section 3 presents the results from simulation studies in order to compare the proposed method with competing methods. Section 4 presents a data application to a head and neck squamous cell carcinoma (HNSCC) dataset. Section 5 discusses some limitations and future extensions of this study.

2. Statistical Models

2.1. Modeling copy number data

For copy number data, we adapt the Bayesian HMM proposed by Guha et al. [16] to account for the spatial dependence among neighboring genes in CNA status. Guha's model has four CNA states: copy number loss, copy-neutral state, single copy gain, and amplification (i.e., multiple copy gain). In an ideal situation, the single copy gain in the log₂ space is $lo{g}_2\left(\frac{3}{2}\right)\approx 0.58$. But, in real applications, the mean of CNAs could be greatly affected by the fact that some patients have certain copy number gains, yet other patients do not. The observed copy number gain at the population level is an average of the patients with copy gain and those without, so it may be hard to clearly distinguish the single copy gain state from the other states at the population level. Therefore, we merge this state with the amplification state in our model.

Let X_ij denote the copy number ratio of tumor vs. normal samples (in the log₂ space) in the i-th array for gene j, where X_ij follows a normal distribution with mean a_j and variance ${\sigma }_{xj}^2$ for i ∈ (1, . . . , I₁) and j ∈ (1, . . . , J) (i.e., I₁ arrays and J genes in total). For each gene j, D_j represents its CNA status:

$$\{\begin{array}{cc}{D}_j=-1\hfill & \text{if gene}j\text{is in a deletion region}\hfill \\ D_j=0\hfill & \text{if gene}j\text{is in a normal region}\hfill \\ D_j=1\hfill & \text{if gene}j\text{is in an amplification region}\hfill \end{array}\phantom{\}}$$

Furthermore, we assume that for gene j, given the CNA status D_j, the mean measurement a_j follows a normal distribution, namely

$$\begin{array}{cc}\hfill a_j\mid D_j=-1\sim & N({\alpha }_{-},{\tau }_{a-}^2);\hfill \\ \hfill a_j\mid D_j=0\sim & N(0,{\tau }_{a0}^2);\hfill \\ \hfill a_j\mid D_j=+1\sim & N({\alpha }_{+},{\tau }_{a+}^2),\hfill \end{array}$$

where α₋ < 0 < α₊. If gene j is in a normal region, its mean log-ratio should be close to 0 and so the mean of a_j is fixed at 0 for these genes. Here we do not force the a_js to be exactly zero because real data suggest that the mean log-ratios could vary from zero.

A hidden Markov chain is used to model the spatial dependence of D_js among adjacent genes on chromosome. The CNA status D_j of gene j is a hidden state that can not be observed directly, while the observed copy number ratio X_ij depends on the unobserved D_j that takes an integer value (−1, 0, 1), and D_j only depends on D_j–1. Let Λ be the transition matrix of the HMM,

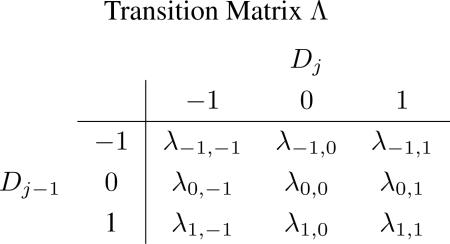where the (s, t)th element in Λ is defined by λ_s,t ≡ P(D_j = t|D_j–1 = s).

For the s-th row of Λ:

$${\overrightarrow{\lambda }}_s=({\lambda }_{s,-1},{\lambda }_{s,0},{\lambda }_{s,1})$$

with

$${\lambda }_{s,-1}+{\lambda }_{s,0}+{\lambda }_{s,+1}=1\text{for}s=-1,0,1.$$

Let (D_j–, D_j0, D_j+) be the corresponding indicator vector of D_j, where (D_j–, D_j0, D_j+) =(1,0,0), (0,1,0) and (0,0,1) represent D_j = –1, 0, 1, respectively. Then

$$(D_{j-,}{D}_{j0},D_{j+})\mid D_{j-1}=s,\Lambda \sim \text{multinomial}(1,{\lambda }_{s,-1},{\lambda }_{s,0},{\lambda }_{s,1}).$$

The row vector of stationary probabilities, $\overrightarrow{\rho }=({\rho }_{-1},{\rho }_0,{\rho }_1)$, satisfies $\overrightarrow{\rho }\cdot \Lambda =\overrightarrow{\rho }$.

2.2. Modeling gene expression data

Let Y_ij denote the expression intensity ratio of tumor sample vs. normal sample (in log₂ space) in the i-th array for gene j, where Y_ij follows a normal distribution with mean b_j and variance ${\sigma }_{yj}^2$, for i ∈ (1, . . . , I₂) and j ∈ (1, . . . , J) (i.e., I₂ arrays and J genes in total). For each gene j, the indicator variable E_j describes its gene expression status:

$$\{\begin{array}{cc}{E}_j=-1\hfill & \text{if gene}j\text{is under-expressed}\hfill \\ E_j=0\hfill & \text{if gene}j\text{is equally expressed}\hfill \\ E_j=1\hfill & \text{if gene}j\text{is over-expressed}\hfill \end{array}\phantom{\}}$$

Furthermore, it is assumed that given the expression status E_j, the mean expression level of gene j follows a normal distribution, namely,

$$\begin{array}{cc}\hfill b_j\mid E_j=-1\sim & N({\beta }_{-},{\tau }_{b-}^2);\hfill \\ \hfill b_j\mid E_j=0\sim & N(0,{\tau }_{b0}^2);\hfill \\ \hfill b_j\mid E_j=+1\sim & N({\beta }_{+},{\tau }_{b+}^2),\hfill \end{array}$$

where β_– < 0 < β₊.

We assume that genes in different CNA regions have different probabilities of being over-expressed and under-expressed. Therefore, we set up a conditional probability matrix Φ to link the copy number and gene expression data,

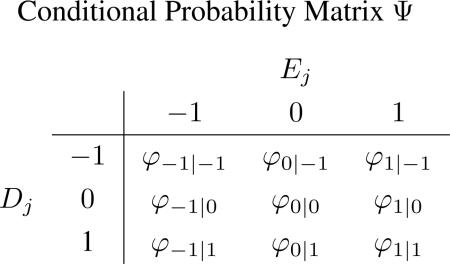where the (s, t)th element in Φ is defined by φ_s|t ≡ P(E_j = t|D_j = s).

For the s-th row of Φ:

$$\overrightarrow{{\phi }_s}=({\phi }_{-1\mid s},{\phi }_{0\mid s},{\phi }_{1\mid s})$$

with

$${\phi }_{-1\mid s}+{\phi }_{0\mid s}+{\phi }_{1\mid s}=1\text{for}s=-1,0,1.$$

Let (E_j–, E_j0, E_j+) be the indicator vector of E_j, where (E_j–, E_j0, E_j+) =(1,0,0), (0,1,0) and (0,0,1) represent E_j = –1, 0, 1, respectively. Then

$$(E_{j-,}{E}_{j0},E_{j+})\mid D_j=s,\Psi \sim \text{multinominal}(1,{\phi }_{-1\mid s},{\phi }_{0\mid s},{\phi }_{1\mid s}).$$

2.3. The full probability model

Let Θ denote all the parameters involved, X denote the copy number data and Y denote the gene expression data. We assume all the variance components are independent. Let ϕ(x|μ, σ²) denote the probability density function (pdf) of a normal distribution with mean μ and variance σ², evaluated at x. Let π(·) denote a general (hyper)prior distribution. Then the full probability model is given by

$$f(\mathbf{X},\mathbf{Y},ϴ)\propto \prod _{i=1}^{I_1}\prod _{j=1}^J\varphi (x_{ij}\mid a_j,{\sigma }_{xj}^2)\cdot \prod _{j=1}^J\varphi (a_j\mid D_j,{\alpha }_{D_j},{\tau }_{a,D_j}^2)\cdot \prod _{i=1}^{I_2}\prod _{j=1}^J\varphi (y_{ij}\mid b_j,{\sigma }_{yi}^2)\cdot \prod _{j=1}^J\varphi (b_j\mid E_j,{\beta }_{E_j},{\tau }_{b,E_j}^2)\cdot \pi \left({\alpha }_{-}\right)\pi \left({\alpha }_{+}\right)\pi \left({\beta }_{-}\right)\pi \left({\beta }_{+}\right)\prod _{j=1}^J\pi \left({\sigma }_{xj}^2\right)\prod _{j=1}^J\pi \left({\sigma }_{yj}^2\right)\cdot \pi \left({\tau }_{a-}^2\right)\pi \left({\tau }_{a0}^2\right)\pi \left({\tau }_{a+}^2\right)\pi \left({\tau }_{b-}^2\right)\pi \left({\pi }_{b0}^2\right)\pi \left({\tau }_{b+}^2\right)\cdot {\rho }_{D_1}\cdot \prod _{j=1}^J{\lambda }_{D_{j-1},D_j}\cdot \prod _{j=1}^J{\phi }_{E_j\mid D_j}\cdot \pi \left({\overrightarrow{\lambda }}_{-1}\right)\pi \left({\overrightarrow{\lambda }}_0\right)\pi \left({\overrightarrow{\lambda }}_1\right)\pi \left({\overrightarrow{\phi }}_{-1}\right)\pi \left({\overrightarrow{\phi }}_0\right)\pi \left({\overrightarrow{\phi }}_1\right).$$

Other details for full conditional posterior distributions are presented in the Appendix.

2.4. Prior specification

For the population-level means, we use independent noninformative flat priors; that is, α_– ~U(–L_α , 0), α₊ ~U(0, L_α), β_– ~ U(–L_β , 0) and β₊ ~ U(0, L_β). Independent conjugate inverse gamma priors, IG(u, v), are assigned to all the variance components. For row vectors ${\overrightarrow{\lambda }}_s$ of the transition matrix Λ and ${\overrightarrow{\phi }}_s$ of the conditional probability matrix Φ(s = –1, 0, 1), we consider a Dirichlet prior $Dirichlet\left(\overrightarrow{\delta }\right)$.

As to specification of the hyperparameters involved, we can specify the upper bounds

$$L_{\alpha }=\underset{ij}{\max }{X}_{ij};{\lambda }_{\beta }=\underset{ij}{\max }{Y}_{ij},$$

so that the corresponding flat priors provide a sufficient coverage to all possible values of the means. Another way to specify L_α (or L_β ) conservatively is to find the mean and standard deviation of all X_ijs (or Y_ijs), say X̄, sd_x (or Ȳ, sd_y), then set

$$L_{\alpha }=\stackrel{‒}{X}+10s{d}_x;L_{\beta }=\stackrel{‒}{Y}+10s{d}_y.$$

The hyperparameters of the inverse gamma priors u and v are chosen to make the priors very vague, for example, u = 0.01 and v = 0.01. For the Dirichlet prior, we choose $\overrightarrow{\delta }=(1,1,1)$ so that they are noninformative.

2.5. Statistical inference and implementation

Since the full posterior conditionals are all known distributions (see the Appendix), a Gibbs sampler can be used to draw posterior samples readily from the joint posterior distribution f(Θ|X, Y). We ran 8,000 iterations for each dataset in our numerical experiments. The first 4,000 iterations were used as burn-in samples, and iterations 4,001-8,000 were used as posterior samples for statistical inference. We also tried 20,000 iterations in our simulation studies, and the results were similar.

The goal of the analysis is to identify the driver genes which have both abnormal expressions and CNAs. We can use the posterior probabilities of E_js and D_js to detect DE genes and genes with CNAs, respectively. For driver genes, we used the posterior probabilities Pr(E_j = 1&D_j = 1) and Pr(E_j = –1&D_j = –1). In the HNSCC data example, we selected genes with Pr(E_j = 1&D_j = 1) > 0.8 or Pr(E_j = –1&D_j = –1) > 0.8 as the identified driver genes.

For convergence detection, we used trace plots. We also ran several chains with different initial values, and then used the Gelman and Rubin's statistics [33] to confirm the chains were converged. To check the sensitivity of the Bayesian analysis, we tested different values of hyper-parameters v, u, δ_–, δ₀, and δ₊ and the results were similar, indicating the analysis is robust against different values of hyper-parameters.

Our approach was implemented with C++ and the statistical part of GNU Scientific Library (GSL). It would take about 5 minutes to get results when the proposed method is applied to the simulated data with 1,000 genes, 15 copy number arrays and 15 gene expression arrays. The time would increase to 1 hour for the real data application in HNSCC data, where we have 10,844 genes with same number of arrays. We provide the integrative analysis software (FIBA: Fully Integrated Bayesian Approach) as a web-based service on our Galaxy server (http://galaxy.qbrc.org/?tool_id=FIBA).

3. Simulation

We conducted eight simulation studies to examine the performance of the proposed method. In Studies 1-3 we compared the performance of our joint modeling approach in detecting driver genes with four existing methods, edira [29], SIM [30], intCNGEan [31], and DLMM [32], all developed for integrative analysis of copy number and gene expression data. The implementation details for different methods are summarized in Table A.1. Next, Studies 4 and 5 evaluated our model with data generated from underlying models that are different from the assumed model. We found that, overall, our approach outperformed the other four methods. Furthermore, to shed light on how our integrated Bayesian approach leads to superior performance and to further understand its behavior, we conducted Studies 6-8, in which we compared the proposed joint modeling approach with the analysis using one data source only.

In all of the simulation studies, we simulated a chromosome with 1,000 genes which has two amplification regions and two deletion regions. Each of the four regions contains 50 genes, and the remaining 800 genes are in the normal regions. Fifteen arrays were simulated for both copy number and gene expression data, following the HNSCC dataset in our application.

3.1. Comparison in detecting candidate tumor driver genes

Here, we considered three different levels of association (strong, moderate and zero) between the copy number and gene expression data. Then, we investigated how the association level affects the relative performance of the five methods, edira, SIM, intCNGEan, DLMM and our joint modeling approach.

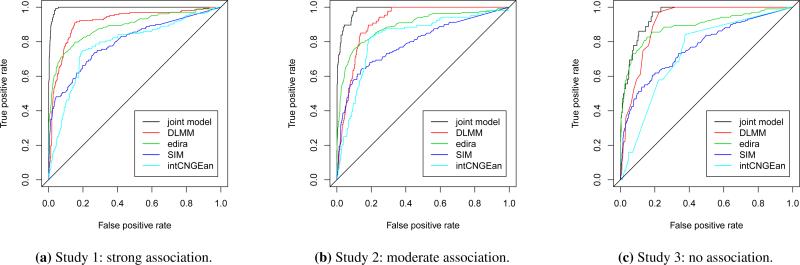
Study 1 is a relatively ideal scenario, where the gene expression is strongly dependent on the CNA status. Specifically, 80% of genes in amplification regions are over-expressed and 80% of genes in deletion regions are under-expressed, while among genes in normal regions, 10% of genes are over-expressed and 10% of genes are under-expressed. All other genes are equally expressed. In Study 2, we assume a moderate level of association. Specifically, 50% of genes in amplification regions are over-expressed, 50% of genes in deletion regions are under-expressed, 10% over-expressed and 10% under-expressed genes in normal regions, and all other genes are equally expressed. In Study 3, we assume there is no association between copy number and gene expression data; that is, we randomly select 10% of genes as over-expressed genes and another 10% of genes as under-expressed genes, so that the gene expression status E_j is independent of the CNA status D_j. For a summary of the association setups, see Table 1.

Table 1.

The conditional probability matrix Ψ for simulation studies 1 to 3 and 6 to 8.

	Study 1&6			Study 2&7			Study 3&8
	Dj = –1	Dj = 0	Dj = 1	Dj = –1	Dj = 0	Dj = 1	Dj = –1, 0, 1
Ej = –1	0.8	0.1	0	0.5	0.1	0	0.1
Ej = 0	0.2	0.8	0.2	0.5	0.8	0.5	0.8
Ej = 1	0	0.1	0.8	0	0.1	0.5	0.1

For copy number data, we generated X_ij from N(a_j, 1.0²) for i = 1, . . . , 15, where a_j ~ N(0, 0.4²) for genes in the normal regions, a_j ~ N(–0.6, 0.6²) for genes in the deletion regions, and a_j ~ N(0.6, 0.6²) for genes in the amplification regions. For gene expression data, we generated Y_ij from N(b_j, 1.0²) for i = 1, . . . , 15, where b_j ~ N(0, 0.4²) for equally expressed genes, b_j ~ N(–1, 0.6²) for under-expressed genes, and b_j ~ N(1, 0.6²) for over-expressed genes. All of the parameter values used here were estimated from the HNSCC dataset in our data application (distributions of the real and simulated datasets are presented in the Figure A.1).

Figure 1 reports the Receiver Operating Characteristic (ROC) curves for the joint model, edira, SIM, intCNGEan and DLMM in Simulation Studies 1-3. The joint model performs much better than all of the other approaches in detecting driver genes when there is a strong association between the copy number and gene expression data (Study 1, Figure 1(a)). Similarly, in Study 2, where there is a moderate association, the proposed joint model also outperforms edira, SIM, intCNGEan and DLMM (Figure 1(b)). Finally, the joint model still performs slightly better than the other four methods even when there is no association between the two data sources (Figure 1(c)). In summary, the proposed joint modeling approach improves the performance of detecting the candidate tumor driver genes, and the improvement appears to increase as the association between the copy number and gene expression data increases.

Figure 1.

Comparison of ROC curves for the proposed joint model, edira, SIM, intCNGEan and DLMM under three different levels of association (strong, moderate and zero) between the copy number and gene expression data. The ROC curves were calculated by ranking the genes according to the measurement scores summarized in Table A.1, and comparing the gene rankings with the simulation truth.

In order to evaluate the performance of our model with data generated from underlying models different from our proposed model, we designed Studies 4 and 5. To better mimic the real data scenario, Study 4 differs from the assumed model in the following ways:

1. For CNA data, we set different alteration levels. Particularly, we set the means of the CNA log ratios in the first amplification region to be from N(0.9, 0.6²) while that of the second amplification region is from a N(0.6, 0.6²). We did the same thing to deletion regions, by simulating the means of CNA log ratios of the first deletion region to be from N(–0.9, 0.6²), while that from the second deletion region is from N(–0.6, 0.6²). In this way, we can test whether the proposed method has flexibility to accommodate different levels of alterations.

2. We simulated the CNA from the individual patient level. For each amplified region, it has 60% probability to be amplified in each individual sample, and the same for the deleted region. This reflects the fact that the alteration occurs at the individual level; i.e., some patients have the alterations, while others do not.

3. For a gene located in an amplified region for a specific patient, it has 60% probability to be over-expressed in the patient. Similarly, for a gene located in a deleted region for a specific patient, it has 60% probability to be under-expressed in the patient. This modification reflects the fact that some driver genes may not lead to changes in gene expression level.

In order to study the robustness of our proposed method against the normal assumption, we used a t mixture distribution [34], instead of a normal mixture distribution, in Study 5 to simulate the data, while keeping the other settings the same as in Study 4. Particularly, the a_j|D_j's in the CNA data were generated from a t distribution with degrees of freedom 5, and location parameter equal to α_–, 0, α₊, respectively, for D_j equals to −1, 0, and 1. The location parameters were chosen so that the sample mean of a_j|D_j's was the same as the previous settings. Similarly, b_j|E_j's in the gene expression data were generated from a t distribution with degrees of freedom 5, and location parameter equal to β_–, 0, β₊, respectively, for E_j equals to −1, 0, and 1.

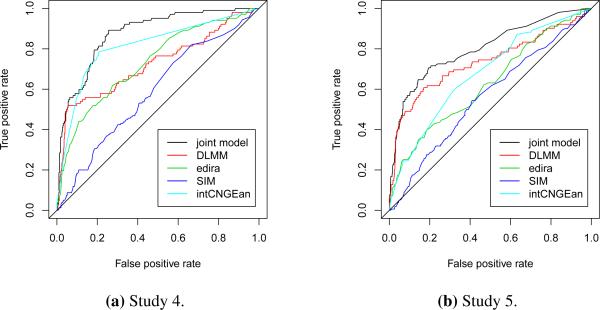
The ROC curves for all five methods in Simulation Studies 4 and 5 were reported in Figure 2, and the AUCs of different methods were summarized in Table 2 (the simulation for each study were repeated ten times, the means and standard deviations of AUCs were reported there). We can see that when data was not generated from the assumed model, the joint modeling approach still outperformed the other methods in Studies 4 and 5.

Figure 2.

Comparison of ROC curves for the proposed joint model, edira, SIM, intCNGEan and DLMM in Studies 4 and 5.

Table 2.

AUC summary for different methods.

	joint model	DLMM	edira	SIM	intCNGEan
Study 1	0.96(0.02)	0.92(0.03)	0.90(0.04)	0.80(0.04)	0.78(0.07)
Study 2	0.95(0.02)	0.90(0.02)	0.88(0.04)	0.76(0.03)	0.73(0.10)
Study 3	0.93(0.03)	0.89(0.03)	0.87(0.05)	0.74(0.05)	0.69(0.11)
Study 4	0.89(0.04)	0.75(0.07)	0.76(0.07)	0.63(0.06)	0.68(0.12)
Study 5	0.79(0.05)	0.71(0.07)	0.67(0.03)	0.57(0.05)	0.65(0.06)

3.2. Understanding the behavior of the joint modeling approach

We conjecture that the observed superior performance of the proposed method comes from explicitly modeling the association between the two types of data sources through an integrated Bayesian approach. To aid our intuition, in Simulation Studies 6-8, we examined the performance of the proposed approach in detecting DE genes and genes with CNAs under different association levels, and compared them with those using either copy number or gene expression data alone. To make a direct comparison, we used the HMM described in Section 2.1 for copy number data alone (named CN alone). We also applied edira for CNA detection to copy number data alone. (Note that the other software (SIM, intCNGEan and DLMM) do not provide the CNA detection results from the single data source analysis.) For gene expression data, we compared the proposed method with its Bayesian counterpart using the hierarchical model described in Section 2.2 (named GE alone), as well as a popular method SAM-t [35]. None of the edira, SIM, intCNGEan and DLMM methods can provide results for differentially expressed gene detection. For the method GE alone, the conditional probability matrix becomes a vector $\overrightarrow{\phi }=({\phi }_{-1},{\phi }_0,{\phi }_1)$, which is independent of the CNA status. Again, for both CN alone and GE alone, we specified the same noninformative priors, and used Gibbs samplers to draw samples from the posterior distributions, as in the proposed method. In this way, the advantage of the Bayesian joint modeling, if any, can be shown through this direct comparison.

As summarized in Table 1, Simulations 6-8 are for strong, moderate and no association between copy number and gene expression data, respectively, which are the same as in Simulations 1-3. We also kept the parameter settings unchanged, except for the noise level in the copy number data, which increases from τ_a– = τ_a+ = 0.6 and τ_a0 = 0.4 in settings 1-3, to τ_a– = τ_a+ = 1.0 and τ_a0 = 0.8 in settings 6-8, in order to further test the robustness of our Bayesian method. (Note that in these new settings, DLMM did not perform properly, because the noise level was too high for DLMM to converge.)

To examine the behavior of the proposed method under this elevated noise level, we report the mean and standard deviation (SD) of the posterior samples for the joint model parameters from Simulation Studies 6-8 in Figure A.3. Also, Table A.2 provides the summary statistics of the posterior samples for the conditional probability matrix Φ in Simulation Study 6 as an example. We find that all of the 95% credible intervals contain the true values of the parameters, indicating the model and posterior sampling procedures worked well.

Next, we compare the joint model with CN alone, edira, SAM-t and GE alone, using ROC curves under the three different association levels. Figure A.2(a) shows the ROC curves for detecting genes with CNAs, and Figure A.2(b) presents those for detecting DE genes (no matter over- or under-expressed) in Study 6 (strong association). In this study, the joint model performs much better than using either copy number or expression data alone. Similarly, in Study 7 (moderate association), the joint model outperforms the analysis using either copy number or gene expression data alone (Figure A.2(c) and (d)), but the improvement is not as large as in Study 6. Finally, the joint model performs similarly to that using either data source alone (Figure A.2(e) and (f)) in Study 8 (no association), which indicates that even if there is no conditional dependency, the proposed method provides a reliable performance. In summary, when there is a positive association between copy number and gene expression data, the joint modeling approach can take advantage of this feature, via an integrated Bayesian approach, to improve the performance in detecting both DE genes and genes with CNAs, leading to the superior performance in identifying candidate tumor driver genes.

4. Application to HNSCC Data

In cancer research, most tumor cells are characterized by CNAs, such as regional or focal amplifications/deletions in chromosomes. Although some driver genes might not lead to expression changes at the mRNA level, a gene is likely to be a tumor driver gene if its CNA-associated expression change alters the transcriptional activities of many downstream genes and leads to cancer. The proposed method can integrate the information from both copy number and gene expression data to better identify candidate tumor driver genes. In this study, we applied our method to a head and neck squamous cell carcinoma (HNSCC) dataset in order to demonstrate the potential advantages of the joint modeling method.

We downloaded the HNSCC dataset from Louhimo et al. 2012 [36], which contains the gene expression (Affymetrix Human Exon 1.0 microarrays) and copy number (Agilent Human 244A comparative genomic hybridization microarrays) data measured in 15 cancer cell lines and one normal control line. We used the 10,844 genes measured in both copy number and gene expression microarray platforms. All genes were aligned and sorted by their chromosome locations. The log₂ ratios between the tumor samples and the control sample were used as input data for the proposed Bayesian joint model. We used the posterior probability Pr(E_j = 1&D_j = 1) or Pr(E_j = –1&D_j = –1) as a criterion to identify candidate tumor driver genes, and then applied Ingenuity Pathway Analysis (IPA) to study the biological functions of identified genes. Interestingly, ‘Cancer’ was identified as the top hit of diseases and disorders for both under-expressed (Table A.3) and over-expressed genes (Table A.4), which indicates the proposed method could identify biologically meaningful genes.

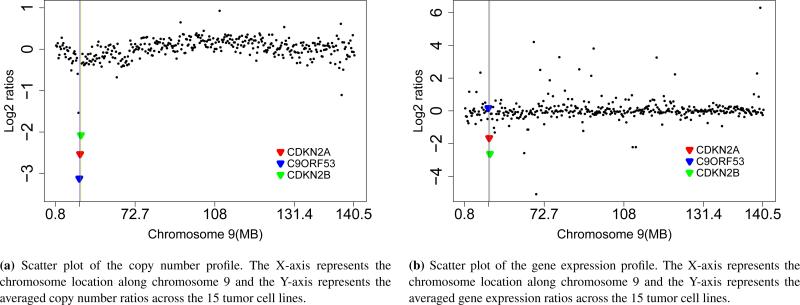
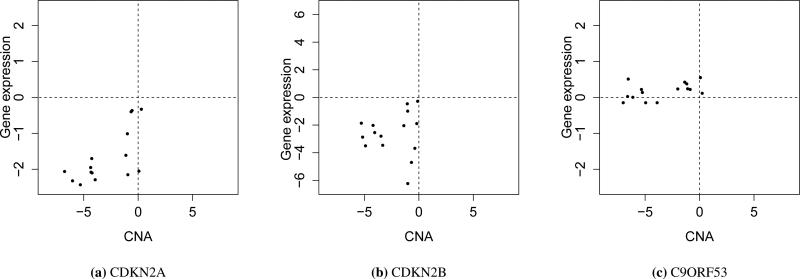
Figure 3 shows the copy number profile (a) and gene expression profile (b) along Chromosome 9. Clearly, there is a copy number deletion region near 22MB. The joint modeling approach identified two tumor driver genes, CDKN2A and CDKN2B, both located in a copy number deletion region with under-expression in the tumor samples, compared to the control sample. Studies [37, 38] have shown that under-expression of CDKN2A through homozygous deletion or promoter hypermethylation leads to HNSCC. CDKN2B is one of the strongest genetic susceptibility loci for HNSCC [39]. In addition, both CDKN2A (p16) and CDKN2B are known to be important tumor suppressor genes in other cancer types, so both genes are likely to be the true driver genes for HNSCC. Another interesting gene, C9ORF53, has an even lower CNA level than both CDKN2A and CDKN2B, but the expression of C9ORF53 gene is not under-expressed in tumor samples. Therefore, it was not identified as a driver gene by the joint modeling approach, indicating the advantage of integrating copy number and gene expression data in identification of candidate tumor driver genes. The scatter plots of copy number and gene expression across 15 tumor cell lines for CDKN2A, CDKN2B and C9ORF53 are shown in Figure 4. We can see from Figure 4 that both CDKN2A and CDKN2B have CNA-associated expression changes, but C9ORF53 does not.

Figure 3.

The position and mean of copy number and gene expression data for CDKN2A (red), CDKN2B (green), and C9ORF53 (blue).

Figure 4.

Scatter plots for CDKN2A, CDKN2B, and C9ORF53. The X-axis represents CNAs and the Y-axis represents gene expression changes throughout 15 tumor cell lines (in log₂ space).

We also applied edira, SIM, intCNGEan and DLMM methods to this dataset. DLMM identified C9ORF53 (score 0.124, rank 1) as the most likely potential gene associated with copy number deletion on chromosome 9, followed by CDKN2A (score 0.108, rank 3) and CNKN2B (score 0.032, rank 23). Similarly, both edira and SIM identified all three of the genes CDKN2A, CDKN2B and C9ORF53 as driver genes. But intCNGEan did not identify any of them with its default setting. These results suggest that our approach performs better in identifying candidate tumor driver genes, compared with the other existing methods.

5. Discussion

Recently, several methods have been proposed to integrate copy number and gene expression data, especially for identifying candidate tumor driver genes [24, 25, 26, 27, 28]. However, most of them focused on either the overlap between genes with CNAs and expression changes, or the correlation between CNAs and expression changes, which might not efficiently capture the wide-range and probabilistic relationships between CNAs and gene expression changes in a complex genomic context. In this study, we propose to model the dependency of gene expression change on CNA status through conditional probabilities under a fully integrated Bayesian framework. By modeling the two types of data simultaneously and capturing the probabilistic relationship between them, we can borrow strength across the different data types and improve the statistical inference for each type of data, which leads to better identification of candidate tumor driver genes. Both simulation studies and a data application have shown that the joint modeling approach compared very favorably with other existing approaches, edira, SIM, intCNGEan, and DLMM; and, more importantly, it may reveal novel tumor driver genes as potential therapeutic targets for cancer treatments.

Among the five methods (edira, SIM, DLMM, intCNGEan and the proposed), all developed for integrative analysis of copy number and gene expression data, we note that the proposed method and DLMM share several common characteristics: (1) both of them rely on model-based Bayesian approaches for coherent inference; (2) both adopt formal Bayesian hierarchical setups for modeling gene expression and copy number data, respectively; and (3) both explicitly model spatial patterns to account for spatial dependence existing in copy number data. All of these features are attractive, leading to improved detection of candidate tumor driver genes, as opposed to purely algorithm-based ad hoc approaches. However, there exist major differences between the two, which may explain their performance difference, especially for data with high noise levels. First, DLMM takes a segmentation-based approach to model spatial dependence in the copy number data, and the breakpoint arrangement is updated by reversible jump Markov Chain Monte Carlo, which needs a build-in Metropolis-Hastings algorithm. In contrast, we adapted an HMM to model spatial dependence, which has led to a much simpler Gibbs sampler with known distributions for all full posterior conditionals. The algorithm is easy to implement through direct sampling, converges quickly, and appears to be robust to high noise levels. DLMM, due to its complexity, tends to be more sensitive, and usually converges more slowly. Second, DLMM does not directly distinguish the direction of changes; that is, its status variables (Z and W ) for aberrant copy number and differential gene expression are binary (0 or 1) instead of three states (−1, 0, +1). Therefore, it takes complicated extra steps that rely not only on Z and W , but also several other continuous variables, in order to calculate the over-expression and under-expression scores. Also, due to the binary setup of Z or W , DLMM has to use a common distribution for genes with any changes for each type of data, without explicitly distinguishing genes with positive changes from those with negative changes. This might cause loss of efficiency, besides the extra effort in inference, when compared to our proposed method.

While CNAs in some genes are constitutively altered in some cancers, those in other genes are only altered in some individual patients. Currently, most computational methods for copy number data are focused on detecting CNA at the individual level. In this study, we attempt to identify the CNA at a population level. Therefore, in our model, the CNA status only depends on genes, not individual subjects. By doing so, the model is more robust and can converge quickly, as we have better statistical power to detect the candidate tumor driver genes at the population level. On the other hand, our model cannot detect the CNA and candidate tumor driver genes for each individual. With some relatively simple modifications, our model can be extended to detect the candidate tumor driver genes for individuals, but the statistical power might be an issue. As we found in the simulation studies, the DLMM method, which models the CNA status at the individual level, only converges when the noise level in copy number data is relatively low.