Maximum Entropy Reconstruction and Nonuniform Sampling in Multidimensional NMR

CONSPECTUS

NMR spectroscopy is one of the most powerful and versatile analytic tools available to chemists. The discrete Fourier transform (DFT) played a seminal role in the development of modern NMR, including the multidimensional methods that are essential for complex biomolecules, but it suffers from well-known limitations. Chief among these is the difficulty of obtaining high-resolution spectral estimates from short data records. For multidimensional NMR experiments, this imposes a sampling burden, because the time required to perform an experiment is proportional to the number of data samples. At high magnetic field, where spectral dispersion is greatest, the problem becomes particularly acute. Consequently multidimensional NMR experiments that rely on the DFT either must sacrifice resolution in order to be completed in reasonable time, or they must use inordinate amounts of time to achieve the potential resolution afforded by high-field magnets. Maximum entropy (MaxEnt) reconstruction is a non-Fourier method of spectrum analysis capable of providing high-resolution spectral estimates from short data records. It can also be used with nonuniformly sampled data sets. Since resolution is substantially determined by the largest evolution time sampled, nonuniform sampling enables high resolution while avoiding the need to uniformly sample at large numbers of evolution times. The Nyquist sampling theorem does not apply to nonuniformly sampled data, and artifacts that attend the use of nonuniform sampling can be viewed as frequency-aliased signals. Strategies for suppressing nonuniform sampling artifacts include careful design of the sampling scheme and special methods for computing the spectrum.

Time savings of a factor of three for each of the N-1 indirect dimensions of an N-dimensional NMR experiment are now routinely reported, making practical high-resolution 3- and 4-dimensional experiments that were previously prohibitively time consuming. Conversely, tailored sampling in the indirect dimensions has been utilized to improve sensitivity. Improvements in nonuniform sampling strategies appear poised to enable further reductions in sampling requirements for high resolution NMR spectra, and the combination of these strategies with robust non-Fourier methods of spectrum analysis (such as MaxEnt) represent a profound change in the way multidimensional experiments are conducted. The potential benefits will enable more advanced applications of multidimensional NMR spectroscopy to biological macromolecules, metabolomics, natural products, dynamic systems, and other areas where resolution, sensitivity, or experiment time are limiting. Just as the development of multidimensional NMR methods presaged multidimensional methods in other areas of spectroscopy, we anticipate that nonuniform sampling approaches will find application in other forms of spectroscopy.

Introduction

NMR spectroscopy can probe all states of matter and quantify the composition of mixtures, structures of molecules, dynamics of rate processes, and thermodynamics of association. This versatility comes at a price; useful sensitivity and high resolution requires expensive magnets and lengthy experiments. The introduction of Fourier Transform (FT) NMR enabled dramatic improvements in sensitivity and resolution¹. In FT-NMR, the response of spins to a strong RF pulse is recorded, and the discrete FT (DFT) is used to compute the spectrum. In 2D NMR, for example, a delay between two RF pulses, representing an “indirect” time dimension, is parametrically sampled by repeating the experiment using different values for the time delay. Successive Fourier transformation along the rows and the columns of the resulting data matrix yields a two-dimensional spectrum. FT-NMR readily generalizes to arbitrary numbers of dimensions², enabling the resolution of individual nuclear resonances in complex systems.

The time required for a multidimensional NMR experiment is directly proportional to the number of samples in the indirect dimensions. Together, the requirements of uniform sampling (required by the DFT) with sufficiently small increments of the delay time to span the width of the spectrum (the Nyquist condition³) and long evolution times (for high resolution) mean that high-resolution spectra require lengthy experiments. Conversely, shorter experiments result in lower resolution spectra. Conventional uniform sampling in a high-resolution 3D experiment can require over a week of measuring time. While 3D experiments have become routine, resolution along the indirect dimensions is usually substantially less than the acquisition dimension. 4D experiments are far from routine, because of the time required to collect data sufficient for even moderate resolution.

The subject of this Account is the use of nonuniform sampling (NUS) methods in multidimensional NMR. NUS permits high-resolution spectra to be obtained from short data records, drastically reducing experiment times. NUS can also be tailored to increase sensitivity. We focus on maximum entropy (MaxEnt) reconstruction, one of a number of non-Fourier methods of spectrum analysis suitable for NUS data, because it is particularly versatile and robust. Fast NMR methods are a burgeoning area of development⁴, and NUS represents just one approach, but one of the most general.

The MaxEnt method

MaxEnt reconstruction finds the spectrum that maximizes the entropy while maintaining consistency with the measured data. The use of entropy as a measure of missing information originated with Shannon and is the foundation for information theory⁵. Consistency of the computed spectrum f with the measured data d is defined by the condition

$$C(\mathbf{f},\mathbf{d})=C_0$$ (1)

where C(f, d) is the unweighted χ-squared statistic,

$$C(\mathbf{f},\mathbf{d})=\sum _{i=0}^{M-1}\mid m_i-d_i{\mid }^2=\sum _{i=0}^{M-1}\mid \text{iDFT}{(\mathbf{f})}_i-d_i{\mid }^2$$ (2)

and C₀ is an estimate of the noise level; iDFT is the inverse DFT, and m is a “mock data” vector given by iDFT(f). The constrained optimization problem is converted to an unconstrained optimization through introduction of a new objective function

$$Q(\mathbf{f},\mathbf{d})=S(\mathbf{f})-\lambda C(\mathbf{f},\mathbf{d}),$$ (3)

where S(f) is the entropy. The unconstrained problem is to find the f that minimizes Q(f, d), where the value of the Lagrange multiplier λ is adjusted to obtain C = C₀. C(f,d) and S(f), and thus Q(f,d), readily generalize to multiple dimensions. The seminal development of the “Cambridge” algorithm⁶, which is both robust and highly efficient, launched the modern application of the maximum entropy principle in NMR. Extensions to the Cambridge algorithm have provided additional performance gains and adapted it to the requirements of phase-sensitive NMR data³.

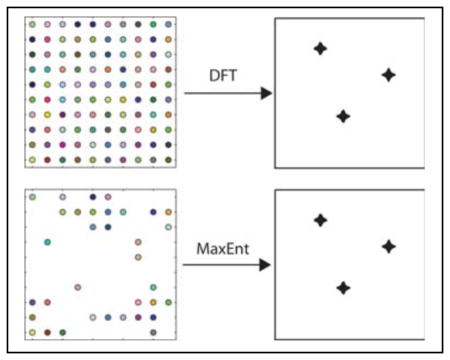
A schematic diagram for MaxEnt reconstruction is shown in Figure 1. Details of the algorithm have been given previously³, however there are a number of features that are important for applications to NUS. At each iteration, m is computed from the current value of f. The computation of C(f,d) can be limited to arbitrary subsets of m; this is the basis for the application to nonuniform sampling methods. The value of λ is normally chosen so that C(f,d) converges to a value (C₀) that is comparable to the noise level in the data. For multidimensional spectra that are reconstructed by computing sub-spectra, e.g. obtaining a 2D spectrum from a series of 1D spectra, using a fixed C₀ value can result in variations in λ that produce slight variations in the nonlinearity of the reconstruction. An alternative, called the fixed-λ algorithm⁷, instead employs a fixed value of λ for all sub-spectra, with λ chosen so that the average value of C(f,d) over all sub-spectra is comparable to the noise. Another alternative is to constrain the reconstruction to match the empirical data very closely, i.e. small C₀ (or large λ). In this approach MaxEnt reconstruction becomes nearly linear⁸. While the formal derivation of the MaxEnt algorithm specifies criteria for determining the value of C₀ and another parameter that appears in the complex entropy functional, applying those criteria in practice can be challenging. Fortunately the results of MaxEnt reconstruction are not terribly dependent on the precise values of the parameters, over a wide range. A heuristic algorithm has been shown to automatically find useful values for the adjustable parameters.⁹

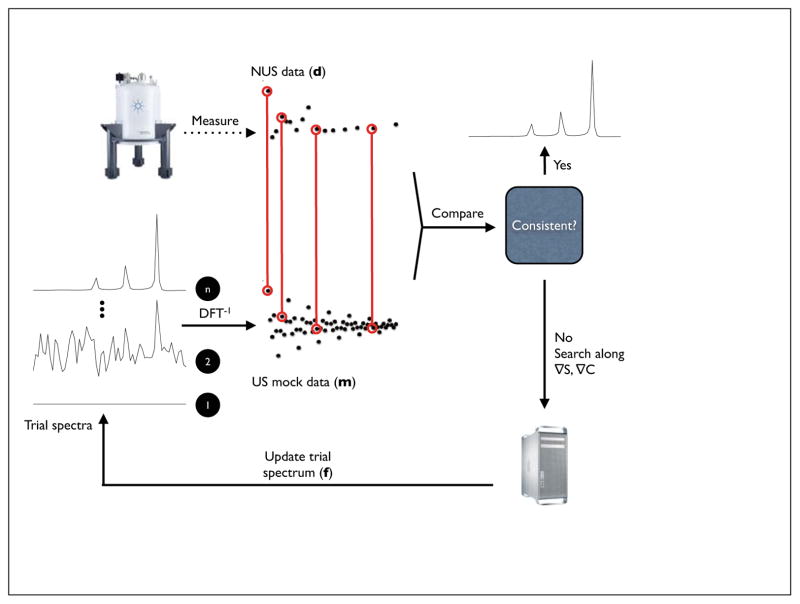
Figure 1. Schematic diagram for MaxEnt.

MaxEnt reconstruction begins with empirical data and a preliminary trial spectrum f (typically a blank spectrum). f is inverted (DFT⁻¹) to create “mock” data (m) that is compared with the empirical data (d). An update to the trial spectrum is computed by searching along the gradients of the entropy and the constraint (the agreement between the empirical and mock data). The algorithm converges to the unique MaxEnt solution when the gradient of the objective function O = S-λC is zero and the gradients of S and C are antiparallel.

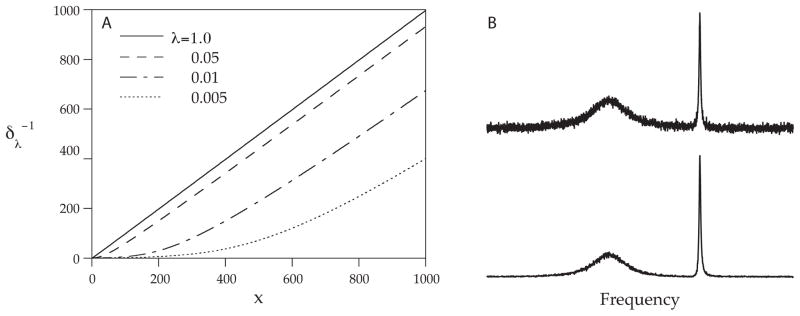
While numerical solution is required in the general case, there is a special case where MaxEnt reconstruction has an analytical solution that gives insights into how MaxEnt reconstruction works. When N (the number of points in the reconstructed spectrum) is equal to M (the number of experimental data points), Parseval’s theorem³ permits the constraint statistic to be computed in the frequency domain. The MaxEnt solution¹⁰ corresponds to a nonlinear transformation, applied point-by-point to the DFT of the time domain data. Figure 2 illustrates the transformation ${\delta }_{\lambda }^{-1}(x)$ for various values of λ (panel A). The transformation depends on the value of λ, and has the effect of scaling every point in the spectrum down, but points closer to the baseline are scaled down more than points far above the baseline (panel B). This explains why noise near the baseline is suppressed more effectively than noise superimposed on top of broad features. This result implies an important distinction between signal-to-noise-ratio (SNR) and sensitivity. Applying the same transformation to both the signal and the noise cannot improve sensitivity, since peaks that are comparable in height to the noise level will be reduced by the same amount as the noise. The SNR may increase, but small peaks will be just as difficult to distinguish as before. In this special case, gains in SNR in the MaxEnt reconstruction are purely cosmetic. In the more general case, there may be real sensitivity gains^11,12. However, a prudent investigator will always question whether gains in SNR really correspond to gains in sensitivity.¹⁰

Figure 2. Nonlinear transformation for analytic MaxEnt.

In the special case that MaxEnt is used to compute the n-element spectrum from an n-element FID, the MaxEnt spectrum is equivalent to applying a monotonic nonlinear transformation to the DFT of the FID. The nonlinear transformation (A) depends on the value of λ ; in the limit of large λ (the constraint weighted more heavily than the entropy), the transformation becomes nearly linear. For small λ, the transformation scales down small amplitude signals more than large amplitude signals (B).

The nonlinearity of MaxEnt has important implications when quantification of peak intensities or volumes is required, such as nuclear Overhauser effect measurements. One approach is to tightly constrain the reconstruction to match the data, which forces the reconstruction to be nearly linear (although at the expense of noise suppression)^8,13. Another is to inject synthetic signals into the time domain data prior to reconstruction. A calibration curve can then be constructed by comparing measured intensities or volumes to the known amplitudes of the injected signals¹⁴.

MaxEnt is just one of a host of methods that have been developed as alternatives to the DFT for reconstructing spectra from NUS data. Some methods place restrictions on the way the data are sampled, for example along radial vectors in time. Others support arbitrary sampling schemes. Among the methods suitable for NUS data, MaxEnt is arguably the best characterized and most versatile. Strengths and weaknesses of the various methods have been compared recently⁴.

Sampling fundamentals

The Nyquist sampling theorem states that to unambiguously determine frequencies, the sampling interval Δt must be at least as short as the reciprocal of the spectral width SW spanned by frequency components in the signal. Frequencies higher than 1/Δt are aliased, or mirrored about the spectral limits. The interval between frequency elements (the digital resolution) of the DFT is 1/NΔt, where N is the number of samples collected; NΔt is the maximum evolution time. The number of samples required to maintain a given maximum evolution time increases with magnetic field strength, because increasing field increases SW.

NUS schemes that sample a subset of the evolution times normally sampled using uniform sampling are called on-grid. In schemes such as radial, spiral or concentric ring, the samples do not fall on this Cartesian grid¹⁵. Exponentially-biased random (on-grid) sampling was the first general NUS approach applied to multidimensional NMR¹⁶. By analogy with matched filter apodization¹⁷, biasing the sampling scheme toward shorter evolution times, using an exponential weighting to match the decay rate of the signal envelope, improves sensitivity. We refer to this as envelope-matched sampling (EMS). Generalizations to sine-modulated signals, where the signal is small at the beginning, and constant-time experiments, where the signal envelope does not decay, utilize the same rationale^18,19. Distributions other than random have been employed; Poisson gap sampling²⁰ avoids long gaps between samples while ensuring the samples are approximately randomly distributed.

It bears emphasizing that Nyquist condition does not apply to NUS: NUS invariably introduces sampling artifacts that are a form of aliasing²¹. To a good approximation, the positions and amplitudes of the sampling artifacts relative to true signals can be derived a priori from the sampling scheme. The point-spread function (PSF) is the spectrum of a real-valued sampling function K consisting of the value 1 for samples included in the NUS scheme and the value zero for samples not included in the scheme. For on-grid sampling, the PSF can be computed using the DFT. K has the property that when it multiplies a uniformly sampled data vector, element-wise, it results in a data vector in which the values not sampled in the NUS scheme have the value zero. The DFT of this zero-augmented NUS data (referred to as nonuniform DFT, nuDFT²²) is equal to the convolution of the DFT spectrum of the uniformly sampled data with the PSF. Thus estimating the spectrum of an NUS data set is equivalent to deconvolving the PSF from the DFT spectrum of the zero-augmented data. While nuDFT provides useful insights into the nature of NUS artifacts, it is not a DFT of NUS data, nor is it a very good estimator of the spectrum of NUS data.

The PSF typically consists of a main central component at zero frequency surrounded by smaller non-zero frequency components. Because the PSF enters into the DFT of the zero-augmented data through convolution, each non-zero frequency component of the PSF gives rise to a sampling artifact for each signal component, with positions relative to the signal components that are the same as the relationship of the satellite peaks to the central component in the PSF. The amplitudes of the sampling artifacts are proportional to the amplitude of the signal component and the relative height of the satellite peaks in the PSF. Thus the largest sampling artifacts arise from the largest-amplitude components of the signal spectrum. The useful dynamic range (ratio between the magnitude of the largest and smallest detectable signal components) of the DFT spectrum of the zero-augmented data can be directly estimated from the PSF as the ratio between the amplitudes of the zero-frequency component and largest non-zero frequency component; this ratio is the peak-to-sidelobe ratio (PSR). The ability of a method of spectrum analysis to suppress sampling artifacts is ultimately limited by both the noise and the dynamic range of the signal.

In addition to the PSR, another useful metric for sampling schemes is the sensitivity relative to uniform sampling. The relative sensitivity depends on the sampling scheme and the nature of the signals, principally the decay rate (or $R_2^{\ast }$) of the signal envelope; in contrast the PSR depends only on the sampling scheme. The relative sensitivity r(K) of a sampling scheme with sampling function K for a hypothetical signal can be estimated from the signal amplitude captured by a NUS scheme divided by that for uniform sampling having the same maximum evolution times t_max. For an exponentially decaying signal, the relative sensitivity of a scheme K spanning a two-dimensional grid with size n₁ by n₂ is approximately given by²³

$$r(\mathbf{K})=\frac{{\mathrm{\sum }}_{i=1}^{n_1}{\mathrm{\sum }}_{j=1}^{n_2}{K}_{ij}{p}_{ij}}{{\mathrm{\sum }}_{i=1}^{n_1}{\mathrm{\sum }}_{j=1}^{n_2}{p}_{ij}}$$ (4)

where the elements of p are given by

$$p_{ij}=\mathit{exp}\left\{-\left(\frac{(i-1)R_2(1)}{SW(1)}\right)-\left(\frac{(j-1)R_2(2)}{SW(2)}\right)\right\},$$ (5)

R₂(1) and R₂(2) are the signal envelope decay rates, and SW(1) and SW(2) are the spectral widths in the two dimensions. A more accurate estimate would include the amount of noise captured by the NUS scheme, compared to uniform sampling. Recently systematic efforts to improve sensitivity using NUS have been reported^8,24.

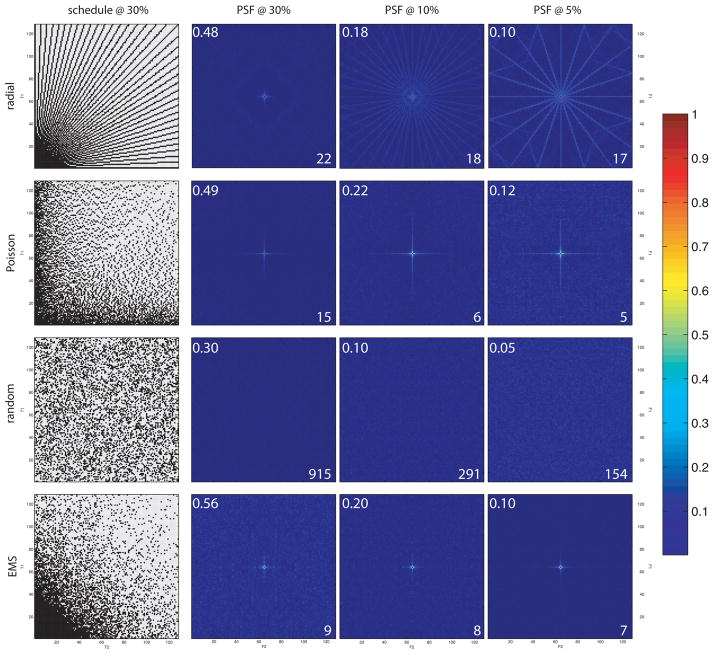
The magnitudes of artifacts in NUS spectra depend on the distribution of sampled evolution times and the sampling coverage γ(K)=k/N, with k equal to the number of nonzero entries in K and N the total number of elements in K, which is the fraction of the evolution times from a uniform grid that are sampled by K. For the example above, $\mathrm{\gamma }(\mathbf{K})=\frac{k}{(n_1\times n_2)}$. In general, the PSR increases with increasing γ, with only the zero-frequency element of the PSF having a non-zero value for γ=1. Because large values of the nonzero frequency components result from correlations among the sampled evolution times, K composed of random evolution times will have the smallest sampling artifacts, and highest PSR, for a given coverage. For decaying sinusoids, a random sampling scheme will not have the highest sensitivity. A compromise between sensitivity and small artifacts leads to biased random sampling distributions, such as EMS¹⁷. PSFs, together with PSRs and relative sensitivity are shown in Fig. 3 for some representative sampling schemes, for sampling coverages of 0.3, 0.1, and 0.05. The importance of randomness in sampling schemes for suppressing sampling artifacts has been explored in depth^21,25.

Figure 3. Examples of NUS schemes and PSFs.

Examples of NUS sampling functions and PSFs in two nonuniformly sampled dimensions. Purely random sampling (third row) yields the smallest sampling artifacts for a given level of coverage (the central zero-frequency component is extremely narrow, making it hard to discern the red dot). Values for the relative sensitivity and PSR (both unitless) are displayed in the upper left and lower right, respectively, for each PSF.

The resolution of any sampling scheme along a given dimension, whether uniform or nonuniform, is largely determined by t_max. Using the DFT, resolving spectral features separated by the natural linewidth requires sampling at evolution times of πT₂ or longer, but sampling beyond 1.26T₂ results in diminishing returns on sensitivity²⁶. (Without apodization, SNR reaches it maximum at 1.26T₂. Using matched filter apodization, SNR does not reach a maximum, but reaches 96% of the limiting value at 1.26T₂.) With MaxEnt, sampling to 1.26T₂ usually resolves spectral components separated by the natural linewidth, and thus represents a reasonable compromise between sensitivity and resolution for decaying signals. For experiments in which the evolution period is constant-time, the signal decay is determined mainly by field inhomogeneity (RF and B₀), and so practical limits on t_max are imposed by the inhomogeneity or length of the constant time period, rather than T₂.

The degree to which reducing sampling coverage via NUS can reduce experiment time, compared to uniform sampling, depends on a number of factors in addition to the randomness of the sampling scheme. Dynamic range of the signals and their amplitude relative to noise are key determinants. Because sampling artifacts enter through convolution, high dynamic range signals present challenges. Instead of being additive, the amplitudes of the largest sampling artifacts are determined by the amplitude of the strongest signal component. When the dynamic range is large, these artifacts may exceed the amplitude of weak signal components. Thus more aggressive reductions in sampling coverage are feasible for high sensitivity experiments that have low dynamic range, and are more challenging for experiments with low sensitivity or high dynamic range. Dimensionality and sparsity (the fraction of values with amplitudes close to zero) of the spectrum have also been shown to play a role^27,28. Increasing dimensionality helps in two ways, by decreasing the coherence of sampling and by increasing the sparsity of the spectrum. Sparsity helps because non-Fourier methods of spectrum analysis such as MaxEnt and l₁-norm reconstruction work best for recovering sparse spectra²⁸. As we show below, sampling coverage can conservatively be around 1/3 for each NUS dimension (e.g. roughly an order of magnitude reduction relative to uniform sampling for two indirect dimensions), even for challenging signals with high dynamic range, while more aggressive reductions have been used successfully for low dynamic range signals.

Optimal sampling

As noted above in the discussion of sensitivity, optimizing sampling schemes can be challenging. Additional optimization can be realized by adjusting the sampling grid. Nonuniform sampling on an oversampled grid has been shown to shift artifacts to the edges of the spectrum, outside the desired spectral window, although the magnitude of sampling artifacts is not affected²⁹. Because a sampling scheme that is optimal for one signal will not necessarily be optimal for a signal containing different frequency components, the design of efficient sampling schemes involves tradeoffs. Simply put, no single NUS scheme will be best suited for all experiments. Despite these challenges, prior knowledge about the signal can successfully inform the design of efficient sampling schemes. One approach is to use “greedy” or adaptive sampling, in which a sampling scheme is iteratively generated by asking what sample (corresponding to a specific combination of indirect evolution times), added to samples already measured, will most improve some metric of performance. Suitable metrics can be derived from the PSF (to minimize sampling artifacts), the relative sensitivity, the ability to resolve expected resonances based on statistical knowledge of chemical shift distributions³⁰, or from characteristics of the spectrum reconstruction prior to the next sample^31,32. A caveat is that while prior knowledge can greatly improve sampling efficiency when it is accurate, highly-tailored sampling schemes can be less robust than more general sampling schemes when there are deviations from the underlying assumptions²³ or high levels of experiment noise.

NUS in action

One compelling reason for adopting NUS in multidimensional NMR experiments is dramatic savings in data collection time, without loss of resolution. The potential savings increase with magnetic field strength and with dimensionality. The time required for a multidimensional experiment is directly proportional to the number of evolution times sampled in the indirect dimensions,

$$t_{\mathit{exp}}=(t_{\mathit{acq}}+t_{rc})\times n_t\times k\times 2^{d-1}$$ (6)

where t_acq is the time required to sample one FID, t_rc is the recycle time between transients, n_t is the number of FIDs co-averaged, k is the number of samples in the indirect dimensions (for uniform sampling $k={\prod }_{j=1}^{d-1}{n}_j$ with n_j the number of samples in dimension j and the product is over the d-1 indirect dimensions of a d-dimensional experiment), and the factor of 2 per indirect dimension reflects quadrature detection. For a fairly typical uniformly sampled 3D experiment averaging two FIDs with 64 evolution times sampled in each of two indirect time dimensions, a t_acq of 0.6 s, t_rc of 1.2 s, t_exp is 16.4 hr. Contrast this time to an experiment in which the maximum evolution time in the indirect dimensions correspond to the Rovnyak limit²⁶ of 1.26T₂ for optimizing sensitivity, or πT₂ for resolving components separated by the natural linewidth. Typical ¹³C and ¹⁵N linewidths for a 20 kDa protein at 14.1 T (600 MHz for ¹H) are 17.5 and 5.8 Hz, respectively. The chemical shift dispersion for ¹³C and ¹⁵N is 10,500 and 2,100 Hz, respectively. With sampling intervals of 0.0952 ms and 0.476 ms required by the Nyquist condition, 241 samples in the ¹³C dimension and 145 samples in the ¹⁵N dimension would be required to sample uniformly to 1.26T₂; 573 and 345 samples are needed to reach πT₂. t_exp for 1.26T₂ is 140 hr, or 795 hr for πT₂. The total number of samples required for uniform sampling to either limit greatly exceeds the number typically acquired or the time devoted to data collection³³. This means that higher dimensionality experiments that employ uniform sampling are usually sub-optimal both in sensitivity per unit time and in resolution.

In their seminal application of NUS and MaxEnt, Barna et al.³⁴ demonstrated rather conservative coverage ranging from 0.25 to 0.125. More substantial reductions in sampling coverage have subsequently been reported for 3D and 4D experiments, with coverages well below 0.01 common³⁵, and reaching 0.0016³⁶. NUS is not the only means for reducing the time required for multidimensional NMR experiments; in the SOFAST approach, the time between FIDs is reduced³⁷. As SOFAST (and related methods) and NUS are complementary, they can be combined, achieving greater speedup than either approach alone^29,38.

Rovnyak et al. exploited NUS to resolve separate resonances reflecting magnetically inequivalent ¹⁷O nuclei in the unit cell of hydroxyapatite crystals³⁹. NUS has also been used to obtain high-resolution spectra for disordered proteins, which exhibit narrow spectral dispersion and hence crowded spectra^38,40,41. The higher resolution afforded by NUS has also enabled novel assignment strategies for protein spectra that are not practical with uniform sampling^35,42. For example 4D HCC(CO)NH-TOCSY spectra obtained using NUS for the three indirect dimensions can be obtained in 1.5 days, a rather dramatic speedup, rendering high-resolution 4D experiments practical. The resulting resolution in the indirect dimensions is sufficient to capture unique carbon-proton connectivities, enabling a novel and efficient scheme for assigning protein side-chain resonances. Similar approaches have also been reported for backbone resonance assignment employing 3D experiments ^42,43.

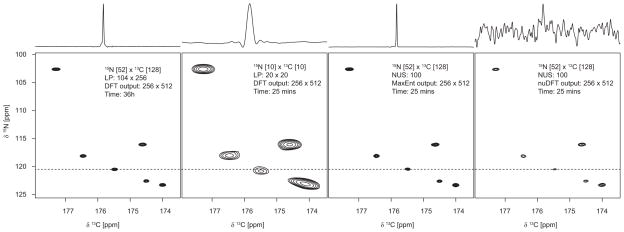
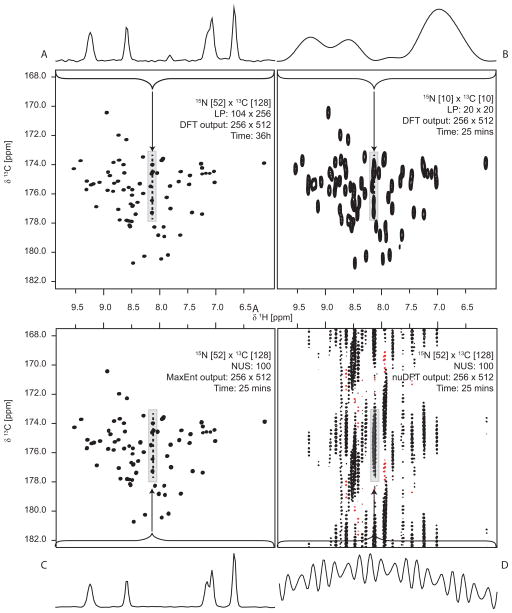
Examples illustrating important characteristics of NUS are shown in Figs. 4 and 5. Fig. 4 depicts 2D cross-sections through the HNCO spectrum of ubiquitin; 1D cross-sections at the frequency indicated by the dashed line are shown above each contour plot. Panel A shows the spectrum obtained using conventional uniform sampling and DFT processing, requiring 34 hours to complete the experiment. Panel B shows the results using uniform sampling with a truncated data set requiring 25 minutes to collect; the reduction in resolution is severe. Panels C and D show the results from an experiment also using 25 minutes of measuring time, but using NUS instead of uniform sampling. In Panel C MaxEnt is used to compute the spectrum; in panel D, nuDFT was employed. Fig. 5 depicts contour plots for 2D projections of the HNCO spectrum for ubiquitin onto the ¹H-¹³C plane. Panel A shows the projection obtained using the uniformly-sampled data set of Fig 4a. Panels B and C show the projections obtained from the truncated uniform and NUS data sets (corresponding to Figs 4B and 4C, respectively). Panel D shows the projection obtained nuDFT instead of MaxEnt (4C); 4D dramatically reveals the poverty of nuDFT, because the coherent sampling artifacts are accumulated by the projection. The nearly 90-fold reduction in experiment time, with no loss of sensitivity or resolution, makes a convincing case for NUS and MaxEnt.

Figure 4. 3D HNCO spectra for Ubiquitin at 14.1 T (600 MHz for ¹H).

¹³C/¹H planar cross-sections at a ¹H frequency of 8.14 ppm. The one-dimensional cross-sections through the plots are of the ¹³C row at the weakest peak (¹⁵N frequency of 120.5 ppm), scaled so that the highest and lowest amplitudes are aligned. A) Using a full dataset, 6656 data samples, processed using LP extrapolation in each indirect dimension, shifted sine-bell apodization, and DFT; this data set required 36 hours of data collection B) using 100 uniformly-sampled data points (10 increments in each indirect dimension); this data requires 25 minutes of data collection. The spectrum was computed by LP extrapolation in each indirect dimension, apodization using a shifted sine-bell, and DFT. C) using NUS, with 100 random samples selected according to an exponentially weighted distribution, reconstructed using MaxEnt; this data also requires 25 minutes of data collection. D) Same as C), except using nuDFT instead of MaxEnt. The weak peak near the center of the ¹³C trace in A is the “tail” of a peak at a nearby ¹H frequency; this disappears because of the narrower peaks in C.

Figure 5. 3D HNCO spectra for Ubiquitin at 14.1 T (600 MHz for ¹H).

Projections of the full spectrum onto the ¹³C/¹H plane. The one-dimensional cross-sections through the plots are expansions depicted by the rectangular boxes, scaled to align the maxima and minima. A) Using the full 6656 sample data set, processed using LP extrapolation in the indirect dimensions, shifted sine-bell apodization, and DFT (36 hours of data collection) B) using 400 uniformly-sampled data points (20 increments in each indirect dimension, 25 minutes of data collection). The spectrum was computed by LP extrapolation in each indirect dimension, apodization using a shifted sine-bell, and DFT. C) using NUS, with 400 random samples selected according to an exponentially weighted distribution, reconstructed using MaxEnt; this data also requires 25 minutes of data collection. D) Same as C), except using nuDFT instead of MaxEnt.

Concluding remarks

The debate over optimal sampling schemes and the best reconstruction method is far from settled. A comprehensive critical comparison remains elusive, in part because metrics of spectral quality (sensitivity, resolution) that are valid for linear methods, such as DFT, are frequently not suitable for non-Fourier methods. In addition to a lack of consensus on appropriate metrics, critical comparison is made difficult by the absence of a “shared task” comprised of a standard set of data. Nevertheless, a number of basic tenets of NUS have achieved broad consensus. It is abundantly clear that NUS approaches are essential for fully realizing the potential resolution afforded by modern high field magnets in the indirect dimensions of multidimensional experiments. Also widely appreciated is the importance of randomness in the design of sampling schemes in order to minimize sampling artifacts. Although the design of efficient sampling schemes remains an active area of investigation, it is understood that sampling more frequently when the signal envelope has greater amplitude improves sensitivity. The flexibility of NUS approaches for reducing measuring time, increasing resolution, or enhancing sensitivity, and in some cases two or more of these simultaneously, make NUS an indispensable tool for enhancing the utility and power of multidimensional NMR. These improvements will enable new and challenging applications of multidimensional NMR to larger, more complex, less abundant, and fleetingly stable systems.

Biographies

Jeffrey Hoch is Professor of Molecular Biology and Biophysics and Director of the Gregory P. Mullen NMR Structural Biology Facility at the University of Connecticut Health Center. He obtained is Ph.D. from Harvard (1983) with Martin Karplus and Chris Dobson.

Mark Maciejewski is Assistant Professor of Molecular Biology and Biophysics and Manager of the Gregory P. Mullen NMR Structural Biology Facility at the University of Connecticut Health Center. For the past 20 years he has utilized NMR for structural characterization of biomolecules and worked on NMR data processing.

Mehdi Mobli is an Australian Research Council Future Fellow at the Centre for Advanced Imaging at the University of Queensland, Australia. His research interests lie in developing and applying advanced NMR methods to solving difficult biological problems, including the structure and function of membrane proteins as well as characterizing weak intermolecular interactions.

Adam Schuyler is an Assistant Professor of Molecular Biology and Biophysics at the University of Connecticut Health Center. His research interests include computational aspects of structural biology.

Alan Stern is a Staff Computational Scientist at Harvard’s Rowland Institute. He has worked on NMR data processing for over 25 years.