Nanobiomechanics of living cells: a review

Abstract

Nanobiomechanics of living cells is very important to understand cell–materials interactions. This would potentially help to optimize the surface design of the implanted materials and scaffold materials for tissue engineering. The nanoindentation techniques enable quantifying nanobiomechanics of living cells, with flexibility of using indenters of different geometries. However, the data interpretation for nanoindentation of living cells is often difficult. Despite abundant experimental data reported on nanobiomechanics of living cells, there is a lack of comprehensive discussion on testing with different tip geometries, and the associated mechanical models that enable extracting the mechanical properties of living cells. Therefore, this paper discusses the strategy of selecting the right type of indenter tips and the corresponding mechanical models at given test conditions.

1. Introduction

The mechanical properties of living cells can affect their physical interactions with their surrounding extracellular matrix [1,2], potentially influencing the process of mechanical signal transduction in living tissues [3–7]. Alterations in cell properties are of fundamental importance for a wide range of processes, and changes in cell mechanics are associated with conditions such as osteoarthritis [8], asthma [9], cancer [10], inflammation [11] and malaria [12]. The mechanical properties of living cells have been quantified using various testing methods, such as micropipette aspiration [8,13], magnetic twisting cytometry [14], optical tweezers [15–17] and nanoindentation [18–20]. Although there are some good review papers on cell mechanics [21,22], they mainly focus on using micropipette aspiration techniques. From the perspective of cell mechanics, one should be aware of what is measured with respect to particular techniques. For example, it is often observed that the cell appears softer [23] during micropipette aspirations compared with cytocompression [24] or indentation with a large spherical tip [25]. During micropipette aspirations, it was observed that the cytoskeleton can be disrupted [26,27]. In such a case, there is no (or very limited) tensile stress in the actin fibres, which significantly contributes to cell stiffness. Therefore, cell mechanics can be approximated, as cytosol reinforced with bundles of actin fibres (with diameter of 9–10 nm). The weight concentration of actin fibres is 1–10% for non-muscle cells and 10–20% for muscle cells, and the elastic modulus of these actin fibres is 1.3–2.5 GPa [28].

This paper will shed light on the nanoindentation techniques, because investigation of mechanical properties of living cells at the nanometre (or submicrometre) scale is essential for understanding how cells interact with the surrounding materials. Cells would sense and respond to the nanoscale (or microscale) features on the materials surface. For example, when in contact with implanted devices or scaffold materials, cells interact with nanoscale (or submicroscale) surface features in topography [29,30] and surface chemistry [31,32]. Therefore, the nanobiomechanics of the living cells is very important for surface design of the implanted materials and the scaffold materials for tissue engineering. In addition, it also helps us to improve the understanding of cell interaction with nanoparticles, which is important for nanotoxicology [33] and nanomedicine [34]. Compared with other measurement techniques, nanoindentation has the advantage of in situ imaging of the indented cells with a high resolution, a very good control of the probe position and loading (or unloading) speed, and the flexibility of using different probe geometries (e.g. flat punch spherical, pyramidal and conical). It also has the unique feature of mapping the measured mechanical properties over the investigated surface of the sample [35]. However, data interpretation for nanoindentation of living cells is often difficult.

Despite abundant experimental data reporting nanobiomechanics of living cells, there is a lack of comprehensive discussion on testing with different tip geometries and mechanical models.

Therefore, the goals of this study were (i) to present the strategy of selecting the right type of indenter tips; (ii) to illustrate cell mechanics at different test conditions; (iii) to discuss the mechanical models that enable extracting the mechanical properties of living cells during nanoindentation.

2. Experimental aspects

2.1. Nanoindenter apparatus and atomic force microscope

Nanoindentation is also known as depth sensing indentation, in which the indentation load–depth–time (P – δ – t) profile is recorded. It enables probing the mechanical properties at the nanoscale or microscale. For such a small-scale indentation, there are different approaches to take with respect to the testing instrumentation. In general, we could divide them into nanoindenter apparatus and atomic force microscope (AFM). The key difference between the commercial nanoindentation apparatus and the AFM is on the different transducer operation mechanisms: the former uses electrical capacitance gages (figure 1a) or magnetic coils to directly drive the indenter into the sample. When a voltage is applied, an electrostatic force is generated between the pick-up electrode and drive plates (as depicted in figure 1a), resulting in the movement of the pick-up electrode between the drive plates. While the AFM actuates the tip indirectly via the bending of a cantilever, the AFM operates by measuring attractive or repulsive forces between a tip and the sample, which causes vertical deflection of the cantilever. To detect the displacement of the cantilever, a laser is reflected at the back of the cantilever and collected in a photodiode (figure 1b).

Figure 1.

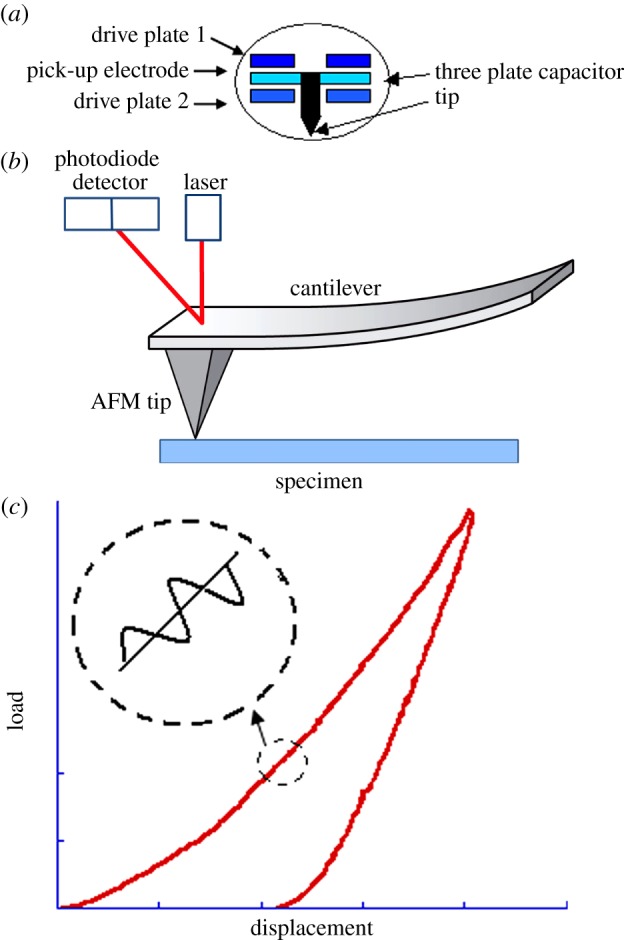
(a) Schematic of electrical capacitance gages that drives nanoindenter, (b) the bending of a cantilever that actuates the AFM tip and (c) dynamic drive signal superposed with the force curve which enables dynamic mechanical measurement during nanoindentation. (Online version in colour.)

In addition to quasi-static loading, a dynamic drive signal can be superposed with the force curve (figure 1c) in both the nanoindenter apparatus [36] and the AFM [37]. This enables measurement of the storage modulus, loss modulus and phase angle, which can be converted to the instantaneous modulus, equilibrium modulus and viscosity [38].

The nanoindenter apparatus allows better control of the indentation force and displacement. The AFM offers the unique advantages of applying very small indentation forces (below 100 pN), but accurate calibration is not easy [39]. Owing to ultra-high resolutions in force and displacement, AFM nanoindentation is particularly useful for probing living cells and subcellular components such as the cell membrane and cytoskeleton.

2.2. Choice of appropriate atomic force microscope tips

There are various tip geometries that can be fitted with the AFM cantilever for nanoindentation tests. The advantages and disadvantages of these tips are discussed as follows. The shape of cells can be spherical or spreading in morphology, depending on the physiological conditions and microenvironment of the living cells and cell types. The choice of appropriate AFM tips depends on cell morphology, cell type and what is of interest (cellular mechanics or subcellular mechanics). This would provide useful guidelines for designing experimental protocols.

2.2.1. Flat punch

Indentation of cells with a flat-ended cylindrical punch (figure 2) is also known as cytoindentation [19]. In this case, the size of the flat punch is much smaller than the cell. This type of indenter is preferred for a very soft and fragile cellular or subcellular structure. The advantage is that data interpretation is relatively straightforward because it avoids the complication of determining the contact area. The contact area is less likely to be affected by thermal drift or creep. The drawback is the spatial resolution is relatively limited compared with the pointed indenter (e.g. pyramid and conical tip); therefore, it is not suitable to characterize fine features. In addition, there are also other practical concerns for using flat punches, such as alignment, detection of contact point and force concentration around edges. The tips are usually made of silicon or glass.

Figure 2.

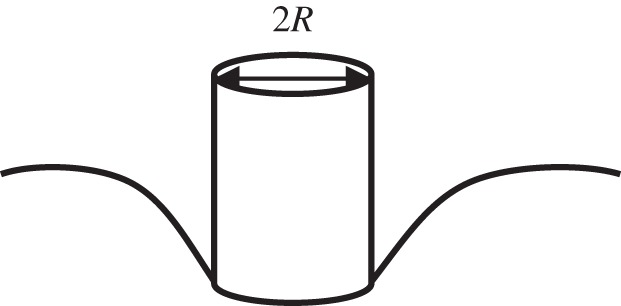
Schematic of nanoindentation by a flat-ended cylindrical punch.

2.2.2. Spherical tip

This type of indenter (figure 3) is also ideal for very soft and fragile cellular or subcellular structures. This type of tip would be particularly useful if the elastic properties of the materials were to change with strain. As the effective strain is related to the ratio of the contact radius and the tip radius, it enables determining the stress–strain curves of the indented materials. The typical spherical tip is made of glass which is easy to manufacture. Similar to the flat punch probe, the spherical glass probe is less likely to cause damage to cells [40]. Again, this may not be good for probing fine features. The typical radius of the probe for indentation of cells is 2.5–10 μm. The representative strain for the spherical tip is the ratio of the contact radius over the effective tip radius [41].

Figure 3.

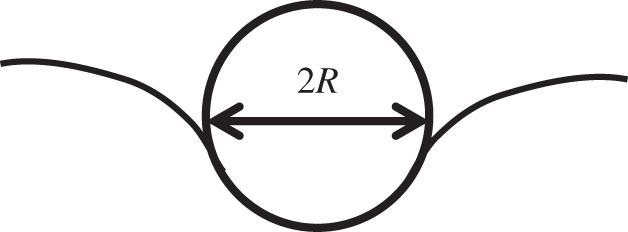
Schematic of nanoindentation by a spherical tip.

2.2.3. Pyramid tip

At a given penetration, the pyramid indenter (figure 4) yields a much smaller contact area compared with the spherical and flat punch tips. It is particularly useful to probe fine features such as the cytoskeleton. Owing to the crystalline structure of silicon, it can be easily etched at certain plane directions, enabling massive production of the probes. The drawback is that the sharp edges may damage the fragile cell membrane or nuclear membrane; therefore, it is not recommended for indentation of living cells.

Figure 4.

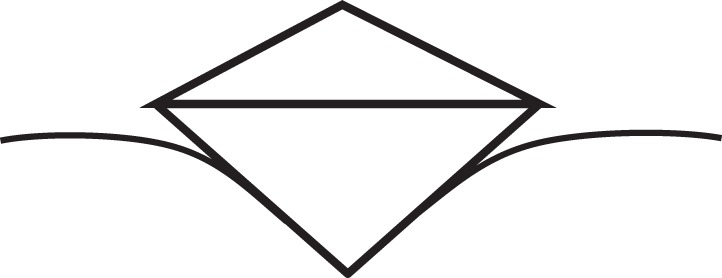
Schematic of nanoindentation by a pyramid tip.

2.2.4. Conical tip

Similar to the pyramid tip, the conical tip (figure 5) yields a much smaller contact area compared with the spherical and flat punch tip. Compared with the pyramid tip, it is less likely to cause damage in lateral directions because it does not have sharp edges. It also circumvents complicated data interpretation owing to coupling of anisotropic soft materials and orientation of the pyramid tip. In principle, the semi-included angle of the probe will not affect the measured elastic or plastic properties, if the appropriate models are used. But it affects the relationship between the yield strength and hardness. At a given penetration, the deformation-affected volume is related to the semi-included angle of the probe [42,43]. Therefore, to eliminate the effect of the substrate or the surrounding matrix, one may need to choose a tip with smaller semi-included angle although the increased stress intensity underneath the very sharp tip might cause puncture of the cell membrane. The tip radius also contributes to the effective deformation zone as discussed in [42,44]. But this influence is not that significant if the tip radius is much smaller than the penetration. When using this probe to do indentation at shallow penetration, it would only sense localized properties mainly resulting from the cell membrane with the underlying cortex or individual cytoskeleton. Sometimes, it may simply measure the bending stiffness of the cell membrane. In such a case, it is unlikely to obtain the mechanical properties of the whole cell. For similar geometries such as a cone (a cylindrical punch can be treated as cone with a semi-apical angle of 90°) and a pyramid, the effective strain is a constant and related to the semi-apical angle (θ) [41].

Figure 5.

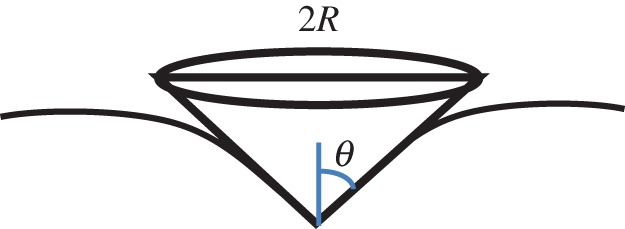
Schematic of nanoindentation by a conical tip.

2.2.5. Extended atomic force microscope testing rigs

In recent years, another type of indentation, cytocompression [45,46], has been widely used to assess the mechanical properties of single cells. In principle, this is an extended AFM indentation on top of cytoindentation. The primary difference in the deformation mechanisms for cytoindentation and cytocompression is in the relative size between the flat punch and the cell. The former has a flat punch diameter well below that of cell. The latter (figure 6) has a flat punch diameter exceeding that of the cell. In such a case, data interpretation is the same as in normal compression tests. The indenter (i.e. the flat plate) is often made of glass, which enables in situ observation of cell deformation [20,47].

Figure 6.

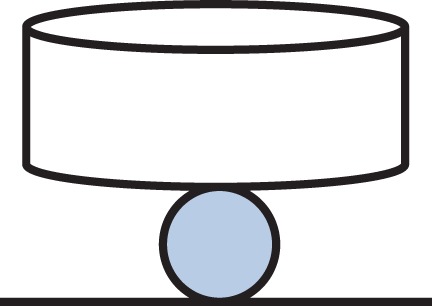
Schematic of cytocompression of a spherical cell.

2.2.6. Summary

Tables 1 and 2 summarize the effective contact radius, effective contact stress and representative strain for various tip geometries. Where, δ_c is the contact depth.

Table 1.

Terms and explanations.

terms	description
P	force
δ	displacement
t	time
T	normalized time constant
a	contact radius
R	tip radius
θ	semi-included angle of indenter
D	diffusivity
V	Poisson's ratio
K	permeability
η	viscosity
G	shear modulus
G∞	equilibrium shear modulus
G0	instantaneous shear modulus
E	Young's modulus
E∞	equilibrium elastic modulus
E0	instantaneous elastic modulus
HA	aggregate modulus
γ	surface energy

Table 2.

The summary of the effective contact radius, effective contact stress and representative strain for various tip geometries.

tip geometry		effective contact radius (ac)	effective contact stress	representative strain
sphere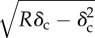
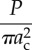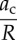cylindrical punch		R		0.1433cos2θ + 0.205cosθ + 0.0191a
cone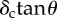
pyramid	triangle-base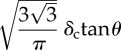
	square-base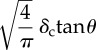

^aThis empirical expression is based on best fitting of the raw data in [41], see appendix A.

Table 3 summarizes brief guidelines of recommended tip geometries of cells with varied morphologies.

Table 3.

The summary of a brief guideline of recommended tip geometries for cells with varied morphologies.

	flat punch	spherical tip	pyramid tip	conical tip
rounded cell	✓	✓
spreading cell
soft cell	✓	✓
stiff cell	✓	✓		✓
subcellular structure			✓	✓

3. Mechanical modelling

Estimation of cell mechanics requires the use of analytical models (or empirical models) of which there are two principal types, namely structure-based models and continuum models. The former include tensegrity [48,49] and percolation models [50], which consider cell mechanics to be dominant by the collective discrete loading bearing element. The latter include linear elastic [51–53], hyperelastic [54–56], poroelastic (also known as biphasic model) [57] and viscoelastic models [8,58]. The continuum model may be interpreted as load-bearing elements that are infinitesimally small relative to the size of the cell.

3.1. Structure-based models

3.1.1. Tensegrity model

The tensegrity model is based on the use of isolated components under compression inside a net of continuous tension, in such a way that the compressed members (usually bars or struts) do not touch each other and the pre-stressed, tensioned cables [59], as shown in (figure 7). This model was coined by Buckminster Fuller in the 1960s. Such a concept was then introduced by Ingber [48] to cell mechanics. It assumes that a cell stabilizes its structure by incorporating compression-resistant elements to resist the global pull of the contractile cytoskeleton [48]. This simple stick and string tensegrity model predicts that a cell appears round when unattached (owing to the internal tension) or attached with a very soft substrate, and spreads out when attached to a stiff substrate. All these agree well with experimental observations [48,61].

Figure 7.

A schematic tensegrity model of cell structure for a spherical cell [60].

3.1.2. Percolation models

The percolation theory describes the behaviour of connected clusters in a random manner. It was introduced in mathematics and then it was applied to materials science. Recently, such a theory was introduced to describe the cell structure and its mechanics [50]. The percolation cluster shown in figure 8 contains substructures of tensegrity on a small scale. These tensegrity substructures are likely to contribute to inherent tension in the cytoskeleton. Owing to the random nature of their interconnection, percolation networks are so flexible that they can easily adapt to the dynamic conditions that affect cells [50].

Figure 8.

A schematic percolation model of cell structure. The smaller interior cube representing the nucleus is supported by the pre-stressed cytoskeletal network [50].

3.1.3. Summary of structure-based models

The percolation and tensegrity models of the cytoskeleton are not mutually exclusive, but complementary. As commented in [50], it is possible that during evolution certain locally ordered tensegrity-type structures may have emerged from more randomly interconnected percolation structures. These structure-based models are very successful at explaining a range of physical observations on cell mechanics such as cell spreading [62], cell migration [63], cell detachment [64] and mechanosensation [65], etc. But it is difficult to quantify the mechanical properties of living cells or subcellular structures.

3.2. Continuum models

Despite neglecting microstructural features, continuum models enable quantifying the mechanical properties of cells under various conditions that could provide essential information of cellular subpopulations [25], disease [18], malignant transformation and cell–materials interactions [2]. However, it is worth pointing out that there is no universal mechanical model available to quantify the mechanical properties of living cells at various physiological and microenvironmental conditions, because living cells can dynamically adapt to their environment. The feasible methodology is to choose appropriate models according to testing conditions (or microenvironment) for a given cell type. Therefore, this paper will focus on the discussion of the feasibilities of various continuum models at given test conditions.

3.2.1. Elastic model

If the tests were performed slowly such that the cell reaches equilibrium, then it is reasonable to use elastic models. At relatively small deformation, a simple linear elastic model may be used to find the Young modulus of the cell (E). Evidence has been shown that this simple elastic model can still reveal useful insights of cell mechanics such as the stiffness ratio of the nucleus over the cytoplasm [51].

If the cell undergoes large deformation, then it may reach the nonlinear elastic region. The neo-Hookean (NH) model, also known as the Gaussian model, is one of the most widely used nonlinear elastic (or hyperelastic) models owing to its simplicity. For example, it has been successfully used to model the deformation of single cells in cytocompression tests [66]. For incompressible materials, the NH model has the following energy function [67]

3.1

where W is the strain energy density, l_j(j = 1,2,3) are the three principal stretch ratios. The Young modulus E is given by

3.2

Other more sophisticated hyperealstic models have also been developed, such as the polynominal and Ogden models. The strain energy function for the former is given by the flowing equation [68]:

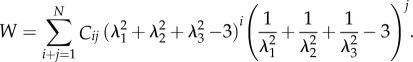3.3

The Young modulus E is given by

3.4

The Ogden model can describe a wide range of strain-hardening characteristics, and it takes the following form as described in previous studies [67–69]:

3.5

where α_i is strain-hardening (or stiffening) exponent. The constants μ_i are related to the initial Young modulus E, by

3.6

This model has been adopted to describe cell mechanics when the chondrocyte is embedded in various hydrogel scaffolds [2].

3.2.2. Poroelastic model

The poroelastic model attributes the time-dependence to the flow of a fluid through an elastic (or viscoelastic) porous solid. Such a model was first proposed by Biot [70] and was based on the assumptions of linearity between the stress (s_ij, p) and the strain (ε_ij, ρ) and reversibility of the deformation process. With the respective addition of the scalar quantities p and ρ to the stress and strain group, the linear constitutive relations can be obtained by extending the known elastic expressions. The most general form for isotropic material constitutive behaviour response is described as follows [70]:

3.7

and

3.8

where K and G are bulk and shear modulus of the drained elastic solid. The parameters H and M characterize the coupling between solid and fluid stress and strain.

This model was originally developed for soil mechanics and it was then applied to describe the mechanics of hydrogels [71] and tissues such as bone [72] and cartilage [73]. Very recently, it has also been applied to cell mechanics [24]. When it comes down to cell mechanics, the material properties of interest include the shear modulus G (or aggregate modulus H_A), and Poisson's ratio of the solid matrix and Darcy permeability k. The permeability could be analogous to the diffusion coefficient, but driven by the mechanical gradient instead of the chemical gradient.

During stress relaxation, it gives [74]

3.9

where P(∞) and P(0) signify the force at infinite time (t = ∞) and t = 0, respectively.

Where the normalized time τ is given by

3.10

where a is the contact radius and t is time.

The diffusivity D is given by

3.11

where v, G, k and η are Poisson's ratio, shear modulus and permeability of the solid matrix and viscosity of the solvent, respectively.

The equilibrium Young modulus E is given by

3.12

The relation between the aggregate modulus and the Young modulus is given by

3.13

This poroelastic model is quite similar to the biphasic theory of the mixture of an incompressible solid and incompressible fluid which was independently developed by Mow et al. [75] and Bowen [76]. In addition, by replacing the elastic media with viscoelastic media to account for the intrinsic viscoelastic properties of the actin filaments, a more complex model (poro-viscoelastic) [77] can be used to describe soft tissue or cell mechanics. When the cell is exposed to an ionic solution, the ionic charge also contributes to the mechanical responses of cells. In such a case, a third phase (i.e. the ionic phase) can be included in the constitutive equation, which is called the triphasic model [78].

3.2.3. Spring-dashpot viscoelastic models

The basic premise of viscoelasticity of this type is that it replaces some elastic springs with a time-dependent dashpot as shown in figure 9. These spring-dashpot models usually refer to viscoelastic models. In a general manner, the empirical Prony series [79] has been used to describe the material's time-dependent constitutive response in the experimental time domain.

Figure 9.

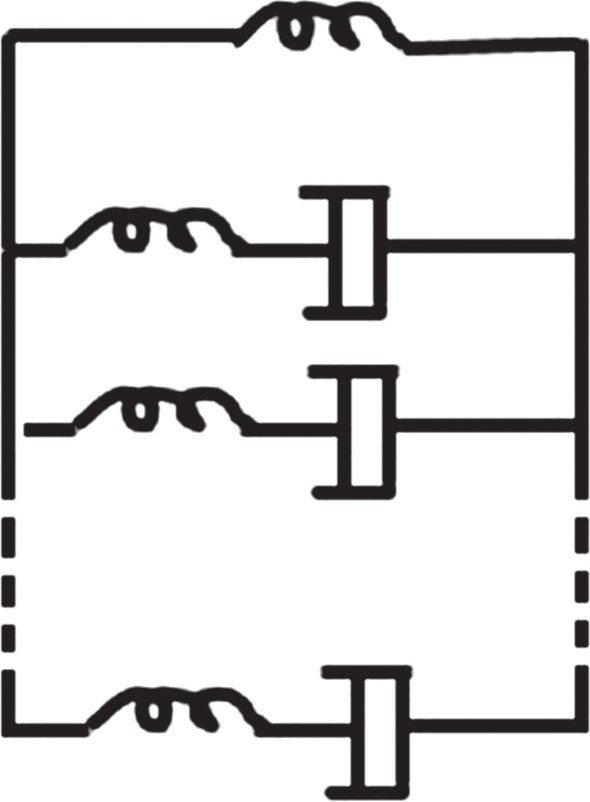
Schematic of the generalized Maxwell model.

For stress relaxation, the relaxation shear modulus G(t) in an empirical Prony series is given by

3.14

where G_∞ is the equilibrium shear modulus and the instantaneous shear modulus 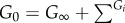or creep, the creep compliance J(t) in an empirical Prony series is given by

3.15

where the parameters C_i are associated with compliance values (inverse shear modulus).

The stress relaxation modulus and the creep compliance are not explicitly inverse in the time domain but are in the Laplace domain (i.e. ).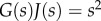

The equilibrium shear modulus (G_∞) and the instantaneous shear modulus (G₀) can be determined by the following equations:

3.16

and

3.17

3.2.4. Power-law rheology

Power-law rheology (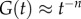, where n is a positive constant) has also been adopted to describe the mechanics of certain cells. For example, it is found that n = 0.2 for lung epithelial cells during stress relaxation [80]. The physical basis of this power law may be related to molecular adjustment of the cytoskeleton matrix, which is similar to soft glassy materials close to the glass transition [80]. Such a model may work better for those cells that do not have a strong cytoskeleton structure. For example, such a power-law rheology model has also been applied to neutrophils and macrophages [81].

3.2.5. Summary

The advantage of the elastic models is that they eliminate the number of elastic parameters, which are easy for empirical curve fitting and numerical simulations. It was argued that poroelastic models provide physical constants related to the material microstructure, compared with the empirical spring-dashpot viscoelastic models. However, it must be pointed out that poroelastic models homogenize the whole structure and may not be able to predict structure reorganization of the cell during external stimuli (e.g. cell migration and cell spreading) compared with those structure-based models (e.g. tensegrity model). Therefore, one should also treat structure-based models and the continuum models as complementary to each other.

4. Nanoindentation models

As mentioned earlier, only the nanoindentation models (continuum based) for the tips (i.e. flat punch, spherical and conical tip) suitable for testing living cells will be discussed in detail. Once the AFM deflection–displacement curves are converted to force–displacement curves, indentation theories would be applicable. The models below are based on assumptions of small deformation and negligible tip–cell adhesions. More detailed discussion is provided in §5, when these assumptions are invalid.

4.1. Elastic nanoindentation models

Flat punch: the force–displacement (P − δ) relation is given by [82]

4.1

where R and ν are the radius of the flat punch and Poisson's ratio, respectively.

Spherical tip: the force–displacement relation is given by the Hertz elastic model [83]

4.2

where R are the radius of the spherical indenter.

Conical tip: the force–displacement relation is given by [84]

4.3

where θ is the semi-included angle of the conical indenter.

4.2. Poroelastic–nanoindentation models

Flat punch: the force–time (P − t) relation is given by [74]

4.4

and

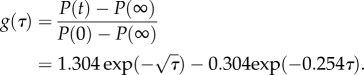4.5

Spherical tip: the force–time relation is given by [74]

4.6

and

4.7

Conical tip: the force–time relation is given by [74]

4.8

and

4.9

where a is the contact radius, and τ is the normalized time constant as defined earlier.

A simpler poroelastic model to describe cell mechanics has been presented in [85,86], which considers fluid propagates through a cell owing to a local pressure increase in a two-dimensional manner. This model requires other techniques to determine the pore size and viscosity, rather than relying on the analysis of the force–time–displacement curve alone. For pore size, it can be estimated by hindered tracer particle diffusion experiments, and for viscosity it can be estimated by a nanoparticle diffusion experiment [85,86].

4.3. Viscoelastic-nanoindentation models

When viscoelastic models were adopted, experimentalists used either the stress relaxation (for tests performed under displacement control) or creep (for tests performed under force control) period to determine viscoelastic parameters. It is advantageous to use stress relaxation or creep for data analysis because they circumvent the possible complexity in nonlinear changes during ramping.

Flat punch: the following force–time and the displacement–time relations can be obtained by incorporating the viscoelastic model into equation (3.16)

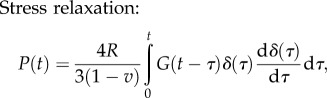4.10

and

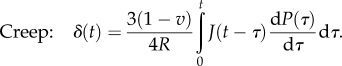4.11

More rigorous analytical solutions were given by [87], which consider that the elastic components may have different Poisson's ratios.

Spherical tip: the force–time and the displacement–time relations are given by [88,89]

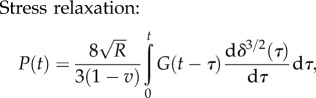4.12

and

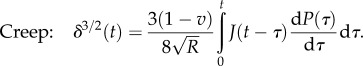4.13

Conical tip: the force–time and the displacement–time relations are given by [90]

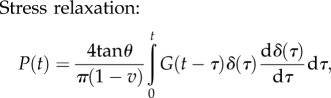4.14

and

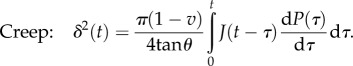4.15

For complicated load–time or displacement–time histories, Boltzmann hereditary integrals can be used to find full P – δ – t profiles [58,91].

5. Discussion

It must be pointed out that most researchers compared measured cell mechanical properties across published results without analysing the experimental techniques related to controlling factors on cell mechanics. These factors include tip geometry, indentation penetration, cell morphology, cell type and mechanical models. Therefore, it is essential to discuss how these factors affect the measured cell mechanical properties.

5.1. Cell mechanics determined by different models

Depending on the models to be adopted, it may affect the values of determined mechanical properties of cells. Table 4 summarizes the elastic properties of bovine articular chondrocytes determined by the biphasic and spring-dashpot viscoelastic models. It can be seen that these two models give similar results. However, the cell actually experiences large deformation, which was not considered in both models.

Table 4.

Elastic properties of bovine articular chondrocytes determined by the biphasic and spring-dashpot models [24].

continuum models	elastic modulus (kPa)
biphasic model	1.38 ± 0.46a
spring-dashpot model	1.48 ± 0.35

^aNote that the original aggregate modulus value of H_A (2.58 kPa) for biphasic model is converted to the equilibrium modulus based on equation (3.13), with Poisson's ratio of 0.38 [25].

Although many researchers adopted viscoelastic models to describe the time-dependent behaviour of cell mechanics [8,25,26,92], other researchers found that poroelastic models are more appropriate in their experimental test protocols [86,93]. However, it has been shown that neither the poroelastic model nor the viscoelastic model is capable of capturing the complete mechanical responses of cells during creep or stress relaxation [94,95]. A recent paper published in Nature Materials [95] has demonstrated that the poroelastic model captures the time-dependent mechanics of cells at a short-time scale (less than 0.5 s), but the viscoelastic model appears to work better at a long-time scale [95]. This may suggest that, at a short-time scale, it is fluid diffusion that governs the time-dependent behaviour of cells. At a long-time scale, it is likely that the collective viscoelastic behaviour of the polymer-like materials inside cell and cytoskeleton dynamics governs the time-dependent behaviour of the cell. Therefore, a further improved model, poro-viscoelastic model presented in [77,96–98] may be more appropriate. If the cell is exposed to an osmotic environment, then it passively swells or shrinks. The poroelastic (biphasic) model is limited to describe the effective materials parameters that vary with extracellular osmolality [99]. The triphasic model [78] has the capability to better describe the mechanochemical coupling by introducing both mechanical and chemical parameters in the governing equations, which could better describe the mechanochemical equilibrium of the cells [99].

It must be pointed out that, in the poroelastic (biphasic) model and triphasic model, small deformation and incompressible solid matrix are assumed. In a real test or physiological loading, cells may experience large deformation. In addition, the solid matrix in cells may not be incompressible. It would be very complex to include all these in the constitutive equations of poroelastic models and triphasic models. However, for viscoelastic models, it is straightforward to account for the large deformation and compressibility of the solids via the hyperviscoelastic model.

The above-mentioned models deal with static loading. Indeed, oscillatory measurement associated with the AFM can be used to determine the viscoelastic properties of the living cell. More details can be found in [37,100].

5.2. Cell mechanics determined by different indenters

As discussed in §2, at a given force, the effective deformation zone varies significantly with tip geometry. Consequently, this can affect the measured mechanical properties of cells. In general, when using a pyramid tip with low penetration, the results are more likely to be affected by spatial heterogeneity, as observed in [101]. Table 5 summarizes the comparison of elastic moduli (determined by elastic contact model) for osteoblastic cells (spread morphology) measured by a pyramidal and spherical tip. It has been shown that elastic moduli measured by a pyramidal tip are about four times higher compared with those measured by a spherical tip. When using a sharp conical or pyramid tip for spreading cells, it senses the region near an actin filament, as observed by Hoh et al. [104]. In such a case, the probed elastic response may be significantly affected by this stiff filament (with elastic modulus on the order of GPa).

Table 5.

The comparison of elastic moduli (determined by elastic contact model) for osteoblastic cells (spread morphology) measured by pyramidal and spherical AFM tip.

elastic parameters	pyramidal tip	spherical tip
E	14 kPa [102]	3.18 kPa [103]

Table 6 summarizes the comparison of elastic moduli (determined by the elastic contact model) for lung epithelial cells measured by a pyramidal and a flat punch tip. In this test, large penetration of 3 µm was applied via a pyramid tip, and the indentations were not far from the nucleus. In that case, it probes the overall cell mechanics. That is why it yields a similar result to that determined by a flat punch tip. However, it should be pointed out that the thin-layer effect was not considered in the original paper. Table 7 summarizes the comparison of viscoelastic properties for a single bovine chondrocyte using cytoindentation and cytocompression. The indenter diameter for cytoindentation is 5 μm [106], which is almost half of the cell diameter. The penetration for cytoindentation is similar to the cell radius; therefore, it is expected that it senses the properties of the whole cell instead of local cellular properties. In such a case, it would be expected that the elastic properties determined by cytoindentation are similar to those by cytocompression. As shown in table 7, the equilibrium moduli and viscosity determined by these two indenters are quite similar. However, the instantaneous modulus determined by cytoindentation is over three times higher than cytocompression. This may suggest that indenter size might affect the instantaneous mechanical responses of cells.

Table 6.

The comparison of elastic moduli (determined by elastic contact model) for lung epithelial cells measured by a pyramidal and a flat punch tip.

elastic parameters	pyramid [100]	flat punch (average radius 0.53 μm) [105]
E	0.53 ± 0.11 kPa	0.5 kPa

Table 7.

The comparison of viscoelastic properties for single bovine chondrocyte (spherical morphology) using cytoindentation and cytocompression.

viscoelastic parameters	cytoindentation [106]	cytocompression [46]
E∞ (kPa)	1.09 ± 0.40	1.48 ± 0.35
E0 (kPa)	8.00 ± 4.41	2.47 ± 0.85
η (kPa s)	1.50 ± 0.92	1.92 ± 1.80

5.3. Cell morphology on cell mechanics

As cells are living materials, they respond to mechanical, physical and chemical stimuli. Cells will change their morphology after being removed from their native environment. Depending on the physical properties or surface chemistry of the substrate that they are seeded on, cells may spread along the substrate or retain a spherical shape. Figure 10 displays a typical example that shows the substrate stiffness regulates the shape of fibroblasts. Table 8 summarizes the mechanical properties of the different cell types and the change in their morphology. In that case, a borosilicate glass sphere (5 µm diameter) probe was used for the AFM nanoindentation [107].

Figure 10.

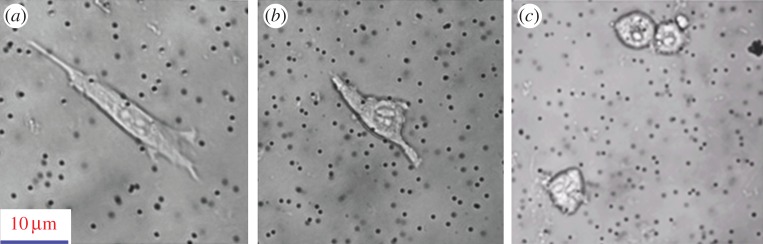
The morphology of fibroblast cultured on polyacrylamide gels with varied stiffness: (a) 10.4 kPa, (b) 3.31 kPa and (c) 0.56 kPa.

Table 8.

Comparison of viscoelastic properties for AFM indentation (with a spherical tip) of osteoblasts, chondrocyte, adipocytes, adipose-derived adult stem cells (ADAS) and mesenchymal stem cells (MSCs) in spread and spherical morphologies [107].

cell morphology	cell type	E∞ (kPa)	E0 (kPa)a	η (kPa s−1)a
spread	Osteoblast	4.5 ± 2.3	11.6 ± 33.9	112.2 ± 450
	chondrocyte	1.0 ± 1.6	1.70 ± 3.13	5.80 ± 14
	ADAS cell	1.7 ± 1.1	3.81 ± 15.4	20.2 ± 47.8
	MSC	2.3 ± 2.1	4.23 ± 14.4	20.5 ± 128
spherical	osteoblast	0.60 ± 0.78	2.1 ± 3.7	10.3 ± 21.4
	chondrocyte	0.45 ± 0.42	0.91 ± 1.3	4.5 ± 8.9
	ADAS cell	0.37 ± 0.31	1.6 ± 2.6	8.8 ± 16.6
	MSC	0.52 ± 0.60	5.3 ± 16.1	46.3 ± 140

^aNote that the values of E₀ and viscosity η were recalculated based on the raw data in [107].

For all the above-presented models, they assume a sample with infinite thickness and width compared with indentation depth. When probing the spreading cells, if the indentation size is comparable to the local thickness, then it invalidates these assumptions. Therefore, the estimation of cell mechanical properties will be affected by the stiffness of the underlying substrate. In such a case, the thin-layer model proposed by Darling et al. [108] could be applicable. This model introduces a geometry factor to describe the force–displacement relation. For example, for a spherical tip, the original elastic model can be modified as follows:

5.1

where f₁(χ) is geometrical correction factor which is given by

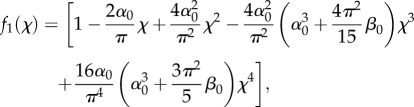5.2

and

5.3

where h is the cell thickness,

5.4

and

5.5

This geometry factor f₁(χ) can be easily incorporated into the above-mentioned viscoelastic models.

For the thin-layer-based poroelastic model, empirical correction parameters can be obtained based on finite-element simulation [109]. For example, the following empirical model is for spherical indenter [109]:

5.6

5.7

and

5.8

It needs to be pointed out that depending on where the indentation is located, one needs to use different thin-layer models (i.e. non-adhered thin-layer model [110] or adhered thin-layer model [111,112]). For example, it was found that when indentation was made at a thin region relatively near the edge of the fibroblast, the adhered thin-layer model is more appropriate [37]. Although when indenting a thin region further from the edge of the fibroblast, the non-adhered thin-layer model may be more suitable [37]. One needs to be aware that all these thin-layer models are valid for cells with approximately uniform thickness (i.e. well-spread). Otherwise, computational models are required, which will be discussed in §5.7. To minimize the thin-layer effect, a tip with a smaller half-angle is preferred [113].

When indenting a specimen with finite thickness and finite width, there is complex coupling between the stiffening effect, caused by the underlying substrate, and the softening effect, caused by a free edge in the lateral direction. A typical example is to use a spherical tip indenting into a spherical cell at a large deformation. Thus, another model has been presented to deal with this coupling effect [58].

The following empirical geometry factor f₂(χ) can then be used [58]:

5.9

and

5.10

This geometrical factor can be incorporated into the viscoelastic models [58], and it has been successfully applied to extract viscoelastic properties of spherical chondrocytes adherent to a glass plate.

5.4. A special case: cell trapped inside a well

Microfabricated well arrays have been proposed to trap cells before nanoindentation [113–115]. This would enable automatic indentation for high-throughput screening methods that may prove useful for cells sorting. All the existing contact mechanics-based models only deal with indented materials placed on a flat surface (i.e. the bottom surface is constrained vertically), free from lateral constraint. Little work has been carried out for indented materials placed within a well (figure 11); in that case, the assumptions in the classic Hertz model and thin-layer models have been violated. This problem has recently been dealt with by Chen [116]. Interestingly, it introduces a similar correction parameter to f₂(χ).

Figure 11.

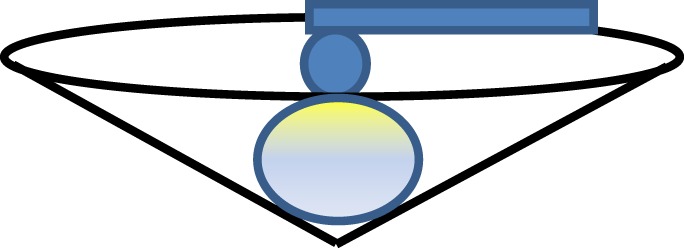
The schematic of AFM indentation of an isolated chondrocyte by a spherical probe.

5.5. Substrate modulation

The substrate physics may affect the cell mechanical properties, even if the cell maintains the same morphology. Table 9 summarizes the comparison of elastic moduli (determined by the elastic contact model) for the same murine NIH3T3 fibrobalst cell line (spread morphology) cultured on different substrates indented by a spherical tip. Table 10 summarizes the comparison of elastic moduli (determined by elastic contact model) for adult bovine chondrocytes (spherical morphology) placed on tissue culture plastic and on uncoated glass, probed by cytocompression. In both cases, it is evident that the substrates can significantly regulate cell mechanical properties even if the cell shape is retained.

Table 9.

The comparison of elastic moduli (determined by elastic contact model) for the same murine NIH3T3 fibrobalst cell line (spread morphology) cultured on different substrates indented by a spherical tip.

elastic parameters	collagen-I-coated glass	uncoated glass
E	1–2 kPa [117]	0.6 kPa [37]

Table 10.

The comparison of elastic moduli (determined by elastic contact model) for adult bovine chondrocytes (spherical morphology) are placed on a tissue culture plastic and on an uncoated glass, determined by cytocompression.

elastic parameters	tissue culture plastic	uncoated glass
E	2.55 kPa [24]	1.17 kPa [46]

Similar behaviour of the matrix modulating cell mechanics was also found in a three-dimensional scaffold. For example, when a bovine chondrocyte cell line were seeded in different scaffolds, they maintained a spherical morphology, but different mechanical properties with regard to the three-dimensional scaffold [2].

5.6. Cell–tip adhesion

Some degree of tip–cell adhesion may be unavoidable in nanoindentation. This would be affected by the composition and surface chemistry of the tip. There are different models that incorporate tip–sample adhesion, such as the Johnson–Kendall–Roberts (JKR) [118], Derjaguin–Muller–Toporov [119] and Maugis–Dugdale [120] models. Among which, the JKR model is appropriate for the indentation of relatively compliant materials with probes of relatively large radii and strong adhesive forces. This would be preferred to compliant materials such as cells, in particular for a spherical indenter in contact with spherical cells [121].

During unloading, one may observe the negative force resulting from the surface adhesion, as shown in figure 12. Such a pull-out force is related to the surface energy (γ) at the cell–tip interface and is given by [83]

5.11

Figure 12.

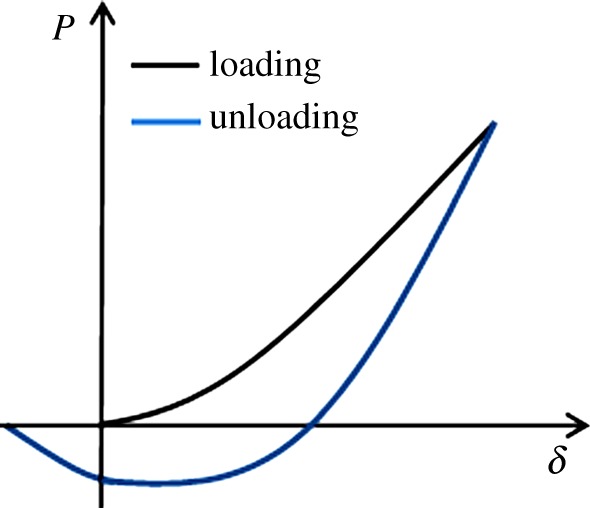
Schematic of force–displacement curve for a typical adhesive indentation. (Online version in colour.)

In such a case, one needs to replace the force (P) in all the equations above by P + P_pull. More detailed discussions about the adhesive contact during AFM indentation has been summarized by Lin & Horkay [122].

5.7. Inverse finite-element analysis

All the previous mechanical models work properly when the irregularity of cell shape is negligible. For example, when indenting a spread cell (with non-uniform thickness) with a conical tip at small depth, the effective-deformed region is mainly confined within the dotted region, as shown in figure 13. In that case, the cell can be assumed a regular shape with a single radius, so that the previous models in §4 are applicable. However, at greater penetration, the effective deformation zone spreads out, and the irregularity of cell shape becomes important. In that case, one should treat the previous thin-layer model with caution, because the non-uniform thickness and the change of curvature becomes important. Therefore, three-dimensional finite-element analysis (FEA) with the true cell shape is necessary. Figure 14 displays a flowchart of inverse FEA to determine the mechanical properties of cells during nanoindentation. In that case, the three-dimensional model a of cell and its nucleus model can be reconstructed from the sliced images obtained by confocal microscopy [123].

Figure 13.

Schematic of indenting a spread cell (with non-uniform thickness) with a conical tip at small depth; in that case, the cell can be assumed as regular shape.

Figure 14.

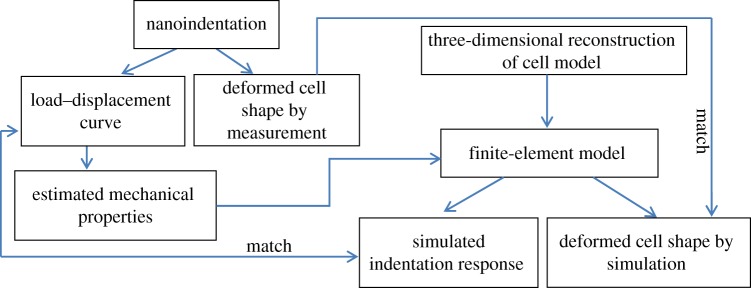
Flowchart of finite-element analysis to determine the mechanical properties of cells during nanoindentation.

In addition, in order to obtain the mechanical properties of a subcellular structure of living cells without mechanical or chemically separating them from living cells, FEA is also essential. For example, finite-element simulations have been used to do inverse analysis to obtain the mechanical properties of cytoplasm [2,51,54], nucleus elastic properties [2,51,54] or the pericellular matrix [114]. As living materials, the external force may trigger passive stress generation in the cell. FEA can be used to investigate how the passive stress may affect the elastic modulus by treating it as residual stress [124].

5.8. Summary of strategy of selecting tip geometry and mechanical models

Prior to discussing the strategy to select tip geometry and size, it is good to recall the cellular structure. A eukaryotic cell (excluding the red blood cell) is composed of cell membrane, cytoplasm (including cytosol, cytoskeleton and other suspended organelles) and nucleus (including nucleus membrane, nucleoplasm, a structure layer nuclear lamina, nucleus and other suspended organelles). In this paper, we discuss the design indentation protocols and the associated indentation models with regard to the cell morphology, because cell morphology will affect the boundary conditions of the indentation models. In addition, cell morphology can be regulated by the substrate as shown in figure 10. Cell type is also important, and we will generally classify the cell as a cell with a strong cytoskeleton (such as osteoblast, chondrocyte and muscle cells), medium strong cytoskeleton (such as fibroblast cell, epithelial cell and endothelial cell) and weak cytoskeleton (such as fat cell, neutrophils, blebbing cell and mesenchymal stem cell).

If one is interested in the mechanics of the cell membrane (with thickness of approx. 7 nm), then a very small indentation (blow 1 nm) should be made with a conical or pyramid tip with a small semi-included angle. This is due to the fact that the tip with a smaller semi-included angle could restrict the effective deformation zone. A simple mechanical model such as an elastic model is acceptable.

If one is interested in the mechanics of cytoplasm, a small indentation, less than 10% of the vertical distance from the nucleus (i.e. less than 0.1d as shown in figure 15) should be made with a conical tip. The suitable penetration depth varies with the semi-included angle. Alternatively, one can locate the indentation near the edge, away from the nucleus. The poroelastic model is more appropriate. It is also recommended to use a cone with a big angle to prevent high strain-induced nonlinear elasticity. For a typical commercial AFM probe, the tip radius is 4–10 nm. One may need to use the modified models for a blunt cone or truncated pyramid as discussed by Lin & Horkay [122], when penetration is comparable to the tip radius.

Figure 15.

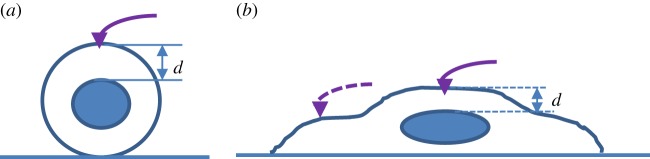
Schematic of indentation of (a) a spherical and (b) spread cell.

If one is interested in the mechanics of the whole cell (mixed responses of cytoplasm and nucleus), then a bigger indentation (more than 0.1d) should be made with a flat punch or a spherical tip. For a well-spread cell (i.e. thickness is small), a conical tip with a big semi-apical angle is appropriate. In this case, poroelastic, viscoelastic and more complex poro-viscoelastic models are appropriate for the cells with a strong or medium strong cytoskeleton. If the cell undergoes large deformation, then the hyperviscoelastic model is more appropriate [66], particularly for cells with a strong cytoskeleton. The power-law rheology model may be more suitable for cells with a weak cytoskeleton.

The guidelines about the relative penetration above are a rough estimation based on a coating/substrate system [44]; some dedicated computational modelling is required to further reveal this rule of thumb to better guide the experimentalists to design test protocols.

If cells are exposed to osmotic pressure, then the poroelastic model (or poro-viscoelastic models) should be used. If the ionic charge is important, then a triphasic model is more appropriate [78,125]. If penetration is comparable to the cell thickness (typically for a spread cell), then a thin-layer model in combination with a viscoelastic/poroelastic model should be used. When the contact radius is comparable to cell width and thickness, the model proposed by Chen & Lu [58] should be used to account for coupling of the free edge effect and the thin-layer effect.

6. Conclusion and perspectives

The exploration of nanobiomechanics of living cells helps us to understand a range of processes such as disease progression and cell–materials interactions. This provides essential information for cellular therapy and tissue engineering. A range of mechanical models has been discussed. The structural models have the advantage in predicting how cells rearrange their structure (e.g. cell spreading and cell migration) according to external stimuli. The continuum models enable quantifying the mechanical properties in cells under various conditions that could provide essential information of cellular subpopulations, disease, malignant transformation and cell–materials interactions.

It is almost impossible to get an accurate universal physical model to quantify the mechanical properties of cells during indentation, owing to the complex cell structure and the complicated mechanotransduction mechanisms (e.g. via cytoskeleton and nuclear lamina). Therefore, it is more realistic to use the averaged continuum model accompanied by appropriate testing protocols if the overall cell mechanics is of interest. One should also treat structure-based models and the continuum models as complementary to each other. Various factors (e.g. cell morphology, substrate, tip geometry and relative indentation penetration with regard to cell size) that affect quantifying the mechanical properties of cells have been evaluated. When researchers compare the measured cell mechanical properties across the literature, they should be aware that interpretation of the results can be significantly affected by the mechanical models adopted at given test conditions. Accordingly, this paper presents strategies to select tip geometries and the associated mechanical models at given test conditions. When the irregular shape of a cell plays an important role in cell mechanics, it violates the boundary conditions of all the analytical and semi-analytical mechanical models. In that case, FEA incorporating the true cell shape is essential.

The way that cells sense and respond to the substrate is expected to be temporal in nature [126]. In addition, passive stresses may be generated in the cell during indentation. Therefore, the outlook for modelling cell mechanics should be to incorporate these dynamic effects to the mechanical modelling and FEA.

Appendix A

Figure 16 presents how the effective strain changes with the semi-apical angle of the conical tip, with the raw data taken from [41].

Figure 16.

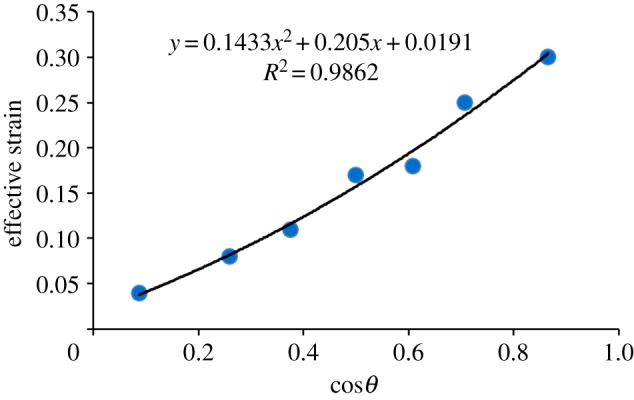
The effective strain changes with the semi-apical angle of the conical tip, with the raw data taken from [41].

Funding statement

This work is partially supported by ‘A new frontier in design: the simulation of open engineered biological systems’, EP/K039083/1 and EPSRC-Newcastle University sandpit workshop award.