Fast and Efficient Estimation of Individual Ancestry Coefficients

Abstract

Inference of individual ancestry coefficients, which is important for population genetic and association studies, is commonly performed using computer-intensive likelihood algorithms. With the availability of large population genomic data sets, fast versions of likelihood algorithms have attracted considerable attention. Reducing the computational burden of estimation algorithms remains, however, a major challenge. Here, we present a fast and efficient method for estimating individual ancestry coefficients based on sparse nonnegative matrix factorization algorithms. We implemented our method in the computer program sNMF and applied it to human and plant data sets. The performances of sNMF were then compared to the likelihood algorithm implemented in the computer program ADMIXTURE. Without loss of accuracy, sNMF computed estimates of ancestry coefficients with runtimes ∼10–30 times shorter than those of ADMIXTURE.

INFERENCE of population structure from multilocus genotype data is commonly performed using likelihood methods implemented in the computer programs STRUCTURE, FRAPPE, and ADMIXTURE (Pritchard et al. 2000a; Tang et al. 2005; Alexander et al. 2009). These programs compute probabilistic quantities called ancestry coefficients that represent the proportions of an individual genome that originate from multiple ancestral gene pools. Estimation of ancestry proportions is important in many respects, for example in delineating genetic clusters, drawing inference about the history of a species, screening genomes for signatures of natural selection, and performing statistical corrections in genome-wide association studies (Pritchard et al. 2000b; Marchini et al. 2004; Price et al. 2006; Frichot et al. 2013).

Individual ancestry coefficients can be estimated using either supervised or unsupervised statistical methods. Supervised estimation methods use predefined source populations as ancestral populations. Classical supervised estimation approaches were based on least-squares regression of allele frequencies in hybrid and source populations (Roberts and Hiorns 1965; Cavalli-Sforza and Bodmer 1971). Unsupervised approaches attempt to infer ancestral gene pools from the data, using likelihood methods. An undesired feature of likelihood methods is that they can be computer intensive, with typical runs lasting several hours or more. With the use of dense genomic data and increased sample sizes, reducing the time lag necessary to perform estimation is a major challenge of population genetic data analysis.

A fast approach to the estimation of ancestry coefficients is by using principal component analysis (PCA) (Patterson et al. 2006). PCA is an exploratory method that describes high-dimensional data, using a small number of dimensions, and makes no assumptions about sampled and ancestral populations. Using PCA can lead to results surprisingly close to likelihood methods, and connections between methods have been intensively investigated during recent years (Patterson et al. 2006; Engelhardt and Stephens 2010; Frichot et al. 2012; Lawson et al. 2012; Lawson and Falush 2012). But a drawback of PCA is that interpretation in terms of ancestry is often difficult, as it can be confounded by demographic factors or irregular sampling designs (Novembre and Stephens 2008; McVean 2009; François et al. 2010).

In this study, we introduce computationally fast algorithms that lead to estimates of ancestry coefficients comparable to those obtained with STRUCTURE or ADMIXTURE. The algorithms were implemented in the computer program sNMF based on sparse nonnegative matrix factorization (NMF) and least-squares optimization (Lee and Seung 1999; Kim and Park 2007; Kim and Park 2011). Like PCA, NMF algorithms are flexible approaches that are robust to departures from traditional population genetic model assumptions. In addition, NMF algorithms produce estimates of ancestry proportions with runtimes that are much shorter than those of STRUCTURE or ADMIXTURE. This study assesses the utility of NMF algorithms when analyzing population genetic data sets and compares the performances of the algorithms implemented in sNMF with those implemented in ADMIXTURE on the basis of human and plant data.

Materials and Methods

To provide statistical estimates of ancestry proportions using multilocus genotype data sets, we implemented sparse NMF least-squares optimization algorithms in the computer program sNMF.

Modeling ancestry coefficients

We considered allelic data for a sample of n multilocus genotypes at L loci representing single-nucleotide polymorphisms (SNPs). The data were stored into a genotypic matrix (X), where each entry records the number of derived alleles at locus ℓ for individual i. For autosomes in a diploid organism, the number of derived alleles at locus ℓ is then 0, 1, or 2. In our algorithm, we used 3 bits of information to encode each 0, 1, or 2 value as an indicator of a heterozygote or a homozygote locus. In other words, the value 0 was encoded as 100, 1 was encoded as 010, and 2 as 001. The use of a binary coding warrants that the entries sum up to L for each row of the transformed data matrix.

Admixture models generally suppose that the genetic data originate from the admixture of K ancestral populations, where K is unknown a priori. Given K populations, the probability that individual i carries j derived alleles at locus ℓ can be written as

$$p_{i\ell }\left(j\right)={\displaystyle \sum _{k=1}^K{q}_{ik}{g}_{k\ell }\left(j\right),}j=0,1,2,$$ (1)

where q_ik is the fraction of individual i’s genome that originates from the ancestral population k, and g_kℓ(j) represents the homozygote (j = 0, 2) or the heterozygote (j = 1) frequency at locus ℓ in population k. Since it makes no assumption about Hardy–Weinberg equilibrium, the above framework is appropriate to deal with inbreeding and outbreeding in ancestral populations. Using our binary coding, Equation 1 writes as

$$P=QG,$$ (2)

where P = (p_iℓ) is an n × 3L matrix, Q = (q_ik) is an n × K matrix, and G = (g_kℓ(j)) is a K × 3L matrix. The Q matrix records ancestry proportions for each individual in the sample. Although the focus of the above framework is on estimating ancestry estimates for each sampled individual, it can be easily modified to provide ancestry estimates based on allele frequencies in population samples.

Least-squares estimates of ancestry proportions

We approached the inference of ancestry coefficients by using least-squares (LS) optimization algorithms (Engelhardt and Stephens 2010). Estimates of the Q and G matrices were obtained after minimizing the least-squares criterion

$$\mathrm{LS}\left(Q,G\right)={\left|\left|X-QG\right|\right|}_{\mathrm{F}}^2,$$ (3)

where ||M||_F denotes the Frobenius norm of a matrix M (Berry et al. 2007). Without constraints on Q and G, the solutions of the LS problem are given by the singular value decomposition of the matrix X, and the resulting matrices Q and G contain the scores and loadings of a PCA. To obtain ancestry coefficients, the matrices Q and G must have nonnegative entries such that

$${\displaystyle \sum _{k\mathrm{=}1}^K{q}_{ik}}=1,{\displaystyle \sum _{j=0}^2{g}_{k\ell }\left(j\right)}=1.$$ (4)

With the constraints of Equation 4, estimating ancestry coefficients and genotypic frequencies is equivalent to performing NMF of the data matrix, X. NMF was previously applied to gene expression data (Kim and Park 2007), and algorithms for NMF were surveyed and compared in Kim and Park (2011). In sNMF, estimates of Q and G were computed using the alternating nonnegativity-constrained least-squares (ANLS) algorithm with the active set (AS) method (Berry et al. 2007; Kim and Park 2011). We modified the ANLS-AS algorithm as follows.

Our algorithm begins with the initialization of the Q entries with nonnegative values. Then it iterates the following cycles until convergence. The first step of an algorithm cycle consists of computing a nonnegative matrix G that minimizes the quantity

$$\mathrm{L}{\mathrm{S}}_1\left(G\right)={\left|\left|\begin{array}{c}X-QG\end{array}\right|\right|}_{\text{F}}^2,G\ge 0.$$ (5)

The G matrix was obtained by setting all negative entries to zero, after solving classical linear regression equations. The obtained solution was then normalized so that its entries satisfy Equation 4.

Given G, the second step of the cycle consists of computing a nonnegative matrix Q that minimizes the quantity

$$\mathrm{L}{\mathrm{S}}_2\left(Q\right)={\left|\left|\begin{array}{c}\left(\begin{array}{c}{G}^T\\ \sqrt{\alpha }{e}_{1\times K}\end{array}\right)Q-\left(\begin{array}{c}{X}^T\\ 0_{1\times n}\end{array}\right)\end{array}\right|\right|}_{\text{F}}^2,$$ (6)

where e_1×K is a row vector having all entries equal to 1, 0_1×n is a vector of length n with all entries equal to 0, and α is a nonnegative regularization parameter. This minimization problem was solved using the block principal pivoting method proposed by Kim and Park (2011). The obtained solution, Q, was then normalized so that the row entries sum up to 1. Iterations were stopped based on a stationarity criterion derived from the Karush–Kuhn–Tucker conditions (Kim and Park 2011) and when the relative difference between two successive values of the criterion was less than a tolerance threshold of ε = 10⁻⁴.

For α > 0, the algorithm amounts to performing sparse NMF for the data matrix X. We tested values α > 0 because they can reduce the variance of Q and G estimates for the smaller data sets, force irrelevant estimates to zero, and improve the numerical behavior the ANLS minimization algorithm. In addition, the programming structures used in sNMF optimized the time spent in memory access. Several algorithmic methods were also used to accelerate computation of matrix products. While we evaluated sNMF runtimes using a single computer processor unit (2.4 GHz, 64 bits, Intel Xeon), a multithreaded version of the sNMF program was also developed for multiprocessor systems.

Data sets

Ancestry inference and runtime analyses were performed on six worldwide samples of genomic DNA from 52 populations of the Human Genome Diversity Project–Centre d’Etude du Polymorphisme Humain (HGDP-CEPH). Five panels were extracted from the Harvard HGDP-CEPH database. These panels were given identification nos. HGDP00778, HGDP00542, HGDP00927, HGDP00998, and HGDP01224 and contained precisely ascertained genotypes of n = 934 individuals. The genotypes were specifically designed for population genetic analyses (Patterson et al. 2012). Each marker was ascertained in individuals of Han, Papuan, Yoruba, Karitiana, and Mongolian ancestry, and the data matrices included 78,253, 48,531, 124,115, 2635, and 10,664 SNPs, respectively (Patterson et al. 2012, Table 1). A sample of 1043 individuals from the HGDP-CEPH Human Genome Diversity Cell Line Panel was also analyzed. The genotypes were generated on Illumina 650K arrays (Li et al. 2008), and the SNP data were filtered to remove low-quality SNPs included in the original files. In addition, we used data from the 1000 Genomes Project. The 1000 Genomes Project data contain the genomes of 1092 individuals from 14 populations, constructed using a combination of low-coverage whole-genome and exome sequencing [phase 1 data (1000 Genomes Project Consortium 2012)]. The data matrix included 2.2 million polymorphic sites across the human genome (Table 1).

Table 1. Data sets used in this study.

Data set	Sample size	No. SNPs	Reference
HGDP00778	934	78,000	Patterson et al. (2012)
HGDP00542	934	48,500	—
HGDP00927	934	124,000	—
HGDP00998	934	2,600	—
HGDP01224	934	10,600	—
HGDP-CEPH	1,043	660,000	Li et al. (2008)
1000 Genomes	1,092	2,200,000	1000 Genomes Project Consortium (2012)
A. thaliana	168	216,000	Atwell et al. 2010)

To examine the robustness of sNMF to departures from classical population genetic hypotheses, additional analyses were performed on a sample of n = 168 European accessions of the plant species Arabidopsis thaliana. A. thaliana is a widely distributed self-fertilizing plant known to harbor considerable genetic variation and complex patterns of population structure and relatedness (Atwell et al. 2010). We analyzed 216,130 SNPs spread across the genome of A. thaliana (Atwell et al. 2010, Table 1).

Comparisons with ADMIXTURE

The computer program ADMIXTURE (version 1.22) estimates ancestry coefficients based on the likelihood model implemented in STRUCTURE. In ADMIXTURE, the assumption of Hardy–Weinberg equilibrium in ancestral populations translates into a binomial model for allele counts at each locus. Considering unrelated individuals, the logarithm of the likelihood can thus be computed as

$$\begin{array}{l}\mathrm{ℒ}\left(\text{Q},\text{F}\right)\\ ={\displaystyle \sum _i{\displaystyle \sum _{\ell }\left(x_{i\ell }\log \left({\displaystyle \sum _k{q}_{ik}{f}_{k\ell }}\right)+\left(1-x_{i\ell }\right)\log \left({\displaystyle \sum _k{q}_{ik}\left(1-f_{k\ell }\right)}\right)\right)}}\end{array}$$

up to an additive constant that does not influence estimation algorithms. In this formula, Q = (q_ik) represents the matrix of ancestry coefficients for all individuals, and F = (f_kℓ) represents a matrix of allele frequencies for all loci. The F matrix can be converted to a G matrix comparable to the one computed by sNMF, using the binomial model, g_kℓ(0) = (1 − f_kℓ)², g_kℓ(1) = 2f_kℓ(1 − f_kℓ), and $g_{k\ell }\left(2\right)=f_{k\ell }^2.$ ADMIXTURE provides numerical estimates of Q and F that maximize the quantity ℒ(Q, F). The local optimization algorithm relies on a block relaxation scheme, using sequential quadratic programming for block updates, coupled with a quasi-Newton acceleration of convergence.

A difficulty with optimization algorithms used by ADMIXTURE and sNMF is that the solutions produced can be dependent on the initial values used for Q, F, or G. To enable comparisons with estimates obtained with ADMIXTURE, the clusters output by runs of each program was permuted using CLUMPP (Jakobsson and Rosenberg 2007). Differences in ancestry estimates obtained with ADMIXTURE (Q^ADM) and with sNMF (Q^sNMF) were assessed by two measures. The first measure was defined as the root mean-squared error (RMSE) between the matrices Q^ADM and Q^sNMF obtained from each program,

$$\mathrm{RMSE}={\left(\frac{1}{nK}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{k=1}^K{\left(q_{ik}^{\mathrm{ADM}}-q_{ik}^{\mathrm{sNMF}}\right)}^2}}\right)}^{1/2}.$$

Although G matrices could be mainly considered as nuisance parameters for our estimation problem, a similar RMSE criterion was defined for comparing them. The second measure was defined as the squared Pearson correlation coefficient (R²) between the matrices Q^ADM and Q^sNMF. When simulations with known Q matrices were analyzed, one of the two matrices was replaced by the true Q matrix used to generate the simulated data.

Runs of ADMIXTURE and sNMF were performed for values of the number of clusters set to K = 2−10, 15, and 20 for human data sets and set to K = 2−7 for A. thaliana. For sNMF, the values of the regularization parameter (α) ranged between 0 and 10,000, using a log₁₀ scale (5 values). Each run was replicated five times for a total of 1410 experiments. Missing data imputation was initially performed after resampling missing genotypes from empirical frequencies at each locus. The missing values were updated using predictive probabilities after 20 sweeps of the algorithm (see below).

Cross-entropy criterion

We employed a cross-validation technique based on imputation of masked genotypes to evaluate the prediction error of ancestry estimation algorithms (Wold 1978; Eastment and Krzanowski 1982). The procedure partitioned the genotypic matrix entries into a training set and a test set. To build the test set, 5% of all genotypes were randomly selected and tagged as missing values. The occurrence probabilities for the masked entries were computed using the program outputs obtained from training sets according to the formula

$$p_{i\ell }^{\text{pred}}\left(j\right)={\displaystyle \sum _{k=1}^K{q}_{ik}{g}_{k\ell }\left(j\right)},j=0,1,2.$$ (7)

ADMIXTURE predicts each masked value by $E\left[x_{i\ell }|Q^{\mathrm{ADM}},F^{\mathrm{ADM}}\right]=2{\displaystyle {\sum }_k{q}_{ik}^{\mathrm{ADM}}{f}_{k\ell }^{\mathrm{ADM}}}$ and the prediction error is estimated by averaging the squares of the deviance residuals for the binomial model (Alexander and Lange 2011). Extending the approach employed by ADMIXTURE to our nonparametric approach, the predicted values were compared to the masked values, x_iℓ, by averaging the quantity defined as $-\log p_{i\ell }^{\text{pred}}\left(x_{i\ell }\right)$ over all SNPs in the test set. In statistical terms, our criterion provides an estimate of the quantity

$$H\left(p^{\text{sample}},p^{\text{pred}}\right)=-{\displaystyle \sum _{j=0}^2{p}^{\text{sample}}\left(j\right)\log p_{i\ell }^{\text{pred}}\left(j\right)},j=0,1,2.$$ (8)

This quantity corresponds to the sum of the Kullback–Leiber divergence between the sampled (p^sample) and predicted (p^pred) allelic distributions and the Shannon entropy of the sample distribution. It also corresponds to the cross-entropy between p^sample and p^pred. The number of ancestral gene pools (K) and the regularization parameter (α) were chosen to minimize the cross-entropy criterion. In general, smaller values of the criterion indicate better algorithm outputs and estimates. The standard error of the cross-entropy criterion is of order $1/\sqrt{n_L},$ where n_L is the number of masked genotypes. For data sets including 1000 individuals genotyped at >20,000 SNPs, the third digit of the cross-entropy criterion can be significant.

Simulated data analysis

We adopted a simulation approach to compare RMSEs between the Q matrix computed by ADMIXTURE or by sNMF and a known matrix used to generate the simulated data. In addition, we assessed whether the correct value of K could be identified by sNMF, using the cross-entropy criterion.

In a first series of simulations, we used the 1000 Genomes Project data set to generate artificial data showing various levels of admixture. As ancestral populations, we chose the Han Chinese (CHB), British (GBR), and Yoruba (YRI) samples (1000 Genomes Project 2012). We considered 50,000 SNPs in linkage equilibrium, exhibiting no missing genotypes. The allele frequencies observed in our three ancestral populations were used as the true values for the F matrix. The genotypic matrix was constructed according to the binomial model used by ADMIXTURE. For 1000 individuals in each simulated data set, a Q matrix was simulated from a Dirichlet probability distribution, and several parameters were explored. Our experiments reproduced the parameters used for evaluating the accuracy of ADMIXTURE in a previous study (Alexander et al. 2009). Runs of sNMF were performed for values of the number of clusters set to K = 2−5 (α = 0), and the choice of K was made on the basis of the cross-entropy criterion. For K = 3, the values of the regularization parameter (α) were varied between 0 and 100.

Additional data sets were created to mimic the population structure of European populations of A. thaliana, using 10,000 SNPs (168 individuals). To define ancestral frequencies, we used the western European populations, grouping samples from the United Kingdom, Belgium and France (23 individuals); central European populations, grouping samples from the Czech Republic (24 individuals); and northern European populations, grouping samples from Finland and Northern Sweden (13 individuals). ADMIXTURE and sNMF grouped these samples within three well-separated clusters exhibiting low levels of admixture with other plant populations. The empirical frequencies computed from the three populations were considered as the true frequencies for a generative model with K = 3 ancestral populations. From empirical frequencies, we computed genotypic frequencies, f_kℓ, using four distinct values of population inbreeding coefficient, F_IS = 25–100%, that corresponded to moderate and strong levels of inbreeding. For 168 individuals, 10,000 genotypes were simulated using the sampling equation $p\left(x_{i\ell }=j\right)={\displaystyle {\sum }_k{q}_{ik}{g}_{k\ell }\left(j\right)},$ where q_ik corresponds to the Q matrix computed from the full empirical data set (216,000 SNPs). In addition, simulated data sets were generated with or without missing data (0 or 20%). Fifty replicates were created for each value of the inbreeding coefficient and for each value of the ratio of missing data.

Results

We used the program sNMF to implement nonnegative matrix factorization algorithms and to compute least-squares estimates of ancestry coefficients for worldwide human population samples and for European populations of the plant species A. thaliana. As in the likelihood model implemented in the computer programs STRUCTURE and ADMIXTURE, sNMF supposes that the genetic data originate from the admixture of K parental populations, where K is unknown, and it returns estimates of ancestry proportions for each multilocus genotype in the sample (Pritchard et al. 2000a; Alexander et al. 2009). To estimate ancestry coefficients, sNMF solves a constrained least-squares minimization problem, using an alternating algorithm based on a block principal pivoting method (Kim and Park 2011) (see Materials and Methods).

Comparison of ancestry estimates for HGPD data sets

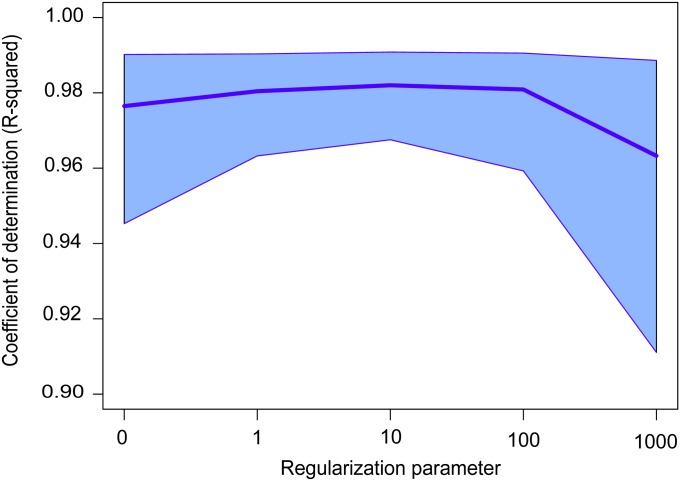
First we evaluated the ability of ADMIXTURE estimates to be accurately reproduced by sNMF for five Harvard HGDP panels and for the HGDP-CEPH data set (Li et al. 2008; Patterson et al. 2012). For each run of ADMIXTURE, we computed a maximum squared correlation coefficient (R²) and a minimum RMSE over runs of sNMF performed with the same number of clusters (K). For K ranging from 5 to 10, squared correlation coefficients remained >0.96 across all runs (480 runs, Figure 1). Average values of the RMSE remained <5.5% across all runs (Supporting Information, Table S1). These results provided evidence that sNMF estimates closely reproduce those obtained with ADMIXTURE across the six HGDP data sets.

Figure 1.

Correlation between sNMF and ADMIXTURE estimates. Shown is squared correlation (coefficient of determination, R²) between the ancestry coefficients estimated by each program. For each number of clusters (K), the result corresponds to the maximum correlation over five runs, averaged over values of the regularization parameter <1000 and over six HGDP data sets. The shaded area corresponds to a 95% confidence interval displayed for each value of the regularization parameter, α.

Runtime analysis

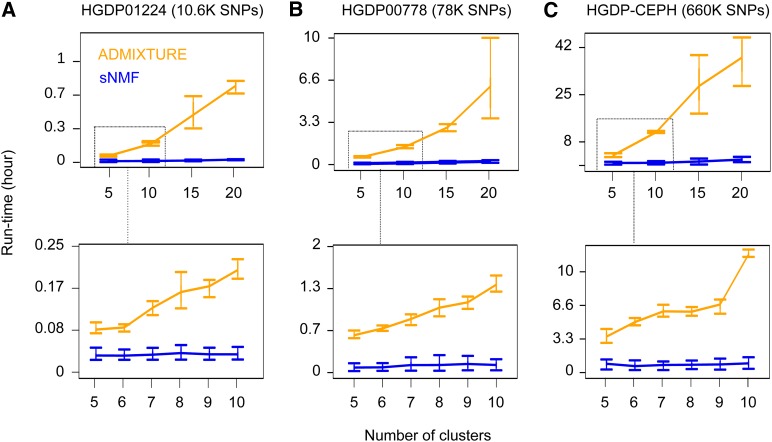
Next we performed runtime analyses for ADMIXTURE and for sNMF, using the 1000 Genomes Project phase 1 data in addition to the previous HGDP data sets. The runtimes were averaged over distinct random seed values for each value of K. Runtimes increased with the number of SNPs in the data set and with the number of clusters in each algorithm (Figure 2, Table 2, Figure S1). For data set HGDP01224 (10,600 SNPs), it took on average 0.8 min (1.7 min) for sNMF to compute ancestry estimates for K = 10 (K = 20) clusters. For ADMIXTURE, the runtime was on average 11 min (48 min) for K = 10 (K = 20) clusters. For panel HGDP00778 (78,000 SNPs), it took on average 7.2 min (15 min) for sNMF to compute ancestry estimates for K = 10 (K = 20) clusters. For ADMIXTURE, the average runtime was 1.5 hr (6.2 hr) for K = 10 (K = 20) clusters. For the CEPH-HGDP data sets (660,000 SNPs), it took on average 55 min (2.1 hr) for sNMF to compute ancestry estimates for K = 10 (K = 20) clusters. For ADMIXTURE, the average runtime was 12 hr (38 hr) for K = 10 (K = 20) clusters. Runtimes increased in a quadratic fashion with K for ADMIXTURE whereas they increased linearly for sNMF (Figure 2). For the values of K used in our analyses, sNMF ran 5–30 times faster than ADMIXTURE when these programs were applied to HGPD data sets. Regarding the 1000 Genomes Project phase 1 data set, the average runtimes of sNMF were ∼2.8 hr (4.6 hr) for K = 5 (K = 10) clusters. The ADMIXTURE runs led to similar estimates of Q, but a single run on the phase 1 data set took >19 hr for K = 5 (59 hr for K = 10).

Figure 2.

Runtimes for sNMF and ADMIXTURE runs. Averaged time elapsed before the stopping criterion of the sNMF (blue) and ADMIXTURE (orange) programs is met. Time is expressed in unit of hours. (A) Runtime analysis for Harvard HGDP panel 01224 (10,600 SNPs). (B) Runtime analysis for Harvard HGDP panel 00778 (78,000 SNPs). (C) Runtime analysis for the HGDP-CEPH data (660,000 SNPs).

Table 2. Runtime summary for sNMF and ADMIXTURE: Average values and their 95% confidence intervals.

		K = 5		K = 10		K = 20
Data set (no. SNPs)	Time unit	sNMF	ADMIXTURE	sNMF	ADMIXTURE	sNMF	ADMIXTURE
HGDP01224	min	0.68	4.4	0.8	11	1.7	48
(10,600)		[0.1, 1.6]	[3.4, 4.9]	[0.18, 1.7]	[9.9, 12]	[1.3, 1.8]	[41, 55]
HGDP00778	hr	0.087	0.61	0.12	1.5	0.25	6.2
(78,000)		[0.03, 0.15]	[0.55, 0.66]	[0.044, 0.12]	[1.3, 1.5]	[0.14, 0.34]	[3.8, 9.4]
HGDP-CEPH	hr	0.9	3.7	0.92	12	2.1	38
(660,000)		[0.33, 1.3]	[3, 4.3]	[0.38, 1.5]	[11, 12]	[1.3, 3.0]	[29, 45]
1000 Genomes Project	hr	2.8	(19)	4.6	(59)	—	—
(2,200,000)		[1.1, 4.7]	—	[1.5, 8.3]	—	—	—

Terms in brackets represent 95% confidence intervals. Terms in parentheses represent values obtained from a single program run.

Prediction of masked genotypes

To decide which program options could provide the best estimates, we employed a cross-validation technique based on the imputation of masked genotypes (Wold 1978; Alexander and Lange 2011). The cross-validation method partitions the genotypic matrix entries into a training set and a test set that are used for estimation and validation sequentially. To build test sets, 5% of the genotypic matrix entries were tagged as missing values. The masked entries were then predicted using estimates obtained from training sets. Predictions were assessed using a cross-entropy criterion that measured the capability of an algorithm to correctly impute masked genotypes (see Materials and Methods). Lower values of the cross-entropy criterion generally indicate better predictive capabilities of an algorithm.

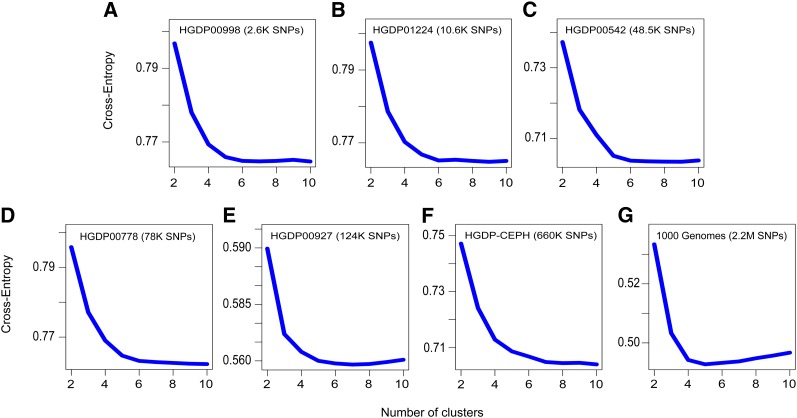
Using the cross-entropy criterion, we performed an extensive analysis of sNMF program outputs to assess which values of the number of clusters (K) and the regularization parameter (α) could provide the best prediction of masked genotypes (Figure 3, Figure S2). For HGDP data sets with moderate size (panels HGDP00998 and HGDP01224), values of K ∼ 7–8 provided the best predictive results. For larger human data sets, cross-entropy values did not stabilize for K ≤ 10, indicating that >10 clusters were necessary to describe population structure. Choices of regularization parameter values >1000 were generally discarded by the cross-entropy criterion. For panels of moderate size, the best ancestry estimates were obtained for values ∼α = 100. The influence of the regularization parameter was substantial for the smallest data sets, but for the largest ones a wide range of values led to comparable imputation results (Figure S2). Regardless of the value of the regularization parameter, K = 5 clusters led to the best results for the 1000 Genomes Project data set (Figure 3). This last result is in accordance with the criteria used for choosing populations included in the 1000 Genomes Project.

Figure 3.

Values of the cross-entropy criterion for sNMF runs (human data sets). (A–G) Minimal values of the cross-entropy criterion over five runs of sNMF for (A–E) five Harvard HGDP panels, (F) HGDP-CEPH data, and (G) the 1000 Genomes Project data. The number of clusters ranged from 2 to 10.

Ancestry estimates

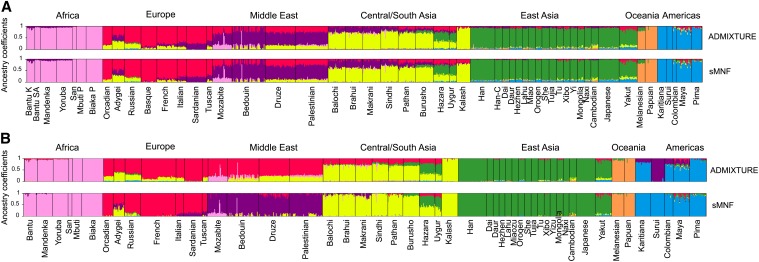
To compare ancestry estimates obtained from particular runs of sNMF and ADMIXTURE, we displayed the Q matrices computed by each program for the Harvard HGPD panel HGDP00778 (78,000 SNPs), the HGDP-CEPH data (660,000 SNPs), the 1000 Genomes Project phase 1 data (2.2 million SNPs), and European populations of A. thaliana (216,000 SNPs). Using K = 7 ancestral populations for the Harvard HGPD panel HGDP00778, the cross-entropy criterion was 0.747 for the ADMIXTURE run, and it was 0.762 for the sNMF run. The criterion favored ADMIXTURE in this case, but the two runs led to very close estimates of the Q matrix (R² = 0.99, Figure 4). When the programs were applied to the HGDP-CEPH data (K = 7), the cross-entropy criterion was 0.691 for the ADMIXTURE run and 0.704 for sNMF (Figure 4). This particular ADMIXTURE run identified clusters that separated the African hunter–gatherer populations from the other populations, whereas sNMF identified a unique cluster in Africa. In the sNMF run, Middle East populations were separated from European populations (Figure 4). The differences between ADMIXTURE and sNMF results disappeared when additional runs were performed with distinct random seeds. Using K = 5 for the 1000 Genomes Project phase 1 data, sNMF identified clusters that correspond to the main geographic regions of the world, similarly to ADMIXTURE (Figure 5, cross-entropy = 0.5010). Substantial levels of European ancestry in African-Americans, Mexican-Americans, Puerto Ricans, and Colombians were inferred by sNMF and by the other program. An interesting case was with the application of ancestry estimation programs to European populations of A. thaliana, a selfing plant characterized by high levels of inbreeding (Atwell et al. 2010). Using K = 3, the cross-entropy criterion for ADMIXTURE was 0.641 on average, while the average value for sNMF was 0.483. The value of the criterion suggests that sNMF estimates were more accurate than those obtained from ADMIXTURE. The graphical output of the Q matrix displayed clinal variation of ancestry coefficients occurring along an East–West gradient separating two clusters, and Northern Swedish accessions were grouped into a separate cluster. These results supported previous estimates based on sequence data (Figure S3) (François et al. 2008).

Figure 4.

Graphical representation of ancestry estimates obtained for HGDP data sets (K = 7). (A) HGDP00778 panel (78,000 SNPs). Shown are estimated ancestry coefficients using ADMIXTURE (top, cross-entropy = 0.747) and sNMF (bottom, cross-entropy = 0.762 and α = 100). (B) HGDP-CEPH data set (660,000 SNPs). Shown are estimated ancestry coefficients using ADMIXTURE (top, cross-entropy = 0.691) and sNMF (bottom, cross-entropy = 0.704 and α = 100).

Figure 5.

Graphical representation of ancestry estimates obtained for the 1000 Genomes Project data set. (A) Estimated ancestry coefficients using sNMF with K = 5 and α = 10,000 (cross-entropy = 0.5010). (B) Estimated ancestry coefficients using sNMF with K = 6 and α = 10,000 (cross-entropy = 0.5011) (FIN, Finnish; GBR, British; IBS, Spanish; CEU, CEPH Utah residents; TSI, Tuscan; CHS, Southern Han Chinese; CHB, Han Chinese; JPT, Japanese; YRI, Yoruba; LWK, Luhya; ASW, African-American; PUR, Puerto Rican; CLM, Colombian; MXL, Mexican-American).

Simulated data analysis

To further ascertain the accuracy of sNMF estimates and to compare those estimates with ADMIXTURE, we employed computer simulations based on the 1000 Genomes Project and A. thaliana data sets. We also assessed the ability of the cross-entropy criterion to correctly identify the value of K when it is known.

In a first series of simulations, we used the 1000 Genomes Project data to generate genotypes showing various levels of admixture. As our ancestral populations, we chose the CHB, GBR, and YRI samples (1000 Genomes Project 2012), and true Q matrices were created using several parameterizations of the Dirichlet distribution (Table 3). Genotypic matrices were simulated according to the binomial model used by ADMIXTURE. In this context, ADMIXTURE estimates are thus expected to be more accurate than sNMF estimates. For the range of parameters explored in the simulations, root mean-squared errors comparing the estimated and true values of the Q matrix remained <2% for both programs (Table 3). For moderate levels of admixture, differences in statistical errors were <1% regardless of the value of the regularization parameter, α, used in sNMF. This result indicated that sNMF estimates are generally accurate and that relatively small values of α do not influence sNMF outputs for data sets of size comparable to those used in simulations. Root mean-squared errors comparing the estimated and true values of the G matrix were slightly lower for ADMIXTURE than for sNMF (Table 3). This could be explained as we simulated from a binomial model (unrelated individuals) and as the number of degrees of freedom in sNMF is twice the number of degrees of freedom in ADMIXTURE. Regarding the choice of the number of clusters, the cross-entropy criterion was minimal for K = 3 for every simulated data set (Table S2).

Table 3. Statistical errors for ADMIXTURE and sNMF on simulated data sets.

Ancestry estimation	Dir(1, 1, 1)	Dir(0.5, 0.5, 0.5)	Dir(0.1, 0.1, 0.1)	Dir(0.2, 0.2, 0.05)	Dir(0.2, 0.2, 0.5)	Dir(0.05, 0.05, 0.01)
Q matrix
ADMIXTURE	0.023	0.012	0.004	0.006	0.010	0.003
sNMF α = 0	0.020	0.011	0.007	0.007	0.013	0.009
sNMF α = 100	0.024	0.014	0.006	0.006	0.014	0.006
G matrix
ADMIXTURE	0.029	0.022	0.016	0.022	0.022	0.022
sNMF α = 0	0.034	0.027	0.021	0.028	0.028	0.028
sNMF α = 100	0.034	0.027	0.021	0.028	0.028	0.028

Dir: Dirichlet distribution used to simulate “true” admixture coefficients, using three ancestral populations.

To evaluate the relative impact of linkage disequilibrium (LD) on sNMF and ADMIXTURE ancestry estimates, we considered subsets of SNPs sampled from the 1000 Genomes Project data set. We compared ancestry estimates computed by each program for data sets containing blocks of >30 SNPs spaced <20 kb apart and for data sets containing SNPs separated by >20 kb (20,000 SNPs, 20 replicates). Using linked blocks of SNPs, the average value of the RMSE over all runs was 0.0859 (0.0297 for unlinked SNPs) for sNMF whereas it was 0.0976 for ADMIXTURE (0.257 for unlinked SNPs). Our results show that LD had an impact on the accuracy of ancestry estimates regardless of the program used and that the magnitude of the effect was similar for ADMIXTURE and sNMF (Figure S4).

We used another series of simulated data to evaluate the sensitivity of ADMIXTURE and sNMF estimates to the presence of related individuals and inbreeding in the sample. Based on empirical data, we used simulation models that mimicked the population structure of European populations of A. thaliana. First, we verified that the true value of the number of ancestral populations was correctly recovered by the sNMF program, using the cross-entropy criterion (K = 3). Next, we evaluated statistical errors for ADMIXTURE and sNMF estimates of the Q matrix. RMSEs remained <4% for both programs. These results showed that the two programs produced accurate estimates of the Q matrix in the presence of inbreeding and missing data (Figure 6).

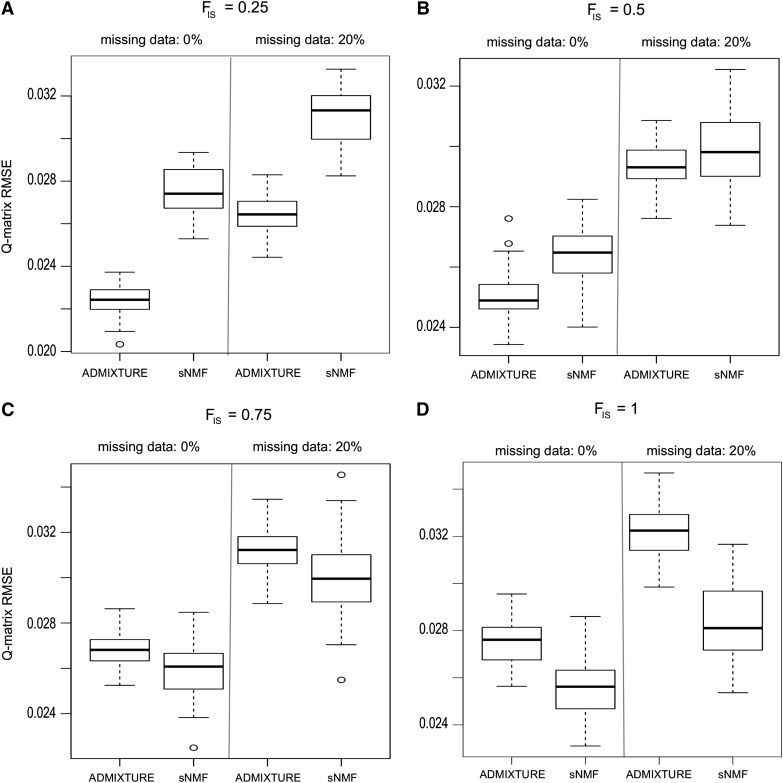
Figure 6.

Accuracy of ADMIXTURE and sNMF in the presence of related individuals. Shown are RMSEs between estimated Q matrices and a known matrix used to generate simulated data. Simulations mimicked the population structure of European populations of Arabidopsis thaliana. (A and B) Moderate levels of inbreeding, F_IS = 25–50%. (C and D) Strong levels of inbreeding, F_IS = 75–100%.

ADMIXTURE estimates were robust to the inclusion of moderate levels of inbreeding in the sample. When the values of the inbreeding coefficient were 0.25−0.5, ADMIXTURE ancestry estimates were more accurate than sNMF estimates. When the values of the inbreeding coefficient were >0.5 and for fully inbred lines, sNMF produced better estimates than ADMIXTURE (Figure 6). The cross-entropy criterion was smaller for sNMF than for ADMIXTURE, showing that sNMF produced better prediction of masked genotypes than ADMIXTURE (Figure S5). This result can be explained by a more accurate estimation of genotypic frequencies for sNMF than for ADMIXTURE in the presence of strong levels of inbreeding.

Discussion

We applied the computer program sNMF to the estimation of individual ancestry coefficients, using large population genetic data sets for humans and for A. thaliana, and compared the program performances to those of ADMIXTURE. For six HGDP data sets, ancestry estimates obtained with sNMF and ADMIXTURE strongly agreed with each other. In addition, the sNMF program was able to analyze the 1000 Genomes Project phase 1 data set within a few hours, using a standard computer processing unit. Without significant loss of accuracy, sNMF computed estimates of admixture proportions within runtimes that were ∼10–30 times faster than those of ADMIXTURE.

The approach used by sNMF is based on theoretical connections between likelihood approaches, PCA, and NMF methods (Ding et al. 2008; Engelhardt and Stephens 2010; Lawson et al. 2012; Parry and Wang 2013). Several methods can be applied to computing NMF estimates, including the multiplicative update algorithm, the projected-gradient method, and the alternating least-squares algorithm (Brunet et al. 2004; Berry et al. 2007; Kim and Park 2011). For population genetic data, we found that alternating least-squares algorithms coupled with the active set method provided the best trade-off between speed and accuracy and improved performance significantly over other NMF implementations (Kim and Park 2011).

To decide which algorithm yielded the best estimates, we introduced a predictive criterion based on the computation of cross-entropy and the imputation of masked genotypes. For HGDP data sets, the cross-entropy criterion discarded large values of the sNMF regularization parameter (>1000). For the large data sets, a wide range of values of the regularization parameter reached similar predictive values. For data sets having <10,000 SNPs, we found that parsimony (i.e., large values of α) could improve estimation of ancestry coefficients. We observed that a likelihood approach could benefit the analysis of modest-sized data sets or data containing a large number of missing genotypes. For larger data sets and missing <20% genotypes, sNMF ancestry estimates were statistically close to those obtained with ADMIXTURE, and both programs were equally efficient at predicting masked genotypes. Statistical theory actually predicts that errors in evaluating the cross-entropy criterion are of order $O\left(1/\sqrt{n_L}\right),$ where n_L is the number of masked genotypes. For Harvard HGDP panels, differences between the ADMIXTURE and sNMF results could be considered hardly significant and estimates were statistically similar. The example of the Harvard HGDP panels showed that the cross-entropy criterion could also be used to discriminate among program runs regardless of the program used.

The assumptions underlying STRUCTURE and ADMIXTURE rely on simplified population genetic hypotheses. More specifically, the assumptions include absence of genetic drift and Hardy–Weinberg and linkage equilibrium in ancestral populations. The coding used by sNMF enabled the estimation of homozygote and heterozygote frequencies and avoided Hardy–Weinberg equilibrium assumptions. Although ADMIXTURE analyses were robust to small departures from Hardy–Weinberg equilibrium in human data, sNMF was more appropriate to deal with inbred lineages. For European populations of A. thaliana, the values of the cross-entropy criterion indicated better predictive results for sNMF than for ADMIXTURE. The difference between sNMF and ADMIXTURE predictions could be explained as the binomial model of ADMIXTURE is not suited to the high levels of inbreeding observed in A. thaliana populations (Atwell et al. 2010). As seen from Equation 1, an implicit assumption underlying NMF predictions is that genotypic frequencies can be formed according to instantaneous mixtures of ancestral frequencies without genetic drift. Interpretations of admixture using estimates obtained using likelihood and least-squares methods can be confounded by the existence of phylogenetic relationships among population samples (see Patterson et al. 2012 for an alternative approach) or by complex demographic scenarios such as spatial range expansion (François et al. 2010).

Comparing the relative computational performances of ADMIXTURE and sNMF was a difficult task because runtimes are dependent on several factors. These factors include the size and other characteristics of each data set, the tolerance threshold used when stopping program iterations, the use of multiprocessor algorithms, and the initial values of the Q and G matrices. For example, runtimes could be shortened by using initial values obtained after running the program on reduced data sets.

We explain the relative speed of the NMF algorithm by looking at algorithmic complexity for each program. The ANLS algorithm iterates cycles that solve linear regression equations for Q and G. The complexity of a single cycle of sNMF is of order O(KLn), where K is the number of clusters, n the number of individuals, and L the number of loci. The complexity of a single cycle of ADMIXTURE is of order O(K²Ln) (Alexander et al. 2009). Since the default tolerance threshold in this program implies that the program generally runs a small number of cycles (e.g., <40 cycles for the 78,000-SNPs Harvard HGDP panel), we observed that least-squares algorithms ran significantly faster than likelihood algorithms when analyzing large population genomic data sets with large values of K. The sNMF program can be downloaded from http://membres-timc.imag.fr/Olivier.Francois/snmf.html.