Elements Required for an Efficient NADP-Malic Enzyme Type C4 Photosynthesis^,,,

A systems model of C4 photosynthesis facilitates studies of C4 photosynthesis to quantitatively evaluate the control of different anatomical and biochemical features over light and nitrogen use efficiencies.

Abstract

C4 photosynthesis has higher light, nitrogen, and water use efficiencies than C3 photosynthesis. Although the basic anatomical, cellular, and biochemical features of C4 photosynthesis are well understood, the quantitative significance of each element of C4 photosynthesis to the high photosynthetic efficiency are not well defined. Here, we addressed this question by developing and using a systems model of C4 photosynthesis, which includes not only the Calvin-Benson cycle, starch synthesis, sucrose synthesis, C4 shuttle, and CO₂ leakage, but also photorespiration and metabolite transport between the bundle sheath cells and mesophyll cells. The model effectively simulated the CO₂ uptake rates, and the changes of metabolite concentrations under varied CO₂ and light levels. Analyses show that triose phosphate transport and CO₂ leakage can help maintain a high photosynthetic rate by balancing ATP and NADPH amounts in bundle sheath cells and mesophyll cells. Finally, we used the model to define the optimal enzyme properties and a blueprint for C4 engineering. As such, this model provides a theoretical framework for guiding C4 engineering and studying C4 photosynthesis in general.

C4 photosynthesis has a higher potential energy conversion efficiency compared with C3 photosynthesis as a result of a CO₂ concentrating mechanism that largely eliminates photorespiration (Zhu et al., 2008); similarly, C4 photosynthesis has higher water and nitrogen use efficiencies (Sage, 2004). The Food and Agriculture Organization of the United Nations predicted that 70% more basic food stuffs will be required to feed the world in 2050 and at current rates of global crop yield improvement, there will be a shortfall (Long, 2012). Introducing C4 photosynthesis into C3 crops such as rice (Oryza sativa) is therefore viewed as a strategy to achieving the needed jump in genetic yield potential (Hibberd et al., 2008; Zhu et al., 2010; von Caemmerer et al., 2012). Most C4 plants compartmentalize photosynthetic reactions into two distinct cell types, bundle sheath cells (BSCs) and mesophyll cells (MCs), each with a distinct chloroplast type. A key requirement, unique to C4 photosynthesis, is efficient transport of key metabolites between the two cell types and their distinct chloroplasts (Weber and von Caemmerer, 2010; Furbank 2011). Although the basic anatomical, cellular, and biochemical features of C4 photosynthesis have long been well defined, our current understanding of the key quantitative steps in coordination and regulation is still rather limited (Sage and Zhu, 2011). To achieve informed engineering of a C4 photosynthetic system into a C3 plant, a primary requirement is knowledge of the qualitative and quantitative importance of each component of the system to the efficiency of the process. This will be a key to setting priorities in the practical engineering of the conversion of a C3 to a C4 crop.

Historically, genetic engineering of C4 photosynthetic systems (e.g. increasing or decreasing the expression of individual enzymes) has been used to study the contribution of individual components on C4 photosynthetic efficiency. For example, the effects of decreasing the amount of Rubisco, pyruvate orthophosphate dikinase (PPDK), and NADP-malate dehydrogenase (NADP-MDH) on photosynthesis in Flaveria bidentis was studied systematically. This showed that in saturating light, the control coefficients were approximately 0.7 for Rubisco, 0.2 to 0.3 for PPDK, and zero for NADP-MDH (Furbank et al., 1997). The control coefficient for phosphoenolpyruvate carboxylase (PEPC) was estimated in Amaranthus edulis at approximately 0.35 under saturating light and ambient CO₂ levels (Bailey et al., 2000). Matsuoka et al. (2001) summarized the control coefficients of photosynthetic enzymes in different C4 plants. However, these were mainly constrained to a few enzymes under a few light and CO₂ conditions. The contribution of each enzyme to C4 photosynthetic efficiency still needs to be systematically evaluated under different light and CO₂ conditions. Given that the control coefficient of a particular enzyme in a metabolic system is not a property of the enzyme itself; rather, it depends on the levels of all enzyme activities in the whole metabolic system (Fell, 1997) and the physicochemical environment.

However, with millions of potential permutations in quantities of enzymes and transporters, plus potential pleiotropic effects, experimental manipulation of all possibilities would be impractical. Besides the influence of metabolic or enzymatic properties on C4 photosynthetic efficiency, many anatomical and cellular features related to C4 photosynthesis also influence its efficiency. Because many anatomical or cellular features can influence more than one biochemical or biophysical process simultaneously, the impact of modifying these properties to C4 photosynthesis is even more difficult to define than in C3 photosynthesis. Although a high density of plasmodesmata between the MCs and BSCs has long been recognized as a characteristic of C4 leaves, their quantitative role is poorly defined. Because the BSC wall is suberized in most C4 species, plasmodesmata represent the only path for metabolite diffusion between BSCs and MCs. However, the plasmodesmata also provides a path for leakage of CO₂ concentrated from the BSCs. Because a decrease in plasmodesmata permeability would lower metabolite diffusion but limit CO₂ leakage at the same time, the impact is not intuitive. Plasmodesmata are used here to show one of several features in which quantitative significance is nonintuitive. Others include presence of different decarboxylation pathways, which operate simultaneously to varying degrees, and metabolite transporters in the plastid envelope and plasmalemma of the two cell types.

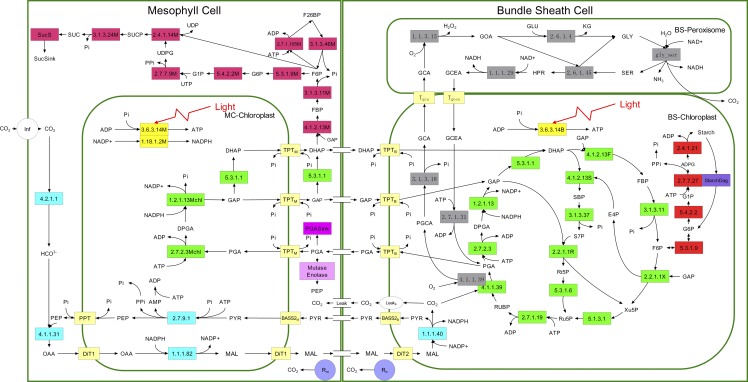
In recent years, in silico experiments based on systems modeling have emerged as an effective way to understand control properties of the C3 photosynthetic system and focus practical engineering on key targets (Fell, 1997; Poolman et al., 2000; Zhu et al., 2007, 2012). Steady-state models of C4 photosynthesis were first developed over 30 years ago (Berry and Farquhar, 1978; Collatz et al., 1992; von Caemmerer, 2000), and the metabolite transport processes of C4 photosynthesis were simply described (Hatch and Osmond, 1976). These models have been widely used to understand the physiology and ecology of C4 photosynthesis because of their simplicity and robustness. They have also been used to understand the significance of properties such as the resistance to CO₂ back-diffusion from the BSCs (von Caemmerer and Furbank, 2003). However, as a result of their lack of an explicit description of the individual reactions of the C4 photosynthetic pathway, these steady-state models cannot be used directly to study the impact of manipulating a particular gene or anatomical feature on C4 photosynthetic efficiencies from a whole systems perspective. A metabolic systems model of C4 photosynthesis, which incorporated the major metabolic reactions involved in C4 photosynthesis, was developed by Laisk and Edwards (2000), and was used to estimate the metabolic control coefficients of different enzymes. Here we extended this model and developed a comprehensive dynamic systems model of NADP-malate enzyme type (NADP-ME) C4 photosynthesis (referred to hereafter as the C4 model; Fig. 1). The NADP-ME pathway was chosen because major C4 food crops such as maize (Zea mays) and Sorghum bicolor as well as key C4 bioenergy crops Miscanthus giganteus and Saccharum officinarum, together with the model C4 plant Setaria viridis are all of this subtype. Furthermore, this pathway has been chosen as the target C4 photosynthetic pathway to be engineered into rice.

Figure 1.

The structure of the systems model of NADP-ME type C4 photosynthesis. The rectangles indicate enzymes or transporters; colors differentiate these by function (green, Calvin-Benson cycle; pale yellow, transporters; gray, photorespiratory pathway; cyan, C4 dicarboxylate cycle; red, starch and Suc synthesis; yellow: light reactions). Enzymes are denoted by their EC numbers (Tables I and II; Supplemental Table 1). R_m and R_b represent mitochondria respiration in MCs and BSCs. [See online article for color version of this figure.]

Because roles of individual steps in the process, as shown above, can be nonintuitive, it was considered necessary to expand on previous models by including all discrete steps in C4 NADP-ME carbon metabolism from CO₂ assimilation in the MC cytoplasm to carbohydrate end-product synthesis in the BSCs. Therefore, this C4 model includes all reactions of the Calvin-Benson cycle, photorespiration, starch synthesis, and Suc synthesis, as well as the C4 shuttle, CO₂ leakage, and metabolite transport processes between BSCs and MCs. The model was validated against the measured CO₂ assimilation rate (A) and metabolite levels under different light and CO₂ levels. In this study, we systematically quantified the impacts of modifying different biochemical and anatomical features of C4 photosynthesis to the efficiency of CO₂ uptake. These were used to predict the critical changes required to engineer an artificial C4 system into a C3 leaf.

RESULTS

Model Validation

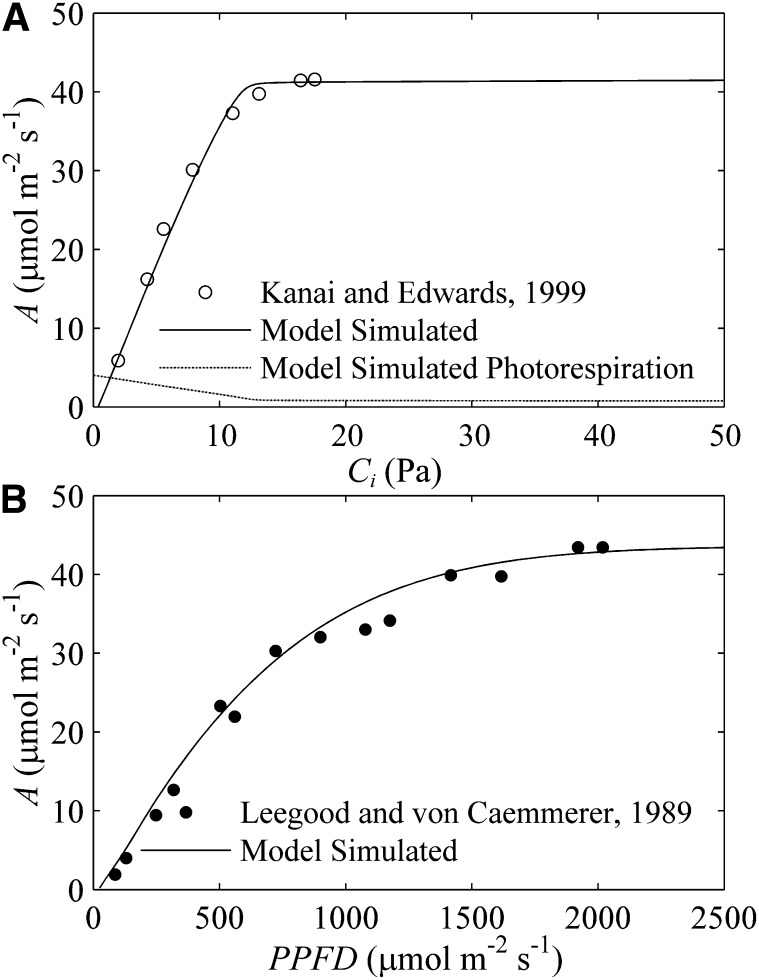
The model realistically predicted the response of the CO₂ uptake rate (A) to intercellular CO₂ concentration (C_i) and the response of A to the photosynthetic photon flux density (PPFD; Fig. 2). The predicted photorespiration rate was 0.75 μmol m⁻² s⁻¹ under ambient [CO₂] and [O₂] conditions, which is comparable with the measured value of approximately 1.6% of A in maize (Deveau and Burris, 1989). The predicted CO₂ compensation point was approximately 0.7 Pa, which is a unique feature of C4 plants (Meidner, 1962; Moss, 1962). The simulated maximum quantum yield of 0.057 mol/mol (mol CO₂ per mol photon) is also comparable with previously reported quantum yields of NADP-ME subtype plants (Ehleringer and Björkman, 1977; Monson et al., 1982; Ehleringer and Pearcy, 1983; Dai et al., 1993).

Figure 2.

Model predicted photosynthetic CO₂ uptake rate. A, The predicted photosynthetic CO₂ uptake rate (A) versus intercellular CO₂ concentration curve (C_i; black line) at a PPFD of 1,600 μmol m⁻² s⁻¹. The dotted line is the predicted photorespiratory rate. Circles are experimental data from Kanai and Edwards (1999). B, The predicted A versus PPFD curve. The black dots are experimental data from Leegood and von Caemmerer (1989).

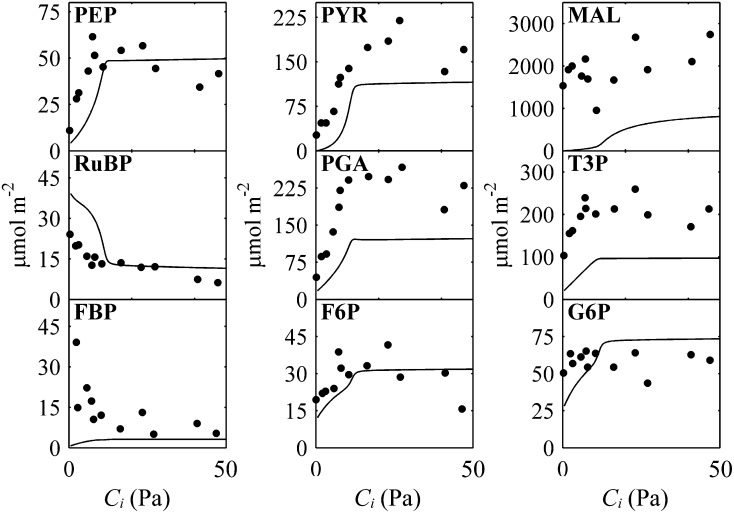
We further examined the responses of metabolite concentrations to changes in C_i (Fig. 3). Most of the predicted trends are broadly similar to experimental data (Leegood and von Caemmerer, 1989), except in the case of fructose-bisphosphate (FBP). The predicted FBP trend is contrary to experimental measurement. The predicted responses of C4-related photosynthetic intermediates to changes in PPFD are similar to experimental data (Supplemental Fig. S1). The predicted pool sizes of 3-phosphoglycerate (PGA) and triose phosphate (T3P) are about half of the measured values.

Figure 3.

Predicted changes in steady-state contents of key metabolites of photosynthetic carbon metabolism with increase in C_i. Black lines represent model predictions using and black dots are experimental data from Leegood and von Caemmerer (1989). The PPFD used in the simulation was 1,600 μmol m⁻² s⁻¹. F6P, Fructose-6-phosphate; G6P, glucose-6-phosphate; MAL, malate; PEP, phosphoenolpyruvate; PYR, pyruvate.

Significance of Different Enzymes to C4 Photosynthetic Efficiency

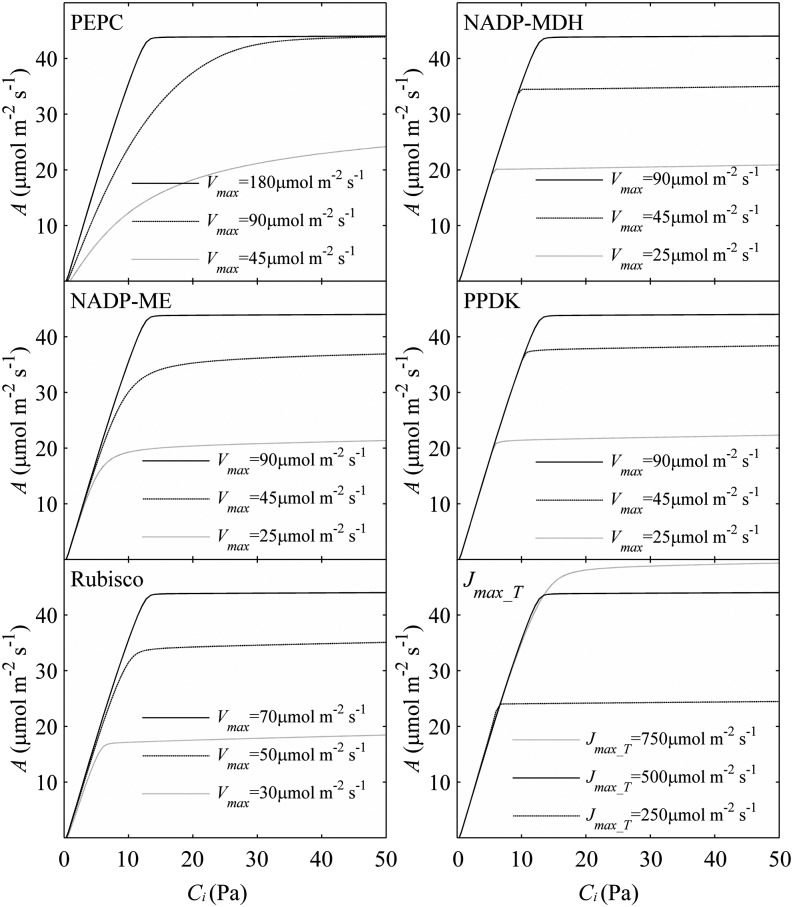
Five enzymes (PEPC, NADP-ME, PPDK, Rubisco, and MDH) have usually been regarded as exerting the greatest metabolic control over the rate of C4 photosynthesis (Furbank et al., 1997; Bailey et al., 2000; Matsuoka et al., 2001). We used the C4 model to predict the influence of manipulation of activities of these five enzymes on the A-C_i curve (Fig. 4). Of these five enzymes, only PEPC activity influenced the initial slope of the A-C_i curve; NADP-ME and Rubisco activities influenced both the convexity and maximal CO₂ uptake rate of the A-C_i curve, whereas NADP-MDH and PPDK activities affected the maximal CO₂ uptake rate of the A-C_i curve. Under a high PPFD of 2,500 μmol m⁻² s⁻¹, the maximum rate of photosynthetic electron transport (J_{max_T}) was a limiting factor for the CO₂ assimilation. J_{max_T} is defined as the total electron transport capacity that includes the maximum rate of linear electron transport in MCs (J_{max_m}) and the maximum rate of cyclic electron transport in BSCs (J_{max_b}).

Figure 4.

Model predicted A versus C_i curves under different maximal enzyme activities (V_max) and maximum electron transport rates (J_{max_T}). The PPFD was 2,500 μmol m⁻² s⁻¹.

The model was then used to calculate the flux control coefficient (CC) of each enzyme with respect to the CO₂ uptake rate (Tables I and II; Supplemental Table S1). The results suggested that under a high PPFD of 2,000 μmol m⁻² s⁻¹, J_{max_T} and Calvin-Benson cycle enzymes (e.g. Rubisco and sedoheptulose-1,7-bisphosphatase [SBPase]) had the greatest CC under an ambient C_i of 15 Pa. PEPC and mesophyll conductance (g_m) showed the greatest CC under a low C_i of 5 Pa (Tables I and II). Under a PPFD of 200 μmol m⁻² s⁻¹, PPFD and J_{max_T} had the greatest CC (Tables I and II).

Table I. Flux CCs determined from their effect on A of enzymes.

We simulated the following scenarios: high light, PPFD = 2,000 μmol m⁻² s⁻¹, C_i = 15 Pa; low light, PPFD = 200 μmol m⁻² s⁻¹, C_i = 15 Pa; and low CO₂, PPFD = 2,000 μmol m⁻² s⁻¹, C_i = 5 Pa. PGAK, Phosphoglycerate kinase; GAPDH, glyceraldehyde-3-phosphate dehydrogenase; PGAsink, PGA used for amino acid synthesis or other metabolic pathway; I, photosynthetic active radiation. The definitions of abbreviations are listed in Supplemental Data File S1.

Enzyme Abbreviation	EC No.	Vmax	Flux CC
			High Light	Low CO2	Low Light
		μmol m−2 s−1
CA	4.2.1.1	200,000	0.001	0.185a	0.000
PEPC	4.1.1.31	170	0.004	0.364a	0.000
Rubisco_CO2	4.1.1.39	65	0.254a	0.099a	0.073a
SBPase	3.1.3.37	29.18	0.030a	0.000	0.010
PRK	2.7.1.19	1,170	0.026a	0.000	0.028a
PGAK_M and GAPDH_M	2.7.2.3M and 1.2.1.13M	300	0.002	−0.123a	0.009
Rubisco_O2	4.1.1.39	7.15	−0.017	0.029a	-0.063a
PGAsink	PGA Sink	2	0.005	−0.008	0.037a
Jmax_T		500	0.600a	−0.018	0.074a
I		2,000 or 200	0.134a	−0.008	0.969a

^aFlux CCs above 0.02.

Table II. Flux CCs determined from their effect on diffusion-related parameters.

We simulated the following scenarios: high light, PPFD = 2,000 μmol m⁻² s⁻¹, C_i = 15 Pa; low light, PPFD = 200 μmol m⁻² s⁻¹, C_i = 15 Pa; and low CO₂: PPFD = 2,000 μmol m⁻² s⁻¹, C_i = 55 Pa. D_{mal_pd}, Diffusion coefficient of malate in plasmodesmata; D_{co2_pd}, diffusion coefficient of CO₂ in plasmodesmata; P_{co2_Bchl}, permeability coefficient of CO₂ in BSC chloroplast envelope; Φ, the fraction of the BSC-MC interface cross-sectional area that is permeated by plasmodesmata; L_pd, the length of plasmodesmata.

Diffusion Parameter	Value	Flux CC
		High Light	Low CO2	Low Light
gm	7 μmol m−2 s−1 Pa−1	0.002	0.495a	0.000
Dmal_pd	6.77 × 10−10 m2 s−1	0.000	0.041a	0.000
Dco2_pd	1.7 × 10−9 m2 s−1	−0.045a	−0.047a	−0.042a
Pco2_Bchl	20 μm s−1	−0.023a	−0.004	−0.020
Φ	0.03	−0.045a	−0.028	−0.040a
Lpd	400 nm	0.044a	0.028	0.040a

^aFlux CCs above 0.02.

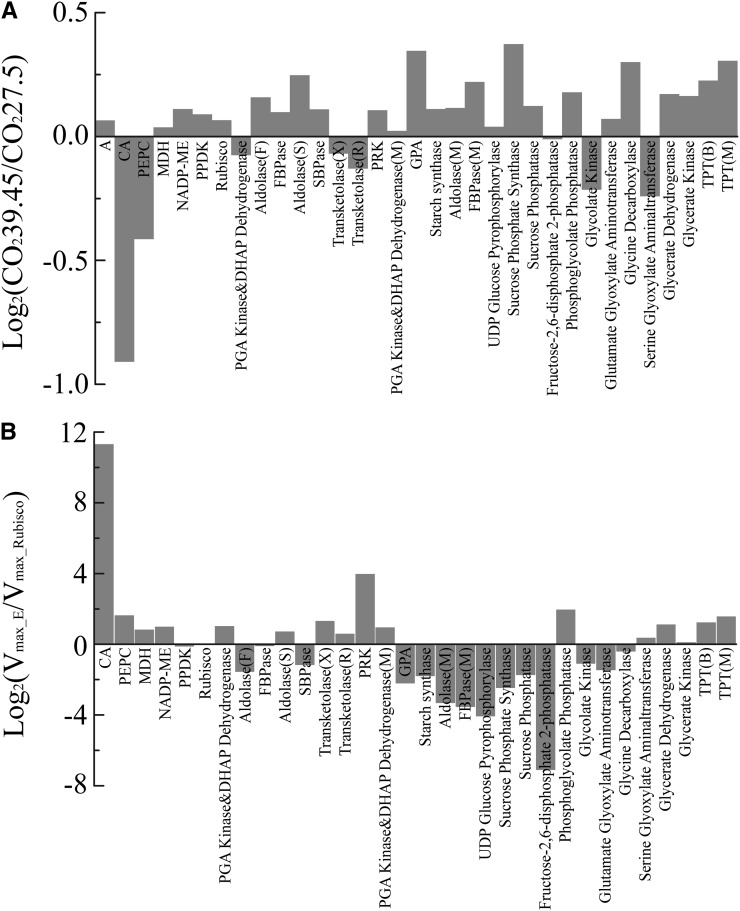
An optimization algorithm was applied to identify the optimal amounts of active enzymes required to achieve maximal A under a fixed total amount of protein nitrogen. Compared with the optimal enzyme activities under an ambient preindustrial [CO₂] of 27.5 Pa, less carbonic anhydrase (CA) and PEPC were required to gain an optimal CO₂ uptake under the current ambient [CO₂] of 39.45 Pa, whereas the optimal amounts of most other enzymes required were higher (Fig. 5A).

Figure 5.

The optimized distribution of nitrogen resources between photosynthetic enzymes for maximize light-saturated A. A, The ratio of optimal enzyme concentrations identified by the evolutionary algorithm required to reoptimize the system for a preindustrial atmospheric CO₂ concentration (C_a) of 27.5 Pa, relative to today’s C_a of 39.45 Pa. In this simulation, C_i = 0.4 C_a was assumed (Leakey et al., 2004). B, The enzyme and transporter activities relative to Rubisco activity that optimization predicts for ambient CO₂ concentration (C_a = 39.45 Pa). DHAP, Dihydroxyacetone phosphate; FBPase, fructose-bisphosphate. The capital letters in brackets are used to distinguish reactions that catalyzed by the same enzyme between different product or location. F, FBP; S, SBP; X, xylulose 5-phosphate; R, ribose 5-phosphate; M, mesophyll cell; B, bundle sheath cell.

Given that Rubisco is a critical enzyme for CO₂ fixation in the Calvin-Benson cycle and a major goal of C4 engineering is to repress Rubisco’s ribulose 1,5-bisphosphate (RuBP) oxygenation activity, we optimized the ratios of activities of different enzymes to that of Rubisco for the current atmospheric CO₂ condition (Fig. 5B). Compared with Rubisco activity, the optimal activities of CA and the major enzymes involved in the C4 shuttle (i.e. PEPC, MDH, and NADP-ME) were higher for higher A (Fig. 5B). In addition, more triose phosphate transporter (TPT), which transports PGA and T3P across the chloroplast envelope, would be needed (Fig. 5B).

Many enzymes functioning in C4 photosynthesis, which play important metabolic roles in C3 plants (Aubry et al., 2011), have undergone specific changes in their amino acid sequence and correspondingly in their catalytic properties during their cooption into C4 photosynthesis; that is, the homologs used in C4 photosynthesis differ from their C3 homologs (Engelmann et al., 2003; Aubry et al., 2011; Chastain et al., 2011; Maier et al., 2011). Thus far, it is unclear how much difference introducing the C4 homologs versus using the endogenous C3 homologs might have on the photosynthetic CO₂ uptake rate and nitrogen use efficiency during C4 engineering. We evaluated the effect of C4 or C3 homologs of C4 photosynthetic enzymes on both the photosynthetic CO₂ uptake rate and nitrogen cost. The nitrogen cost ratio was defined as the ratio of nitrogen required for synthesis of a C3 homolog of enzyme to that needed for synthesis of a C4 homolog. The nitrogen cost was calculated based on catalytic constant (k_cat) and M_r (Table III; Supplemental Table S2) of both C3 and C4 homologs. Compared with the C3 homolog, the C4 homolog of PEPC has a higher affinity to HCO₃⁻, whereas the C4 homologs of NADP-MDH, PPDK, NADP-ME, and Rubisco all have lower affinities to their substrate and higher turnover numbers (Table III; Supplemental Table S2). Simulation results indicated that a lower substrate binding affinity did not decrease reaction rates (Table III), possibly because the lower affinity was compensated by increased substrate concentrations. On the other hand, higher k_cat values of these enzymes are indeed beneficial through decreasing the nitrogen demand for a given V_max.

Table III. Comparison of the impacts of using different homologs of C4-related enzymes on A and nitrogen cost.

Kinetic parameters for C3 and C4 homologs of the enzymes involved in C4 photosynthesis were used as inputs to the model to predict CO₂ uptake rates under low and high CO₂ conditions. The CO₂ uptake ratio is the ratio of CO₂ uptake rates predicted using kinetic parameters from a C3 homolog to that using a C4 homolog. Nitrogen cost for the synthesis of an enzyme was calculated based on the k_cat, M_r, and V_max of the enzyme. The nitrogen cost ratio was defined as the ratio of nitrogen required for synthesis of a C3 homolog to that for a C4 homolog.

Comparison (C3/C4)	PEPC	NADP-MDH	PPDK	NADP-ME	Rubisco
CO2 uptake ratio
Ci = 5 Pa	0.35	1.00	1.00	1.00	1.03
Ci = 15 Pa	0.51	1.00	1.00	1.00	1.03
Nitrogen cost ratio	1.10	5.14	1.20	1.39	1.24

Predicted Changes of Carbon Isotope ¹³CO₂ Discrimination Signals

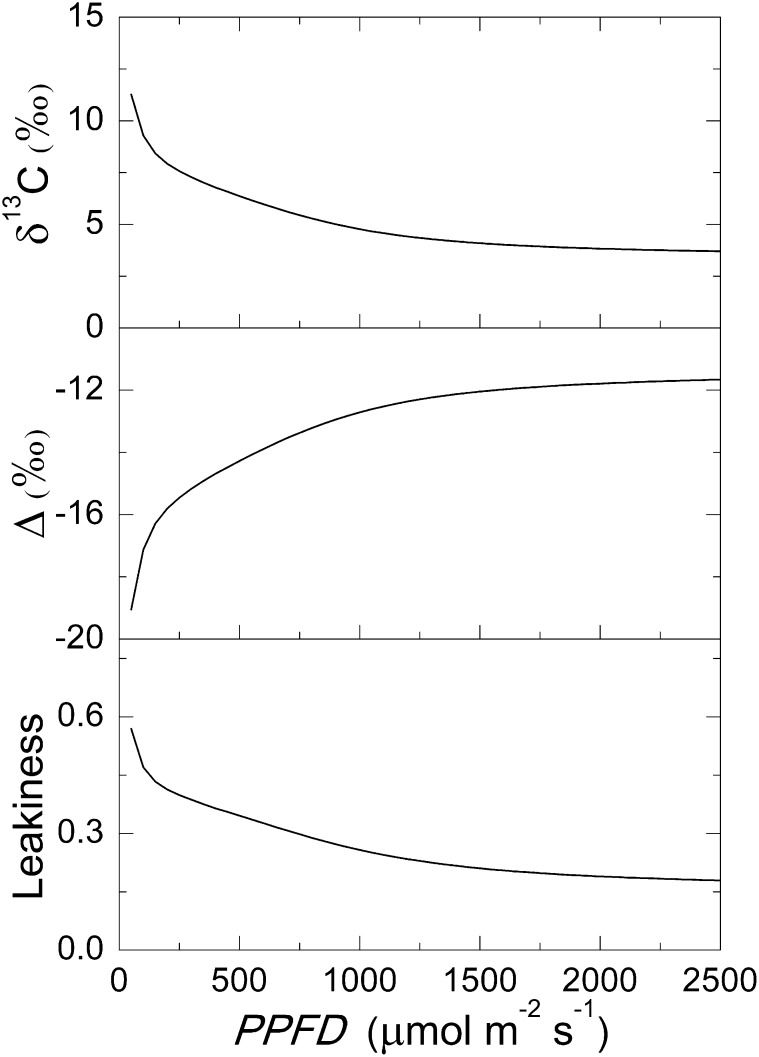
We compared the predicted carbon isotope composition (δ¹³C) and discrimination (Δ) with reported values. C3 and C4 plants have distinct Δ and δ¹³C values; thus, both are commonly used to distinguish these two photosynthetic types. Typical δ¹³C for C3 species are between −30‰ and −22‰ (Troughton et al., 1974), but are approximately −12‰ for C4 plants (Cousins et al., 2006). Typically, a C3 plant has a Δ value of approximately −20‰, and a C4 plant has a Δ value around 4‰ (Farquhar et al., 1989). Our model predicted a C4 δ¹³C value of 12.4‰ and a Δ value of 4.1‰ under a PPFD of 1,500 μmol m⁻² s⁻¹ (Fig. 6). Interestingly, the model predicted decreased Δ, and increased δ¹³C together with concurrent decrease in CO₂ with increasing light intensity (Fig. 6).

Figure 6.

Predicted carbon isotope discrimination (Δ; A), composition (δ¹³C; B), and CO₂ leakiness (C) versus PPFD. C_i was 15 Pa.

The Influence of Intracellular and Intercellular Metabolite Transport Processes on C4 Photosynthetic Efficiency

Compared with C3 photosynthesis, C4 photosynthesis requires extensive metabolite transport between different cell types and organelles. Properties of the metabolite transport processes and CO₂ diffusion can influence A. Our model assumes that metabolite transport through chloroplast envelopes in both MCs or BSCs follow typical Michaelis-Menten kinetics. Metabolite movements between BSCs and MCs are assumed to be a simple diffusion process through plasmodesmata, as previously suggested by Stitt and Heldt (1985b). In this model, CO₂ transport between the two cell types and across the chloroplast envelope were both modeled as simple first-order diffusion processes.

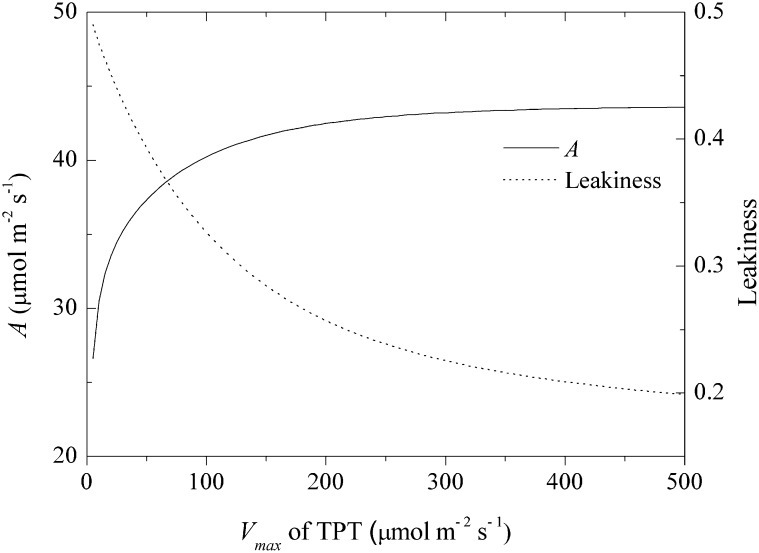
Figure 7 demonstrates the effect of variation in the activity of the TPT, which transports PGA and T3P across the chloroplast envelope, on A. The simulated results indicated that a high TPT rate is required to obtain a high CO₂ assimilation rate and to decrease CO₂ leakage (Fig. 7).

Figure 7.

Effect of TPT rate on A and CO₂ leakiness. This simulation assumes that TPTs in MCs and BSCs have the same maximal rate at a PPFD of 2,000 μmol m⁻² s⁻¹and a C_i of 15 Pa.

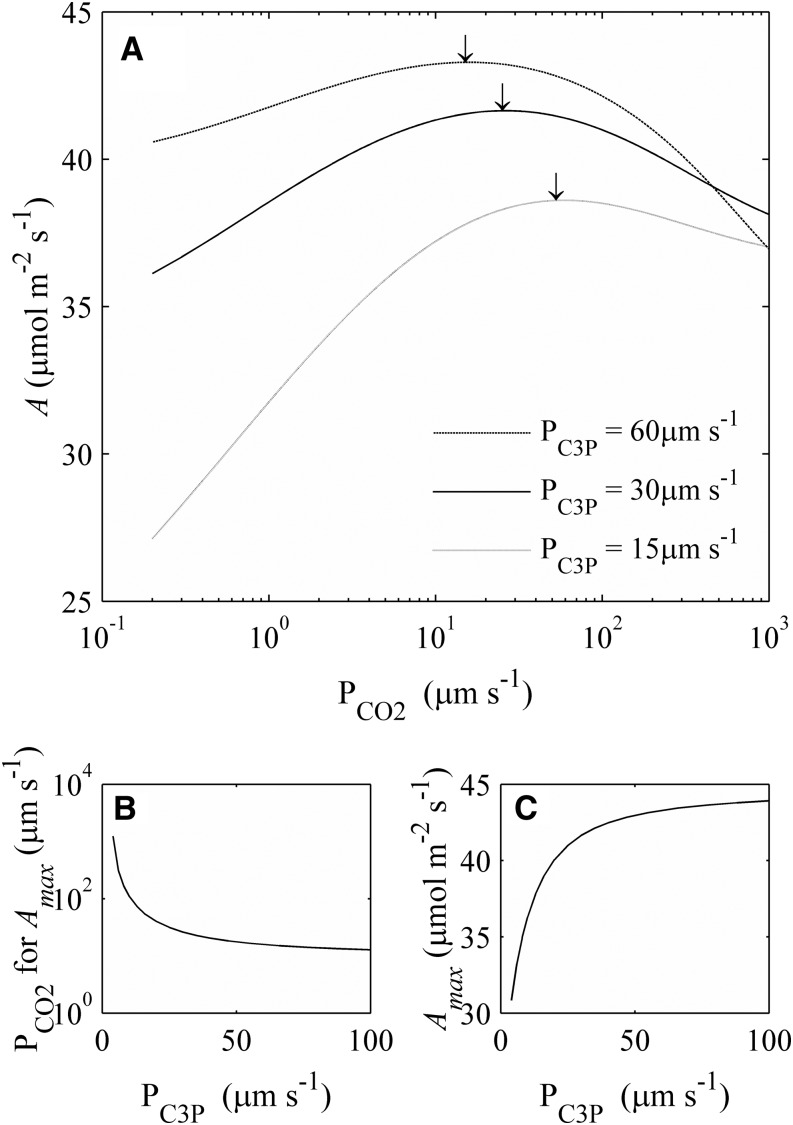
In maize, there is a large concentration difference of many metabolites, such as PGA, T3P, and malate, between BSCs and MCs (Leegood, 1985; Stitt and Heldt, 1985a, 1985b), which indicates that metabolite transport through plasmodesmata is likely a limiting factor of CO₂ assimilation. Here we used the C4 model to systematically examine how different factors related to metabolite transport influence A. First, the permeability to each metabolite was varied to determine its influence on A. As expected, increasing the permeabilities to malate and pyruvate increased A (Supplemental Fig. S2). In the simulation, the same permeability was assumed for both T3P and PGA (C3P [compounds containing three carbons and a phosphate group]), because they have the same diffusion properties (Sowiński et al., 2008). At a given permeability to C3P transport, increasing the permeability of plasmodesmata to CO₂ first increases and then decreases A (Fig. 8A). For any given C3P permeability, there is an optimal permeability to CO₂ that achieves the maximum A (Fig. 8, A and C). Increased C3P permeability resulted in a higher light-saturated A (A_max; Fig. 8B). Furthermore, a higher optimal CO₂ permeability is predicted for A_max under a lower C3P permeability (Fig. 8C).

Figure 8.

The predicted influence of the permeability to C3P (PGA and T3P) and CO₂ between BSCs and MCs on A. A, The permeability of CO₂ and C3P across the BSC-MC interface affects the CO₂ uptake rate. Black arrows indicate the maximum CO₂ uptake rate (A_max). B, The permeability of CO₂ needs to be coordinated with the permeability of C3P to obtain A_max. C, The A_max increases with an increase in the permeability of C3P between the bundle sheath and mesophyll cell. PPFD used in the simulation was 2,000 μmol m⁻² s⁻¹, and C_i was 15 Pa.

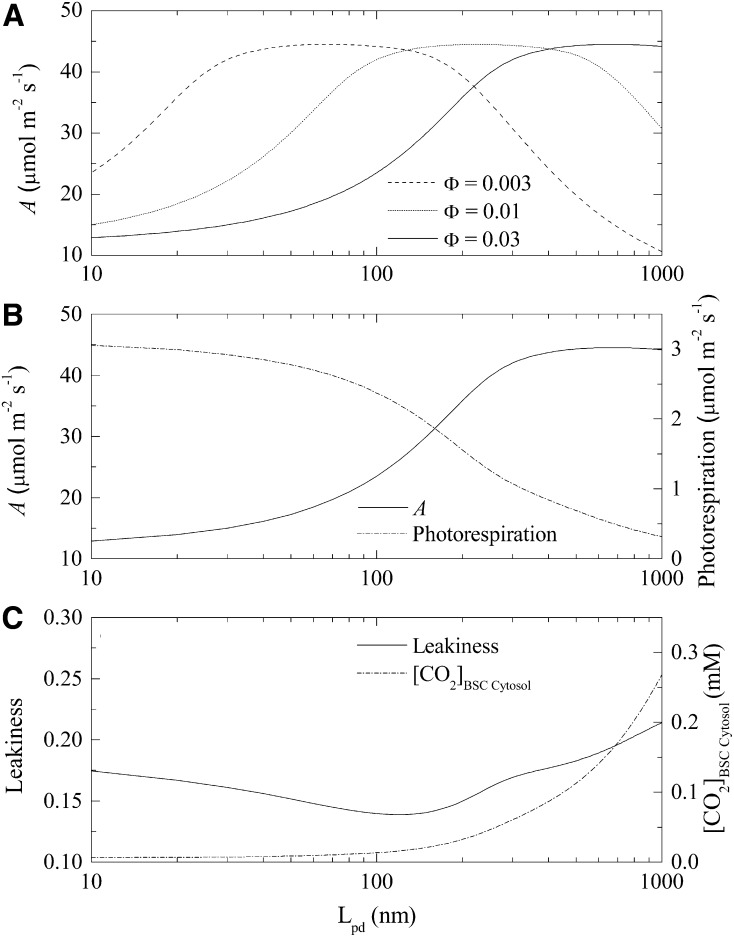
Diffusion of metabolites across the cell walls at the BSC-MC interface depends on the length and quantity of plasmodesmata and the metabolite diffusion coefficient. Based on these principles, impacts of varying the properties of the plasmodesmata on A were explored. The simulated impact of changing the surface fraction of plasmodesmata (Φ) and BSC-MC interface cell wall thickness (L_pd) on A is shown in Figure 9A. At any given Φ, increasing L_pd first increases and then decreases A (Fig. 9A). The optimal L_pd for maximal A is as Φ is increased (Fig. 9A). At Φ equal to 0.03, increased L_pd lowered the rate of photorespiration (Fig. 9B) as a result of increased [CO₂] in the BSCs (Fig. 9C), which subsequently increased A (Fig. 9B). The increased CO₂ concentration also led to an enhanced CO₂ leakage (Fig. 9C). A was maximal at an L_pd between 500 nm and 800 nm (Fig. 9B). CO₂ leakiness reached a minimum at an L_pd value of approximately 150 nm (Fig. 9C).

Figure 9.

Effect of plasmodesmata properties on A. A, Predicted effect of plasmodesmata length (L_pd) on photosynthetic CO₂ uptake rates at different surface fractions of plasmodesmata in the interface (Φ). B, Plasmodesmata length influences the CO₂ uptake rate and photorespiration rate (Φ = 0.03). C, Plasmodesmata length influences the CO₂ concentration in BSC cytosol and CO₂ leakiness from BSC to MC (Φ = 0.03). PPFD used in the simulation was 2,000 μmol m⁻² s⁻¹, and C_i was 15 Pa.

DISCUSSION

This section summarizes the novelties of this model compared with earlier models. Then, the significance of different biochemical and anatomical features on C4 photosynthetic efficiency, as revealed by the model, are then discussed. Finally, the application of the model in guiding selection of components process for engineering C4 photosynthesis into C3 crops is examined.

Novelty and Capacity of This C4 Photosynthesis Model

The large increase in, and wider availability of, computational power over the past decade provides support for more complex kinetic models than available when the previous model of C4 photosynthesis by Laisk and Edwards (2000) was completed. As a result, this model of C4 photosynthesis incorporates many new features and reactions to provide a more complete description of the C4 photosynthetic process combined with Kranz leaf anatomy. This model not only includes more detailed and updated description of the BSC and MC metabolism (e.g. incorporation of the Calvin-Benson cycle, starch, Suc, mitochondria respiration, and photorespiration in a cell-specific manner), but also incorporates detailed diffusion of metabolites between these two cell types. For example, Suc synthesis is assumed to occur in the cytosol of MCs according to experimental data (Lunn and Furbank 1997; Furbank et al., 1985). The metabolite transport between BSCs and MCs was described as a diffusional process through plasmodesmata, and the metabolite transport across chloroplast envelope was assumed to follow Michaelis-Menten kinetics according to Stitt and Heldt (1985b) and Weber and von Caemmerer (2010). Incorporation of the effects of different plasmodesmata properties on diffusion coefficients enables the model to evaluate the implications of changing these anatomical features on photosynthetic efficiency. We also assumed that starch synthesis and breakdown occur at the same time (Stitt and Heldt, 1981). Finally, the electron transfer rate directly linked to ATP and NADPH synthesis. This is in contrast with the work of Laisk and Edwards (2000), in which the ATP production rate was determined by the NADPH production rate via NADP-ME in BSCs.

This C4 model accurately predicted the experimentally measured A under different [CO₂] and PPFD (Figs. 1 and 2). The model predicted a photorespiratory rate, a CO₂ compensation point, and a maximum quantum yield that are all comparable with previously measured values in C4 plants (Meidner, 1962; Moss, 1962; Ehleringer and Björkman, 1977; Monson et al., 1982; Ehleringer and Pearcy, 1983; Deveau and Burris, 1989; Dai et al., 1993).

Most of the predicted trends of metabolite concentrations to variation in [CO₂] and PPFD were similar to experimental observations (Leegood and von Caemmerer 1989; Fig. 3; Supplemental Fig. S1), except for [FBP]. The discrepancy between modeled and experimentally observed responses of [FBP] to variations in [CO₂] may have two causes. First, Fru-bisP plays a role not only in the Calvin-Benson cycle and Suc synthesis, but also in glycolysis and the pentose phosphate pathway, which are currently not included in this model. Slowly labeled FBP in a ¹³CO₂ labeling experiment in Arabidopsis (Arabidopsis thaliana) indicated that a large part of the FBP pool is not directly involved in Calvin-Benson cycle (Szecowka et al., 2013). Second, the regulatory mechanisms controlling the activity of the enzymes of photosynthetic carbon metabolism were not described in the model. Additional features incorporated into this model may be able to further improve the model’s predictive ability. A low rate of starch breakdown can replenish fructose-6-phosphate in BSCs, and this has enabled the model to correctly predict the increasing response of the RuBP pool with decreasing [CO₂] (Fig. 3) as observed in experiments (Usuda, 1987; Leegood and von Caemmerer, 1989). This simulated RuBP response is in contrast with previous model simulation in which low ambient [CO₂], RuBP concentration decreased when ambient [CO₂] decreased (Laisk and Edwards, 2000). The predicted pool sizes of PGA and T3P were lower than experimental data, but they can be improved by increasing total phosphate concentration in bundle sheath plastid and increasing Michaelis-Menten constants (K_m) for PGA and T3P in related enzymes is another way to specifically modify PGA and T3Ps contents (Supplemental Figs. S3–S5). Similarly, the pool size of FBP also can be increased by increasing the K_m for FBP in cytosolic fructose-bisphosphatase (Supplemental Fig. S6). More research is needed to determine whether one or combinations of these possibilities or others might be contributed to the predicted lower than measured metabolite levels.

The model predicted a δ¹³C and a Δ value that are within the range of values for a typical C4 plant (Fig. 6; Farquhar et al., 1989). The model further predicted that carbon isotope discrimination and CO₂ leakiness were reduced with increasing PPFD (Fig. 6), which is consistent with experimental observations (Farquhar et al., 1989; Henderson et al., 1992; Cousins et al., 2006; Kromdijk et al., 2008; Tazoe et al., 2008). These results demonstrate that the C4 model can realistically simulate the experimentally observed carbon isotope discrimination of C4 species.

Even with all the above-mentioned features and capacity, this C4 model should be regarded as a living model (i.e. one designed to support continual improvement). First, our model assumes that two-thirds of the light energy is absorbed by MCs and that one-third is absorbed by BSCs. However, reliable estimates of this partitioning are not yet available. Second, though we conducted a comprehensive literature search, kinetic parameters for a number of the enzymes of the C4 system had to be taken from the literature for C3 plants. Parameters that are currently unavailable for C4 plants include kinetic parameters describing transporters, concentrations of components of the electron transfer chain in both BSCs and MCs, and the diffusion properties of the membranes, cell walls, and plasmodesmata for different metabolites. Even the exact diffusion properties of the cytosol are not well characterized to date. Possibly as a reflection of all these uncertainties, our predicted pool sizes and BSC/MC concentration gradients of T3P and PGA (Fig. 3; Supplemental Fig. S1) are lower than those reported in literature (Stitt and Heldt, 1985a, 1985b; Leegood and von Caemmerer, 1989). More accurate measurements of kinetic parameters, metabolite concentrations (especially metabolites concentrations in different compartments of both BSCs and MCs), and metabolite fluxes under varied [CO₂] and PPFD will undoubtedly help improve the C4 systems model. Fortunately, various techniques in metabolomics (Fiehn, 2002; Sumner et al., 2003; Weckwerth, 2003; Kopka et al., 2005; Oksman-Caldentey and Saito, 2005) and fluxomics (Fernie et al., 2005; Wiechert et al., 2007; Szecowka et al., 2013) are rapidly emerging, which can help fill this data demand.

Despite these caveats, the model is shown to predict A-PPFD, A-C_i, with quantitative and qualitative reality, as well as responses of metabolite concentrations to varying PPFD and C_i levels. Thus, it is already well suited to serve as a platform to study the properties of C4 photosynthesis and to identify key elements required for efficient NADP-ME C4 photosynthesis.

Control Properties of Key Enzymes for C4 Photosynthetic Efficiency

The biochemical models of C4 photosynthesis described by Collatz et al. (1992) and von Caemmerer (2000) predict the C4 photosynthetic rate assuming that the A is limited by three enzymes (i.e. Rubisco, PEPC, and PPDK), at steady state. The wide use of these models in predicting C4 photosynthetic rates warrants a systematic test of these assumptions. Here we tested these assumptions by predicting the impacts of varying activities of these enzymes on A-C_i curves (Fig. 4). Our analysis confirmed that PEPC and Rubisco are two major enzymes influencing the A-C_i response curves. Consistent with the steady-state models, our simulations suggested that PEPC controls the initial slope of the A-C_i response curve and Rubisco controls the plateau of the A-C_i response curve (Collatz et al., 1992; von Caemmerer, 2000).

In addition to the effect of PEPC and Rubisco, our results suggested that PPDK, NADP-ME, and NADP-MDH also affect the A-C_i response (Fig. 4). NADP-ME influenced both the convexity and maximal CO₂ uptake rate of the A-C_i curve, which is consistent with previous experimental observations (Pengelly et al., 2012).

Besides enzymes directly involved in the C4 shuttle, some Calvin-Benson cycle enzymes, e.g. SBPase and phosphoribulokinase (PRK), showed certain CCs over A under certain conditions, such as under high light (Tables I and II), suggesting that these enzymes may be targets to engineer for improving C4 photosynthesis. Interestingly, many of these identified enzymes were experimentally shown to influence C3 photosynthetic efficiency, such as SBPase (Lefebvre et al., 2005; Tamoi et al., 2006), PRK (Paul et al., 2000), and glyceraldehyde-3-phosphate dehydrogenase (Price et al., 1995); therefore, these predicted impacts on C4 photosynthetic efficiency warrant future transgenic testing. Of particular significant here is the observation that in C3 crops, plants transgenically overexpressing SBPase showed a greater increase in A at elevated [CO₂] than in ambient [CO₂] (Rosenthal et al., 2011). This suggests that increased SBPase may be of particular value in the elevated [CO₂] environment of the BSCs of C4 crops.

One caveat here is that the predicted flux CC of an enzyme depends on the default V_max of all enzymes in the model and also the percentage of decrease of the enzyme under study. For example, in this article, we presented the CC calculated by the difference in the A when V_max was decreased and increased by 1% only. In this case, our predicted CC for PPDK was zero, suggesting that in this system with default V_max values for all enzymes, PPDK confers no control over the photosynthetic rate. However, if the V_max of PPDK decreased by 50%, we predicted a decrease of A of approximately 13% (Fig. 4), which is consistent with the reported decrease of A (Furbank et al., 1997).

To address the issue of uncertainties in the V_max involved in the model, we conducted a systematic sensitivity analysis. Specifically, V_max of each enzyme was decreased by 20% to calculate CC individually (Supplemental Table S2). To gain a precise estimate of the CC for an enzyme in a species grown under a particular environment, accurate measurements of the V_max of the involved enzymes in the system are essential. Another potential reason that underlies the difference in the predicted CC and the measured CC is the pleiotropic effect of manipulation a particular gene on other metabolic processes. The CC predicted from this model therefore only represents the control coefficient of the particular enzyme assuming that properties of all other enzymes are maintained as constant.

An evolutionary algorithm was applied to the system to determine the optimal investment of nitrogen between the proteins of the pathways and transporters, as depicted in Figure 1, to maximize the light-saturated rate of CO₂ uptake at preindustrial and current atmospheric [CO₂]. This optimization predicted that in order to maximize A under elevated [CO₂], nitrogen needs to be reallocated from PEPC and CA to enzymes in the Calvin-Benson cycle, starch, and Suc synthesis (Fig. 5A). Previous optimization on a C3 photosynthetic metabolism model suggested that Rubisco activity should be reduced under elevated [CO₂], but our simulated results show that the optimized Rubisco activity increased under elevated [CO₂] in C4 photosynthesis (Fig. 5A). Rubisco is the first enzyme to fix CO₂ in C3 photosynthesis; by contrast, in C4 photosynthesis, CO₂ is first fixed by PEPC with the help of CA. If environmental [CO₂] increases, the CC of the enzyme that first fixes CO₂ will decrease. This explains why in the optimization process, nitrogen moved away from Rubisco in C3 photosynthesis, and nitrogen moved away from PEPC and CA to other enzymes including Rubisco in C4 photosynthesis.

Figure 5B shows optimal ratios of different enzyme activities to Rubisco activity under ambient CO₂ condition, which provided a blueprint to guide C4 metabolic engineering. Although the predicted optimal combinations of enzymes can result in an efficient C4 photosynthetic system, the optimization results provided here might not necessarily represent the unique optimal combination of enzymes for the highest C4 photosynthesis efficiency (i.e. a local maximum might be identified by our optimization algorithm).

The Role of TPT in C4 Photosynthetic Efficiency

The assimilation of one CO₂ in the Calvin-Benson cycle needs two NADPH for PGA reduction, whereas only one NADPH is produced when one CO₂ is released by NADP-ME catalyzed malate decarboxylation in BSCs (Fig. 1). Because PSII activity in BSC chloroplasts is negligible in many NADP-ME type C4 plants (e.g. maize; Majeran et al., 2008), the MCs have to provide additional NADPH required for PGA reduction. C4 plants achieve this by transporting a portion of PGA from the BSC chloroplasts to the MC chloroplasts, where it is reduced to T3P. Most of T3P is then transported back to the BSC chloroplasts to complete the Calvin-Benson cycle (Hatch, 1987; Weber and von Caemmerer, 2010). The transport of PGA and T3P across MC and BSC chloroplast envelopes is facilitated by TPT (Weber and von Caemmerer, 2010). Therefore, TPT is critical to balance NADPH production and utilization between BSCs and MCs. The model suggests that a high TPT capacity is required to obtain a high A and to decrease the CO₂ leakage (Fig. 7). Indeed proteomic studies indicate that TPTs were highly abundant in C4 plants (Bräutigam et al., 2008; Majeran et al., 2010), which supports the prediction here that TPTs in both BSCs and MCs are critical for effective C4 photosynthesis. It follows that when the goal of converting a C3 plant to a C4 is to achieve increased A, then these high levels of TPT in both plastid types will also be key.

The Role of CO₂ Leakage to C4 Photosynthetic Rate

CO₂ leakage, or back-diffusion of CO₂ from the BSCs to MCs, is usually considered detrimental to the C4 photosynthetic rate. Because the C4 dicarboxylate cycle needs ATP for phosphoenolpyruvate regeneration, more leakage of CO₂ out of the BSC increases the ATP requirement for fixing one CO₂. The rate of CO₂ leakage from the BSCs depends on the permeability of the BSC-MC interface to CO₂ and the gradient of [CO₂] between these two cell types, which in turn is determined by the relative biochemical capacities of the C4 and C3 cycles (von Caemmerer and Furbank 1999; von Caemmerer, 2000). Across a range of C4 species, leakiness has been estimated to vary between 0.08 and 0.29 (Hatch, et al., 1995; von Caemmerer and Furbank, 2003). A low CO₂ permeability across the BSC-MC interface is usually regarded as an essential feature in gaining a high C4 A (von Caemmerer and Furbank, 2003). Simulations in this study suggested that under high PPFD when the capacity of C3P transport is limited, leakage can, counterintuitively, be beneficial for the C4 photosynthetic rate (Fig. 8, A and C). This is because under high light, when ATP supply is high, NADP-ME catalyzes generation of CO₂ and NADPH from malate in BSC. The leakage of CO₂ from BSC will increases the NADPH-CO₂ ratio of BSCs, which can alleviate the lack of NADPH in BSCs and thus help decrease demand of PGA transporters and TPTs between BSCs and MCs. However, in some C4 plants (e.g. maize), Asp was also used as a C4 acid, which transferred from MCs to BSCs (Saccardy et al., 1996; Furbank, 2011). The usage of Asp will also change the NADPH-CO₂ ratio in BSCs because Asp does not bring NADPH from MCs to BSCs.

The Effects of Varying Plasmodesmata Length on C4 Photosynthetic Efficiency

According to Equation 12, the rate of metabolite movement through the plasmodesmata is determined by the length of the pathway, the BSC-MC interface per unit leaf area, the surface fraction of plasmodesmata, and the diffusion coefficient for the given metabolite. The diffusion coefficient is determined not only by the physical properties of the molecule, but also by those of the medium through which the metabolite diffuses. Our simulation results suggested complex impacts of altering the properties of plasmodesmata on A. Figure 9A shows that both the surface fraction of plasmodesmata (Φ) and plasmodesmata length (L_pd, assuming it is equal to cell wall thickness) can affect A. L_pd also influences leakiness and photorespiratory flux (Fig. 9, B and C). Taking L_pd as an example to illustrate this complex relationship, a longer diffusion path through the plasmodesmata helps maintain a high [CO₂] in BSCs and decrease photorespiration (Fig. 9B). The high CO₂ gradient between BSCs and MCs, however, can increase CO₂ leakage (Fig. 9C). A thickened cell wall will also inevitably decrease the rate of metabolite transport between the two cell types, which will correspondingly decrease A (Supplemental Fig. S7). Therefore, it is not intuitive to predict the responses of A to changes in the density or length of these plasmodesmata. Simulations suggested that an optimal cell wall thickness to minimize leakiness is around 150 nm (Fig. 9C). To reduce photorespiratory flux, a thicker cell wall is always better (Fig. 9B). However, to maximize A, an optimal cell wall thickness is around 500 nm, at Φ was 0.03 (Fig. 9B). When the BSC/MC interface has little resistance (Fig. 9C), the CO₂ concentration in BSC cytosol is close to C_i. The BSC chloroplast membrane is an important barrier for CO₂ leakage, helping to keep CO₂ around Rubisco and maintain a part of the C4 photosynthesis rate (Fig. 9B).

The above predictions were made assuming that metabolites diffuse through plasmodesmata with defined permeability constants. However, detailed biophysical properties of these plasmodesmata are still far from being well understood. For example, a high density of plasmodesmata at the MC-BSC interface has been found in C4 species (Evert et al., 1977; Botha, 1992) and large concentration gradients between two cell types has been observed (Leegood, 1985; Stitt and Heldt, 1985a, 1985b). This indicates that a rapid diffusion between BSCs and MCs can potentially be supported. However, a recent theoretical analysis based on plasmodesmatal structure and its diffusional properties showed that the required metabolite gradient between BSCs and MCs to support observed rate of C4 photosynthetic CO₂ uptake should be at least three orders of magnitude higher than experimentally measured (Sowiński et al., 2008). Recent and historical measurement indicated that unidirectional transport of fluorescent protein through plasmodesmata exists in unique surfaces (Arisz, 1969; Christensen et al., 2009), which suggested that active transport or accelerated diffusion of small molecules of certain size may occur through plasmodesmata. However, the underlying mechanism is still unclear and no kinetic studies on this phenomenon are available. Understanding the movement of metabolites through plasmodesmata will be key to developing the engineering framework for conversion of C3 to C4 crops.

Choice of Enzymes with Kinetic Properties Suitable for C4 Engineering

C4 photosynthesis differs from C3 photosynthesis not only in the required leaf anatomical structure, cellular biology, and metabolism (Hatch, 1987), but also in the kinetic properties of specific enzymes. Although it is usually considered that C4 engineering requires expression of the C4 homologs of the involved enzymes into C3 systems, this has not been quantitatively examined. The C4 homolog of PEPC in the mesophyll cytoplasm has a higher affinity for HCO₃⁻ than its C3 and heterotrophic counterpart, whereas the C4 homologs of NADP-MDH, PPDK, NADP-ME, and Rubisco all have lower affinities to their substrates but higher k_cat (Supplemental Table S2). Are all of these changes needed to build an effective C4 leaf? The model developed here was used to systematically evaluate the impacts on A of using these alternative homologs of these enzymes. Simulation results showed that for NADP-ME, PPDK, NADP-MDH, and Rubisco, the lower substrate binding affinities do not decrease A under both current and even low CO₂ concentrations (Table III). This is because the substrate concentrations are sufficiently high to eliminate the potential negative effects of low enzyme affinity on their reaction rates. It is worth noting that the predicted results depend on the V_max values of used enzymes. When V_max is too high, further modifying their kinetic parameters will not affect CO₂ uptake rates and result in a near-zero flux in CCs (Tables I and II).

However, the lower k_cat of the C3 homologs of these enzymes increases the required nitrogen input for achieving a given V_max (Table III). For example, to achieve the same V_max, only 20% of the protein nitrogen is required when the C4 homolog of NADP-MDH is used (Table III). Similarly, there is substantial nitrogen saving if the C4 homolog of Rubisco is used for C4 engineering. Therefore, the analysis suggested that although all enzymes required to establish the C4 photosynthetic pathway exist in C3 plants (Aubry et al., 2011), kinetic properties of the C4 homologs would provide major benefits in resource use efficiency replacing the C3 Rubisco in BSCs. However, this would only apply if [CO₂] can be elevated in the BSCs to the level of C4 crops such as maize. If the CO₂ concentration around Rubisco in C4 rice is not as high as the typical C4 plant, the C4 homolog of Rubisco may not be appropriate because of the lower specificity compared with that of C3 plants.

Elements and Steps Needed to Engineer C4 Rice with High Photosynthetic Efficiency

A number of earlier studies explored the major features (Hatch, 1987; Leegood, 2002; Kajala et al., 2011) required for an NADP-ME type C4 photosynthesis. In this study, through quantitative studies, we showed a number of features that are critical for gaining efficient NADP-ME type C4 photosynthesis. These mainly include a proper combination of cell wall thickness and plasmodesmata density to balance CO₂ leakage and metabolite transport and the choice of C4 homologs of the key enzymes, which are needed to improve nitrogen use efficiency when aiming to gain the sustainability benefits of C4 photosynthesis in converting a C3 crop.

CONCLUSION

This article presents a new systems model of C4 photosynthesis, which can effectively simulate the responses of CO₂ uptake rates, metabolite concentrations, and isotope discrimination signals. The control properties of different enzymes on C4 photosynthetic efficiency were systematically characterized using this model. We further used this model to demonstrate the following: (1) TPTs are critical elements for an efficient NADP-ME type C4 photosynthesis, (2) CO₂ leakage can also help balance ATP and NADPH amounts in BSCs and MCs, (3) the plasmodesmata density and cell wall thickness need to be considered simultaneously to improve the CO₂ uptake rate, and (4) C4 versions of the enzymes used in C4 engineering can dramatically increase nitrogen use efficiency. Based on these results, we proposed required elements and procedures to engineer a NADP-ME type C4 photosynthetic pathway into a C3 plant. In summary, this C4 model be used cannot only as a platform to study systems properties and controls over C4 photosynthesis, but also as a tool to guide engineering C4 photosynthesis for improved light and nitrogen use efficiency in either C4 plants or in a plant with C3 photosynthetic machinery.

MATERIALS AND METHODS

Development of the C4 Kinetic Model

The overall C4 model developed here is depicted diagrammatically in Figure 1. The carbon metabolism part of photosynthetic C3 carbon assimilation and photorespiratory C2 metabolism (Zhu et al., 2007) was used as a basis of the kinetic model of C4 metabolism, upon which MC-BSC metabolite transfer reactions were added. The four major components required for developing this C4 model are described below.

Rate Equations

In the C4 model, the reactions were divided into six categories: enzymatic reactions, light reactions, metabolite transport across the chloroplast envelope, metabolite transport between MCs and BSCs, Suc and starch synthesis, and photorespiration.

Enzymatic Reactions.

Rate equations describing each discrete step of carbon metabolism were either taken from the literature or developed based from standard Michaelis-Menten rate equations. The complete set of rate equations and parameters is presented in Supplemental Data Files S2 and S3. Reactions were categorized as either equilibrium or nonequilibrium reactions based on their equilibrium constants. The interconversion between the following compounds were assumed to be in equilibrium: (1) glyceraldehyde-3-phosphate and dihydroxyacetone phosphate independent of the location of the reactions; (2) xylulose-5-phosphate, Rib-5-P, and ribulose-5-phosphate in the chloroplast stroma of the BSCs; and (3) Fru-6-P, Glc-6-P, and Glc-1-P independent of the location of the reactions (Fig. 1).

With the exception of reactions catalyzed by Rubisco, ADP-Glc pyrophosphorylase, and Gly decarboxylase, all nonequilibrium reactions were assumed to obey Michaelis-Menten kinetics, modified as necessary for the presence of inhibitor(s) or activator(s). Equations for the three exceptions were as given by Zhu et al. (2007). Otherwise, a general reversible reaction of the form A + B < → C + D was assumed, following the standard kinetic equation of a reversible reaction with two substrates and two products (Cleland, 1963), as in Zhu et al. (2007).

Light Reactions.

A biochemical model (Ögren and Evans, 1993; von Caemmerer, 2000) was used to calculate the electron transport rate (J):

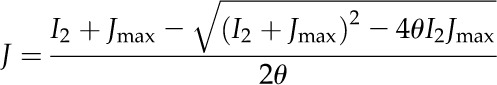(1)

where I₂ is the photosynthetic active radiation absorbed by PSII, J_max is the maximal electron transport rate, and θ is an empirical curvature factor (default value is 0.7; Evans, 1989; von Caemmerer, 2000).

This model assumes that linear electron transport process operate in MCs, whereas only the cyclic electron transport through PSI operates in BSCs. The electron transport rates in MCs and BSCs were calculated as follows:

(2)

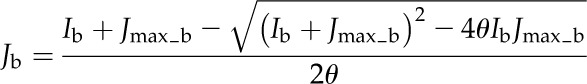(3)

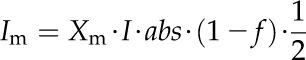(4)

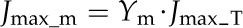(5)

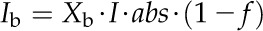(6)

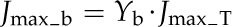(7)

where abs represents the leaf absorbance (the default value is 0.85) and f accounts for the spectral distribution of light, that is, a proportion of the absorbed light cannot be effectively used by photosystems (0.15; Evans, 1987). X_m and X_b are light partition coefficients for MCs and BSCs. The sum of X_m and X_b is 1. Y_m and Y_b also sum to 1 and partition the maximum rate of photosynthetic electron transport (J_{max_T}) between MCs and BSCs, respectively. Here we assume MCs receive two thirds of the absorbed light (i.e. X_m = two-thirds) and the J_{max_T} partition coefficient for MCs is 0.6 (i.e. Y_m = 0.6; Supplemental Fig S8).

J, either J_m or J_b, is the electron transport rate that is used to directly calculate the rates of ATP (or NADPH) synthesis in the model. The maximum rate of ATP and NADPH synthesis reactions were described as follows:

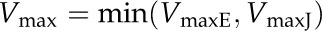(8)

where V_maxE is the maximum rate of ATP and NADPH synthesis determined by the kinetic properties of ATP synthase and NADP⁺ reductase. V_maxJ is the maximum rate of ATP (or NADPH) synthesis as limited by the electron transport rate:

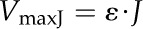(9)

where ε is the ATP-e⁻ ratio or the NADPH-e⁻ ratio.

Metabolite Transport across the Chloroplast Envelope.

Metabolite transport across membranes was described as for enzyme-catalyzed reactions in the following generalized equation:

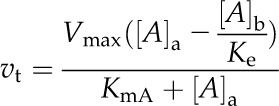(10)

where v_t is the flux of metabolite A, [A]_a is the concentration of metabolite A in compartment a; [A]_b is the concentration of metabolite A in compartment b. The direction of transport is from compartment a to compartment b, and K_m is the Michaelis-Menten constant for A, reflecting the affinity of the transporter for the metabolite.

Metabolite Transport between MCs and BSCs.

Metabolite fluxes via the plasmodesmata (v_{A_pd}) spanning the BC-MSC interface were calculated as follows:

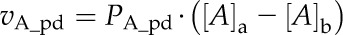(11)

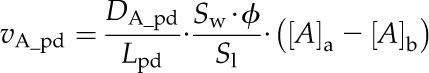(12)

These two equations assume that metabolite transport process is entirely driven by diffusion; that is, the rate is determined by both the permeability (P_{A_pd}) and the concentration gradient of the metabolite between these two compartments ([A]_a − [A]_b). Equation 12 assumes that the permeability between BSCs and MCs is determined by the length of plasmodesmata (L_pd), the cell wall area at the BSC-MC interface per unit leaf area (S_w/S_l), the fraction of the BSC-MC interface cross sectional area that is permeated by plasmodesmata (Φ) and the diffusion coefficient of a metabolite (D_{A_PD} for metabolite A) in the cytosol. It further assumes that the cytosol of the BSCs and MCs is continuous through the cytoplasmic sleeves of the plasmodesmata (Eq. 12).

Different metabolites have different diffusion coefficients in the cytosol (D_cyt), according to molecular sizes. In this model, the D_cyt of C3P is assumed to be 5.25 × 10⁻¹⁰ m² s⁻¹ (Sowinski et al., 2008). CO₂ leakage is described also as a diffusion process with a diffusion coefficient in the cytosol of 1.7 × 10⁻⁹ m² s⁻¹ (Evans et al., 2009). Apoplastic diffusion of CO₂ is not considered because the outer cell wall of the BSCs of NADP-ME plants usually includes a suberin band, which effectively eliminates apoplastic leakage of CO₂ (Dengler and Nelson, 1999). CO₂ flux across the BSC chloroplast envelopes is simulated as a simple diffusion process with a permeability coefficient of 2 × 10⁻⁵ m s⁻¹ (Uehlein et al., 2008; Evans et al., 2009; Supplemental Fig. S9; Supplemental Data File S4). We used an assumed value of BSC chloroplast surface area per unit leaf area, which is 10 m²/m² to convert the unit. Rate equations and parameters are listed in Supplemental Data Files S2 and S3.

Suc and Starch Synthesis.

Suc is limited to the cytosol of the MCs and starch synthesis is in the chloroplasts of the BSCs (Fig. 1), as indicated by observed localization of relevant substrates, products, and enzymes (Furbank et al., 1985; Lunn and Furbank, 1997). Although immunohistological (Cheng et al., 1996), activity (Ohsugi and Huber, 1987), and proteomic analyses have indicated that Suc-P-synthase, a key enzyme in Suc synthesis, was also found in the BSC cytosol (Majeran et al., 2010), the Suc-P-synthase is assumed to be involved in Suc synthesis during starch degradation at night rather than participating in photosynthesis during the day. Following Stitt and Heldt (1981), starch synthesis and degradation are assumed to occur simultaneously. For simplicity, starch degradation was simplified to one reaction (i.e. a hypothetical reaction that directly converts starch to Glc-6-P).

Photorespiration.

For photorespiration, although glycerate kinase has been identified in MC chloroplasts (Usuda and Edwards, 1980), we simplified the model by assuming that reactions related to photorespiration only occur in BSCs, because most of the enzymes of the photorespiratory pathway have been shown to be localized to the BSCs of C4 plants (Majeran et al., 2005).

Equations for Conserved Quantities

The total concentration of the adenylate nucleotide ([CA]) chloroplast was assumed constant (Pettersson and Ryde-Pettersson, 1988; Poolman et al., 2000; Zhu et al., 2007, 2012). Similarly, the sum of [NADPH] and [NADP] in chloroplast stroma ([CN]) was assumed constant in both the MCs and BSCs. The sum of inorganic phosphate and sugar-bound phosphate in chloroplast stroma ([CP]) was also assumed constant in both BSCs and MCs (Fliege et al., 1978; Zhu et al., 2007). These conserved quantities were expressed as algebraic equations following Zhu et al. (2007).

Ordinary Differential Equations

The rate of metabolite concentration change was calculated as the difference between the rate of the reaction generating the metabolite (v₁) and the rate of the reaction consuming the metabolite (v₂). A parameter, Vol (the volume per unit leaf area for a compartment; L m⁻²) was used to convert the unit of V₁ and V₂ from mmol m⁻² s⁻¹ to mmol L⁻¹:

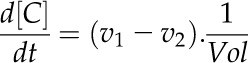(13)

The complete system of ordinary differential equations for the C4 model is listed in Supplemental Data File S2. The proportion of MC and BSC volume was based on maize (Zea mays) leaf cross sections, and subcellular volumes were based on barley (Hordeum vulgare) leaf (Winter et al., 1993). All of the volume-related parameters are listed in Supplemental Data File S3. There were 56 differential equations to calculate 56 metabolite concentration variables in the model.

Numerical Integration

The ode15s procedure of MATLAB (version 2008a; MathWorks) was chosen to solve the system. The solution of the ordinary differential equation provided by ode15s is the time evolution of the concentration of each metabolite in each compartment, which in turn allows calculation of leaf CO₂ and O₂ fluxes.

CO₂ Assimilation Rate Calculation

During the simulation, we assume that the model has reached a steady state when simulated metabolite concentrations do not change any more with time. The steady-state metabolite concentrations and flux rates were extracted from the model for CO₂ assimilation rate calculation and further analysis. The CO₂ assimilation rate (A) was calculated as follows (Farquhar et al., 1980):

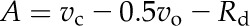(14)

where v_c and v_o are the rates of RuBP carboxylation and oxygenation respectively. R_d is the rate of mitochondrial respiration. The default value for R_d is 1 µmol m⁻² s⁻¹ with the rate of respiration in both BSCs (R_b) and MCs (R_m) being equal as 0.5 µmol m⁻² s⁻¹.

In von Caemmerer’s C4 model (von Caemmerer, 2000), CO₂ assimilation was calculated by two equations. In addition to Equation 14, the following equation was also used:

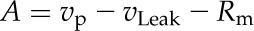(15)

The minimum of Equations 14 and 15 determines the actual A. In our model, both calculation methods always reach the same result at the steady state (Supplemental Data File S5 for detailed derivations).

Parameterization

Kinetic constants for the enzymes of the Calvin-Benson cycle, photorespiratory C2 metabolism, and starch and Suc synthesis were as provided in detail by Zhu et al. (2007). For Rubisco, the kinetic properties reported for maize (Cousins et al., 2010) were used to replace those used in the earlier C3 model (Zhu et al., 2007). Kinetic properties and their sources for the unique C4 enzymes are given in the Supplemental Data File 2 and S3.

Model Validation

The model was validated by comparing the predicted and measured patterns of response photosynthetic CO₂ uptake rate (A) and metabolite concentrations to variation in C_i and PPFD (Leegood and von Caemmerer, 1989; Kanai and Edwards, 1999).

Model Applications

Identification of Key Enzymes Controlling Different Phases of the Steady-State A-C_i Response Curve

The model was first used to simulate A under high light and increasing C_i to develop an A-C_i curve. Subsequently, the V_max values of specific enzymes were decreased individually to evaluate the impact of these enzymes on the initial slope of the A-C_i response and the maximal A at saturating C_i.

Calculation of the CCs for Specific Features of C4 Photosynthesis

The V_max of each enzyme was increased and decreased by 1% individually in the model to calculate new A (A⁺ and A⁻) for two different conditions of light and C_i. The flux CC of each enzyme was calculated as follows:

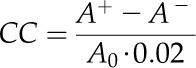(16)

Identification of Optimal Distribution of Enzymes Related to C4 Photosynthesis to Maximize Photosynthetic Efficiency

Following Zhu et al. (2007), a genetic algorithm was used to identify, assuming a constant leaf nitrogen level, the optimal investment in the proteins of the photosynthetic apparatus to maximize photosynthetic rate. A MATLAB GA Toolbox, GATBX (The Genetic Algorithm Toolbox, developed by the University of Sheffield), was used. Briefly, this genetic algorithm mimics the process of natural biological evolution (i.e. reproduction, mutation, recombination, natural selection, and survival of the fittest). Candidate sets of the enzyme concentrations play the role of individuals in a population and the CO₂ assimilation rate is used as the selection pressure in the algorithm. Mutation here was limited to altering the amount of an enzyme, but the enzyme properties were otherwise unchanged.

Prediction of Changes of Carbon Isotope Discrimination Signals

To estimate ¹³C discrimination, ¹³CO₂ and H¹³CO₃⁻ were included as metabolites in the model together with the dominant ¹²CO₂ and H¹²CO₃⁻. The model includes the difference between the binary diffusivities of ¹³CO₂ and ¹²CO₂, and differences between the kinetic constants for ¹²CO₂ and ¹³CO₂ in Rubisco catalyzed reactions, and for H¹³CO₃⁻ and H¹²CO₃⁻ at phosphoenolpyruvate carboxylase. Taking Rubisco as an example:

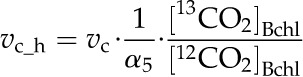(17)

where v_{c_h} is the ¹³CO₂ fixation rate of Rubisco and v_c is the ¹²CO₂ fixation rate of Rubisco. α₅ is the isotope effect of Rubisco with the value taken from Farquhar et al., (1989), [¹³CO₂]_Bchl and [¹²CO₂]_Bchl are ¹³CO₂ and ¹²CO₂ concentrations in BSCs chloroplast respectively. The complete set of rate equations and parameters are presented in Supplemental Data Files S2 and S3.

δ¹³C is the established value for expressing the ratio of ¹³C to ¹²C and was calculated as follows:

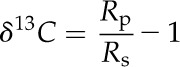(18)

where R_s and R_p are the molar abundance ratios of ^l3C-¹²C of the standard and photosynthetic product. The R_s was calculated based on carbon in carbon dioxide generated from a fossil belemnite from the Pee Dee Formation, denoted PDB (R_s = 0.0112372; Craig, 1957). Farquhar and Richards (1984) proposed the use of Δ as an alternative measure of the carbon isotope discrimination by plants:

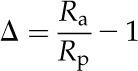(19)

where R_a is the isotopic abundance in the air. In this model, we assumed a R_a of free atmosphere as 0.0111473 (Farquhar et al., 1989). In contrast with δ, Δ is independent of R_a (Farquhar and Richards, 1984).

In the model, the steady-state ¹³CO₂ and ¹²CO₂ fixation flux of Rubisco were used to calculate R_p as follows

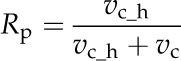(20)

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure S1. Predicted changes in contents of key metabolites with changes in PPFD (as for Fig. 3, but the response of metabolites to light).

• Supplemental Figure S2. Effects of metabolite permeability between BSCs and MCs on A and CO₂ leakiness.

• Supplemental Figure S3. The effects of modifying phosphate concentration in bundle sheath plastid on steady-state contents of key metabolites of photosynthetic carbon metabolism.

• Supplemental Figure S4. The effects of modifying PGA- and T3P-related enzyme kinetic parameter effects on key metabolite contents.

• Supplemental Figure S5. The effects of modifying phosphate concentration and enzyme kinetic parameters on key metabolite contents.

• Supplemental Figure S6. The effects of modifying cytosolic Fru-bisphosphatase enzyme kinetic parameters on key metabolite contents.

• Supplemental Figure S7. Effect of plasmodesmata length on A and metabolite fluxes between MCs and BSCs.

• Supplemental Figure S8. The proportion of J_{max_T} partitioned into BSCs (Yb) influences CO₂ leakiness, A, and proportion of PGA transport to MCs.

• Supplemental Figure S9. The effect of the chloroplast envelope permeability to CO₂ on photosynthesis, photorespiration, and leakiness.

• Supplemental Table S1. Photosynthetic flux CCs of enzymes and diffusion-related parameters.

• Supplemental Table S2. Comparison of the impacts of using C3 and C4 homologs of enzymes related to C4 photosynthesis on A and nitrogen demand.

• Supplemental Data File S1. List of abbreviations and definitions for the C4 photosynthesis systems and their definitions.

• Supplemental Data File S2. Equations used in the C4 photosynthesis systems model.

• Supplemental Data File S3. Parameters used in the C4 photosynthesis systems model.

• Supplemental Data File S4. Rationale underlying the choice of the default CO₂ permeability coefficient.

• Supplemental Data File S5. Rationale underlying the choice of the rate equation used to calculate CO₂ uptake rates.

Glossary

BSC

bundle sheath cell

MC

mesophyll cell

PPDK

pyruvate orthophosphate dikinase

NADP-MDH

NADP-malate dehydrogenase

PEPC

phosphoenolpyruvate carboxylase

NADP-ME

NADP-malate enzyme

PGA

3-phosphoglycerate

T3P

triose phosphate

CA

carbonic anhydrase

RuBP

ribulose 1,5-bisphosphate

TPT

triose phosphate transporter

PPFD

photosynthetic photon flux density

MDH

malate dehydrogenase