Reconstruction algorithm for improved ultrasound image quality

Abstract

A new algorithm is proposed for reconstructing raw RF data into ultrasound images. Prior delay-and-sum beamforming reconstruction algorithms are essentially one-dimensional, as a sum is performed across all receiving elements. In contrast, the present approach is two-dimensional, potentially allowing any time point from any receiving element to contribute to any pixel location. Computer-intensive matrix inversions are performed once-and-for-all ahead of time, to create a reconstruction matrix that can be reused indefinitely for a given probe and imaging geometry. Individual images are generated through a single matrix multiplication with the raw RF data, without any need for separate envelope detection or gridding steps. Raw RF datasets were acquired using a commercially available digital ultrasound engine for three imaging geometries: a 64-element array with a rectangular field-of-view (FOV), the same probe with a sector-shaped FOV, and a 128-element array with rectangular FOV. The acquired data were reconstructed using our proposed method and a delay-and-sum beamforming algorithm, for comparison purposes. Point-spread-function (PSF) measurements from metal wires in a water bath showed the proposed method able to reduce the size of the PSF and/or its spatial integral by about 20 to 38%. Images from a commercially available quality-assurance phantom featured greater spatial resolution and/or contrast when reconstructed with the proposed approach.

I. Introduction

The reconstruction of raw radiofrequency (RF) data into ultrasound images typically includes both hardware-based and software-based operations [1]. One especially important step, called ‘delay-and-sum beamforming’ as it involves applying time delays and summations to the raw RF signal, can be performed very rapidly on dedicated hardware. Such hardware implementations of the delay-and-sum beamforming algorithm have made ultrasound imaging possible at a time when computing power was insufficient for entirely-digital reconstructions to be practical. But improvements in computer technology and the introduction of scanners able to provide access to digitized RF signals [2–6] have now made digital reconstructions possible. Software-based reconstructions are more flexible [6–11], and may allow some of the approximations inherited from hardware-based processing to be lifted. A main message of the present work is that delay-and-sum beamforming is not a particularly accurate reconstruction algorithm, and that software-based remedies exist which are capable of providing significant image quality improvements, especially in terms of spatial resolution and contrast.

Delay-and-sum beamforming is essentially a one-dimensional operation, as a summation is performed along the ‘receiver element’ dimension of the (properly delayed) RF data. Several improvements upon the basic scheme have been proposed, whereby different weights are given to different receiver elements in the summation to control apodization and aperture. More recently, sophisticated strategies have been proposed to adjust these weights in an adaptive manner, based on the raw data themselves, to best suit the particular object being imaged [12–17]. In the ‘minimum variance beamforming’ method for example [12–15], weights are sought that minimize the L2-norm of the beamformed signal (thus making reconstructed images as dark as possible), while at the same time enforcing a constraint that signals at focus be properly reconstructed. The overall effect is to significantly suppress signals from undesired sources while preserving for the most part signals from desired sources, thus enabling a number of different possible improvements in terms of image quality [18]. Such adaptive beamforming approaches will be referred to here as ‘delay-weigh-and-sum’ beamforming, to emphasize that elaborately selected weights are being added to the traditional delay-and-sum beamforming algorithm. It should be noted that irrespective of the degree of sophistication involved in selecting weights, delay-weigh-and-sum beamforming remains essentially one-dimensional in nature. In contrast, the approach proposed here is two-dimensional, allowing any time sample from any receiver element to potentially contribute, in principle at least, toward the reconstruction of any image pixel. Image quality improvements are obtained as correlations between neighboring pixels are accounted for and resolved. Reductions in the size of the point-spread-function (PSF) area by up to 37% and increases in contrast by up to 29% have been obtained here, as compared to images reconstructed with delay-and-sum beamforming.

In the proposed approach, the real-time reconstruction process consists of a single step, a matrix multiplication involving a very large and very sparse reconstruction matrix, without any need for separate envelope detection or gridding steps. Throughout the present work, considerable attention is given to the question of computing load, and of whether computing power is now available and affordable enough to make the proposed approach practical on clinical scanners. Computing demands for reconstruction algorithms can be separated into two very different categories: Calculations performed once and for all ahead of time for a given transducer array and imaging geometry, and calculations that must be repeated in real-time for every acquired image. While long processing times may be acceptable for the first category (algorithms performed only once, ahead of time), fast processing is necessary for the second category (real-time computations). While the method does involve a heavy computing load, the main bulk of these calculations fit into the first category above, i.e., for a given probe and FOV geometry they can be performed once and for all. The actual real-time reconstruction involves multiplying the raw data with the calculated reconstruction matrix. In the present implementation, depending on field-of-view (FOV) and raw dataset sizes, this multiplication took anywhere between about 0.04 and 4 s per time frame. In the future, further algorithm improvements and/or greater computing power may enable further reductions in processing time. Even in cases where frame rates sufficient for real-time imaging could not be reached, the present method could still prove useful for reconstructing the images that are saved and recorded as part of clinical exams.

It may be noted that the proposed approach is not adaptive, in the sense that the reconstruction matrix depends only on the probe and on the geometry of the imaging problem, and does not depend on the actual object being imaged. As such, the proposed approach should not be seen as a competitor to adaptive beamforming, but rather as a different way of addressing different limitations of the traditional delay-and-sum bemforming algorithm. Ideas from the adaptive beam-forming literature may well prove compatible with the present approach, thus enabling further improvements in image quality. More generally, the 2D approach proposed here might prove a particularly suitable platform for modeling and correcting for image artifacts, to obtain improvements beyond the increases in spatial resolution and contrast reported in the present work.

II. Theory

A. Regular (delay-and-sum beamforming) reconstructions

Ultrasound imaging (USI) reconstructions typically rely on delay-and-sum beamforming to convert the received RF signal into an image [1]. Other operations such as TGC, envelope detection and gridding may complete the reconstruction process. The acquired RF signal can be represented in a space called here ‘e-t space’, where ‘e’ is the receiver element number and ‘t’ is time.

This space is either 2- or 3-dimensional, for 1D or 2D transducer arrays, respectively. A single e-t space matrix can be used to reconstruct a single ray, multiple rays, or even an entire image in single-shot imaging [19, 20]. In the notation used below, all of the points in a 2D (or 3D) e-t space are concatenated into a single 1D vector, s. The single-column vector s features N_t × N_e rows, i.e., one row for each point in e-t space, where N_e is the number of receiver elements and N_t the number of sampled time points. As further explained below, a regular delay-and-sum beamforming reconstruction can be represented as:

$$\widehat{\mathit{o}}=A\{\mathbf{G}\times V\{{\mathbf{D}}_0\times {\mathbf{T}}_0\times \mathit{s}\}\}=A\{\mathbf{G}\times V\{{\mathbf{R}}_0\times s\}\},$$ [1]

where ô is the image rendering of the ‘true’ sonicated object o; it is a 1D vector, with all N_x × N_z voxels concatenated into a single column. Time gain compensation (TGC) is performed by multiplying the raw signal s with the matrix T₀, which is a diagonal square matrix featuring N_t × N_e rows and columns. Delay-and-sum beamforming is performed by further multiplying with D₀, a matrix featuring N_l × N_ax rows and N_t × N_e columns, where N_l is the number of lines per image and N_ax is the number of points along the axial dimension. The content and nature of D₀ will be described in more details later. The operator V{·} performs envelope detection, which may involve non-linear operations and thus could not be represented in the form of a matrix multiplication. Gridding is performed through a multiplication with the matrix G featuring N_x × N_z rows and N_l × N_ax columns. The operator A{·} represents optional image-enhancement algorithms, and will not be further considered here. The reconstruction matrix, R₀, is given by D₀ × T₀. An example of an RF dataset in e-t space and its associated reconstructed image ô (rendered in 2D) is shown in Fig. 1a and 1b, respectively. Figure 1b further includes graphic elements to highlight regions-of-interest (ROI) that will be referred to later in the text (white boxes and line). A main goal of the present work is to improve R₀ in Eq. 1 as a means to increase the overall quality of reconstructed images ô such as that in Fig. 1b.

Fig. 1.

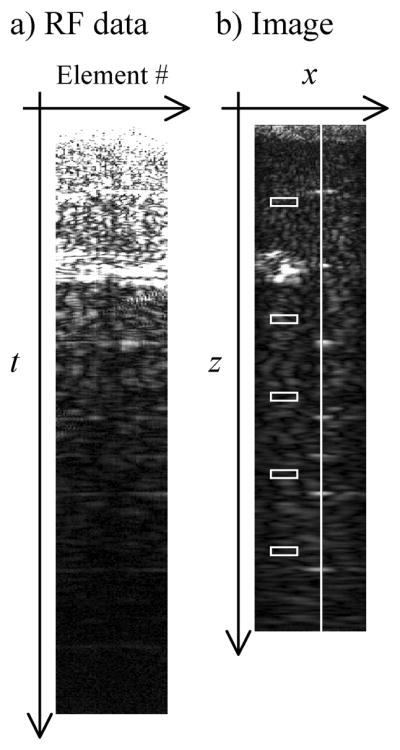
a) Raw RF data in the element vs. time space, called e-t space here, can be reconstructed into the image shown in (b) using a regular delay-and-sum beamforming reconstruction. Note that the carrier frequency of the raw signal was removed in (a) for display purposes, as it would be difficult to capture using limited resolution in a small figure (the raw data was made complex and a magnitude operator was applied). Regions of interest are defined here in (b) for later use (white boxes and line).

B. An improved solution to the reconstruction problem

As assumed in delay-and-sum beamforming reconstructions, the signal reflected by a single point-object should take on the shape of an arc in the corresponding e-t space RF signal. The location of the point-object in space determines the location and curvature of the associated arc in e-t space. For a more general object, o, the raw signal would consist of a linear superposition of e-t space arcs, whereby each object point in o is associated with an e-t space arc in s. The translation of all object points into a superposition of e-t space arcs can be described as:

$$T_0\times \mathit{s}={\mathbf{E}}_{\mathit{arc}}\times \mathbf{o},$$ [2]

where E_arc is an encoding matrix featuring N_t × N_e rows and N_l × N_ax columns. The matrix E_arc is assembled by pasting side-by-side N_l × N_ax column vectors that correspond to all of the different e-t space arcs associated with the N_l × N_ax voxels to be reconstructed. The reconstruction process expressed in Eq. 1 is actually a solution to the imaging problem from Eq. 2: Multiplying both sides of Eq. 2 with E_arc⁺, the Moore-Penrose pseudo-inverse of E_arc, one obtains o ≈ E_arc⁺×T₀×s. Upon adding the envelope detection and gridding steps, one can obtain Eq. 1 from Eq. 2 given that:

$${\mathbf{D}}_0={{\mathbf{E}}_{\text{arc}}}^{+}.$$ [3]

On the other hand, the operations involved in a digital delay-and-sum beamforming reconstruction (i.e., multiplying the raw signal in e-t space with an arc, summing over all locations in e-t space, and repeating these steps for a collection of different arcs to reconstruct a collection of different image points) can be performed by multiplying the RF signal with E_arc^H, where the superscript H represents a Hermitian transpose. In other words, D₀ in Eq. 1 is given by:

$${\mathbf{D}}_0={{\mathbf{E}}_{\text{arc}}}^{\text{H}}.$$ [4]

Combining Eqs 3 and 4 gives a relationship that captures one of the main assumptions of delay-and-sum beamforming reconstructions:

$${{\mathbf{E}}_{\mathit{arc}}}^{+}={{\mathbf{E}}_{\mathit{arc}}}^{\text{H}}.$$ [5]

In other words, delay-and-sum beamforming reconstructions assume that assembling all e-t space arcs together in a matrix format yields an orthogonal matrix. This assumption is very flawed, as demonstrated below.

An example is depicted in Fig. 2 where the e-t signal consists of a single arc (Fig. 2a), meaning that the object o should consist of a single point. However, reconstructing this arc using Eqs 1 and 3 does not give a point-like image, but rather the broad distribution of signals shown in Fig. 2b. This is because E_arc^H, and thus D₀ through Eq. 4, is only a poor approximation to E_arc⁺.

Fig. 2.

a) A point in the imaged object is typically assumed to give rise to an arc in e-t space. b) However, reconstructing the arc in (a) with delay-and-sum beamforming does not yield a point in the image plane, but rather a spatially broad distribution of signal. c) At least in principle, when applied to artificial signals such as that in (a), the proposed approach can reconstruct images that are vastly improved in terms of spatial resolution as compared to delay-and-sum beamforming.

Instead of using the approximation from Eq. 5, the imaging problem as expressed in Eq. 2 can be better handled through a least-square solution. Equation 2 is first multiplied from the left by E_arc^H to obtain the so-called normal equations [21]: E_arc^H×(T×s) = E_arc^H×E_arc×o. Inverting the square normal matrix E_arc^H×E_arc and multiplying from the left with (E_arc^H×E_arc)⁻¹ allows o to be estimated: ô = (E_arc^H×E_arc) ⁻¹×E_arc^H×(T×s). Upon the addition of a damped least-squares regularization term λ²L, and the insertion of Ψ⁻¹ as part of a preconditioning term E_arc^H×Ψ ⁻¹, an equation is obtained which exhibits the well-known form of a least-square solution [7, 11, 22, 23]:

$$\begin{array}{l}{\mathbf{D}}_1={({{\mathbf{E}}_{\mathit{arc}}}^{\text{H}}\times {\mathbf{\Psi }}^{-1}\times {\mathbf{E}}_{\mathit{arc}}+{\lambda }^2\mathbf{L})}^{-1}\times {{\mathbf{E}}_{\mathit{arc}}}^{\text{H}}\times {\mathbf{\Psi }}^{-1},\\ \widehat{\mathit{o}}=\mathbf{G}\times V\{{\mathbf{D}}_1\times {\mathbf{T}}_1\times \mathit{s}\}=\mathbf{G}\times V\{{\mathbf{R}}_1\times \mathit{s}\}.\end{array}$$ [6]

In the present work Ψ is simply an identity matrix, and L will be discussed in more details later. The signal ‘s’ may here include both legitimate and noise-related components, and ô is a least-square estimate of the actual object ‘o’. The image in Fig. 2c was reconstructed using Eq. 6. Compared to Fig. 2b, Fig. 2c presents a much more compact signal distribution and a greatly improved rendering of the point-object. But even though images reconstructed using the R₁ matrix (e.g., Fig. 2c) may prove greatly superior to those reconstructed with delay-and-sum beamforming and the associated R₀ matrix (e.g., Fig. 2b) when dealing with artificial e-t space data such as those in Fig. 2a, such improvements are typically not duplicated when using more realistic data instead. The reason for this discrepancy is explored in more details in the next section.

C. Including the shape of the wavepacket into the solution

Datasets acquired from a single point-like object do not actually look like a simple arc in e-t space. In an actual dataset, the arc from Fig. 2a would be convolved with a wavepacket along t, whereby the shape of the wavepacket depends mostly on the voltage waveform used at the transmit stage and on the frequency response of the piezoelectric elements. A wavepacket has both positive and negative lobes, while the arc in Fig. 2a was entirely positive. Even though the delay-and-sum beamforming assumption in Eq. 5 is very inaccurate, negative errors stemming from negative lobes largely cancel positive errors from positive lobes. For this reason, delay-and-sum beamforming tends to work reasonably well for real-life signals, even though it may mostly fail for artificial signals such as those in Fig. 2a.

The reconstruction process from Eq. 6 avoids the approximation made by delay-and-sum beamforming as expressed in Eq. 5, but it remains inadequate because it is based on E_arc, and thus assumes object points to give rise to arcs in e-t space. While E_arc associates each point in the object o with an arc in the raw signal s through Eq. 2, an alternate encoding matrix E_wav associates each point with a wavepacket function instead. Because E_wav features several non-zero time points per receiver element, the reconstruction process truly becomes two-dimensional in nature, as whole areas of e-t space may get involved in the reconstruction of any given pixel location, as opposed to one-dimensional arc-shaped curves as in delay-and-sum beamforming. Sample computer code to generate E_wav is provided in the Appendix.

The solution presented in Eq. 6 is duplicated in Eq. 7 below, but it now involves a more accurate model relying on E_wav rather than E_arc:

$$\begin{array}{c}{\mathbf{D}}_2={({{\mathbf{E}}_{\mathit{wav}}}^{\text{H}}\times {\mathbf{\Psi }}^{-1}\times {\mathbf{E}}_{\mathit{wav}}+{\lambda }^2\mathbf{L})}^{-1}\times {{\mathbf{E}}_{\mathit{wav}}}^{\text{H}}\times {\mathbf{\Psi }}^{-1},\\ \widehat{\mathit{o}}={\mathbf{D}}_2\times {\mathbf{T}}_2\times \mathit{s}={\mathbf{R}}_2\times \mathit{s},\end{array}$$ [7]

where the TGC term T₂ may be equated to T₁ in Eq. 6, T₂ = T₁. Note that no envelope detection and no gridding operation are required in Eq. 7, unlike in Eqs 1 and 6. As E_wav already contains information about the shape of the wavepacket, envelope detection is effectively performed when multiplying by D₂. Furthermore, because a separate envelope detection step is not required, there is no reason anymore for reconstructing image voxels along ray beams. Accordingly, the N_vox reconstructed voxels may lie directly onto a Cartesian grid, removing the need for a separate gridding step. For a rectangular FOV, the number of reconstructed voxels N_vox is simply equal to N_x × N_z, while for a sector-shaped FOV it is only about half as much (because of the near-triangular shape of the FOV). As shown in the Results section and in the Appendix, a prior measurement of the wavepacket shape, for a given combination of voltage waveform and transducer array, can be used toward generating E_wav. Note that unlike E_arc, E_wav is complex.

Equation 8 below is the final step of the present derivation. The index ‘2’ from Eq. 7 can now be dropped without ambiguity, and a scaling term (I + λ²L) is introduced, where I is an identity matrix, to compensate for scaling effects from the λ²L regularization term:

$$\begin{array}{c}\mathbf{D}={({{\mathbf{E}}_{\mathit{wav}}}^{\text{H}}\times {\mathbf{\Psi }}^{-1}\times {\mathbf{E}}_{\mathit{wav}}+{\lambda }^2\mathbf{L})}^{-1}\times (\mathbf{I}+{\lambda }^2\mathbf{L})\times {{\mathbf{E}}_{\mathit{wav}}}^{\text{H}}\times {\mathbf{\Psi }}^{-1},\\ \widehat{\mathit{o}}=\mathbf{D}\times \mathbf{T}\times \mathit{s}=\mathbf{R}\times \mathit{s}.\end{array}$$ [8]

Based on Eq. 8, an image ô can be generated in a single processing step by multiplying the raw RF signal s with a reconstruction matrix R.

D. Geometrical analogy

There is a simple geometrical analogy that may help understand at a more intuitive level the least-square solution in Eq. 8. Imagine converting a 2D vector, s⃗=s₁i⃗+s₂j⃗, from the usual x-y reference system defined by unit vectors i⃗ and j⃗ to a different reference system defined by the unit vectors $\overrightarrow{u_1}=(\overrightarrow{i}+\overrightarrow{j})/\sqrt{2}$ and by $\overrightarrow{u_2}=(\overrightarrow{i}-\overrightarrow{j})/\sqrt{2}$ instead. This can be done through projections, using a dot product: $\overrightarrow{s}={\displaystyle \sum _l}(\overrightarrow{s}·\overrightarrow{u_l})\overrightarrow{u_l}$. Projections are appropriate in this case because the basis vectors u⃗_l form an orthonormal set: $\overrightarrow{u_l}·\overrightarrow{u_k}={\delta }_{lk}$. In contrast, projections would not be appropriate when converting s⃗ to a non-orthonormal reference system, such as that defined by $\overrightarrow{v_1}=(\overrightarrow{i}+\overrightarrow{j})/\sqrt{2}$ and by $\overrightarrow{v_2}=\overrightarrow{i}$. In such case, the coefficients s_α and s_β in $\overrightarrow{s}=s_{\alpha }\overrightarrow{v_1}+s_{\beta }\overrightarrow{v_2}$ should instead be obtained by solving the following system of linear equations:

$$\left(\begin{array}{c}{s}_1\\ s_2\end{array}\right)=\left(\begin{array}{cc}1/\sqrt{2}& 1\\ 1/\sqrt{2}& 0\end{array}\right)\left(\begin{array}{c}{s}_{\alpha }\\ s_{\beta }\end{array}\right);\left(\begin{array}{c}{s}_{\alpha }\\ s_{\beta }\end{array}\right)={\left(\begin{array}{cc}1/\sqrt{2}& 1\\ 1/\sqrt{2}& 0\end{array}\right)}^{-1}\left(\begin{array}{c}{s}_1\\ s_2\end{array}\right)=\left(\begin{array}{cc}0& \sqrt{2}\\ 1& -1\end{array}\right)\left(\begin{array}{c}{s}_1\\ s_2\end{array}\right)=\left(\begin{array}{c}\sqrt{2}{s}_2\\ s_1-s_2\end{array}\right).$$ (9)

Direct substitution confirms that $s_{\alpha }=\sqrt{2}{s}_2$ and s_β= (s₁ – s₂) is indeed the correct solution here, as it leads to $\overrightarrow{s}=s_{\alpha }\overrightarrow{v_1}+s_{\beta }\overrightarrow{v_2}=s_1\overrightarrow{i}+s_2\overrightarrow{j}$. The delay-and-sum beamforming reconstruction algorithm, which aims at converting e-t space signals into object-domain signals, is entirely analogous to a change of reference system using projections. Every given pixel is reconstructed by taking the acquired signal in e-t space and projecting it onto the (arc-shaped) function associated with this particular pixel location. Such projection-based reconstruction algorithm neglects any correlation that may exist between pixels, and a better image reconstruction algorithm is obtained when taking these correlations into account, as done in Eqs 8 and 9.

E. Generalization to multi-shot imaging

As presented above, Eq. 8 involved reconstructing a single e-t space dataset s from a single transmit event into an image ô. However, Eq. 8 can readily be generalized to multi-shot acquisitions, whereby transmit beamforming is employed and only part of the image is reconstructed from each transmit event. In such case, data from all N_shot shots are concatenated into the column-vector s, which would now feature N_shot × N_t × N_e elements. The number of columns in the reconstruction matrix R also increases to N_shot × N_t × N_e. In the simplest scenario, where any given image voxel would be reconstructed based on RF data from a single transmit event (rather than through a weighted sum of multiple voxel values reconstructed from multiple transmit events), the number of non-zero elements in R would remain the same as in the single-shot imaging case. As shown in the results section, the number of non-zero elements in R is the main factor determining reconstruction time. While the increased size of s and R may cause some increase in reconstruction time, the fact that the number of non-zero elements in the sparse matrix R would remain unchanged suggests that such increase may prove modest.

F. On extending the proposed model

The present work offers a framework whereby information anywhere in the e-t space can be exploited, in principle at least, toward reconstructing any given image pixel. This more flexible, two-dimensional approach may conceivably lend itself to the modeling and correction of various effects and artifacts. Two possible examples are considered below:

1) Multiple reflections

The number of columns in the encoding matrix E_wav could be greatly increased to include not only the e-t space response associated with each point in the reconstructed FOV, but also a number of extra versions of these e-t space responses shifted along the t axis, to account for the time delays caused by multiple reflections. Such increase in the size of E_wav could however lead to a prohibitive increase in terms of memory requirements and computing load.

2) Effect of proximal voxels on more distal voxels

Ultrasound waves are attenuated on their way to a distal location, which may give rise to the well-known enhancement and shadowing artifacts, but they are also attenuated on their way back to the transducer, which may affect the e-t space function associated with distal points. For example, whole segments of the e-t space signal might be missing if one or more proximal hyperintense object(s) would cast a shadow over parts of the transducer face. The model being solved through Eq. 8 is linear, and cannot accommodate for the exponential functions required to represent attenuation. One would either need to opt for a different type of solution, possibly an iterative solution, or to make the model linear through a truncated Taylor series, e^x ≈ (1 + x). We did pursue the latter approach, and obtained encoding matrices the same size as E_wav, to be used in solutions of the same form as Eq. 8. At least in its current form, the approach proved very impractical for two main reasons: A) Although no bigger than E_wav in its number of rows and columns, the new encoding matrix was much less sparse than E_wav, leading to truly prohibitive reconstruction times and memory requirements. B) Maybe more importantly, the encoding matrix becomes dependent on the reconstructed object itself so that most of the processing would have to be repeated in real-time for each time frame, rather than once-and-for-all ahead of time.

III. Methods

A. Experimental set-up and reconstruction

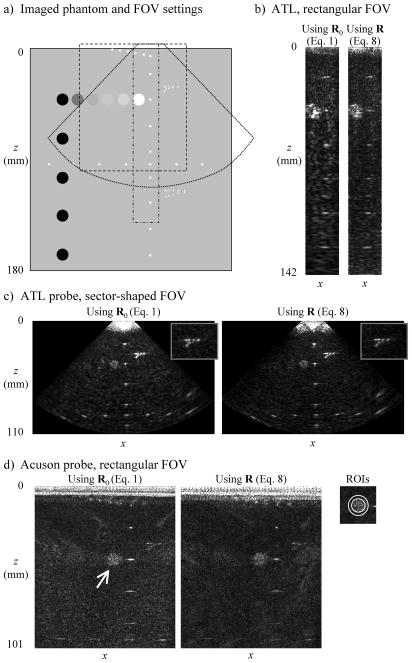
All data were acquired with a Verasonics system (Redmond, WA, USA) model V-1, with 128 independent transmit channels and 64 independent receive channels. Two different ultrasound phantoms were imaged: A phantom manufactured by CIRS (Norfolk, VA, USA) model 054GS with a speed of sound of 1540 m/s and an attenuation coefficient of 0.50 ± 0.05 db/cm-MHz, and a homemade phantom consisting of a single metal wire in a water tank. Two different probes were employed: An ATL P4-2 cardiac probe (2.5 MHz, 64 elements, pitch of 0.32 mm) and an Acuson probe (3.75 MHz, 128 elements, pitch of 0.69 mm). The ATL probe was used either in a rectangular-FOV mode (all elements fired simultaneously) or in a sector-FOV mode (virtual focus 10.24 mm behind the transducer face), while the Acuson probe was used only in a rectangular-FOV mode. When using the Acuson probe, signal from the 128 elements had to be acquired in two consecutive transmit events, as the imaging system could acquire only 64 channels at a time. The system acquired 4 time samples per period, for a 10⁻⁷ s temporal resolution with the ATL probe and 6.7×10⁻⁸ s with the Acuson probe. About 2000 time points were acquired following each transmit event (either 2048 or 2176 with the ATL probe, and 2560 with the Acuson probe). The reconstructed FOV dimensions were 2.05 × 14.2 cm for the ATL probe in a rectangular-FOV mode, 17.7 × 11.0 cm for the ATL probe in a sector-FOV mode, and 8.77 × 10.1 cm for the Acuson probe in a rectangular-FOV mode.

Reconstruction software was written in the Matlab programming language (MathWorks, Natick, MA, USA) and in the C language. Sample code for key parts of the processing is provided in the Appendix. The reconstruction problem from Eq. 8 was solved using either an explicit inversion of the term (E_wav^H× Ψ⁻¹×E_wav+λ²L), or a least-square (LSQR) numerical solver. While the LSQR solution was vastly faster than performing an explicit inverse, and proved very useful throughout the developmental stages of the project, it would be impractical in an actual imaging context as the LSQR solution requires the actual RF data, and thus cannot be performed ahead of time. In contrast, performing the explicit inverse may take a long time, but it is done once and for all ahead of time and the result reused indefinitely for subsequent datasets, potentially allowing practical frame rates to be achieved. Reconstruction times quoted in the Results section were obtained using either an IBM workstation (Armonk, New York, USA) model x3850 M2 with 4 quad-core 2.4 GHz processors and 128 GB of memory, or a DELL workstation (Round Rock, Texas, USA) Precision T7500 with 2 quad-core 2.4 GHz processors and 48 GB of memory. The DELL system was newer and overall significantly faster, allowing shorter reconstruction times to be achieved, while the IBM system proved useful for early developments and for reconstruction cases with more stringent memory requirements.

B. Optimization of reconstruction parameters

1) Time-gain-compensation

The dataset shown in Fig. 1 was reconstructed several times using Eq. 1 and Eq. 6 while adjusting the TGC matrices T₀ and T₁ from one reconstruction to the next. The different TGC matrices were computed based on different attenuation values, in search for matrices able to generate fairly homogeneous image results. The effects of reconstructing images one column or a few columns at a time rather than all columns at once were also investigated, as a way of gaining insights about the proposed algorithm.

2) Regularization

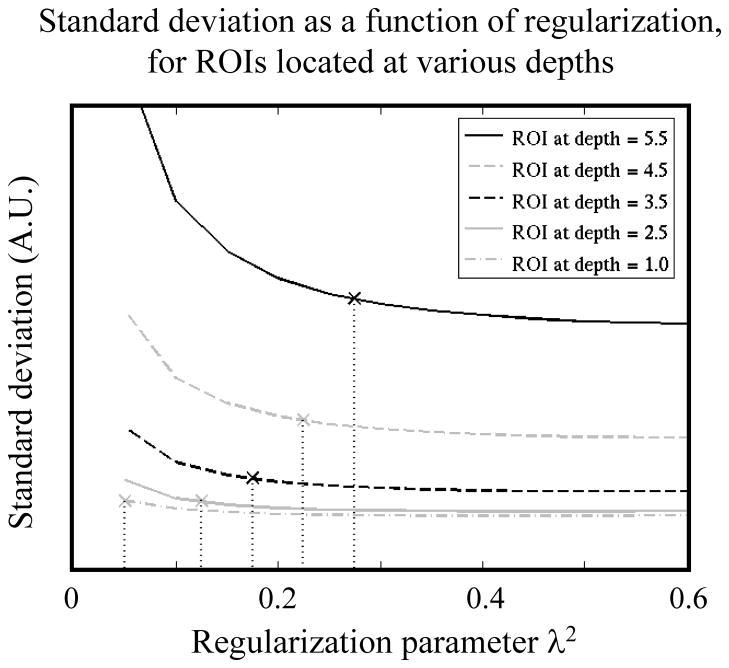
The dataset shown in Fig. 1 was reconstructed using several different settings for the regularization term λ²L in Eq. 8, by varying the value of the scalar λ² and using L = I, an identity matrix. Although a single time frame was shown in Fig. 1, the full dataset actually featured N_fr = 50 time frames. A standard deviation along the time-frame axis was calculated, and ROIs at various depths were considered (shown in Fig. 1b). As a general rule, the regularization term should be kept as small as possible to avoid blurring, but large enough to avoid noise amplification if/when the system becomes ill conditioned. A depth-dependent regularization term λ²L is sought, with L ≠ I, whereby an appropriate amount of regularization is provided at all depths.

3) Maintaining sparsity

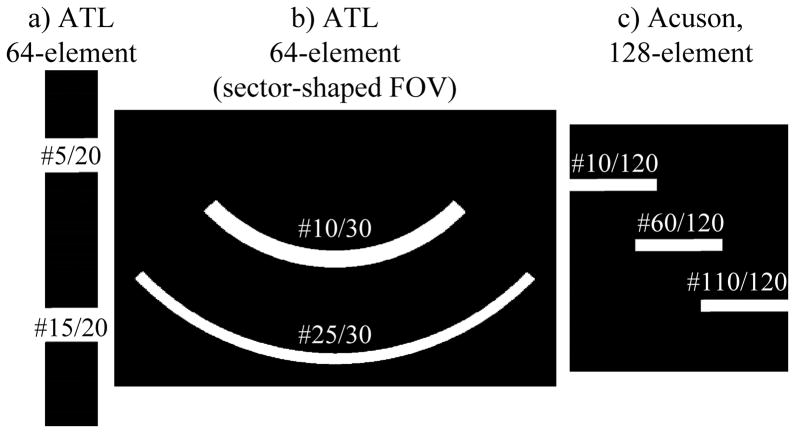
The proposed approach involves manipulating very large matrices featuring as many as hundreds of thousands of columns and rows. The approach may nevertheless prove computationally practical because these matrices, although large, tend to be very sparse. Only the non-zero elements of a sparse matrix need to be stored and manipulated, and one needs to make sure that all matrices remain sparse at all times throughout the reconstruction process. If large amounts of nearly-zero (but nevertheless non-zero) elements were generated at any given processing step, processing time and memory requirements could readily grow far beyond manageable levels. Three main strategies were used to ensure sparsity: A) As shown in the results sections, the wavepackets used as prior knowledge when constructing E_wav were truncated in time so as to keep only N_wpts non-zero points, to help keep E_wav sparse. B) Instead of solving for all of D in one pass, the areas of D where non-zero values are expected were covered using a series of N_patch overlapping regions, each one only a small fraction of D in size. In the image plane, these patches can be thought of as groups of voxels that are located roughly a same distance away from the virtual transmit focus. For rectangular-FOV geometries, different patches simply correspond to different z locations (Fig. 3a) and additional reductions in processing requirements can be achieved by further sub-dividing the x-axis as well (Fig. 3c), while for sector-shaped FOV geometries they correspond to arc-shaped regions in the x-z plane (Fig. 3b). Alternatively, these patches can be understood as square sub-regions along the diagonal of the square matrix (E_wav^H × E_wav + λ²L) ⁻¹, which are mapped onto the non-square D and R matrices through the multiplication with E_wav^H in Eq. 8. C) Once all patches are assembled into a D or an R matrix, the result gets thresholded so that only the largest N_nz values may remain non-zero. Preliminary thresholding on individual patches may also be performed. Smaller settings for N_nz lead to sparser R matrices and shorter reconstruction times, but potentially less accurate image results. The need for fast reconstructions must be weighed against the need for image accuracy.

Fig. 3.

To reduce computing requirements, processing is performed over several overlapping patches rather than for the whole FOV at once. Results from all patches can be combined into single reconstruction matrix R. Examples in the x-z plane are shown, for all three FOV geometries used in the present work.

After selecting a reasonable setting of N_patch = 20 for the dataset in Fig. 1 (see Fig. 3a), images were generated using a number of different values for N_nz while noting the effect on reconstruction speed and accuracy. The so-called ‘artifact energy’ was used as a measure of image accuracy:

$$E_{\mathit{Nnz}}=(\sum _{\mathit{voxels}}{\mid {\widehat{\mathit{o}}}_{\mathit{Nnz}}-{\widehat{\mathit{o}}}_{\mathit{ref}}\mid }^2)/(\sum _{\mathit{voxels}}{\mid {\widehat{\mathit{o}}}_{\mathit{ref}}\mid }^2),$$ [10]

where ô_Nnz and ô_ref were obtained with and without thresholding, respectively. The number of non-zero elements in R should be made as small as possible to achieve shorter reconstruction times, but kept large enough to avoid significant penalties in terms of image quality and artifact energy.

C. Comparing reconstruction methods

1) PSF

The metal-wire phantom was imaged using the ATL P4-2 cardiac probe both in a rectangular-FOV and a sector-FOV mode, and the Acuson probe in a rectangular-FOV mode. The acquired datasets were reconstructed using both delay-and-sum beamforming (Eqs 1 and 4) and the proposed approach (Eq. 8). E_arc in Eq. 4 consisted of about N_vox×N_e non-zero elements, in other words, one non-zero element per receive channel for each imaged pixel. Any interpolation performed on the raw data would be built-in directly into E_arc, and would lead to an increase in the number of non-zero elements. Interpolating the raw data might bring improvements in terms of secondary lobes suppression [24], but would also degrade the sparsity of E_arc by increasing the number of non-zero elements.

Because the water-wire transition had small spatial extent, resulting images were interpreted as a point-spread-function (PSF). The full-width-half-max (FWHM) of the signal distribution was measured along the x and z axes, giving FWHM_x and FWHM_z. The size of the PSF was interpreted here as the size of its central lobe, as approximated by (π × FWHM_x × FWHM_z/4). A second measurement was performed which involved the whole PSF distribution, rather than only its central lobe: After normalizing the peak signal at the wire’s location to 1.0 and multiplying with the voxel area, the absolute value of the PSF signal was summed over an ROI about 3 cm-wide and centered at the wire. The result can be understood as the minimum area, in mm², that would be required to store all PSF signal without exceeding the original peak value anywhere. This measure corresponds to the L1-norm of the PSF, and along with the size of the central lobe it was used here to compare PSF results obtained from different reconstruction methods.

2) Phantom imaging

The CIRS phantom was imaged using the same probes as for the metal-wire phantom (above), and the datasets were reconstructed using both delay-and-sum beam-forming (Eq. 1) and the proposed approach (Eq. 8). Resulting images were displayed side-by-side for comparison. Small hyperechoic objects allowed differences in spatial resolution to be appreciated, while a larger hyperechoic object allowed differences in contrast to be measured.

IV. Results

A. Optimization of reconstruction parameters

1) Equivalence of implementations

Figure 4 shows 1D images obtained from the same da-taset as in Fig. 1, for a 1D FOV that passes through the line of beads from Fig. 1b. Of particular interest are the 3 results plotted with the same black line in Fig. 4a. These results are indistinguishable in the sense that differences between them were much smaller than the thickness of the black line in Fig. 4a. One was obtained using delay-and-sum beamforming and R₀ from Eq. 1, the two others using R₁ and Eq. 6 while including only one ray (i.e., one image column) at a time into the encoding matrix. Results from Eq. 6 diverged from delay-and-sum beamforming results only when many or all image rays were included at once in the same encoding matrix (gray and dashed lines in Fig. 4a). The main point is that differences between our approach and delay-and-sum beamforming reported here do not appear to come from one being better implemented than the other, but rather from our method resolving the correlation between adjacent voxels and rays, as it was designed to do.

Fig. 4.

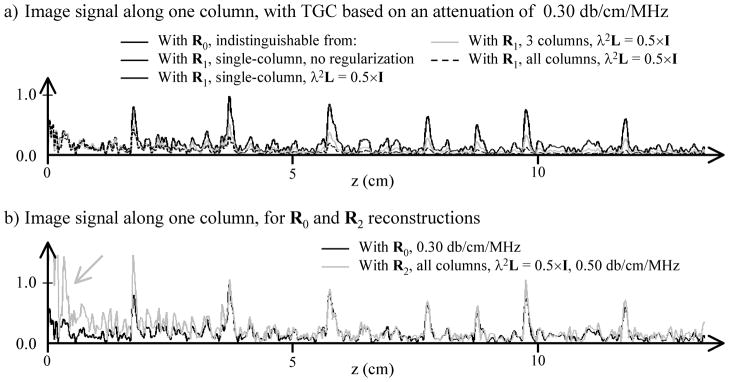
A single column from a phantom image, highlighted in Fig. 1b, is plotted here for different reconstruction algorithms and settings. a) When reconstructing one column at a time, our modified reconstruction from Eq. 6 gives results that are essentially identical to the delay-and-sum beamforming reconstruction from Eq. 1 (black solid line). As more columns are included into the reconstruction, our method diverges from delay-and-sum beamforming (gray solid and black dashed lines). b) With all columns included into the reconstruction, the TGC must be changed from 0.30 to about 0.50 db/cm-MHz to restore the magnitude at greater depths. The nominal attenuation value for this phantom is 0.50±0.05 db/cm-MHz, in good agreement with the TGC compensation required with our method. However, signal becomes overcompensated at shallow depths (gray arrow). The plots use a linear scale, normalized to the maximum signal from the curve in (a).

2) Time-gain-compensation

Figure 4b shows that with delay-and-sum beamforming and R₀ in Eq. 1, a TGC term based on a 0.30 db/cm-MHz attenuation seemed appropriate, as it would keep the amplitude of the various beads in Fig. 1b roughly constant with depth. On the other hand, when using R₁, a correction based on a higher attenuation of 0.50 db/cm-MHz proved more appropriate. Documentation on the CIRS phantom lists the true, physical attenuation as 0.50±0.05 db/cm-MHz, the same value as used here with our proposed reconstruction method. It would appear that with the proposed reconstruction, TGC might become a more quantitative operation based on true signal attenuation. On the other hand, as shown in Fig. 4b (gray arrow), signals at shallow depths tend to be overcompensated when employing a value of 0.50 db/cm-MHz. To prevent the near-field region from appearing too bright in the images presented here, further ad hoc TGC was applied over the shallower one-third of the FOV. Furthermore, an ad hoc value of 0.35 db/cm-MHz (rather than 0.50 db/cm-MHz) had to be used when reconstructing data from the higher-frequency Acuson array, so that homogeneous-looking images could be obtained. Overall, although the TGC operation does appear to become more quantitative in nature with the proposed approach, ad hoc adjustments could not be entirely avoided.

3) Regularization

The 50-frame dataset from Fig. 1 was reconstructed several times using different values for λ², the regularization parameter. For each reconstruction, the standard deviation along the time-frame direction was computed and then spatially averaged over 5 ROIs located at different depths (shown in Fig. 1b as white rectangular boxes). Figure 5 gives the mean standard deviation associated with each one of these ROIs, as a function of the regularization parameter λ². For each curve in Fig. 5, an ‘×’ indicates the amount of regularization that appears to be roughly the smallest λ² values that can be used, while still avoiding significant noise increases. Defining a normalized depth $r=\left(\sqrt{x^2+{(z+d_{vf})}^2}-d_{vf}\right)/w_{\mathit{probe}}$, where d_vf is the distance to the virtual focus behind the transducer and w_probe is the width of the transducer probe in the x direction, the location of the ‘×’ marks in Fig. 5 correspond to λ² = r/20. Because having no regularization at r = 0 might be problematic, a minimum value of 0.1 was used for λ², so that λ² = max(r/20, 0.1). In practice, the regularization parameter in Eq. 8 was equated to the constant part of this expression, λ² = 1/20, while the diagonal of the N_vox by N_vox matrix L was equated to the variable part, so that λ²×diag(L) = max(r/20, 0.1), where j ranges from 1 to N_vox.

Fig. 5.

A 50-frames dataset was reconstructed several times, with different settings for the regularization parameter λ². The standard deviation across all 50 frames was taken as a measure of noise, and averaged over the 5 ROIs shown in Fig. 1b. With d = z/w_probe, the ROIs were located at a depth of d = 1.0, 2.5, 3.5, 4.5 and 5.5. For each ROI, the standard deviation is plotted as a function of the regularization parameter λ², and a ‘×’ mark indicates the λ² = d/20 setting selected here.

More generally, this expression cannot be expected to hold for all FOV and probe geometries. For example, when using the ATL probe in a sector-FOV mode rather than the rectangular-FOV mode employed in Fig. 5, a much larger number of voxels get reconstructed from essentially the same number of raw-data points, suggesting that conditioning might be degraded and that a higher level of regularization might prove appropriate. For both the sector-FOV results and the Acuson-probe results presented here, regularization was scaled up by a factor of 4 compared to the expression above, leading to λ²×diag(L) = max(r_j/5, 0.1).

4) Maintaining sparsity

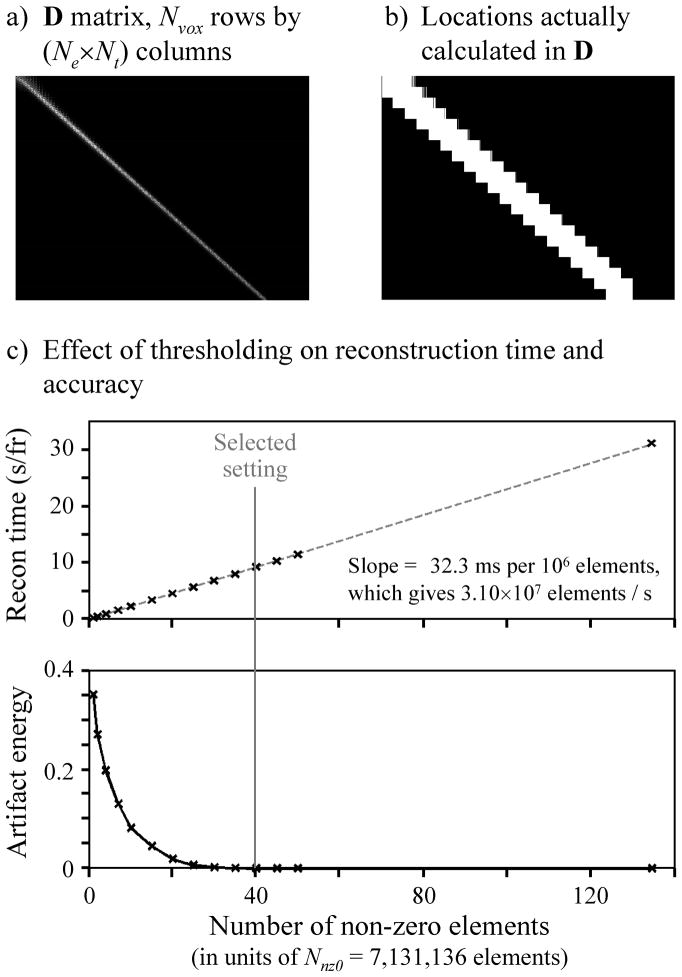
The dataset from Fig. 1a was reconstructed using the proposed method, and the magnitude of the N_vox by (N_e×N_t) matrix D is shown in Fig. 6a. Because D is very sparse, one can greatly decrease computing requirements by calculating only the regions with expected non-zero signals, using a series of overlapping patches. The calculated regions, where elements can assume non-zero values, are shown in Fig. 6b. R is calculated from D, and the plots in Fig. 6c show the effect that thresholding R had on reconstruction time and accuracy. The horizontal axis in Fig. 6c is expressed in terms of N_nz0 = 7131136, the number of non-zero elements in R₀, as obtained when performing a regular delay-and-sum beamforming reconstruction on the same data (Eq. 1). As seen in the upper plot in Fig. 6c, reconstruction time scales linearly with the number of non-zero elements in R with a slope equivalent to 3.10×10⁷ non-zero elements per second, for the IBM workstation mentioned in the Methods section. Based on the lower plot a setting of N_nz = 40×N_nz0 was selected, which is roughly the lowest value that can be used while essentially avoiding any penalty in terms of artifact energy. As compared to the non-thresholded case, an N_nz = 40×N_nz0 setting enabled about a 3-fold reduction in reconstruction time.

Fig. 6.

a) The D matrix (Eq. 8) tends to be very sparse. b) The areas where non-zero signal is expected are covered using many overlapping smaller ‘patches’, greatly reducing the computing requirements as compared to solving for the entire D matrix all at once. c) The R matrix (Eq. 8) and/or the D matrix can be thresholded, so that only the N_nz largest values are allowed to remain non-zero. The smaller N_nz becomes, the faster the reconstruction can proceed, as about 32.3 ms were needed for every 10⁶ non-zero elements, on the IBM workstation used here. But too aggressive a thresholding leads to increased artifact contents. A compromise was reached in this case for N_nz = 40×N_nz0 = 2.852×10⁸ elements.

B. Comparing reconstruction methods

1) PSF

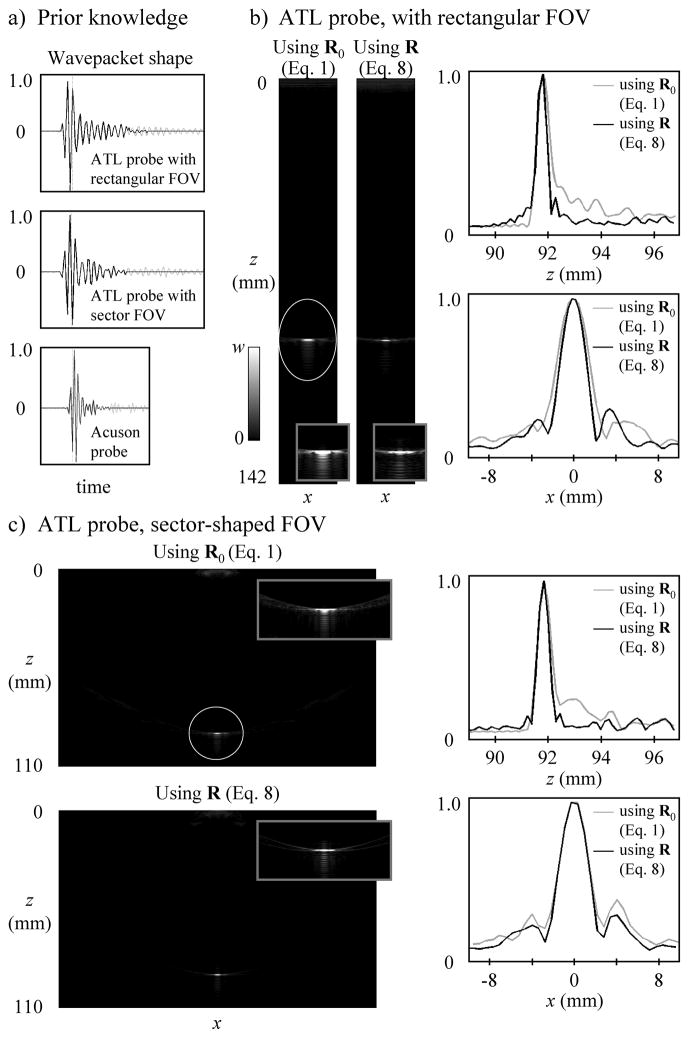
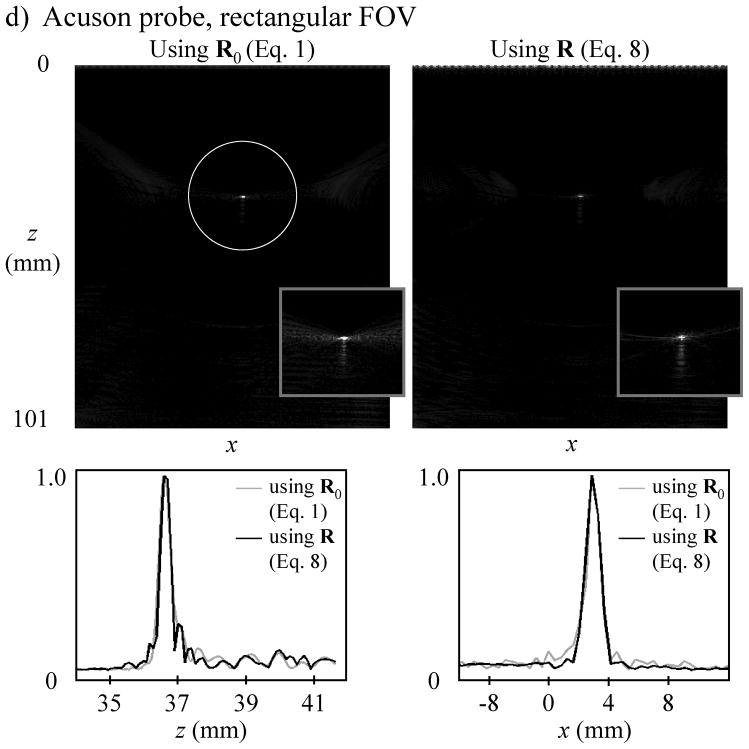
The wavepacket shapes used toward calculating E_wav are shown in Fig. 7a, for all probe and FOV geometries used here. As shown with black curves in Fig. 7a, the wavepackets were cropped to only N_wpts non-zero points to help maintain sparsity in E_wav. In Fig. 7a and in all reconstructions a setting of N_wpts = 50 points was used. Images of the wire phantom are shown in Fig. 7b–d, both for a delay-and-sum beamforming reconstruction (Eq. 1) and for our proposed method (Eq. 8), along with profiles of the PSFs along the x and z directions. All images shown here are windowed such that black means zero or less, white means signal equal to the window width w or more, and shades of gray are linearly distributed in-between. Area and L1-norm measurements of the PSF are provided in Table 1, while Table 2 lists reconstruction times and matrix sizes. Note that delay-and-sum beamforming results were reconstructed with very high nominal spatial resolution (λ×λ/8, Table 2), to help ensure a fair comparison.

Fig. 7.

Imaging results from a metal-wire phantom are interpreted here in terms of a point-spread-function (PSF). a) Prior knowledge about the shape of the wavepacket is used as part of the reconstruction. b–d) Single-shot images reconstructed with delay-and-sum beamforming (R₀ in Eq. 1) and with the proposed approach (R in Eq. 8) are shown side-by-side. All images are windowed such that black is zero or less, white is equal to the window width w or above, and all possible shades of gray are linearly distributed in-between. The ROIs indicated by white ellipse/circles were used for the calculations of the L1-norms listed in Table 1 (3 cm in diameter, 2 cm minor diameter for the ellipse in (a)). Gray boxes show the area surrounding the point-object using a window width w four-time lower than the one used for the corresponding main images, to better show background signals. Profiles across the location of the point-object are also shown, both along the z and the x directions, for delay-and-sum beamforming (gray curves) and for the proposed method (black curves). All plots use a linear scale normalized to the maximum response.

Table 1.

Measurements of PSF size and L1-norm for delay-and-sum beamforming and for our proposed approach (‘practical’ processing in black and ‘optimal’ processing in gray), for different probes and FOV settings

	Point-object x-z location (cm)	Delay+sum central lobe (mm2)	Our method central lobe (mm2)	Improvement	Delay+sum L1-norm (mm2)	Our method L1-norm (mm2)	Improvement
ATL P4-2 rectangular FOV	(0.0, 9.2)	1.55	0.973	37.3%	9.20	6.640	27.8%
			0.972	37.4%		6.53	29.0%
ATL P4-2 sector FOV	(0.0, 9.2)	1.51	1.26	16.6%	11.3	8.28	26.7%
			1.23	18.5%		8.11	28.3%
Acuson rectangular FOV	(0.3, 3.7)	0.324	0.322	0.64%	6.13	3.81	37.8%

Table 2.

Matrix sizes and reconstruction times, for our proposed approach (in black) and for delay-and-sum beamforming (in gray), for different probes and FOV settings

	Raw data size	Image size	Npatch	Voxel size (with λ =c/f)	Nnz	Recon time, stage 1	Recon time, stage 2
ATL P4-2, rectangular FOV	64×2176	64×924	10	pitch × λ/4	3.03e8	13.6 hrs/0 s	0.039±0.004 s/frc
	same	64×1850	1	pitch × λ/8	7.40e6	31.62 s/0 s	0.044 s/fr
ATL P4-2, sector FOV	64×2048	286×716	15	λ× λ/4	1.05e9	66.7 hrs/0 s	1.70±0.06 s/frc
	same	286×1434	1	λ× λ/8	2.58e7	4.17 min/0 s	0.18 s/fra
Acuson, rectangular FOV	128×2560	213×985	3×40	λ× λ/4	3×8.58e8	3×52.2 hrsb/0 s	3(1.39±0.06) s/frc
	same	213×1971	1	λ× λ/8	4.75e7	16.0 minb/0 s	0.30 s/fr

^aDoes not include gridding time

^bPerformed on the 128 GB IBM system

^cProcessed using a C program with 8 threads

As seen in Table 1, the size of the PSF was reduced by up to 37% (ATL probe with rectangular FOV), while the L1-norm of the PSF was reduced by up to 38% (Acuson probe with rectangular FOV). As compared to the ATL probe results, using the wider 128-element Acuson array and reducing the depth of the metal-wire location to only about 4 cm lead to very compact PSF distributions (0.32 mm², from Table 1). In this case our method had very little room for improvements in terms of PSF size (1% improvement, from Table 1), but a 38% reduction of the L1-norm of the PSF was achieved. Reductions of the L1-norm mean that less signal may leak away from high-intensity features, and that higher contrast might be obtained, as verified below using the CIRS phantom.

Gray numbers in Table 1 refer to an ‘optimized’ reconstruction tailored to the metal-wire phantom, whereby a 1.5 by 1.5 cm square region centered at the object-point location was reconstructed using a single patch (N_patch = 1) and high spatial resolution (λ × λ/4, where λ is the wavelength = c/f). Such ‘optimized’ reconstructions were performed for comparison purposes on both datasets obtained with the ATL probe, with rectangular- and sector-shape FOV. Note that the optimum reconstruction brought very little further improvements in terms of PSF size or L1-norm (see Table 1, gray vs black numbers).

2) Phantom imaging

Because the R₀ and R matrices had already been calculated for the PSF results shown in Fig. 7, no further processing was required and the pre-computed matrices were simply reused for reconstructing the images in Fig. 8. The fact that no new processing was needed is emphasized in Table 2 using “0 s” entries in the “Recon time, stage 1” column.

Fig. 8.

a) Imaging results were obtained from the phantom depicted here. b–d) Single-shot images reconstructed with delay-and-sum beamforming (R₀ in Eq. 1) and with the proposed approach (R in Eq. 8) are shown side-by-side. A zoom of the region surrounding the axial-lateral resolution targets is shown in (b) (the window width, w, was increased by 250% to better show the individual objects). Overall, spatial resolution appears to be improved in the images reconstructed with the proposed method (i.e., with R in Eq. 8). Contrast was improved with the proposed method in (d), as tested using the circular ROI covering the hyperechoic region indicated with a white arrow and the ring-shaped region that surrounds it. See text for more details.

A schematic of the imaged phantom is provided in Fig. 8a, and single-shot images are shown in Fig. 8b–d for both the delay-and-sum beamforming (R₀ matrix) and the present reconstruction method (R matrix), for the 3 imaging geometries considered here. The side-by-side comparison appears to confirm that the present approach (as expressed through Eq. 8), succeeds in increasing spatial resolution as compared to a delay-and-sum beamforming reconstruction (as expressed through Eq. 1), at least in results obtained with the 64-element ATL probe. Using the wider 128-element Acuson linear, the improvement in spatial resolution appears to be subtler. On the other hand, the reduction in the L1-norm of the PSF (Table 1) does appear to have detectable effects in the images shown in Fig. 8d. Using the ROIs defined in Fig. 8d, and with S_C the mean signal over the inner circular ROI and S_R the mean signal over the ring-shaped ROI that surrounds it, contrast for the hyperechoic circular region (arrow in Fig. 8d) was defined as (S_C − S_R)/(S_C + S_R). The inner circular ROI had an 8 mm diameter, equal to the known size of the phantom’s hyperechoic target, and the surrounding ring-shaped ROI had an outer diameter of 12 mm. Because a lesser amount of signal was allowed to ‘bleed’ away from the hyperechoic region when using our proposed reconstruction approach, contrast as defined above was increased by 29.2% compared to the delay-and-sum beamforming results, from a value of 0.248 to a value of 0.320.

V. Discussion

An image reconstruction method was presented that offers advantages over the traditional delay-and-sum beamforming approach. Without any increase in risk or exposure to the patient, and without any penalty in terms of ultrasound penetration, spatial resolution and/or contrast could be increased through a more accurate reconstruction of the acquired data. The proposed reconstruction process involved a single matrix multiplication without any need for separate envelope detection or gridding steps, and improvements by up to 38% in the area and/or the L1-norm of the PSF were obtained for three different FOV and probe configurations. As a limitation of the results presented here, the acquired data enabled a quantitative characterization of the PSF at only a single location within the imaged FOV. A series of measurements involving different relative positions between the imaging probe and the imaged metal wire would be required if spatial maps of PSF improvements were to be obtained, rather than a single spatial location. Although more qualitative in nature, results from a CIRS imaging phantom suggested that improvements in PSF may be occurring throughout the imaged FOV.

It is worth noting that the amounts of spatial resolution and contrast improvements reported here do not necessarily represent a theoretical limit for the proposed algorithm, but merely what could be achieved with the present implementation. In principle at least, in a noiseless case where the encoding matrix is perfectly known, the PSF could be reduced to little more than a delta function (e.g., see Fig. 2c). In more realistic situations, limitations on the achievable spatial resolution result from inaccuracies in the encoding matrix, the need to use regularization, and limits on both memory usage and reconstruction time. It is entirely possible that with a more careful design for E_wav and/or for the regularization term λ²L, or greater computing resources, greater improvements in spatial resolution and/or contrast might have been realized. On the other hand, in especially challenging in vivo situations where processes such as aberration may affect the accuracy of E_wav, lower levels of improvement might be obtained instead. The possibility of including object-dependent effects such as aberration into E_wav, although interesting, is currently considered impractical because of the long processing time required to convert E_wav into a reconstruction matrix R (Eq. 8).

Prior information about the transmitted wavepacket was obtained here from a single transducer element, during a one-time reference scan, using a phantom consisting of a metal wire in a water tank. Interestingly, when using the proposed reconstruction scheme, the TGC part of the algorithm became more exact and less arbitrary in nature, as the nominal 0.5 db/cm-MHz attenuation coefficient of the imaged phantom could be used directly toward calculating attenuation corrections. Scaling difficulties did however remain, especially in the near field, and ad hoc corrections could not be entirely avoided.

A main drawback of the proposed approach may be its computing load. Although the ‘real-time’ part of the processing consists of a single multiplication operation between a matrix R and the raw data s, the R matrix tends to be very large and the multiplication is computationally demanding. The use of ‘graphics processing unit’ (GPU) hardware, which enables extremely fast processing in some applications, may not be appropriate here. In current systems at least, the graphics memory is still fairly limited and physically separate from the main memory, meaning that much time might be wasted transferring information to and from the graphics card. While GPU processing may prove particularly beneficial in situations that require a large amount of processing to be performed on a relatively small amount of data, it is not nearly as well suited to the present case where fairly simple processing (a matrix multiplication) is performed on a huge amount of data (mainly, the matrix R). For this reason, ‘central processing unit’ (CPU) hardware is exploited here instead, and a multi-threaded reconstruction program was written in the C language. Reconstruction times in the range of about 0.04 to 4 s per image were obtained here, using 8 processing threads on an 8-processor system. Using more threads on a system featuring more cores would represent an obvious way of reducing processing time. Further improvements in our programming and future improvements in computer technology may also help. If necessary, sacrifices could be made in terms of voxel size, spatial coverage and/or artifact content, to further reduce the number of non-zero elements in R and thus reduce processing time. It should be noted that even in cases where frame rates required for real-time imaging could not be achieved, the present method could still be used to reconstruct images saved and recorded as part of clinical ultrasound exams.

Unlike for the ‘real-time’ operation R × s, the processing speed for the initial one-time evaluation of R is considered, for the most part, of secondary importance. In the present implementation, processing times ranged from about 7 hours to well over 100 hours, depending on probe and FOV geometry. While reducing this time through algorithm improvements and/or parallel processing would be desirable, it is not considered an essential step toward making the method fully practical. Because these lengthy calculations can be re-used for all subsequent images acquired with a given transducer, excitation voltage waveform and FOV setting, long initial processing times do not prevent high frame rates to be achieved. In practice, several R matrices corresponding to different transducers and a range of FOV settings can be pre-computed, stored, and loaded when needed.

VI. Conclusion

An image reconstruction method was introduced that enabled valuable improvements in image quality, and computing times compatible with real-time imaging were obtained for the simplest case considered here (0.039 s per frame). The method proved capable of reducing the area and/or L1-norm of point-spread-functions by up to about 38%, allowing improvements in spatial resolution and/or contrast at no penalty in terms of patient risk, exposure or ultrasound penetration.

VII. Appendix

A. Generating the E_wav matrix

The generation of the E_wav matrix in Eq. 8 can be considered of central importance to the proposed approach. Prior knowledge about the shape of the wavepacket (see Fig. 7a), stored in a row-vector ‘wvpckt’ featuring N_t elements, is transformed here to the temporal frequency domain and duplicated N_e times into the N_e by N_t array ‘wvpckt_f’:

wvpckt_f = repmat (fft (wvpckt, [], 2), [Ne 1]);

For each voxel ‘ivox’ to be reconstructed, a corresponding arc-shaped e-t space wavepacket function is calculated through modifications to wvpckt_f. First, a ‘travel_time’ vector with N_e entries is obtained:

d_travel = d_to_object + d_from_object;
t_travel = d_travel/sound_speed;

With ‘t_ref’ the time point within the wavepacket to be considered as the origin, a phase ramp is placed on wvpckt_f that corresponds to the appropriate element-dependent time shift:

t_travel = t_travel - t_ref;
ph_inc =-(2*pi/Nt) * (t_travel/dt + 1);
ph_factor = ph_inc * (0:Nt/2-1);
arc = zeros(Ne, Nt);
arc(:,1:Nt/2) = wvpckt_f(:,1:Nt/2).*exp(1i*ph_factor);
arc = ifft (arc, [], 2);

To maintain sparsity in E_wav, only a relatively small number of time points (50 here) can be kept for each wavepacket in ‘arc’ (see Fig. 7a). A sparser version of ‘arc’ is thus obtained, called ‘arc_sparse’, stored into a 1D column-vector featuring N_t × N_e rows, and normalized so that its L2-norm is equal to 1:

E_1vox(:) = arc_sparse(:);
scaling = sqrt (sum(abs(E_1vox(:)).^2,1));
E_1vox(:) = E_1vox(:) ./(scaling+epsilon);

Finally, the calculated result for voxel ‘ivox’ can be stored at its proper place within E_wav:

Ewav(:,ivox) = E_1vox(:,1);

The process is repeated for all ‘ivox’ values, to obtain a complete E_wav matrix.

B. Matrix inversion and image reconstruction

For each patch within D (see Fig. 6b), and with ‘E’ representing the corresponding region within E_wav, the inversion in Eq. 8 can be performed through:

Ep = E’;
EpE_inv = inverse(Ep*E + lambda_L);
EpE_inv = double(EpE_inv);

where inverse(·) is part of a freely-downloadable software package developed by Tim Davis, http://www.mathworks.com/matlabcentral/fileexchange/24119. Alternatively, the readily available Matlab inv(·) function may be used instead, although it is generally considered less accurate:

EpE_inv = inv(Ep*E + lambda_L);

The reconstruction times provided in Table 2 were obtained using Matlab’s inv(·) function. As shown in Eq. 8, the (E_wav^H × E_wav + λ²L) ⁻¹ term gets multiplied by (I + λ²L) and by E_wav^H:

EpE_inv = EpE_inv * (speye(Nvox_patch,Nvox_patch)+lambda_L);
D = EpE_inv * Ep;

Optional thresholding may be performed on D. The current patch, which involves all voxels listed into the array ‘i_vox’, can then be stored at its proper place within the matrix R:

R(i_vox,:) = R(i_vox,:) + W*D*T;

where T is for TGC and W is a diagonal matrix with a Fermi filter along its diagonal, to smoothly merge contiguous overlapping patches. The matrix R is thresholded, and the image corresponding to time frame ‘ifr’ can be reconstructed with:

s = zeros(Nt*Ne,1);
s(:) = data(:,:,ifr);
O_vec = R*s;

The N_vox by 3 array ‘voxs’ is a record of the x, z and matrix location for every image voxel being reconstructed. The 1D vector ‘O_vec’ gets converted into a ready-for-display 2D image format through:

O = zeros(Nz, Nx);
O(voxs(:,3)) = O_vec;