Structural Determinants of Water Permeation through the Sodium-Galactose Transporter vSGLT

Abstract

Sodium-glucose transporters (SGLTs) facilitate the movement of water across the cell membrane, playing a central role in cellular homeostasis. Here, we present a detailed analysis of the mechanism of water permeation through the inward-facing state of vSGLT based on nearly 10 μs of molecular dynamics simulations. These simulations reveal the transient formation of a continuous water channel through the transporter that permits water to permeate the protein. Trajectories in which spontaneous release of galactose is observed, as well as those in which galactose remains in the binding site, show that the permeation rate, although modulated by substrate occupancy, is not tightly coupled to substrate release. Using a, to our knowledge, novel channel-detection algorithm, we identify the key residues that control water flow through the transporter and show that solvent gating is regulated by side-chain motions in a small number of residues on the extracellular face. A sequence alignment reveals the presence of two insertion sites in mammalian SGLTs that flank these outer-gate residues. We hypothesize that the absence of these sites in vSGLT may account for the high water permeability values for vSGLT determined via simulation compared to the lower experimental estimates for mammalian SGLT1.

Introduction

The Na⁺-glucose transporter (SGLT) is a member of a broad class of cotransporters that harness the energy stored in ionic gradients to drive the transport of substrates across membranes. Specifically, SGLTs are symporters that use sodium gradients to pump simple sugars into the cell (1,2). In addition to its primary role as a sugar transporter, it is well accepted that mammalian SGLTs, such as human SGLT isoform 1 (hSGLT1), are permeable to water (3–7). Additionally, intestinal water absorption is closely linked to the coupled absorption of salt and sugar, and this provides the basis for oral rehydration therapy (ORT). It is estimated that ORT has reduced the mortality of children with acute diarrhea from 4.6 million in 1980 to 1.5 million in 2000 (8). Although there is no dispute that glucose-stimulated water absorption is directly linked to Na⁺/glucose cotransport by SGLTs, the exact nature of the coupling is controversial.

There is broad consensus that SGLTs facilitate passive water flow across membranes in response to osmotic gradients (5–7,9), and this property has been observed for several other transporters (10). Passive water flow is independent of the presence or absence of galactose, but it is sensitive to the conformational state of the transporter, since flow is blocked by inhibitors known to trap SGLTs in an outward-facing conformation (11). In addition to its role as a passive water channel, it has been observed that SGLT1 undergoing normal transporter turnover energized by a Na⁺ or glucose gradient can move water from a region of low osmolyte concentration to a region of high osmolyte concentration. Two general classes of model have been developed to explain this observation: molecular-based models involving the cotransport of water (4,11–14), or an unstirred-boundary-layer model, which posits the existence of local osmotic gradients due to the build-up of sugar near the membrane (5,6,9,15).

Experiments supporting the water cotransport hypothesis show that each transport cycle of SGLT1 delivers 260 water molecules into the cell, along with two Na⁺ and one sugar, in a tightly coupled manner (4). These models rely on the alternating-access mechanism (1,16), in which a water-filled cavity is first presented to the extracellular solution to bind ion and substrate (outward-facing state), and then closed to the extracellular solution and opened toward the interior of the cell (inward-facing state) via a rocking mechanism. The water-filled cavities contain a substantial number of water molecules, and the inward movement of ion and substrate moves these water molecules with them via a number of potential mechanisms nicely outlined by Zeuthen and MacAulay (17). Contrary to the cotransport models, the unstirred-boundary-layer hypothesis suggests that SGLTs are not able to actively pump water molecules, but rather that water movement occurs passively due to the establishment of a local osmolyte concentration gradient (5,6,9,15). In this model, SGLT activity increases the intracellular concentration of Na⁺ and sugar at the membrane due to slow intracellular diffusion while at the same time depleting the extracellular concentration. Together, these changes set up an osmotic gradient that is favorable for water entry into the cell through a conformational state of the transporter, which is permeable.

In the absence of a high-resolution structure of hSGLT1, structures of the bacterial homolog from Vibrio parahaemolyticus, vSGLT, provide a useful model for beginning to understand the molecular underpinning of water transport in the broader sodium solute symporter families (SSS and NSS). vSGLT shares significant sequence identity with SGLT1 and retains even higher conservation among key residues involved in gating and ligand binding (2,18–23). Unfortunately, no experimental data exist for the water permeability of vSGLT due to its poor expression levels in Xenopus oocytes (24), thus preventing a direct comparison. However, all-atom molecular dynamics (MD) simulation coupled with the crystallographic structure of vSGLT provides a way of tracking the motions of the solvent, substrate, and transporter with the high temporal and spatial resolution required to provide a dynamical account of their coupling. Using this approach, our group performed, to our knowledge, the first simulations showing the existence of an aqueous pathway traversing vSGLT (14). This pathway allows water to permeate the inward-facing state. This observation was later confirmed by other groups (15,25,26).

In this study, we used trajectories collected from a series of MD simulations, each 500–1800 ns in length, to sample water flow through the inward-facing state of vSGLT before, during, and after substrate release. This ensemble of 21 simulations, which includes 10 spontaneous sugar escapes, permits a careful analysis of the role of both sugar and transporter motions in controlling water flow through the transporter. We observe the formation of transient water-conducting states in which residues in the outer gate of the transporter undergo a conformational transition to open a pore connecting the aqueous lumen of vSGLT to the extracellular bulk. Although sugar does not influence the passive water permeability of SGLT1, our simulations show that bound galactose occludes the water channel, reducing permeability. Fluctuations in the inward and outward flow of water give rise to net water movement over short periods of time, but this net movement occurs outward as much as inward, as we would expect at equilibrium, and it was poorly correlated with galactose exit from the binding site. Based on the location of key residues along the water permeation pathways and multiple sequence alignments, we propose that two large, conserved extracellular loops found in SGLT1 and SGLT 2 from higher organisms, but not in prokaryotic homologs, may explain differences between the permeabilities calculated from our simulations and those measured experimentally for mammalian SGLT1 (27).

Methods

MD simulations

Four independent all-atom models of monomeric vSGLT embedded in a lipid bilayer were constructed based on the x-ray structure of the inward-occluded, galactose-bound state (PDB ID 3DH4) (21) using MODELLER (28) and the CHARMM-GUI Membrane Builder (29). The model was parameterized using the CHARMM22 force field (30) with CMAP corrections (31) for the protein, the CHARMM36 lipid force field (32), the CHARMM pyranose monosaccharides parameter set for the galactose (33), and the TIP3P explicit water model (34). Each model was minimized and equilibrated using NAMD 2.7 (35), and then coordinates and velocities from these runs were used to initiate simulations on the Anton special-purpose supercomputer (36).

The first model (M0) was equilibrated for 20 ns without restraints, during which time the sodium ion bound in the Na2 site exited and migrated into bulk solution before a 2.8 μs production simulation was initiated on Anton. For the remaining three models (M1–M3), the sodium ion remained bound throughout the 20 ns equilibration period. We then extended each simulation an additional 70 ns and selected snapshots of the simulation spaced 10 ns apart to use as starting points for 21 separate production runs on Anton. Upon initializing these simulations on Anton, both galactose and the Na2-site sodium ion were placed near their crystallographic poses. In nine of the simulations, the galactose had a root mean-square deviation (RMSD) of <1 Å from the 3DH4 coordinates, whereas in the remaining simulations, the RMSDs were between 2 and 7 Å. Fourteen of the simulations began with sodium within 2 Å of the crystallographic position, with the remainder exhibiting RMSDs of <3.5 Å.

We consider the resulting set of trajectories to be effectively independent, since the distribution of water molecules and the RMSD of the protein decorrelate on the 10 ns timescale. Each production trajectory was run until either both the sodium and galactose escaped into the bulk solvent phase or the simulation reached ∼480 ns. Initially, coordinates were recorded every 100 ps. For the 10 simulations in which sugar exited the transporter, we resampled the exit event at a 1 ps interval to track the movement of individual water molecules with high fidelity. Additional details about the preparation of the systems and simulations are provided in the Supporting Material.

Water-flow calculations

Water molecules in the simulation could exchange between the intracellular and extracellular solutions by permeating through the transporter, or by crossing the upper and lower simulation boundaries along the z direction due to the periodicity of the simulation box. The latter mechanism is an artifact of the simulation method and is explicitly removed from the analysis, as described below. Crossings mediated by the protein-lipid interface were negligible and do not affect the overall statistics.

We confine our analysis to permeation events wherein water molecules pass directly through the transporter as they move from one bath to the other. After centering the sugar-binding site of the transporter at the origin, we divided the simulation box into three regions using two planes oriented parallel to the membrane in the xy plane. The planes were placed at ±15 Å along the z axis, and all water molecules were initially assigned to a region based on the coordinates of the oxygen atom at the start of the trajectory. Time-dependent assignments for every water molecule were calculated, and we counted only permeation events that sequentially passed from one bulk phase region to another by way of the central region. Using this method makes it possible to distinguish events that move up through the transporter from those that move down through the transporter. The numbers of permeation events in each direction were averaged over 1 ns windows, and the net water flow through the transporter is defined as the cumulative sum of upward events minus downward events.

Water molecules cannot cross the entire transporter in <1 ps, so it is possible to unambiguously determine vSGLT-facilitated movement from one bulk to the other using our 1 ps sampling data. However, the distance that water can diffuse in 100 ps is significantly larger, especially in the bulk phase. At that temporal resolution of sampling, errors arise in correctly assigning the order in which a water molecule visits each region. We estimate that by downsampling our 1 ps data sets to 100 ps, statistics gathered using the longer sampling interval undercount the true number of permeation events by ∼6% after correcting for systematic errors caused by the periodic boundary (see the Supporting Material).

Path-based method for calculating pore size

We developed a, to our knowledge, novel method for determining the narrowest region along a water permeation pathway by using the atomic positions of water molecules recorded from MD trajectories. Identifying this region can be challenging for irregular three-dimensional pathways through a protein, especially when there are multiple pathways and cavities that bifurcate from the main channel and residues lining the channel are dynamic. To address this problem, we enumerate the number of distinct water chains that pass from the extracellular space to the intracellular solution through the transporter for each frame of a trajectory. A water chain, or path, is defined as a series of contiguous water molecules where the distance between adjacent oxygen atoms in the chain, d_c, is ≤3.2 Å.

First, we wrap the simulation cell for all trajectories such that the center of mass of the protein coincides with the origin. The entire system is then rotated to superimpose the instantaneous coordinates of the protein’s nonhydrogen atoms onto the crystallographic reference structure. We then calculate the pairwise distances between the oxygen atoms of all water molecules separated by no more than $d_c$ and within a cylinder 25 Å in radius with ends at +35 Å and −35 Å in the z-direction. These pairwise distances are used to construct an adjacency matrix describing the network of water molecules in and around the transporter.

Starting from the water whose oxygen atom is closest to (0, 0, −30) Å, Dijkstra’s algorithm (37) is employed to calculate the shortest path through the network terminating above $z=30$ Å. If a chain is found that successfully connects the two bulk phases through the transporter, all water molecules in the path are pruned from the network, and the shortest path on the subset of remaining water molecules is calculated. This iterative process is repeated until no additional pathways can be found. The resulting set of pathways are independent, as the set of water molecules within a path are unique to that path (i.e., the pathways are nonoverlapping). The number of water chains that connect the bulk regions is then a measure of the width of the channel at its narrowest point. Failure to find a pathway for a given frame indicates that the intra- and extracellular regions are separated by a dehydrated constriction zone.

Identification of residues that gate the water channel

The pathfinding algorithm described in the previous section provides not only an estimate of the size of the water pathway, but a direct way to identify the moieties that disrupt water flow through the transporter. For each frame that lacks a continuous water chain connecting the intra- and extracellular regions, we attempted to identify the closest water molecules on each side of the discontinuity to enumerate the intervening residues or substrate molecule that restricted water movement through that region. In these frames, by definition, oxygen atoms on either side of the discontinuity are separated by more than the 3.2 Å cutoff, $d_c$. To isolate these water molecules, the original cutoff distance is supplemented by a second cutoff that is increased gradually in 0.5 Å steps until a continuous pathway can be found. Those pairs of oxygen atoms whose distance is >$d_c$ but less than the second cutoff are penalized by a factor of $\alpha =10$ during the calculation of the shortest path using Dijkstra’s algorithm. This penalty term ensures that the method preferentially selects oxygen atoms separated by the shorter distance when available in building the path. Once the second cutoff is increased to a sufficient distance to create a continuous path through the discontinuity, all pairs of oxygens separated by >$d_c$ are recorded.

For each recorded oxygen pair, we then create a cylindrical volume formed by the line segment between the pair and extending outward 2 Å in radius from the axis. We record all nonhydrogen atoms belonging to either the protein or the galactose molecule within the volume. The corresponding residues play at least a transient role in gating water movement through the transporter by occluding the pathway.

Sequence alignment

The sequence of vSGLT (NCBI accession number AAF80602.1) was obtained from GenBank along with the corresponding sequences for SGLT1 and SGLT2 from human, rabbit, and rat (accession numbers P13866.1, P11170.1, P53790.1, P31639.1, P26430.1, P53792.1, respectively). The sequences of several prokaryotic homologs with known functional conservation to the SGLT family, including the proline transporter, PutP (accession number ZP_03034013.1), and the pantothenate permease, PanF (accession number P16256.2), both from E. coli, were obtained from the same source. A sequence alignment of the residues corresponding to the 10 core transmembrane helices in vSGLT, from Faham et al. (21), has been used previously to construct an experimentally validated homology model of hSGLT1 (23). We started with this alignment, which included the partial sequences of vSGLT, hSGLT1, and PutP and extended it using TM-Coffee (38) to include the SGLT isoforms from rabbit and rat, as well as PanF, for the complete sequences of each transporter.

Results

Water permeation is correlated with the transient formation of a continuous water channel through the extracellular gate

The amount of water permeating vSGLT fluctuates significantly during our simulations, as the transporter appears to interconvert between putative water-conducting and nonconducting states. Although water readily moves through the transporter for periods of hundreds of nanoseconds (Fig. S2, A–D, in the Supporting Material), we also detect quiescent states with substantially less water permeation (Fig. S2, E–H). These changes are not mediated by large-scale conformational changes in vSGLT, as the RMSD of the core-transporter domain with respect to the starting x-ray structure remains small throughout the trajectory (see Fig. S3).

To understand the subtle structural rearrangements in the transporter that were controlling these changes in water flow, we attempted to identify the water pathways through the transporter. Initially, we used the programs HOLE (39) and 3V (40) to identify channels and cavities in static snapshots of the protein extracted from the simulation trajectories. Unfortunately, unlike many ion channels, the water pathways through vSGLT are convoluted and lack axial symmetry, and using these software packages failed to reliably identify pathways whose biophysical properties quantitatively correlated with the magnitude of water flux.

To overcome this issue, we developed a, to our knowledge, novel path-based algorithm to identify water chains through the protein directly from simulation snapshots, allowing us to calculate the effective radius of the water channel created by the protein as a function of time. The method first marks all water molecules near the transporter, and then traces out single water pathways from the bulk intracellular solution to the bulk extracellular solution using Dijkstra’s algorithm. Two water molecules are assumed to be in contact if their oxygen atoms are within $d_c=3.2$ Å of each other. After a pathway is identified through the transporter, all waters in the path are removed and the process is repeated until a path can no longer be found. This occurs when a dehydrated zone appears in the transporter in which water molecules are separated by >$d_c$. The total number of identified pathways approximates the size of the water channel at its narrowest point.

Fig. 1 shows the total number of paths detected in 1 ns blocks together with the maximum instantaneous water influx and efflux. The number of nonoverlapping paths correlates well with the water transport, suggesting that water flow is strongly coupled to the size of the constriction zone along the water permeation pathway. There are, however, periods in which flow and path number are poorly correlated (see 100–150 ns in Fig. 1 A and 375–400 ns in Fig. 1 B). Closer qualitative inspection of the simulations revealed a primary channel encompassing most pathways (Fig. 1 C, red path) and a secondary, transient channel that branches from the primary channel (Fig. 1 C, green path). The secondary channel diverges from the primary channel passing between the interface of the extracellular half of TM10 above G432 and TM helices 11 and 12. This bifurcation occurs above the galactose binding site, circumventing the extracellular gate. Water in the secondary channel is far less dynamic than that in the primary channel; consequently, the secondary channel has a significantly reduced permeability. When we removed contributions from the secondary channel from our calculation of the number of permeant paths, the discrepancies previously noted were largely ameliorated (Fig. 1, D and E).

Figure 1.

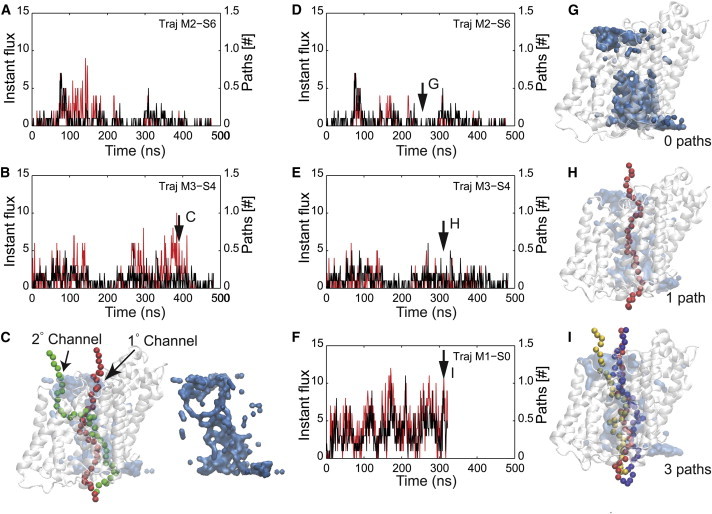
Instantaneous water flow and the identification of water channels. (A and B) Total number of independent water pathways (red) and maximum instantaneous water flow (black) versus time for two representative trajectories. Instantaneous water flux is defined as the number of upward or downward permeation events in 1 ns, and the maximum instantaneous water flux is the larger of these two values. The independent water pathways are the average number of paths identified from the lower bulk to the upper bulk averaged over 1 ns. The red and black curves show marginal agreement, but there are noticeable exceptions, for instance at 375 ns in B, where there are many paths through the transporter even though the water flux is low. The black arrow in B indicates the time from which the snapshot in C is taken. (C) Visualization of the water pathways when the instantaneous water flow and the total pathways are poorly correlated. The snapshot corresponds to the time indicated in B (black arrow). In the snapshot at left, vSGLT is white, and the molecular surface representation of the water is light blue. Two pathways are present: the main channel (red) and a secondary channel (green). Additional analysis revealed that water movement through the secondary channel is slow, and that the primary channel is responsible for the majority of the water flux. At right, the water surface is pictured alone to show clearly the trajectories of the two independent and contiguous pathways. (D–F) Removal of secondary-channel data results in excellent correlation between pathway numbers (red) and maximum instantaneous water flow (black). Pathways that ran through the secondary site (C, green path) were systematically removed, resulting in marked improvement in the correlations shown in A and B, as can be seen in D and E, respectively. Simulations represented in D–F show an increasing degree of channel openness, as well as an increasing degree of water flux. (G–I) Snapshots with zero (G), one (H), and three (I) independent pathways corresponding to the plots in D–F, respectively. The color scheme is as in C. In each snapshot, the oxygen atoms from independent pathways are represented by different colors. To see this figure in color, go online.

Next, we used our method to determine which residues were responsible for occluding the aqueous channel. We started by selecting every frame from the trajectories in which no continuous paths were detected. Focusing on the constriction zones along these pathways, as described in Methods, we identified the residues that lie in the dehydrated region. We tallied the number of times that a particular residue was involved in blocking the pathway and plotted the probability of finding any given residue in any gap (Fig. 2 A). Picking a cutoff of 5% (dashed line), our analysis reveals that the side chains of residues S76, Y87, N245, D336, Q422, F424, Q425, and Q428, along with the bound galactose, are responsible for interrupting the continuous water pathway through the transporter. A subset of these residues (Y87, F424, and Q428) were recently identified as lining the constriction zone based on direct observation of simulations (25), and Y87 and F424 were proposed to form part of the extracellular gate along with M73, based on visualization of the static x-ray structure (21). Using grand canonical Monte Carlo simulations of the transporter, Sasseville et al. also identified Y87, Q425, and Q428, as well as A259, F479, and M483, as components of a constriction zone that acted as a barrier to water permeation through vSGLT (15). It is not surprising that some of these amino acids have bulky hydrophobic side chains capable of occluding and drying pathways in particular rotameric states, whereas others are charged or polar and form interactions between adjacent TM helices to hold the outer gate shut.

Figure 2.

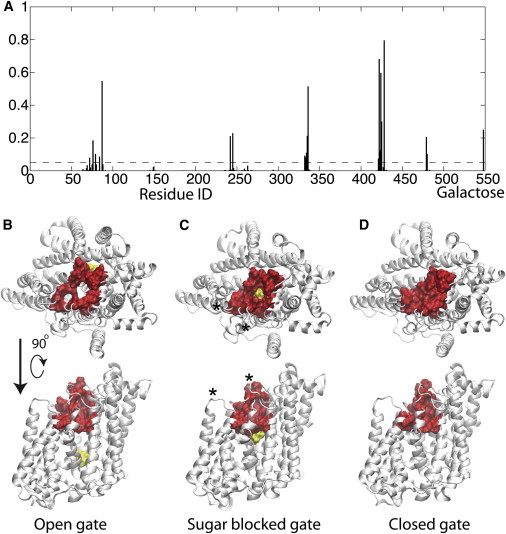
Identification of residues that control the number of water pathways. (A) Probability of a protein residue or galactose being identified in a gap region. Probability is calculated as the number of total observations divided by the total frames involving water gaps. The x axis is the protein residue number in vSGLT with galactose (1–547), with the galactose being the final value. The dashed line corresponds to a 5% (0.05) probability. (B–D) All residues observed in >5% of gaps were highlighted (red) on the vSGLT structure (white) in high water flux (B) and in two low-water-flux states (C and D). Galactose is yellow. Each structure is shown from the extracellular space (upper) and from the membrane (lower). In B, the residues form an annulus with an open center. The side view shows that all residues are localized to the extracellular side of the transporter. In C, the residues form an open annulus, but with the sugar plugging the hole, which explains why no water pathways are found in this snapshot. The asterisks indicate the positions of the insertion sites described in Fig 4 and the Discussion. In D, it can be seen that the outer residues all come together to occlude the outer gate and prevent water pathways through the channel. All of the molecular images were rendered using VMD (61). To see this figure in color, go online.

We highlighted the primary gating residues on the vSGLT structure in a high-water-flux configuration (Fig. 2 B) and two low-water-flux configurations (Fig. 2, C and D). As can be seen from the lower row of structures in Fig. 2, B–D, the identified residues all localize to the outer-gate region above the galactose binding site on the extracellular side of the protein. In addition, the residues form an open annulus when the water flux is high (Fig. 2 B) and a completely closed mass when the water flux is low (Fig. 2 D). Interestingly, we realized that the residues were sometimes open, as in Fig. 2 C, despite a very low water flux. In these cases, the galactose molecule occludes the water channel, preventing water flow (see Fig. 2 C).

We also examined the role of galactose in controlling water flow through the transporter. As shown in Fig. S4, when the sugar has an RMSD of <2 Å with respect to the crystallographic pose, the average water flow is nearly four times smaller than when the sugar is in bulk solution. The fluctuations in flow are also dramatically suppressed when sugar occupies the binding site. This is consistent with the ability of the gating residues to occlude the permeation pathway in the absence of substrate. A similar dependence of water flow on sugar occupancy was previously observed in simulations carried out by the Tajkhorshid lab (25).

Diffusional and osmotic water permeabilities of vSGLT

Additional insight into the biophysical nature of the permeation mechanism was obtained from a comparison of the osmotic permeability coefficient, $p_f$, and the coefficient of diffusional water exchange, $p_d$. We estimated these quantities directly from our equilibrium simulations using the theory developed by Zhu et al. (41), as done in our previous work with vSGLT (14). Water movement in the system must be accurately tracked to provide high-fidelity estimates of the water-diffusion and osmotic-permeability coefficients. All simulations were recorded at either 1 ps or 100 ps intervals. The 100 ps sampling introduces some uncertainty in the tracking of water movement, as described both in Methods and in the Supporting Material. Our analysis indicates, however, that the error associated with the calculation of $p_d$ from the trajectories sampled at 100 ps intervals is only 6%. We therefore used our entire collection of trajectories, with an aggregate total simulation time of 6.5 μs, to calculate $p_d=5.1\times {10}^{-14}$ cm³/s with a 95% confidence interval of $p_d=\left(4.6,5.7\right)\times {10}^{-14}$ cm³/s.

The osmotic permeability coefficient, however, is much more sensitive to the sampling interval, so accurate estimates could only be made using our 1 ps sampling data. Using this smaller subset of the data, we determined that $p_f=2.7\times {10}^{-13}$ cm³/s with a 95% confidence interval of $p_f=\left(2.2,3.1\right)\times {10}^{-13}$ cm³/s. The discrepancy between the values of $p_f$ reported in this study and in our previous work (14) and the much smaller value presented in Li et al. (25) are discussed in the Supporting Material.

Experimentally, $p_f$ measured in SGLT1 from rabbit is 4.5 $\times {10}^{-16}$ cm³/s (27), which is 600 times smaller than our reported value. The $p_f$ and $p_d$ values reported here are consistent with results from previous simulations, where the high $p_f$ compared to the experimental value was originally noted (14). We will return to this topic in the Discussion. The ratio $p_f\text{/}{p}_d$ is related to the structure of water in the channel (42) and is a measure of the degree of cooperativity in the transport process, with values close to 1 indicative of large pores that lack cooperativity and values >10 indicative of a high degree of cooperativity in transport, as observed for single-file transport in aquaporins (41). Our simulations indicate this ratio for vSGLT is $p_f/p_d=5.3$, in good agreement with other transporters and water channels (43).

Directional water flow is not correlated with substrate release

Previous analysis of a single vSGLT simulation suggested that the inward release of galactose to the intracellular space is coupled to the inward cotransport of water (14). The simulation showed that 70–80 water molecules entered the intracellular space during the time that galactose left the central binding pocket and exited the protein through a narrow intracellular cavity. It was hypothesized that the galactose acted as a plug in the tight confines of the exit cavity, causing water to move inward as the galactose unbound. To determine whether water and galactose movement are correlated, we examined the net water flow and transient fluctuations from eight independent galactose unbinding simulations and 11 other simulations in which galactose remained bound to the transporter.

Fig. 3 shows a representative subset of nine of these trajectories, where the position of the galactose relative to the center of mass of the sugar binding site is plotted along with the cumulative net water flow through the transporter. We observe transient directional flow through the transporter that does not appear to correlate with substrate release. Although there are trajectories in which water moves in the same direction as the galactose during exit, consistent with our previous observation (14) (Fig. 3, C, E, F, and G), there are nearly as many instances where water moves against the direction of galactose exit (Fig. 3, A and B) or fails to flow at all (Fig. 3 D). Further, there are two trajectories in which galactose remains bound during the entire simulation, yet the water fluctuations are comparable in magnitude to values observed during galactose exit (Fig. 3, H and I). These results suggest that the directional flux of water observed by Choe et al. (14). represented a transient fluctuation that was coincident with galactose exit, rather than tight coupling to the movement of galactose.

Figure 3.

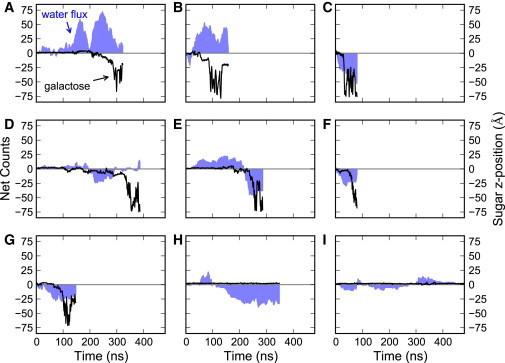
Water flow and movement of galactose as a function of time. (A–I) For each trajectory, the cumulative net flow of water (blue-shaded areas), defined as the difference between cumulative efflux and influx through the transporter, is shown alongside the position of the galactose relative to the sugar binding site projected onto the z axis (black). Net efflux through the transporter corresponds to positive values, whereas net influx results in negative values. Panels A-G show examples of simulations in which galactose was released into the bulk intracellular solution. In panels H and I, the sugar is stable in the binding site for the entire simulation. To see this figure in color, go online.

Discussion

We have used a series of long, 500- to 1800-ns MD simulations, starting from a sugar and sodium-bound inward-facing state, to probe the structural basis of water movement through vSGLT. A major advance of this study is our observation of multiple independent events of sugar unbinding from the intracellular space, where previously we had observed only a single unbinding event (14). Thus, this analysis provides a statistical description of solute-coupled water flow, which has allowed us to refine our initial hypothesis. In addition, we have significantly more simulation of the substrate-bound conformation, as well as outer-gate conformations, allowing us to discern the roles of binding-site occupancy and protein conformations in modulating water permeation.

For the inward-facing conformation, we find that the magnitude of the passive water flow is controlled by small structural rearrangements in the outer gate, as well as the occupancy of galactose in the binding site. Although the conformation of vSGLT corresponding to the crystal structure (21) is nearly impermeable to water, due to the tight packing of side chains in the gate region, the thermalized system permits water to leak through the outer gate during transient excursions to more permissive conformations. To properly account for the aqueous pathways, we developed a believed novel procedure for detecting continuous water chains connecting the two bulk solvent phases in the simulation cell. The hole that forms in the outer gate varies in size from the diameter of a single-file chain of waters, reminiscent of aquaporins (44), to a large pore several water molecules in diameter. We found that the number of water paths closely matched the magnitude of the water flow, acting as a surrogate for the effective radius of the pore, despite the complicated geometry of the gate. For this reason, we believe that our method will be widely applicable for the detection of narrow water channels with complex geometry in other systems.

These longer simulations confirm our previous finding that water permeates vSGLT through the sugar-binding site. Estimates of the diffusional and osmotic permeabilities are also consistent with our previous measurements (14). The data presented here, however, do not support a mechanism of water transport in which the exiting sugar forces water in the lumen of the transporter into the intracellular solution. Instead, the net water movement exhibits large, apparently stochastic, fluctuations that are not strongly correlated with the motion of the exiting substrate. This finding indicates that the hyperosmotic (12) and Brownian piston (14) models of active water pumping are most likely not correct for vSGLT. Water is able to move past galactose while it is in the binding site and the intracellular exit tunnel, which explains why the inward movement of galactose is not coupled to water motion. We still believe that the piston mechanism could rectify water flow in a more tightly constricted exit tunnel or during different stages of the transport process. In addition, active pumping mechanisms that rely on water being expelled in a unidirectional manner by large-scale protein conformational changes (17) cannot be addressed by this work, since we did not observe major rearrangements. Such changes occur on the millisecond timescale for alternating access and are hard to capture by simulation (45).

In agreement with our previous simulations of vSGLT, we find that the osmotic water permeability is nearly 600–900 times greater (14) than that reported for mammalian homologs (7). It is possible that this difference arises due to deficiencies in the underlying force field or because experiments average the water flow over the entire transport cycle and our simulations are limited to the inward-facing state only. For instance, if the inward-facing state is the only conformation that allows water permeation, and if the fraction of time spent in this state is 1/1000, then there would be excellent agreement between our vSGLT simulations and experiments on mammalian homologs. However, kinetic models of hSGLT1 transport suggest that a significant amount of time is spent in the inward-facing state (46), pointing to the possibility that there are structural differences between the prokaryotic and eukaryotic transporters.

To investigate this possibility, we performed a multiple-sequence alignment between vSGLT and several of its closely related family members. The resulting alignment revealed two extracellular loops that are present in the mammalian transporters but notably absent in vSGLT and other prokaryotic homologs. These insertion sites and the conserved flanking transmembrane helices are shown in Fig. 4 for vSGLT, the proline permease from E. coli, PutP, hSGLT1, and hSGLT2. Insertion site 1 (Fig. 4 A) is 13 residues long and is positioned in the extracellular loop connecting TM5 and TM6, between S239 and N240 in vSGLT (C255–R267 in hSGLT1). The second insertion site (Fig. 4 B) results in an additional 18 residues inserted in the loop between TM11 and TM12, and it is flanked by residues L475 and S476 (A505 and C522 in hSGLT1). It is predicted, based on the alignment, that both of these insertion sites will lie proximal to the extracellular gate and the residues that control water permeation through the inward-facing state of vSGLT. In Fig 2C, the asterisks indicate where the loops would be inserted on vSGLT. These loops, absent in vSGLT, might further occlude the water pathway to the extracellular solution in the mammalian transporter by forming a steric block. Alternatively, the loops may help maintain the outer gate in a closed, water-tight conformation without sterically hindering the water pathway directly. We believe that the hypothesis that vSGLT possesses an intrinsically leakier outer gate may also explain why experiments predict that galactose binding fails to alter water flow, whereas simulations suggest that it does. If movement of water through a tightly sealed outer gate is rate-limiting in mammalian transporters, then the presence or absence of galactose occluding the permeation pathway would not be detectable with such a small water flow.

Figure 4.

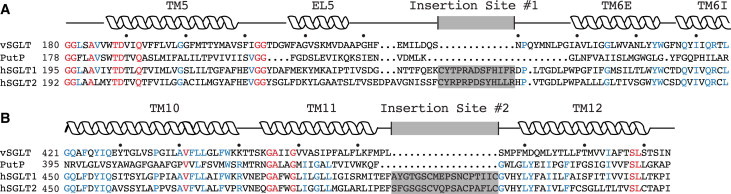
Insertion sites in mammalian transporters near the extracellular gate. Alignment of the primary sequences of vSGLT, PutP, hSGLT1, and hSGLT2 showing the regions around the two insertion sites found in mammalian transporters, which are absent in the bacterial homologs. Secondary-structure elements are shown above the sequences based on the structure of vSGLT. Strictly conserved and highly conserved residues are shown in red and blue, respectively. Insertion sites 1 (A) and 2 (B) are shown as gray boxes. To see this figure in color, go online.

Both loops contain a number of highly conserved residues that are present in both hSGLT1 and hSGLT2, as well as isoforms from rat and rabbit. Among the conserved residues, C255 at the N-terminal end of insertion site 1 and C511 near the center of insertion site 2 are hypothesized to form a disulfide bridge (47,48). Such a link would orient the loop corresponding to insertion site 2, toward the opening of the water permeation pathway that we have identified, consistent with the proposed proximity of C255 and C511 to the sugar binding site (48). Although these differences are suggestive, any effect of sequence differences on the functional behavior of the transporters would require experimental validation. Nonetheless, these protein elements may be critical in controlling the flow of material across the membrane and may play a role in regulating key steps in the alternating-access cycle.