Mycobacterium tuberculosis Type II NADH-Menaquinone Oxidoreductase Catalyzes Electron Transfer through a Two-Site Ping-Pong Mechanism and Has Two Quinone-Binding Sites

Abstract

Type II NADH-quinone oxidoreductase (NDH-2) catalyzes the transfer electrons from NADH to the quinone pool and plays an essential role in the oxidative phosphorylation system of Mycobacterium tuberculosis (Mtb). The absence of NDH-2 in the mammalian mitochondrial electron transport chain makes this enzyme an attractive target for antibiotic development. To fully establish the kinetic properties of this enzyme, we studied the interaction of Mtb NDH-2 with substrates, NADH, and various quinone analogues and their products in both membrane and soluble environments. These studies, and comparative analyses of the kinetics with thio-NAD⁺ and quinone electron acceptors, provided evidence that Mtb NDH-2 catalyzes the transfer electrons from NADH to quinone substrates by a nonclassical, two-site ping-pong kinetic mechanism whereby substrate quinones bind to a site that is distinct from the NADH-binding site. Furthermore, the effects of quinols on Mtb NDH-2 catalytic activity demonstrate the presence of two binding sites for quinone ligands, one favoring the reduced form and the other favoring the oxidized form.

There is an increasing need for the development of antibiotics against new physiological targets to combat the emergence of bacteria resistant to current front-line drugs. TMC207 (Bedaquiline), a potent and specific inhibitor of mycobacterial ATP synthase, is a new antibiotic that is approved for use in the treatment of multi-drug resistant (MDR) tuberculosis (TB).¹ This success has validated the oxidative phosphorylation system (OxPhos) of Mycobacterium tuberculosis (Mtb) as a potential target for the development of new antibiotics. The OxPhos pathway is composed of the respiratory chain (electron transport chain), which produces the proton motive force that drives ATP synthase. In mycobacteria, electrons are introduced into the electron transport chain primarily via type II NADH-quinone (Q) oxidoreductase (Mtb NDH-2), a membrane-bound enzyme composed of a single polypeptide chain of 45 kDa and a single FAD cofactor that mediates electron transfer. NDH-2 catalyzes the oxidation of NADH to NAD⁺ with concomitant reduction of menaquinone to menaquinol.² There is no NDH-2 counterpart in vertebrate mitochondria, which utilize a much larger, complex oxidoreductase, type I NADH-quinone oxidoreductase (Complex I or NDH-1), to initiate electron transport. Thus, Mtb NDH-2 is an attractive target for the development of selective antimycobacterial agents, and a detailed understanding of NDH-2 kinetics will be valuable to guide the development process.

Steady-state kinetic studies from our laboratory showed that Mtb NDH-2 catalyzes the transfer electrons from NADH to quinone by a ping-pong mechanism.³ Similar studies of NDH-2 counterparts in Saccharomyces cerevisiae (Ndi1)^4,5 and Yarrowia lipolytica(6) also concluded that electron transfer occurs by a ping-pong mechanism. More recently, however, a mechanism proceeding through a ternary complex has been proposed for Ndi1. This mechanism was based on the appearance of a broad spectral peak at 740 nm characteristic of a charge transfer complex between NAD⁺ and FADH₂ that underwent an increase in intensity upon addition of electron acceptors,⁷ and quinol inhibition kinetics suggesting separate binding sites for NADH and quinone.⁷ It was suggested that the ping-pong kinetics seen previously might be an artifact of enzyme solubilization by detergents and/or activity measurements using small, soluble quinone substrates that can interact at the NADH-binding site.⁷

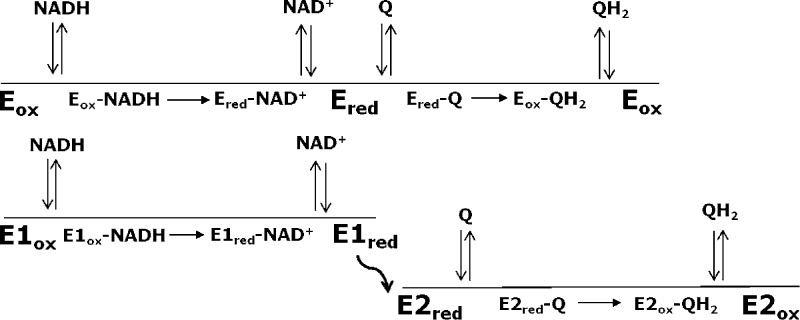
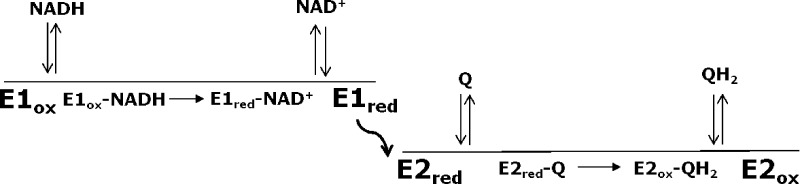
Recently, two independent laboratories have published atomic-resolution structures of Ndi1.^8,9 Both structures revealed globally similar protein folds but different modes of interaction of the FAD with quinone substrates. In the structure published by Iwata et al.,⁸ sites for NAD⁺ and quinone substrates appeared to overlap on the same face of the isoalloxazine ring of the FAD cofactor, suggesting that donation of electrons from NADH and abstraction of electrons by quinone occur on the same face of FAD. The suggestion of overlapping substrate-binding sites is difficult to reconcile with the formation of a ternary complex but is consistent with a classical (one-site) ping-pong mechanism (Scheme 1; see Experimental Procedures). In the structure published by Feng et al.,⁹ NADH and quinone substrates were observed to bind at sites located on opposite faces of the isoalloxazine ring of the FAD cofactor. Structures containing bound substrates showed the nicotinamide ring of the NADH substrate bound proximal to the re face of the isoalloxazine ring, whereas the sites for the two quinone ligands were adjacent to the si face of the flavin. Independent binding sites for the electron donor and acceptor would favor a nonclassical (two-site) ping-pong mechanism (Scheme 2).

Scheme 1.

Scheme 2.

In this study, we characterized the kinetics of various quinone substrates and reaction products on the NADH-Q reductase activity of Mtb NDH-2 in both soluble and membrane environments and defined the kinetics of NADH-thio-NAD⁺ transhydrogenase activity catalyzed by Mtb NDH-2. By comparing the kinetic properties of the two activities, we showed that Mtb NDH-2 catalyzes the transhydrogenase reaction through a one-site ping-pong mechanism and the physiologically relevant NADH-Q reductase reaction through a two-site ping-pong mechanism. Furthermore, the data revealed the existence of two quinone-binding sites with widely different preferences for oxidized and reduced quinones. The two-site ping-pong mechanism and two quinone sites elucidated in this kinetic study are more consistent with the Ndi1 crystal structure of Feng et al.⁹ than with that of Iwata et al.⁸

Experimental Procedures

Materials

NADH, NAD⁺, quinone substrates (UQ₀, UQ₁, UQ₂, and menadione), HEPES buffer, and cosolvents glycerol and DMSO were from Sigma-Aldrich (St. Louis, MO). Thio-NAD⁺ was from Cell Sciences (Canton, MA), and Big CHAP was from Affimetrix (Santa Clara, CA). The TALON metal affinity column was from Clontech (Mountain View, CA), and the Superose 6 column was from GE Healthcare Life Sciences (Pittsburgh, PA).

Recombinant Mtb NDH-2

NDH-2 was purified according to the method of Yano et al.,³ with the following modifications. Mtb NDH-2 was overexpressed in Mycobacterium smegmatis mc² 4157 with a T7-based expression vector (pYUB derivative).¹⁰M. smegmatis was aerobically grown in an autoinduction medium¹¹ in the presence of 20 μg/mL kanamycin and 50 μg/mL hygromycin at 37 °C for 3 days, and the cells were harvested by centrifugation at 5000g for 10 min. Membrane fractions were prepared according to the method of Yano et al.³ and were detergent-solubilized in buffer containing 2% (w/v) Big CHAP. The solubilized membrane fraction was passed over an immobilized metal affinity column and the bound NDH-2 was eluted with an imidazole solution containing 0.25% Big CHAP and was concentrated by ultrafiltration. The concentrated material was further purified by size exclusion chromatography on a Superose 6 HPLC column equilibrated with a solution of 50 mM HEPES/K⁺ (pH 7.0), 300 mM KCl, 2 mM MgCl₂, 0.25% Big CHAP, and 20% (v/v) glycerol. NDH-2 fractions were combined and concentrated by ultrafiltration to 2–3 mg/mL. The final preparation was stored in liquid nitrogen until it was used.

NADH-Quinone (Q) Reductase and NADH-tNAD⁺ Transhydrogenase Activity Assays

Activity measurements were typically performed at room temperature in 0.5 or 1.0 cm cuvettes using a Beckman 640 spectrophotometer. NADH oxidation was measured by absorbance at 340 nm; tNAD⁺ reduction was measured at 398 nm. Absorbance measurements were taken at 1.0–3.0 s intervals, and initial activities were determined from linear-least-squares fitting of progress curves over 0.5–3.0 min periods where <10% of the substrates were consumed. The reaction mixture in NADH-Q reductase assays consisted of 0.1 M HEPES/Na⁺ (pH 7.0) (NADH-Q buffer), substrates, and 2–5 nM enzyme, and in transhydrogenase assays, it consisted of 50 mM HEPES/K⁺ (pH 7.0), 2 mM MgCl₂ (transhydrogenase buffer), substrates, and 10–50 nM NDH-2. Unless otherwise indicated, reactions were initiated by addition of purified recombinant NDH-2 or membrane preparations from cells overexpressing NDH-2. The dilution of the purified enzyme or membrane to start reactions was >100-fold. This dilution virtually removed any influence of the detergent on purified enzyme activity or substrate solubility. In studies with less soluble substrates (UQ₁, UQ₂, and menadione), 10% (v/v) DMSO was included in the assay buffer. Removal of detergent and addition of DMSO did not result in a loss of activity during the assay period, which were usually followed until NADH consumption was complete (10–20 min).

To obtain k_cat or turnover numbers (TN), the change in absorbance was converted into NADH consumed using an extinction coefficient of 6.22 cm^–1 mM^–1 for NADH (ε₃₄₀) or 11.9 mM^–1 cm^–1 for tNADH (ε₃₉₈)¹² and divided by NDH-2 concentration. The stock concentration of purified NDH-2 was determined by FAD measurement. The amount of membrane-bound NDH-2 was estimated assuming it had the same specific activity as purified NDH-2. Under assay conditions of 0.3 mM NADH, 2.0 mM UQ₀, and HEPES buffer (pH 7.0), 1.0 nM NDH-2 produced a change in Abs₃₄₀ of 0.1 min^–1.

Assays in the Presence of Reaction Products

Most studies that included reaction products were assayed as just described except for the addition of NAD⁺ or quinols. NAD⁺ stock solutions were made in water or 50 mM HEPES-KOH buffer (pH 7.0) containing 2 mM MgCl₂. Ubiquinols (Q₀H₂, Q₁H₂, and Q₂H₂) were prepared from commercially available ubiquinone substrates by reduction with sodium borohydride. Briefly, quinones were dissolved in 50 mM HCl/DMSO at 20–100 mM and reduced with a stoichiometric excess of sodium borohydride at room temperature, followed by the addition of 12 N HCl to quench unreacted sodium borohydride. The quinol solution was neutralized with HEPES buffer and confirmed by the loss of visible absorption. Studies to determine the effect of NAD⁺ on NADH-Q reductase activity were performed in a TECAN M-1000 plate reader by monitoring the change in absorbance at 340 nm. Assays contained 50 mM HEPES (pH 7.0) with 10% glycerol and were initiated with NADH. Initial velocities were determined by linear regression of progress curves.

Kinetic Mechanisms, Equations, and Data Analysis

Kinetic studies were analyzed as described by Cook and Cleland.¹³ Scheme 1 depicts a classical (one-site) mechanism, and Scheme 2 depicts a nonclassical (two-site) ping-pong mechanism.¹³ Both mechanisms proceed through two half-reactions: (1) transfer of a hydride from NADH to FAD in the oxidized enzyme (E_ox), producing a reduced, modified enzyme (E_red) and the product NAD⁺, and (2) transfer of electrons from FADH₂ in the reduced enzyme to quinone, generating the quinol product and regenerating the oxidized enzyme. Arrows denoting the progress of the chemical reactions point in one direction because both the overall reaction and each half-reaction are highly exergonic and thus effectively irreversible. In accord with the crystal structures discussed in the introductory section, in the one-site ping-pong mechanism both NADH oxidation and quinone reduction occur on the same face of the isoalloxazine ring. Consequently, the binding of each substrate is mutually exclusive because of the overlap between binding sites. This overlap permits competitive inhibition between substrates as well as between each reaction product with the substrate from the other half-reaction. In the case of the two-site mechanism, oxidation of NADH and reduction of quinone occur on different faces of the isoalloxazine ring, permitting separate binding sites for each substrate denoted by E1 and E2 in Scheme 2. The curved arrow connecting the two sites is intended to convey the delivery of an electron to one face of the isoalloxazine ring and the transfer of an electron from the other face. In this mechanism, competitive inhibition can occur between only the substrate and product of the same half-reaction.

The steady-state rate equation describing ping-pong kinetics is the same for both classical and nonclassical mechanisms (eq 1). A ternary complex mechanism differs from a ping-pong mechanism in that both substrates have to bind before products are generated or released. As a result, there is no modified enzyme formed (E_red in Schemes 1 and 2). The rate equation for a ternary complex mechanism is the same as eq 1 except that the factor K_ia^NADHK_M^Q is added to the denominator, where K_ia^NADH is the dissociation constant for the binding of NADH to the enzyme.

1

Cook and Cleland¹³ point out that a ping-pong mechanism can be distinguished from ordered or random mechanisms proceeding through a ternary complex in studies where initial velocities are measured as a function of the concentration of both substrates varied at a constant ratio. In the case of a ping-pong mechanism, a double-reciprocal plot of data will be linear as depicted by eq 2, where [Q] = α[NADH], but in the case of a ternary complex mechanism, it will be parabolic because of the added factor in the denominator, as described by eq 3.

2

3

To determine the kinetic parameters for Mtb NDH-2 catalysis, a series of velocity (v) versus substrate concentration curves were obtained with one substrate varied (NADH or Q) and the other held constant. The resulting plots, determined at two or three different concentrations of the nonvaried substrate, were globally fit using eq 4, which is a rearranged version of eq 1. The constant term, K_M^NADH/V_max, and the apparent V_max are the fitted parameters; the apparent V_max is the factor multiplying [NADH] in the denominator. V_max for the reaction was estimated from a secondary plot of 1/V_{max apparent} versus 1/[Q]. K_M for NADH was estimated using V_max and the constant K_M^NADH/V_max obtained from the global fit. K_M for Q was determined using V_max and the slope of the secondary plot. The rate equation with Q as the varied substrate and NADH as the fixed substrate has the same form as eq 4, except the positions in the equation for NADH and Q are reversed. To account for the apparent competitive inhibition between substrates in the transhydrogenase reaction when tNAD⁺ was the varied substrate and NADH was the fixed substrate, K_M^NADH in the apparent V_max term was modified by the factor 1 + [tNAD⁺]/K_si^tNAD+. Global fitting was by nonlinear least-squares regression analysis using Igor Pro (Wavemetrics).

4

Reaction irreversibility precludes reversible product inhibition; therefore, inhibition kinetics by NAD⁺ were assumed to be due to the formation of dead end complexes competing with substrate binding. Inhibition was initially analyzed using the Michaelis–Menten rate equation to determine the type of inhibition. Depending on the outcome of these analyses, the data were then fit to eq 5 to determine relevant K_i values modifying the K_M of each substrate where [S]_V and [S]_C are the concentrations of the variable and constant substrates, respectively, and the modifying inhibition factors β₁ and β₂ are 1 + [NAD⁺]/K_i′ and 1 + [NAD⁺]/K_i″, respectively. To obtain values for inhibition constants K_i′ and K_i″, fits used K_M, V_max, and K_si values obtained from other analyses.

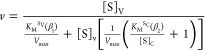5

Quinol inhibition of the transhydrogenase and NADH-Q reactions did not appear to be competitive and therefore was evaluated using a relationship assuming binding to a single discrete site as described by eq 6, where FA is fractional activity and f is the fraction of activity remaining at an infinite quinol concentration.

6

Results

Kinetics of NADH-Q Reductase Activity

To examine the validity of the proposed ping-pong mechanism for Mtb NDH-2, we evaluated its kinetic properties with a series of quinone substrates (UQ₀, UQ₁, UQ₂, and menadione) using both detergent-solubilized and membrane-bound enzyme preparations. The latter membrane preparations were isolated from bacteria in which recombinant Mtb NDH-2 was overexpressed. These membranes contained 50–100-fold more NDH-2 activity than wild-type membranes based on NADH reductase activity in the presence of exogenous UQ₀.

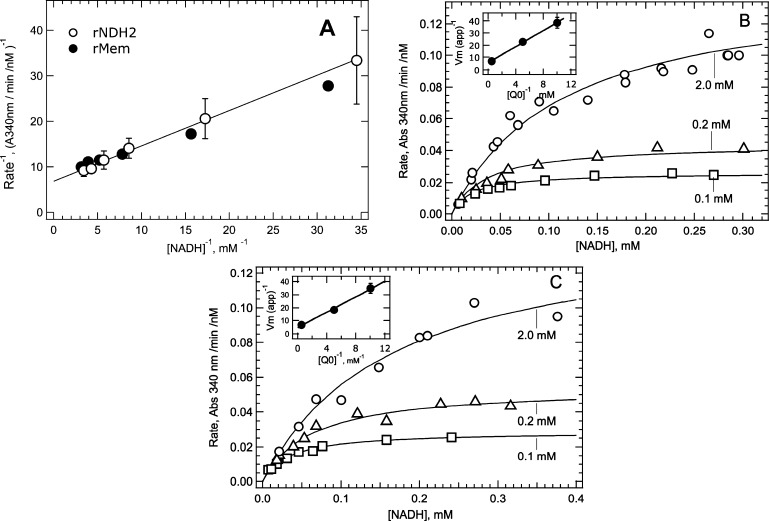
As pointed out by Cook and Cleland,¹³ an ordered or random sequential mechanism can be distinguished from a ping-pong mechanism (classical or non-classical) by the dependence of activity on the concentration of both substrates varied together at a fixed ratio (eq 2, Experimental Procedures). In Figure 1A, the NADH-Q reductase activity of purified Mtb NDH-2 and Mtb NDH-2 overexpressed membranes was measured at varying concentrations of NADH and UQ₀ set to a fixed concentration ratio of [UQ₀] = 6.25[NADH]. As discussed in Experimental Procedures, the linearity of the double-reciprocal plots for both soluble and membrane-bound NDH-2 preparations strongly supports a ping-pong mechanism.

Figure 1.

Kinetic analysis of NADH-UQ₀ reduction by membrane-bound and purified (soluble) Mtb NDH-2. (A) Double-reciprocal plots of the initial velocity vs substrate concentration where both substrates were varied while maintaining a constant ratio of [UQ₀] = 6.25[NADH]. The line through the data is the fit of soluble Mtb data to eq 2. Error bars show the range from duplicate experiments. (B) Analysis of NADH-UQ₀ kinetics with soluble NDH-2. Initial velocities were determined with NADH as the varied substrate and three different concentrations of UQ₀ as the fixed substrate. Lines through the data were determined by global fitting of the three data sets to eq 4. Insets represent secondary plots used to determine V_max for the reaction and K_M values. (C) Plots are similar to those in panel B but were obtained using membranes isolated from M. smegmatis overexpressing recombinant Mtb NDH-2.

K_M values for NADH and UQ₀ were determined from velocity versus substrate concentration data, as shown in panels B and C of Figure 1. Initial velocities were determined as a function of the concentration of a varied substrate, NADH, at three fixed concentrations of the second substrate, UQ₀. The data were globally fit using eq 4 to obtain the constant parameter K_M^NADH/V_max, which is characteristic of a ping–pong mechanism, and the apparent V_max at each of the constant substrate concentrations. Soluble and membrane-bound enzyme data were fit well by eq 4 (solid lines through data). Insets are secondary plots used to obtain K_M and k_cat values as described in Experimental Procedures. The kinetic parameters are listed in Table 1 along with values obtained with UQ₀ as the varied substrate. The K_M value for NADH with soluble NDH-2 (average of 0.13 mM) is somewhat lower than the K_M for membrane-bound NDH-2 (average of 0.28 mM). The K_M for UQ₀ varied between 0.23 and 0.64 mM with both free and membrane-bound enzymes. The k_cat for the NADH-UQ₀ reductase reaction ranged between 330 and 580 s^–1. These results indicate that detergent solubilization of NDH-2 from the membrane does not significantly alter electron transfer kinetics.

Table 1. Kinetic Parameters for NADH Oxidation Catalyzed by NDH-2 from Soluble and Overexpressed Membrane Preparations with Various Electron Acceptors^a.

	[NADH] varied	[quinone] varied	ratio plot
NDH-2 Overexpressed Membranes with UQ0
KMNADH (mM)	0.24 ± 0.07b	0.32 ± 0.15	–
KMUQ0 (mM)	0.64 ± 0.20	0.23 ± 0.10	–
kcat (s–1)	580.0 ± 170	570.0 ± 200	330 ± 15
Soluble NDH-2 with UQ0
KMNADH (mM)	0.14 ± 0.02	0.12 ± 0.2	–
KMUQ0 (mM)	0.58 ± 0.11	0.35 ± 0.5	–
kcat (s–1)	480.0 ± 60	425.0 ± 35	390 ± 70
Soluble NDH-2 with UQ1
KMNADH (mM)	ndc	ndc	0.13d
KMUQ1 (mM)	ndc	ndc	0.050 ± 0.02e
kcat (s–1)	ndc	ndc	500.0 ± 50
Soluble NDH-2 with UQ2
KMNADH (mM)	0.12 ± 0.2	ndc	0.12
KMUQ2 (mM)	<0.02	ndc	0.051 ± 0.05
kcat (s–1)	640.0 ± 40	ndc	1150.0 ± 350
Soluble NDH-2 with Menadione
KMNADH (mM)	ndc	0.23 ± 0.01	0.23
KMmenadione (mM)	ndc	0.10 ± 0.01	0.04 ± 0.02
kcat (s–1)	ndc	423.0 ± 70	400.0 ± 25

^aKinetic constants determined by global fitting using eq 4 in Experimental Procedures.

^bErrors are standard errors from fits or propagation errors calculated from fitted values when division of errors was necessary.

^cNot determined.

^dThe K_M value is the average for NADH with UQ₀ and UQ₂.

^eK_M calculated according to eq 2 assuming K_M for NADH where K_M^UQ₁ = α(slope × V_max – K_M^NADH).

To provide additional support for a ping-pong mechanism and to evaluate whether apparent ping-pong kinetic behavior might be an artifact of the use of the soluble quinone substrate UQ₀, the NADH-Q reductase reaction was assayed with quinone substrates having one or two isoprenoid units at position 5 of the benzoquinone ring (UQ₁ and UQ₂), and with menadione, which shares the same naphthoquinone headgroup as the physiological substrate in Mtb membranes, menaquinone-9. Because all of these quinones are less soluble than UQ₀ in water, 10% DMSO was included in the assay buffer to increase the solubility of each analogue and ensure a broader concentration range for kinetic measurements. Addition of DMSO reduced NADH-UQ₀ activity by approximately 10%.

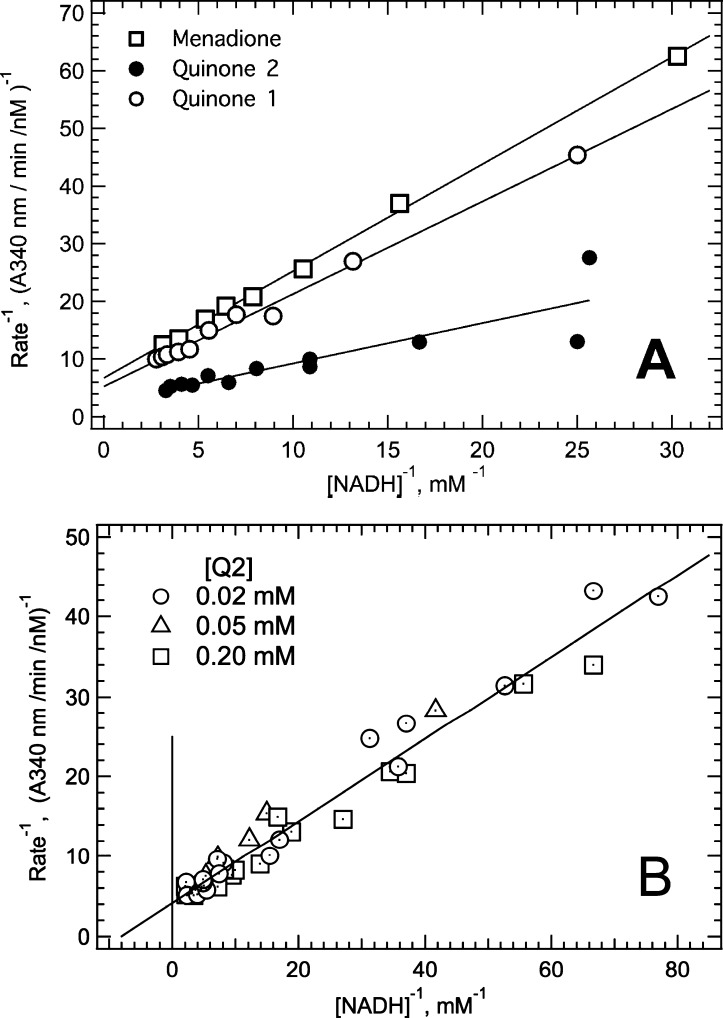
Soluble NDH-2 reduced UQ₁, UQ₂, and menadione more efficiently than UQ₀. At a constant substrate concentration ratio, double-reciprocal plots of NADH-Q reductase activity versus NADH were linear for the three quinone analogues, indicating the general applicability of the ping-pong mechanism (Figure 2A). Kinetic parameters for UQ₂ and menadione were determined from velocity versus substrate concentration plots using eq 4. The K_M value for UQ₁ was estimated from the plots in Figure 2A as described in the footnotes of Table 1. While K_M values for NADH were relatively constant with all quinones (∼0.15 mM), the K_M values for quinones decreased approximately 10-fold relative to those for UQ₀ with each added isoprenoid unit. A double-reciprocal plot for UQ₂ in Figure 2B shows the virtual overlap of velocity versus NADH concentration plots at UQ₂ concentrations ranging from 0.02 to 0.2 mM, indicating that NDH-2 was saturated with UQ₂ at all concentrations analyzed and that the K_M for UQ₂ is <0.02 mM.

Figure 2.

Kinetics for reduction of various quinones by soluble NDH-2. Assays were conducted in NADH-Q buffer containing 10% (v/v) DMSO. (A) Double-reciprocal plots of velocity vs substrate concentration data obtained with NADH and quinone concentrations maintained at a constant ratio. Ratios were [UQ₁] and [UQ₂] = 0.28[NADH] and [menadione] = 0.68[NADH]. To minimize spontaneous reoxidation, the assay with menadione was performed under anaerobic conditions by addition to the assay of an oxygen scavenging reaction mixture consisting of 0.2 μg/mL glucose oxidase and 1.0 mM glucose. (B) Double-reciprocal plots describing UQ₂ reduction kinetics by soluble NDH-2.

Unlike K_M values for quinones, k_cat values were similar in all cases, including when menadione was the electron acceptor. Naphthoquinone has a lower midpoint redox potential than benzoquinone (−70 to −110 mV vs 70–110 mV), demonstrating that k_cat values were not simply a function of the midpoint redox potential of each quinone. This observation indicates that the transfer of an electron from FADH₂ to quinone substrates does not contribute appreciably to the rate-limiting step of the reaction and that the transfer of a hydride from NADH to FAD may be the rate-limiting in the NADH-Q reductase reaction. It should be noted that all quinone substrates exhibited exclusively two-electron reduction reactions, as determined by the stoichiometry of NADH consumption relative to quinone concentration under assay conditions where NADH was in excess.

The decreased K_M values for quinones with longer isoprenoid side chains indicate that hydrophobicity is an important determinant of quinone binding affinity, and that the quinone-binding site can accommodate at least two isoprenoid units. Importantly, we did not observe any evidence of substrate inhibition of NADH oxidation by any of the quinone substrates examined, including UQ₂ for which the K_M is at least 10-fold lower than that of NADH (see Figure 2B). The absence of detectable substrate inhibition is consistent with a nonclassical ping-pong mechanism (Scheme 2).

Characterization of NADH-tNAD⁺ Transhydrogenase Activity

Product inhibition studies are routinely employed to distinguish between classical and nonclassical ping-pong kinetic mechanisms. However, in the case of NADH-Q reduction, product inhibition is not feasible because the highly exergonic nature of both half-reactions renders each effectively irreversible. Under these conditions, products (NAD⁺ and QH₂) can function only as dead-end inhibitors. To discriminate between classical and nonclassical ping-pong mechanisms, we turned to a comparison of the NADH-Q oxidoreductase and transhydrogenase activities of NDH-2. As a member of the flavoprotein disulfide reductase family, Mtb NDH-2 is capable of catalyzing the transfer of a hydride from NADH via FAD to various NAD⁺ analogues in vitro.(14) The midpoint redox potential for the tNAD⁺/tNADH couple (E_m,7 = −270 mV) is slightly higher than that for the NAD⁺/NADH couple (E_m,7 = −320 mV), making tNAD⁺ reduction favorable. Given that the electron acceptor for the transhydrogenase reaction [thio-NAD⁺ (tNAD⁺)] resembles NADH, we predicted that the transhydrogenase reaction should proceed through a classical (one-site) ping-pong mechanism, with both the donor and the acceptor interacting with NDH-2 at the NADH site. Markedly different properties of the transhydrogenase and NADH-Q reductase activities of NDH-2 toward substrates and reaction products acting as dead-end inhibitors might therefore provide evidence for discriminating between classical and nonclassical ping-pong mechanisms.

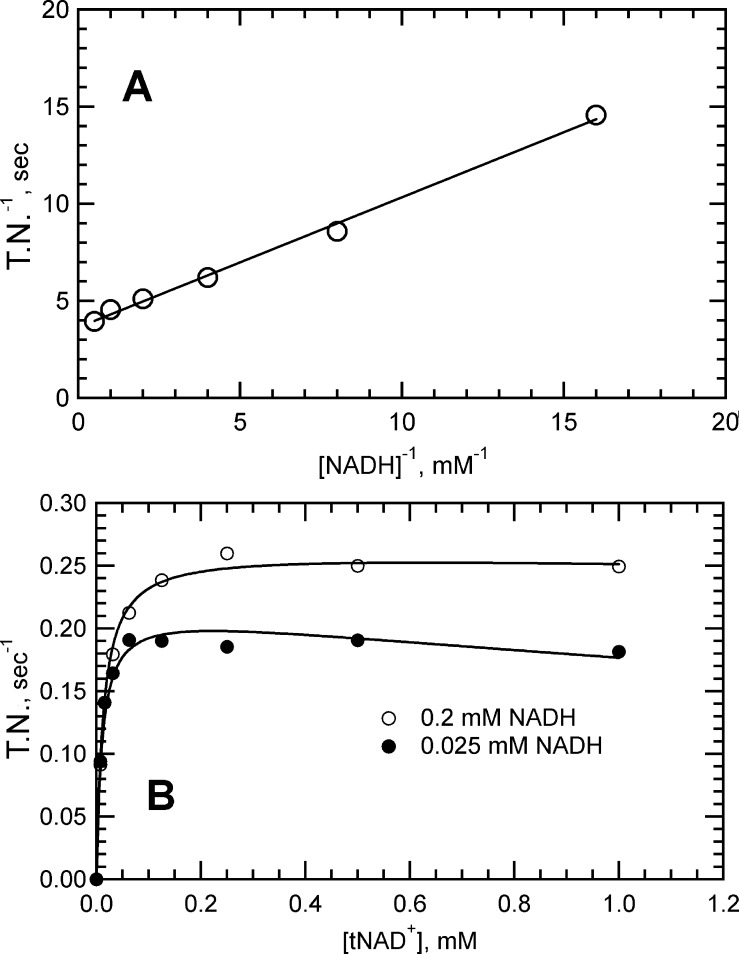
Characterization of the NDH-2 kinetics using tNAD⁺ as the electron acceptor is shown in Figure 3. Assays monitored tNAD⁺ reduction by an increase in absorbance at 398 nm, a wavelength at which tNADH exhibits significant absorbance and NADH has virtually no absorbance. Shown in Figure 3A is a double-reciprocal plot of velocity versus substrate data obtained at a fixed concentration ratio of NADH = tNAD⁺. The k_cat value obtained from the y-intercept was 0.275 s^–1, which is ∼1000-fold lower than the k_cat observed with quinone acceptors. The linear relationship observed is consistent with a ping-pong mechanism. The dependence of velocity on tNAD⁺ concentration with NADH fixed at two different concentrations is shown in Figure 3B. The curve at high NADH concentrations reached a plateau indicative of saturation, whereas the curve at the lower NADH concentration trended downward at the higher tNAD⁺ concentrations. The downward curvature is indicative of competition between the two substrates, which is consistent with a one-site ping-pong mechanism.

Figure 3.

NADH-tNAD⁺ transhydrogenase reaction catalyzed by soluble Mtb NDH-2. Initial velocity data converted to turnover numbers (TNs) as described in Experimental Procedures. (A) Double-reciprocal plots of velocity vs substrate concentration data where substrates were maintained at a fixed ratio of [NADH] = [tNAD⁺]. The reaction mixture contained 40 nM NDH-2. (B) Initial velocity vs substrate concentration plots to obtain kinetics of the transhydrogenase reaction. The reaction mixture contained 48 nM NDH-2, varying concentrations of tNAD⁺, and 200 μM NADH (○) or 25 μM NADH (●). Solid lines through the data were produced from global fits to eq 4 modified with a term to account for substrate inhibition.

To obtain the K_M values for the reaction, the data were fit to eq 4 with an added term to account for substrate inhibition of NADH by tNAD⁺ (see Experimental Procedures). The V_max term in eq 4 was assigned the k_cat value determined from the intercept in Figure 3A (0.25 s^–1), reducing the fitted parameters to three values. K_M values for NADH and tNAD⁺ were 0.01 and 0.02 mM, respectively, and the substrate inhibition constant (K_si^tNAD+) for tNAD⁺ was 0.90 mM (values listed in Table 2). The k_cat for the transhydrogenase reaction is roughly 2000-fold lower than that observed for NADH-Q reductase activity (∼500 s^–1), suggesting that the rate-determining step may have changed from the first to the second half-reaction, i.e., transfer of a hydride from FADH₂ to tNAD⁺ instead of transfer of a hydride from NADH to FAD. A change in the rate-determining step would be consistent with the marked decrease in the K_M for NADH (see the Supporting Information). The presence of substrate inhibition alters eq 2, making it no longer linear. Curvature was not evident in the double-reciprocal plot of Figure 3A because the magnitude of K_si was 50-fold higher than the K_M for NADH, thereby minimizing its influence on the reaction velocities in this analysis.

Table 2. Kinetic Parameters Determined for the NADH-tNAD⁺ Transhydrogenase Reaction Catalyzed by Mtb NDH-2 and Inhibition Constants Produced by Addition of NAD⁺ to Each Reaction Mixture^a.

	NADH-UQ0 reductase reaction	NADH-tNAD+ transhydrogenase reaction
KMNADH (mM)	0.13–0.15b	0.01 ± 0.001c
KMtNAD+ (mM)	–	0.02 ± 0.003c
KitNAD+ (mM)	1.0 ± 0.13d	–
KsitNAD+ (mM)	–	0.90 ± 0.35c
Ki′NAD+ (mM)	0.54, 1.37e	1.4 ± 0.34
Ki″NAD+ (mM)	–	0.03–0.05f

^aReaction steps represented by constants are noted on Schemes 3–5 in Figures 4 and 5. Values were obtained from global fits using eq 4 or 5 as described in Experimental Procedures. Analyses of NAD⁺ inhibitory activity were performed with each substrate varied (see Figure 4); hence, two values are reported for these constants.

^bData taken from Table 1.

^cFitted parameters obtained from a global fit of data in Figure 3B to a modified eq 3, assuming the k_cat value (0.25 s^–1) for the transhydrogenase reaction determined from data in Figure 3A.

^dValue obtained from progress curves in Figure 5.

^eFitted parameter obtained from data in panels C and D of Figure 4.

^fFitted parameters obtained from data in panels A and B of Figure 4.

NAD⁺ Inhibition of Mtb NDH-2 Transhydrogenase and NADH-Q Reductase Activities

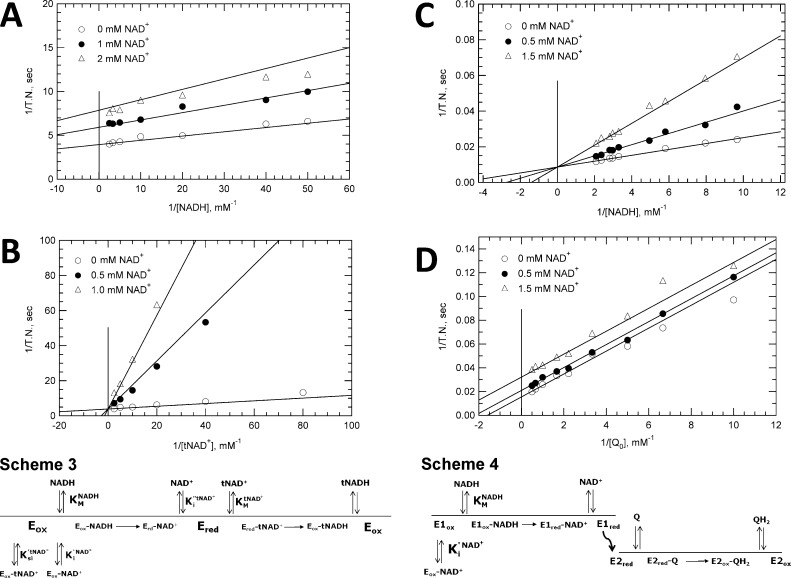
The kinetics of NAD⁺ inhibition of transhydrogenase and NADH-UQ₀ reductase activities are characterized in Figure 4. In panels A and B of Figure 4, inhibition of transhydrogenase activity was measured with NADH and tNAD⁺ as the varied substrates, respectively. Data shown are presented in double-reciprocal form with velocities converted to turnover numbers (TNs); velocity versus substrate concentration plots were used in global fits to obtain inhibition constants. Hyperbolic plots of this data are presented in the Supporting Information. With NADH as the varied substrate, a marked decrease in apparent k_cat values was evident, whereas a decrease in K_M was seen with tNAD⁺ as the varied substrate. Given the structural similarity of NAD⁺ with each substrate, the inhibition constants fitted using eq 5 were assumed to modify the K_M of each substrate. K_M values of each substrate and the K_si value for substrate inhibition were assumed from the studies in Figure 3 (listed in Table 2), so that the only fitted constants in eq 5 were inhibition constants for NAD⁺. The inhibition kinetics with NADH (Figure 4A) as the varied substrate were best described by noncompetitive (mixed) inhibition, with a weak effect on the K_M for NADH (K_i′^NAD+ = 1.4 ± 0.34 mM) and a much stronger effect on k_cat (K_i″^NAD+ = 0.03–0.05 mM). With tNAD⁺ as the varied substrate (Figure 4B), the inhibition was best described as being competitive with a strong effect on the K_M for tNAD⁺ (K_i″^NAD+ = 0.03 mM). The results are fully consistent with a classical (one-site) ping-pong mechanism (Scheme 3 in Figure 4), wherein NAD⁺ is a competitive inhibitor of both the electron donor and acceptor. Substrate inhibition between tNAD⁺ and NADH is added in Scheme 3. The kinetics in Figure 4B appear to be competitive rather than noncompetitive as expected because the relatively high NADH concentrations used in the study minimized NAD⁺/NADH competition, virtually eliminating an effect on the apparent k_cat.

Figure 4.

Kinetics of NAD⁺ inhibition for NADH-tNAD⁺ transhydrogenase and NADH-UQ₀ reductase activities. Data are presented in double-reciprocal plot form. Lines through data were generated using kinetic and inhibition constants from global fits of the original velocity vs substrate data with assumptions as described in the text. (A) Inhibition of transhydrogenase activity by NAD⁺ with NADH as the varied substrate. Reaction mixtures contained 25 nM NDH-2 and 1.0 mM tNAD⁺ as the fixed substrate with 0.0 mM NAD⁺ (○), 1.0 mM NAD⁺ (●), or 2.0 mM NAD⁺ (△). Fitting of data to obtain K_i values assumed noncompetitive inhibition. (B) Inhibition of transhydrogenase activity by NAD⁺ with tNAD⁺ as the varied substrate. Reaction mixtures contained 25 nM NDH-2 and 0.2 mM NADH with 0.0 mM NAD⁺ (○), 0.2 mM NAD⁺ (●), or 1.0 mM NAD⁺ (△). Data were fit assuming competitive inhibition. (C) NAD⁺ inhibition of NADH-UQ₀ activity with NADH as the variable substrate and UQ₀ at a fixed concentration. Reaction mixtures contained 5.0 nM NDH-2 and 2.0 mM UQ₀ with 0.0 mM NAD⁺ (○), 0.5 mM NAD⁺ (●), or 1.5 mM NAD⁺ (△). Data were fit globally assuming uncompetitive inhibition. (D) Inhibition of NAD⁺ on NADH-UQ₀ reductase activity with UQ₀ as a variable substrate and NADH at a fixed concentration. Reaction mixtures contained 5.0 nM NDH-2, buffer, and 0.125 mM NADH with 0.0 mM NAD⁺ (○), 0.5 mM NAD⁺ (●), or 1.5 mM NAD⁺ (△). Data were fit assuming competitive inhibition.

A parallel study with UQ₀ replacing tNAD⁺ as the electron acceptor is shown in panels C and D of Figure 4. The NAD⁺ inhibition pattern observed is markedly different from that describing the transhydrogenase reaction. Fitting of the data using either the Michaelis–Menten rate law or eq 5 with the appropriate substitutions found competitive inhibition by NAD⁺ when NADH was the varied substrate (Figure 4C) and uncompetitive inhibition when UQ₀ was the varied substrate (Figure 4D). This inhibition pattern indicates that the only kinetic constant affected by NAD⁺ was the K_M for NADH. The inhibition constant (K_i′^NAD+) obtained in both studies using eq 5 varied between 0.5 and 1.3 mM. Both values (average of 0.9 mM) are comparable to the corresponding constant for NAD⁺ competitive inhibition of NADH in the transhydrogenase reaction (Table 2).

The singular effect of NAD⁺ on the K_M for NADH in the NADH-Q reductase reaction could be consistent with either a one-site or a two-site ping-pong mechanism. However, to be consistent with the one-site mechanism, NAD⁺ would have to be a very poor competitive inhibitor of UQ₀ so that inhibition would go undetected in our measurements. This does not appear to be the case because NAD⁺ was a relatively strong inhibitor of tNAD⁺ exhibiting a K_i of 0.03–0.05 mM, which is approximately 10-fold lower than the K_M of UQ₀. Therefore, the absence of competition between NAD⁺ and UQ₀ for the reduced enzyme strongly supports a two-site ping-pong mechanism (Scheme 4 in Figure 4) where NAD⁺ and UQ₀ interact at discrete, independent sites.

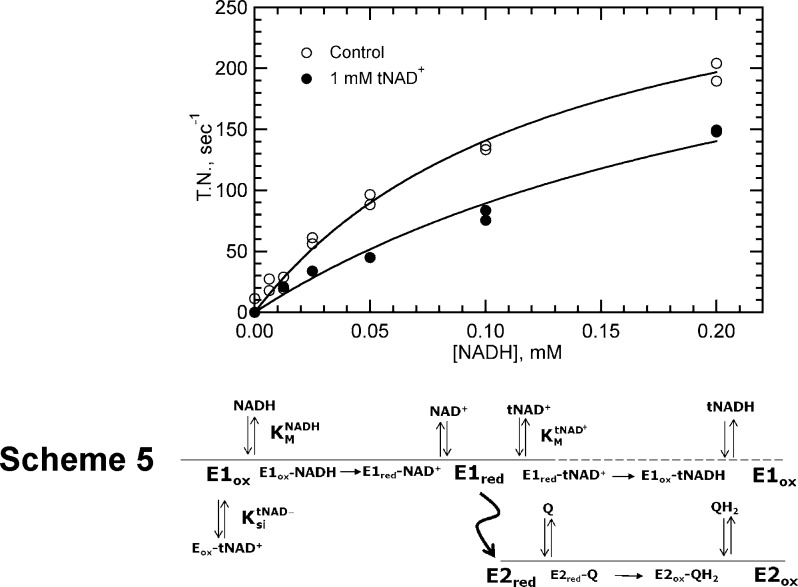
NDH-2 Kinetics When Electron Acceptors UQ₀ and tNAD⁺ Are Present in the Same Reaction Mixture

Kinetic studies with electron acceptors, tNAD⁺ and UQ₀, in the same reaction mixture were performed to determine if there was any competition between the two acceptors. NADH consumption monitored in the presence of UQ₀ alone or with both UQ₀ and tNAD⁺ as electron acceptors is shown in Figure 5. The UQ₀ concentration in both data sets was 4-fold higher than its K_M value, and the tNAD⁺ concentration in the data set with the electron acceptor mixture was 100-fold higher than its K_M value. The concentration of tNAD⁺ was at enzyme saturation levels to maximize the potential effect of its low K_M on the reaction (K_M values differ by >30-fold), and the concentration of UQ₀ was somewhat greater than its K_M to distinguish its higher rate of reduction from that of tNAD⁺ (k_cat values differ by >10³-fold). The curve with UQ₀ alone reflects the high activity observed with this electron acceptor. A similar study with tNAD⁺ alone at a concentration of 100K_M would have a maximal turnover number of <1, which was therefore not graphed. When both electron acceptors were present in the reaction mixture, the activity was reduced only slightly and in a manner consistent with competitive inhibition as determined using the Michaelis–Menten rate equation or eq 5 to fit the data (Scheme 4).

Figure 5.

Effect of tNAD⁺ and UQ₀ on NADH-UQ₀ oxidoreductase activity with NADH the varied substrate. The reaction mixture contained 5.0 nM NDH-2, 0.2 mM NADH, and 2.0 mM UQ₀ in the absence (○) or presence (●) of 1.0 mM tNAD⁺. Data were fit globally using eq 4 assuming competitive inhibition.

These findings are best explained by Scheme 5, which shows the transhydrogenase reaction proceeding by a one-site ping-pong mechanism and the NADH-UQ₀ reductase reaction proceeding in parallel through a two-site ping-pong mechanism. Because electron acceptors tNAD⁺ and UQ₀ bind to different sites in the two-site mechanism, they are not competitive with each other for interaction with the reduced form of the enzyme. If they were, tNAD⁺ would have prevented UQ₀ from binding given its concentration was at virtual saturation (100K_M). Instead, the reaction rate appeared mostly to reflect the difference in rate constants governing abstraction of electrons by each acceptor from reduced FAD. Because the half-reaction for UQ₀ reduction is much more efficient than that for tNAD⁺ reduction, the electron flux likely proceeds exclusively through UQ₀ and the two-site pathway (the dashed line in Scheme 5 signifies the absence of electron flux in the tNAD⁺ half-reaction). The rapid rate of UQ₀ reduction maintains the enzyme predominately in the oxidized form, a form to which tNAD⁺ binds weakly as a competitive inhibitor of NADH (K_i^tNAD+ in Table 2). Via substitution of the appropriate values into eq 5, a K_i value in the range of 1.0 mM was obtained for the competitive inhibition, which is similar to that obtained for substrate inhibition in Figure 3.

This kinetic study was repeated monitoring tNADH production instead of NADH oxidation. In accord with the interpretation mentioned above, the presence of UQ₀ in the assay inhibited tNAD⁺ reduction. These studies further demonstrate that tNAD⁺ and UQ₀ do not bind to the same site and that the transhydrogenase reaction proceeds through a one-site ping-pong mechanism, whereas NADH-UQ₀ reductase activity proceeds through a two-site ping-pong mechanism.

Effects of Quinols on Mtb NDH-2 Catalyzing Transhydrogenase and NADH-UQ Reductase Activities

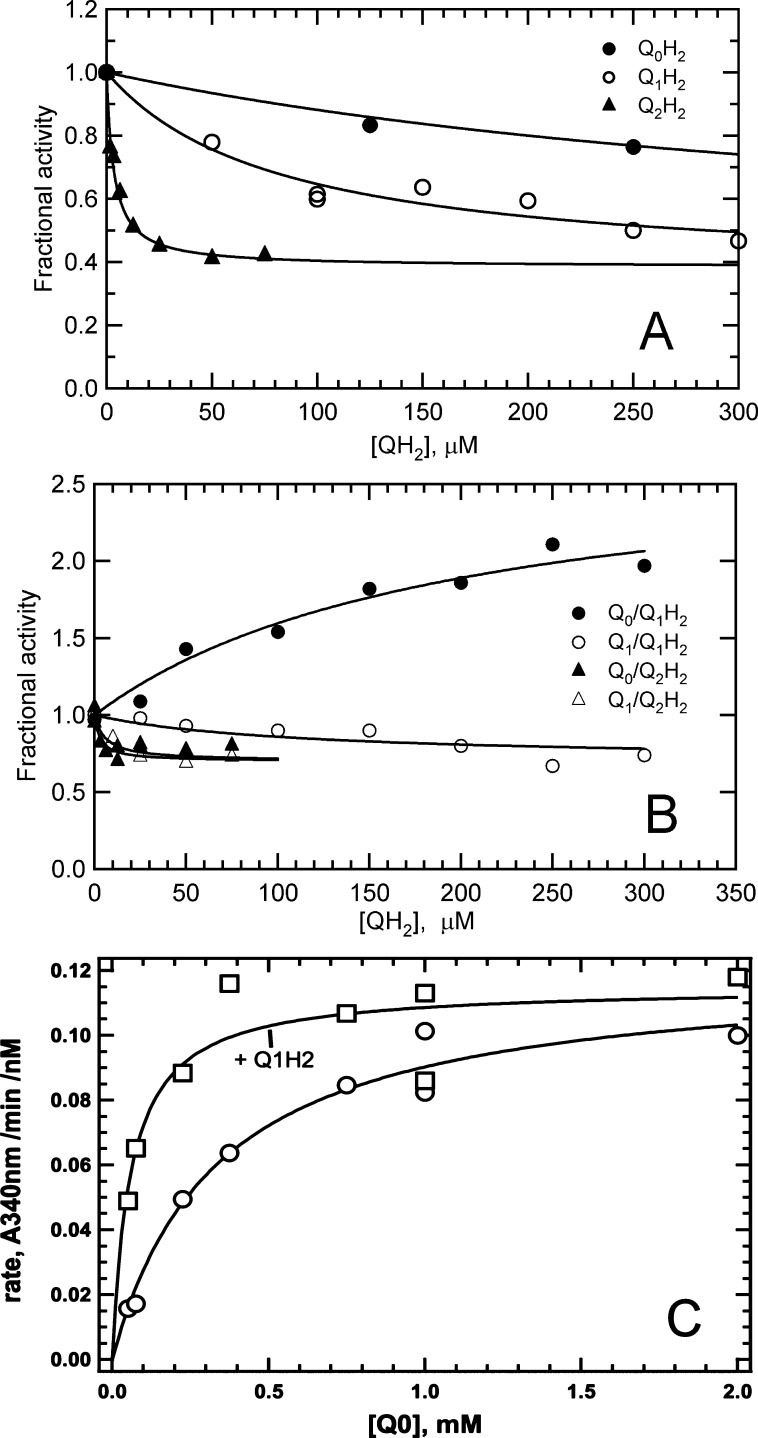
To further substantiate the two-site ping-pong mechanism and explore the properties of the quinone-binding site, inhibition of NDH-2 transhydrogenase and NADH-Q reductase activities by quinol products was evaluated. Because of the irreversible reaction, quinols, like NAD⁺, can act as only dead end inhibitors. Given the above evidence establishing different binding sites for NADH/tNAD⁺ and UQ₀, we were surprised to find that reduced forms of UQ₀, UQ₁, and UQ₂ inhibited the transhydrogenase reaction (Figure 6A). The inhibition was not complete and was observed despite virtually saturating concentrations of NADH and tNAD⁺ being used. The maximal level of inhibition of transhydrogenase activity was ∼60% for all three quinols. Apparent K_i values roughly estimated by fitting the data in Figure 6A to a model assuming a single discrete binding site (eq 6, Experimental Procedures) were ∼0.4 mM for UQ₀H₂, 0.08 mM for UQ₁H₂, and 0.003 mM for UQ₂H₂. The decrease in K_i values with an increasing isoprenoid chain length mirrors K_M values for the parent quinone substrates in the NADH-Q reductase reaction (Table 1). In the presence of 0.05 mM UQ₂H₂, which should be near saturating according to the K_i reported above, the K_M values for NADH and tNAD⁺ were unaffected while k_cat decreased by 60% (data not shown), further indicating that the inhibitory effects of quinol ligands on the transhydrogenase reaction are not mediated by binding to the NADH/tNAD⁺ substrate-binding site.

Figure 6.

Effect of quinols on NDH-2 transhydrogenase and NADH-Q reductase activities. (A) Effect of quinols on the transhydrogenase activity of soluble NDH-2. Reaction mixtures contained 20 nM NDH-2, transhyrogenase buffer, 0.2 mM NADH, 0.2 mM tNAD⁺, and varying concentrations of UQ₀H₂ (○), UQ₁H₂ (●), or UQ₂H₂ (△). Fractional activities were plotted as a function of quinone concentration, and plots were fit with eq 6. (B) Effects of UQH₂ on the NADH-Q reductase activity of soluble NDH-2. Reaction mixtures contained 0.3 mM NADH, 0.025–0.05 mM UQ, 1–5 nM NDH-2, and varying concentrations of UQH₂. Activities relative to those of control reaction mixtures that contained no reduced quinone were plotted as a function of UQH₂ concentration. Activation was fit with a modification of eq 6. (C) Kinetic studies characterizing UQ₁H₂ activation of membrane-bound NADH-UQ₀ reductase activity. Reaction mixtures contained 0.1 μL of recombinant membrane, NADH-Q buffer, and 0.3 M NADH in the absence (○) or presence (●) of 0.1 M Q₁H₂. Data were fit to the Michaelis–Menten rate equation (—) to obtain kinetic constant values.

The effects of quinols on NADH-Q reductase activity also showed incomplete inhibition, except for the activation of UQ₀ activity by UQ₁H₂ (Figure 6B). To maximize the possibility of demonstrating competitive inhibition by quinol products, NADH-Q activity was measured at subsaturating concentrations of substrate quinones. Modest, partial inhibition was again observed for most combinations of quinone and quinol ligands, plateauing in the range of 35–40% inhibition. Estimates of inhibition constants were made as described above. UQ₂H₂ exhibited relatively strong inhibition of activity when UQ₀ and UQ₁ (K_i = 0.003–0.006 mM) were the electron acceptors. UQ₁H₂ also inhibited activity when UQ₁ was the electron acceptor, but ∼10-fold more weakly than UQ₂H₂ (K_i ≈ 0.070 mM). In contrast to the general inhibitory activity of most quinols, UQ₁H₂ activated NADH oxidase activity 2-fold when UQ₀ was the electron acceptor. Although the inhibition constants mirror the K_M values observed with quinone substrates, the observation that quinol binding is not competitive with either NADH or quinone substrates suggests that quinol inhibition results from binding to a unique site that affects both NADH-Q and transhydrogenase activities.

To demonstrate that activation and inhibition were not artifacts of enzyme solubilization and purification, parallel experiments were repeated with membrane-bound recombinant NDH-2 under conditions similar to those described in the legend of Figure 1. Consistent with the results obtained with soluble NDH-2, addition of 1.0 mM UQ₁H₂ to an assay containing 0.05 mM UQ₁ as an electron acceptor resulted in 30 ± 10% inhibition, whereas the same quinol added to an assay containing UQ₀ as an electron acceptor produced an up to 5-fold increase in activity (data not shown). The dependence of NADH-UQ₀ activation on UQ₁H₂ concentration was hyperbolic, indicative of a discrete site with a binding constant of 0.070 mM. Kinetic analysis of UQ₁H₂ activation of NADH-UQ₀ reductase activity is shown in Figure 6C. The data indicate that activation results from a 5–6-fold decrease in the apparent K_M value for UQ₀ (from 0.35 ± 0.007 to 0.06 ± 0.02 mM; V_max values under both conditions were 0.12 ± 0.01 A₃₄₀ min^–1 nM^–1). Because the K_M for UQ₀ is composed of rate constants for association and dissociation of the substrate as well as the chemical steps for both half-reactions (see the Supporting Information), the precise mechanism through which quinol binding decreases the K_M of UQ₀ is unclear. Nevertheless, in the case of UQ₁H₂ activation of UQ₀, the quinol appears to function as an allosteric activator. The incomplete inhibition of NDH-2 transhydrogenase and quinone reductase activities and apparent allosteric activation of NADH-UQ₀ reduction by UQ₁H₂ provide unequivocal evidence of the existence of at least two binding sites with different affinities for quinone and quinol ligands on Mtb NDH-2.

Discussion

Comparison of the kinetics for Mtb NDH-2 catalysis of the NADH-Q and transhydrogenase reactions allowed us to conclude that the NADH-Q reductase activity follows a nonclassical, two-site ping-pong kinetic mechanism as has been reported for a number of other oxidoreductase systems.¹⁵⁻¹⁷ The establishment of this two-site mechanism differs from the previously reported ternary complex mechanism proposed for the yeast NDH-2 analogue, Ndi1, and supports the recent Ndi1 crystal structure of Feng et al.,⁹ showing separate binding sites for NADH and quinone on opposite faces of the isoalloxazine ring of the FAD cofactor. In addition, studies with quinol products revealed a second quinone-binding site more suited to binding quinol than quinone. Occupation of this second site produced either partial inhibition or activation depending on the specific quinone/quinol pair. It is unclear if these two sites reflect the two sites found in the Ndi1 crystal structure of Feng et al.,⁹ both of which were predicted to play a role in catalysis.

Discrimination between a one-site and a two-site ping-pong mechanism was based on considerable evidence. (1) Kinetic studies with UQ₂ as the electron acceptor found no evidence of competition with NADH, even though its K_M was at least 10-fold lower than that for NADH (Figure 2B). The absence of substrate competition under these conditions is consistent with independent electron donor- and acceptor-binding sites. In contrast, the transhydrogenase reaction, which was predicted to follow a one-site ping-pong mechanism, displayed substrate inhibition between NADH and tNAD⁺; K_M values for NADH and tNAD⁺ were approximately equal in this reaction (Figure 3B). (2) NAD⁺ was a potent competitive inhibitor of tNAD⁺ in the transhydrogenase reaction, consistent with overlap in donor- and acceptor-binding sites. In contrast, NAD⁺ inhibited NADH-UQ₀ activity only weakly, despite UQ₀ having a K_M 30-fold higher than that of tNAD⁺ (Figure 4C,D). The lack of appreciable competition between NAD⁺ and UQ₀ strongly indicates that donor and acceptor substrates bind to different sites, consistent with a two-site ping-pong mechanism. (3) Finally, in a reaction mixture containing both UQ₀ and tNAD⁺, initial NADH oxidation rates reflected the high k_cat of the NADH-UQ₀ reductase reaction instead of the low k_cat of the transhydrogenase reaction (Figure 5). On the basis of a K_M for tNAD⁺ 30-fold lower than that for UQ₀, the concentration of tNAD⁺ in the reaction mixture should have prevented UQ₀ from binding to reduced NDH-2 if both electron acceptors were interacting at the same site.

The relatively low K_i of NAD⁺ for reduced NDH-2 compared to the K_M of NADH (differing by 3-fold) for the oxidized NDH-2 might appear to be counterproductive to overall reaction efficiency, especially in the bacterium where the steady-state NAD⁺/NADH ratio usually favors NAD⁺. However, as discussed above, in the two-site ping-pong mechanism, quinone and NAD⁺ are not competitive for the reduced enzyme, and therefore, NAD⁺ will not impede the reduction of quinone. Furthermore, quinone reduction is fast compared to FAD reduction by NADH, the likely rate-determining step (Table 1). The greater efficiency of quinone reduction will maintain the enzyme largely in the oxidized state to which NAD⁺ binds weakly (K_i ∼5–7-fold greater than K_M for NADH). Our kinetic data also suggest a potential protective role for the tight binding of NAD⁺ to reduced NDH-2. Tight binding of NAD⁺ may limit the reactivity of reduced FAD toward soluble oxidants such as molecular oxygen, thereby suppressing the formation of toxic reactive oxygen species. Physiologically, a two-site ping-pong mechanism is ideal for catalyzing the transfer of electrons from a charged, cytoplasmic electron donor (NADH) to a hydrophobic electron acceptor that is buried in a membrane (menaquinone).

Recently, Yang et al.⁷ proposed a ternary complex mechanism for Ndi1. Their data were heavily based on the appearance of a broad 740 nm spectral peak characteristic of a charge transfer complex. The peak was barely detectable upon addition of NADH but intensified upon addition of an electron acceptor. The need for both substrates to maximize the 740 nm signal was interpreted to indicate that the charge transfer complex was a ternary complex between the enzyme and both substrates and that the oxidation–reduction process was concerted and proceeded through this ternary complex. In support of a ternary complex, Yang et al.⁷ report inhibition kinetics with a quinol consistent with separate binding sites for quinone and NADH. Although this group initially reported a ping-pong mechanism for Ndi1, they recently attributed this result to an artifact resulting from enzyme solubilization and/or the use of small, soluble quinone substrates capable of entering the NADH substrate site.⁵ There is, however, an alternative explanation for their data. First, as shown here, the presence of independent binding sites is consistent with a two-site ping-pong mechanism. Second, the kinetics of the 740 nm peak intensification appeared to be too slow (∼5 min with O₂ or UQ₆) to be consistent with steady-state kinetics. We suggest that the slow intensification may be related to the accumulation of NAD⁺ during the reaction, especially if the interaction of NAD⁺ with the reduced form of Ndi1 is as strong as described for NDH-2 in this study. Broad absorption peaks at 740 nm between reduced flavoprotein (FADH₂, acting as the charge donor) and NAD⁺ (acting as the charge acceptor) have been described for flavoproteins exhibiting ping-pong kinetics, e.g., glutathione reductase and lipoyl dehydrogenase.¹⁸

When Ndi1 was crystallized in the presence of UQ₄, electron density for 2 equiv of quinone ligands (designated UQ_I and UQ_II) was observed on the si face of the FAD isoalloxazine ring, which opens to the face of Ndi1 that associates with the membrane.⁹ The authors further supported this observation through an EPR study, in which two distinct semiquinone species were observed. This structural evidence is consistent with studies of Ndi1, indicating weak and strong quinone-binding sites.⁵ On the basis of their structural and EPR studies, Feng et al.⁹ proposed a model whereby 2 equiv of quinone participates in the transfer of an electron from FADH₂.

In our studies, addition of quinols (UQ₁H₂ and UQ₂H₂) to the NADH-Q and transhydrogenase reaction mixtures produced partial inhibition (maxima of 30 and 60 μM, respectively) in most cases. Thus, they were not competitive inhibitors of NADH, tNAD⁺, or quinones and therefore not interacting at the substrate-binding site(s). The order of inhibitor effectiveness for the various quinols was the same for the transhydrogenase and NADH-Q reactions, consistent with a single quinol-binding site capable of affecting both reactions. Perhaps the best evidence for a unique quinol site is the observation that UQ₀ reduction was activated in the presence of UQ₁H₂ (Figure 6B). Activation resulted from a 5.5-fold reduction in the K_M for UQ₀ (Figure 6C), suggesting an allosteric interaction with NDH-2. A binding constant of 0.07 mM was measured for the activation, which is similar to that observed for Q₁H₂ inhibition of transhydrogenase and NADH-Q reactions. Thus, we believe that both inhibition and activation of NDH-2 reductase activity are mediated through a single quinol-binding site. How this site affects the transhydrogenase reaction remains to be determined. Feng et al.⁹ do not provide information about quinol inhibition for Ndi1 activity, making it difficult to compare their structural results with our kinetic results. However, Yang et al.⁷ report competitive inhibition of Ndi1 catalytic activity by Q₁H₂. This would suggest the Mtb quinol-binding site described in our study is not reflective of either of two quinone sites described in the crystal structure of Feng et al.⁹

This study establishes that Mtb NDH-2 catalyzes quinone reduction through a two-site ping-pong mechanism, which is distinct from the sequential, ternary complex mechanism proposed for yeast homologue Ndil.⁷ Our studies also provide evidence of a binding site that favors quinols over quinones. In other studies, we showed that a drug, trifluoperazine,¹⁹ inhibits NDH-2 in a noncompetitive manner, and the drug clofazimine is a substrate of NDH-2, its reduction leading to ROS production.²⁰ The identification of a unique binding site that favors quinols and can influence activity might help explain the relatively selective interaction of mycobacteria with these drugs and aid in the design of inhibitory agents that target enzyme regulation. Work to fully understand the function and utility of the quinol/quinone-binding sites is underway.

Glossary

Abbreviations

Mtb

M. tuberculosis

NDH-2

type II NADH-quinone oxidoreductase

Complex I or NDH-1

type I NADH-quinone oxidoreductase

MDR

multi-drug resistant

Ndi1

S. cerevisiae NADH dehydrogenase

NAD⁺

nicotinamide adenine dinucleotide, oxidized form

NADH

nicotinamide adenine dinucleotide, reduced form

FAD

flavin adenine dinucleotide, oxidized form

FADH₂

flavin adenine dinucleotide, reduced form

TN

turnover number

UQ

ubiquinone, oxidized form

UQH₂

ubiquinone, reduced form

tNAD⁺

thio-NAD⁺, oxidized form

tNADH

thio-NAD⁺, reduced form

DMSO

dimethyl sulfoxide.

Supporting Information Available

Kinetics of NAD⁺ inhibition for NADH-tNAD⁺ transhydrogenase and NADH-UQ₀ reductase activities that are the same as those depicted in Figure 4 except that data are presented as s–v plots and the data were globally fit using the same parameters used in Figure 4 (Figure S1), microscopic steps for the NADH-Q reductase and transhydrogenase reactions (Scheme S1), and kinetic parameters for the NADH-Q reductase and transhydrogenase reactions depicted in Scheme S1 (Table S1). This material is available free of charge via the Internet at http://pubs.acs.org.

Author Contributions

T.Y., M.R., K.K.A., N.M.S., and C.P.S. performed the experiments, and T.Y., N.M.S., H.R., and C.P.S. wrote the manuscript. All authors have given approval to the final version of the manuscript.

This work supported by National Institutes of Health Grant R01 AI068942 (to H.R.) and the Global Alliance for TB Drug Development.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States