Hunting complex differential gene interaction patterns across molecular contexts

Abstract

Heterogeneity in genetic networks across different signaling molecular contexts can suggest molecular regulatory mechanisms. Here we describe a comparative chi-square analysis (CPχ²) method, considerably more flexible and effective than other alternatives, to screen large gene expression data sets for conserved and differential interactions. CPχ² decomposes interactions across conditions to assess homogeneity and heterogeneity. Theoretically, we prove an asymptotic chi-square null distribution for the interaction heterogeneity statistic. Empirically, on synthetic yeast cell cycle data, CPχ² achieved much higher statistical power in detecting differential networks than alternative approaches. We applied CPχ² to Drosophila melanogaster wing gene expression arrays collected under normal conditions, and conditions with overexpressed E2F and Cabut, two transcription factor complexes that promote ectopic cell cycling. The resulting differential networks suggest a mechanism by which E2F and Cabut regulate distinct gene interactions, while still sharing a small core network. Thus, CPχ² is sensitive in detecting network rewiring, useful in comparing related biological systems.

INTRODUCTION

Numerous methods have been developed for biological network reconstruction, which remains challenging owing to data insufficiency (1). Rather than reconstructing full networks, a shift has been to identify differential interaction patterns across noisy biological networks (2), as they can be linked directly to differences in molecular mechanisms. For example, a co-signaling molecule in a T cell can interact with more than one ligand or counter-receptor and consequently may either stimulate or inhibit immunological functions dependent on a specific molecular context (3). A majority of methods to detect such network rewiring are based on differential correlation—the difference between gene–gene correlation coefficients (4). Generalizing to difference between other statistics obtained separately for each condition, the difference between S-scores, based on a modified t-statistic, was used to identify differential interactions (5). Such a difference-between-statistics paradigm, comparing statistics of patterns but not directly the patterns themselves, is either insensitive or prone to noise. Correlation is a function of both noise and interaction parameters. Unequal noise across conditions can lead to zero differential linear correlation despite distinct slopes (Figure 2). This constitutes the insensitivity deficiency of difference-between-statistics. On the other extreme, reconstruct-then-compare (RTC) (6)—reconstructing interaction patterns first, and then comparing the patterns for difference—ignores uncertainty in the patterns, and false positives tend to arise due to noise. Ouyang et al. (7) overcame these problems by characterizing homogeneity and heterogeneity of parametric interaction patterns while also considering uncertainty for continuous data.

Figure 2.

Conceptual limitations of differential correlation: (a) anti-correlation, (b) shift, (c) reflection and (d) nonlinear interaction patterns. Only anti-correlation in (a) can be detected by differential correlation, while CPχ² detected all four differential interactions. (a) Anti-correlation. Detectable by differential correlation: 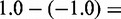2 ≠ 0, and by CPχ²: p_d = 4.9e-6. (b) Shift. Undetectable by differential correlation: 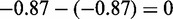. Detectable by CPχ²: p_d = 0.0050. (c) Reflection. Undetectable by differential correlation: 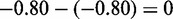. Detectable by CPχ²: p_d = 0.0060. (d) Nonlinear. Undetectable by differential correlation: 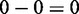. Detectable by CPχ²: p_d = 5.0e-5.

To balance between sensitivity to interaction patterns and robustness to noise, we present a comparative chi-square analysis (CPχ²) to hunt for homogeneous and heterogeneous nonparametric interaction patterns from discrete data. An interaction is an association from one or more parent variables (e.g. transcript quantities of several genes) to a child variable (e.g. another gene’s transcript quantity), represented by the generalized truth table (gtt)—a discrete nonparametric function mapping parent variables to a child variable (8). Nonparametric representation enables detection of complex nonlinear interactions, thus more flexible than parametric approaches including differential correlation (4). A pair of interactions is conserved if both have an identical gtt involving the same parent and child variables; otherwise, it is defined as differential. By decomposing a pair of interactions to measure their homogeneity and heterogeneity, we determine whether interactions are conserved or differential. We show the heterogeneity statistic to be asymptotically chi-square distributed. In a simulation study comparing two pairs of cell cycle models for the budding and fission yeasts, we demonstrate that CPχ² is statistically more powerful than RTC. Broadly, CPχ² is applicable to systems with qualitative states such as Boolean networks and discrete dynamic Bayesian networks for comparing interactions under uncertainty.

MATERIALS AND METHODS

Comparative chi-square analysis of interactions

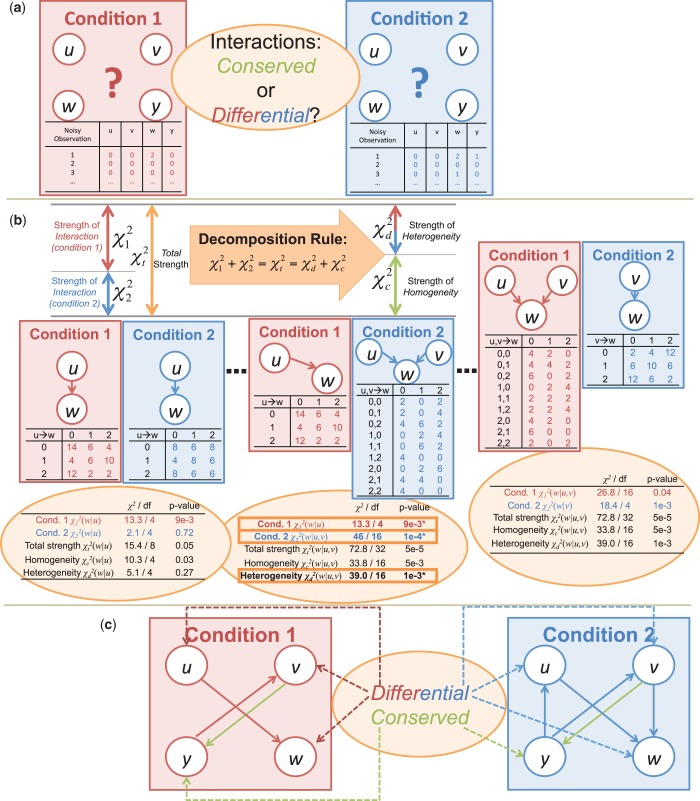
The CPχ² framework is illustrated in Figure 1. The input to CPχ² is observations of nodes, e.g. gene expression, in networks under two or more conditions (Figure 1a). We assume that the networks, of a same set of nodes, may differ in either wiring or strength of interactions. Let 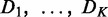be data sets measuring values of nodes in K networks. The output is differential or conserved interactions for each node across the networks (Figure 1c). We first create a contingency table C_k from D_k. Each row index in a contingency table is a specific combinatorial realization of one or more parent variables. Each column index is a specific value the child variable can take. The observed pattern in a contingency table represents how the parent variables interact with the child variable. The chi-square of a contingency table is a discrepancy measure between the observed and expected counts in its cells when parent and child variables are independent. The individual interaction strength 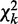, computed from C_k, measures parent–child association separately for condition k. Summing up 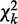over k, we obtain the total strength 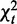, and by further breaking it into to homogeneity 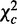and heterogeneity 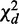, we establish a decomposition rule central to our framework (Figure 1b):

(1)

Figure 1.

Overview of CPχ2. (a) Observations are collected for a network in two contexts. Observed trajectories (shown as tables under each network) are input to the analysis. (b) By the decomposition rule, after adding individual interaction strengths, we obtain the total strength, 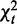, of a pair of interactions, and decompose it to homogeneity 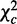and heterogeneity 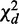. The decomposition is applied on every potential pair of interactions. A pair of interactions showing the best fit to each condition is chosen for each node based on 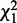and 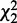. (c) Interactions showing strong heterogeneity are differential and those showing strong homogeneity but insignificant heterogeneity are conserved. These interactions constitute the output.

Under the null hypothesis of noninteracting homogeneity across conditions, 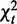is asymptotically chi-squared because it is the sum of independent chi-squares in the K conditions (9). 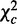is asymptotically chi-squared, as it is computed on a single pooled contingency table. We prove that 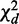is also chi-squared. By statistical significance of these test statistics, differential or conserved interactions are decided.

Interaction homogeneity and heterogeneity via decomposition

By three chi-square tests, we assess total strength, strength of homogeneity and strength of heterogeneity for interactions across K conditions. For a node X, or child, of Q discrete levels in the networks, we evaluate its hypothetical parent sets 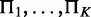under K different conditions via chi-square statistics on contingency tables formed between the parents and the child. We first identify the smallest super parent set 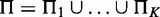. Let R be the number of combinations of discrete levels in Π. Let 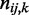be the number of observations in entry 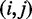of 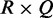contingency table C_k with sample size n_k under condition k. We compute K chi-squares with degrees of freedom (d.f.) 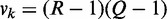to assess the strength of an interaction under each condition by

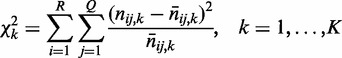(2)

where the expected count in entry (i, j) of C_k is

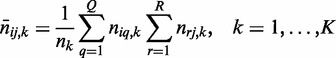(3)

under the null hypotheses that no interaction exists between the given parents and child in each condition. If both 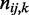and 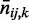are zero for a cell, the cell contributes zero to 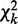. Summing up 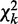’s, we obtain the ‘total strength’ of interaction

(4)

as our first chi-square statistic, measuring evidence of active interactions under ‘some’ of the K conditions, regardless of differential or conserved. The null hypothesis is that no active interaction exists between any parent sets and the child in ‘any’ condition. Under the null hypothesis, 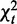asymptotically follows a chi-square distribution with d.f. 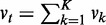and P-value p_t.

To measure the overall agreement of the interactions among all K conditions, we develop a homogeneity test. Then we fill in an 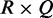contingency table 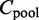using parent superset Π and child values from 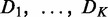. Thus, entry (i,j) of 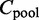contains 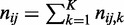observations. We now compute our second χ² statistic as the ‘strength of homogeneity’:

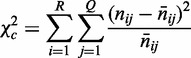(5)

where the expected count in entry (i, j) of 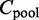is

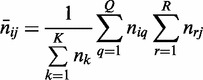(6)

under the null hypothesis that there is no consistent pattern among the interactions between all parent sets and the child in all K conditions. Under this null hypothesis, 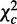asymptotically follows a chi-square distribution with d.f. 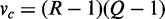and P-value p_c.

To measure the strength of deviation of each interaction from the homogeneous component of all interactions, we define the ‘strength of heterogeneity’ by

(7)

as our third χ² statistic, where 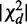is chi-square distributed with d.f. 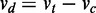and P-value p_d, under the null hypothesis that there are no interactions in any contingency table. 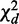measures differential interactions not due to row or column marginal distributions, as explained in Supplementary Methods S3.1. The asymptotic chi-square distribution of 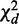is derived from the following theorem:

Theorem 1. —

Under the null hypothesis of K homogeneous noninteracting contingency tables, the heterogeneity statistic is asymptotically chi-square distributed with degrees of freedom.

Here is a sketch of the proof: (i) Normalize each contingency table by subtracting cell means and dividing the standard deviation based on a multinomial distribution of the cell counts. (ii) Transform each normalized contingency table to a matrix of identically and independently distributed (i.i.d.) standard normal variables by using row- and column-Helmert matrices. (iii) Apply the above two steps on the pooled contingency table and obtain a matrix of i.i.d. standard normal variables. (iv) Show that in each cell the sum of normal variables squared minus the square of the pooled normal variable for the same cell is a quadratic form in the normal variables. We prove this quadratic form to be chi-square distributed. (v) The heterogeneity chi-square can then be represented as the sum of these independent chi-square variables in each cell, and is thus also chi-square distributed. A complete proof is given in Supplementary Methods S3.1.

Combining Equations (4) and (7), we obtain the ‘statistical decomposition rule for discrete interactions’:

(8)

with

(9)

which states that the total strength of interactions, as summation of strengths of each individual interaction, can be decomposed into a strength of homogeneity and a strength of heterogeneity. This rule provides the guiding principle underpinning the CPχ² framework.

Parents in a gene interaction, assumed given so far, are often unknown. In our software, the network topology can be either externally provided through an open user interface or the program can internally learn the network topology using various criteria. We can learn network topologies by maximizing network conservation or differentiation if such preference can be justified in advance. Our experience indicates that for networks without a prior tendency toward being conserved or differential, a network topology maximizing fitting to the data for each condition performed the best as demonstrated in our yeast cell cycle simulation study. We also allow the network topologies to differ across conditions but such options are effective only when sufficient data are provided to support the increased complexity.

CPχ² assumed independent two- (or multiple-)sample design, where samples are independent in each condition. This is often satisfied when each biological individual is used exactly once under only one treatment/condition.

Drosophila wing gene expression data and preprocessing

Cell cycle exit occurs in the Drosophila wing at 24 h after puparium formation (h APF) under normal conditions. When E2F or Cabut (Cbt) are overexpressed, wing cells go through at least one extra cycle and instead exit the cell cycle at 36 h APF (10). We therefore used Nimblegen Drosophila expression microarray to study gene expression in the fly wing in response to overexpression of Cbt or E2F at both the normal exit time, 24 h APF and the delayed exit time 36 h APF. RNA sample preparation and data normalization are described in Supplementary Methods S3.5.

To filter out transcripts that were not significantly differentially expressed in the experiments, we used two-way analysis of variance on time (24 h/36 h), condition (E2F+/Cbt+/wild type) and their interaction. This resulted in 6711 transcripts out of the total 15 473 retained for comparative analysis. To align the analysis with other biological evidence, we compiled a priority list of 4653 transcripts, from the total 15 473, selected for gene ontology terms suggesting roles in controlling gene expression, developmentally important signaling pathways or functions in cell cycle control. A total of 3768 priority transcripts are statistically significantly differentially expressed and thus included in the 6711 set.

Observations of many transcripts are apparently linearly correlated likely owing to either the small sample size (24) for a large number of priority transcripts (3768) or truly linearly correlated biological function. To avoid favoring by chance anyone of them as a parent to a child, we group them into linearly correlated clusters to serve as parents. When an interaction from a parent cluster to a child gene is identified, all members in the parent cluster are considered candidates to a potential biological interaction. By hierarchical variable clustering, the 3768 priority transcripts formed 491 groups of linearly correlated genes and 34 groups of a single transcript, based on 24 observations at time points 24 h APF and 36 h APF, with four replicates under three conditions. As transcripts in a same cluster are either positively or negatively linearly correlated, in quantization to be done next, each transcript in the same cluster as parents (including those negatively correlated) would lead to similar chi-square values for a given child. Thus we consider them mathematically equivalent in the context of CPχ² and only choose a cluster representative for further analysis. The cluster representative is a transcript with largest median correlation coefficients with all other transcripts in the same cluster.

Next, we discretized continuous gene expression data to three discrete levels of low, intermediate and high. Discretization is achieved by a joint-likelihood quantization using sequential dynamic programming (11). The average estimated noise level is 0.22 over all quantized transcripts (Supplementary Figure S3). The maximum likelihood estimation of noise level is described in Supplementary Methods S3.3.

The above preprocessing generates the input to CPχ² analysis, including three files of gene expression levels under the conditions of E2F+, Cbt+ and the wild type control, respectively. Each file contains eight discrete samples with value 0, 1 or 2 for each of the 7202 (=491 + 6711) transcripts. Each file also specifies that only representatives of the 525 clusters of priority transcripts can be used as a parent (potential regulator) for a child transcript (any of the 7202).

Highlighting differential gene interaction networks in fruit fly wing development

We performed CPχ² analysis across the three experimental conditions E2F+, Cbt+ and the normal wild type. Cbt and E2F delay cell cycle exit and cause ectopic cell cycles by regulating distinct but largely overlapping sets of genes (Supplementary Figure S1). Thus, we hypothesized that overexpression of E2F or Cbt gives rise to differential gene interactions in reference to the wild type unperturbed state.

In evaluating each potential parent–child relationship, the parent candidates were chosen from the priority gene clusters, and the potential children include every transcript and priority gene cluster. We inspected the parent–child relationships at the same time point, at a zero Markovian order. The maximum number of parents per child was set to 1 as the sample size does not provide a sufficient statistical power to detect interactions with more parents. We did not allow change in parent identity for the same child in interactions to anticipate strength change in gene interactions. All differential interaction P-values were adjusted by the Benjamini–Hochberg method (12) to account for the multiple testing effect by controlling the false discovery rate.

We obtained a network topology that maximized the fit to both E2F+ and Cbt+ data sets, capturing active interactions in both data sets regardless of conserved or differential. Then for each interaction in this active network, we classified it into one of three groups: (i) Conserved between E2F+ and Cbt+ but differential from control, if and only if p_d(E2F+ and Cbt+ versus control) 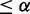, p_d(E2F+ versus Cbt+) 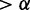and p_c(E2F+ versus Cbt+) 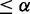; (ii) Differential between E2F+ and control and differential between E2F+ and Cbt+, if p_d(E2F+, control) 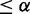and p_d(E2F+, Cbt+) 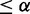; and (iii) Differential between Cbt+ and control and differential between E2F+ and Cbt+, if p_d(Cbt+, control) 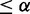and p_d(E2F+, Cbt+) 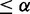. All these differential interactions require statistically significant change in the distribution of each involved gene, which we call working zone change as detailed in Supplementary Methods S3.2.

Motif finding in Drosophila differential gene networks

For the chosen genes that are differential between E2F+ or Cbt+ and the control, sequences upstream of the transcriptional start site was obtained using the UCSC Drosophila Genome Browser (13) or Regulatory Sequence Analysis Tools (14). Sequences were entered into Multiple EM for Motif Elicitation (MEME) (15) and the top five scoring motifs (of widths 6–12 bases) were obtained. Using MEME we looked for motifs enriched in gene clusters displaying differential interactions with working zone changes as well as the top 200 most strongly E2F1 and Cbt co-upregulated genes. The rationale was that we could identify motifs specific to E2F and Cbt target gene sets that overlap in the co-regulated target gene clusters. TOMTOM (16) was used to compare the MEME identified motifs to known Drosophila motifs. As proof of principle, we were able to readily identify two distinct E2F binding sites. On examination of Cbt regulated genes, we identified a novel Drosophila Mad-like motif (Supplementary Figure S2).

RESULTS

Sensitivity of CPχ2 to interaction heterogeneity over alternative approaches

We first evaluated the sensitivity of CPχ² to interaction heterogeneity over differential correlation and RTC.

In several conceptual examples shown in Figure 2, the differential correlation method can be completely insensitive to some truly heterogeneous interaction patterns because each pair of patterns has identical correlation coefficients.

RTC is an intuitive alternative for comparing interactions. We illustrate it with the generalized logical network reconstruction algorithm we developed previously based on chi-square testing (8). Using the same basic chi-square statistic enables a fair experiment to study interaction comparison strategies. RTC first reconstructs a gtt for each node using parents with a smallest P-value of 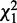for the first network, and generates in isolation another gtt based on 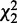for the second network. Then it compares the difference between each pair of reconstructed gtts to declare a conserved or differential interaction. An interaction is conserved if its gtts are the same across two conditions and at least one gtt is significant (P-value 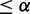, a false-positive threshold). An interaction is differential if the two gtts are different and at least one is significant. If both are insignificant, the interaction is inactive or null. Such direct gtt comparison ignores data uncertainty.

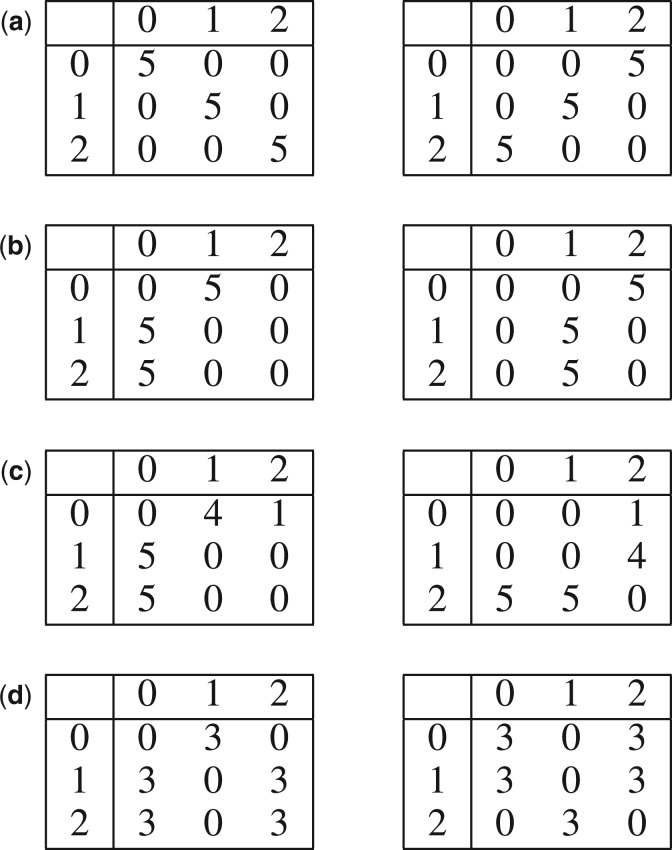
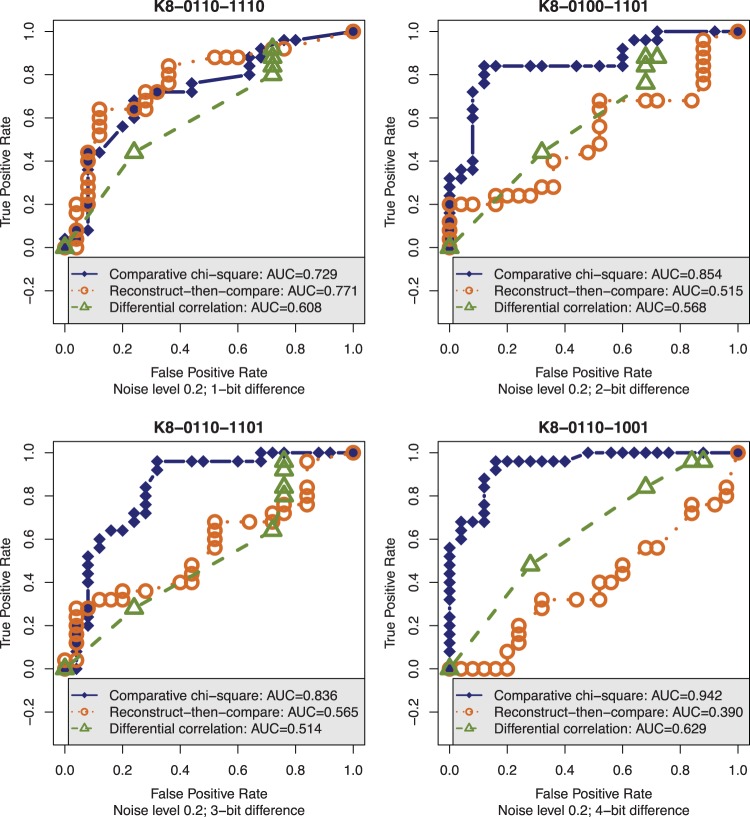
A second set of examples in Figure 3 illustrates a decisive advantage of CPχ² in sensitivity to interaction heterogeneity over differential correlation and RTC at a small sample size. We created a pair of conserved and four pairs of differential Boolean interactions. Each interaction, with two parents and one child, forms a 4-bit truth table. The four pairs of differential interactions have increasing heterogeneity from 1 to 4 bits in their truth tables. With these 10 truth tables, we simulated data sets of a small sample size 8 at the noise level of 0.2 using a noise model defined in Supplementary Methods S3.3. Both the sample size and the noise level of 0.2 are consistent with the Drosophila gene expression data set (Supplementary Figure S3). Then, we applied the three methods on the simulated data sets. The receiver operating characteristic (ROC) curves and area under ROC curves (AUCs) are qualitative and quantitative indicators of the performance. Figure 3 shows that the sensitivity of CPχ² becomes progressively pronounced as interaction heterogeneity increases and is maximized when the truth tables differ the most at 4 bits: the gain of CPχ² in AUC is remarkably 31% over differential correlation or 55% over RTC.

Figure 3.

Sensitivity to interaction heterogeneity. CPχ² shows decisive advantage in sensitivity to heterogeneity on data sets with sample size (8) and noise level (0.2) consistent with the Drosophila gene expression data set. The true positives are based on four pairs of differential Boolean interactions with two parents, and the false positives are based on one pair of conserved interactions. As interaction heterogeneity increases from 1 (top left), 2 (top right), 3 (lower left) to 4 (lower right) bits, the improved performance of CPχ² in AUC contrasts sharply with the either stagnant or deteriorating performance of differential correlation or RTC.

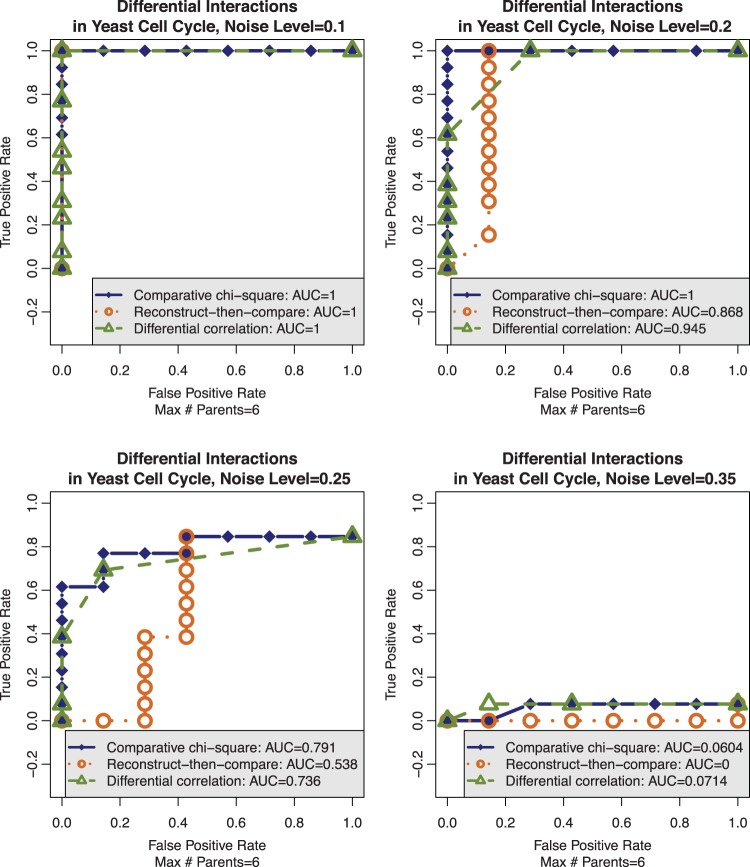
Benchmarking robustness to noise on yeast cell cycle networks

We benchmarked the performance of CPχ² on comparing two pairs of gene networks in budding and fission yeast, respectively, against RTC and differential correlation, using ROC curves at four noise levels (Figure 4). The two pairs of cell cycle gene networks are plotted in Supplementary Figures S6 and S8 and the corresponding generalized logic rules are described in Supplementary Figure S7, S8, S10 and S11. The first pair of budding yeast models (17,18) is similar in network topology; the second pair of fission yeast models (18,19) differs considerably in both network topology and logic. Altogether there are 13 differential and 7 conserved interactions in the two pairs. From each model, we simulated a number of trajectories, each lasting 2–13 time points, to cover all states of the networks. Then we added various levels of independent random noise to each gene in every state of each trajectory using the noise model defined in Supplementary Equation (S28). The noise does not modify the length of the trajectory. The trajectory pairs are input to CPχ² to obtain differential and conserved interactions.

Figure 4.

Robustness to noise in comparative analysis of two pairs of yeast cell cycle models. Data were simulated from the four yeast cell cycle models at increasing noise levels (0: no noise, 0.5: maximum possible noise). CPχ² again performs better in AUC than differential correlation or RTC at the intermediate noise levels of 0.2 and 0.25, most consistent with what was observed in Drosophila gene expression data. When noise is at 0.35, their distinction nearly diminishes. Here, ROC curves become flat and cannot reach a true positive rate of 1 owing to a no-false-parent requirement.

In Figure 4, we define a true positive as a pair of true differential interactions declared as such involving no false parents. A false positive is a pair of true nondifferential interactions declared as differential. A true negative is a pair of true nondifferential interactions declared as such. A false negative is a pair of true differential interactions declared either with incorrect parents or as nondifferential. Here, nondifferential refers to either conserved or null interactions. At each noise level, we collected accumulated results against the groundtruth. Then we plotted ROC curves for detecting differential interactions. The increase in AUC from RTC or differential correlation to CPχ² is evident at the noise levels of 0.2 and 0.25, consistent with what we encountered in biological data. Specifically, CPχ² improved the AUC by ∼5.5% from differential correlation and by ∼13–25% from RTC. Therefore, CPχ² is more robust to noise in detecting differential interactions than its alternatives. Full detail of the yeast cell cycle simulation study is provided in Supplementary Methods S3.4.

Cbt regulates distinct and overlapping gene interactions with E2F in cell cycle

We then extended CPχ² to examine in vivo genetic interactions in response to the ectopic expression of two transcription factors that promote cell proliferation in the wings of Drosophila melanogaster. The Drosophila wing is used to study cell cycle control because it is highly homogeneous and normally undergoes a well-characterized naturally synchronous cell cycle exit to become permanently postmitotic during metamorphosis (10,20,21). Consistent with its role in promoting the cell cycle, the E2F complex is a well-established target for negative regulation by tumor suppressor proteins such as Retinoblastoma (22) and is positively regulated by oncogenes such as SV40 Large T and Adenovirus E1A (23). We have found the E2F complex to regulate the expression of a number of cell cycle regulators, chromatin modifiers and other factors comprising the ‘E2F transcriptional program’ in the fly wing (24). Activation of the E2F complex can delay the process of cell cycle exit and cause ectopic cycling in the wing by promoting the expression of hundreds of cell cycle regulators, chromatin modifiers and other factors (24). Surprisingly, we have recently found that overexpression of another, unrelated zinc finger transcription factor Cbt (25–27), not previously known to play a role in cell cycle regulation, can also delay cell cycle exit and cause ectopic cycling. We have thus applied CPχ² to detect differential genetic interactions that might mediate the overlapping, yet distinct transcriptional outputs to these two transcription factors.

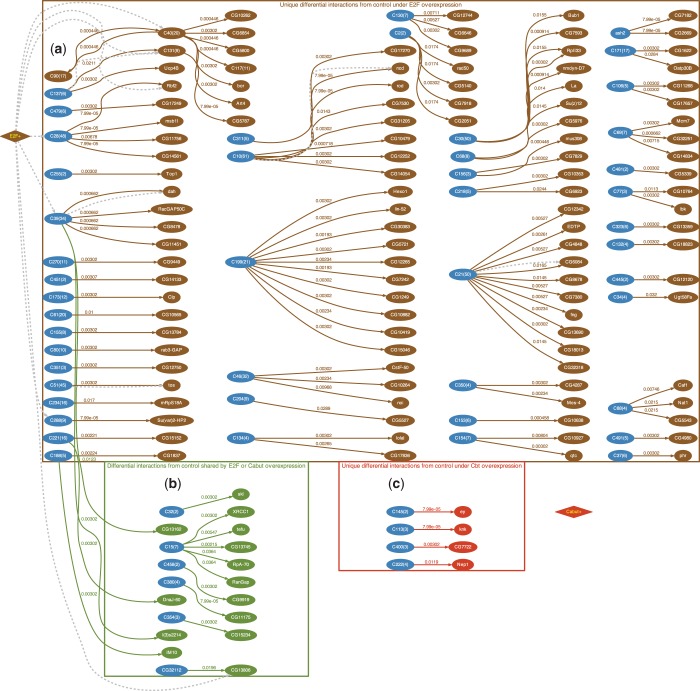
In addition to their many shared transcriptional targets, Cbt and E2F also regulate a distinct nonoverlapping group of transcripts (Supplementary Figure S1) and have differing effects on the level of cell proliferation, tissue patterning and apoptosis in the wing. Thus comparing responses to their overexpression provides an ideal opportunity to examine both conserved and differential interactions in vivo. We applied CPχ² on the corresponding expression array data collected with overexpression of E2F (E2F+), Cbt (Cbt+) and the normal wild type (control). We found that E2F+ and Cbt+ are associated with different sets of differential gene interactions from the control, albeit sharing a small portion involved in promoting proliferation. Specifically, we identified 111 unique differential interactions in E2F+ versus the control (Figure 5a), 14 differential interactions from the control but conserved between the E2F+ and Cbt+ conditions (Figure 5b), and 4 unique differential interactions in Cbt+ versus control (Figure 5c).

Figure 5.

Differential gene networks detected when proliferation is promoted in Drosophila wings by two perturbed transcription factors E2F and Cbt. Adjusted p_d-values for each detected differential interaction are marked on corresponding edges. All gene nodes are differentially expressed. Blue nodes are not children in any significant differential interactions detected, but are parents in other significant differential interactions. Dashed lines are known gene interactions obtained from BioGRID. (a) Unique significant differential interactions (dark tan) due to overexpression of E2F. (b) Consistent significant differential interactions (green) due to overexpression of E2F or Cbt. (c) Unique significant differential interactions (red) due to overexpression of Cbt.

BioGRID (28) searches confirmed five predicted interactions (CG3008 →Ebi, CG8247 →Dah, Ntf-2 →CG6084, CG9938 → tos and sub →ncd) and eight genes (DREF, CycA, brm, dap, Ebi, CG13900, Rbf2 and CG13806) known to interact with E2F. These 13 interactions, marked with dashed lines in Figure 5, are discussed for their biological function in Supplementary Table S1. An evaluation of the evidence suggests that they underpin a network of genes for proliferation by acting cooperatively to promote S-phase and mitosis in response to ectopic E2F or Cbt activity. Figure 5 also predicted parent–child interactions for genes that do not have any known interactions within BioGRID. Importantly, the 14 gene interactions shared by E2F and Cbt (green nodes in Figure 5b) were conspicuous within this group, suggesting a potential coherent core network modulated to promote proliferation (Supplementary Results). Interestingly, our analysis revealed novel interactions that suggest a role for RIO kinases in modulating the function of a transcriptional repressor Ebi, on cell cycle genes (29). We also uncovered several negative cell cycle regulatory loops predicted to limit proliferation that are uniquely engaged when E2F is activated, but not when Cbt is activated. This is consistent with our previous research demonstrating that E2F, when aberrantly active, also induces robust cell cycle negative-feedback mechanisms to limit abnormal proliferation (24).

To seek further support that the regulatory role of Cbt is distinct from E2F, we identified a novel Mad-like motif (Supplementary Figure S2) in Cbt-regulated and Cbt/E2F co-regulated genes, but not enriched in E2F-only regulated genes. It is striking that this novel motif has such a strong similarity to the Mad binding motif (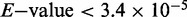), as Cbt and its closest mammalian homolog, KLF10 or TIEG1, are known to impinge on the transforming growth factor β (TGF-β) signaling pathway that converges on the Mad transcription factor (25,27,30). One possibility is that Cbt may bind the identified Mad-like site directly to regulate gene transcription, or it may interact with a DNA binding partner, such as Mad, to regulate target gene expression.

DISCUSSION

E2F and Cbt regulate a largely overlapping, yet distinct, set of cell cycle genes (Supplementary Figure S1). The newly discovered function of Cbt as a cell cycle regulator potentially provides cells with a mechanism for E2F-independent control of cell cycle genes. Cbt is a member of the highly conserved specificity protein/Krüppel-like factor (SP/KLF) family of transcription factors (25,26,31). The ability of Cbt to induce ectopic cell proliferation suggests that it could have oncogenic function. However, the most immediate mammalian homologs of Cbt, KLF10 and KLF11 (members of the TIEG family) are known primarily as cell cycle repressors (32). In mammals, KLF10 and KLF11 are expressed rapidly following induction of TGF-β signaling and function as effectors of TGF-β signaling (30,33–39) with overexpression recapitulating TGF-β–induced cell cycle exit (30,36,39,40). In contrast, in Drosophila the TGF-β family member Dpp plays a well-known role in promoting proliferation and growth in the developing Drosophila wing (41) and Cbt has been shown to act positively on Dpp-signaling in this context (27). In addition, ectopic activity of other members of the SP/KLF family has been linked to a variety of cancerous phenotypes (42–45).

The Cbt-associated motif we identified (Supplementary Figure S2) is present in the promoters of many Cbt and E2F co-regulated genes, as well as in Cbt-only regulated genes. The sequence of the putative Cbt motif is consistent with known DNA-binding data for Drosophila Cbt as well as mammalian homologs, which bind GC-rich promoter sequences (46,47). Additionally, this motif resembles a Mad-like motif and Cbt was recently shown to enhance transcriptional activation of direct Dpp target genes (27). Importantly, recent work has suggested that Drosophila Cbt acts primarily as a transcriptional repressor (48), which runs counter to our simplest hypothesis that Cbt directly binds this motif to activate genes induced on Cbt overexpression. However, we cannot rule out the possibility that Cbt acts indirectly, perhaps via repression of another factor, acting on this motif. Further work exploring these relationships between Cbt, the cell cycle and the TGF-β signaling pathway may help elucidate a new relationship between developmental signaling pathways and cell cycle control.

The computational complexity of CPχ² is linear in both the number of conditions and the number of edges in the network, if network topology is given. If network topology must be learned from the data, the computational complexity increases to be linear in the number of conditions, polynomial in the number of nodes and exponential in the maximum number of parents per node. Exact fast chi-square algorithms exist for binary variables with two parents (49). The implementation of CPχ² already supports parallel computing using the Message Passing Interface protocol (50). In future biological experimental design, where two or more genes are simultaneously disrupted in a network of thousands of genes, fast and probably approximate implementation of CPχ² will be necessary.

The CPχ² method has profound implications for analyzing biological networks. Making minimal assumptions about underlying mechanisms, discrete nonparametric contingency tables are preferable in those systems without known parametric forms of interactions. It strikes a balance between differential correlation that irreversibly compresses interaction patterns and the noise-prone RTC, and offers practical benefits beyond existing differential co-expression methods suggested by our benchmarking. The usefulness of CPχ² is demonstrated here through identifying heterogeneous gene interaction patterns between E2F and Cbt transcription factors in regulating the cell cycle. Applicable to assays where multiple molecules are measured across molecular contexts, CPχ² thus has the potential to underscore diversity in molecular mechanisms implicating complex interaction patterns in differential network biology.

AVAILABILITY

Software is implemented in C++ and freely available to noncommercial users at www.cs.nmsu.edu/∼joemsong/software/CPX2.

ACCESSION NUMBERS

The data in this publication have been deposited in NCBI’s Gene Expression Omnibus (51) and are accessible through GEO Series accession number GSE30484 (http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE30484).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

NIH [5 U54 CA132383 to M.S. and 5 U54 CA132381 to B.A.E.]; NIH [K99/R00 GM086517 to L.B.]; graduate assistantship from an NSF CREST [HRD-0420407 to M.S.]; Developmental Biology Training Grant [T32 HD07183 to A.J.K.]. Funding for open access charge: NIH NCI grant [U54 CA132383], startup funds provided by the University of Michigan, and Excellence Initiative Funding from the Deutsche Forschungs Gemeinschaft (German Research Foundation).

Conflict of interest statement. None declared.