Abstract

The mutually corroborated electrochemical measurements and density functional theory (DFT) calculations were used to uncover the origin of electrocatalytic activity of graphene-based electrocatalysts for oxygen reduction reaction (ORR). A series of graphenes doped with nonmetal elements was designed and synthesized, and their ORR performance was evaluated in terms of four electrochemical descriptors: exchange current density, on-set potential, reaction pathway selectivity and kinetic current density. It is shown that these descriptors are in good agreement with DFT calculations, allowing derivation of a volcano plot between the ORR activity and the adsorption free energy of intermediates on metal-free materials, similarly as in the case of metallic catalysts. The molecular orbital concept was used to justify this volcano plot, and to theoretically predict the ORR performance of an ideal graphene-based catalyst, the ORR activity of which is comparable to the state-of-the-art Pt catalyst. Moreover, this study may stimulate the development of metal-free electrocatalysts for other key energy conversion processes including hydrogen evolution and oxygen evolution reactions and largely expand the spectrum of catalysts for energy-related electrocatalysis reactions.
Introduction
Graphene electrochemistry has gained paramount interest owing to its unique role in energy conversion and storage devices such as fuel cells, water splitting cells, and supercapacitors.1−7 One of the most extensively studied electrocatalytic applications of graphene is the oxygen reduction reaction (ORR) occurring at the cathode of fuel cells and metal-air batteries, in which advanced metal-free graphene-based electrocatalysts are considered as promising alternatives to the state-of-the-art precious Pt catalysts due to their low cost, fuel tolerance, and long-term durability.8−14 Tremendous efforts have been undertaken, both on the experimental and theoretical level, to improve the ORR performance of graphene-based materials by tuning their electronic properties through doping nonmetallic heteroatoms into a graphene matrix.2,15−21 However, the key ORR activity properties (e.g., exchange current density, on-set potential, 4e– pathway selectivity, and kinetic current density) of metal-free materials are still incomparable with those of Pt-based catalysts, which stimulates the ongoing debate on whether graphene is indeed an efficient catalyst for ORR.22 This issue is unresolved, largely due to the lack of knowledge on the origin of graphene activity toward ORR and the effect of the doping of nonmetallic heteroatoms on the graphene’s (electro)chemical properties. In other words, understanding the nature of the ORR process on the surface of doped graphene and recognizing the origin of its electrocatalytic activity open a new era in the design of graphene-based materials with superior electrocatalytic activity toward ORR.
In general, monitoring the reaction intermediates formed on the surface of catalysts represents a possible platform for understanding the pathway and mechanism of ORR electrocatalysis;23,24 however, it is difficult to observe in situ these adsorbed species due to their extremely short lifetimes.25 Importantly, the development of computational quantum chemistry provides a feasible methodology to predict the possible intermediates formed during the ORR process and to evaluate their stabilities on the surface of catalysts in terms of the adsorption free energies. For example, a theoretical methodology has been developed for studying ORR on a wide variety of metal catalyst surfaces, and the free energy diagram for this reaction was constructed together with a volcano-shaped plot that correlates the apparent electrocatalytic ORR activity with inherent oxygen adsorption strength.26−28 Consequently, various Pt and nonprecious metal alloys with superior experimentally measured ORR activities comparable to that of a pure Pt catalyst were designed and developed guided by the prediction of this theoretical methodology.29−34 However, such advanced methodology has not been applied to metal-free catalysts such as the most popular graphene-based catalysts; whether these metal-free counterparts can possess similar catalytic behavior or be even more active than metallic electrocatalysts is unknown from both theoretical and experimental viewpoints.
Here, we extend for the first time the aforementioned methodology used for metal catalysts to metal-free systems by exploring the relationship between the experimentally measured electrocatalytic ORR performance and the theoretically predicted free energy of reaction intermediates for a series of graphenes doped with nonmetal elements. The starting point of this methodology is the construction of the ORR free energy diagrams for various doped graphene models by density functional theory (DFT) calculations. Next, the ORR exchange current density, the on-set potential, and the reaction pathway selectivity are theoretically predicted on the basis of the free energy diagrams for each model catalyst. Also, all these descriptors of the ORR activity are obtained on the basis of the electrochemical voltammograms measured for the synthesized catalysts that correspond to the models studied. The origin of the oxygen reduction activity of the graphene-based catalysts studied is explained in-depth in terms of the molecular orbital theory. By combining experimental and theoretical data, it was possible to predict for the first time the electrocatalytic ORR performance of an ideal graphene-based catalyst (X-graphene) which possesses a 2.1 × 10–6 A/cm2 ORR exchange current density, a 0.33 V on-set potential (vs normal hydrogen electrode, NHE), and a nearly 100% 4e– pathway selectivity; these values are comparable with or even better than those of the state-of-the-art Pt catalyst. This combined computational and experimental study reveals the nature of ORR electrocatalysis for graphene-based materials and paves the way to the molecular design of more highly efficient metal-free electrocatalysts for applications beyond ORR.
Methods
Materials: Synthesis and Structural Characterization
To study the effect of different dopants on the ORR activity of graphene, we designed and synthesized nitrogen (N)-, boron (B)-, oxygen (O)-, sulfur (S)-, and phosphorus (P)-doped graphenes, respectively, as well as undoped graphene. All graphene-based samples were synthesized from chemically exfoliated graphene oxide (GO) prepared by a slightly modified Hummer’s method from graphite.35 After dialysis for one week, the graphite oxide dispersion was diluted, exfoliated, and centrifuged with the resulting GO concentration of ∼0.5 mg/mL. The GO powder was collected by lyophilization for further doping processes. Graphite powder was considered as a representative of pure graphene (G) without any heteroatom doping. Oxygen-doped graphene (O-graphene), which can be considered as reduced GO, was synthesized by thermally reducing initial GO powder at 900 °C in flowing Ar for 3 h without any additional precursor. Due to the strong oxidation process preceding chemical exfoliation of graphite oxide, the latter possesses many oxygen-containing functional groups. During high-temperature thermal reduction (900 °C in Ar atmosphere), most of the oxygen species are removed (oxygen concentration decreases from ∼50 atomic % in pristine GO to ∼5 atomic % in O-graphene); only four relatively stable species are retained. Nitrogen-, boron-, sulfur-, phosphorus-doped graphenes (N-graphene, B-graphene, S-graphene, P-graphene) were produced by annealing GO powder with various heteroatom-containing precursors (the mass ratio of the initial GO to the respective precursor = 1:10) at 900 °C in flowing Ar for 3 h. Melamine (C3H6N6), boron oxide (B2O3), benzyl disulfide (C6H5CH2SSCH2C6H5), and triphenylphosphine ((C6H5)3P) were used as the sources of N, B, S and P elements, respectively.
The X-ray photoelectron spectra (XPS) were measured on a Kratos Axis ULTRA X-ray Photoelectron Spectrometer equipped with a 165 mm hemispherical electron energy analyzer. The incident radiation was monochromatic Al Kα X-rays (1486.6 eV) at 225 W (15 kV, 15 mA). The survey scans were taken at the analyzer pass energy of 160 eV, and the multiple high-resolution scans were recorded at 20 eV. Transmission electron microscope (TEM) imaging was conducted on a FEI Tecnai G2 Spirit TEM at a voltage of 120 kV. Nitrogen-sorption isotherms were collected on a Tristar II, Micromeritics nitrogen sorption analyzer at 77 K. Prior to each measurement, the samples were degassed at 150 °C for at least 10 h. The Brunauer–Emmett–Teller (BET) specific surface area was calculated using adsorption data at a relative pressure range of P/P0 = 0.05–0.25 (Figure S1, Supporting Information [SI]). Raman spectra were recorded on a HORIBA LabRAM with 514.3 nm Ar laser (Figure S2, SI).
Electrochemical Characterization
All electrochemical measurements were performed using the same mass of catalyst (∼0.2 mg/cm2). Linear sweep voltammograms (LSV) were recorded using a glassy carbon rotating disk electrode (RDE, 0.196 cm2, Pine Research Instrumentation, U.S.A.) with a scan rate of 5 mV/s or a rotating ring-disk electrode (RRDE, 0.283 cm2, Pine Research Instrumentation, U.S.A.) with a scan rate of 2 mV/s. The data were recorded using a CHI 760 D potentiostat (CH Instruments, Inc., U.S.A.). The reference electrode was an Ag/AgCl in 4 M KCl solution (all potentials were referenced to NHE by adding a value of 0.205 V) and the counterelectrode was platinum wire. Electrolyte was O2-saturated 0.1 M KOH solution (pH = 13).
Kinetic Current
The kinetic current for ORR occurring on the electrode can be calculated from the intercept of Koutecky–Levich plot using the following equation (Figures S3 and S4, SI):36
| 1 |
where jK is the kinetic current density at a constant potential, jD is the measured current density on RDE, ω is the electrode rotating speed in rpm, and B, the reciprocal of the slope, could be determined from the slope of Koutecky–Levich plot using the Levich equation:
| 2 |
where n is the number of electrons transferred per oxygen molecule, F is the Faraday constant, DO2 is the diffusion coefficient of O2 in 0.1 M KOH, v is the kinetic viscosity, and CO2 is the bulk concentration of O2. The constant 0.2 is adopted when the rotating speed is expressed in rpm.
Electron Transfer Numbers
The overall electron transfer numbers per oxygen molecule involved in a typical ORR process were determined on the basis of RRDE voltammograms recorded by using a RRDE configuration with a 320 μm gap Pt ring electrode. The disk electrode was scanned cathodically at a rate of 2 mV/s, and the ring potential was constant at +0.5 V for oxidizing any OOH– intermediate. The electron transfer number (n) and OOH– intermediate production percentage (%OOH–, which serves as 2e– pathway selectivity) were determined as follows (Figure S5, SI):37
| 3 |
| 4 |
where Id is the disk current, Ir is the ring current, and N is the current collection efficiency of the Pt ring, which was determined to be 0.37.
Tafel Slope and Exchange Current Density
The Tafel analysis of the ORR polarization was evaluated by using the relation between the kinetic current density (jk) and overpotential (η = UNHE – 0.455) as:
| 5 |
where a (V) is the Tafel constant related to the exchange current density (j0) and b (V/dec) is the Tafel slope. A more complete version of this equation can be derived by simplifying the Butler–Volmer equation as:
| 6 |
where R is the ideal gas constant, α is the transfer coefficient, n is the number of electrons transferred, and j0 is the exchange current density. Combination of eq 6 with eq 5 gives the following expression for calculation of the experimental j0 (Table S1, SI):
| 7 |
DFT Calculations
The electrocatalytic active sites and the pathways of ORR on the surface of various electrocatalysts were examined on the basis of hybrid DFT calculations performed by using Gaussian 09 program.38 All the calculations were carried out using UB3LYP/6-31G(d,p) level of theory with all atoms fully relaxed. The solvent (water) effect was considered by the Polarizable Continuum Model (PCM).39 Only intermediate states in the ORR process, as well as the reactant and product states, were proposed and evaluated; extra energy barriers might exist but were not considered due to the unbalanced electron numbers borne by different states.
Free Energy Calculations
The calculation of the free energy diagrams was performed by setting up the reference level as that of the reaction product (Table S2, SI), and the reference electrode was set up to be the NHE; at pH = 0 and 0 V vs NHE, reaction (H+ + e–) ↔ 1/2 H2 is at the equilibrium under standard conditions. The free energies of reactants and each intermediate state at an applied electrode potential U were calculated as follows: G(U) = G – neU, where n is the electron number of such state and G is the free energy obtained by frequency calculations at room temperature (298.15 K) after geometry optimization. Hence, the equilibrium potential U0 for ORR (eq 8) at pH = 13 was determined to be 0.455 V vs NHE where the reactant and product are at the same energy level. The free energy of H2O(l) was derived as GH2O(l) = GH2O(g) + RT × ln(p/p0) since only GH2O(g) can be directly obtained by DFT calculations, where R is the ideal gas constant, T = 298.15K, p = 0.035 bar, and p0 = 1 bar. The free energy of O2(g) was derived as GO2(g) = 2GH2O(l) – 2GH2 – 4.92 eV since the high-spin ground state of oxygen molecule is notoriously poorly described in DFT calculations.40 The free energy of OH– was derived as GOH– = GH2O(l) – GH+, where GH+ = 1/2GH2 – kBTln 10 × pH (kB is Boltzmann’s constant).
The overall reaction scheme of O2 reduction to OH– in alkaline environment is:41,42
| 8 |
with three possible reaction pathways (one dissociative and two associative) as demonstrated in Scheme S1, SI. Specifically, since the surface of a doped graphene features the relatively high energy barrier (>1.2 eV) in the dissociative pathway (Figure S7, SI),43 the following associative mechanism is dominant and considered in our calculations:
| 9a |
| 9b |
| 9c |
| 9d |
where * refers to a given atom in the specific graphene model (i.e., possible active site).
Exchange Current Density
Calculation of the current density at low overpotentials includes the following assumptions: (1) the amount of active sites on different graphene surfaces is the same; (2) the rate constant represents the upper bound of the overall reaction rate; if there are additional barriers to OOH* formation/OH* desorption, the overall reaction rate should be lower.
According to reference (36), the exchange current density for a certain electrocatalytic process can be theoretically calculated as follows:
| 10 |
where n is the electron transfer number, F is Faraday’s constant, k0 is the standard rate constant, Ctotal is the total number of active sites, α is the transfer coefficient (a measure of the symmetry of the potential energy surface, ranging from 0 to 1), and θ is a quantity related to the highest free energy change of the whole reaction (see SI eqs S5–9, Figure S8 for a detailed derivation of this equation and parameter fitting).
Results and Discussion
Synthesis and Characterization of Electrocatalysts
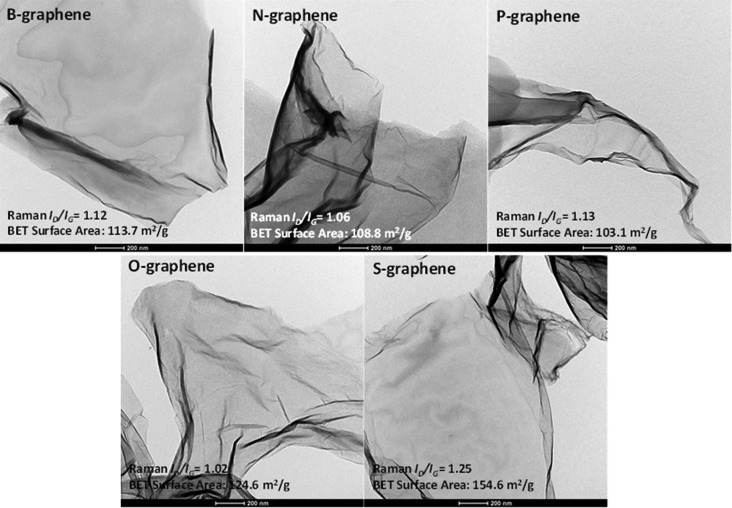
We selected five nonmetallic elements (B, N, P, O, S) with various electron negativities to dope graphenes to obtain single-doped graphene materials.44,45 All the doped graphene electrocatalysts were chemically prepared from GO by using appropriate doping procedures (see the Methods section). In all five resultant samples (B-graphene, N-graphene, P-graphene, O-graphene, S-graphene) the nanosheet morphology of the pristine GO was well preserved without noticeable residues of the solid precursors, as shown in the transmission electron microscopy (TEM) images (Figure 1). Note that the incorporation of different heteroatoms could not change the physicochemical properties of doped graphene samples such as morphology, surface area, and defects. Nitrogen-adsorption studies indicate that all samples show similar surface areas in a range between 100 and 150 m2/g, which also assures similar concentrations of the ORR active sites present on the samples studied (considering that the concentrations of all doped heteroatoms are also similar, between 3 to 5 atomic % based on the XPS survey results; not shown here). The Raman results indicate that all samples have similar concentrations of defects with the ID/IG values in a range of 1.0–1.2, which are closely related to the electrical conductivity of these samples. Therefore, it is presumed that the differences in the electrocatalytic ORR activity of various doped graphene samples do not originate from their physicochemical properties but only from the nature of the dopant affecting their ORR activities.
Figure 1.
TEM images of various single-doped graphene samples. The inset values represent the ID/IG ratios and the specific surface areas obtained from Raman spectra and nitrogen adsorption isotherms, respectively for each sample (see Figures S1 and S2, SI for details).
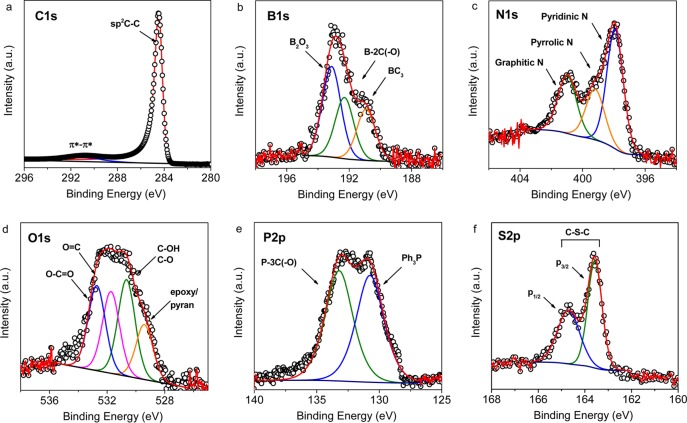
The nature of doping was investigated by analyzing high-resolution XPS spectra shown in Figure 2. Peak deconvolutions were conducted as in the case of the reported respective single-doped graphenes.46−50 The five heteroatoms chemically substituted edge or central carbon atoms in the graphene matrix, yielding 13 different species in- or out-of the graphene basal plane. Specifically, natural graphite was considered as a defect-free (nondoped) graphene with an intensive typical sp2-hybridized carbon (Figure 2a). B-graphene has two boron containing species as central B-3C and edge B-2C–O species (excluding B2O3 precursor residue) (Figure 2b). N-graphene has three nitrogen species as central graphitic nitrogen and edge pyridinic and pyrrolic N in the graphene plane (Figure 2c). O-graphene has two kinds of oxygen species as in-plane central pyran-type oxygen, edge carbonyl and hydroxyl oxygens, and out-of-plane epoxy oxygen (Figure 2d). P-graphene and S-graphene both have one heteroatom doping configuration as P–3C(−O)-type phosphorus (excluding Ph3P precursor residue) (Figure 2e) and edge C–S–C sulfur (Figure 2f), respectively.
Figure 2.
High-resolution XPS spectra of different heteroatoms in doped graphenes: (a) graphite; (b) B-graphene; (c) N-graphene; (d) O-graphene; (e) P-graphene; (f) S-graphene.
Model Construction
We constructed the cluster models (Figure S6, SI) for the aforementioned doped graphenes according to each heteroatom’s chemical environments obtained from the XPS spectra discussed above. The explored models contain 14 hexagonal rings terminated with C–H bonds, which have been previously adopted for investigation of ORR on graphene doped with nitrogen or boron.20,51 Five heteroatoms could induce 13 different doping configurations in graphene clusters with very different electronic properties; concomitantly, 32 possible ORR active sites, either heteroatoms themselves or adjacent carbon atoms, were theoretically studied to build the ORR free energy diagram for each catalyst by obtaining the free energy for each reaction step.
Free Energy Diagram
According to eq 9, the associative 4e– reaction pathways for each doped graphene at the equilibrium potential U0 = 0.455 V vs NHE can be illustrated on a free energy diagram as presented in Figure 3a. From such diagrams, nitrogen- and boron-doped graphene models (gN-G and gB-G) exhibit the lowest overall reaction free energy change at U0, suggesting their ORR performance is the best from the theoretical viewpoint, which has been confirmed by previous reports15,16 and the experiments reported in this work (Figure S3, SI). Taking the gN-G cluster model as an example (black line), the diagram indicates that the first electron transfer step to form OOH* (eq 9a) is an endothermic reaction with a free energy change ΔGeq 9a(U0) = 0.70 eV, while the second electron transfer step (eq 9b) to form chemisorbed O* and the third electron transfer step (eq 9c) to form OH* are all exothermic with ΔGeq 9b(U0) = −0.25 eV and ΔGeq 9c(U0) = −0.54 eV, respectively. The last electron transfer step reflecting OH* desorption (eq 9d) possesses an easily surmountable free energy difference of ΔGeq 9d(U0) = 0.09 eV. Therefore, ΔGeq 9a(U0) is the largest one among the free energy changes of all four reaction steps, which indicates that this step is the most sluggish one and represents the highest resistance for the whole ORR. Such trend is true for all other heteroatom-doped graphene models, indicating that the ORR rate-determining step for these catalysts is the same. Note that each graphene doped by one heteroatom can result in several different cluster configurations, which possess their own reaction pathways. The lines in Figure 3a only represent the model with best performance (i.e., the lowest overall reaction free energy change) among all the investigated cluster models for each dopant. The free energy diagrams for ORR on all possible active sites of each model are presented in Figures S9–S14, SI.
Figure 3.
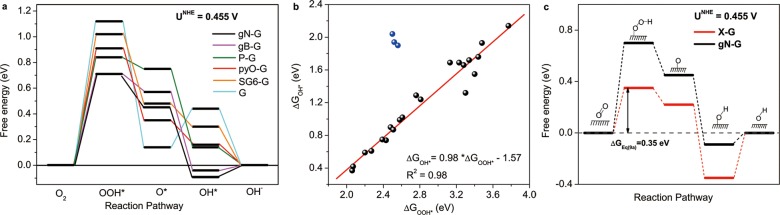
(a) Free energy diagram of different heteroatom-doped graphenes at the equilibrium potential U0. (b) The adsorption free energies of intermediates OOH* (ΔGOOH*) and OH* (ΔGOH*) on the investigated sites of different doped graphene models. Blue points were not considered in the linear fitting because normal OOH* chemisorption did not occur on the corresponding graphene clusters. The specific values of ΔGOOH* and ΔGOH* for different models are provided in Table S3, SI. (c) Calculated free energy diagram of the predicted X-graphene at the equilibrium potential; data for gN-G model are also included for the purpose of comparison. Reaction intermediates for each step are shown as inset animation.
According to the developed theories for metal surfaces,26,52 the ORR electrocatalytic activity descriptors (specifically, the exchange current density, on-set potential, 4e– pathway selectivity, and kinetic current density) of a given catalyst are governed by the adsorption free energies of ORR intermediates including OOH*, O*, and OH*, which are represented by ΔGOOH*, ΔGO*, and ΔGOH*, respectively (equation S1, SI). As shown in Figure 3b, ΔGOOH* for a wide variety of the doped graphene surfaces studied scales roughly with ΔGOH*, similarly as in the case of metal surfaces.53,54 Additionally, the O* chemisorption is more complicated than that of OH* and OOH*, since it could either form single bonding with the adsorption center on graphene or form epoxy-type bonding; within each bonding type, a linear relationship is also observed (Figure S15, SI). On the basis of these linear relationships (ΔGOOH* vs ΔGOH* or ΔGO*), we can predict the ORR free energy diagram of an optimal X-graphene, which is the basis to obtain its corresponding electrocatalytic properties at the macroscopic level. The free energy diagram of X-graphene can be obtained on the basis of the Sabatier principle that an ideal catalyst should bind the reaction intermediates not too strongly nor too weakly;55 therefore, at equilibrium potential U0, the optimal overall reaction pathway on an ideal X-graphene should follow the relationship of ΔGeq9a(U0) = ΔGeq9d(U0). At the same time, ΔGeq9a(U0) and ΔGeq9d(U0) are associated to each other via the linear relationship of ΔGOOH* and ΔGOH* as shown in Figure 3b; therefore by obeying these requirements, ΔGeq9a(U0) for X-graphene is determined to be 0.35 eV, representing the largest free energy change on the overall pathway as shown in Figure 3c (red line, see eq S4, SI for free energy changes of other steps). This predicted free energy difference is lower than those for all other investigated doped graphene models (for example, gN-G denoted by black line) and is close to that calculated for Pt by DFT.26
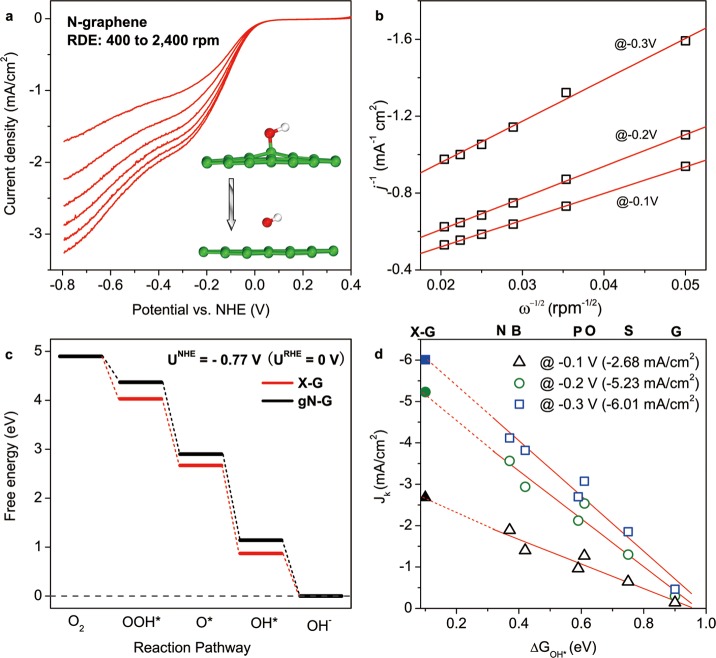
Exchange Current Density (j0)
For a given catalyst j0 is defined as the current density at the equilibrium potential in one direction for a given reaction,36 which reflects the intrinsic catalytic activity of the catalyst. The measured exchange current densities, j0expt, for each synthesized graphene surface can be obtained from the respective Tafel plot as shown in Figure 4a (specific values could be found in Table S1, SI). Simultaneously, knowing the free energy diagram for each graphene model, the theoretical exchange current density, j0theory, can be calculated by using a microkinetic model with one prefactor fitted from j0expt by eq 10.
Figure 4.
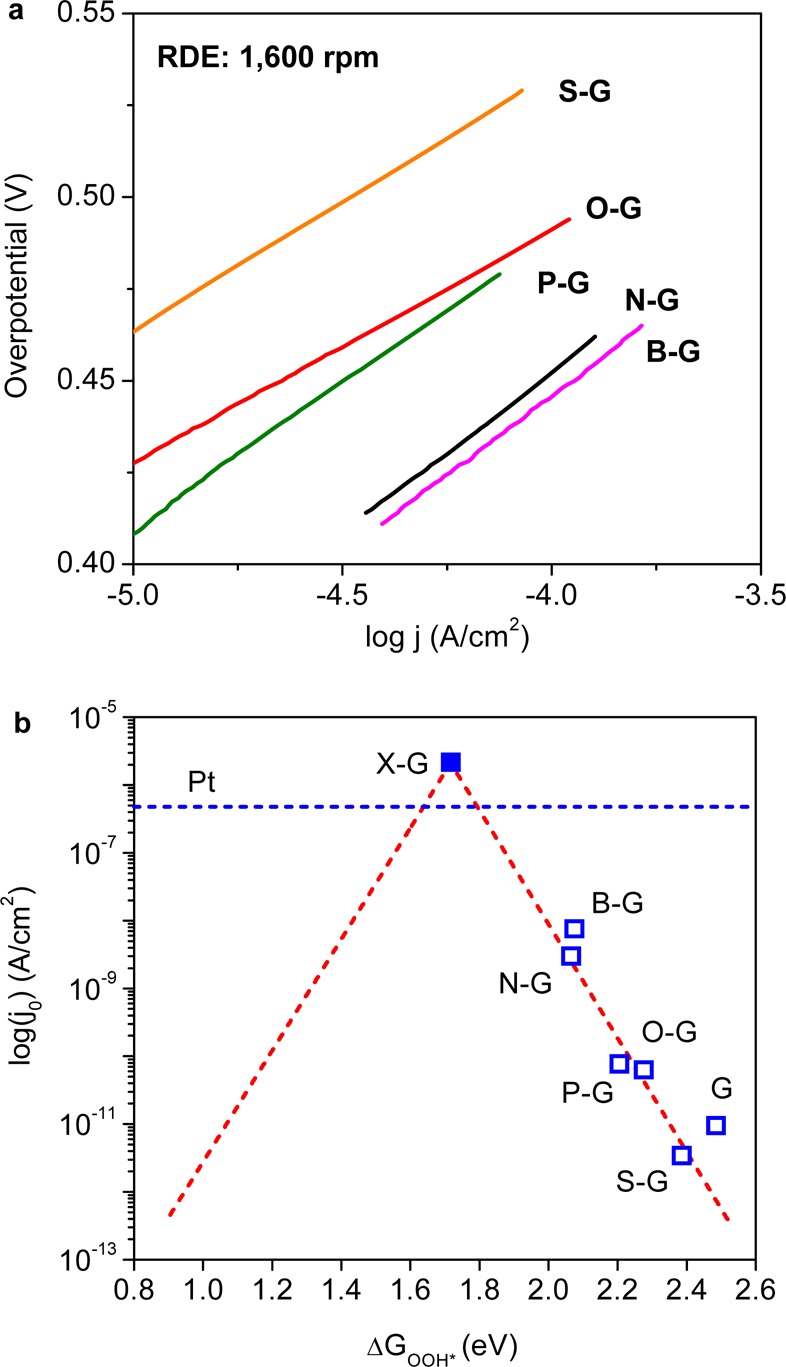
(a) Experimentally determined Tafel plots for different catalysts from ORR polarization curves shown in Figure S3, SI, data were collected at RDE = 1600 rpm. (b) Volcano plot between j0theory and ΔGOOH* with charge-transfer coefficient α = 0.5 (red dashed line). Blue hollow squares are j0expt obtained from Tafel plots and DFT-derived ΔGOOH* for each doped graphene catalyst. ΔGOOH* for X-graphene (blue solid square) was obtained from eq S4e, SI and its j0theory was obtained from eq 10. The j0expt value for Pt was also shown by the blue dashed line as a reference.
The predicted j0theory values for various graphene models form a volcano-shaped plot versus ΔGOOH* (Figure 4b red line), while j0expt for each synthesized sample perfectly follows the trend of this plot (blue squares), similarly as in the case of metal surfaces.26 Additionally, due to the weak binding of OOH* on graphene-based surfaces, the calculated points are all on the right branch of the volcano plot, while an optimal catalyst should possess a higher j0 induced by a ΔGOOH* closer to the volcano center.56 Following such trends, the j0theory value for an ideal X-graphene should be located at the summit of the volcano, with a calculated value of 2.12 × 10–6 A/cm2, which is even ∼5 times higher than that of Pt/C catalyst at same testing conditions (Figure S4c, SI).
On-set Potentials (Uon-set)
Due to the existence of a high free energy difference for the first electron transfer step ΔGeq (9a)(U0) as shown in Figure 3a, the initialization of oxygen reduction requires a potential bias η = Uon-set – U0 to reduce the free energy difference to ΔGeq9a(Uon-set) that could be overcame at room temperature. Taking chemically synthesized N-graphene as an example, the measured on-set potential UNon-set = 0.029 V vs NHE (from the polarization curve shown in Figure 5a). From the theoretical viewpoint (gN-G model), under this potential UNon-set, the free energies of the reactant and intermediates states (Figure 3c black line) shift upward as compared to those under the equilibrium potential (Figure 5b red line); as a result, ΔGeq9a(UNon-set) reduces to an easily surmountable value of 0.26 eV. In the zone of U > UNon-set, ΔGeq9a(U) keeps decreasing with increasing U, which indicates the first electron transfer step is no longer the rate-limiting step for the overall reaction, i.e. the whole ORR process is ‘activated’. A similar trend was also observed for other graphene models as demonstrated in Figures S9–S14, SI.
Figure 5.
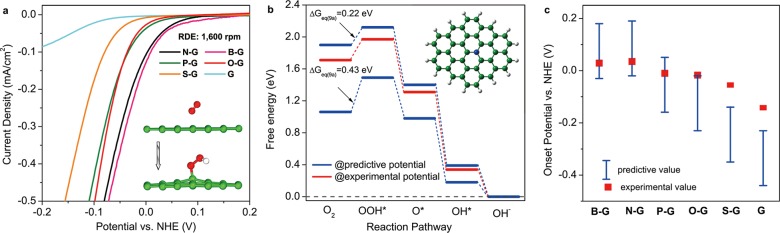
(a) Enlarged LSVs plots at the ORR initial region for different catalysts on RDE at 1600 rpm in an O2-saturated 0.1 M solution of KOH. Inset illustrates the first electron transfer step that is O2 to adsorbed OOH*. (b) Potential corrected free energy diagram for gN-G at experimentally observed on-set potential UNon-set (red) and theoretically predicted UN1 and UN2 which meet ΔGeq9a(UN1) = 0.43 eV and ΔGeq9a(UN2) = 0.22 eV, respectively (blue). Inset shows the atomic configuration of gN-G cluster. (c) Experimentally derived on-set potentials of doped graphenes (red squares), and the predicted values (blue bars).
Theoretically, the on-set potential for a given graphene model can be thermodynamically predicted from its free energy diagram at equilibrium potential by eqs S2–3, SI. First, a range for ΔGeq9a is defined as [0.22 and 0.43] eV on the basis of classical reaction thermodynamics (Table S4, SI).57 It is assumed that, if ΔGeq9a at a given electrode potential possesses a value within this range, the free energy difference can be overcome. The obtained theoretical on-set potentials that satisfy 0.22 eV ≤ ΔGeq9a ≤ 0.43 eV as well as the experimentally determined ones for all chemically synthesized graphenes are shown in Figure 5c. Most of the experimentally obtained values (red squares) are in the theoretically predicted range (blue bars), except for S-graphene and pure graphene samples (slightly above the theoretical range), which could be attributed to the influence of Nafion and glassy carbon working electrodes on the overall current density. Furthermore, based on the same criterion, the predicted on-set potential for X-graphene that corresponds to ΔGeq9a = 0.43 eV was 0.33 V, which is closer to the ORR equilibrium potential than the experimental value obtained for Pt catalyst.58
4e– Pathway Selectivity
Theoretically, as demonstrated in Scheme 1 in SI, ORR can proceed either by two sequential two-electron reactions (2e–) with formation of OOH– intermediate or a more efficient direct four-electron reaction (4e–). Therefore understanding the nature of the 2e– pathway is essential to design more appropriate catalysts for ORR that possesses high 4e– pathway selectivity to enhance the electrocatalytic efficiency. In alkaline solution, the mechanism of 2e– pathway is:
| 11a |
| 11b |
According to previous studies, 2e– and 4e– pathway selectivity is associated with the desorption of OOH* and OH* on a metal surface, respectively;52 therefore, at a given potential U, the probability of 2e– reaction pathway depends on the value of ΔGeq 11b(U) in comparison to ΔGeq 9d(U). Taking gN-G model as an example (Figure 6a), at equilibrium electrode potential for 2e– pathway U2e0 (−0.08 V vs NHE at pH = 1342), the desorption of OOH* (eq 11b) is exothermal with an energy difference of ΔGeq 11b(U2e0) = −0.16 eV, which means 2e– pathway is unavoidable to compensate the 4e– pathway on gN-G model. Experimentally, we used the rotating ring-disk electrode (RRDE) technique to verify this theoretically derived pathway selectivity prediction by monitoring the formation of intermediate peroxide species (e.g., OOH– in the alkaline solution) under different electrode potential as shown in Figure 6b. The measured electron-transfer number at U2e0 was 3.35 for chemically synthesized N-graphene; it corresponds to a mixed 33% 2e– pathway selectivity and 67% 4e– pathway selectivity as shown in Figure 6c. Also note that at more negative electrode potentials, 2e– pathway is always unavoidable due to the negative ΔGeq 11b, which is consistent with the RRDE observation (Figure 6c). Additionally, the same property (mixed 2e– and 4e– pathways for ORR) has been observed for all other chemically synthesized graphene catalysts. To fundamentally eliminate the 2e– pathway, a catalyst surface that binds OOH* strongly enough to induce an endothermic OOH* desorption process is required. This criterion is met by the ideal X-graphene model, as shown by its free energy diagram at U2e0 in Figure 6a (red line): at the equilibrium electrode potential for 2e– pathway U2e0, OOH* desorption on X-graphene is endothermic while OH* desorption is exothermic, which therefore avoids the 2e– reduction pathway to present a nearly 100% 4e– pathway selectivity, similar as in the case of Pt catalyst.
Figure 6.
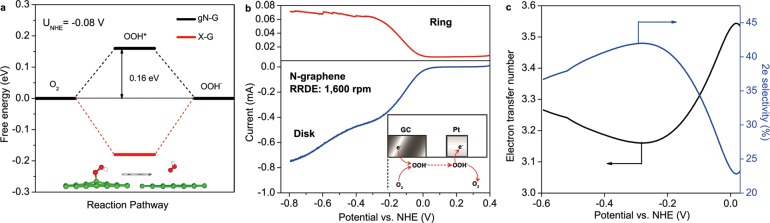
(a) Free energy diagrams of 2e– ORR pathway for gN-G model (black) and X-graphene (red) at equilibrium electrode potential for 2e– pathway U2e0 = −0.08 V vs NHE. Under this potential, the rate-limiting step of ORR on gN-G is the activation of O2 to OOH*, the atomic configuration of which is shown in Figure 5a inset, whereas that for X-graphene is the reduction of OOH* to OOH–, which atomic configuration is shown in the inset of this figure. (b) Experimental ring and disk currents for the synthesized N-graphene catalyst on RRDE at 1600 rpm in an O2-saturated 0.1 M solution of KOH. Inset is the scheme of measuring OOH– production on the Pt ring. (c) RRDE measured electron transfer numbers (black) and corresponding 2e– pathway selectivity (blue) for N-graphene catalyst according to eqs 3 and 4
Kinetic Current Density (jK)
jK is the cathodic oxygen reduction current under the kinetic limitation zone when the reactant mass transfer is efficient enough to keep the concentration of O2 at the electrode surface equal to the bulk value,36 which represents the ORR kinetic electrochemical property at a given electrode potential (always more negative than ORR on-set potential). Experimentally, for N-graphene (Figures 7a,b) and other chemically synthesized graphenes (Figure S3, SI), jK was measured by rotating disk electrode (RDE) voltammogram with different rotating speeds followed by performing Koutecky–Levich plot as presented in eqs 1 and 2 (see the Methods section).
Figure 7.
(a) Electrochemically measured LSV of N-graphene catalyst at different rotating speeds in an O2-saturated 0.1 M solution of KOH. Inset illustrates the last electron transfer step: OH* desorption to generate OH–. (b) Koutecky–Levich plots for N-graphene at −0.3 V, −0.2 V, and −0.1 V vs NHE, data were collected from panel a. (c) Potential corrected free energy diagram for gN-G and X-graphene models at URHE = 0 V (UNHE = −0.77 V). (d) The relationship between ΔGOH* and jK for various synthesized graphene catalysts under different potentials (open symbols), data were collected from Figure S3, SI. The values in parentheses of the legend are jK values for X-graphene, which are predicted by extending the fitted lines to ΔGOH* = 0.10 eV, shown as closed symbols.
From the theoretical perspective, the above electrochemical measured jK values can be related to the free energy change of the last electron transfer step (ΔGOH*) by a linear relationship shown in Figure 7d. The microkinetic scenario of this relationship might be due to the fact that the last step in the reaction pathway, OH* desorption as shown in the inset of Figure 7a, now becomes the rate-determining step of the whole ORR as shown in Figure 7c.52 On the basis of this trend, the predicted jK for X-graphene can be obtained from the value of the extended fitted lines at ΔGOH* = 0.10 eV (obtained by eq S4, SI), as shown in Figure 7d closed symbols, which is 6.01 mA/cm2 at −0.3 V, comparable to Pt catalyst’s value (7.35 mA/cm2 at −0.3 V, calculated from Pt’s LSV plots in Figure S4c, SI). It should be noted that these predicted jK values for X-graphene were obtained on the basis of a mixture of 2e– and 4e– ORR pathways (since the experimentally observed jK for line fitting all contain 2e– pathway as shown in Figure 6c and Figure S5, SI), which could be further enhanced if only 4e– pathway exists like in the case of Pt catalyst.59
Molecular Orbital Origin
On the basis of the former theoretical and experimental observations of j0, Uon-set, 4e– pathway selectivity, and jk for various graphene-based catalysts, we found that all these electrochemical quantities relate well to the binding strength of intrinsic oxygen-containing intermediates (adsorbed species) on the catalyst surface. Inspired by the success of the d-band center theory that the energy level of a metal atom’s d-band center serves as the activity descriptor for metal surfaces,60 we searched for a simple activity descriptor suitable for metal-free catalysts that could accomplish a similar correlation between the binding strength and each ORR active atom’s molecular valence orbital levels. We first investigated the origin of the binding strength for different graphene cluster models via natural bond order (NBO)61 analysis to explore the orbital information of each active site. Since the valence orbital of each active center participates in the bond formation with an oxygen-containing intermediate on the graphene surface (e.g., OH*), the valence orbital level should greatly influence its adsorption energy ΔGOH*. Therefore, we introduced a descriptor Ediff which is defined as the difference between lowest valence orbital energy of the active center and the highest valence orbital energy of the entire graphene cluster (Fermi energy level in the form of natural atomic orbitals) to quantitively represent the valence orbital level. As shown in Figure 8a, ΔGOH* data plotted against Ediff formed a linear relationship for a wide variety of graphene active sites. The principle that underlies this linear relationship is that the valence band (v) of the active sites hybridizes with the bonding (σ) orbital of the adsorbed species to form bonding (v-σ) and antibonding (v-σ)* states, as illustrated in Figure 8b. For the investigated graphene models, the (v-σ) state is full, while the filling of (v-σ)* state depends on the valence orbital levels of the active atom on the graphene surface. An increased filling of the antibonding (v-σ)* state, induced by a lower valence band, could lead to destabilization of the graphene–adsorbate interaction and hence diminish the binding between them; on the other hand, a decreased filling of (v-σ)* state corresponds to an enhanced binding between ORR intermediates and the graphene surface. As a result, a better graphene-based ORR catalyst such as X-graphene should possess higher valence orbital energies of the ORR active atom to induce a smaller Ediff and lead to stronger adsorption of OOH* and OH* intermediates, as marked in Figure 8a, resulting in better ORR activity. Such an X-graphene could in principle be realized by doping with multiple elements,20 introducing structural defects,8 or any possible combination.
Figure 8.
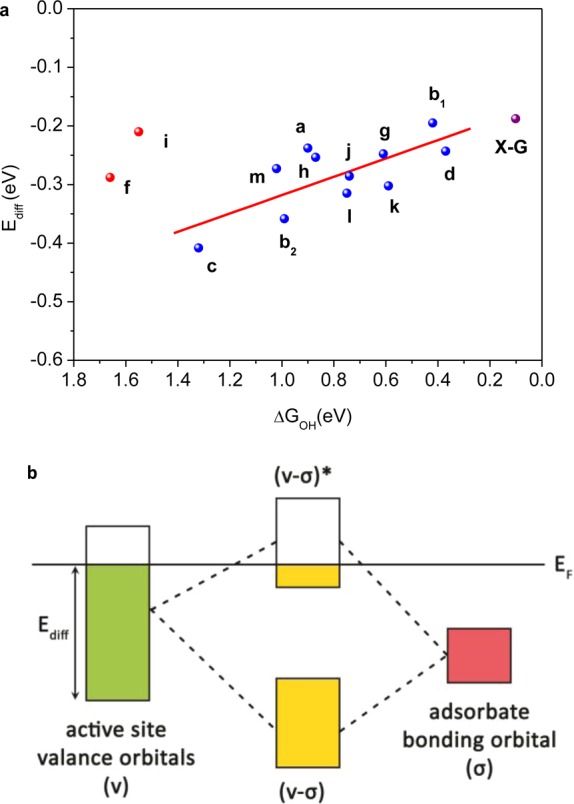
(a) The relationship between ΔGOH* and Ediff; data were collected for the most active site of various doped graphene models and labeled according to the corresponding molecular configurations shown in Figure S6, SI. Red points were not considered in the line fitting. The prediction of X-graphene is shown as pink point. (b) Scheme of orbital hybridization of valence band from active sites and adsorbates bonding orbital. EF refers to highest valence orbital energy of the entire graphene cluster.
Conclusions
In summary, by combining experimental data and DFT calculations, we systematically investigated the nature and origin of ORR activity of a series of heteroatom-doped graphene catalysts. Although the stability of each model, the electric double layer effect, and hydrogen bonding were not considered in the quantum chemistry study, our models are in good accordance with the experimental observations, from the viewpoint of the ORR exchange current density, on-set potential, pathway selectivity, and the kinetic current density. This agreement also validates the predictive capability of the powerful DFT model employed beyond traditional metallic catalysts. Our study shows further that graphene-based metal-free catalysts possess the potential to surpass the ORR performance of the state-of-the-art Pt catalyst. Using ORR as a probe reaction, the explored methodology should be applicable to other energy-related electrocatalysis processes such as oxygen evolution and hydrogen evolution reactions.
Acknowledgments
This work was financially supported by the Australian Research Council (ARC) through the Discovery Project program (DP130104459). The computational part of this research was undertaken with the resources provided at the NCI National Facility systems at the Australian National University through the National Computational Merit Allocation Scheme supported by the Australian Government.
Supporting Information Available
Experimental measurements of electron transfer, Tafel slope, and exchange current densities; graphene cluster models, overall reaction scheme and free energy calculations; adsorption of intermediates on each graphene surface, definition of activation energies, computational derivation of exchange current density. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Contributions
‡ Y.J. and Y.Z. contributed equally.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- Yang X. W.; Cheng C.; Wang Y. F.; Qiu L.; Li D. Science 2013, 341, 534. [DOI] [PubMed] [Google Scholar]
- Qu L. T.; Liu Y.; Baek J. B.; Dai L. M. ACS Nano 2010, 4, 1321. [DOI] [PubMed] [Google Scholar]
- Gong K. P.; Du F.; Xia Z. H.; Durstock M.; Dai L. M. Science 2009, 323, 760. [DOI] [PubMed] [Google Scholar]
- Su C. L.; Acik M.; Takai K.; Lu J.; Hao S. J.; Zheng Y.; Wu P. P.; Bao Q. L.; Enoki T.; Chabal Y. J.; Loh K. P. Nat. Commun. 2012, 3. [DOI] [PubMed] [Google Scholar]
- Su D. S.; Zhang J.; Frank B.; Thomas A.; Wang X. C.; Paraknowitsch J.; Schlogl R. ChemSusChem 2010, 3, 169. [DOI] [PubMed] [Google Scholar]
- Brownson D. A. C.; Kampouris D. K.; Banks C. E. Chem. Soc. Rev. 2012, 41, 6944. [DOI] [PubMed] [Google Scholar]
- Chen D.; Tang L. H.; Li J. H. Chem. Soc. Rev. 2010, 39, 3157. [DOI] [PubMed] [Google Scholar]
- Li Y. G.; Zhou W.; Wang H. L.; Xie L. M.; Liang Y. Y.; Wei F.; Idrobo J. C.; Pennycook S. J.; Dai H. J. Nat. Nanotechnol. 2012, 7, 394. [DOI] [PubMed] [Google Scholar]
- Yu L.; Pan X. L.; Cao X. M.; Hu P.; Bao X. H. J. Catal. 2011, 282, 183. [Google Scholar]
- Wang H.; Maiyalagan T.; Wang X. ACS Catal. 2012, 2, 781. [Google Scholar]
- Zheng Y.; Jiao Y.; Jaroniec M.; Jin Y.; Qiao S. Z. Small 2012, 8, 3550. [DOI] [PubMed] [Google Scholar]
- Dai L.; Chang D. W.; Baek J.-B.; Lu W. Small 2012, 8, 1130. [DOI] [PubMed] [Google Scholar]
- Shao Y.; Sui J.; Yin G.; Gao Y. Appl. Catal., B 2008, 79, 89. [Google Scholar]
- Yu D.; Nagelli E.; Du F.; Dai L. J. Phys. Chem. Lett. 2010, 1, 2165. [Google Scholar]
- Sheng Z. H.; Gao H. L.; Bao W. J.; Wang F. B.; Xia X. H. J. Mater. Chem. 2012, 22, 390. [Google Scholar]
- Yang S. B.; Zhi L. J.; Tang K.; Feng X. L.; Maier J.; Mullen K. Adv. Funct. Mater. 2012, 22, 3634. [Google Scholar]
- Li R.; Wei Z. D.; Gou X. L.; Xu W. RSC Adv. 2013, 3, 9978. [Google Scholar]
- Choi C. H.; Park S. H.; Woo S. I. ACS Nano 2012, 6, 7084. [DOI] [PubMed] [Google Scholar]
- Deng D. H.; Yu L.; Pan X. L.; Wang S.; Chen X. Q.; Hu P.; Sun L. X.; Bao X. H. Chem. Commun. 2011, 47, 10016. [DOI] [PubMed] [Google Scholar]
- Zheng Y.; Jiao Y.; Ge L.; Jaroniec M.; Qiao S. Z. Angew. Chem., Int. Ed. 2013, 52, 3110. [DOI] [PubMed] [Google Scholar]
- Wang S. Y.; Zhang L. P.; Xia Z. H.; Roy A.; Chang D. W.; Baek J. B.; Dai L. M. Angew. Chem., Int. Ed. 2012, 51, 4209. [DOI] [PubMed] [Google Scholar]
- Wang L.; Ambrosi A.; Pumera M. Angew. Chem., Int. Ed. 2013, 52, 13818. [DOI] [PubMed] [Google Scholar]
- Ramaswamy N.; Tylus U.; Jia Q. Y.; Mukerjee S. J. Am. Chem. Soc. 2013, 135, 15443. [DOI] [PubMed] [Google Scholar]
- Mukerjee S.; Srinivasan S.; Soriaga M. P.; Mcbreen J. J. Electrochem. Soc. 1995, 142, 1409. [Google Scholar]
- Norskov J. K.; Bligaard T.; Rossmeisl J.; Christensen C. H. Nat. Chem. 2009, 1, 37. [DOI] [PubMed] [Google Scholar]
- Norskov J. K.; Rossmeisl J.; Logadottir A.; Lindqvist L.; Kitchin J. R.; Bligaard T.; Jonsson H. J. Phys. Chem. B 2004, 108, 17886. [Google Scholar]
- Lima F. H. B.; Zhang J.; Shao M. H.; Sasaki K.; Vukmirovic M. B.; Ticianelli E. A.; Adzic R. R. J. Phys. Chem. C 2007, 111, 404. [Google Scholar]
- Shao M. H.; Liu P.; Zhang J. L.; Adzic R. J. Phys. Chem. B 2007, 111, 6772. [DOI] [PubMed] [Google Scholar]
- Greeley J.; Stephens I. E. L.; Bondarenko A. S.; Johansson T. P.; Hansen H. A.; Jaramillo T. F.; Rossmeisl J.; Chorkendorff I.; Norskov J. K. Nat. Chem. 2009, 1, 552. [DOI] [PubMed] [Google Scholar]
- Friebel D.; Viswanathan V.; Miller D. J.; Anniyev T.; Ogasawara H.; Larsen A. H.; O’Grady C. P.; Norskov J. K.; Nilsson A. J. Am. Chem. Soc. 2012, 134, 9664. [DOI] [PubMed] [Google Scholar]
- Stamenkovic V.; Mun B. S.; Mayrhofer K. J. J.; Ross P. N.; Markovic N. M.; Rossmeisl J.; Greeley J.; Norskov J. K. Angew. Chem., Int. Ed. 2006, 45, 2897. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Iyyamperumal R.; Yancey D. F.; Crooks R. M.; Henkelman G. ACS Nano 2013, 7, 9168. [DOI] [PubMed] [Google Scholar]
- Greeley J.; Markovic N. M. Energy Environ. Sci. 2012, 5, 9246. [Google Scholar]
- Stamenkovic V. R.; Mun B. S.; Arenz M.; Mayrhofer K. J. J.; Lucas C. A.; Wang G. F.; Ross P. N.; Markovic N. M. Nat. Mater. 2007, 6, 241. [DOI] [PubMed] [Google Scholar]
- Li D.; Muller M. B.; Gilje S.; Kaner R. B.; Wallace G. G. Nat. Nanotechnol. 2008, 3, 101. [DOI] [PubMed] [Google Scholar]
- Bard A. J.; Faulkner L. R.. Electrochemical Methods: Fundamentals and Applications; Wiley: New York, 2000. [Google Scholar]
- Liu C. L.; Hu C.-C.; Wu S.-H.; Wu T.-H. J. Electrochem. Soc. 2013, 160, H547. [Google Scholar]
- Frisch M. J.et al. ; Gaussian; Gaussian, Inc.: Wallingford CT, 2009. [Google Scholar]
- Tomasi J.; Mennucci B.; Cammi R. Chem. Rev. 2005, 105, 2999. [DOI] [PubMed] [Google Scholar]
- Jones R. O.; Gunnarsson O. Rev. Mod. Phys. 1989, 61, 689. [Google Scholar]
- Tarasevich M. R.; Sadkowski A. In Kinetics and Mechanisms of Electrode Processes; Conway B. E., Bockris J. O’M., Yeager E., Khan S. U. M., White R. E., Eds.; Comprehensive Treatise of Electrochemistry, Vol. 7; Plenum Press: New York: 1983; p 301. [Google Scholar]
- Zhang T.; Anderson A. B. Electrochim. Acta 2007, 53, 982. [Google Scholar]
- Yan H. J.; Xu B.; Shi S. Q.; Ouyang C. Y. J. Appl. Phys. 2012, 112. [Google Scholar]
- Paraknowitsch J. P.; Thomas A. Energy Environ. Sci. 2013, 6, 2839. [Google Scholar]
- Yang Z.; Nie H.; Chen X. a.; Chen X.; Huang S. J. Power Sources 2013, 236, 238. [Google Scholar]
- Bagri A.; Mattevi C.; Acik M.; Chabal Y. J.; Chhowalla M.; Shenoy V. B. Nat. Chem. 2010, 2, 581. [DOI] [PubMed] [Google Scholar]
- Choi C. H.; Chung M. W.; Kwon H. C.; Park S. H.; Woo S. I. J. Mater. Chem. A 2013, 1, 3694. [Google Scholar]
- Liu Z.; Peng F.; Wang H.; Yu H.; Tan J.; Zhu L. Catal. Commun. 2011, 16, 35. [Google Scholar]
- Raymundo-Piñero E.; Cazorla-Amorós D.; Linares-Solano A.; Find J.; Wild U.; Schlögl R. Carbon 2002, 40, 597. [Google Scholar]
- Yang Z.; Yao Z.; Li G.; Fang G.; Nie H.; Liu Z.; Zhou X.; Chen X. a.; Huang S. ACS Nano 2011, 6, 205. [DOI] [PubMed] [Google Scholar]
- Sidik R. A.; Anderson A. B.; Subramanian N. P.; Kumaraguru S. P.; Popov B. N. J. Phys. Chem. B. 2006, 110, 1787. [DOI] [PubMed] [Google Scholar]
- Viswanathan V.; Hansen H. A.; Rossmeisl J.; Norskov J. K. J. Phys. Chem. Lett. 2012, 3, 2948. [DOI] [PubMed] [Google Scholar]
- Viswanathan V.; Hansen H. A.; Rossmeisl J.; Norskov J. K. ACS Catal. 2012, 2, 1654. [Google Scholar]
- Rossmeisl J.; Logadottir A.; Norskov J. K. Chem. Phys. 2005, 319, 178. [Google Scholar]
- Chorkendorff I.; Niemantsverdriet J. W.. Concepts of Modern Catalysis and Kinetics; Wiley: New York, 2007. [Google Scholar]
- Greeley J.; Jaramillo T. F.; Bonde J.; Chorkendorff I. B.; Norskov J. K. Nat. Mater. 2006, 5, 909. [DOI] [PubMed] [Google Scholar]
- Scudder P. H.Electron Flow in Organic Chemistry: A Decision-Based Guide to Organic Mechanisms; Wiley: New York, 2013. [Google Scholar]
- Schmidt T. J.; Stamenkovic V.; Ross P. N.; Markovic N. M. Phys. Chem. Chem. Phys. 2003, 5, 400. [Google Scholar]
- Damjanovic A.; Genshaw M. A.; Bockris J. O. M. J. Electrochem. Soc. 1967, 114, 1107. [Google Scholar]
- Hammer B.; Norskov J. K. Nature 1995, 376, 238. [Google Scholar]
- Reed A. E.; Weinhold F. J. Chem. Phys. 1983, 78, 4066. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.