Homolog detection using global sequence properties suggests an alternate view of structural encoding in protein sequences

Significance

A Fourier-based sequence distance function for proteins is presented, which exhibits high accuracy in structural homology searches. The significance of this work lies in the fact that there has been no independent method available until now with which to compare homologies generated by sequence alignment. The method avoids the limitations of alignment and has the potential to uncover new classes of homologs and to give significant insight into the organization of the protein universe. Because it is very rapid and able to compare arbitrarily large groups of sequences simultaneously and exactly, it also has great promise as a general tool in biomedical research.

Abstract

We show that a Fourier-based sequence distance function is able to identify structural homologs of target sequences with high accuracy. It is shown that Fourier distances correlate very strongly with independently determined structural distances between molecules, a property of the method that is not attainable using conventional representations. It is further shown that the ability of the Fourier approach to identify protein folds is statistically far in excess of random expectation. It is then shown that, in actual searches for structural homologs of selected target sequences, the Fourier approach gives excellent results. On the basis of these results, we suggest that the global information detected by the Fourier representation is an essential feature of structure encoding in protein sequences and a key to structural homology detection.

Establishment of the folded structure of a protein from its amino acid sequence is one of the central problems in current molecular biophysics, and a question of the greatest practical interest in all areas of biological research. The most reliable method for predicting the structure of a protein from its sequence remains homology modeling (1, 2). In this approach (3), the structure of a target sequence is modeled, based on the known structures of proteins whose sequences are defined as similar to it by predefined criteria. Although this method has led to many encouraging successes, homology modeling cannot be regarded as a solved problem. This can be appreciated by noting the following two persistent difficulties with present approaches:

• i)Any reasonably large group of sequences known to fold to a specified architecture will contain pairs of sequences that are not related by any known criterion. This observation is so well known (4) that it has been dignified with a name (5): the “remote homolog problem.” As a result of this fact, many appropriate homologs for a given homology target will be rejected incorrectly.
• ii)There exist sequences (6) in which the mutation of a single site leads to a complete change in the fold of the protein. These “conformational switches” have also been well studied. All current sequence comparison methods predict that these sequence pairs should have essentially identical structures. As a result, incorrect homologs can be selected for modeling.

Essentially, all current methods for sequence comparison, which provide the framework in which these difficulties arise, are based on alignment techniques. Alignment rests on a number of assumptions whose effects have not been rigorously examined. We briefly list some of these:

• •An implicit assumption that structural similarity between molecules is a result of evolutionary relationships, rather than purely physical mechanisms;
• •A dependence on completely arbitrary penalty functions to account for misregistration (in the form of insertions and deletions) of sequences;
• •Neglect of the possibility that fold encoding may occur in ways that cannot be detected by local, residue-by-residue comparison;
• •Comparison of sequences using parameters that, at best, represent amino acid physical properties only indirectly;
• •A reliance, in developing advanced approaches, on self-referential methods, in which new sequence comparison algorithms are built on the results of previous alignments, and which therefore incorporate previous assumptions in a nonlinear manner;
• •An additional reliance, in constructing more sophisticated alignment procedures, on multiple sequence alignment, which is an NP-hard problem (7) and cannot be solved exactly.

It should be further noted that it is not known whether an exclusive reliance on alignment-based sequence comparison methods biases the classes of homologs which can be detected. In essence, no controlled studies of this question have been carried out.

To circumvent these assumptions, and make such controls feasible, we have developed an alternate approach (8–13) to the representation and comparison of sequences, based on Fourier analysis. In the present work, we address the initial step in homology modeling, the detection of structural homologs of a target sequence of interest. A Fourier-based sequence–sequence distance function is introduced, and its performance compared with that of an independently constructed structure–structure distance function applied to the same set of proteins. We demonstrate the following points:

• •The distances between molecules in the sequence and structure spaces exhibit very high correlation. To the best of our knowledge, parallel distance functions have not been previously developed, nor has such a correlation been attempted.
• •The statistical reliability of the sequence distance function in homologous fold detection is quantitatively examined and shown to be very high.
• •The method is shown to find exact homologs for sequences belonging to well-established structure families.
• •The sequence–sequence distance function is used to search for homologs of difficult targets posed in previous critical assessment of protein structure prediction (CASP) exercises. It is shown that simple selection criteria lead to homolog sets containing structures very similar to those of the targets.

It should be emphasized that the present method is completely different in both conception and execution from alignment-based approaches. It is exact, has been statistically verified over a very large database, and can be applied to the simultaneous comparison of arbitrarily large ensembles of sequences. It should therefore be helpful in the detection of structural homologs of target sequences of interest, as well as in the study of the organization of protein sequence space.

A brief description of the general approach, and details of the present work, are given in Methods.

Results

We examine the reliability and utility of the Fourier-based sequence distance function, which we denote by Δ, from three different viewpoints.

Correlation Between Sequence and Structure Differences.

We begin by asking whether there is any correlation between interprotein distances in the sequence and structure distance spaces. A positive answer to this question is a sine qua non for the applicability of a sequence comparison function to homology modeling. We are not aware of any studies that investigate this point for alignment-based sequence comparison, or superposition-based structural comparison methods. Indeed, it is not at all clear how one would use alignment to meaningfully quantitate the differences between sequences with no detectable alignment-based similarity, and it is not possible to carry out structural superposition on structure pairs with very different sequence lengths. The methods we have developed make it possible to carry out this investigation on arbitrarily different domains in a physically meaningful way.

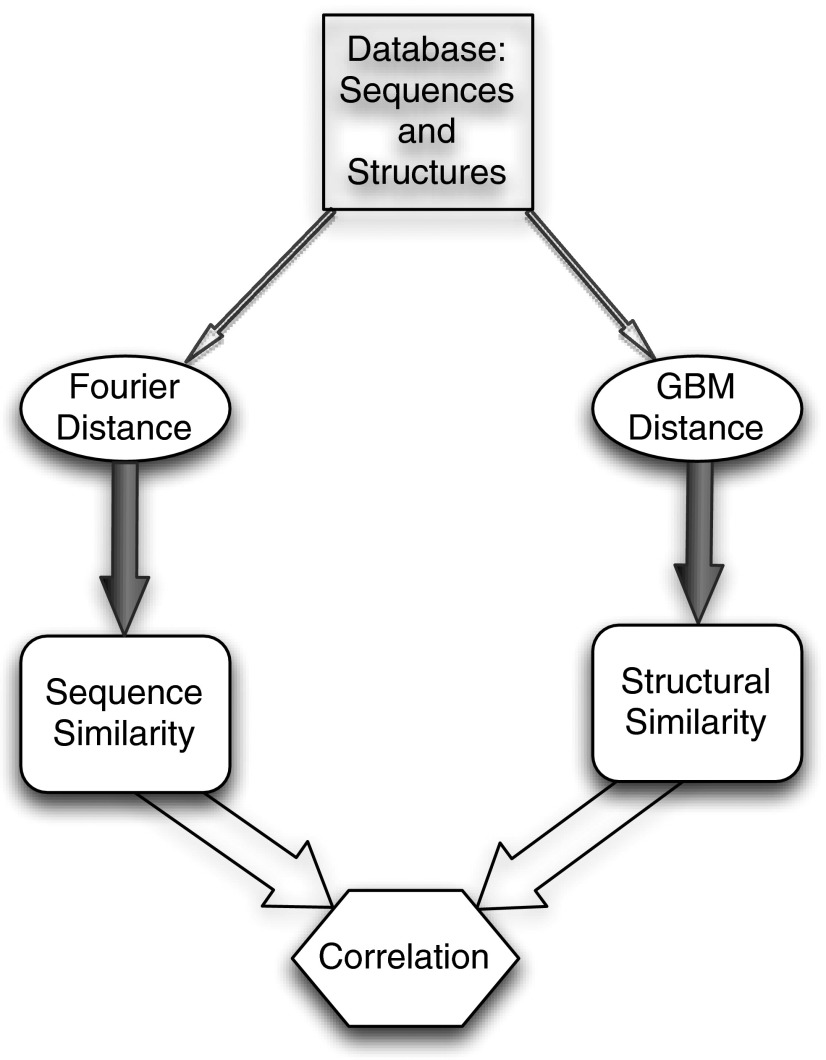
We calculated the correlation coefficient between the sequence-based distance Δ(P,Q) and the structure-based distance δ(P,Q) for the sequence/structure dataset described in Methods. A flowchart for this calculation is shown in Fig. 1. We find that R = 0.8. The two distance functions are indeed highly correlated. It should be pointed out that this correlation is over an extremely large number of sequence distance/structure distance pairs—the 12,227 proteins in the dataset give rise to ∼7.5 × 10⁷ independent measurements. To quantitate the statistical significance of the correlation coefficient, we calculated a standard score (i.e., a centered, normalized value, traditionally denoted by z) for the observed value of R, and find an extremely large value: z ∼ 9,518. We are therefore able to conclusively reject the null hypothesis that R = 0. This provides a far more stringent, and statistically significant, test of the utility of the intersequence distance function than homology searches involving a limited number of target sequences. We shall, nevertheless, examine the results of such searches, to place the present results in the context of currently widespread methods. First, however, we examine the statistical significance of fold detection by Δ from a different perspective.

Fig. 1.

Schematic of the correlation calculation. Here, “GBM” refers to the “generalized bond matrix” structural distance function discussed in the text.

Statistical Significance of Fold Detection.

We ask how many sequences with a given degree of fold similarity to the target are found within a specified neighborhood of each sequence in our dataset. We use a simple K-nearest-neighbor model and characterize fold similarity by the degree of identity in CATH (14) indices. We thus examine the K nearest neighbors (as measured by Δ) of sequence j, which has CATH indices (C_j,A_j,T_j,H_j), and ask what fraction of them have index values C_j, (C_j,A_j), (C_j,A_j,T_j), or (C_j,A_j,T_j,H_j). A match constitutes a correct prediction at the given degree of fold similarity. We can also calculate exactly the expected values of these fractions, and the associated SDs, using straightforward counting arguments from elementary probability. This enables us to calculate a standard score (z value) for each number of nearest neighbors, and thus to determine the extent to which Δ performs better than would be expected on a purely random basis. Data are shown in Table 1 for nearest-neighbor values of 1, 10, and 20. It will be seen that Δ does very much better than would be expected on a purely random basis, except at the lowest degree of fold similarity (the C level) with 10 (z = 1.15) or 20 (z = 0) nearest neighbors. At this low level of similarity, the number of sequences with each value of the index (C) is so large that, for any reasonable number of nearest neighbors, we execute an essentially random selection. However, if we restrict choice by selecting only a single nearest neighbor, Δ performs much better than random selection (z = 41.43) even at the C level.

Table 1.

The statistical significance of fold detection by Δ

Degree	Observed fraction	Predicted fraction*	SD	z
NN = 1
CATH	0.287	0.0051	0.00067	420.75
CAT	0.294	0.03	0.0015	176.0
CA	0.35	0.117	0.0029	80.34
C	0.569	0.395	0.0042	41.43
NN = 10
CATH	0.469	0.047	0.002	211.0
CAT	0.538	0.2	0.005	67.6
CA	0.783	0.625	0.009	17.56
C	0.982	0.967	0.013	1.15
NN = 20
CATH	0.535	0.089	0.003	148.67
CAT	0.617	0.289	0.0068	48.24
CA	0.886	0.789	0.019	7.46
C	0.998	0.998	0.019	0.0

NN is the number of nearest neighbors used in the K-nearest-neighbors test. Degree denotes the degree of fold similarity. “Fraction” denotes the fraction of correct matches in the NN-nearest-neighbor group (see text).

^*The fraction that would be expected on a purely random basis.

We have established the statistical significance of fold detection by the intersequence distance function Δ. We now examine the results of actual homology searches to place the Fourier method in a somewhat more familiar context.

Search for Structural Homologs of Specified Target Sequences.

This effort was divided into two parts. In the first, a set of 12 sequences from the dataset were selected at random. The only requirements imposed on target selection were that each sequence should not be the only member of its CATH class, and that a roughly equal number of representatives should be chosen from classes C = 1, 2, and 3 (helical, sheet/barrel, and mixed structures). A 20-nearest-neighbor search was carried out for structural homologs of each sequence. Structural homologs were identified by correspondence of (C,A,T) or (C,A,T,H) index sets between the target and members of the 20-sequence neighborhood of the target. [It should be remembered that the H index relates to sequence homology properties, so that no more than (C,A,T)-level identity is necessary to indicate structural homology.]

It can be seen from Table 2 that, for all 12 targets, structural homologs are found in a 20-sequence neighborhood. In eight cases, more than one homolog was found. The task that remains for the modeler is to identify the homologs from among the 20 candidates. This can be expected to be dealt with in the course of energy-based optimization of the model structure, using the 20 candidates as starting points.

Table 2.

Structural homolog search results for classified sequences

Target no.	PDB code	C	A	T	H	No. of CATH matches*	No. of CAT matches*
1	16pk001	3	40	50	1,260	2	4
2	1a04A01	3	40	50	2,300	0	1
3	1a0hA01	2	40	20	10	1	1
4	1a17000	1	25	40	10	0	2
5	1a2yB00	2	60	40	10	18	18
6	1a4pA00	1	10	238	10	2	2
7	1a6zA01	3	30	500	10	1	1
8	1a78A00	2	60	120	200	3	3
9	1aoy000	1	10	10	10	1	1
10	1b9oA00	1	10	530	10	3	3
11	1pu3A00	3	10	130	10	2	2
12	1a2wA00	3	10	130	10	5	5

The columns labeled C, A, T, and H give the indices of the targets in the CATH database (see text).

^*The number of CATH or CAT matches out of 20 nearest neighbors.

In the second part of the search investigation, five targets proposed as difficult cases in the CASP8 exercise (15) were chosen. These molecules now have structures deposited in the Protein Data Bank, but have not been classified in the CATH database. To identify structural homologs, therefore, we calculated the structural distances δ(T,N_i) between the target T and each of the nearest neighbors N_i (i = 1, 2,…, 20). The question of interest is now whether, within the set of nearest sequence neighbors, there are any that are also near structural neighbors. With a view to the practicalities of homology searching, and in the absence of classification information, we limited the search for structural homologs in this case to molecules with sequence length within ±10% of that of the target sequence. The results of this investigation are shown in Table 3. For each target, the structural distance of the most similar among the 20 nearest-sequence neighbors is shown in the last column. The structure distances are shown as centered, normalized values ζ, defined explicitly in Eq. 7 below, and the minimum possible value, corresponding to identical structures, is −0.778. It can therefore be seen that, in each case, structurally similar domains were identified solely on the basis of sequence similarity considerations.

Table 3.

Results of structural homology search for CASP8 targets

Target ID	PDB code	Domain	Sequence limits	Minimum structure distance, ζ
T0389	2vsw	D1	1–134	−0.645
T0425	3czx	D1	1–179	−0.638
T0433	3d7l	D1	1–199	−0.588
T0457	3dev	D1	1–194	−0.711
T0507	3do8	D1	1–124	−0.687

The actual structures of these most-similar domains are shown in SI Appendix, Fig. S1. It can be seen that in four of the five cases, the structure is quite similar to that of the CASP target. In one case (T0457), the most similar sequence neighbor has different topology from that of the target, although the distance function, unsurprisingly, has detected significant local similarities between the two domains. It should be remembered, in this context, that the CASP domains, which are difficult targets, may not, in every case, have structural homologs in our database at all. With respect to T0457, we find upon further investigation that this is indeed the case.

Discussion and Conclusions

We have demonstrated the ability of Fourier-based intersequence distance functions to identify structural homologs of target sequences. This has been shown in four different ways:

• i)It was demonstrated that intersequence distances given by the Fourier approach are strongly correlated with interstructure distances for the same proteins, given by an independent structure comparison algorithm.
• ii)It was demonstrated that the ability of the Fourier distance function to correctly classify sequences far exceeds what would be expected on a purely random basis.
• iii)It was shown that the algorithm identifies structural homologs of identical fold for every member of a test set of targets.
• iv)It was shown that the algorithm usually identifies structures that are quantitatively similar to the structures of CASP challenge targets, using only sequence information.

These observations suggest very strongly that the global organization of protein sequences, rather than purely local information, is required to encode structure in amino acid sequence. The Fourier approach is not encumbered by many of the limitations of alignment-based sequence comparison methods, and therefore results generated using this approach can be expected to provide both a useful control on homology results generated from algorithms in common use, and new insights into the global organization of the protein universe.

Methods

The Fourier method differs from currently prevalent alignment-based algorithms in two fundamental ways. These points have been discussed in detail previously (8, 9), and we briefly summarize here:

• i)The 20 naturally occurring amino acids are represented by numerical parameters derived, by factor analysis, from their physical properties (16, 17). Ten property factors have been shown (16) to account for essentially all of the variance of the physical properties, and it is therefore possible to represent each amino acid as a 10-vector, and an N-residue sequence as a set of 10 numerical chains of length N (8, 9). The property factors are complete and orthonormal, by construction, and therefore sequences are represented numerically by parameters that, in addition to being physically based, are both exhaustive and nonredundant.
• ii)The resulting numerically encoded sequences are Fourier transformed. The result of this operation is a set of Fourier coefficients, indexed by two parameters—the wave number k and a property factor index l, which indicates which of the 10 property factor strings gives rise to the coefficient. Each individual coefficient is global in character, because it contains information from the entire sequence. The Fourier coefficients, like the property factors, are complete and orthonormal by construction and, taken together, provide a complete numerical representation of the protein sequence. Note that, in k-space, chain length has been removed as a variable, and therefore chains of different lengths can be compared rigorously; the Fourier coefficients describe properties of the chains which scale with length. It has been shown (9) that the average and variance properties of the Fourier coefficients can be calculated analytically, so that the statistical significance of the magnitude of a given coefficient can be determined exactly.

The Sequence Distance Function.

In very recent work (13), we have demonstrated that architectural families are distinguished from one another by Fourier coefficients at a very limited set of low-k wave numbers. The only values of k at which there are statistically significant differences between sets of sequences with different folds are 0 ≤ k ≤ 6.

This observation is central to the present work, because it provides a basis for the construction of the intersequence distance function. As in previous work (9), we define a standard score for the Fourier coefficient [denoted in this case by Z_k^(l)] for property l, at wave number k, as follows:

where c is the unnormalized sine or cosine Fourier coefficient, the angle brackets denote an average over all permutations of the original N-residue wild-type sequence, and σ is the associated SD. This normalization removes any dependence on sequence composition alone and creates a function that explicitly reflects the influence of the specific linear arrangement of amino acids along the sequence. We then define a k-dependent distance between any two sequences P and Q, Δ_k(P,Q), and the total distance between the sequences as follows:

The exact definition of Δ_k(P,Q), which depends on all 10 property factors, is given in SI Appendix. The distance function is a simple Cartesian metric in the space of centered, normalized Fourier coefficients Z_k^(l) (Eq. 1), but different combinations of sine and cosine coefficients are used at different k values, reflecting statistically significant differences found previously (13).

The Structure Distance Function.

To establish the reliability of the sequence distance function Δ, we must define a parallel, independent distance function that measures the degree of structural similarity between proteins without reference to sequence. We devised such a function in previous work (18, 19) and applied it to the quantitative classification of known protein structures. This approach, the generalized bond matrix (GBM) method, describes a structure in terms of a set of matrices of bond lengths, bond angles, and bond dihedral angles. The method can be applied to any appropriately defined representation of the chain, but here we use the nearest-neighbor virtual bond (C^α) backbone. The size of each matrix is determined by a preselected fragment length. The representation is therefore sensitive to local structural characteristics. At the same time, the complete distribution of these matrices (which describe the overlapping fragments that make up a structure) is a global characteristic of the structure and can be used as a fingerprint. A distance function is then defined, which acts on two fingerprints to quantitate the degree of similarity between the associated structures. Because the fingerprints are normalized by sequence length, it is possible to meaningfully compare the structures of proteins of different size. This approach was independently shown (20) to perform comparably to trusted, “gold standard” superposition-based structure comparison algorithms (21, 22), while being computationally far less intensive. Unlike those methods, the GBM method is suitable for the rapid, simultaneous pairwise comparison of very large sets of structures.

We use here a low-resolution (LRGBM) version of the algorithm, which was demonstrated (19) to give results very similar to the full-resolution comparison method, and which is even more rapid in execution. In the LRGBM formulation, the structure of a protein is represented in a four-dimensional space by integrating over the populations of predefined regions of the high-resolution GBM fingerprint, which are denoted as A_R, E_R, E₀, and E_L (defined in ref. 19). We computed these coordinates for the members of a very large dataset of proteins of known structure (described below). A principal component analysis shows that, in this representation, the space of structures is actually three-dimensional, and the coordinates of a structure are given by the following:

where p(X) is the fractional occupation of region X. The distance δ(P,Q) between proteins P and Q in structure space is again taken to be a simple Cartesian metric, given by the following:

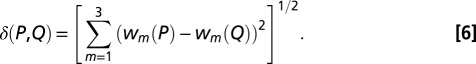This distance can also be given in the form of a standard score which, for clarity, we denote in this case as ζ(P,Q), defined by the following:

The Database.

For the work described herein, we use a protein dataset that is based on the CATH sequence/structure database. The hierarchical organization of this database (in which proteins are classified by class, architecture, topology, and homology) is ideal for the present study. We use a set of 12,227 domains drawn from the CathDomainSeqs.S60.ATOM.v.3.2.0 dataset (www.cathdb.info). The sequences in this set have no more than 60% sequence identity. To the best of our knowledge, this is one of the largest datasets ever used in studies of this type.