Inference on periodicity of circadian time series

Abstract

Estimation of the period length of time-course data from cyclical biological processes, such as those driven by the circadian pacemaker, is crucial for inferring the properties of the biological clock found in many living organisms. We propose a methodology for period estimation based on spectrum resampling (SR) techniques. Simulation studies show that SR is superior and more robust to non-sinusoidal and noisy cycles than a currently used routine based on Fourier approximations. In addition, a simple fit to the oscillations using linear least squares is available, together with a non-parametric test for detecting changes in period length which allows for period estimates with different variances, as frequently encountered in practice. The proposed methods are motivated by and applied to various data examples from chronobiology.

1. Introduction

The identification of periodic patterns is crucial to the understanding of cyclical biological processes such as circadian rhythms found in many living organisms. Circadian clocks are oscillators that are entrained to a 24 h period by physiological forcing such as daily light–dark cycles. Recent experimental techniques allow one to monitor circadian rhythms with good temporal resolution. Examples considered here are high-throughput fluorescent imaging time series of circadian genes (see, e.g. Hall and others, 2003; James and others, 2008), and skin temperature measurements serving as a proxy for core body temperature, identified as a circadian biomarker in the area of cancer chronotherapy (Scully and others, 2011). Many experiments on circadian clocks are in constant physiological conditions where there is no forcing and the period may therefore differ from 24 h. In addition, circadian rhythms may be disrupted by the administration of a specific treatment. In this case, the exact period length is often unknown and may vary under different experimental conditions or treatments. Most circadian clock related studies currently estimate period by approximating the oscillatory gene expression profiles by a sum of sine and cosine functions within a Fourier approximation context (Levine and others, 2002). Software available for gene reporter data analysis, such as Lumicycle (Actimetrics, 2012), attempts to find the period by looking for the largest sinusoidal component in such a representation, but provides no measure of its accuracy. The Fast Fourier Transform Non-linear Least Squares (FFT-NLLS) method by Plautz and others (1997) is widely used and will serve here as a benchmark for comparison. They apply a non-linear least-squares minimization algorithm to estimate the parameters (and corresponding confidence intervals) of the Fourier representation of a time series where the period of the component with the largest amplitude serves as estimator of the period. Other analysis packages, for example, CircWave (Oster and others, 2006), take a similar approach. Various circadian data have non-sinusoidal patterns as well as measurement errors (see, e.g. Edwards and others, 2006). Figure 1 shows examples from human and plant circadian systems that display asymmetric cycles, double peaks, and noise. In this case, period estimation within a Fourier representation approach is more challenging as an increased number of components are required and this poses a burden to the stability of the fitting algorithm. We find that time series with a strong periodic component, such as those encountered in circadian experiments, robustly produce a clear dominant spectral peak even in asymmetric and noisy cases. A motivating example is presented in Section 3 of supplementary material available at Biostatistics online. Combining bootstrap methods (Efron, 1979) with the spectrum allows us to refine the estimate of the period and to obtain confidence bands.

Fig. 1.

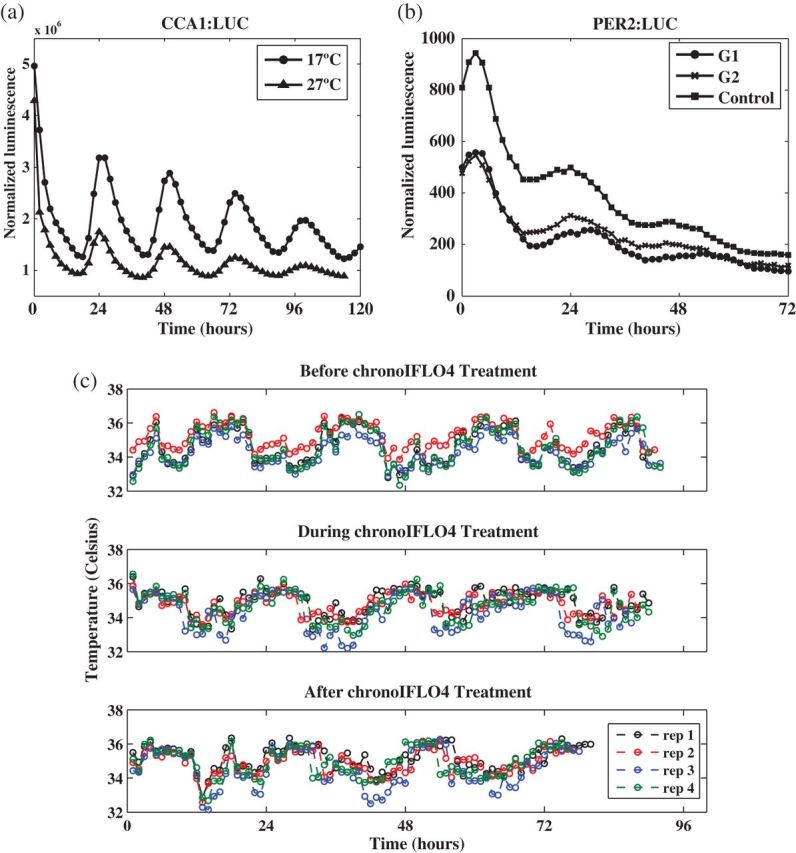
Experimental circadian data. (a) Normalized luminescence of the CCA1:LUC construct for the model plant Arabidopsis thaliana under constant red light and constant temperature of either , or 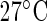, averaged over 62 replicates and sampled ZT 2-120 at 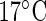, ZT 2-114 at 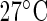. ZT stands for Zeitgeber time. (b) Normalized luminescence levels for the PER2:LUC construct for human cells collected from mouse embryos receiving specific combinations of active compound and dose concentration treatments for lung inflammation (G1 and G2) and a control, averaged over several replicates, and sampled over approximately 3 days. (c) Skin temperature data collected over approximately 3 days (smoothed) from four locations on the skin of a patient suffering from metastatic colorectal cancer at different stages of chronotherapy treatment with four anticancer drugs (chronoIFLO4). In (a) and (b) markers correspond to positions of observed values.

The use of the bootstrap for spectral analysis has recently received considerable attention (see, e.g. Sergides and Paparoditis, 2007; Zoubir, 2010). Franke and Härdle (1992) (FH) use the fact that the relationship between the theoretical and the empirical spectrum can be approximately described by a multiplicative regression model to propose a non-parametric, residual-based bootstrap. They also establish the asymptotic properties of their algorithm for kernel spectral estimates. Dahlhaus and Janas (1996) extend this approach to the class of ratio statistics. A semiparametric methodology is developed by Kreiss and Paparoditis (2003), who fit an autoregressive (AR) model to obtain a set of residuals to which they apply the bootstrap, but define the spectrum through a non-parametric estimator. None of the above approaches directly addresses the problem of period estimation. However, a few spectrum-based methods for period estimation have been developed in the literature. The MESA algorithm of Burg (1972) has been implemented in the context of circadian rhythms (see, e.g. Dowse and Ringo, 1989). The period is estimated using the spectrum of an AR model fitted to the data. This method is, however, sensitive to the number of AR terms (Marple, 1980). Beyond Fourier methods and spectral analysis, software such as WAVECLOCK (Price and others, 2008) uses wavelet analysis to estimate the period of oscillatory circadian data as a smooth function over time but provides no routine for confidence intervals.

Circadian data sets often have replicate time series of the same experiment. Figure 1(c) shows three groups of four time series replicates, each containing measurements on skin temperature for a patient suffering from metastatic colorectal cancer. The groups represent three chemotherapy stages: before, during, and after treatment with chronoIFLO4, a combination of four anticancer drugs (see Scully and others, 2011, for a description of an equivalent study), and the question is whether the period of the clock is affected by the treatment. The replicates correspond to measurements taken at four skin locations of the patient. For testing the hypothesis of equal periodicity between any two groups, one may apply the standard Welch t-test (Welch, 1947) to the estimated periods. However, this test does not allow for the problem that, within a group of replicates, there can be different oscillatory patterns resulting in period estimates with markedly different variances.

The aim of this article is 2-fold: firstly, to provide an estimator for the period with an appropriate confidence interval as a measure of accuracy and, secondly, to introduce a hypothesis test for equality of the period under two different experimental conditions for replicate time series data. Our estimator of period length uses the spectrum estimator of FH. We define confidence intervals for the point estimate based on the bootstrap sample of spectrum functions and study their nominal coverage in a variety of scenarios motivated by real data applications. The current study is the first to investigate the use of FH's spectrum estimator for period estimation in the context of circadian oscillations. We then propose a non-parametric hypothesis test that treats the estimated period lengths within each of two groups of replicates as a sample from a population whose unknown mean value is the true period under the corresponding experimental condition. The null hypothesis that the two means are the same is tested allowing for the possibility that period estimates may have different variances. The paper is organized as follows. After introducing the spectrum resampling (SR) method in Section 2, we present, in Section 3, results of our simulation studies to investigate the performance of the SR method with synthetic circadian data, comparing it with that of the FFT-NLLS routine. The SR method is substantially more robust to non-sinusoidal oscillations and yields more realistic confidence intervals for period length. Given a set of period estimates, a simple regression model, described in Section 4, can be used for fitting the mean of the observed oscillations. In Section 5, we introduce our non-parametric test for the comparison of period lengths in a replicated experimental scenario. Section 6 shows the use of the methods and presents results for our circadian data. Section 7 concludes with some final remarks.

2. The SR method for period estimation

The bootstrap is a resampling technique developed with the aim of gaining information about the distribution of an estimator. The main idea is to treat the original sample of values as the population and to resample from it repeatedly, with replacement, computing the desired estimate each time. This produces a sample of estimates from which a point estimate and confidence intervals can be derived (see, e.g. Davison and Hinkley, 1997). Bootstrap relies on the ability to identify independent components that can be simulated. These can be either the original sample, or the residuals of a suitable model that describes the data. Let 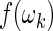and 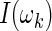be, respectively, the spectrum function and its estimator, called periodogram, evaluated at the Fourier frequencies 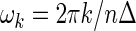, , 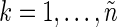, 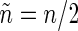where n is the sample size (assumed even) and Δ is the time interval between two consecutive observations (see Section 1 of supplementary material available at Biostatistics online). FH point out that, asymptotically, spectrum estimation can be cast as a multiplicative regression problem,

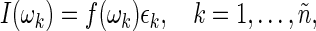(2.1)

where the residuals 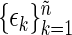are approximately independent and identically distributed (i.i.d.) standard exponential random variables. Tapering and padding can be used to improve the quality of this approximation (Dahlhaus and Janas, 1996; Lee, 1997, see Section 7 of supplementary material available at Biostatistics online). In order to resample from the residuals in (2.1), an initial estimate of the spectrum 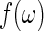is needed. A consistent estimator of 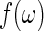can be obtained through a kernel spectrum estimate, say 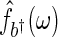, with smoothing parameter 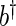(see, BeltraTo and Bloomfield, 1987). Given a set of residuals to the regression in (2.1), bootstrap periodogram values are generated using another kernel estimate 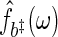with smoothing parameter 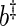. Finally, let b be the smoothing parameter from which the final bootstrap estimate of 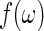, say 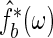, is obtained using the previously generated bootstrap periodogram. The three smoothing parameters are set to 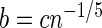, , 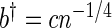, 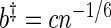with c chosen to minimize an appropriately defined mean square error estimator (Lee, 1997). All three are needed to control the bias and variance of the final kernel spectrum estimator (see Davison and Hinkley, 1997, and Section 1 of supplementary material available at Biostatistics online for details). These are the key steps in FH's algorithm. We proceed to define 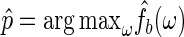as the period estimator of interest. Its distribution can be estimated using the bootstrap procedure described above. Let 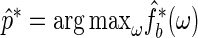. The value of 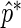provides a point estimate of the true period length p. By repeating the above procedure R times, we obtain a sample of period estimates 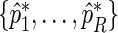from which point estimates and confidence intervals can be derived using percentiles of the bootstrap sample. The value of R typically varies between 1000 and 2000. The algorithm can be easily extended to provide estimates for any number N of relevant period lengths that might be present in the data, provided that the distance between any two such periods is greater than the fundamental period, 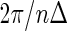. By recording the frequencies corresponding to the N largest peaks in the spectrum, we obtain 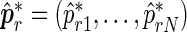, , 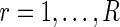an N-dimensional vector of point estimates from which corresponding confidence intervals can be derived. We refer to the proposed period estimation methodology as SR.

3. Simulation study

We evaluate the performance of the SR methodology and compare it with the FFT-NLLS procedure (see Section 2 of supplementary material available at Biostatistics online) using synthetic data from a mathematical clock model. The theoretical framework for understanding the molecular underpinnings governing circadian rhythms is based on a negative transcriptional feedback loop that generates an oscillator with a stable period of around 24 h (see Roenneberg and others, 2008, for an overview on clock models). We simulate synthetic clock data at the mRNA and protein level from a stochastic dynamic model with a delayed negative feedback loop (DNFL) which is considered to be a generic model for molecular clocks (Jensen and others, 2003; Monk, 2003). The manipulation of a set of parameters yields time series with different characteristics of the oscillations (see Section 4 of supplementary material available at Biostatistics online). For each choice of parameter values, we simulated 200 replicate time series. Let p be the true value of the period, which is known for the synthetic data, and 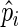represent the period estimate for replicate i. The performance of the estimators is measured by the mean squared error, 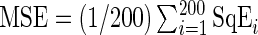, where 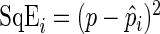. For all simulations, we take R to be 1000. We regard a period estimate to be an “outlier” if it falls outside the circadian range, say [15 h, 35 h].

3.1. Sample size requirements and consistency

Our first simulation study focuses on the properties of the SR estimator in terms of the MSE for varying values of sample size n and number of cycles 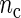. The SR method depends on the autocovariance function of the process through the periodogram (see Section 1 of supplementary material available at Biostatistics online). Hence, in principle, the larger the number of cycles 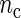, the better will be the performance of the spectrum function in recovering the true period length. However, in most applications the sample size n is fixed a priori so that a compromise must be reached in terms of sampling frequency. Too sparsely measured data reduce identification of the shape of the oscillation, whereas at the same time a minimum number of full length cycles is needed for period estimation. We look at the effects of n and 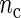separately. For the simulations, we use the DNFL model with parameter values such that the oscillations are sinusoidal in shape with a known true period of around 24 h. We fix n_c = 2,4,8,12, and n = 30,60,120,240, reflecting a range of different situations in terms of the amount of information available. 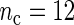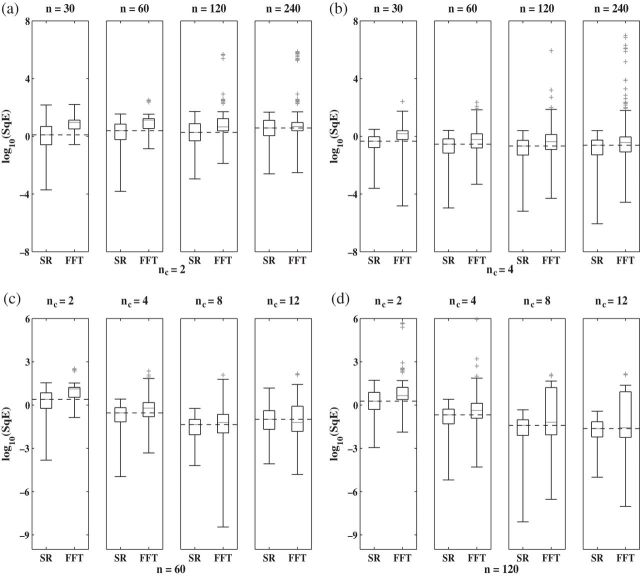For example, and n = 60 corresponds to only 5 observations per cycle, while setting 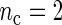and n = 240 yields 120 observations over 2 cycles (see Section 4 of supplementary material available at Biostatistics online). Figure 2 shows boxplots of 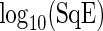of period estimates obtained for synthetic mRNA time series using the SR and the FFT-NLLS method. The value of n was varied while 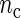was fixed and vice versa. A problem of the FFT-NLLS estimator, also frequently encountered in practice, is that it produces period lengths that are far away from the circadian range, even for relatively sinusoidal oscillations (see Section 3 of supplementary material available at Biostatistics online). In comparison, the SR estimator not only always produces estimates within the desired range but also outperforms the FFT-NLLS estimator in terms of a lower squared error. For fixed 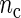, increasing n does not necessarily decrease the estimated MSE of the SR estimator, nor that of the FFT-NLLS estimator. However, for fixed n, increasing 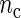tends to improve the SR estimator in terms of lower MSE. The only instance where a rise in MSE was observed corresponds to a very low sampling frequency of almost 5 h (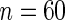, 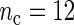), which results in too sparse data.

Fig. 2.

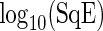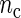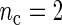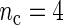Simulation study. Boxplots of for period estimates obtained from synthetic mRNA dynamics for both the SR and the FFT-NLLS (FFT) methods for selected fixed values of and n based on 200 replications. (a) . (b) . (c) 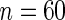observations. (d) 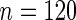observations. For all plots crosses represent values of 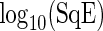associated with non-circadian period estimates.

We also study the asymptotic properties of the SR estimator via a small simulation study where the MSE is estimated for increasing values of n keeping the sampling frequency, say 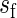(in hours), fixed, so that 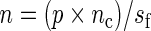. We varie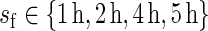d and 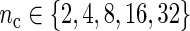. In general, the MSE of the SR estimator tends to decrease as n increases. Moreover, the frequency at which observations are drawn does not seem to affect the rate at which the MSE decays to zero. This is not surprising following the results in Figure 2.

3.2. Non-sinusoidal cycles and noise

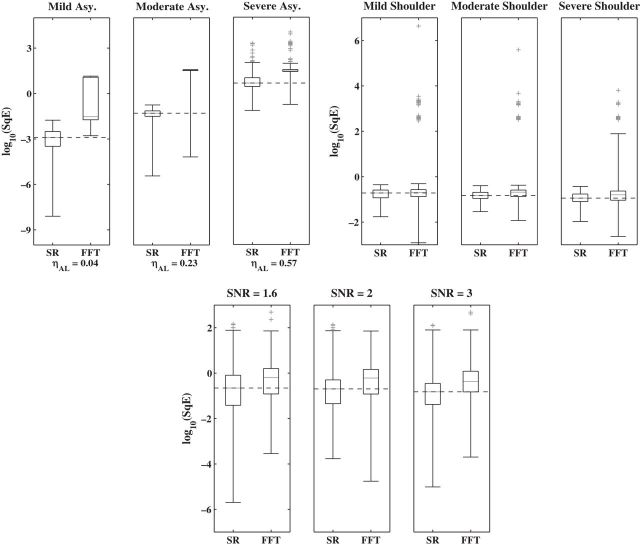
Next we compare SR and FFT-NLLS when cycles are non-sinusoidal or noisy as frequently observed in practice (see Figure 1). We focus on two forms of non-sinusoidal behavior, namely asymmetry, i.e. cycles with a short rise followed by a longer, more gradual decline (or vice versa), and shoulder (or bimodal) patterns, and for each we define three levels: mild, moderate, and severe, each corresponding to different sets of parameter values in the DNFL model, and such that the period is approximately (or equal to) 24 h. To quantify the level of asymmetry in a cycle, we use 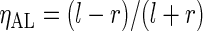, where l and r are, respectively, the distance between the peak of the oscillation and its left and right extremities. The value of 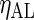varies between 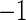and 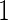, with positive (negative) values corresponding to left (right)-hand side asymmetry, symmetry yielding 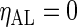. To generate noisy cyclic data, we add independent zero mean Gaussian noise to time series from the DNFL model. The variance is chosen such that the signal-to-noise ratio (SNR) equals preset values 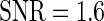, 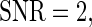and 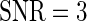. The choice of these values is motivated by signal levels encountered in observed data (see Section 4 of supplementary material available at Biostatistics online). Although the resulting time series are not linear processes, and therefore the model in (2.1) may not be valid, the SR algorithm should be robust to departures from linearity (Franke and Härdle, 1992), and the simulation study should confirm this. The results in Figure 3, where boxplots of 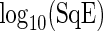are displayed, show that, as can be expected, the MSE of both estimators increases with asymmetry while increasing the level of the shoulder pattern or SNR seems to have less effect on the individual performance of the estimators. It is clear that the SR methodology outperforms the FFT-NLLS for all levels of asymmetry, shoulder pattern, and SNR. In addition, the SR estimator is fairly robust across different levels of the shoulder pattern, even for a severe shoulder level. In contrast, between 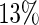and 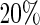of the estimates obtained with the FFT-NLLS were non-circadian. Furthermore, we investigated the coverage probability of the confidence intervals produced by the SR and the FFT-NLLS methods for a nominal level of 95%. The confidence intervals obtained by the SR approach tend to be slightly conservative, as shown in Table 1. In contrast, those obtained by the FFT-NLLS method are not only too narrow, but also, for all cases of asymmetry and shoulder patterns, their coverage probability is unacceptably low.

Fig. 3.

Simulation study. Boxplots of log₁₀(SqE) for period estimates obtained from non-sinusoidal synthetic mRNA dynamics for both the SR and FFT-NLLS (FFT) methods based on 200 replications. (a) Asymmetric cycles. (b) Cycles with shoulder pattern. (c) Cycles with noise. For all plots crosses represent values of log₁₀(SqE) associated with non-circadian period estimates.

Table 1.

Simulation study

	Asymmetry			Shoulder			SNR
Method	Mild	Mod.	Sev.	Mild	Mod.	Sev.	1.6	2	3
SR (%)	100	100	35	100	100	100	93.5	94.5	95
FFT-NLLS (%)	54	16	0	22	16	12	88.5	90	93

Coverage probabilities for period length confidence intervals for non-sinusoidal synthetic data using SR and FFT-NLLS methods based on 200 replicates.

4. Fitted oscillation and phase estimation

In addition to period estimation, one may be interested in phase and amplitude estimation or, more generally, in reconstructing the mean oscillation of the observed process. Here, we take a simple approach that makes use of standard results from spectral theory (see, e.g. Girling, 1995; Brillinger, 2001). Given a time series 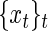, we can represent it as

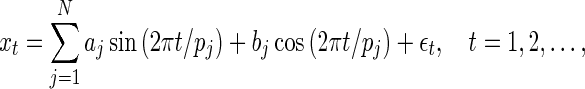(4.1)

where the parameters 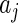and 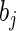are unknown constants, and the 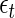's are independent random variables with mean zero. The N period lengths 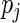are assumed known and fixed. In practice these are estimated using the SR method and correspond to the frequencies of the N ordered largest peaks in the spectrum. Thus, 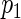is the period yielding the largest spectrum peak and associated with the main oscillation in the data. The remaining periods, 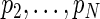, correspond to smaller scale oscillations that may be present in the process. For a set of observations 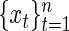, the model in (4.1) can be written in matrix form as 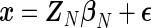, with 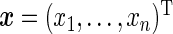and ϵ=(ϵ₁,…,ϵ_n)^T being n-dimensional vectors, β_N=(a₁,b₁,…,a_N,b_N)^T a 2N-dimensional vector, and Z_N the (n×2N) matrix with elements 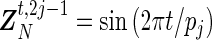and 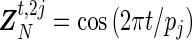, , 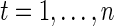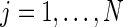. Given a set of period estimates 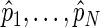, the model in (4.1) is linear in 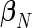and thus an unbiased estimate 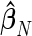can be obtained via least squares (Brillinger, 2001). The number of terms N in (4.1) can be determined by minimizing some information criterion such as the Akaike criterion, say 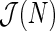. Let 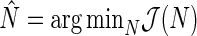. The fitted oscillation is then

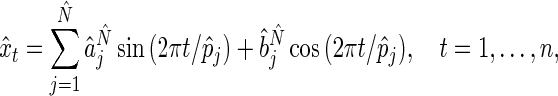(4.2)

with 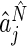and 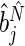the 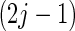th and 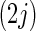th elements of 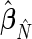, respectively. Estimates for both phase and amplitude of the oscillations can be obtained from the estimated periods 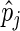(Girling, 1995). We can write 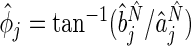and 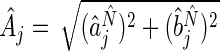as, respectively, the estimated phase, and amplitude of the oscillation with period length 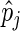. Together with 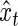in (4.2), the sets of period, phase, and amplitude estimates 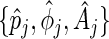, , 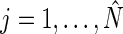provide a complete description of the mean of the true process 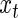underlying the observed oscillation. Note that the Fourier representation in (4.1) is used here only to obtain a simple presentation of the observed oscillation, and not for period estimation. Other methods, such as non-parametric regression, can also be used to describe the typical shape of an oscillation.

5. A two-sample bootstrap test for the comparison of periods

Next we study the problem of testing whether sets of time series replicates from two different experimental conditions have the same period. Hence, we focus on the comparison between the means of two samples of sizes 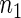and 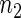given by the number of replicate time series in each experimental group. Let S denote the test statistic of interest with observed value s, and let 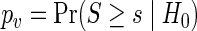be the p-value for some null hypothesis 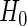. In the bootstrap setting, 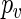is estimated by means of a Monte Carlo experiment comparing the observed statistic s to R independent values of S obtained from simulated samples satisfying 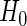. Let these be denoted by 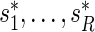then, under 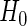, all 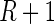values 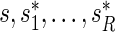are equally likely values of S, and so 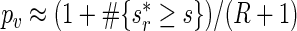. In this setting, the value of R typically varies between 99 and 999 (see, e.g. Davison and Hinkley, 1997, and the references therein). Suppose that the estimated period of each replicate time series, say 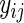, carries a known positive weight 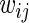, , 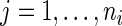, 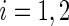and that 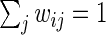, 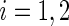. The weights correspond to normalized versions of the inverse of the relative error of the period estimate, defined as the ratio between half the width of the estimate's confidence interval and the period estimate itself. Theoretically, the relative error takes values in 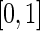, with values closer to zero indicating a more precise estimate. This definition of relative error is reminiscent of the relative amplitude error of the FFT-NLLS period estimator. A test of equality of the mean periodicity is formulated by the model

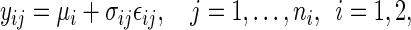(5.1)

where the 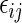's have zero mean and variance 1, and are i.i.d. over j given i. We complete the model in (5.1) with the heterogeneity assumption 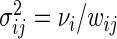for some 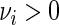. Intuitively, this means that the value of the variance of replicate period estimates depends on the accuracy of the particular estimate, as defined by 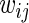(more accurate estimates having smaller variance). These can differ between replicates due to, for example, measurements being taken by different experimentalists, or at different times of the day. The null hypothesis to be tested is 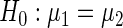, against the alternative 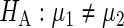. 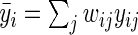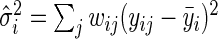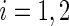We consider the following weighted estimates of the sample mean and overall variance, , and , , respectively. The pooled mean under 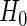is defined as 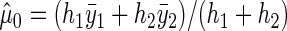, with 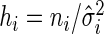, 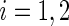. Hence, the sample with higher sample variance, or lower sample size, will contribute less to 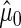. Let 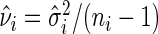. It can be shown that if the error terms in (5.1) are normally distributed, 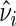is the uniformly minimum variance unbiased estimator of 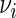(Goldberg and others, 2005). The observed test statistic is defined as 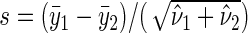(Davison and Hinkley, 1997). Specify 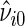as the estimate of 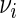under 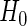, i.e. 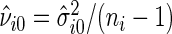, where 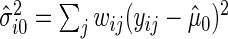, and let 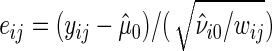be the null model studentized residuals. Bootstrap data sets satisfying 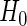are generated as 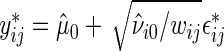, with 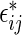sampled with replacement from the set of 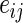's. The p-value 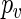can then be estimated as above (see Section 5 of supplementary material available at Biostatistics online).

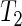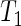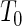The above general procedure is termed test . We examine its size and power properties in a small simulation study, details of which are given in Section 6 of supplementary material available at Biostatistics online. For completeness, we also consider the homogeneous variance case and the two-sample Welch's t-test (Welch, 1947), and , respectively. Both assume 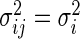, 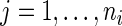. In addition, 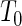also assumes that the 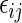's in (5.1) are normally distributed, in which case the test statistic S above follows a Student-t distribution with degrees of freedom given by the Welch–Satterthwaite equation (Satterthwaite, 1946; Welch, 1947). Although here 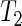uses the proposed SR period estimator, it can be based on other estimators and their estimated variances. In general, all three tests attain the correct nominal size. Test 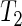shows a slight advantage in terms of power, especially when attempting to detect larger differences in mean, even if some power loss is expected for 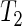(and 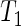) due to the finite number of bootstrap samples used (Davidson and MacKinnon, 2000).

6. Applications

6.1. Chronotherapy study

Chronotherapy involves the administration of treatments according to the circadian rhythm of patients. This approach has been shown to improve cancer treatment tolerability and efficacy (Scully and others, 2011). In humans, skin temperature can act as a biomarker for the circadian system. Figure 1(c) shows skin temperature recordings for a patient with colorectal cancer taken at four different skin locations (replicates) before, during, and after treatment with the anticancer drugs chronoIFLO4. The data are part of a larger study aiming to optimize and personalize chemotherapy according to the patient's circadian rhythm. The question is whether the circadian clock period changes with the administration of the drugs. The original data have temperature measurements taken every minute which results in noisy, low-frequency fluctuations which shift the spectrum away from the desired circadian range. Hence, we first smooth the data by applying a non-overlapping moving average window such that the resulting data, shown in Figure 1(c), have a frequency of 1 h (see Sections 8 and 9 of supplementary material available at Biostatistics online). Figure 4(a) shows the smoothed data for replicate 2 together with the fitted mean oscillation (4.2). Using the SR method, we clearly see a shift in period during treatment (Figure 4(b)). Moreover, after treatment the periods seem to be more variable suggesting that monitoring temperature at multiple skin locations is indeed useful. We used test 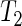for all pairwise comparisons and concluded that the period during treatment is significantly different from the period before (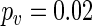) and after (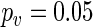) treatment, but that there is no significant difference between the period before and after treatment. Hence, this patient's daily rhythm is altered while receiving the anticancer drugs, and a personalized chronotherapy should take this into account.

Fig. 4.

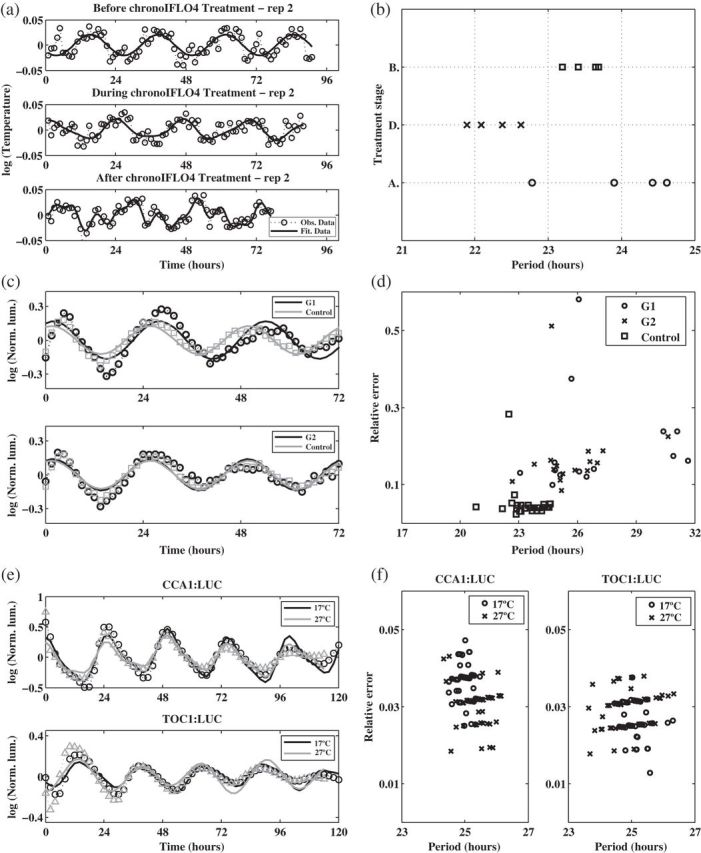
Applications. (a) Detrended smoothed observed skin temperature time series recorded from replicate 2 (dotted line) and fitted theoretical oscillation (solid line). (b) SR period estimates for each replicate and each treatment stage in the chronotherapy study (B, Before; D, During; A, After). (c) Detrended observed averaged PER2:LUC normalized luminescence (Norm. lum.) for treatments G1, G2, and control (dashed lines) together with fitted theoretical oscillations (solid line). (d) Relative error plot for individual replicates of PER2:LUC expression for treatments G1, G2, and control using the SR method. (e) Detrended observed average CCA1:LUC and TOC1:LUC normalized luminescence (dashed lines) together with fitted theoretical oscillations (solid line). (f) Relative error plot for individual replicates of the CCA1:LUC and TOC1:LUC constructs using the SR method. In (c) and (e) markers correspond to positions of observed values.

6.2. Human gene luminescence data

Time series data on the expression level of the human circadian clock gene PER2 was made available to us. Different treatments for inflammation in the lung are applied to cells from mouse embryos, and expression of the PER2:LUC construct is measured over several days at 1.5 h intervals. Figure 1(b) shows the average profile for two treatment groups, G1 and G2 (details of which are subject to a confidentiality agreement), each with 16 replicates, and a control group with no treatment with 36 replicates (see Section 10 of supplementary material available at Biostatistics online). We apply the SR method to the log-transformed averaged data to obtain the fitted oscillations from (4.2) and displayed in Figure 4(c). They suggest that cells to which G1 is applied have a longer period than cells in the G2 and control groups. Indeed, for the averaged profiles, the SR method estimated a period length of 26.09 h for G1, and 23.94 h and 24.17 h for G2 and control, respectively. We apply the SR method to each of the individual replicates. The results can be found in Figure 4(d), where the period estimate for each replicate is plotted against its estimated relative error as defined in Section 5. The results of test 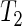conclude that G1 has a different period from G2 (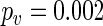) and control (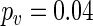), while G2 and control yield the same period (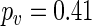). Thus, for the two treatments considered here, the one identified as G1 alters the period of the clock.

6.3. Plant luminescence data

The plant data in Figure 1(a) is part of a comprehensive study on the effect of temperature on the circadian clock of the model plant Arabidopsis thaliana. High-throughput data on the expression levels of circadian clock genes are recorded for different temperatures under constant red light using luminescence constructs. Here, we focus on data for TOC1:LUC and CCA1:LUC at 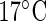and 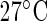. A total of 64 replicate time series are recorded for TOC1:LUC at each temperature, and 62 for CCA1:LUC (see Section 11 of supplementary material available at Biostatistics online). The results of applying the SR method can be found in the plots of Figures 4(e) and (f). The estimated mean period across replicates is 25.08 h and 24.90 h for TOC1:LUC at 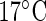and 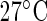, respectively, and 24.99 h and 25.34 h for CCA1:LUC, respectively. Note that from these plots it is not possible to say whether the change in temperature leads to a change in period. Our test 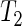gave 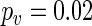for TOC1:LUC and 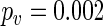for CCA1:LUC, strongly suggesting that this is the case.

7. Discussion

In this study, we propose an improved estimator for the period of an oscillatory time series using bootstrapping of spectral estimates. In a comparison based on simulated data from circadian clock models, we find that the SR method outperforms the currently used FFT-NLLS routine based on Fourier series approximations. Our SR method is substantially more robust to non-sinusoidal patterns and the presence of noise. Confidence intervals are readily available and are found to be substantially more realistic than those provided by the FFT-NLLS method. Given a set of estimated period lengths, one can obtain a simple oscillation fit using linear least squares methods. If required, phase and amplitude estimates are also available although the definition of phase remains somewhat arbitrary in the context of circadian systems. The fundamental difference between the SR and the FFT-NLLS methodologies is that the FFT-NLLS attempts to find the period by coercing the data into a parsimonious sum of sinusoidal functions, while the SR method simply makes use of the fact that the spectrum function breaks down the observed variance in the signal into asymptotically independent contributions, making no assumptions on the underlying process other than stationarity. Moreover, the spectrum is a transformation of the autocorrelation function which is quite robust to the particular shape of the oscillation. The simulation results using non-sinusoidal time series reveal the superiority of this approach. The SR methodology is simple to implement and is currently developed as freely available software. It should be noted that a key assumption to any period estimation technique, including the SR method, is that the time series are stationary. In practice, this can often be achieved through detrending of the data. We found that a cubic polynomial provides enough flexibility to accommodate the trends encountered in all our experimental data. In addition, the logarithmic transformation is beneficial, in particular if the oscillations are found to dampen with time. We have also focused on the scenario where groups of replicate time series from different experimental conditions are available to study the hypothesis that the period is the same. We have introduced a non-parametric test 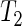, which can be seen as a generalization of the t-test, allowing for heteroscedasticity within each group as this assumption is more realistic for our experimental data. Simulation studies indicate that the test attains correct nominal size and that allowing for within-group heteroscedasticity resulted in some improvement of the power. In principle, 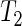could be applied to any other period estimator, provided an estimate of the variance is available. Some limitations remain. For example, the confidence intervals produced by the proposed methodology using the percentile approach tend to be conservative. Other definitions, as proposed in Carpenter and Bithell (2000), could be used, but we chose the percentile method as it is simple and inexpensive to compute. The SR methodology requires a minimum of two complete cycles worth of observed data. However, it seems that most data sets resulting from circadian experiments do fulfill this requirement. We have shown applications to various observed circadian data which originally motivated our study. The SR method is able to cope with departures from sinusoidal behavior and the presence of noise by consistently retrieving period length estimates within the circadian range that match the observed rhythms, while the non-parametric test has proved very useful in situations where a difference in period between two experimental groups is not clear from the relative error plots. We believe that the methods have wide applicability in chronobiology.

8. Software

Software implementing the SR methodology is freely available and can be used with appropriate citation, http://go.warwick.ac.uk/systemsbiology/software/. Automated SR analysis will also be available from the BioDare repository, http://www.biodare.ed.ac.uk/.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This research was funded by BBSRC and EPSRC under the SABR initiative. M.J.C. and B.F. are funded by ROBuST grant BB/F005261/1. J.F. and K.H. are funded by ROBuST grant BB/F005237/1. P.D.G. and A.H. are funded by ROBuST grant BB/F005318/1. D.A.R. holds an EPSRC Senior Research Fellowship (EP/C544587/1) and his work was also funded by the European Union BIOSIM Network Contract 005137.