Seizure prediction in hippocampal and neocortical epilepsy using a model-based approach

Abstract

Objectives

The aim of this study is to develop a model based seizure prediction method.

Methods

A neural mass model was used to simulate the macro-scale dynamics of intracranial EEG data. The model was composed of pyramidal cells, excitatory and inhibitory interneurons described through state equations. Twelve model’s parameters were estimated by fitting the model to the power spectral density of intracranial EEG signals and then integrated based on information obtained by investigating changes in the parameters prior to seizures. Twenty-one patients with medically intractable hippocampal and neocortical focal epilepsy were studied.

Results

Tuned to obtain maximum sensitivity, an average sensitivity of 87.07% and 92.6% with an average false prediction rate of 0.2 and 0.15/h were achieved using maximum seizure occurrence periods of 30 and 50 min and a minimum seizure prediction horizon of 10 s, respectively. Under maximum specificity conditions, the system sensitivity decreased to 82.9% and 90.05% and the false prediction rates were reduced to 0.16 and 0.12/h using maximum seizure occurrence periods of 30 and 50 min, respectively.

Conclusions

The spatio-temporal changes in the parameters demonstrated patient-specific preictal signatures that could be used for seizure prediction.

Significance

The present findings suggest that the model-based approach may aid prediction of seizures.

1. Introduction

As one of the most common neurological disorders, epilepsy affects more than approximately 1% of the population worldwide (Engel, 1989). This wide-spread disorder is characterized by episodic interruptions of cerebral electrical activities caused by abnormal hypersynchronous discharges of neuronal populations, commonly referred to as seizures (Jackson, 1873). Further, 25% of epilepsy patients exhibit intractable epilepsy (Beghi et al., 1986). Reliable seizure prediction systems may lead to new ways of controlling seizures and hence improving the quality of life by assisting epilepsy patients in adjusting their preventive behavior accordingly (Murray, 1993).

Due to its high temporal resolution, electroencephalography (EEG) is one of the effective and widely used tools to investigate physiological and pathological activities of the brain. Over the past decades, investigations using both linear and nonlinear analyses on seizure prediction in intracranial or scalp EEG recordings have led to findings that show gradual interictal-to-ictal transitions involving dynamical changes minutes to hours prior to upcoming seizures (Lehnertz et al., 2003; Mormann et al., 2006). Although these investigations have achieved high sensitivities in seizure prediction, these methods were also limited by high false prediction rates, i.e., prediction alarms with no seizure occurring within seizure occurrence periods (Mormann et al., 2006). From a clinical point of view, high false prediction rates can increase the psychological stress of epilepsy patients. Accordingly, a maximum false prediction rate per hour has been defined as a metric for quantifiably assessing seizure prediction tools intended for clinical use (Winterhalder et al., 2003).

Due to the complexity of seizure-precipitating factors, current seizure prediction methods may still be too rudimentary to extract all relevant parameters reflecting dynamical changes in the EEG signals preceding epileptic seizures (Mormann et al., 2007). The seizure prediction problem thus becomes exceedingly difficult when multiple regions of the brain are involved in the preictal transition. Even if there is a well-defined spatiotemporal preictal state as revealed by linear and nonlinear analyses of the EEG (Mormann et al., 2006), there still remains no established physiological correlation between preictal changes and the underlying neurophysiologic process taking place within the preictal state (Lopes da Silva et al., 2003a,b).

In general, the dynamics of the preictal transition appear to be complex, as observed even in a patient exhibiting preictal periods of different durations. Therefore, a different approach incorporating physiological parameters is desirable to improve the performance of seizure prediction. Such an approach has merits that it may explain why false predictions that exhibit the same dynamical changes of neuronal networks as that of true predictions, do not lead to epileptic seizures.

In the present study, our goal is to develop a model-based method to predict seizures in patients with hippocampal and/or neocortical seizures. We used a neural mass model incorporating biophysical parameters such as connectivity strengths (between excitatory and inhibitory subpopulations), to investigate whether the periods preceding neocortical and hippocampal seizures could be characterized by changes in the parameters of the model in comparison with interictal periods far from seizures. Towards this objective, the model was fit to the spectra of intracranial EEG (iEEG) data. A patient-specific rule-based system was then designed to spatiotemporally integrate preictal changes in order to capture the essence of the transition from interictal state to ictal activity. Finally, we assessed the system performance for preictal identification at single-subject and group levels.

2. Material and methods

2.1. Patient characteristics and iEEG recordings

In this study, we analyzed long-term iEEG data of 21 patients with medically intractable epilepsy. The iEEG data were obtained from the publicly available Freiburg Seizure Prediction EEG (FSPEEG) database (Maiwald et al., 2004) with permission. The data had been recorded from grid, strip, and depth electrodes surgically placed on the cortex of the patients or inserted in their brain. The patients underwent iEEG monitoring as part of a presurgical evaluation for hippocampal and/or neocortical focal epilepsy, at the Epilepsy Center of the University Hospital of Freiburg, Germany. Intracranial recordings had been acquired using a Neurofile NT digital video-EEG system with 128 channels. A sampling frequency of 256 or 512 Hz had been used to record the iEEG data using a common referential montage relative to the contact recording with no epileptic activity. For each patient in this database, six contacts had been selected by a certified epileptologist who visually inspected iEEG data. Out of six contacts, three had been chosen from the contacts inside the epileptogenic zone that exhibited the earliest signs of seizure activity, and three contacts from the remote locations defined as either the cerebral regions, which were not involved at all or the regions of which seizure activity was observed during the seizure propagation. The expert had also determined the onset and offset times of seizures based on identification of epileptic patterns preceding clinical manifestation of seizures in the iEEG recordings.

For each patient, iEEG data with epileptic seizures including at least 50-min preictal data were available. At least 24 h of seizure-free iEEG recordings had also been collected for each patient. For 13 patients, the interictal iEEG data were continuous. However, for the remaining eight patients interictal iEEG data were discontinuous including joined interictal data of less than 24 h (Schelte et al., 2006).

In total, we analyzed 596 h of iEEG data containing 87 seizures. No hyperventilation or photo-stimulation had been used to provoke seizures. However, medication had been reduced in most patients during the recording period. Table 1 summarizes the patients’ characteristics and the iEEG data used in this study. It is of note that regardless of type and number of seizures, location of seizure onsets in the brain, and record quality we analyzed all iEEG records as provided in the FSPEEG database in which the data and channel selection as well as the determination of onset and offset times of the seizures had been carried out independently and objectively by the expert at the Epilepsy Center of the University Hospital of Freiburg, Germany.

Table 1.

Patient specific characteristics of the intracranial EEG data.

Patient	Sex	Age	Seizure type	HC/NC	Origin	Electrodes	# Seizures		Interictal EEG duration (h)
							Training set	Test set	Training set	Test set
1	F	15	SP,CP	NC	Frontal	g,s	1	3	4	20
2	M	38	SP,CP,GTC	HC	Temporal	d	1	2	4	20
3	M	14	SP,CP	NC	Frontal	g,s	1	4	4	20
4	F	26	SP,CP,GTC	HC	Temporal	d,g,s	1	4	4	20
5	F	16	SP,CP,GTC	NC	Frontal	g,s	1	4	4	20
6	F	31	CP,GTC	HC	Temporo/occipital	d,g,s	1	2	4	20
7	F	42	SP,CP,GTC	HC	Temporal	d	1	2	4	20.6
8	F	32	SP,CP	NC	Frontal	g,s	1	1	4	20
9	M	44	CP,GTC	NC	Temporo/occipital	g,s	1	4	4	20
10	M	47	SP,CP,GTC	HC	Temporal	d	1	4	4	20.5
11	F	10	SP,CP,GTC	NC	Parietal	g,s	1	3	4	20
12	F	42	SP,CP,GTC	HC	Temporal	d,g,s	1	3	4	21
13	F	22	SP,CP,GTC	HC	Temporo/occipital	d,s	1	1	4	20
14	F	41	CP,GTC	HC,NC	Fronto/temporal	d,s	1	3	4	20
15	M	31	SP,CP,GTC	HC,NC	Temporal	d,s	1	3	4	20
16	F	50	SP,CP,GTC	HC	Temporal	d,s	1	4	4	20
17	M	28	SP,CP,GTC	NC	Temporal	s	1	4	4	20
18	F	25	SP,CP	NC	Frontal	s	1	4	4	21
19	F	28	SP,CP,GTC	NC	Frontal	s	1	3	4	20.4
20	M	33	SP,CP,GTC	NC	Temporo/parietal	d,g,s	1	4	4	21.6
21	M	13	SP,CP	NC	Temporal	g,s	1	4	4	20
Total	13F/8M						21	66	84	425
Mean							1	3	4	20.2

SP, simple partial; CP, complex partial; GTC, generalized tonic-clonic; HC, Hippocampal; NC, Neocortical; g, grid; s, strip; d, depth.

2.2. Model-based seizure prediction

At macroscopic scales, intracranial contacts placed on the cortex and/or inserted in the brain measure the mean local field potentials generated by synchronous activity of large assemblies of neurons including pyramidal cells as well as excitatory and inhibitory interneurons located in the vicinity of the contact (Ullah and Schiff, 2009).

To date, many computational models incorporating explicit biophysical parameters have been proposed to elucidate the mechanisms underlying the generation of physiological and pathological cerebral activity such as alpha activity, event related potential, and epilepsy (Lopes da Silva et al., 1974; Jansen and Rit, 1995; Wendling et al., 2002; Suffczynski et al., 2006; Moran et al., 2007). These computational models rest on four main assumptions (Freeman, 1972; Wilson and Cowan, 1972; Suffczynski et al., 2006). First, it is assumed that neurons inside the mass are densely distributed with random multi-scale inter-neuron connections. Second, the neural activity of the mass is assumed to be the average of postsynaptic potentials over all synchronously activated assemblies of neurons inside the mass. In other words, the instantaneous single neurons within the neuronal population receive the same average influence exerted to them from the ensemble. This assumption is the so-called mean field approximation, which is crucial to determine the steady-state behavior of the mass (Suffczynski et al., 2006; Daunizeau et al., 2011). Third, temporal neural events are also assumed to be the ensemble average over the electrical activities of the microscopic neural structure inside the mass. Therefore, relaxation times for action potentials and synaptic potentials for individual neurons are ignored. In this case, the state equations governing the model only describe the neural mass states at a macroscopic scale with no explicit reference to action potentials, thresholds, and refractory periods (Freeman, 1972). Finally, the main assumption in developing these models is that the neural mechanism is mainly dependent on the interaction of excitatory and inhibitory cells (Wilson and Cowan, 1972; Suffczynski et al., 2006).

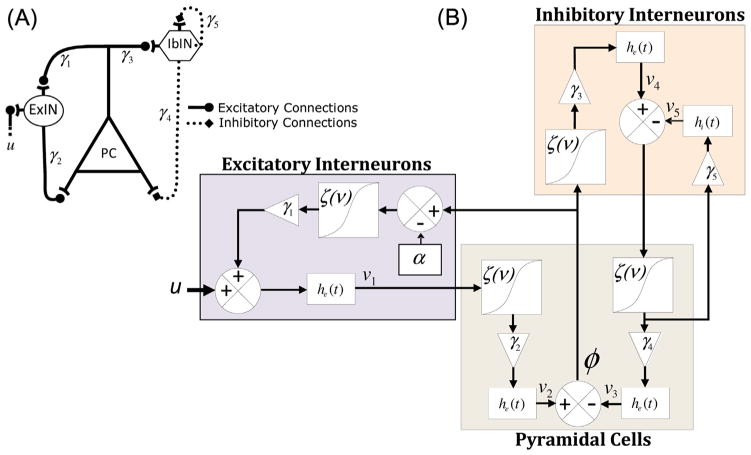
Among the computational models mentioned above, we were interested in the neural mass model incorporating lumped parameters, originally developed by Lopes da Silva et al. (1974) to explain the origin of the alpha activity. The model was later modified by Jansen and Rit (1995) who developed a nonlinear model of a cortical column to simulate event-related potentials. The modified model was built based on the incorporation of excitatory Pyramidal Cells (PC) receiving inputs from Excitatory InterNeurons (ExIN), Inhibitory InterNeurons (IbIN), and extrinsic input (u) coming from other cerebral regions (Fig. 1A). In this model, the synapses of excitatory or inhibitory neurons convert the average density of pre-synaptic action potentials into the average postsynaptic membrane potential by convolving their respective impulse response functions h_e(t) and h_i(t) with the input.

Fig. 1.

Canonical neural mass model (A), and schematic diagram of the neural mass model (B) described by the state Eq. (1). ExIN, excitarory interneurons; IbIN, inhibitory interneurons; PC, pyramidal cells. See Table 2 for parameter description.

$$h_{e/i}(t)=\left\{\begin{array}{ll}(H_{e/i}/{\tau }_{e/i})texp(-t/{\tau }_{e/i})\hfill & t\ge 0\hfill \\ 0\hfill & t<0\hfill \end{array}\right\}$$ (1)

where H_e and H_i determine the maximum amplitude of the excitatory and inhibitory post-synaptic potentials, respectively, and τ_e and τ_i represent the average time constants of passive membrane and other spatially distributed delays in the dendritic tree in the excitatory and inhibitory feedback loops, respectively. At mesoscopic scales of neuronal interactions, the impulse responses of the synaptic junctions can be formulated through a state-space representation by a second-order differential equation (David and Friston, 2003) as follows.

$$\ddot{v}=(H_{e/i}/{\tau }_{e/i})u(t)-(2/{\tau }_{e/i})\stackrel{.}{v}(t)-{(2/{\tau }_{e/i})}^{2}v(t)$$ (2)

where v is the average postsynaptic membrane potential for the excitatory or inhibitory interneurons.

In the model proposed by Jansen and Rit, the average postsynaptic membrane potential is converted to outgoing density of action potentials by a nonlinear static sigmoid function ζ(v)

$$\zeta (v)=\frac{2e_0}{1+exp(-r(v_0-v))}$$ (3)

where e₀ represents the maximum firing rate of the neural population, v₀ is the postsynaptic potential achieved with a 50% firing rate, and r determines the steepness of the sigmoid function.

The model configuration makes it unique for investigating preictal state in epilepsy patients because the unbalanced interactions between PC, ExIN (positive feedback), and IbIN (negative feedback) appear to play an important role in generating epileptic EEG activities, as described by Suffczynski et al. (2006). Later, the Jansen and Rit model has been extended and enhanced by Moran et al. (2007) by adding several specific parameters which met our needs to design a model-based seizure predictor. The main advantage of this model over others is that the model incorporates a recurrent connection (γ₅ in Fig. 1B) added to the inhibitory sub-unit. This self-feedback has been proven to be indispensible for the model to replicate fast activities in the gamma frequency band, especially in the hippocampus (Wendling et al., 2002; Moran et al., 2007). Not only can this structure be used to model the neocortical networks, it can also replicate the activity generated by the hippocampus containing a network of richly interconnected excitatory cells (e.g. pyramidal neurons) that are regulated by a wide diversity of inhibitory interneurons (Freund and Buzsaki, 1996).

The state equations governing the extended model (see Moran et al. (2007) for more details) are formulated as:

$$\begin{array}{l}{\ddot{v}}_1=(H_e/{\tau }_e)({\gamma }_1\zeta (\varphi -\alpha )+u)-(2/{\tau }_e){\stackrel{.}{v}}_1-(1/{\tau }_e^2)v_1\\ {\ddot{v}}_2=(H_e/{\tau }_e){\gamma }_2\zeta (v_1)-(2/{\tau }_e){\stackrel{.}{v}}_2-(1/{\tau }_e^2)v_2\\ {\ddot{v}}_3=(H_i/{\tau }_i){\gamma }_4\zeta (v_4-v_5)-(2/{\tau }_i){\stackrel{.}{v}}_3-(1/{\tau }_i^2)v_3\\ {\ddot{v}}_4=(H_e/{\tau }_e){\gamma }_3\zeta (\varphi )-(2/{\tau }_e){\stackrel{.}{v}}_4-(1/{\tau }_e^2)v_4\\ {\ddot{v}}_5=(H_i/{\tau }_i){\gamma }_5\zeta (v_4-v_5)-(2/{\tau }_i){\stackrel{.}{v}}_5-(1/{\tau }_i^2)v_5\\ \varphi =v_2-v_3\\ \zeta (v)=\frac{1}{1+exp(-{\rho }_1(v-{\rho }_2))}-\frac{1}{1+exp({\rho }_1{\rho }_2)}\end{array}$$ (4)

where v₁–v₅ represent the average postsynaptic membrane potentials for the excitatory interneurons, pyramidal cells and inhibitory interneurons, respectively (Fig. 1B). φ is the local field potential (herein the EEG signal), and ρ₁ and ρ₂ are the parameters that control the shape and position of the sigmoid function ζ(ν). In this model, α is the spike-frequency adaptation whose dynamics conforms to the universal model (see Benda and Herz (2003) for a detailed description of the mechanisms for adaptation):

$$\stackrel{.}{\alpha }=(a_{\infty }-a)/{\tau }_{\alpha }$$ (5)

The time constant τ_α determines how quickly α moves toward its steady state α_∞, which determines the rate beyond which the neuron stops firing. Since adaptation occurs over large timescales (from a few 100 ms to 2 s), it has a slow trend independent of any spike-generating process, the effect of the adaptation was therefore formulated as a shift in the firing rate – input curve, ζ(ν−α) (Moran et al., 2007). Finally in the extended model only the excitatory interneurons were considered to adapt to the extrinsic input (Fig. 1B).

ρ₁, ρ₂ and α are the unique parameters of the model that increase the adaptability of the model and its ability to replicate the spectral power density of real EEG (Moran et al., 2008).

Table 2 describes the model parameters used in the state Eq. (4) and their physiological interpretation. For the sake of simplicity, we refer to γ₁ and γ₂ as the coupling strengths of the excitatory feedback loop. Similarly, γ₃ and γ₄ are referred as the coupling strengths of the inhibitory feedback loop.

Table 2.

Parameters used in the state equations governing the model and their interpretation and standard values.

Parameters	Physiological interpretation	Physical role in the model	Standard value
ρ1	Determines the steepness of the sigmoid function	Alters the sensitivity of the neuron to its membrane potential	2 mV−1
ρ2	Determines the position of the sigmoid function	Increases the excitability of the of the neuronal population	1 mV
He	Maximum excitatory post-synaptic potentials	Alters average excitatory synaptic gain	4 mV
Hi	Maximum inhibitory post-synaptic potentials	Alters average inhibitory synaptic gain	32 mV
τe	Average time constant in the excitatory feedback loop	Alters average time constant of excitatory dendritic tree	4 ms
τi	Average time constant in the inhibitory feedback loop	Alters average time constant of inhibitory dendritic tree	16 ms
γ1	Average number of synapses in the path connecting PC to ExIN	Alters the strength of coupling between PC and ExIN	128
γ2	Average number of synapses in the path connecting ExIN to PC	alters the strength of coupling between ExIN and PC	128
γ3	Average number of synapses in the path connecting PC to IbIN	Alters the strength of coupling between PC and IbIN	64
γ4	Average number of synapses in the path connecting IbIN to PC	Alters the strength of coupling between IbIN and PC	64
γ5	Average number of synapses in the self-feedback inhibitory path	Alters the strength of recurrent inhibitory gain	16
τα	Adaptation rate constant	Determines how fast the firing rate adapts	512 ms

2.3. Seizure prediction system

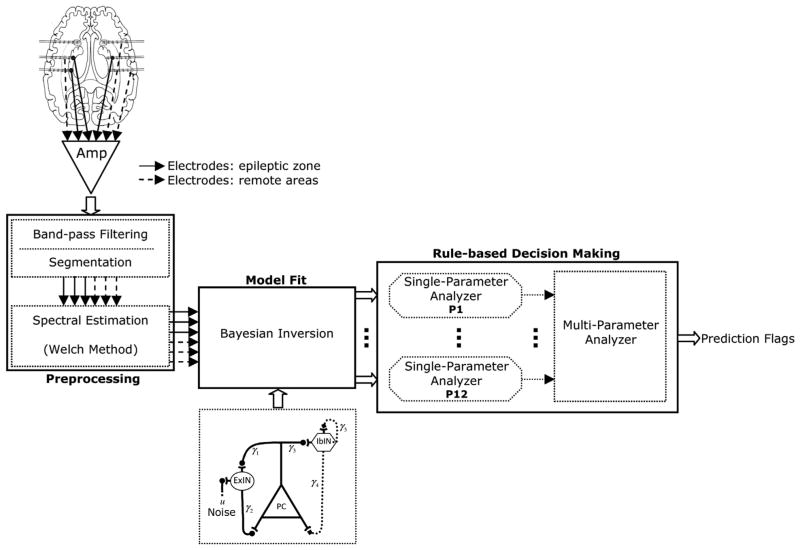
Our model-based seizure prediction system comprises three stages (Fig. 2). First, the iEEG data are band-pass filtered to remove dc offset components and high frequency noise and divided into quasi-stationary segments. The neural mass model is then fitted to the frequency spectrum of the iEEG segments on a channel-by-channel basis. The resulting parameters are thresholded using the statistics of a reference window selected as the baseline distant in time from any seizure. The thresholded parameters of single channels are then spatially integrated using a rule-based patient-specific decision making approach to identify seizure precursors. Each stage of the system is described in detail in the following sections.

Fig. 2.

Schematic diagram of the model-based seizure prediction system.

2.4. Preprocessing

The EEG data were first band-pass filtered between 0.5 and 100 Hz, and then notch filtered at 50 Hz to eliminate possible power line interference. Then, for each patient, the iEEG data were split into independent training and testing sets. The training set included one randomly selected sample seizure with a preictal period of 50 min and 4-h seizure free interictal iEEG data used as the reference window. The 4-h reference window was considered large enough to include intra-individual temporal variations of interictal activity. A shorter baseline had strong impact on the Gaussianity of the distributions of the model parameters estimated within the reference state (numerically tested). On the other hand, for each patient we tried to keep the baseline as short as possible to use a large portion of interictal data for testing the system. The testing sets containing the remaining seizures and interictal data as listed in Table 1 were used to assess the performance of the system. The data included in the training and testing sets were then broken down into nonoverlapping 10-s segments assumed to be quasi-stationary as investigated by Esteller et al. (2001).

We computed the power spectral density of 10-s iEEG segments using the Welch spectral estimation method (Welch, 1967) which divided the data into short segments overlapped by 50% and applied a Hamming window and the Fourier transform to each. The power spectrum was then computed by taking the squared magnitude of the averaged transforms. The Welch spectral estimation method reduces noise as well as the variance of the iEEG spectral estimate by windowing and averaging methods (Welch, 1967).

2.5. Model fit

For the sake of simplicity, we ignored connectivities between neuronal mass models used to characterize the neural activities of the six intracranial contacts. Therefore, we only modeled the iEEG activity of each contact separately. We used the Bayesian inference method (Moran et al., 2008) to estimate the parameters of the model by inverting the power spectral density of iEEG segments. The main assumption in the inversion process is that the spectral profile of the measured signal (herein iEEG signal) is a linear mixture of different frequency modes (Valdes et al., 1999; Friston, 2002; Zavaglia et al., 2008).

In brief, to invert the model, a linear transfer function is first provided in the state space by linearizing the state Eq. (4) (Moran et al., 2007). This transfer function describes the relationship between the steady-state spectral response of the neuronal population under investigation and the model parameters. The endogenous input (u in Fig. 1) passing through the transfer function of the neural mass model is assumed to be stochastic as a mixture of white, pink or 1/f noise, with no sensory or event based inferences (Moran et al., 2008). Then, the inversion method uses the specification of a likelihood model. The priors are used as constraints on the parameters, and an Expectation Maximization method is employed to estimate the posterior probability of the model parameters. The posterior distribution is defined via Bayes’ Theorem as the normalized product of the prior density and the likelihood. Defining the prior distributions (mean and covariance) ensured the stability and convergence to a global minimum (Moran et al., 2008). We assigned the standard values listed in Table 2 to the mean of the prior distributions. The same prior expectations for the parameters as used by Moran et al. (2008) were used in this study to ensure positivity under Gaussian priors.

We only applied the Bayesian inversion method as implemented in the SPM5 software (see Moran et al. (2008) for more details) to seizure-free interictal activities as well as to preictal periods. Thus, iEEG signals of ictal and postictal states were not analyzed. The model parameters estimated from iEEG segments were then used for seizure prediction under two assumptions. First, we assumed that the model parameters remained unchanged within the quasi-stationary iEEG segments and the amplitude and frequency content of the iEEG signal did not change by possible nonlinearity of the recording machine. Second, since the inversion method used the linearized state equations to estimate the model parameters using the power spectral density of EEG activity, the linearization process did not involve the model nonlinear mechanism, which was indispensible to generate spike-like activity (Moran et al., 2007). Therefore, the inversion process was unable to estimate the model parameters for segments containing spikes. In general, spikes are considered as short-time isolated events, which less contribute to the low frequency ranges. To ensure that the total spectral power of the iEEG segments was not affected significantly by high-energetic spikes or series of spikes, we rejected segments highly contaminated by spike-like activity. For this purpose, we first used a simple amplitude thresholding method to identify segments affected by high amplitude sporadic spikes. In order to determine the location of spikes for each segment, we computed the background amplitude of the segment by averaging the absolute values of the amplitudes of the EEG signal in each segment (Gotman, 1985). Any waveforms with amplitudes greater than four times the background amplitude were considered spikes. If the average energy ratio of the segment was more than 5%, that segment was excluded from further analysis. The average energy ratio (R) for a N-sample segment was defined as:

$$\begin{array}{l}R=\frac{P_{\text{Spikes}}}{P_{\text{Segment}}}\times 100\%,P_{\text{Spikes}}=\frac{1}{M}\sum _{m=1}^M{(\mid y[m]\mid )}^2,\\ P_{\text{Segment}}=\frac{1}{N}\sum _{n=1}^N{(\mid x[n]\mid )}^2\end{array}$$ (6)

where M is the number of samples within the spiky portion of the segment, P_Spikes is the power of the spike-like activities within the segment, and P_Segment is the power of the segment.

2.6. Rule-based decision making

The time profiles of the twelve parameters (listed in Table 2) extracted from consecutive iEEG segments for each patient were first smoothed using a backward-moving-average filter of 5 min in length, and then thresholded using the following method. This filter length has been reported by Mormann et al. (2005) as the optimal length for seizure prediction methods to achieve higher performance. The thresholding was used to identify outliers in the temporal profiles of the parameter values. This procedure was intended to locate significant preictal changes. For each channel and parameter, the parameter values were normalized using (y−ŷ)/σ, where y was the parameter value, and ŷ and σ were the respective expectation and standard deviation of the parameter values within the reference window. Since the baseline was relatively long, we expected a normal distribution for the values of each parameter within the reference window. However, we found one standard deviation to be more appropriate to identify outliers because the parameter distribution was shown to be non-Gaussian in some cases (numerically tested). However, increasing the thresholds could reduce the sensitivity of our seizure prediction system where preictal changes in parameters were not highly significant in comparison with the reference window. Once identified, the location and the parameter value of the iEEG segments that exhibited values greater than (ŷ + σ) or lower than (ŷ−σ) were saved for further analysis.

Using the Mann–Whitney U-test (Mann and Whitney, 1947) as a two-sided rank sum statistical test, we tested the null hypothesis that the parameter values within the reference period and the ones within the preictal period on the same channel were independent samples from identical distributions with equal medians. The alternative hypothesis was that the parameter values did not have equal medians, with a level of significance of P < 0.05. We used the Mann–Whitney U-test to identify the parameters and channels that exhibited the significant changes within the 50-min preictal period of the sample seizures for all of the patients.

To determine a preictal increase or decrease in each parameter for each patient, the parameter values within the 50-min preictal period of the sample seizure (training set) were statistically compared with the ones from the reference window in a channel-by-channel basis. If the preictal period was significantly different from the respective reference window for a specific parameter and channel, then, a label H or L was assigned to the preictal state of the parameter on that channel. The label H or L indicated that the median of the parameter values in the preictal period was respectively greater or less than the one computed in the reference period. If the preictal period did not show any significant changes in comparison with the reference window, a label E representing equality was assigned to the parameter and channel. This procedure was repeated for all the other parameters and channels for each patient in order to identify significant preictal changes. For each patient, all of the labels obtained for the parameters were then arranged in a vector called spatial parameter pattern vector (SFPV) and saved as the spatiotemporal preictal profile of the parameters. The resulting profiles of the twelve parameters were then fed to the parameter analyzers as described in the Supplementary Material. As guidelines, the SFPVs were used to establish patient-specific rules, which were consequently employed to identify recurrences in the preictal pattern as observed in the sample seizure in the testing set.

The single- and multi-parameter analyzers were designed to integrate parameter values spatio-temporally by rules established in the form of “if-then” rules, which allowed a mapping from parameter-channel space into decisions made about seizure prediction (see the Supplementary Material for details).

2.7. System evaluation

The system evaluation was performed by dividing the patients’ iEEG data into training and testing sets. The system parameters were optimally adjusted using the training set for each patient. Then, the performance of the seizure prediction system was assessed on the testing sets using the commonly used performance parameters including sensitivity, specificity, false prediction rate, mean prediction time, and portion of time under false predictions (Mormann et al., 2006); see the Supplementary Material for definitions).

The performance parameters were calculated for maximum seizure occurrence periods of 30 and 50 min and a minimum seizure prediction horizon (SPH) of 10 s.

The performance of the system was evaluated using the optimal thresholds described in the Supplementary Material for the maximum sensitivity and maximum specificity strategies. The system sensitivity was also compared with the sensitivity values obtained using the random and periodical prediction methods as described in Maiwald et al. (2004) (see the Supplementary Material).

3. Results

3.1. Percentage of rejected spiky segments

To obtain the percentage of iEEG segments excluded from our analysis, for each patient and channel, iEEG segments containing high-energy spiky transients were first identified based on the energy criterion described in the model fit section. The channel-related percentage was then obtained by calculating the ratio of the number of identified spiky segments to the total number of segments analyzed for the patient. This process was repeated for all of the patients.

Supplementary Table S1 lists the percentage of rejected iEEG segments for electrodes positioned within the epileptic zone and remote areas for each patient. For the majority of channels, less than 5% of segments contained high-energy spiky transients. Therefore, based on the energy criterion that we defined, no channels were precluded from the seizure prediction process. More importantly, as we described earlier, for any segment to be declared as a seizure precursor, prediction flag Is have to be raised on at least two channels. Therefore, rejecting isolated spiky segments may not affect significantly the performance of the seizure prediction system. Only a very low percentage of segments showed spike-like activities on all channels simultaneously in the preictal periods for patients 6 and 16.

3.2. Threshold optimization

In Supplementary Table S2 lists the mean and absolute deviation of the optimal values for the thresholds (T_c1, T_c2, N_P, and N_ch) used for seizure prediction in all patients over ten randomly selected reference windows. All thresholds were obtained using the optimization process for both the maximum sensitivity and maximum specificity strategies (see Supplementary Material for more details). As shown, for the majority of the patients, the system needed at least two parameters and six channels to identify seizure precursors. The system also showed higher sensitivity to the threshold T_c2 used to filter out flag IIIs with non-significant values.

3.3. Cross-validation results: maximum sensitivity vs. maximum specificity

Supplementary Tables S3 and S4 list the results on the performance evaluation of the entire system using the maximum sensitivity and maximum specificity strategies. Grand statistics were calculated using out-of-sample seizure-free interictal data and seizures (see Supplementary Material for more information). The results showed no statistically significant differences in the system performance when different baselines were used. However, increasing the sensitivity of the system caused a slight increase in false prediction rates and vice versa. The periods preceding the seizures could be characterized by increases and decreases in parameters on different intracranial electrodes with a mean prediction time of 15 min. However, the performance of the system depended on the individual patient.

The overall performance of the system was computed by averaging the performance values obtained across seizures. Using the maximum sensitivity strategy, the system achieved an average sensitivity of 87.07% and 92.6% with an average false prediction rate of 0.2 and 0.15/h, and an average specificity of 95.8%, respectively, for seizure occurrence periods of 30 and 50 min and SPH = 10 s. Using the maximum specificity strategy, the system’s sensitivity decreased to 82.9% and 90.05%, respectively, for seizure occurrence periods of 30 and 50 min and SPH = 10 s. However, the respective false prediction rates were improved to 0.16 and 0.12/h.

In Supplementary Tables S3 and S4, for each patient, the ranges of changes in portion of time under false predictions and mean prediction time have been reported for each patient. The mean prediction time implies directly the duration of the identified preictal periods within which significant preictal changes in parameters were observed.

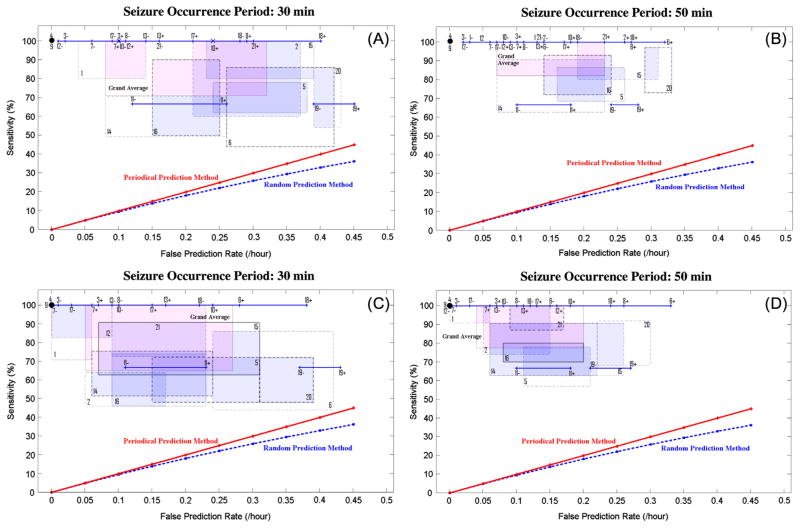
Figs. 3A–D depict the variation range of the sensitivity of the system versus that of false prediction rate for seizure occurrence periods of 30 and 50 min and a seizure prediction horizon of 10 s for each patient.

Fig. 3.

Sensitivity versus false prediction rate for each patient (as indicated by patient number in Table 1) and for the grand average across patients (labeled in pink as grand average) using seizure occurrence periods of 30 min (A and C), and 50 min (B and D) and a seizure prediction horizon of 10 s. Results for the maximum sensitivity and maximum specificity strategies are shown in (A–B) and (C–D), respectively. For each patient, a box shows the range of variation of sensitivity versus false prediction rate obtained using different randomly selected reference windows. It is of note that a line (e.g. for patient 11) or a dot (e.g. for patient 4) represents the results where no variations in sensitivities or/and in false prediction rates were observed. Plus and minus signs used with the patients’ number denote the upper and lower bounds of the corresponding ranges of variation. The performances of the random and periodical prediction methods as described in the Supplementary Material are shown in all four panels (A–D). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Using both strategies, the seizure prediction method obtained significantly higher sensitivities compared to the random and periodical prediction methods with a maximum false prediction rate of less than 0.45/h. Accordingly, Fig. 3C and D illustrate how the system’s sensitivity deteriorated when the system was optimized using the maximum specificity strategy. However its false prediction rate was improved.

3.4. Frequency content analysis

For each patient, the power spectral densities of iEEG segments within the reference windows and preictal periods were averaged over the intracranial electrodes located within the epileptogenic zone or remote areas. The average frequency content of segments within the reference windows and preictal periods were relatively similar with specific differences in two distinct frequency peaks: a low frequency peak in the frequency band below 5 Hz within the EEG theta band, and a high frequency peak in the low-gamma bands between 20 and 40 Hz (Fig. 4). It is also important to note that both the low frequency and high frequency peaks occurred in all patients during the preictal and reference periods.

Fig. 4.

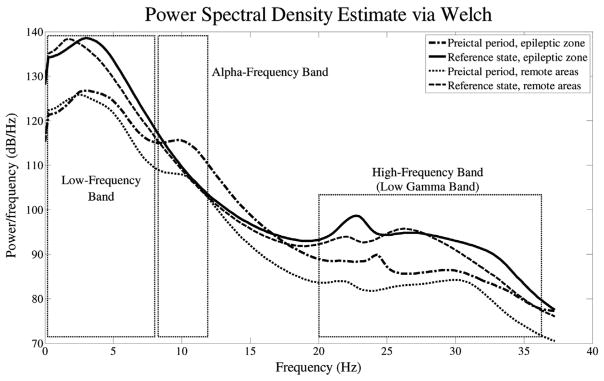
Spectra for preictal and reference state, averaged over the electrodes within the epileptic zone and remote areas.

4. Discussion

Motivated by the existence of neuronal population models, we have developed a model-based method with the objective of modeling intracranial EEG to infer physiological changes underlying interictal and preictal activities. The parameters of a physiologically inspired neural mass model fitted to the power spectral density of iEEG segments were spatio-temporally integrated using the patient-specific rules established from the characteristics of the preictal periods to predict hippocampal and neocortical onset seizures in patients with medically intractable epilepsy. We tested the patient-specific system on blinded long-term iEEG recordings after tuning its parameters using a training set for each patient. We then evaluated the system using common performance parameters including sensitivity, specificity, and false prediction rate. Using the maximum sensitivity strategy, our rule-based seizure prediction system achieved an average sensitivity of 87.07% and 92.6% with an average false prediction rate of 0.2 and 0.15/h, and an average specificity of 95.8% for seizure occurrence periods of 30 and 50 min, respectively. Similarly, using the maximum specificity strategy, the system sensitivity decreased to 82.9% and 90.05% for seizure occurrence periods of 30 and 50 min, respectively. However, the false prediction rate was reduced to 0.16 and 0.12/h accordingly.

Our model-based seizure prediction method was able to capture preictal changes at least 15 min before electrographic onset. The predictive power of the system substantially increased within prediction occurrence periods of 30 and 50 min. The transitional preictal states differed from seizure-free interictal control periods on intracranial electrodes located within the epileptic zone and remote areas. The characteristic differences in the model parameters between periods preceding the seizures and baselines were statistically significant. The system also largely outperformed the random and periodic prediction methods.

Implementations of the estimation process using the Bayesian inversion algorithm used in this study can be found in the statistical parametric mapping package (SPM5, available from http://ltfat.sourceforge.net). The estimation procedures were run on a Windows 7 platform with a Pentium 5, 3.4 GHz CPU, 4 GB of memory. On average, the running time needed to estimate the model parameters for a 10-s segment of iEEG data was 5 s using MATLAB (Math Works Inc.). However, a further substantial improvement can be obtained by compiling the MATLAB program in C/C++ codes for real-time applications.

4.1. Comparison to other seizure prediction methods

To date, many research groups have attempted to identify preictal changes preceding epileptic seizures by linear and nonlinear analyses, all with a varying degree of success (Lehnertz et al., 2003; Mormann et al., 2006). The international EEG database (FSPEEG) has been used for evaluating seizure prediction tools employing the correlation dimension (Aschenbrenner-Scheibe et al., 2003), the dynamical similarity index (Winterhalder et al., 2003; Schelte et al., 2006), the mean phase coherence (Schelte et al., 2006), and a phase and lag synchronization measure (Winterhalder et al., 2006). Maiwald et al. (2004) carried out a study to compare the performance of the dynamical similarity index, the accumulated energy, and the effective correlation dimension for seizure prediction. With a false prediction rate (FPR) of less than 0.15/h and a seizure occurrence period (SOP) of up to 30 min, these three methods achieved sensitivity ranges of 21–42%, 18–31% and 13–30%, respectively. Using bivariate signal analysis, Mirowski et al. (2009) extracted features including cross-correlation, nonlinear interdependence, dynamical entrainment and phase synchrony-based measures from 5-s segments of iEEG data from the FSPEEG database. They aggregated extracted features into spatio-temporal, or spatio-temporal and frequency-based patterns and classified them into the preictal or interictal categories using patient-specific machine learning-based classifiers. Using convolutional networks combined with wavelet coherence, they achieved a sensitivity of 71% with zero false positives on 15 (out of 21) patients on average 60 min before the seizure onset. They reported that for each patient in this database, at least one method based on bivariate measures could predict seizures with a sensitivity of 100% 60 min prior to the seizures with no false alarm. Recently, a seizure prediction system developed by Feldwisch-Drentrup et al. (2010) used the “AND” and “OR” combination of different seizure prediction algorithms including the mean phase coherence (Mormann et al., 2000) and the dynamic similarity index (Le Van Quyen et al., 1999), for the purpose of improving prediction performances. They evaluated their system on a database with 182 h of continuous long-term iEEG recordings with an average of 19.1 seizures per patient. They achieved a mean sensitivity of 25% for the individual methods and mean sensitivities of 43.2–35.2% and 55–50% for a maximum false prediction rate of 0.15/h respectively for the “AND” and “OR” combinational systems using seizure occurrence periods of 30 and 50 min.

In a very recent study, we developed a rule-based seizure prediction algorithm using combined univariate and bivariate nonlinear measures. Using the rule-based seizure prediction system, we achieved an average sensitivity of 79.9% and 90.2%, and an average false prediction rate of 0.17 and 0.11/h, respectively, for seizure occurrence periods of 30 and 50 min and a fixed seizure prediction horizon of 10 s (Aarabi and He, 2012). In comparison, in the present approach, we achieved a higher average sensitivity of 87.07% and 92.6%, and average false prediction rates of 0.2 and 0.15/h for seizure occurrence periods of 30 and 50 min, respectively. A key parameter that discriminates the present approach from other approaches is that other approaches used discriminative relevant nonlinear parameters of the iEEG data to distinguish preictal periods from interictal states considered as the baseline. In contrast, our present approach implied characterization of neurophysiological processes underlying iEEG through inference on the parameters of a biophysical model. The changes in these parameters may reflect fundamental physiological differences between interictal and preictal states. Our present results suggest the existence of a preictal period that occurs several minutes before the first electrical changes associated with the seizures are observed. In most of the cases, preictal changes were related to both sites where seizure emerged as well as to remote areas. In some patients, the preictal changes were more significant in remote areas than in the epileptogenic zone, which suggests the existence of spatio-temporal changes in the EEG dynamics driven by neocortical and hippocampal networks prior to seizures.

4.2. Model considerations

Mathematical models (Traub et al., 1987; Lopes da Silva et al., 1994; Lytton et al., 1997; Traub et al., 1997; Wendling et al., 2002; Suffczynski et al., 2004) and experimental models (Walther et al., 1986; Hawkins and Mellanby, 1987; Jefferys, 2003) have been successfully used to study mechanisms underlying seizure generation. The computational models have shown great computational power to reproduce large variety of MEG/EEG patterns (Nunez, 1974; Jansen and Rit, 1995; Lopes da Silva et al., 1997; Valdes et al., 1999; Robinson et al., 2001; Suffczynski et al., 2001; Rennie et al., 2002; David and Friston, 2003; Wendling et al., 2000, 2002, 2005). Specifically, based on the impaired balance between neural excitation and inhibition, Wendling et al. (2000, 2002, 2005) have used neural mass models to simulate epileptic patterns. But to the best of our knowledge, no physiologically inspired models have been used so far to investigate preictal changes in real EEG data recorded from epileptic patients with focal epilepsy. In this study, we have used the dynamic causal modeling using the Bayesian inversion method described by Moran et al. (2007, 2008) to infer changes in physiological parameters in the preictal period prior to the hippocampal and neocortical onset seizures. This modeling scheme incorporates explicit biophysical parameters including coupling strengths between excitatory and inhibitory interneurons and other intrinsic parameters defined at a macroscopic level. The resulting model has been developed under the physiological basis consistent with the experimental and theoretical work of others (Wendling et al., 2002, 2005). Furthermore, the model has been validated successfully through a correct prediction of changes in synaptic parameters using simulated data and experimental recordings from animals. For example, the model inversion has provided consistent predictions about the level of extracellular glutamate as measured experimentally in the prefrontal cortex of rats (Moran et al., 2008). This neural mass model is the modified version of the dynamic causal model used by David et al. (2006) to study event-related potentials with distinctive parameters (Moran et al., 2007, 2008).

4.3. Seizure prediction considerations

The short-term preictal changes in parameters were analyzed based on amplitude and duration for identifying seizure precursors. With this approach we obtained a good performance for the system. However, the preictal changes in parameters were strongly affected by the differences between patients. Furthermore, no sustained increases or decreases in parameters were observed in the periods preceding the seizures in some patients.

We observed discriminant preictal increases or decreases in the model parameters in comparison to baselines in all three intracranial electrodes near the focus as well as in those located in remote areas in the neocortex and hippocampus with certain variation from seizure to seizure interindividually and across patients. Our findings are in accordance with other observations, which suggest that the seizure generation process may involve recording sites within the epileptic focal area as well as distant brain structures (see Mormann et al., 2006, 2007).

In our model-based seizure prediction approach, one neural mass model was considered for each of the six intracranial contacts. Therefore, six models for each patient were considered independent from each other (non-coupled neuronal population models). This uncoupled modeling approach provided us with means to investigate the behavior of intrinsic parameters with no influence from other cerebral regions. However, our main assumption was that the neural activity within one region is independent from the activity of other cerebral regions. This assumption may not be valid especially when one deals with epileptic networks, because interactions between different regions of the brain during the epileptogenic process have been considered to be closely associated with changes in the spatiotemporal dynamics of ictogenesis.

Lastly, as described earlier, due to the linearization of the nonlinear state equations, the inversion process could not be employed to estimate the model parameters for segments containing spikes, which are caused by the inherent non-linear nature of the state equations. Therefore, we discarded iEEG segments with spike-like events from seizure prediction process based on the hypothesis that interictal spikes are generated by a random process. This hypothesis does not hold in situations where spike rates may decrease or increase in the pre-ictal periods in a patient-specific way. Therefore, the process of discarding spiky segments may systematically affect the performance of the system for patients with preictal periods characterized by spiky activities. On the other hand, it is probable that removing segments with spike-like events would improve the performance of the other methods that we earlier compared our system with. As a result, one may envisage use of neural mass model being able of producing oscillatory background activities with low amplitude dynamics as well as high amplitude spike–wave discharges. This bistable model would help to understand the mechanism of transition from interictal state to seizure activity with time-invarying parameters with an emphasis on spatial interactions in the model (Goodfellow et al., 2011). This property provides a better characterization of the transition from spontaneous background EEG into ictal activity by considering a larger number of coupled compartments. Other data-driven neural field models have also been developed for estimating intracortical connectivity and synaptic dynamics from electrophysiological data (Freestone et al., 2011). This therefore motivates the future application of models that allow for interregional coupling.

5. Conclusion

In summary, our model-based seizure prediction tool achieved a clinically acceptable performance across the patients studied. It also provided a substantial ground for identifying preictal states by investigating changes in the neural mass model’s parameters estimated using the spectrum of iEEG signals. The spatio-temporal changes in the neurophysiological parameters of the model demonstrated patient-specific preictal signatures that could be used for seizure prediction in the majority of the seizures with hippocampal and neocortical origins.

Further investigations will focus on using coupled neural mass models to investigate interregional influences and their relation to mechanisms underlying the transition from interictal to ictal states. The results obtained in this study will then be compared with those to be obtained using the model with interregional connections. As the second step to improve the performance of our seizure prediction tool, the improved Bayesian inversion method which includes the second-order moment of the posterior density on the model’s parameter (Daunizeau et al., 2011) will be used to minimize dependencies between the estimates of parameters.

HIGHLIGHTS.

• Sensitivity of >90% and false prediction rate of <0.15/h from intracranial EEG (iEEG).

• The neural mass model revealed patient-specific preictal patterns.

• Preictal changes were observed independent of locations of intracranial electrodes.

Appendix A. Supplementary data

Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.clinph.2013.10.051.