Relating Nanoparticle Properties to Biological Outcomes in Exposure Escalation Experiments

Abstract

A fundamental goal in nano-toxicology is that of identifying particle physical and chemical properties, which are likely to explain biological hazard. The first line of screening for potentially adverse outcomes often consists of exposure escalation experiments, involving the exposure of micro-organisms or cell lines to a library of nanomaterials. We discuss a modeling strategy, that relates the outcome of an exposure escalation experiment to nanoparticle properties. Our approach makes use of a hierarchical decision process, where we jointly identify particles that initiate adverse biological outcomes and explain the probability of this event in terms of the particle physicochemical descriptors. The proposed inferential framework results in summaries that are easily interpretable as simple probability statements. We present the application of the proposed method to a data set on 24 metal oxides nanoparticles, characterized in relation to their electrical, crystal and dissolution properties.

1. INTRODUCTION

Nanomaterials are a large class of substances engineered at the molecular level to achieve unique mechanical, optical, electrical and magnetic properties. Unusual properties of these particles can be attributed to their small size (with one dimension less than 100nm), chemical composition, surface structure, solubility, shape and aggregation behavior. One often refers to these particle characteristics as physicochemical properties. These very properties allow for increasingly diverse biological interactions, therefore defining potential hazard concerns. Furthermore, the potential bio-hazard or these compounds is coupled with increased likelihood of environmental and occupational release as nano-tech applications are ever growing in science, medicine and industry (Nel et al. 2006; Stern and McNeil 2008).

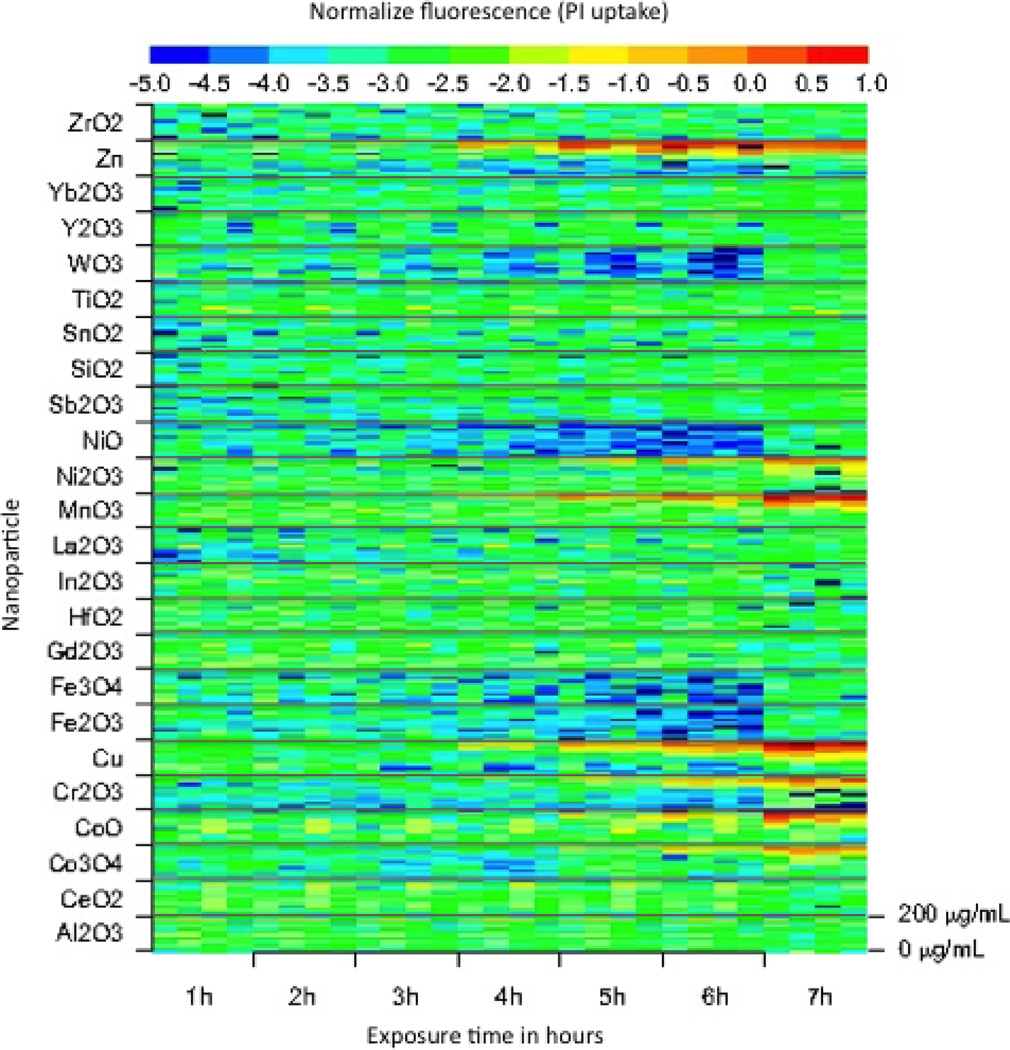
A first line of screening for potentially hazardous particles is often represented by invitro studies, where micro-organisms or cell cultures are exposed to nanomaterials in a controlled experimental setting. A typical in-vitro study would measure a biological outcome (LDH, MTS, etc.) in relation to a dose escalation protocol, though, more generally, in-vitro studies aim to measure how a biological response y(w) changes in relation to a prescription of increased particle exposure w, varying according to an exposure escalation protocol 𝒲, (Meng et al. 2010; George et al. 2011; Zhang et al. 2011). In Fig. 1, for example, we illustrate a more general design, where 24 metal-oxide nanoparticles are monitored in relation to a cellular membrane damage assay (Propidium Iodide (PI) absorption), measured contemporaneously over a grid of eleven doses and seven hours of exposure.

Figure 1. PI uptake of BEAS-2B.

Normalized PI uptake associated with exposing BEAS-2B cells to increased doses of nanomaterials (from 0µg/ml to 200µg/ml). This image summarizes data for an exposure escalation experiment involving a library of 24 nano metal oxides. The exposure escalation protocol includes 11 dose levels and 7 hours of exposure. Each dose by duration combination is replicated 4 times.

A first statistical challenge is encountered in relation to modeling the outcome y(w). Standard dose-response models focus almost exclusively on dose-escalation protocols and often rely on parametric assumptions, defining dose-response relationships as sigmoidal curves (Ritz 2010, Piegorsch et al. (2013)). This practice is likely not warranted, when considering more general exposure escalation designs. Sigmoidal dose-response curves may be inadequate, for example, if one considers non-lethal assays (intracellular calcium flux, mitochondrial depolarization, etc.) as they carry assumptions of monotonicity. Furthermore, particle solutions at varying concentrations may result in different particle aggregation behavior, potentially reducing total cellular exposure at higher concentrations (Hinderliter et al. 2010). These considerations challenge standard dose-response summaries, e.g. effective concentrations (ECα), slope coefficients, no adverse effect dose levels, benchmark dose levels, etc., and motivate our work. In §2 we replace parametric assumptions about dose-response relationships with a general smooth surface response model over 𝒲 and propose a statistical notion of toxicity, based on mixture modeling (McLachlan and Peel 2000).

Beyond the identification of potentially hazardous particles in the observed sample, from a predictive and inferential perspective it is important to understand how particles physical and chemical properties affect the way they interact at the nano-bio interface. The use of a combination of molecular properties to predict a compound’s behavior with respect to biological end-points is a well accepted concept in the predictive toxicology of chemicals (Schultz et al. 2003). In nano-informatics, the literature refers to this class of models as nano quantitative structure-activity relationships (nano-QSAR) models (Shaw et al. 2008; Puzyn et al. 2011; Liu et al. (2011)). Shaw et al. (2008) present a nano-QSAR model based on hierarchical and consensus clustering. Nanoparticles are classified into groups and clustering patterns are informally compared in relation to particles properties, that tend to be assigned to the same class. Puzyn et al. (2011) characterize particle toxicity in terms of the dose concentration that brought about 50% reduction in bacterial cell viability (EC50). Given this summary, the relationship between EC50 values and particle descriptors is modeled via linear regression, with selection of covariates based on minimizing a cross validation error. Similarly, Liu et al. (2011) use logistic regression to model the probability that a particle is toxic, given covariates. A particle is defined as toxic at a given concentration, based on a statistically significant difference in mean response, as compared to the background response in unexposed cells.

These techniques often rely on previously defined data summaries (effective concentrations, dose-response slopes, benchmark doses, etc.) and fail to account for the uncertainty inherent in the estimation of these summaries, when relating them to covariate information (particles physicochemical properties). We propose a modeling strategy that provides a definition of toxicity in relation to very general exposure escalation protocols and, at the same time, represents the probability of toxicity as a function of particle physical and chemical properties, without the loss of information associated with step-wise procedures. The proposed methodology is appropriate for limited data sets and easily includes data integration and a framework for advanced dimension reduction through variable selection.

The remainder of this manuscript is organized as follows. In §2 we introduce the proposed model. In §3 we discuss parameter estimation and associated inferential details. We illustrate the application of the proposed methodology in §4 through the analysis of 24 metal-oxide nanomaterials. We discuss our proposal, potential limitations and extensions in §5.

2. MODEL FORMULATION

2.1. A Statistical Definition of Toxicity

Standard protocols for in-vitro assays aim to measure the biological response y_ij(w) associated with exposure to particle i, (i = 1, …, n). The experiment is replicated m times, with replicates indexed by j, (j = 1, …,m) and the response y is evaluated with respect to a protocol of increased exposure to nanoparticles indexed by w ∈ 𝒲 ⊂ ℝ^ν+. Increased exposure is most often implemented as a dose escalation experiment, in which case ν = 1 and 𝒲 = [0,D], where D is the largest dose. However, experimental protocols considering both dose escalation and repeated measurements, obtained over a total exposure duration interval (t ∈ (0, T]), are becoming more prevalent (George et al. 2011; Patel et al. 2011). In this last case ν = 2 and 𝒲 = [0,D] × [0, T]. We assume that raw data have been normalized and purified from experimental artifacts.

In this general setting, it is indeed difficult to identify an obvious notion of toxicity. In fact, some biological assays may not address toxicity all-together and simply measure sublethal biological reactions. To be precise, in the absence of reasonable expectations for a standard sigmoidal dose-response curve, common measures of toxicity, including effective concentrations or hill coefficients are clearly ill-defined. Some progress can be made when considering a test library of n nanomaterials, by defining toxicity using empirical evidence about the existence of subgroups of particles. Our approach is based on defining two possible exposure-response categories, as follows:

$${\gamma }_i=0\text{if particle}i\text{is non-toxic}{\gamma }_i=1\text{if particle}i\text{is toxic}.$$

The foregoing model supports both the statistical definition of toxicity, via a mixture approach, and the formulation of probability statements describing the relationships between toxicity and nanoparticle properties. Let y_i be a vector of measurements collecting all evidence associated with particle i.^† For each particle i, we define a sampling model

$${\mathit{y}}_i|{\gamma }_i~f_{i{\gamma }_i}(·),{\gamma }_i\in \{0,1\},i=1,\dots ,n.$$

Densities f_i0(·) describe sampling variability over the entire exposure escalation domain 𝒲, which is not distinguishable from the the case of no exposure. This invariance of f_i0(·) with respect to 𝒲 allows for the interpretation of f_i0(·) as a model for normal biological variation associated with exposure to non-toxic particles. Densities f_i1(·) describe sampling variability as a function of the exposure escalation protocol 𝒲, therefore allowing for the interpretation of f_i1(·) as model of biological variation associated with exposure to toxic or bio-active particles. If we identify with π_i = P(γ_i = 1) the pre-experimental probability of particle i being toxic, then for each particle we can readily convert exposure escalation measurements y_i into a probability of toxicity $p_i^{+}$. Specifically, we have

$$p_i^{+}=P({\gamma }_i=1|{\mathit{y}}_i,f_{i0,}{f}_{i1},{\pi }_i)=\frac{{\pi }_i{f}_{i1}({\mathit{y}}_i)}{(1-{\pi }_i)f_{i0}({\mathit{y}}_i)+{\pi }_i{f}_{i1}({\mathit{y}}_i)}.$$ (1)

These quantities offer an interpretable and unequivocal scale of evidence in the classification of potentially hazardous nanomaterials. From a modeling perspective, the limitations of standard dose-response analysis and the importance of mixture modeling ideas have a been recognized by several authors (Boos and Brownie 1991, Piegorsch et al. 2013), even though, to our knowledge, we are the first to apply this strategy in the joint analysis of multiple biological stressors, specifically nanomaterials.

2.2. Distributional Assumptions and Semi-parametric Representation

Let y_ij(w) denote a response corresponding to nanoparticle i (i = 1, …, n) and replicate j (j = 1, …,m), at exposure w ∈ 𝒲. In practice, observations are obtained over a discrete exposure sampling grid (w₁, …,w_k) ∈ 𝒲 ⊂ ℝ^ν+. However, for ease of presentation and without loss of generality, we assume that exposure points are defined in a continuous domain. We make precise our definition of toxicity by introducing the following smooth response model

$$y_{ij}(w)={\alpha }_i+{\pi }_i{m}_i(w)+{\epsilon }_{ij}(w),$$ (2)

where α_i represents the background signal at exposure zero, m_i(w) is an exposure-response curve or surface, ${\epsilon }_{ij}(w)~N(0,{\sigma }_{\epsilon }^2/{\tau }_i)$ and τ_i | ν Gamma(ν/2, ν/2).

More precisely, assuming m_i(w) ≠ 0 for at least one w ∈ 𝒲, the forgoing representation describes a particle i to be bio-active with probability π_i. The coefficient α_i is interpreted as the background signal and m_i(w): 𝒲 → ℝ is interpreted as the above-background response hyper-surface, defining signal variation over the exposure-escalation domain 𝒲. More stringent constraints can be required if there is no possibility of cellular proliferation. In which case: m_i(w) ≥ 0 for all w ∈ 𝒲 and m_i(w) > 0 for at least some w ∈ 𝒲 defines a model of strict toxicity. For the moment we think of m_i(w) as a general smooth function defined over a p-dimensional space and describe practical representation issues later in the manuscript.

The sampling distribution of y_ij(w) is modeled in terms of the error term ε_ij(w) as a scale mixture of normal random variables. The error variance is defined in terms of the measurement error ${\sigma }_{\epsilon }^2$, and a particle-specific random variance inflation parameter τ_i, resulting marginally in a t-distributed error structure, with ν degrees of freedom (West 1984).

It is convenient to introduce a data-augmented representation of the model in (2). More precisely, we define a n-dimensional vector of latent binary indicators γ = (γ₁, …, γ_n)′ ∈ {0, 1}ⁿ, with γ_i | π_i ~ Bern(π_i). Conditioning on γ_i we have

$$E[y_{ij}(w)|{\gamma }_i]=\{\begin{array}{cc}{\alpha }_i\hfill & \text{if}{\gamma }_i=0\hfill \\ {\alpha }_i+m_i(w)\hfill & \text{if}{\gamma }_i=1.\hfill \end{array}$$ (3)

This representation makes explicit the trans-dimensional nature of the proposed model and will be used as a key component in the construction of a covariate model. We note that likelihood identifiability is contingent on the condition m_i(w) ≠ 0 for at least one w ∈ 𝒲, which includes possible positivity restrictions on w_i(w) as a special case.

2.3. Modeling Dependence on Covariates

Nanoparticles are often described in terms of their physical and chemical properties. We propose to use these descriptors to inform particles probabilities of toxicity. Let X denote an n × p covariate matrix, x_i be the i-th row of X and g(·): [0, 1] → ℝ denote a general link function. We relate toxicity indicators γ_i to x_i as follows

$$g(P({\gamma }_i=1|\mathit{\lambda };{\mathit{x}}_i))={\mathit{x}}_i^{\prime }\mathit{\lambda },$$ (4)

where λ = (λ₁, …, λ_p)′ is a vector of regression coefficients. Common implementations define g(·) as a probit or logit link, often according to computational or analytical convenience. The specific interpretation of λ will depend on g(·). However, the vector λ can be generally interpreted as a summary of how variability in the particle properties explain variability in the probability of toxicity. This formulation is inherently related to the class of hierarchical mixture of experts introduced by Jordan and Jacobs (1994), as the probability of particle bio-active potential is now informed by the particle’s physicochemical characteristics x_i.

For regularization purposes, especially in instances where p is large in relation to n, it may be appropriate to consider covariate subset selection (George and McCulloch 1993). A possible representation of the problem relies again on data-augmentation, by defining a p-dimensional vector of variable inclusion indicators ρ = (ρ₁, …, ρ_p)′ ∈ {0, 1}^p and a reduced design matrix X_ρ, which only includes the columns of X corresponding to the non-zero elements of ρ. Conditioning on ρ, we assume $g(P({\gamma }_i=1|\mathit{\lambda },\mathit{\rho };{\mathit{x}}_{i\rho }))={\mathit{x}}_{i\rho }^{\prime }{\mathit{\lambda }}_{\rho }$. In the foregoing model, λ_ρ is interpreted as a |ρ|-dimensional vector that includes all nonzero elements of λ. Alternative regularization strategies are easily implemented and may rely, for example, on penalized likelihood formulations (Tibshirani 1996).

2.4. Implementation for a Dose-Duration Escalation Protocol

Our discussion in §2.2 assumed a known exposure response hyper-surface m_i(w): 𝒲 → ℝ^ν. Here we discuss practical representation details in relation to a dose-duration escalation protocol. We illustrate this specific case as experimental protocols designed to monitor a biological outcome over several doses and durations of exposure to nanomaterials are becoming increasingly prevalent (George et al. 2011; Patel et al. 2011). Furthermore, standard dose escalation protocols are easily obtained as a special case of this more general design.

Specifically, we consider the case of 𝒲 = [0,D] × (0, T], so that the dose-response surface m_i(w) = m_i(d, t): [0,D] × [0, T] → ℝ spans two dimensions: dose d ∈ [0,D] and time t ∈ [0, T]. Requiring that m_i(d = 0, t = 0) = 0, allows for the interpretation of α_i as background fluorescence. Furthermore, requiring m_i(d, t) ≠ 0 for at least one dose/time combination insures likelihood identifiability.

It is often appropriate to think of m_i(·) as a smooth function, therefore non-parametric representations may rely on two-dimensional P-splines (Lang and Brezger 2006). The literature about the application of splines to the analysis of dose-response data has often focused on the estimation of curves under shape restrictions (Ramsay 1988; Desquilbet and Mariotti 2010; Wang and Shel 2010). The topic is too vast to review here. However, we point out that strict topological constraints may not be warranted in nanotox experiments and therefore recommend simpler penalization strategies.

We consider the representation of m_i(d, t) using s_d and s_t equally spaced interior knots

$$0<{\eta }_{1_d}<{\eta }_{2_d},\dots <{\eta }_{s_d-1}<{\eta }_{s_d}<D;\text{and}0<{\eta }_{1_t}<{\eta }_{2_t},\dots <{\eta }_{s_t-1}<{\eta }_{s_t}<T.$$

Each set of interior knots generates a corresponding set of M_d = s_d + ℓ, and M_t = s_t + ℓ, B-spline basis functions of order ℓ. Let ℬ_m(·) denote the m^th basis and β_i = (β_i1, ‥, β_i,mdmt, …β_i,MdMt)′ be a (M_dM_t)-dimensional vector of spline coefficients. The function m_i(d, t; β_i) can then be represented as the tensor product of one-dimensional B-splines:

$$m_i(d,t;{\mathit{\beta }}_i)=\sum _{m_d=1}^{M_d}\sum _{m_t=1}^{M_t}{\beta }_{i,m_d{m}_t}{ℬ}_{m_t}(t){ℬ}_{m_d}(d);i=1,\dots ,n.$$ (5)

Using the foregoing representation, the identifiability restriction m_i(d = 0, t = 0; β_i) = 0, is implemented by fixing β_i1 = 0, for all particles. Similarly, if positivity of m_i(·) is required, it is easily implemented by restricting β_i ∈ ℝ^M_dM_t+ for all i = 1, …, n. In our implementation, we will simply require that not all β_iℓ equal 0, (i = 1, …, n; ℓ = 1, …, M_dM_t).

Model complexity and flexibility in m_i(d, t) is a function of the spline order ℓ and the number of interior knots s_d in the dose and s_t in the time domain. Typical implementations rely on cubic splines ℓ = 4 and a large number of interior knots. Automatic smoothing is then obtained via regularization procedures that include penalized likelihood (Eilers and Marx 1996) or smoothing priors (Besag and Kooperberg 1995, Lang and Brezger 2004).

3. ESTIMATION AND INFERENCE

3.1. Bayesian Hierarchical Representation

Estimation of the model parameters and inference can be carried out using several inferential strategies. In particular, penalized likelihood estimation could be implemented in order to account for regularization of the exposure response surface and regression coefficients in the covariate model.

A more natural representation of the proposed probability scheme is based on hierarchical models (Carlin and Louis 2000). This choice is guided by the fact that the proposed model is defined in terms of large vectors of related parameters and Bayesian hierarchical models lead to shrinkage estimates with good statistical properties (Berger 1985).

In this article we consider the following representation.

• Stage 1: Sampling Model. We rewrite the model first introduced in (2), conditioning on all coefficients defining its semi-parametric structure. We have,

  $$y_{ij}(w)|{\gamma }_i,{\alpha }_i,{\mathit{\beta }}_i,{\sigma }_{\epsilon }^2,{\tau }_i~N({\alpha }_i+I({\gamma }_i=1)m_i(w,{\mathit{\beta }}_i),{\sigma }_{\epsilon }^2/{\tau }_i);$$ (6)

  for particles i = 1, …, n; j = 1, …, m, w ∈ 𝒲.

• Stage 2: Particle Level Model. At the level of particle i, we specify a model for the toxicity indicators γ_i and the response surface coefficients β_i.

The probability of toxicity is assumed to depend on a subset of covariate X_ρ, indexed by inclusion indicators ρ. We follow Albert and Chib (1993) and introduce a n-dimensional vector of latent variables z = (z₁, …, z_n)′, so that we can write

$${\gamma }_i|z_i=I(z_i>0),\text{and}{z}_i|\mathit{\lambda },\mathit{\rho };{\mathit{x}}_{i\rho }~N({\mathit{x}}_{i\rho }^{\prime }{\mathit{\lambda }}_{\rho },1).$$ (7)

The foregoing implementation defines a probit link for γ and represents covariate selection as introduced in §2.3.

Distributional assumptions for β_i are based on considerations of smoothness and conjugacy (Besag and Kooperberg 1995, Lang and Brezger 2004). Specifically, we use a prior based on the Kronecker product of penalty matrices defined in of the dose and time domain, so that

$${\mathit{\beta }}_i~N_{M_d{M}_t}(0,{\mathbf{\Sigma }}_{\mathit{\beta }}={\sigma }_{\beta }^2{(K_d\otimes K_t)}^{-1}).$$ (8)

The penalty matrices K_d : M_d × M_d and K_t : M_t × M_t, are constructed as follows:

$$K_d=\left[\begin{array}{ccccccc}\hfill 1+\delta \hfill & \hfill -2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill -2\hfill & \hfill 5\hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill 1\hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill -4\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill -4\hfill & \hfill 6\hfill & \hfill -4\hfill & \hfill 1\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill 1\hfill & \hfill -4\hfill & \hfill 5\hfill & \hfill -2\hfill \\ \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -2\hfill & \hfill 1+\delta \hfill \end{array}\right];\delta >0.$$ (9)

The matrix K_t is similarly constructed. A small positive constant δ is introduced to insure propriety of the prior, without fundamentally changing the spatial smoothing properties of the proposed distribution. Detailed derivations and alternatives are discussed in Clayton (1996), as well as Lang and Brezger (2004).

For completeness the prior on the background level is chosen to be conjugate and non informative, so that ${\alpha }_i|{\sigma }_{\epsilon }^2,{\tau }_i~N(0,c{\sigma }_{\epsilon }^2/{\tau }_i)$, where c is set to a large value.

• Stage 3: Priors. Our choice of priors is guided by conditional conjugacy as well as principles of multiplicity correction. In particular we consider a Zellner g-prior (Zellner 1986) for the covariate model coefficients ${\mathit{\lambda }}_{\rho }|\mathit{\rho }~N(0,g_{\rho }{({\mathit{X}}_{\rho }^{\prime }{\mathit{X}}_{\rho })}^{-1})$ and an exchangeable Bernoulli prior for the inclusion indicators ρ, so that p(ρ|ψ) = ψ^|ρ|(1 − ψ)^p−|ρ|. As described by Lee et al. (2003), choosing small values for ψ, leads to parsimonious models by restricting the number of covariates included. The values of ψ can also be tuned to include prior knowledge about the importance of certain physicochemical properties. Most commonly, a prior is placed on ψ, such that ψ ~ Beta(a_π, b_π), and multiplicity correction is achieved automatically, as described by Scott and Berger (2006). A data dependent g_ρ is often recommended and we follow Fernandez et al. (2001) in setting g_ρ = max(n, |ρ|²).

Finally, we complete the model by specifying conditionally conjugate prior distributions on variance components:^‡

$$1/{\sigma }_{\epsilon }^2~\mathit{\text{Gamma}}(a_{\epsilon },b_{\epsilon });1/{\sigma }_{{\alpha }_i}^2~\mathit{\text{Gamma}}(a_{{\alpha }_i},b_{{\alpha }_i});1/{\sigma }_{\beta }^2~\mathit{\text{Gamma}}(a_{{\beta }_i},b_{{\beta }_i}).$$

3.2. Posterior Simulation via MCMC

We base our inference on Markov Chain Monte Carlo (MCMC) simulations. Closed-form full conditional distributions are available for all parameters, therefore the proposed posterior simulation algorithm utilizes a Gibbs sampler to directly update parameters component-wise (Geman and Geman 1984, Gelfand and Smith 1990).

Specific steps in the simulation are inherently trans-dimensional and some care is needed in the identification of Gibbs components to be updated jointly. In particular, we implement a chain with transition kernels moving toxicity indicators γ and covariate inclusion indicators ρ, always with respect to their marginal posterior distributions, integrating over β and λ respectively. Given γ and ρ, the model structure and dimension is fully determined and other model parameters can be updated in a standard fashion. The proposed sampling scheme can be summarized as follows.

1. Trans-dimensional updates

We begin by drawing γ from its marginalized conditional distribution, obtained by integrating the conditional posterior over β. More precisely, for each particle i (i = 1,…, n)

$$p({\gamma }_i|{\mathit{y}}_i,\mathit{\alpha },\mathit{\lambda },{\sigma }_{\epsilon }^2,\mathit{\tau },\mathit{\rho })\propto \int p({\mathit{y}}_i|{\mathit{\beta }}_i,\mathit{\alpha },{\mathit{\sigma }}_{\epsilon }^2,\mathit{\tau })p({\mathit{\beta }}_i|{\gamma }_i,{\mathbf{\Sigma }}_{\mathit{\beta }})\mathrm{d}{\mathit{\beta }}_{i}p({\gamma }_i|\mathit{\lambda },\mathit{\rho });$$

where defining ${\mathbf{\Omega }}_{{\beta }_i}=\frac{{\tau }_i}{{\sigma }_{\epsilon }^2}{\mathit{H}}_{\mathit{i}}^{\prime }{\mathit{H}}_{\mathit{i}}+{\mathbf{\Sigma }}_{\mathit{\beta }}^{-\mathbf{1}}$, gives us

$$P({\gamma }_i=1|{\mathit{y}}_i,\mathit{\alpha },\mathit{\lambda },{\sigma }_{\epsilon }^2,\mathit{\tau },\mathit{\rho })={[\frac{\mathrm{\Phi }(-{\mathit{x}}_{i\rho }^{\prime }{\mathit{\lambda }}_{\rho })}{\mathrm{\Phi }({\mathit{x}}_{i\rho }^{\prime }{\mathit{\lambda }}_{\rho })|{\mathbf{\Sigma }}_{\mathit{\beta }}{|}^{-\frac{1}{2}}|{\mathbf{\Omega }}_{{\beta }_i}{|}^{-\frac{1}{2}}\text{exp}\left\{\frac{{\tau }_i^2}{2{\sigma }_{\epsilon }^4}{\mathit{ỹ}}_i^{\prime }{\mathit{H}}_i{\mathbf{\Omega }}_{{\beta }_i}^{-1}{\mathit{H}}_i^{\prime }{\mathit{ỹ}}_i\right\}}+1]}^{-1}.$$

In the foregoing formula, Φ(·) is the cdf of a standard normal distribution. The derivation of this result, and precise construction of the vectors ỹ_i and matrices H_i are provided in Appendix A. If β is subjected to positivity restrictions, the foregoing integral must be evaluated over a positive hyper-quadrant, therefore requiring approximate Monte Carlo evaluation. Alternatively a reversible jumps transition scheme may be deviced to move jointly over the space of (γ_i, β_i) (Green 1995).

A similar scheme was adapted for sampling from ρ | λ, z, γ. The marginalized conditional distribution of ρ, obtained by integrating over λ is given by

$$p(\mathit{\rho }|\mathit{z},\psi )\propto \int p(\mathit{z}|\mathit{\rho },\mathit{\lambda })p(\mathit{\lambda }|\mathit{\rho })d\mathit{\lambda }p(\mathit{\rho }|\psi )\propto \frac{1}{\sqrt{(1+g_{\rho })}}\mathit{\text{exp}}[\frac{g_{\rho }}{2(1+g_{\rho })}\mathit{z}\prime {\mathit{X}}_{\rho }{({\mathit{X}}_{\rho }^{\prime }{\mathit{X}}_{\rho })}^{-1}{\mathit{X}}_{\rho }^{\prime }\mathit{z}]{\psi }^{|\mathit{\rho }|}{(1-\psi )}^{1-|\mathit{\rho }|}.$$

2. Fixed dimensional updates

Given the current state of the latent indicators γ, response surfaces are uniquely defined as in (3). Posterior sampling here is standard, and proceeds by updating spline coefficients β_i, background response parameters α_i, and variance parameters τ_i and ${\sigma }_{\epsilon }^2$ and ${\sigma }_{\beta }^2$, from their full conditional distributions via direct simulation. Similarly, given latent indicators ρ, the covariate model is uniquely defined as in (7). Again, posterior sampling is standard and proceeds by updating regression coefficients λ_ρ from p(λ_ρ | ρ, z), and, z from p(z | y, λ, ρ), via Gibbs sampling. Full conditional distributions are given in Appendix A.

4. STRUCTURE ACTIVITY RELATIONSHIPS OF NANO METAL OXIDES

4.1. Case Study Background

We illustrate the proposed methodology by analyzing data on human bronchial epithelial cells (BEAS-2B), exposed to a library of 24 nano metal-oxides including: ZnO, CuO, CoO, Fe₂O₃, Fe₃O₄, WO₃, Cr₂O₃, Mn₂O₃, Ni₂O₃, SnO₂, CeO₂, Al₂O₃, among others. We consider a measure of cellular membrane damage as measured by Propidium Iodine (PI) uptake. Specifically, cell cultures are treated with Propidium Iodide (PI) and in cells with damaged membranes PI is able to permeate the cell and bind to DNA, where it causes the nucleus to emit a red florescence. Each sample was also stained with a Hoechst dye, which causes all cell nuclei to emit a blue florescence, and allows for a count of the total number of cells. An analysis of the fluorescence readout, measured at varying wavelengths, results in a measure of the percentage of cells positive for each response. The outcome is measured over a grid of eleven doses and seven times (7-hours) of exposure over four replicates. The final response was purified from experimental artifacts and normalized using a logit transformation (Fig. 1).

All particles were characterized in terms of their size, dissolution, crystal structure, conduction energies, as well as many other particle descriptors (Zhang et al. 2012). Burello and Worth (2011) hypothesized that comparing the conduction and valance band energies to the redox potential of the reactions occurring within a biological system could predict nanoparticle toxicity of oxides. The normal cellular redox potential is in the range (−4.12 to −4.84 Ec). The conduction band energy of a particle is a measure of the energy sufficient to free an electron from an atom, and allow it to move freely within the material. Therefore, we are interested in the relationship between particles with conduction band energies within and outside the range of the cellular redox potential and their cytotoxicity profiles.

Another measure of interest is the metal dissolution rate of a particle. Particles that are highly soluble have the ability to shed metal ions, which can lead to nanoparticle toxicity (Xia et al. 2008; Xia et al. 2011; Zhang et al. 2012). Other potential risk factors include the particle primary size, a measure of length that defines the crystal structure (b(Å)), lattice energy (ΔH_lattice), which measures the strength of the bonds in the particles, and the enthalpy of formation of gaseous cation Meⁿ⁺ (ΔH_Meⁿ⁺), which is a combined measure of the energy required to convert a solid to a gas and the energy required to remove n electrons from that gas.

4.2. Case Study Analysis and Results

The model described in §2 was fit to the metal-oxide data-set described in the previous section. We placed relatively diffuse Gamma(.01, .01) priors on the 1/σ_ε parameter, Gamma(1, .1) priors on all remaining precision parameters, and c = 100 as the prior variance inflation constant of α_i. We also placed a prior distribution on the degrees of freedom parameter ν, for the t-distributed error described in Section 2.2. Specifically, the prior was modeled using a discrete uniform distribution on 1,2,4,8,16, and 32 degrees of freedom (Besag and Higdon 1999). Finally, for the covariate model we consider a default U(0, 1) prior for ψ.

In structuring the covariate matrix X, we model log(dissolution) in a non-linear fashion as a spline function with a change point at log(dissolution) of 2.3. This choice is motivated by the fact that the nanoparticle library is really comprised of two separate classes, a set of particles with low dissolution and two particles (ZnO and CuO) with high dissolution, therefore it is wise to allow for a discontinuity at the boundary. Conduction band energy was coded as a binary covariate (I{Ec ∈ (−4.12, −4.84}), and all other ENM characteristics described above as continuous linear predictors.

Our inferences are based on 20,000 MCMC samples from the posterior distribution, after discarding a conservative 60,000 iterations for burn-in. MCMC sampling was performed in R version 2.10.0, and convergence diagnostics were performed using the package CODA (Convergence Diagnostics and Output Analysis), (Plummerm et al. 2006).

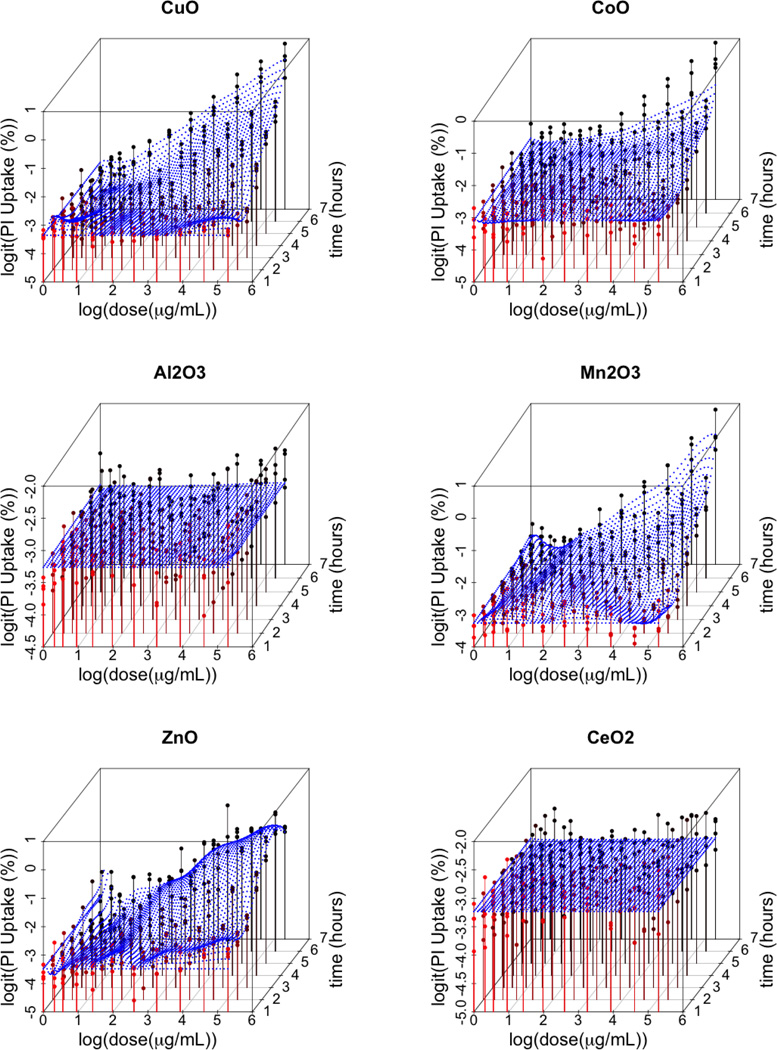
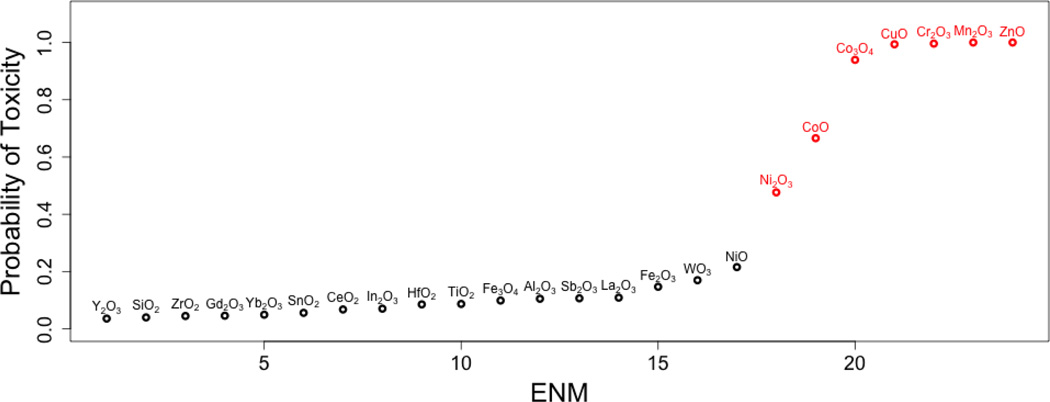
Figure 2 illustrates data and the posterior expected dose-time response for a sample of particles examined in this study. Figure 3 provides a plot of the estimated probability of toxicity for each of the 24 nanomaterials. We find that CuO, Mn₂O₃, ZnO, Cr₂O₃, CoO, CO₃O₄, and Ni₂O₃ nanomaterials have a pronounced dose/time effect, as compared to the other 17 materials. These seven particles all have posterior mean probabilities of toxicity above 0.5 (Fig. 3), suggesting that they are highly likely to induce cytotoxicity. It is important to stress the fact that our chosen cut-off value of 0.5 is, in a sense, arbitrary and that reporting results as we did in Figure 3 is essential to illustrate the full spectrum of bio-active potential in the particle sample.

Figure 2. Fitted response surfaces for CuO, CoO, Al₂O₃, Mn₂O₃, ZnO, CeO₂ ENMs.

Estimated smooth response surfaces of cellular membrane damage, as measured by Propidium Iodine (PI) uptake, as a function of log(dose) and time. The color red represents response values corresponding to lower time points and the color black represents response values corresponding to higher time points.

Figure 3. Posterior mean probability of toxicity for each ENM.

Particles with a probability of toxicity greater then .5 are indicated in red.

An estimate of the inclusion probability, ρ̂ was used to select a single covariate model. Specifically we follow Scott and Berger (2006) by selecting the median model, that is including all covariates for which ρ̂_k > 0.5, (k = 1, …, p). The median model included log(metal dissolution) and conduction band energy. Table 1 provides estimates of posterior inclusion probabilities and model averaging posterior summaries. Results for the median model are reported in Table 2, where we provide posterior summaries for the model including conduction band energy and log(metal dissolution rate) alone.

Table 1. Posterior summaries for regression coefficients corresponding to the model which includes predictors for seven different ENM physicochemical properties.

Posterior inclusion probabilities as well as posterior mean and associated 95% posterior intervals are provided for the model regression coefficients.

Parameter	Inclusion Probability	Posterior Summaries
Intercept	1.00	−0.50(−16.17,18.31)
Conduction Band Energy	0.77	1.62(0.00, 3.81)
log(Metal Dissolution Rate)<2.3	0.69	0.07(−0.19, 0.39)
log(Metal Dissolution Rate)>2.3	0.69	2.81(−0.19,12.90)
log(Primary Size)	0.31	0.00(−0.72, 0.71)
log(Crystal Structure (b(Å)))	0.35	−0.03(−2.11, 1.97)
log(Enthalpy of Formation (ΔHMen+))	0.38	−0.20(−2.38, 1.37)
log(Lattice Energy (ΔHlattice))	0.36	−0.18(−1.89, 2.10)

Table 2. Posterior summaries for regression coefficients corresponding to the final model.

The final model includes model includes predictors for to conduction band energy and log(metal dissolution rate). Posterior mean estimates and associated 95% posterior intervals are provided for the model regression coefficients.

Parameter	Posterior Summaries
Intercept	−1.22(−2.45, −0.20)
Conduction Band Energy	2.02(0.49, 3.75)
log(Metal Dissolution Rate)<2.3	0.11(−0.19, 0.41)
log(Metal Dissolution Rate)>2.3	3.52(−0.18, 8.49)

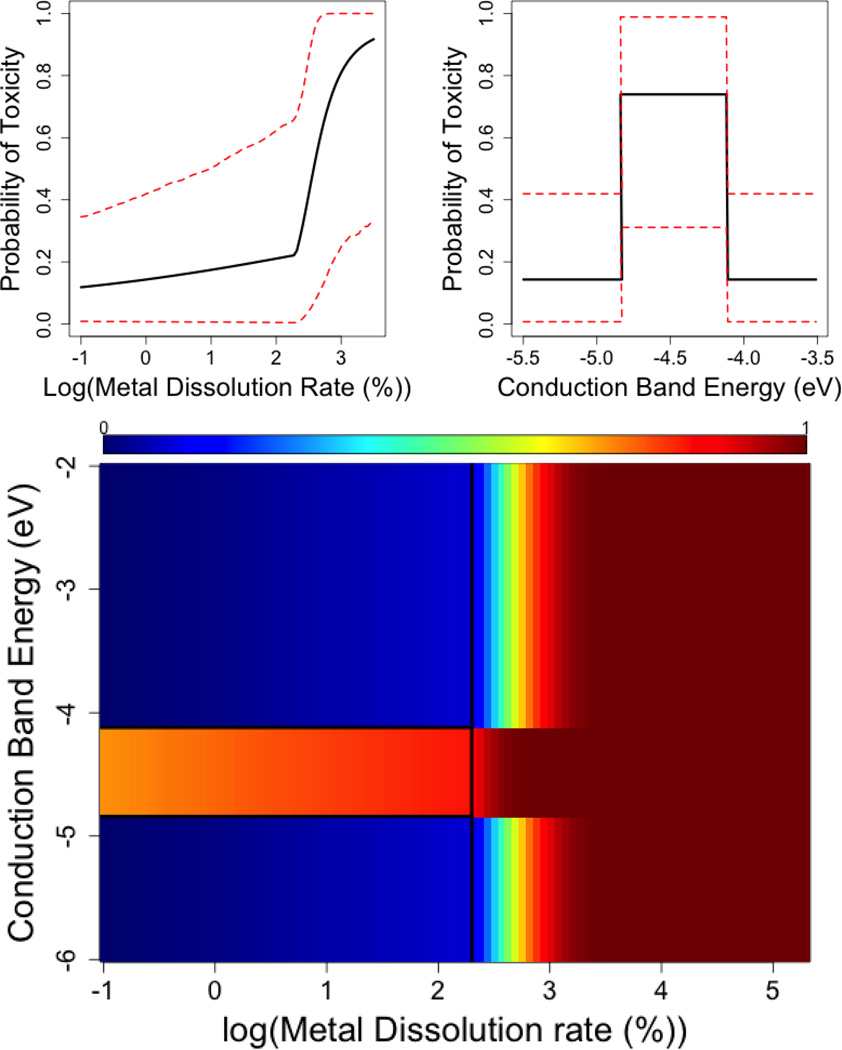
These regression coefficients are easily interpreted as simple probability statements related to changes in the probability of toxicity, as one varies a particle’s physical and chemical properties. Figure 4 illustrates summary plots of the posterior probability of toxicity (with 95% credible bands) as a function of conduction band energy and metal dissolution. The bottom panel of Figure 4 provides the posterior mean probability of toxicity, as a function of both conduction band energy and log(metal dissolution). We find that conduction band energies inside the redox potential of the cell, predict high probability of cytotoxicity. Similar inference is drawn for particles with a high metal dissolution rate. The mechanistic interpretation of our findings is based on the idea that oxidizing and reducing substances can create an imbalance in the normal intracellular state of the cell, either by the production of oxygen radicals or by reducing antioxidant levels. In particular, the potential for oxidative stress might be predicted by comparing the energy structure of oxides, as measured by their conduction and valance band energy levels, to the redox potential of the biomolecules maintaining the cellular homeostasis. When these two energy levels are comparable, it can possibly allow for the transfer of electrons, and subsequent imbalance in the normal intracellular state. Our model confirms the substantive findings in Burello and Worth (2011) and Zhang et al. (2012)).

Figure 4. Posterior summaries of the probability of toxicity as a function of conduction band energy and log metal dissolution rate.

(Top) Posterior mean (black) and 95% posterior intervals (red) for the probability of toxicity as a function of log(metal dissolution rate), given conduction band energy outside the range of the cell redox potential. (Middle) Posterior mean (black) and 95% posterior intervals (red) for the probability of toxicity as a function of conduction band energy, given no metal dissolution. (Bottom) Posterior mean probability as a function of conduction band energy and log(metal dissolution rate). Red colored regions indicate greater probability of toxicity, whereas blue colored regions indicate low probability of toxicity.

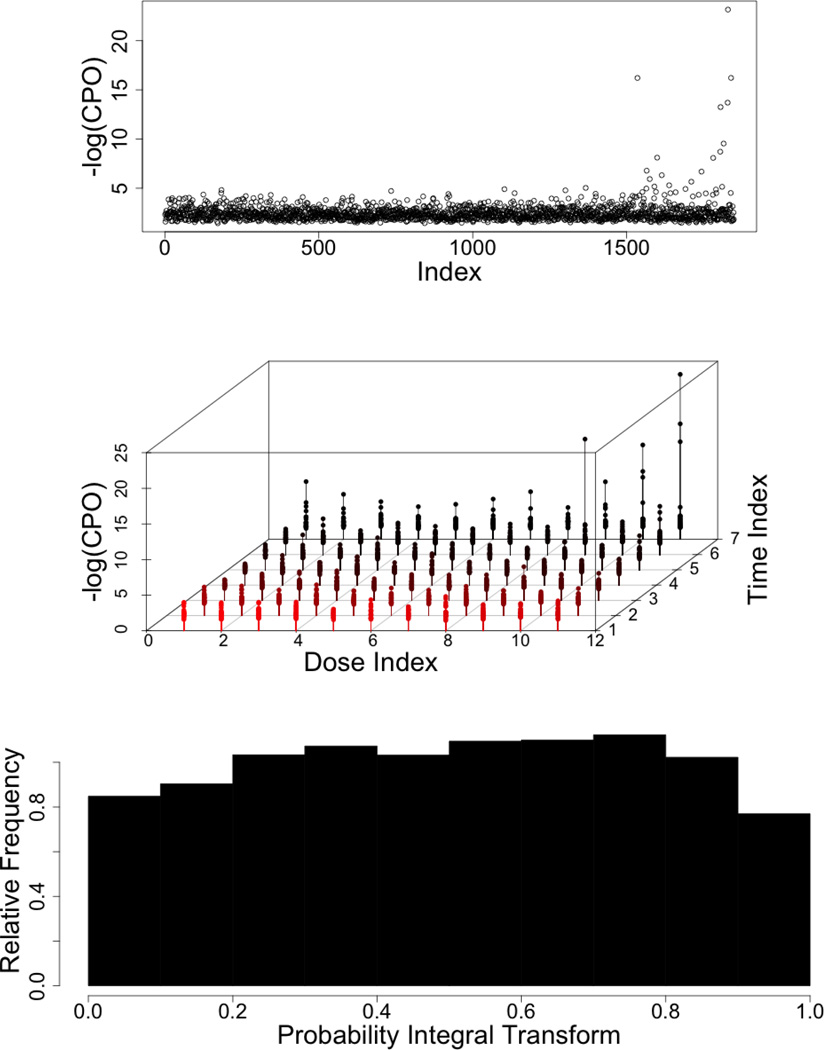
Finally, we assess goodness of fit using posterior predictive checks. The conditional predictive ordinate (CPO), as defined by Geisser (1980), is the predictive density of observation ℓ, given all other observations, and can be used as a diagnostic tool for detecting observations with poor model fit. Large values of −log(CPO) indicate observations that are not being fitted well. The top panel of Figure 5, provides a plot of −log(CP̂O_i(d, t)) for our final model. In general, low values of −log(CPO_i(d, t)) indicate good model fit. The middle panel indicates that the largest values of −log(CP̂O_i(d, t)) tend to be observations with large exposure times. This is expected, as cell death is sometimes followed by the dissolution of cell nuclei, hindering the measurement of cellular response. Next, we provide plots of the probability integral transform histogram for the entire model, as described by Gneiting et al. (2007). The plot is provided in the bottom panel of Figure 5, and visual assessment indicates that it is close to uniformity, suggesting relatively good posterior predictive calibration. In this case study, a subsequent analysis performed excluding potentially influential data-points revealed no changes in our inferences. We would however like to stress the importance of final model diagnostics any times one reaches for highly structured models for data analysis. Additional summaries and formal definition of these diagnostic tools are detailed in Appendix B.

Figure 5. Graphical model diagnostics.

(Top) Estimate of −log(cpo_i(d, t)) for detecting observations with poor model fit. (Middle) Plot of −log(cpo_i(d, t)) as a function of dose and time, indicating any relationship between outlying observations and the administered dose or duration of exposure. (Bottom) Probability Integral Transform assessing empirical calibration of the posterior predictive distribution.

5. DISCUSSION

In this manuscript we propose a modeling framework for general exposure escalation experiments, based on a newly defined measure of toxicity. Precisely, we consider the representation and estimation of the probability that each particle or compound would initiate adverse biological reactions. This measure is seamlessly integrated into very general exposure escalation protocols, including multi-dimensional models, that account for dose and duration kinetics jointly. Furthermore, the proposed summary is warranted with respect to non-lethal biological outcomes, as well as for experiments in nano-toxicology, where particle aggregation behavior may hinder reasonable expectations of sigmoidal dose response trajectories.

One dimension that is potentially lost in the model, if implemented in terms of a general exposure-response surface, is the possible interpretation of standard dose-response parameters for canonical risk assessment. However, if parametric assumptions are warranted by the experimental setting, our model is easily represented in terms of these standard parametric formulations. Furthermore, most quantities related to standard risk assessment parameters can still be easily obtained numerically, by post-processing posterior samples.

We show how the probability of toxicity can be used to link nanomaterials physicochemical properties to non-linear and multidimensional cytotoxicity profiles, while accounting for the uncertainty in the estimation of this summary. This is in stark contrast with the current practice of step-wise analyses. In our case study we chose to carry out the analysis through the use of standard diffuse prior setting on the latent regression model, which in turn translates into over dispersed Beta priors on the pre-experimental probabilities of toxicity. It is however important to stress how the proposed formulation allows for the explicit inclusion of pre-experimental evidence through prior calibration related to particle properties that are known to be potentially hazardous. This last exercise may be crucial in risk assessment settings, where large amounts of evidence already exist in relation to specific classes of nanomaterials. The proposed methodology is also appropriate for limited data sets, as it includes data integration and a framework for advanced dimension reduction through variable selection. We account for the non-robust nature of the data by allowing for particle specific variance inflation, resulting in a t-distributed model for the error structure. Finally, the hierarchical representation of the model allows for easy and robust estimation, as well as rich inference and informative model diagnostics.

Our proposal is easily extended to account for multiple cytotoxicity parameters, in the form of multivariate dependent observations. A reasonable dependence scheme can, for example, assume data to be dependent within outcome and particle, as well as between outcomes for the same particle. Further generalizations may relax the assumption of linearity relating particle properties to probabilities of toxicity. This exercise would however, find justification only if larger sets of nanomaterial libraries become available for biological testing.