Computational approaches to understanding protein aggregation in neurodegeneration

Abstract

The generation of toxic non-native protein conformers has emerged as a unifying thread among disorders such as Alzheimer's disease, Parkinson's disease, and amyotrophic lateral sclerosis. Atomic-level detail regarding dynamical changes that facilitate protein aggregation, as well as the structural features of large-scale ordered aggregates and soluble non-native oligomers, would contribute significantly to current understanding of these complex phenomena and offer potential strategies for inhibiting formation of cytotoxic species. However, experimental limitations often preclude the acquisition of high-resolution structural and mechanistic information for aggregating systems. Computational methods, particularly those combine both all-atom and coarse-grained simulations to cover a wide range of time and length scales, have thus emerged as crucial tools for investigating protein aggregation. Here we review the current state of computational methodology for the study of protein self-assembly, with a focus on the application of these methods toward understanding of protein aggregates in human neurodegenerative disorders.

Introduction

The transition of native proteins to partially unfolded and aggregated species has been implicated in numerous human neurodegenerative disorders. In healthy individuals, the formation of potentially toxic aggregates is counteracted by various quality control mechanisms, including endoplasmic reticulum-associated degradation and the activity of chaperones that process unfolded, misfolded, and aggregated proteins (Barral et al., 2004). In conditions of stress or in aged individuals, insufficient capacity of quality control mechanisms may allow aggregate formation to predominate and, eventually, to cross a pathogenic threshold. However, aggregation can also occur in the absence of excessive cellular stress, even in cases where the native state of a protein is highly thermodynamically favorable (Chi et al., 2003). Aggregation propensity also depends on subcellular localization of a protein and its accessibility to the various quality control mechanisms that maintain proteostasis (Monsellier et al., 2008). Therefore, differences in both native structures and cellular microenvironments of intrinsically disordered proteins and peptides, folded cytosolic proteins, and membrane proteins underlie their widely varying aggregation propensities (Linding et al., 2004; Monsellier et al., 2008).

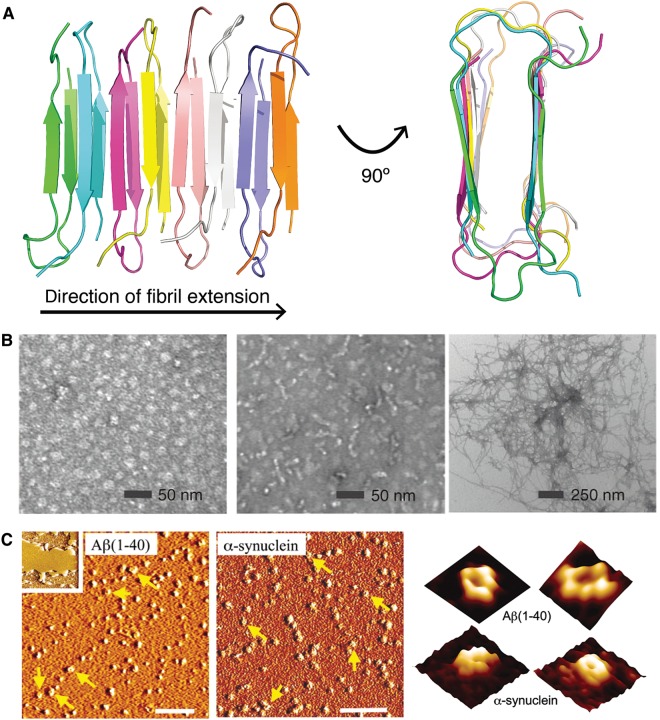
Protein aggregates are found in both fibrillar (ordered) and amorphous (disordered) forms. One of the most common structural features found in ordered protein aggregates is the amyloid fold (Toyama and Weissman, 2011). Amyloid fibrils contain a characteristic cross-β architecture, which consists of β-strands running parallel to each other, but perpendicular to the direction of fibril extension (Figure 1A) (Eanes and Glenner, 1968; Jahn et al., 2010; Qiang et al., 2012). Amyloid aggregates can exhibit various gross morphologies, such as twisted ribbons, twisted ropes, sheets, and tubes, based on differing arrangements of protofibrillar units (Stromer and Serpell, 2005). Although the common propensity of multiple aggregation-prone proteins to form amyloid is well established, there is an emerging view that neurotoxicity related to protein aggregation occurs mainly in lower-order disordered oligomers (soluble assemblies larger than the native oligomeric state that may be pre-fibrillar intermediates or species not on the fibrillization pathway; examples of oligomers, protofibrils, and fibrils of amyloid beta (Aβ) peptide are shown in Figure 1B) (Uversky, 2010; Denny et al., 2013). One of the mechanisms demonstrated to facilitate early stages of aggregation in association with membranes, which can result in membrane disruption and subsequent cell death (Aisenbrey et al., 2008). During the process of protein misfolding at the surface of a membrane, pre-fibrillar oligomers form non-specific ion channels (Figure 1C) (Quist et al., 2005); the resultant alteration of membrane permeability disrupts ion homeostasis, causing mitochondrial dysfunction and impaired synaptic transmission, among other neurotoxic consequences (Kagan, 2006). Conformational features of disordered and pre-fibrillar oligomers of various neurodegeneration-linked proteins are discussed in more detail in the latter half of the review.

Figure 1.

Diverse morphologies of protein aggregates. (A) The characteristic amyloid cross-β structure, as seen in a fibril model of the Iowa mutant (D23N) of Aβ₄₀ (PDB ID: 2lnq (Qiang et al., 2012)). Individual polypeptide chains are colored differently. (B) From left to right: transmission electron microscopy images of Aβ₄₂ oligomers, protofibrils, and fibrils. Reprinted by permission from Ahmed et al. (2010), copyright 2010 Macmillan Publishers Ltd. (C) Atomic force microscopy (AFM) images of Aβ₄₀ (left) and α-synuclein (middle) incubated with lipid bilayers. Inset shows a lipid bilayer in the absence of peptide/protein. Scale bar, 100 nm. At right, high-resolution AFM images (image size: 25 nm) showing individual pores formed by Aβ₄₀ and α-synuclein within lipid bilayers. Reprinted from Quist et al. (2005), copyright 2005 National Academy of Sciences, USA.

Computational methods for studying protein misfolding and aggregation

Computational models, especially when combined with experimental approaches, are increasingly useful for the characterization of changes in protein dynamics and identification of rare molecular events that lead to aggregation (Sharma et al., 2008). In this section, we discuss computational strategies that are commonly employed to study protein aggregation, starting with algorithms that predict aggregation propensity on the basis of amino acid sequence alone or in the context of protein tertiary structure. We then discuss methods for simulating protein aggregation and modeling aggregate structures using molecular dynamics (MD) simulations, including the incorporation of strategies to reduce the computational burden of simulations involving large polypeptides and long time scales.

Assessment of sequence determinants of protein aggregation

The question of how amino acid composition influences aggregation propensity is highly relevant to protein design, as well as to our understanding of protein evolution and the pathogenicity of certain amino acid substitutions. Given the fact that hydrophobic interactions are a major driving force of protein self-assembly, it is expected that increased hydrophobic content in a peptide would lead to increased aggregation propensity, while a net charge on the peptide would impede aggregation. Also, with the evidence for common cross-β architecture among amyloid fibrils of diverse proteins (Nelson et al., 2005), a stretch of amino acids with enhanced propensity to adopt β-strand secondary structure would be expected to promote formation of fibrils. Such physicochemical properties of amino acids are the basis of most of the algorithms that predict either the rate or propensity of aggregation of different regions of a protein.

Predictors based on overall protein composition

One of the first attempts to rationally predict the effect of protein sequence on its aggregation propensity was based on the prediction of the effect of a point mutation on the aggregation kinetics of a protein (Chiti et al., 2003). This method was based on fitting the coefficients of an empirical formula with a set of existing data for the aggregation kinetics of 50 point mutants of human muscle acylphosphatase (AcP), as compared with the wild-type protein (Chiti et al., 2003). The empirical formula was a linear equation incorporating the change in hydrophobicity, net charge, and helix-β-sheet conversion propensity upon mutation. This is a simplistic model since it treats protein properties as a simple sum, without accounting for position of the mutation in the structure. Additionally, two terms of the three-term equation, hydrophobicity and net charge, are highly dependent on each other. Even with these limitations, predictions of the changes in aggregation rate associated with 27 mutations in a variety of both disease-associated and model proteins obtained using this model had statistically significant correlation with experimental values. This study highlights the role of physicochemical properties of amino acids in determining, to a large extent, the differences in aggregation rate. The two limitations of this model, namely interdependent terms and fitting of free parameters, were overcome in a more sophisticated model from the Caflisch group (Tartaglia et al., 2004). Depending on the type of mutation (e.g. polar to apolar or apolar to polar), the terms of their equation included changes in aromaticity, dipole moment, ratio of accessible surface area, and β-sheet propensity. This equation is more complicated than the simple linear relationship of Chiti et al. but does not have redundant terms and, importantly, does not have free parameters that must be obtained from fitting the equation to a training set. The model of Chiti et al. was extended to predict absolute aggregation rate by incorporating extrinsic factors like ionic strength and pH at which aggregation occurs in vitro (DuBay et al., 2004). Similarly, the updated model from the Caflisch group can also predict absolute aggregation rates (Tartaglia et al., 2005). The models described thus far all consider the starting state of the protein to be denatured.

Predictors of peptides in amyloidogenic proteins

These types of predictors are based on the assumptions of a well-folded starting state and the amyloidogenic potential of a peptide within a protein instead of just a sum over the entire protein. TANGO (Fernandez-Escamilla et al., 2004) is one of the models incorporating these criteria. Instead of a simple linear equation for the entire protein, the TANGO algorithm is based on the assumption that a given amino acid position in a protein can assume four possible states: helix, turn, unfolded, and β-aggregated. The propensity of a particular residue to exist in each state is based on its secondary structure propensity, solvation penalty and charge–charge interactions. TANGO calculates the partition function of these different states for each residue, assuming that the probability of one polypeptide chain having more than two amyloidogenic regions is negligible. This assumption limits the ability of TANGO to estimate aggregation propensities of proteins larger than 50 amino acids. To address the fact that the folded state is the starting point of aggregation, the stability of the folded state is taken into consideration in the TANGO algorithm using Fold-X (Guerois et al., 2002) calculations. For practical purposes, TANGO is more useful for identifying whether a protein is likely to aggregate, rather than predicting absolute aggregation rates. Given these caveats, in benchmark tests of disease-associated proteins and their mutants, TANGO was successful in predicting the stretches of these proteins that were experimentally known to be prone to aggregation. The latest extension of this approach is WALTZ (Maurer-Stroh et al., 2010), which, among other developments, significantly expanded the peptide training set in order to reduce biases in the original algorithm that were attributed to the smaller training set. In the same class of predictors of aggregation-prone stretches of amino acids in a protein, there are several additional algorithms, including an extension of the original method of Chiti et al. (as surveyed by Belli et al. (2011)). There even exists a server that combines the results of several of these algorithms and provides a consensus prediction (Hamodrakas et al., 2007).

Predictors that consider tertiary structure of an amyloid

TANGO, WALTZ, and a similar program, Zyggregator (Tartaglia and Vendruscolo, 2008), implicitly consider tertiary structure by incorporating protein stability measurements. However, there are two classes of algorithms that explicitly consider structure of the final amyloid. One option to obtain this information is to perform coarse-grained MD simulations (discussed below) of peptides or proteins to estimate their amyloidogenicity (Cecchini et al., 2006; Ding et al., 2012). Another option is to assume the cross-β architecture (Figure 1A) described in published models of amyloid fibrils and ‘thread’ the sequence of a protein onto this template structure, in order to observe whether certain regions are able to stably adopt this conformation (Thompson et al., 2006; Trovato et al., 2006; Zhang et al., 2007). The advantage of these methods over the purely sequence-based methods described above is that they explicitly account for subtle structural features of amyloid fibrils, including twist in the β-strands and tertiary contacts between amino acids resulting from electrostatic and steric effects. However, the superiority of these methods over the sequence-based methods is not clear, mainly because the actual structures of some amyloids may not be identical to the cross-β models assumed in these methods. Khare et al. (2005a) applied a hybrid approach, separately examining sequence and structural determinants of the per-residue aggregation propensity of Cu, Zn superoxide dismutase (SOD1). Overlapping heptapeptide fragments spanning the entire SOD1 sequence were threaded onto idealized dimeric and tetrameric β-strand templates and conformational free energy was calculated following MD simulations, in order to assess the energetic favorability of a given region of the SOD1 adopting an amyloidogenic conformation. To identify ‘hot spots’ of SOD1 amyloidogenicity in the context of misfolding of the native dimeric structure, in silico conditions under which SOD1 forms domain-swapped oligomers were used to identify regions of protein structure that participate in non-native intermonomer contacts. Evaluating amyloidogenicity in these two distinct approaches implicated the same regions of SOD1, suggesting that aggregation ‘hot spots’ in this protein arise from multiple factors: the inherent propensity of certain sequence regions to adopt β-strand-rich conformations, as well as the position of these regions within the context of the native protein as it misfolds.

Applications and limitations

An important application of the methods described above is the ability to scan proteomes of several organisms to observe the prevalence of amyloidogenic sequences throughout evolution. Such studies have yielded interesting conclusions: (i) evolution disfavors the adoption of amyloidogenic sequences by intrinsically disordered proteins (Linding et al., 2004; Chen and Dokholyan, 2008); (ii) to allow hydrophobic cores, stably folded proteins must also tolerate amyloidogenic sequences (Linding et al., 2004); (iii) stably folded proteins circumvent amyloidogenic sequences by having ‘gatekeeper’ residues like glycine, proline, and charged amino acids near the amyloidogenic stretches, which counteract their high aggregation propensities (Rousseau et al., 2006); and (iv) proteins that form homooligomeric complexes have lower aggregation propensities than proteins that do not exist as homooligomers (Chen and Dokholyan, 2008). Furthermore, proteins that are essential to organismal fitness have lower aggregation propensities than nonessential proteins. Another application of intense interest is the use of these algorithms to predict mutations that reduce aggregation propensities of specific proteins (Fowler et al., 2005). This application is especially useful in designing mutations to stabilize protein-based biotechnological products, including therapeutic agents.

There has been a reasonable degree of progress made toward the prediction of sequence determinants of aggregation. However, there are significant challenges that remain. The best correlations between experiments and predictions can be attributed to simple physicochemical properties. For example, some of the best predictions involve introduction of charged residues. These methods also suffer from excessive false positive predictions, which are accompanied by the fact that even the most sophisticated algorithm does not take into account the protein structure/sequence as a whole. Thus, at this stage, we can conclude that simple rules may explain a significant portion of protein aggregation mechanisms, but to reach more thorough understanding, aggregation must be studied in the context of the tertiary structure of the entire protein. To enable such studies, significant advancements in computational resources and/or significant improvements in algorithms to simulate protein conformational states are essential.

Modeling of protein aggregate structures with MD

Structural and dynamic properties of protein states populated along the aggregation pathway are important for our understanding of misfolding and aggregation mechanisms, and also for the development of strategies for therapeutic inhibition. Although the aggregate structures of several short peptide segments of amyloidogenic proteins have been solved by X-ray crystallography (Nelson et al., 2005; Sawaya et al., 2007; Neudecker et al., 2012), the structures of aggregates and pre-fibrillar intermediates of many misfolding-prone proteins are not known. These intermediate states are often transient in nature, making them difficult to capture and thus challenging to characterize experimentally. As a result, atomic structures of protein aggregates are a major subject of computational modeling studies (Ma and Nussinov, 2006).

MD simulations utilize the input of a set of spatial coordinates of the system of particles (atoms, amino acid residues, or their equivalents) to evaluate the potential energy of the system. The traditional simulation engine iteratively solves Newton's equations of motion over small time steps. The output of the simulation is a trajectory of spatial coordinates describing the behavior of the system over time, like a movie of a virtual experiment. Direct observation of the formation of oligomers is currently not achievable using all-atom MD simulations due to the requirement of extensive sampling. To increase computational efficiency of biomolecule simulations, researchers have developed discrete molecular dynamics (DMD), an event-driven algorithm in which adaptive discretization of the potential function is combined with optimized treatment of hydrogen bonds and implicit solvent interactions (Dokholyan et al., 1998; Ding et al., 2008; Dagliyan et al., 2011; Shirvanyants et al., 2012). DMD has been used to study conformational dynamics and molecular mechanisms of self-assembly for a wide variety of proteins and peptides (Ding et al., 2002, 2005a, 2012; Peng et al., 2004; Khare et al., 2005b).

Another method for reducing the computational burden of oligomerization simulations is to start simulations from experimentally obtained structures. For example, Jang et al. (2010) utilized structures of the Aβ peptide from NMR and electron microscopy in MD simulations to examine the conformations of β-barrel channels that are proposed to be toxic. Using 12-, 16-, and 20-mer structures, the authors obtained results similar to those found using atomic force microscopy (AFM), emphasizing the possible heterogeneity of structures formed by Aβ oligomers. The near-native structure and dynamics of oligomers and pre-fibrillar aggregates can be explored using experimentally solved structures, but in order to observe de novo aggregation and other events occurring on longer time scales, current limits on computational power dictate that researchers simplify their representation of these structures.

Coarse-graining for complex systems

MD simulations with all-atom modeling have been used to study the early stages of protein misfolding and aggregation (as reviewed by Straub and Thirumalai (2010)). However, the typical time scales accessible by atomistic simulations are ∼100 nsec to ∼μsec, or ∼msec with state-of-the-art, hardware-accelerated supercomputers (Lindorff-Larsen et al., 2011); these time scales are far shorter than the days, years, or even decades sometimes required for protein aggregation. The propensity to aggregate appears to be a sequence-independent property of all polypeptide chains (Dobson, 1999) that is governed by fundamental interactions (such as hydrophobicity and electrostatics); therefore, coarse-grained simulations with simplified representations of proteins represent a tractable method for recapitulating physiologically relevant aggregation events (reviewed by Wu and Shea (2011)). Coarse-graining of a system simplifies groups of atoms into beads, with each bead usually representing more than one atom: for instance, a bead could represent an amino acid residue, part of a residue, or a particular chemical group. In exchange for the reduction in accuracy due to simplification, coarse-grained simulations have the capability to reach longer time and length scales on account of the fewer particles and therefore fewer calculations necessary at each time step. Some commonly used coarse-grained protein models include MARTINI (Marrink et al., 2007) and PRIME (Voegler Smith and Hall, 2001).

A disadvantage of the coarse-graining of protein systems is the difficulty of modeling large changes in secondary structure, which are common in processes of misfolding and aggregation. To address this issue, researchers have introduced phenomenological coarse-grained models, which represent specific peptides based on steps in their misfolding processes. Pellarin et al. (2007) utilized a two-state peptide model, comprising an amyloid-competent and an amyloid-protected state, with Langevin dynamics to simulate an amphipathic peptide. By varying only the relative stabilities of the two states, the authors demonstrated control over the roughness of the free energy surface and the heterogeneity of the fibril elongation pathway. Increasing the energy gap between the two states, equivalent to decreasing the β-aggregation propensity, roughened the free energy surface, creating additional intermediates along the elongation pathway.

In addition to phenomenological models, physics-based coarse-grained models are widely employed for studying protein aggregation. These models rely on physical force fields to define the energy of the system, instead of assigning parameters meant to mimic experimental observations, and are therefore more applicable to generalized real-world systems. Physics-based models have been used to assess the effect of β-sheet propensity on peptide aggregation with a three-bead model (Bellesia and Shea, 2009), and to reveal the amyloidogenesis mechanisms of Aβ peptides (Peng et al., 2004) and Src SH3 domain (Ding et al., 2005b) using two-bead models.

Multi-scale approaches that bridge coarse-grained and all-atom simulations

Molecular modeling with fully atomistic representation provides the most accurate description of the structure and dynamics of the molecular system. However, all-atom simulations have limited ability to reach long time scales and large polypeptide length scales because they are required to compute all of the detailed interactions and dynamics of the system. For this reason, all-atom simulations have been mainly applied to study early events of protein misfolding and aggregation. On the other hand, coarse-grained simulations with simplified representation of the molecular system have the ability to reach longer time scales and model larger systems, but with the drawback of less accurate description of the molecular systems. Multi-scale modeling approaches have been proposed as a means of combining both all-atom and coarse-grained simulations in order to cover a wide range of time and length scales. The challenges of multi-scale modeling include the choice and development of a coarse-grained force field, the inter-conversion of molecular models with different resolutions, and the coupling between simulations of different scales.

Multi-scale modeling has allowed the investigation of the structure and dynamics of lipid membranes, proteins, and DNA (as reviewed by Ayton et al. (2007) and Tozzini (2010)). These methods often involve conformational sampling with coarse-grained simulations, all-atom reconstruction, and subsequent energetic evaluation with atomistic simulations (Heath et al., 2007; Samiotakis et al., 2010). Similar multi-scale modeling approaches have also been applied to study protein misfolding and aggregation. For example, coarse-grained simulations are often used to generate an ensemble of possible aggregate conformations to serve as starting structures for all-atom simulations, allowing the evaluation of the thermodynamic viability and structural features of different assemblies (Urbanc et al., 2004a; Ding et al., 2005a). This approach was used to identify atomic-level differences in dimers of Aβ₄₀ and those of the more toxic Aβ₄₂ alloform (Barz and Urbanc, 2012). Multi-scale methods can also be employed in the reverse order: all-atom simulations were used to analyze the structural elements in SOD1 that are prone to form the core of fibrillar aggregates, and this information was incorporated into subsequent coarse-grained simulations to model the formation of large SOD1 aggregates (Ding et al., 2012). Therefore, by combining high-accuracy atomistic simulations with coarse-grained simulations that are able to sample long time scales, multi-scale modeling approaches offer the opportunity to cover a wide range of time and length scales, which is important for bridging the gaps between experimental observations and underlying molecular systems.

Application of computational methods to the study of protein aggregation in human diseases

Aβ and Alzheimer's disease

Aβ is a peptide of variable length (36–43 residues) that is formed by the sequential cleavage of Aβ precursor protein (APP) by β- and γ-secretases in the ER lumen and transmembrane domain (TMD), respectively (Golde et al., 1992; Chiti and Dobson, 2006). The most abundant Aβ peptides derived from the TMD of APP are Aβ₄₀ and the toxic Aβ₄₂ (Figure 2A), where Aβ₄₀ is 10 times more populated than Aβ₄₂ (Näslund et al., 1994). Both Aβ₄₀ and Aβ₄₂ can populate a range of oligomeric states, but Aβ₄₂ is more prone to adopt transient oligomeric conformations that rearrange to form protofibrils (Bitan et al., 2003). Unlike monomeric Aβ₄₂, these early soluble oligomers and protofibrils of Aβ₄₂ are suggested to be the major contributors to the onset of neurodegeneration in Alzheimer's disease (AD) (Chiti and Dobson, 2006). As in other protein aggregation diseases, protein misfolding is thought to be the initiating process of AD pathology, and can be induced by destabilizing conditions such as low pH, high temperature, and amino acid substitution (Bucciantini et al., 2002; Dobson, 2003). The assembly of Aβ into soluble oligomers and amyloid fibrils has been investigated with various experimental methods (Chiti and Dobson, 2006); however, it is still experimentally challenging to characterize oligomerization-triggering events at the atomic level due to the transient equilibria between various orders of oligomers. Therefore, computer simulations can provide experimentally inaccessible insights into early Aβ oligomerization steps that could be targeted for drug discovery efforts.

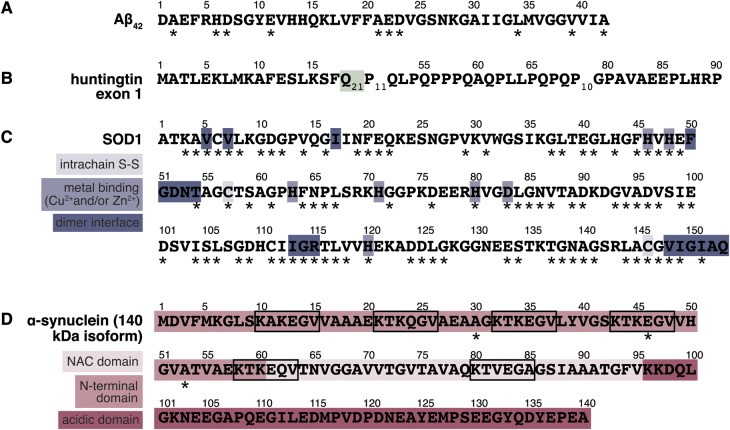
Figure 2.

Primary structures of neurodegeneration-linked proteins and peptides discussed in this review. (A) Amino acid sequence of Aβ₄₂; the sequence of Aβ₄₀ is identical except for the C-terminal isoleucine and alanine. (B) Sequence of the protein product of an HTT exon 1 variant with 21 CAG repeats. The site of the variable-length polyQ tract is shaded. (C) Sequence of SOD1, shaded to indicate amino acids that participate in the intramolecular disulfide bond, coordination of Cu²⁺ or Zn²⁺, and formation of the homodimer, steps in SOD1 maturation that contribute to the stability of the native state. (D) Sequence and domains of α-synuclein, shaded to indicate the N-terminal domain, containing multiple conserved imperfect KTKEGV repeats (enclosed in boxes), and the non-Aβ component of plaque (NAC) domain, which is characterized by a high content of hydrophobic residues and promotes α-synuclein aggregation. The N-terminal and NAC domains form transient α helical structures and are involved in binding to membranes (Breydo et al., 2012). The C-terminal acidic domain is indicated by dark shading; this domain contains a high content of proline, aspartate, and glutamate residues and is the site of numerous interactions with proteins and ligands such as dopamine and its analogs, calcium, copper, and iron (Breydo et al., 2012). Asterisks mark sites of amino acid substitutions linked to AD (A), HD (B), ALS (C), and PD (D); substitution sites reflect entries from the Human Gene Mutation Database (http://www.hgmd.org), the Alzheimer Disease and Frontotemporal Dementia Mutation Database (http://www.molgen.ua.ac.be/ADMutations/), and the ALS Online Genetics Database (http://alsod.iop.kcl.ac.uk/) as of January 2014.

MD simulations have been employed to probe the structural features of Aβ oligomers and fibrils, as well as the key interactions mediating their assembly. Based on MD simulations and solid-state NMR experiments, a structural model of amyloid fibrils formed by Aβ₄₀ peptides was built (Petkova et al., 2002). In this fibril model, the first 10 residues are disordered while residues 12–24 and 30–40 form parallel β-sheets, which interact with each other through side-chain interactions involving residues 25–29. Residues Asp-23 and Lys-28 in the core form salt bridges that stabilize the cross-β unit, which consists of a double-layered β-sheet structure with hydrophobic core and face (Petkova et al., 2002; Baumketner and Shea, 2007). MD simulations have revealed the effects of Aβ₄₀ on the competence of Aβ₄₂ to form fibrils: β strand content of the Aβ₄₂ monomer was found to decrease in the presence of Aβ₄₀, leading to increased flexibility of the Asp-23-Lys-28 salt bridge and residues 18–33 of Aβ₄₂, thus decreasing fibril stability (Viet and Li, 2012). Calculations from DMD simulations indicated no significant free energy difference between formation of Aβ₄₀ dimers and Aβ₄₂ dimers, suggesting that thermodynamically stable planar β-strand dimers do not initiate Aβ oligomerization (Urbanc et al., 2004a). The distinct oligomer formation of Aβ₄₀, Aβ₄₂, their versions containing an AD-causing substitution (E22G), and their N-terminally truncated versions were investigated with a four-bead DMD model (Urbanc et al., 2004b, 2010; Meral and Urbanc, 2013). Consistent with experimental findings (Bitan et al., 2003), these computational studies revealed that two C-terminal residues in Aβ₄₂ cause the difference in oligomer size distribution between Aβ₄₀ and Aβ₄₂, whereas N-terminally truncated versions show increased aggregation propensity. Furthermore, Yun et al. (2007) showed that electrostatic interactions facilitate oligomerization of both Aβ₄₀ and Aβ₄₂ into trimers and tetramers, while Aβ₄₂ can also form nonamers and tetradecamers due to its extended C-terminus via a quasi-stable turn. The crystal structure of an Aβ_18–41 tetramer (Streltsov et al., 2011) supported the oligomeric structures suggested in these DMD studies.

In addition to elucidating Aβ aggregation mechanisms and structures of oligomers and fibrils, results from computational studies have been used to propose a number of therapeutic approaches for blocking Aβ aggregation. One strategy for blocking Aβ aggregation is the generation of peptides that mimic the structure of a portion of Aβ, such that they will bind to a growing fibril but cannot serve as a template for further extension. Fibril formation was found to be reduced by chemically-modified pentapeptides that mimic Aβ_17–20 (LVFF), but act as β-sheet breakers (Permanne et al., 2002; Adessi et al., 2003). In another study, docked conformations of Aβ_17–20-mimicking peptides were used to design 3D-pharmacophores for virtual screening. Based on docking scores and physicochemical features, 16 diverse small molecule compounds were selected for experimental tests. At 2–3 μM concentrations of the selected hit compound, Aβ aggregation was reversed in vitro and in vivo (Chen et al., 2009). The relationship between aggregation rate and binding affinity of the β-sheet breaker peptides KLFVV and LPFFD was investigated with all-atom MD simulations, which showed that KLVFF is less effective than LPFFD at preventing aggregation of Aβ_16–22 peptides. Analysis of the relative affinities of these two peptides using the Molecular Mechanics Poisson–Boltzmann surface area method revealed that the greater efficacy of LPFFD is attributable to its higher affinity for Aβ_16–22. These simulations also showed that although total β-sheet content is elevated in the presence of β-sheet breaker peptides, aggregation rate is decreased due to a reduction in β-sheet content of fibril-prone regions (Viet et al., 2011).

In light of the emerging view of Aβ oligomers, as opposed to fibrils, as primary disease-causing toxic species, computational approaches have also focused on the therapeutic potential of targeting these species. Inhibitors based on Aβ peptide fragments reduce toxic effects of Aβ₄₂ without preventing Aβ₄₂ oligomerization; simulations with a four-bead DMD model revealed that these peptides form large assemblies with Aβ₄₂ and reduce their β-strand content (Urbanc et al., 2011). These results highlight the therapeutic potential of stabilizing Aβ in a relatively benign conformation, even when the abundance of oligomers is largely unaltered. Computational characterization of mechanisms by which inhibitors reduce Aβ toxicity, as well as of Aβ folding and structures of oligomers and aggregates, was recently reviewed by Shea and Urbanc (2012).

Huntingtin and Huntington's disease

The interesting transcript 15 (IT15), also called the huntingtin gene (HTT), encodes a ∼350 kDa multidomain protein that is essential for brain development (MacDonald et al., 1993; Reiner et al., 2003). The protein product, huntingtin protein (htt), contains a polymorphic glutamine/proline rich domain close to its amino-terminus (Figure 2B) (MacDonald et al., 1993). The polymorphic nature of the 5′ region of HTT results in a variable size of the protein product with anomalous polyglutamine (polyQ) expansions; the presence of htt with expanded polyQ tracts is characteristic of aggregates found in neurons of Huntington's disease (HD) patients. HD is a late-onset autosomal-dominant neurodegenerative disorder characterized by acute motor dysfunction, cognitive decline, and psychiatric disturbances (Landles and Bates, 2004). The age of onset of HD symptoms is inversely proportional to the length of polyQ expansion (Bates, 2005). Although ubiquitously expressed and localized to several subcellular compartments, the normal function of htt has not been established due to its lack of homology to other known proteins (Harjes and Wanker, 2003). Roles for htt in numerous cellular processes are suggested by its ability to bind to proteins involved in apoptosis, vesicle transport, morphogenesis, and transcriptional regulation (Harjes and Wanker, 2003; Li and Li, 2004). Recent reports suggest that htt is involved in modulation of gene transcription via direct interaction with genomic DNA (Bates, 2005).

Biochemical and biophysical studies have established that regardless of length, polyQ expansions result in the formation of aggregates with common structural features (Klein et al., 2007; Vitalis et al., 2009). However, detailed structural information pertaining to polyQ-htt is difficult to obtain experimentally, as even short polyQ tracts make htt insoluble at the high concentrations required for crystallography or NMR studies (Truant et al., 2008). Computational approaches, on the other hand, have provided atomistic details of the structural organization of polyQ-htt of different lengths and oligomeric states (Marchut and Hall, 2007). Several structural models, including the triangular β-helix model and the antiparallel β-sheet model, were proposed and have geometries compatible with existing experimental data (Stork et al., 2005; Esposito et al., 2008). Classical MD simulations have provided valuable insights into the stability, toxicity, folding, and three-dimensional organization of monomeric and aggregated polyQ-htt (Finke et al., 2004; Armen et al., 2005; Khare et al., 2005b; Sikorski and Atkins, 2005; Stork et al., 2005; Barton et al., 2007; Esposito et al., 2008; Lakhani et al., 2010). In addition to MD simulations, force field-based Monte Carlo simulations have also been employed to study the aggregation characteristics of polyQ (Vitalis et al., 2009). Several studies have focused on the dependence of the structural stability of the circular β-helix and other possible structures on polyQ extension length (Khare et al., 2005b; Stork et al., 2005; Marchut and Hall, 2007; Ogawa et al., 2008; Lakhani et al., 2010; Rossetti et al., 2011). Although conflicting views prevail, these studies are in general agreement that polyQ extensions of 30 Qs or more impart maximal stability to the resulting β-helix structures (Stork et al., 2005; Merlino et al., 2006; Ogawa et al., 2008). In contrast to these results, experimental and computational studies have proposed and validated the formation of annular units smaller than the circular β-helix structures (Marchut and Hall, 2006a, 2007). In addition, using enhanced sampling techniques, several groups have demonstrated the dependence on sequence context of the aggregation propensity of polyQ tracts (Kelley et al., 2009; Lakhani et al., 2010).

As outlined above, atomistic details of the association of monomeric polyQ-htt of a given length to form mature fibrils remain a matter of controversy. Although computational studies can provide atomistic details of such molecular processes, they are largely limited by the long time scales required to observe such events. A common methodology used to overcome this limitation is the use of coarse-grained modeling of protein–protein interactions. Simplified models of polyQ have been developed to study their aggregation propensities (Marchut and Hall, 2006a, b, 2007). Using DMD, Barton et al. (2007) demonstrated that the formation of inter-glutamine hydrogen bonds defines the dominant interactions involved in aggregation of unfolded intermediates. More recently, it was demonstrated using enhanced sampling techniques that the amino acid sequences flanking the huntingtin repeats influence the misfolding propensity of the polyQ-htt, in agreement with experimental observations (Ding et al., 2008; Lakhani et al., 2010; Shirvanyants et al., 2012). Applications of computational methods toward understanding the molecular mechanisms of HD are discussed by Rossetti and Magistrato (2012).

SOD1 and ALS

The link between SOD1, a homodimeric antioxidant metalloprotein (Figure 2C), and amyotrophic lateral sclerosis (ALS), a late-onset neurodegenerative disorder specifically affecting motor function, was first discovered in the early 1990s (Rosen et al., 1993) and over 150 mutations in the gene encoding SOD1 have since been identified in ALS patients. ALS-linked mutants of SOD1 range from completely inactive to wild type-like in their dismutase activities, with no correlation between enzymatic activity and disease severity, but many SOD1 mutations have a common effect of decreasing stability of the native homodimeric conformation (Khare et al., 2006; Shaw and Valentine, 2007); more destabilizing mutations having a tendency to cause ALS with earlier onset and/or more rapid progression (Wang et al., 2008).

Pathophysiology of ALS, like that of other neurodegenerative disorders, is extraordinarily complex; it is difficult to distinguish between deleterious phenomena that initiate disease onset from those appear subsequently. Soluble misfolded SOD1, present as monomers and non-native dimers, trimers, and higher-order oligomers (Banci et al., 2007; Gruzman et al., 2007), directly disrupts neuronal homeostasis by interacting with components essential to processes such as axonal transport, mitochondrial function, proteasomal efficiency, and ER-associated degradation (Ferraiuolo et al., 2011; Redler and Dokholyan, 2012). In addition to destabilizing mutations, SOD1 can be induced to misfold and aggregate by non-genetic factors such as oxidation, which induces wild-type SOD1 to adopt similar conformations to that of ALS-linked mutants and also exacerbates the destabilizing effects of some mutations (Bosco et al., 2010; Proctor et al., 2011; Mulligan et al., 2012). SOD1 aggregation, particularly the formation of soluble oligomers, is thus considered to be a potentially widespread factor in ALS pathogenesis.

MD simulations have been instrumental in studying the contributions of individual residues to SOD1 stability, folding, and misfolding. DMD was used to identify residues most essential to the thermodynamic stability and two-state folding kinetics of wild-type SOD1 (Khare et al., 2003). As monomeric SOD1 containing ALS-linked mutations and lacking bound metal ions and/or the native intramolecular disulfide bond represent the most aggregation-competent species, much effort has been focused on characterization of their stability and dynamics. From simulations of 75 ALS-linked SOD1 mutants using the explicit solvent/implicit solvent (ES/IS) method, Khare et al. (2006) calculated the effect of each mutation on thermodynamic stability of dimers and monomers, finding that over 90% of the mutations studied decrease dimer stability, increase dimer dissociation propensity, or both. All-atom MD simulations with explicit solvent also revealed a common tendency of ALS-causative mutations to weaken the native hydrogen-bonding network by restricting correlated movements between subunits in the dimer, showing the importance of dynamic coupling to SOD1 stability (Khare and Dokholyan, 2006). An altered network of hydrogen bonds was also shown for the G37R mutant using implicit solvent MD (Milardi et al., 2010). A4V-SOD1, in addition to exhibiting the increased loop and active site fluctuations seen in most ALS-linked mutants (Shipp et al., 2003; Tiwari and Hayward, 2003; Rodriguez et al., 2005; Tiwari et al., 2005), has higher solvent exposure of Cys-111, which is susceptible to destabilizing post-translational modification (Proctor et al., 2011; Redler et al., 2011) and has been shown to modulate aggregation propensity (Cozzolino et al., 2008). Results from MD simulations also indicated that, unlike the wild-type protein, A4V forms α-sheet and α-bridge structures that have been observed in other amyloidogenic proteins (Schmidlin et al., 2009).

To determine the relative contributions of metal binding and the native disulfide bond to SOD1 misfolding, Ding and Dokholyan (2008) used all-atom DMD simulations of wild-type SOD1 in the presence and absence of these stabilizing elements. Coordination of metals contributes more to thermodynamic stability than does the native disulfide bond, while both disulfide reduction and metal loss lead to loss of intersubunit contacts important to dimer stability. The reduced dimer stability of metal-free, disulfide-reduced SOD1 can be explained by the observation of increased flexibility in the Glu-49-Asn-53 loop and resultant weakening of intersubunit contacts. In addition to elucidating the contribution of native post-translational modifications to SOD1 stability, MD simulations have also enabled characterization of the structural consequences of two modifications reported to be abundant in SOD1 from human tissue: Thr-2 phosphorylation and Cys-111 glutathionylation (Wilcox et al., 2009). In simulations utilizing all-atom DMD with replica exchange, Proctor et al. (2011) report that both modifications, individually and in combination, destabilize dimers of wild-type and mutant SOD1 and increase the energetic favorability of populating a misfolded intermediate state.

α-synuclein and Parkinson's disease

α-synuclein is a neuronal protein that plays a central role in Parkinson's disease (PD) and dementia with Lewy bodies, as well as other neurodegenerative diseases such as AD and multiple system atrophy (Jellinger, 2009; Breydo et al., 2012). PD involves massive death of dopaminergic neurons in the substantia nigra, leading to reduction of striatal dopamine levels and motor dysfunctions such as tremor, rigidity of the limbs and trunk, bradykinesia, and postural instability (Ferrer et al., 2012). Mutations in the gene encoding α-synuclein (SNCA, also known as PARK1) corresponding to A30P, E46K, and A53T substitutions have been discovered in patients with early onset familial PD (Figure 2D), and evidence suggests that these mutations promote α-synuclein aggregation (Breydo et al., 2012). Like Aβ, α-synuclein is an intrinsically disordered protein that forms morphologically diverse aggregates, including spherical or ring-like oligomers, amorphous aggregates, and amyloid fibrils (Breydo et al., 2012). Toxic oligomers also may be released and sequestered by fibrils (Cremades et al., 2012).

As in several other protein conformational disorders, multiple cytotoxic mechanisms have been proposed for α-synuclein monomers and aggregates. α-synuclein oligomers induce oxidative stress in neurons (Cremades et al., 2012) and can bind to lipid membranes, permeabilizing bilayers, and sometimes forming ion-conducting pores (Breydo et al., 2012). A detailed review of oligomer toxicity was recently presented (Kalia et al., 2013). Mechanisms of α-synuclein aggregate neurotoxicity include impairment of α-synuclein degradation via proteasome inhibition by the aggregated species, as well as copper-dependent generation of reactive oxygen species (Breydo et al., 2012; Zhou et al., 2012). α-synuclein aggregation is also reported to underlie inflammation and immune abnormalities present in PD, including aberrant microglial activation (Bennett, 2005).

Computer simulations have been instrumental in analysis of α-synuclein structure and interactions, both of the native state and of pathological aggregates. Simulations coupled with NMR (Dedmon et al., 2005; Bortolus et al., 2008; Allison et al., 2009; Wu et al., 2009) and FRET experiments (Nath et al., 2012) provided evidence that the native state of α-synuclein is more compact than would be expected for a random coil, and that it forms transient oligomeric structures mediated by contacts made by the C-terminus. In implicit solvent Monte Carlo simulations (Jónsson et al., 2012), two-phase behavior of α-synuclein was observed in solution: one phase is structurally disordered and another has significant β-strand content. Destabilization of the native state is promoted by disease-associated mutations, as was shown in MD studies for A53T (Coskuner and Wise-Scira, 2013), A30P (Wise-Scira et al., 2013a), and E46K (Wise-Scira et al., 2013b). Structural changes promoted by these mutations result in more open states, biased to aggregation (Hazy et al., 2011). Results of atomistic simulations (Tsigelny et al., 2008) suggest that the transient oligomers formed by α-synuclein may be the species capable of interacting with lipid membranes. A MD study of aggregation kinetics (Matthes et al., 2012) indicates a two-phase process of fibril formation, where formation of the contact interface by mostly disordered chains is followed by structural transition and accumulation of β-sheet content. It also suggests a critical role of protein–solvent interactions in α-synuclein aggregation. Structures of fibrils have also been a focus of computer-assisted studies. Fibril rupture simulations agree with AFM experiments and indicate the presence of highly mechanically stable structures in α-synuclein fibrils with high β-sheet content (Jónsson et al., 2013).

Concluding remarks

Protein aggregation has been implicated in numerous neurodegenerative disorders whose etiologies are poorly understood and for which there are no effective treatments. In particular, early-stage soluble oligomers are thought more likely to be toxic, but their heterogeneity and/or transience often precludes experimental characterization that could allow the development of strategies to prevent their assembly or toxicity. Therefore, the high-resolution structural, dynamic, and mechanistic insights afforded by computational studies of protein aggregation have a unique potential to enable the rational manipulation of oligomer formation. Such capability will facilitate further direct testing of the ‘cytotoxic oligomer hypothesis’ and reveal potential strategies for inhibiting formation of toxic oligomers in neurodegenerative disorders.

Funding

This work was supported by National Institutes of Health Awards R01GM080742 (to N.V.D.), F31NS073435 (to R.L.R.), and F31AG039266 (to E.A.P.). O.D. is a Howard Hughes Medical Institute International Student Research Fellow.

Conflict of interest: none declared.