On Detecting Incomplete Soft or Hard Selective Sweeps Using Haplotype Structure

Abstract

We present a new haplotype-based statistic (nS_L) for detecting both soft and hard sweeps in population genomic data from a single population. We compare our new method with classic single-population haplotype and site frequency spectrum (SFS)-based methods and show that it is more robust, particularly to recombination rate variation. However, all statistics show some sensitivity to the assumptions of the demographic model. Additionally, we show that nS_L has at least as much power as other methods under a number of different selection scenarios, most notably in the cases of sweeps from standing variation and incomplete sweeps. This conclusion holds up under a variety of demographic models. In many aspects, our new method is similar to the iHS statistic; however, it is generally more robust and does not require a genetic map. To illustrate the utility of our new method, we apply it to HapMap3 data and show that in the Yoruban population, there is strong evidence of selection on genes relating to lipid metabolism. This observation could be related to the known differences in cholesterol levels, and lipid metabolism more generally, between African Americans and other populations. We propose that the underlying causes for the selection on these genes are pleiotropic effects relating to blood parasites rather than their role in lipid metabolism.

Introduction

Since the generation of the first genetic variation data more than 40 years ago, much research has focused on methods for detecting selection. In particular, after the emergence of genome scale population level DNA genotyping and sequencing in humans, numerous studies have been published identifying genes in the human genome that have been targeted by selection (Bustamante et al. 2005; Carlson et al. 2005; Kelley et al. 2006; Voight et al. 2006; Wang et al. 2006; Kimura et al. 2007; Sabeti et al. 2007; Tang et al. 2007; Williamson et al. 2007). Many of the studies focus on a model in which selected de novo mutations are swept to fixation in the population (Kimura et al. 2007; Sabeti et al. 2007). Such a model, known as a hard sweep, classic selective sweep, or standard selective sweep model, has been extensively explored (Kim and Stephan 2002; Przeworski 2002; Maynard-Smith and Haigh 2007). This model can be contrasted with models in which selection acts on previously neutral alleles already segregating in the population, that is, selection on standing genetic variation, or with models in which multiple independent mutations at a single locus are all favored and increase in frequency simultaneously until the sum of the frequencies is 1 (polygenic adaptation). Both of these models are often referred to as “soft sweeps” (Hermisson and Pennings 2005; Przeworski et al. 2005; Pennings and Hermisson 2006b, 2006c; Pritchard and Rienzo 2010). Examples of soft sweeps have been documented in several studies including studies on three-spined sticklebacks (Feulner et al. 2013) and beach mice Peromyscus polionotus (Domingues et al. 2012). In humans, most cases of selection have been assumed to be hard sweeps, although several cases of selection on standing variation have been reported (Bhatia et al. 2011; Peter et al. 2012; Seixas et al. 2012), and results of genome-wide association studies are increasingly being used to infer selection that has been acting on polygenic traits (Casto and Feldman 2011; Turchin et al. 2012).

Lewin and Foley (2004) argued that, given the currently accepted assumptions regarding human demography (a small effective population size and migration out of Africa 50–100 ka), there may have been little time for new beneficial mutations to occur. Thus, the hard sweep model may not be entirely appropriate for describing the process of adaptation in recent human history (Pritchard et al. 2010). Instead, adaptation to the local environments might more likely have proceeded from standing variation (Przeworski et al. 2005).

Numerous empirical (Hamblin and Rienzo 2000; Tishkoff et al. 2007; Scheinfeldt et al. 2009) and theoretical (Innan and Kim 2004; Hermisson and Pennings 2005) studies suggest selection on standing variation might be important in recent human evolution. In particular, selection on standing variation occurring on more than one loci (polygenic adaptation from standing variation) has been suggested to be an important, if not the most important, mechanism of adaptation in humans (Pritchard and Rienzo 2010).

Current methods for detecting recent adaptation use summary statistics based on the site frequency spectrum (SFS), linkage disequilibrium (LD), length of high-frequency haplotypes, proportions of common derived alleles, decreases in local diversity, or changed allele frequencies between geographically separated populations. These methods are good at detecting hard sweeps. Nonetheless, many of them are expected to have low power to detect sweeps from standing variation because of the weak effects soft sweeps have on linked sites (Kim and Stephan 2002, 2003; Hermisson and Pennings 2005; Pennings and Hermisson 2006b, 2006c). For example, a sweep from standing variation may not have the distribution of allele frequencies and resulting SFS as expected under a hard sweep. However, haplotype patterns will clearly change even when selection is acting on multiple haplotypes. Haplotype-based statistics are, therefore, an obvious avenue to pursue when designing methods for detecting sweeps from standing variation.

There are numerous different statistics used to detect selection based on haplotype homozygosity. The most commonly used statistic is iHS (Voight et al. 2006), which is based on the decay of haplotype homozygosity as a function of recombination distance. The distribution of most of the commonly used neutrality statistics depends to varying degree on the recombination rate. Somewhat disturbingly, O’Reilly et al. (2008) found that most scans for selection in the human genome had a strong bias toward identifying regions of low recombination. Perhaps, part of the effect is caused by an increased power to detect selection in regions of low recombination. However, the possibility that many results in fact are false positives due to reduced recombination is worrying.

A dependence on recombination rates will in particular be true for haplotype homozygosity as it is closely related to LD. In part to address this problem, iHS is based on taking the ratio of haplotype homozygosity for the haplotypes carrying the derived iHH_D and ancestral allele iHH_A in a candidate site. Using this ratio increases the robustness of the statistic toward varying mutation rate and/or recombination rate, and possibly to deviations from the assumed demographic model as well. Nonetheless, as we shall show later in the article, the distribution of the statistic still depends on the recombination rate.

In this article, we describe a haplotype-based statistic akin to iHS, which combines information on the distribution of fragment lengths, defined by pairwise differences, with the distribution of the number of segregating sites between all pairs of chromosomes. We show that this method is able to identify selective sweeps, both hard and soft. Using theoretical and simulation results, we demonstrate the robustness of this statistic to misspecification of the recombination rate and to a variety of demographic factors, such as population subdivision, bottlenecks in population size, and population growth. We compare the power of the new statistic with those of other methods, under a variety of selective sweep models. Additionally, using the HapMap3 data set from the International HapMap Project (The International HapMap 3 Consortium 2010), we show that our method is less influenced by the variation in recombination rate than other similar methods. We also discuss our biological findings of the HapMap3 data. In particular, we describe a very strong signal for selection in West African populations in genes related to cholesterol transporters.

Definition of Statistics

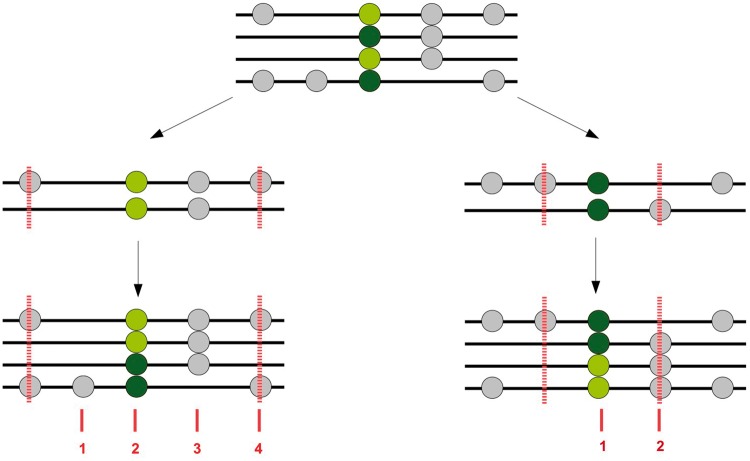
Here, we present a single-population haplotype-based statistic (nS_L: number of segregating sites by length) designed to detect the signature of positive selection acting to increase haplotype homozygosity. This statistic combines information on the distribution of fragment lengths between mutations with the distribution of the number of segregating sites between all pairs of chromosomes, and is based on taking the ratio of haplotype homozygosity for the derived and ancestral alleles, an approach also taken by iHS. However, the crucial difference between nS_L and iHS is that nS_L measures the length of a segment of haplotype homozygosity between a pair of haplotypes in terms of number of mutations in the remaining haplotypes in the data set in the same region (fig. 1). As a consequence, a genetic map is not required to calculate the statistic, and robustness toward recombination and/or mutation rate variation is increased.

Fig. 1.

Length of a segment of haplotype homozygosity. A sample of four chromosomes (black horizontal bars) carrying two copies of the derived allele (light green circles) and two copies of the ancestral allele (dark green circles) at a segregating site. On the left side, the haplotype homozygosity for the pair of chromosomes carrying the derived allele is shown. The haplotype is defined by the closest pairwise difference upstream and downstream of the segregating site, indicated by vertical dashed red lines. The length of the haplotype is given in terms of the number of segregating sites contained within the haplotype boundaries (vertical dashed red lines) using the entire sample. The number of polymorphic sites within the boundaries is given by the numbers in red. On the right side, the haplotype homozygosity for the pair of chromosomes carrying the ancestral allele is shown. The haplotype boundaries and haplotype length are set up as described for the derived allele.

The nS_L statistic is defined as follows: We organize phased data as an n× S_n matrix H with rows corresponding to the n sampled haplotypes and columns corresponding to the S_n segregating sites, with H_ik = 1 if the ith haplotype carries the derived allele at the kth segregating site, and 0 otherwise. For each segregating site, we define the following sets of haplotypes carrying the ancestral and derived alleles:

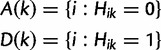and let n_A(k) and n_D(k) denote the sizes of these respective sets.

We let p_k be the position, in units of recombination distance, of the kth segregating site. It will be useful to refer to single nucleotide polymorphisms (SNPs) by their recombination position, rather than ordinal position in H, so we let 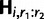denote the row vector corresponding to segregating sites of the ith haplotype which lie in the open interval (r₁, r₂)

For haplotypes i and j, we define L_ij to be as follows:

This is the number of consecutive segregating sites, in the interval containing x, over which haplotypes i and j are identical by state (IBS). At the kth segregating site, our statistic is defined in terms of the mean value of L_ij over pairs of haplotypes which either both carry the ancestral or derived allele:

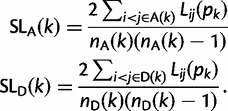Finally, nS_L is defined in a manner analogous to iHS by taking the log ratio of ancestral and derived statistics:

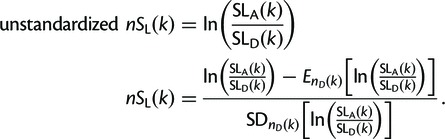Therefore, this new statistic is mathematically very similar to iHS. The related statistic EHH^w is defined to be the probability that a pair of randomly chosen haplotypes, both carrying the same allele, are IBS in a window of length w. Using our notation, EHH^w computed with respect to the derived allele is given by:

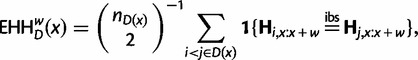If w is positive then the window is to the right of x, while if it is negative, it is to the left. iHH is defined as the integral of EHH with respect to w. Rearranging the integral gives the following:

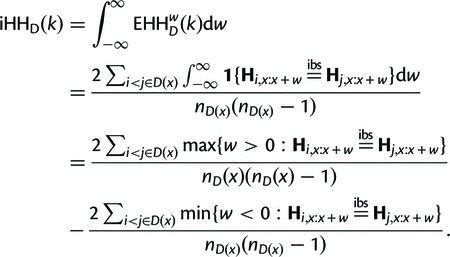These extremal points must occur at a pairwise difference between haplotypes i and j, so if we define

we get that

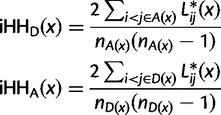Note that the expression in the sum is almost the same as the expression for L_ij, except for r – l has been replaced by p_r – p_l. Finally,

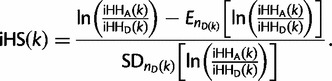Both nS_L and iHS are defined at every polymorphic site so they give one value for each SNP. The same is true for extended haplotype homozygosity (EHH) since for the purposes of this article the core haplotypes of interest are defined by the presence or absence of a single SNP. The main difference between the nS_L and iHS statistics is in how they measure distance. The nS_L statistic uses segregating sites as a proxy for distance, while the iHS statistic uses the recombination distance. Therefore, iHS can be viewed as nS_L with some additional randomness due to the spacing between segregating sites.

Moreover, because variance due to SNP spacing has a strong dependence on the recombination rate, this also predicts that the distribution of iHS will be more sensitive to the recombination rate. In particular, when the recombination rate is low, and hence SNP spacing is less uniform, the ratio of iHS variance to nS_L variance will be higher. This result was seen in simulations, as well as in HapMap3 data.

A program, and associated open source code for computing nS_L is available at http://cteg.berkeley.edu/~nielsen/ (last accessed March 3, 2014).

Results

Using simulations, we compared the performance of nS_L to four well-established statistics: Tajima’s D, Fay’s and Wu’s H, EHH, and iHS (Tajima 1989; Fay and Wu 2000; Sabeti et al. 2002; Voight et al. 2006). We used the program ms (Hudson 2002) to generate the null distribution of each statistic under different demographic models and recombination rates. We then used the program mbs (Teshima and Innan 2009) to evaluate the power of these same statistics under a range of selection scenarios. Finally, we applied the nS_L statistic to HapMap3 data to illustrate the utility of the method.

Robustness to Demographic Assumptions

We explored the robustness of the five statistics under three scenarios modeling possible deviations from the standard neutral reference model of a single population of constant size: exponential population growth, a population bottleneck, and population structure. We quantified deviations from the standard distribution using the total variation distance between the distribution of the test statistic under the standard model and the corresponding distribution under the alternative demographic model. If the distribution of a statistic is completely unchanged under one of these scenarios, then the total variation distance will be 0, while if the resulting distribution has no overlap with the reference distribution at all, then the total variation distance will attain its maximum possible value of 1. As the test statistics can be applied in many ways, for example using different significance levels, the total variation distance provides an attractive application-agnostic heuristic for comparing the robustness of these methods. However, we also examine false-positive rates at specific significance levels.

For the neutral model, we used a population of constant size with 4N_eµ equal to 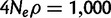(see Materials and Methods). Three different exponential growth rates were used for the models of exponential growth (α = 10, 100, and 1,000), where α is the coalescent-scaled growth rate. For the population bottleneck model, we simulated three models with bottlenecks of different severities (r = 0.25, 0.10, and 0.05) occurring 1,200 generations ago and lasting 800 generations, where r is the ratio of population size during the bottleneck relative to other time periods. For the model with population structure with migration, we simulated an island model with two islands and we varied the migration rates between the two islands (M = 0.1, 1, and 10), where M = 4Nm was the coalescent-scaled migration rate between islands. This rate was assumed to be symmetric and constant in time. We drew all the samples from one island. For each variation of the standard neutral model, we generated 100 simulations with 20 chromosomes per simulation. Notice that each of the test statistics can be calculated using different choices of window sizes. For the SFS-based statistics, as well as for nS_L, the window sizes are the lengths in number of segregating sites of the window in which the statistic is calculated. For iHS, the window size is the haplotype homozygosity threshold used to set the limits of integration. For EHH and relative EHH (rEHH), the window size corresponds to the genetic distance over which the IBS of the haplotypes is determined.

Robustness to Assumptions Regarding Population Growth, Bottlenecks, and Population Structure

The distributions of all statistics depend on the demographic model assumptions (table 1). For example, for a growth rate parameter of α = 1,000, the total variation distance between the standard neutral reference distribution and the true distribution varies between 0.23 and 0.99 depending on the choice of statistic. In models with exponential population growth or a population bottleneck, the SFS-based statistics, and Tajima’s D in particular, seem most affected. Perhaps a bit surprisingly, the haplotype-based statistics are also strongly affected by both population growth and bottlenecks. For example, depending on window size, the total variation distance varies between 0.34 and 0.87 for rEHH under strong exponential population growth (α = 1,000). Haplotype statistics seem more robust to population growth and bottlenecks than the SFS-based statistics, but cannot be claimed to be robust generally. For example, even at moderate growth rates (α = 10), the total variation distance is 0.59 for rEHH when calculated with a window size of 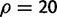. In general, nS_L is among the most robust statistics to population growth. For moderate growth rates, the total variation distance is never larger than 0.07 for nS_L, whereas it is at least 0.13 for all other statistics including iHS. The robustness of both EHH and rEHH depends strongly on choice of window size, but with a sufficiently large window size, EHH and rEHH can be as robust, or more robust than nS_L. The same does not hold true for weaker population growth. Table 1 highlights cases where other statistics are as robust (underlined) or more robust (underlined and italicized) than nS_L.

Table 1.

Total Variation Distance between the Reference Distribution and the True Distribution under Different Models for Five Different Statistics.

	Population Growth (α = 0)			Population Bottleneck (r = 1)			Population Subdivision (M = 0)			Recombination Rate Variation’ (ρ = 2,000)
	10	100	1000	0.25	0.10	0.05	0.1	1	10	0	400	4,000
nSL (200)	0.03	0.19	0.38	0.11	0.15	0.11	0.13	0.06	0.02	0.04	0.03	0.03
nSL (500)	0.04	0.21	0.40	0.09	0.13	0.11	0.10	0.04	0.04	0.04	0.03	0.04
nSL (1,500)	0.07	0.23	0.40	0.10	0.14	0.12	0.08	0.04	0.05	0.05	0.04	0.04
iHS (0.25)	0.20	0.41	0.53	0.20	0.28	0.29	0.11	0.05	0.03	0.11	0.09	0.08
iHS (0.10)	0.16	0.40	0.59	0.17	0.23	0.24	0.09	0.05	0.04	0.09	0.08	0.07
iHS (0.05)	0.13	0.35	0.53	0.14	0.18	0.19	0.08	0.05	0.05	0.08	0.06	0.05
EHH (2)	0.20	0.30	0.46	0.18	0.22	0.26	0.14	0.19	0.25	0.08	0.06	0.05
EHH (20)	0.41	0.61	0.83	0.35	0.40	0.46	0.23	0.25	0.31	0.21	0.16	0.12
EHH (200)	0.16	0.21	0.23	0.14	0.16	0.18	0.11	0.11	0.11	0.10	0.08	0.04
rEHH (2)	0.20	0.27	0.40	0.13	0.19	0.23	0.10	0.17	0.24	0.07	0.05	0.04
rEHH (20)	0.59	0.77	0.87	0.43	0.54	0.68	0.26	0.30	0.41	0.25	0.20	0.19
rEHH (200)	0.24	0.34	0.34	0.18	0.26	0.27	0.12	0.14	0.12	0.14	0.12	0.09
Tajima’s D (41)	0.64	0.89	0.96	0.09	0.21	0.47	0.25	0.13	0.10	0.14	0.10	0.06
Tajima’s D (101)	0.73	0.94	0.98	0.20	0.29	0.53	0.19	0.13	0.22	0.26	0.17	0.09
Tajima’s D (201)	0.79	0.95	0.99	0.30	0.37	0.59	0.14	0.18	0.33	0.37	0.22	0.10
Fay’s and Wu’s H (41)	0.37	0.55	0.65	0.25	0.25	0.12	0.39	0.28	0.18	0.18	0.11	0.06
Fay’s and Wu’s H (101)	0.46	0.63	0.72	0.36	0.34	0.13	0.46	0.39	0.31	0.32	0.18	0.08
Fay’s and Wu’s H (201)	0.54	0.69	0.77	0.45	0.42	0.19	0.52	0.47	0.42	0.44	0.23	0.09

Note.—We computed each of the statistics with three window sizes (values within parenthesis following the name of each statistic). For nS_L, Tajima’s D, and Fay’s and Wu’s H the window size is defined as the number of segregating sites. For iHS, the window size value indicates the EHH threshold used to set the limits of integration. For EHH and rEHH the window size corresponds to the recombination rate distance over which the IBS of the haplotypes is determined. Values in the table range from 0 to 1. They correspond to the total variance distance between the standard neutral distribution computed with the parameter of reference (value within parenthesis following each parameter) and the true distribution. Low values indicate high robustness because the lower the value, the smaller the difference between the neutral and the true distribution. Underlined values denote the results that fall in the same range as the results obtained when testing nS_L. Values that are better than those obtained with nS_L are underlined and italicized. Note that, as the population subdivision model assumes sampling from only one population receiving migrants from another population, the M = 0 scenario corresponds to no population subdivision.

In the bottleneck scenarios explored here, nS_L generally appears more robust than any of the other methods. The only exceptions are Tajima’s D for the low bottleneck ratio (r = 0.25), if calculated in a 41 SNPs window, and Fay’s and Wu’s H, if calculated in a 41 SNPs window for the extreme bottleneck ratio (r = 0.05). Perhaps a bit surprisingly, the established haplotype-based statistics are often less robust to the effect of bottlenecks than SFS-based methods. For example, with a window size of 20 and a bottleneck ratio of r = 0.05 the total variance distance for rEHH is 0.68. Under the same conditions, the total variation distance is between 0.12 and 0.19 for Fay’s and Wu’s H. The effect of population growth and bottlenecks on the haplotype-based statistics can perhaps be understood as an effect of growth and bottlenecks on the variance in pairwise coalescence times, which will affect the variance of haplotype homozygosity-based statistics (supplementary fig. S1, Supplementary Material online). In the simulations with population structure, the effect of migration also depends on the statistics. For iHS and nS_L, the total variation distance decreases with M. For other statistics, especially rEHH, the total variation distance increases with M. Supplementary table S3, Supplementary Material online, shows total variance distance results for a wider range of demographic parameters. In all the scenarios, nS_L is the most robust method.

Although the total variance distance is an appropriate summary statistic for illustrating differences between distributions, differences in the tail of the distribution are particularly important in the current context because only the tail of the distribution matters in the hypothesis testing scenario. We, therefore, also show the entire distribution for various population growth rates and bottleneck models for iHS and nS_L in supplementary figure S1, Supplementary Material online. Note that the behavior of the tails of the distributions mimics that expected from the total variance distance, that is, both iHS and nS_L are somewhat sensitive to population growth, and iHS a bit more so than nS_L. In general, iHS and nS_L appear to be the most robust statistics with total variation distance varying between 0.01 and 0.13 depending on migration rate and window size.

We also, in supplementary table S4A and B, Supplementary Material online, provide a table of false-positive rates at the 5% and 1% significance level for the simulations discussed in table 1. In many cases, the variance of the test statistic is smaller than under the standard neutral model, leading to a conservative test when there, for example, is population growth or the population has experienced a bottleneck in the population size. Some notable exceptions include the classical cases of Tajima’s D in the presence of bottlenecks or population growth and Fay’s and Wu’s H in the presence of population structure and migration. Among the haplotype-based statistics, rEHH seems most often to tend to produce an excess of false positives in the presence of nonstandard demographics. Some of the other tests are in some cases highly conservative. This is not a desirable property as it is often associated with correspondingly low power.

Robustness to Assumptions Regarding Recombination and Mutation Rates

To evaluate the effect of assumptions regarding recombination, we simulated data for regions with ρ = 2,000 and θ = 1,000, where ρ is the population-scaled recombination rate under a standard neutral model and θ is two times the population-scaled mutation rate. We compared this distribution with that obtained under values of ρ equal to 0, 400, and 4,000 (table 1), corresponding to no recombination, a 5-fold reduction in recombination rate and a 2-fold increase in recombination rate. As predicted from O’Reilly et al. (2008), all the established statistics are somewhat sensitive to the assumptions regarding recombination rates. For example, for a 5-fold decrease in recombination rate, the total variation distance varies between 0.05 and 0.20 for rEHH and between 0.10 and 0.22 for Tajima’s D. The most robust of the previous test statistics is iHS, which for a 5-fold decrease in recombination rate has total variation distance varying between 0.06 and 0.09. In all the scenarios, nS_L is the most robust method, except when the recombination rate is high (ρ = 4,000). In that case, EHH and rEHH, when respectively calculated in windows of ρ = 200 and ρ = 2, perform similarly to nS_L. For the other recombination rates, nS_L has at least two times smaller variation distance than the rest of methods. Supplementary table S3, Supplementary Material online, shows the robustness of these statistics for some additional recombination rates. In all the scenarios, nS_L is the most robust method. Supplementary table S4A and B, Supplementary Material online, provide false-positive rates for fixed nominal significance levels.

Power

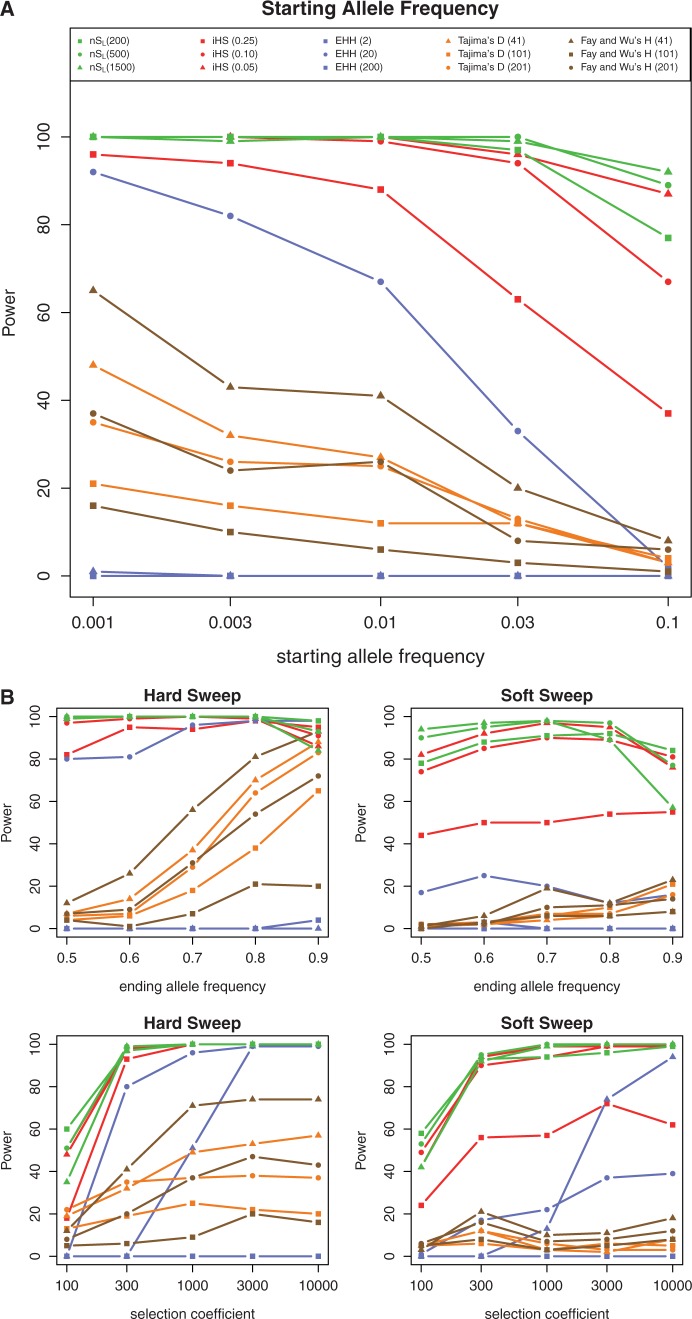
To quantify the power of the various test statistics for detecting selective sweeps, we performed simulations using the program mbs (Teshima and Innan 2009) with selection acting on a de novo mutation (hard sweep) as well as on alleles with initial frequencies of 0.001, 0.003, 0.01, 0.03, or 0.1 (soft sweeps) (fig. 2A). For the simulations under selection, we used θ = ρ = 300. The simulated region was 0.3-cM long and selection was set up to always occur at the center of the region. For the selected allele, we generated 1,000 allele frequency trajectories for each combination of initial and final frequencies. For each trajectory, a sample of 100 chromosomes was produced.

Fig. 2.

(A) The power of five methods (nS_L, iHS, EHH, Tajima’s D, and Fay’s and Wu’s H) for a range of starting allele frequencies (0.001–0.1). Power is defined as the proportion of simulations that reject the neutral null hypothesis at the 5% significance level. Each color corresponds to a method and symbols correspond to the window sizes used to run the methods (the specific window sizes used for the analysis are given in parenthesis). (B) The power of the five methods for a range of ending allele frequencies (0.5–0.9) (top two panels). The bottom two panels show the power of the methods for a range of selection coefficients (4Ns = 100−10,000). The color scheme and symbols in these panels correspond to the legend embedded in (A).

Power is defined as the proportion of simulations that reject the neutral null hypothesis at the 5% significance level. As in the case of the previous simulations, we compared nS_L with Tajima’s D, Fay’s and Wu’s H, EHH, and iHS. Figure 2A shows that when selection occurs on a preexisting allele all the methods examined loose power as the initial frequency of the selected allele increases. However, generally in this scenario haplotype-based methods have more power than SFS-based methods and, nS_L has the highest power. Notice that even for very low initial frequencies (0.1%), where LD-based methods have full power, SFS-based methods have half the power of LD-based methods. As the frequency of the selected allele increases, iHS and nS_L experience a relatively small reduction in power (∼10–30% reduction for allele frequencies >1%), whereas SFS-based methods under the same conditions experience an almost complete reduction in power (∼70–80% reduction in power). The most dramatic loss of power is observed for EHH. At low initial frequencies (0.1%), this method has high power, but the power reduces to close to zero when the initial frequency is high (10% allele frequency). Figure 2A shows the power of the five methods for different window sizes. Notice that the power of all the haplotype-based methods, and EHH in particular is highly dependent on the window size. In general, small window sizes result in low power (supplementary fig. S2A and B, Supplementary Material online).

We also examined the power of these methods using a range of different selection coefficients and current allele frequencies (fig. 2B). The current allele frequency is the allele frequency at the time of sampling. We focused on two scenarios: selection on a new allele (a hard sweep) and selection on a preexisting allele at frequency 1% (a soft sweep). For the hard sweep, haplotype-based methods have higher power than SFS-based methods. However, the power of the SFS-based methods increases as the current allele frequency increases, and becomes comparable with those of haplotype-based methods when the current allele frequency is high (∼90%). This is not surprising, as the haplotype-based methods are known to have most power when the allele frequency is moderately high (65–85%) (Voight et al. 2006), whereas SFS-based methods retain power, and often maximize power, when the allele frequency is at, or near, 100%.

In the case of a soft sweep, we again observe that the haplotype-based methods have more power than SFS-based methods. In general, nS_L performs better, having higher power than the rest of methods, in particular for low allele frequencies. For all the frequencies and selection coefficients we tried, nS_L has the most power except when it is calculated using a large window (1,500 segregating sites), the ending allele frequency is high (70%), and the selection coefficient is intermediate (4Ns = 1,000). With these parameters, the power of the nS_L statistic drops to 50%.

We examined the power of these statistics to detect selection in expanding populations by plotting receiver operating characteristic (ROC) curves under a range of population growth rates and selection coefficients. The areas under the ROC curves are shown in supplementary table S5, Supplementary Material online, and some representative curves are shown in supplementary figure S2C–E, Supplementary Material online. The iHS and nS_L statistics have the largest areas under the curves, with nS_L having slightly higher areas. As expected, for all statistics, the area under the curve is maximized when selection is strong and the growth rate is low.

Analysis of HAPMAP Data

We analyzed phased data for the autosomal polymorphic positions in the 11 human populations from the International HapMap 3 Project (International HapMap 3 Consortium 2010) (http://hapmap.ncbi.nlm.nih.gov/, last accessed March 3, 2014). The analysis was restricted to the subset of SNPs (12487425), for which we could assess the ancestral allele state by comparing chimpanzee, macaque, and human reference sequences.

Robustness in the Analysis of HapMap Data

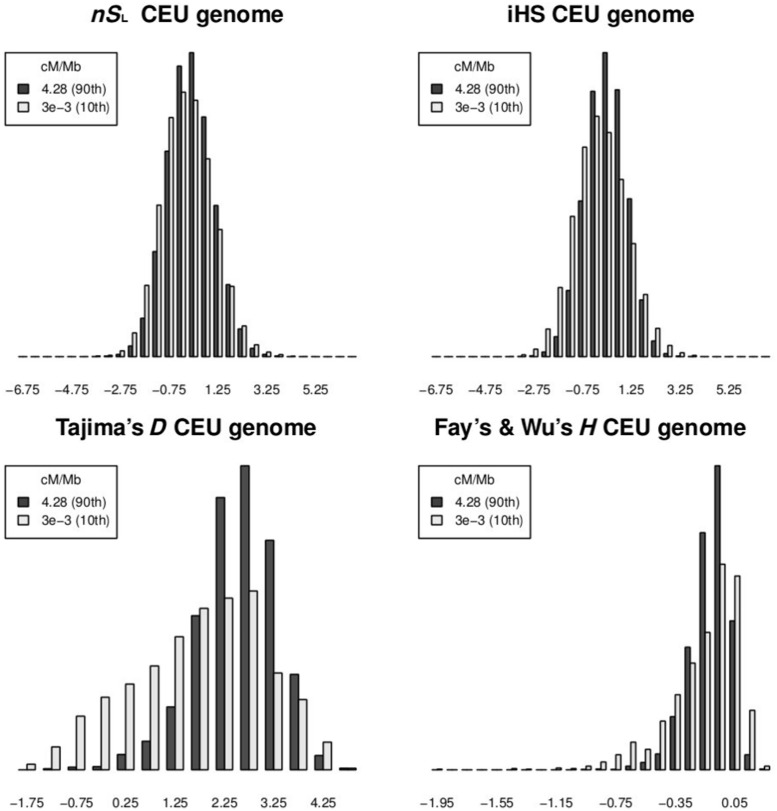
We computed the previously discussed five statistics for the HapMap3 CEU population to examine whether the biases caused by recombination rate variation are also present in real data. Figure 3 shows the distribution of iHS, nS_L, Tajima’s D, and Fay’s and Wu’s H for sites with low or high recombination rates. The distribution of nS_L is similar for low and high recombination rates, whereas the other statistics have higher variance in regions of low recombination. This is consistent with the expectation from the simulation. Examining the top values of each statistic (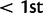 and 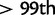, respectively), we find 8% of nS_L values, 9% of iHS values, 7% of Tajima’s D values, and 8% of Fay’s and Wu’s H values fall in regions of low recombination rate 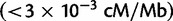, whereas 9%, 5%, 1%, and 1% of their values fall in regions of high recombination rate (>4.28 cM/Mb). These results are concordant with the conclusion from the simulation studies that nS_L is more robust toward variation in recombination rate than other statistics, with iHS as a close second. In contrast, Tajima’s D and Fay’s and Wu’s H are very sensitive to recombination rate variation. These two methods are intended for DNA sequencing data, and the use of ascertained SNP genotyping data may affect their distributions. However, as these results mirror those found in simulations of full sequencing data, they lend further support to the hypothesis that results of genome scans based on these tests are highly sensitive to recombination rate variation (O’Reilly et al. 2008). Similar conclusions will likely be true for other statistics based on the SFS that do not directly incorporate recombination rate variation.

Fig. 3.

Robustness to recombination rate. Distribution of nS_L, iHS, Tajima’s D, and Fay’s and Wu’s H for regions with high (black) and low (gray) recombination rate. Plots are made with whole-genome genotype data for the HapMap3 CEU population (Utah residents with Northern and Western European ancestry from the CEPH collection).

Overview of Selection Signatures in Africa

To date, most genome scans for positive selection have been performed on the three populations originally included in the HapMap project: Europeans (CEU), Asians (CHB and JPT), and Africans (YRI). Signatures of selection within and between these populations have been described elsewhere (Weir et al. 2005; Voight et al. 2006; Wang et al. 2006; Kimura et al. 2007; Sabeti et al. 2007; Tang et al. 2007; O’Reilly et al. 2008), but only a limited number of genome-wide scans have been published on African populations (Andersen et al. 2012; Jarvis et al. 2012). Because of the availability of several populations of African ancestry in the HapMap3 (4 out of 11), we focused on reporting and discussing the results for these populations using nS_L.

As in Voight et al. (2006), we primarily interpret our results as an outlier approach, because it facilitates comparisons between results obtained using different methods (specifically, between nS_L and iHS). However, we also provide P values estimated using simulations (see Materials and Methods). We warn against a strong interpretation of these P values, because as illustrated in the analysis of simulated data, the distribution of any of the neutrality statistics depend on demographic assumptions, although less so for nS_L than for the other statistics. Based on the outlier approach, we identify the genes that have most likely been affected by selection (see Materials and Methods).

Comparisons with iHS: Recombination Rate Variation

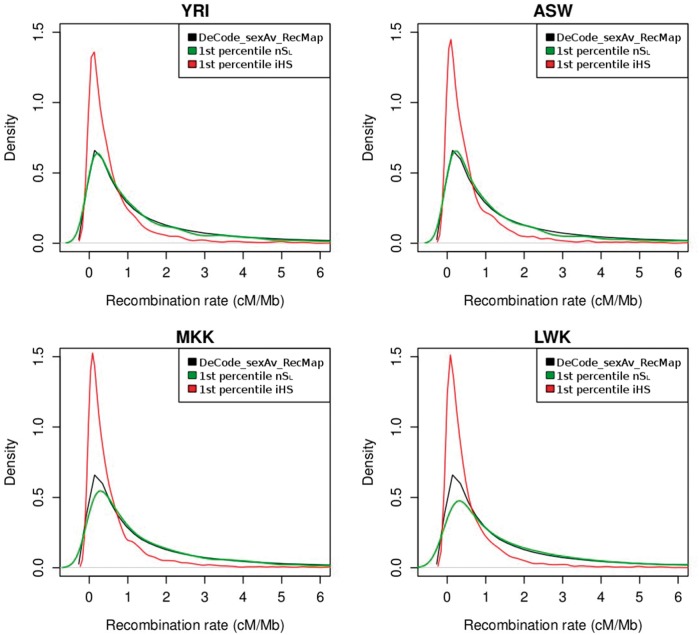
We examined the effect of recombination rate variation by plotting the distribution of recombination rates among the SNPs in the first percentile of the nS_L and iHS distributions and compared these distributions with the distribution of the recombination rate from the entire genome using the DeCode map (fig. 4). The recombination rate distribution of nS_L outliers is similar to the overall distribution of the genome. In contrast, the distribution of the recombination rate for the iHS outliers is shifted toward regions with low recombination rates. This illustrates that iHS tends to detect more outliers in regions of low recombination rates. This phenomenon was observed in all four African populations and it is in agreement with the results obtained using the European population from HapMap 3 (fig. 3) as well as with the simulation results (table 1).

Fig. 4.

Distribution of the recombination rate. Distribution of recombination rate for nS_L and iHS outliers (less than the first percentile of the respective empirical distributions). Recombination rate for nS_L outliers is shown in green, whereas recombination rate for the iHS outliers is in red. The distribution of the recombination rates for the entire genome is shown in black (data taken from the DeCode recombination map). Each panel in the figure corresponds to one HapMap3 population of African ancestry (YRI, ASW, MKK, and LWK).

Comparisons with iHS: Individual Missense Mutations with Strong Signal

To further explore the difference between nS_L and iHS, we analyzed the results for the SNPs with the largest difference between nS_L and iHS scores: rs2267161 and rs10828663. Both SNPs have extreme values of nS_L (−2.92 and −3.00, respectively) but moderate iHS values (−0.38 and −0.55, respectively). To our knowledge, neither of the regions to which these SNPs belong have previously reported as targets of positive selection. The haplotype structure of the haplotypes tagged by the SNPs are in both cases roughly compatible with what would be expected from a classic selective sweep, that is, a single allelic class with reduced haplotype homozygosity (fig. 5). However, the value of iHS does not indicate the presence of selection at these sites, presumably due to a high recombination rate in these regions (3.46 cM/Mb and 2.84 cM/Mb, respectively). One of the SNPs (rs2267161) is located at GAL3ST1; a gene involved in the metabolism of a number of different compounds including hormones and neurotransmitters. The rs2267161 variant itself is associated with increased risk of type 2 diabetes. In the homozygous state, the ancestral allele is associated with lower insulin resistance in females (Roeske-Nielsen et al. 2009). The other SNP (rs10828663) is in a gene with little functional annotation (KIAA1217).

Fig. 5.

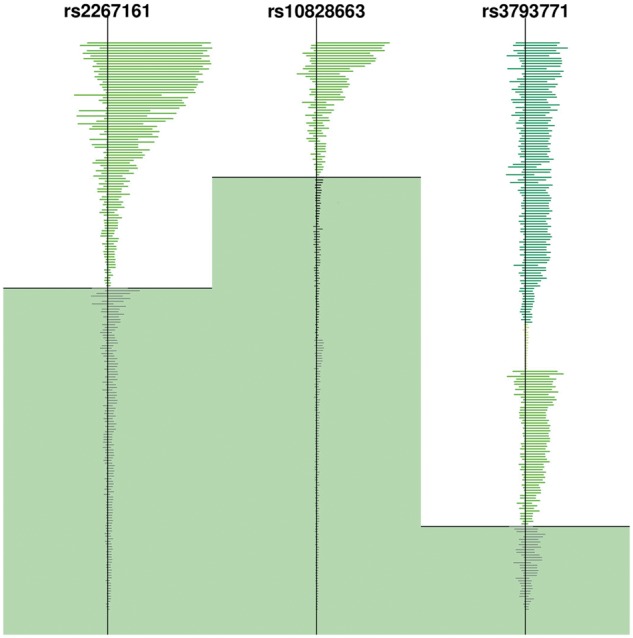
Haplotype pattern for three SNPs in the YRI population. The vertical dark line indicates the location of the SNP (SNPid is shown). The average length of each haplotype is represented by a horizontal line. The different haplotype backgrounds carrying the derived allele are denoted by different tones of green. Each tone of gray indicates a different haplotype background carrying the ancestral allele. All haplotypes carrying the derived allele lie on the white background, whereas haplotypes carrying the ancestral allele lie on the green background.

Finally, we investigated outliers that did not fall in regions of high recombination, but nonetheless showed a strong difference between nS_L and iHS values. An extreme case is rs3793771 with an nS_L value of −2.75 but a value of −1.90 for iHS, although the recombination rate in the region is only 0.26 cM/Mb. As illustrated in figure 5, this SNP might represent a case of selection on standing variation. It falls in WNT8B, a gene with expression restricted to the developing brain (Lako et al. 1998).

Novel Selection Signatures in African

In the following section, we describe, by gene, the top signature(s) of positive selection in African populations using nS_L. We focus on a contrast between the Maasai and the Yoruban populations, which have very distinct and extreme patterns, as illustrated below. A list of the top 30 nS_L outliers ( or percentile) for each HapMap3 population is included in the supplementary table S6A–K, Supplementary Material online.

Top Signatures of Selection in the Maasai Population (MKK)

Among all 11 populations analysed in this study, the Maasai population (MKK) includes the most extreme nS_L value (6.63, P value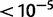; rs16831455). This value, and other similarly high values are found in the region around the LCT gene, for which regulatory variants have previously been shown to be under selection in this population, relating to lactose persistence (Tishkoff et al. 2007). The pattern in the HapMap3 data is so extreme that all top 50 SNPs in the MKK population are within a 3.4-MB region around LCT (supplementary fig. S3, Supplementary Material online) and all have P values less than 10⁻⁵. The highest value falls within the ZRANB3 gene (table 2); a gene encoding a zinc finger protein. This variant is intronic and has a positive nS_L value, which might indicate selection associated with the ancestral allele if selection was acting directly on this SNP. However, the effect we observe is likely due to LD with SNPs not included in the HapMap 3 data. Tishkoff et al. (2007) reported three variants conferring lactose persistence in the Maasai population; these variants are not present in HapMap3 data, but given the high LD around LCT (supplementary fig. S4, Supplementary Material online) the signature of selection found on rs16831455 might be caused by selection acting on the previously identified SNPs. The average recombination rate in this region is 1.56 cM/Mb, partly explaining why the signal of selection spans such a large section. A gene ontology (GO) analysis of the top 3% of genes showed enrichment for two GO components: cell junction (corrected P value = 0.03) and synapse part (corrected P value = 0.03), none of them containing LCT or ZRANB3.

Table 2.

The Top Ten Genes with the Most Extreme nS_L Scores in the Masaai (MKK) and Yoruban (YRI) Populations.

Population	SNPid	Chr	Position	Derived Allele	DAF	nSL	P Value	Function	Rec Rate	Gene
MKK	rs16831455	2	135690238	G	16	6.63	1e–5	Intron	—	ZRANB3
MKK	rs309154	2	136443037	C	25	6.24	1e–5	Intron	—	DARS
MKK	rs16838134	2	137595057	C	22	−6.12	1e–5	Intron	0.024	THSD7B
MKK	rs13390171	2	135493974	A	25	5.97	1e–5	Intron	—	YSK4
MKK	rs6430516	2	134935075	G	29	5.89	1e–5	Intron	1.449	TMEM163
MKK	rs2289959	2	136140374	C	19	5.49	1e–5	Intron	0.004	R3 HDM1
MKK	rs11887041	2	134773894	G	52	5.43	1e–5	Intron	—	MGAT5
MKK	rs3769012	2	136272950	A	73	−5.31	1e–5	Intron	0.003	LCT
MKK	rs4954221	2	135625932	G	70	−5.30	1e–5	Intron	—	RAB3 GAP1
MKK	rs1050115	2	136228287	G	70	−5.25	1e–5	Coding-synon	0.003	UBXN4
YRI	rs7193968	16	69230453	G	2	4.94	5e–5	Unknown	—	IL34*
YRI	rs4312417	19	43489029	A	78	−4.85	1e–5	Intron	0.729	YIF1B*
YRI	rs11880532	19	43550883	T	80	−4.83	1e–5	Intron	—	CATSPERG
YRI	rs2866908	4	108124957	A	14	4.83	1e–5	Intron	—	DKK2*
YRI	rs10231365	7	20398110	C	25	4.82	1e–5	Intron	1.526	ITGB8
YRI	rs2413395	22	34984662	A	7	4.82	1e–5	Intron	2.325	APOL1 (lipid binding)
YRI	rs8136512	22	32461239	C	28	−4.81	1e–5	Intron	1.071	LARGE*
YRI	rs6687226	1	160158180	A	1	4.76	1e–5	Intron	0.057	ATF6*
YRI	rs11292	10	102303597	G	20	4.73	1e–5	Untranslated-3	0.087	HIF1 AN
YRI	rs10234980	7	79958990	T	25	−4.64	1e–5	Intron	—	CD36 (lipid binding)

Note.—The table shows the top ten |nS_L| scores falling within genes in the MKK and YRI populations from HapMap3. The first column indicates the population, next columns show the SNP identification number, the location (chromosome and position) of each SNP based on HG18, the derived allele and derived allele frequency (DAF), the nS_L score and P value (calculated under the demographic model for Yoruba proposed in Gutenkunst et al. [2009]; the function of the SNP, the recombination rate (Rec Rate) in cM/Mb at the site (from the DeCode recombination rate map) and the gene the SNP is located in. In the YRI population, SNPs that are not among the strongest signatures of selection according to Voight et al. (2006) are marked with an asterisk. Genes involved in lipid binding and in the metabolism of cholesterol are indicated in the table with the notation: lipid binding.

Top Signatures of Selection in the Yoruba Population (YRI)

In the YRI population, the most extreme nS_L value is in the IL34 gene. This gene encodes a cytokine that promotes the differentiation and viability of monocytes and macrophages through the colony-stimulating factor-1 receptor (Wei et al. 2010). The SNP with the highest nS_L value (4.94, P = 0.00005) also has a high nS_L in the MKK population (2.86, 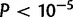). This gene itself has, to our knowledge, not previously been reported as candidate for positive selection.

We performed a gene ontology analysis of the top 3% of genes with extreme nS_L scores to identify enriched GO terms. We emphasize that such enrichment may not in itself demonstrate validity of the results Pavlidis et al. (2012).

This analysis revealed three enriched functional categories in the YRI population: the lipid-binding category, the plasma membrane and the intracellular ligand-gated ion channel activity (corrected P values = 0.05, 0.04, and 0.04, respectively). Interestingly, two out of the top six genes (APOL1 and CD36 are members of the lipid-binding category). They both have important roles in the metabolism of cholesterol. APOL1 is involved in the formation of most cholesteryl esters in plasma and also promotes efflux of cholesterol from cells. Also, it may play a role in lipid exchange and transport throughout the body, as well as in reverse cholesterol transport from peripheral cells to the liver (Duchateau et al. 2000). CD36 is implicated in the binding and internalization of oxidized low-density lipoprotein (Ox-LDL) (Liu et al. 2010). It is involved in cholesterol uptake in monocytes and macrophages (Anwar et al. 2011) and contributes to cholesterol efflux in hepatic cells (Truong et al. 2010). Its expression increases as a result of raised Ox-LDL, as well as raised levels of glucose, insulin resistance, low high-density lipoprotein (HDL) cholesterol and free fatty acid (Gautam and Banerjee 2011). A part from APOL1 and CD36, our top list of candidates includes one more gene related to cholesterol metabolism: ATF6. This gene encodes a transcription factor that is activated during endoplasmic reticulum stress and is processed in response to cholesterol deprivation (Ye et al. 2000). Finally, the lipid-binding category also includes one more high-scoring gene (ranked 22nd) involved in cholesterol metabolism: OSBP2. This gene, also named ORP4, interacts with intermediate filaments and inhibits an intracellular cholesterol-transport pathway (Wang et al. 2002).

It is worth noticing that APOL1 is also involved in parasite killing. Specifically, it is responsible for trypanosome killing through its anionic pore-forming capacity. It triggers uncontrolled osmotic swelling of the lysosome (Pays and Vanhollebeke 2009). This is a type of human innate immunity against trypanosomes, and possibly other parasites. Similarly, CD36 harbors genetic variants associated with susceptibility to malaria (Aitman et al. 2000).

Discussion

We present a haplotype homozygosity-based method (nS_L) for the detection of positive selection using haplotype homozygosity. The method differs from previous methods primarily in measuring genomic distances using counts of segregating sites. Using simulations and real data, we compare this to other methods including both methods based on information regarding the SFS and methods based on haplotype structure. We generally find that most methods are less robust than perhaps previously assumed. In particular, none of the haplotype-based methods are fully robust to demographic assumptions. We also show, in accordance with the results of O’Reilly et al. (2008), that all previous methods lack robustness to assumptions regarding local recombination rate. Among the previous methods, iHS is generally most robust, especially in the presence of population structure. Much of this robustness is achieved by the use of ratios of haplotype homozygosity between derived and the ancestral alleles, in the construction of the test statistic. The new method, nS_L, is more robust than other methods for most of the scenarios investigated here, and in general has the same power or more power than tests based on previously proposed statistics. nS_L is closely related to the iHS statistic, and has very similar properties. However, nS_L is more robust to variation in mutation/recombination rates and is somewhat more robust to assumptions regarding changes in population size. It primarily achieves this robustness by measuring haplotype length in terms of segregating sites rather than true genomic distance, thereby incorporating more information about local total tree length.

We notice that the increased robustness to recombination rate variation is of particular importance in genomic scans, using outlier methods, or more generally in studies focusing on ranked lists of genes. As pointed out by O’Reilly et al. (2008), such methods have a tendency to primarily identify SNPs in regions of low recombination. One possible explanation for this is that regions with low recombination rate are more likely to be affected by genetic hitchhiking. However, when using the nS_L statistic, we do not find a large enrichment in regions of low recombination. Given that nS_L is more robust to recombination rate variation and is at least as powerful as other statistics, this suggests that the enrichment found using other statistics may be due to an increased false-positive rate.

Przeworski et al. (2005) argue that sweeps from standing variation might be more important in recent human history than classic selective sweeps. Many of the most common methods for detecting selection have reasonable power to detect classic sweeps, but less so to detect sweeps from standing variation (Kim and Stephan 2002). Using simulations, we here evaluate the power of nS_L and several previous statistics, to detect sweeps from standing variation. Both nS_L and iHS have considerable power to detect selection on standing variation, perhaps more so than previously appreciated, in particular, when the selection coefficient is high (S > 300) and the initial allele frequency is less than 10%. The power of nS_L is again as high or higher than the power of iHS, but the power is generally very similar between the two methods. In real data analyses, the results differ between these two methods, as illustrated by the result on rs3793771, a missense SNP in a region not previously reported to be targeted by positive selection. This site has two different long haplotypes associated with the derived (and presumably advantageous allele), a possible consequence of a soft sweep (fig. 5). For this SNP, nS_L has an extreme value (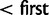 quantile of nS_L empirical distribution) while the value of iHS is moderate ( 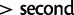quantile of iHS empirical distribution).

All of the methods discussed here rely on a predefined window size, and this window size strongly influences power. The reason for a specification of window size for methods such as Tajima’s D is obvious. However, it is perhaps less obvious for statistics such as EHH, iHS, and nS_L. For these three methods, the window size determines the maximum allowed length of a haplotype. In EHH and iHS, the use of a window size was originally introduced for purely computational reasons to reduce computational complexity. We notice that even under a standard neutral model, the expected length of homozygosity segment is infinite. The expected time to the next mutation or recombination in a fragment with initial coalescence time t between a pair of sequences, is given by 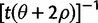(see Definition of Statistics for definitions). The integral of this expectation over the distribution of t in the standard neutral model does not converge. Although perhaps this observation may initially be dismissed as a minor mathematical point, it helps explain the strong effect of window size on the power of the haplotype homozygosity-based statistics observed in our simulations (figs. 3 and 4). There is no simple cutoff for which the haplotype-based statistics in average take on the same value as if no cutoff had been used. For practical purposes, based on our tests, we recommend using SNP density to determine the cutoff. In our case, after testing nS_L using a range of cutoffs on genotyping (HapMap3) and simulated (ms) data, we decided to use a window size of 1,500 SNPs for HapMap3 data and a window of 200 SNPs for ms data.

As an example of the utility of the method, we analyze genotype data from the 11 populations in the HapMap3 project. We report the top nS_L scores in each population and focus on the four populations of African ancestry. Our most interesting finding is perhaps the results on the YRI (Yoruban) population. This population shows an enrichment of nS_L scores in three GO categories: lipid binding, plasma membrane, and intracellular ligand-gated ion channel activity. The lipid-binding category contains genes directly related to cholesterol metabolism. Interestingly, the YRI population is often argued to be the ancestral population of many African Americans (Price et al. 2009), who generally have elevated HDL cholesterol levels (47 mg/dl) and reduced triglyceride levels (102 mg/dl) compared with Americans of Europeans descent (HDL: 44 mg/dl and triglycerides: 134 mg/dl; both with 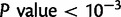) (Haffner et al. 1999).

Several studies have shown that this difference in the cholesterol levels can not be explained exclusively by environmental effects, but likely has a genetic basis (Berbée et al. 2005). In the YRI population, the cholesterol-related gene presenting the most extreme nS_L score is APOL1, a gene encoding a component of HDL. Alleles in this gene are associated with protection against Trypanosoma brucei rhodesiense, but not against T. b. gambiense; both Trypanosoma subspecies cause human sleeping sickness that results in 50,000 deaths per year. So far two variants of APOL1 have been associated to the lysis of some T. b. rhodesiense clones (Genovese et al. 2010), which previously have been argued to have been subject to positive selection (Genovese et al. 2010). Interestingly, the YRI population inhabits a region not influenced by T. b. rhodesiense but by T. b. gambiense, for which these two alleles have been shown not to confer protection (Genovese et al. 2010). The APOL1 SNP with a high nS_L value identified in this study is not linked to the variants described to confer resistance to T. b. rhodesiense and selection at this site could possibly be the consequence of local adaptation to T. b. gambiense, instead. The candidate allele is ancestral, suggesting that selection may possibly affect another linked SNP.

The other major lipid-related protein with extreme nS_L values in the YRI population is CD36. Variants in this gene have been shown to be associated with increased HDL cholesterol levels (Liu et al. 2010). In addition, variants in the gene are also associated with malaria resistance (Aitman et al. 2000; Sirugo et al. 2008). For both CD36 and APOL1, the nS_L values are high in the YRI population but moderate in other African populations. Similarly, only the YRI population shows a GO enrichment of lipid metabolism genes with extreme nS_L values.

For both APOL1 and CD36, selection may likely not primarily have targeted the effect of the genes in terms of lipid transport and cholesterol, but rather the pleiotropic effects on defense against pathogens. It is difficult to establish the exact selective agent of past selection, but the strong direct fitness consequences of T. brucei or malaria infection, here suggest selection might primarily be acting in response to these diseases. If so, the differences in lipid metabolism between certain African populations and other populations might be a secondary effect of the selection relating to blood parasites. With a few exceptions, such as lactose tolerance (Enattah et al. 2002) and altitude adaptation (Simonson et al. 2010; Yi et al. 2010; Peng et al. 2011; Xu et al. 2011), strong selection in humans, particularly local selection, seems to be dominated by selection in response to pathogens (Pennings and Hermisson 2006a; Cagliani et al. 2013). This is perhaps not surprising given the strong effect on human survivorship of many pathogens. The resulting pleiotropic effects of the immune and defense-driven genetic changes may explain differences between different groups of humans in traits such as susceptibility to autoimmune diseases (Fumagalli et al. 2011) and lipid metabolism.

Materials and Methods

The nS_L Statistic

The nS_L statistic is a haplotype-based statistic designed to detect the signature of positive selection in single-population genomic data. This method requires phased data and information on the ancestral/derived status at each segregating site. A formal description of the method is in the Definition of Statistics section.

Dependency on Allele Frequency

As nS_L highly depends on allele frequency (supplementary fig. S5A, Supplementary Material online), we standardized results as in Voight et al. (2006) by binning the SNPs by allele frequency and subtracting the mean and dividing by the standard deviation of each bin. Frequency categories were defined by 1% frequency increments (supplementary fig. S5B, Supplementary Material online).

Simulations under Neutrality and Summary Statistics

We used two summaries of the SFS: Tajima’s D (Tajima 1989) and Fay’s and Wu’s H (Fay and Wu 2000) and two haplotype-based methods: EHH and iHS (Sabeti et al. 2002; Voight et al. 2006) for comparison with nS_L. We applied these five methods on simulated full-sequencing data generated with ms (Hudson 2002). We defined a baseline standard neutral demographic model of one population of constant size with 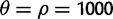(over the locus), where θ and ρ had their standard definitions of 4Nµ and 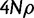. We used a sequence length of 0.3 cM. We then varied this baseline neutral model to produce simulations with 1) a population expansion for a range of growth rates (α = 1, 10, 100, and 1,000); 2) a population bottleneck for a range of bottleneck ratios that occurred 1,200 generations ago and lasted 800 generations (r = 0.5, 0.25, 0.1, and 0.05); a two island model with migration assumed to be symmetric and constant in time. Under this model, we varied the population-scaled migration rate between the two islands and sampled from one of them (M = 0.001, 0.01, 0.1, 1, and 10). α is the growth rate. If t is in coalescent units, then the effective population size as a function of time is given by 2N₀exp(-α* t), where 2N₀ is the effective population size at the present. The bottleneck ratio, r, is 2N₀/2N₁, where 2N₁ is the population size for the duration of the bottleneck and N₀ was assumed to be 10⁴. The population-scaled migration rate, M, is 4Nm, where m is the probability, per generation, that an individual switches populations. Finally, we varied the recombination rate (ρ = 0, 200, 400, 2,000, and 4,000) (supplementary table S3, Supplementary Material online). Under each of these scenarios, we ran 100 simulations with 20 chromosomes per simulation. We also used neutral simulations to investigate the power of nS_L and the other four statistics to reject a neutral hypothesis in favor of a recent selective sweep. For this purpose, we simulated data under a standard neutral model of one population of constant size. Assuming 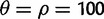and a length of 0.3cM. Data corresponding to selective sweeps were then simulated using the mbs program (Teshima and Innan 2009), as described later. The statistical power of each method was computed as the ratio of simulated data sets, which were rejected to the total number of simulated data sets. For a simulated sample of sequences, nS_L, iHS, and EHH were calculated at a single site in the center of sequence or at the site under selection.

Simulations of Selection

We estimated the power of the new method to detect positive selection through simulations. As mentioned, we used the program mbs (Teshima and Innan 2009) to generate 0.3-cM long regions with a biallelic site under selection at the center of the region. For each of the scenarios described later, 1,000 replicates were simulated with θ = 4Nμ = 1,000 and 100 sampled chromosomes. We tested selection on a new allele and selection on standing genetic variation. In the latter case, we used a range of starting allele frequencies (0.1%, 0.3%, 1%, 3%, and 10%) (fig. 2A). For these simulations, we used a population-scaled selection coefficient of s = 1,000 and an ending allele frequency of 80%. For a starting allele frequency of 0% (selection on a new allele) as well as for a starting allele frequency of 1% (selection on standing variation), we varied the selection coefficient (S = 0.0012, 0.004, and 0.012) and the final allele frequency (from 50% to 90%, in 10% increments) (fig. 2B). We generated the trajectory files for the selected alleles using two programs provided with mbs (forwardtraj.c and backwardtraj.c). Backward simulations were used to create the trajectory of new alleles, whereas a combination of both forward and backward simulations was used to simulate the trajectory of alleles in the soft sweep scenario. In the latter case, we used backward simulations for the trajectory of a neutral allele before it reached 1% frequency in the population (setting S = 0) and then used forward simulations after that time until the allele reached the ending frequency (the frequency at the time of sampling). We used rejection sampling to condition on the ending frequency of the alleles. The underlying demographic model for the simulations under selection was the standard neutral model described in the previous section.

Estimation of P Values

We computed an approximate P value by simulating the distribution of nS_L under an approximating neutral demographic model. This was done while binning SNPs based on their derived allele frequency, to account for dependence in the distribution on allele frequencies. The simulations were carried out with the program ms (Hudson 2002) using the demographic model of Gutenkunst et al. (2009), which models the demographic history of four populations: African, East Asian, European, and Mexican-American. We analyzed data from 11 populations, eight of which can directly be compared with the populations in Gutenkunst’s model: three African (LWK, MKK, and YRI), two East Asian (JPT and CHB), two European (CEU and TSI), and one Mexican-European admixed population (MEX). Two populations are admixed (ASW is African-European admixed and CHD is Asian-European admixed) and GIH is an Indian population for which there is no equivalent in the demographic model we use. For this reason, we omitted GIH when we made comparisons with the null model. Despite the inaccuracies in the demographic model, we compared ASW with Africans and CHD with Asians. As a consequence, every nS_L score in the study is accompanied by a P value, except in the GIH population because the lack of demographic model. Hypothesis testing throughout the article is one-tailed.

Correcting for SNP Ascertainment Bias

Because of SNP ascertainment the allele frequency spectrum (SFS) of HapMap3 data does not agree with the SFS generated by the Gutenkunst demography. We used rejection sampling, as in Voight et al. (2006) to match the frequency spectrum of the simulated data with the observed SFS in the real data.

HapMap Phase 3 Data

We used autosomal phased haplotype data from the 11 populations included in the HapMap Phase3 release 2. These data contain a total of 1,184 samples (supplementary table S1, Supplementary Material online). We excluded closely related individuals by estimating pairwise identity-by-descent (IBD) with the PLINK tool set (Purcell et al. 2007) using the option—genome (http://pngu.mgh.harvard.edu/purcell/plink/, last accessed March 3, 2014). Sites with major allele frequency or missing data rates of more than 5% were not included. We excluded 339 individuals from the analysis because more than 5% of their genomes were estimated to be IBD. A breakdown by population is given in supplementary table S1 (Supplementary Material online). The HapMap consortium phased the data using family information to deterministically resolve phase by transmission, when possible, and used IMPUTE++ (Howie et al. 2009) otherwise. The consensus set of SNPs after imputation contains 1385868 SNPs. The number of SNPs in each chromosome is given in supplementary table S2 (Supplementary Material online).

SNP Position and Function

The position of the SNPs included in the project is based on NCBI36/hg18. We used the UCSC genome browser (http://genome.ucsc.edu/, last accessed March 3, 2014) to determine the functional state of each SNP (nonsynonymous, synonymous, intronic, UTR, or intergenic). We were unable to attribute function to 0.56% of the SNPs because either their function was unknown (776,138 SNPs) or they were not present in UCSC database (1,953 SNPs).

Ancestral State

We used the snp129OrthoPt2Pa2Rm2 table from the UCSC Genome Table Browser to determine the ancestral state of each SNP. This information was available for 99.1% of the SNPs. The ancestral allele was assigned to the human allele that agreed with at least two nonhuman primate species. We did not assign an ancestral state for 4% of the SNPs because they showed discrepancies among the nonhuman primate alleles. Supplementary table S2, Supplementary Material online, also shows the number of SNPs for which we did not assign the ancestral allele.

Identifying Signatures of Selection

To define candidate loci that may have been targeted by selection, we first calculated nS_L for all SNPs and then established a cutoff based on the 1st and 99th percentile of the empirical distributions for each population independently. In addition, we assigned P values to each SNP using parametric simulations, as described in the section Estimation of P values. Results are presented by ranking the absolute normalized nS_L scores in each population. For the nS_L scores in the 1st and 99th percentiles, we performed a hierarchical cluster analysis of the fragment lengths between pairwise differences. Based on this analysis, we determined the number of different haplotypes backgrounds for each allele. This information was used for plotting purposes (visualization of the haplotypes carrying the derived and the ancestral allele).

We used RefSeqGenes (http://www.ncbi.nlm.nih.gov/refseq/rsg/, last accessed March 3, 2014) to assign SNPs to genes, when applicable. For this purpose, we focused solely on genes with transcript products, that is, with mature mRNA. When more than one transcript was available we used the longest transcript product. We then assigned SNPs into genes according to the transcript coordinates. We kept the most extreme 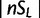score per gene to rank all genes according to this score and performed the Gene Ontology enrichment analysis using the GOrilla tool Eden et al. (2009) with two list of genes; the list of candidates (top 3% of genes) and the list of all genes in the study (from 14,269 to 14,279 genes, depending on the population). Any category belonging to GO process, GO function and GO component was considered significant if having a corrected P value ≤ 0.05. The corrected P value was computed as the P value provided by GOrilla times the number of tested GO terms.

iHS was computed using the code released by Voight et al. (2006). iHS scores were normalized similarly to nS_L. The EHH and rEHH were computed with our own code according to the description given by Sabeti (2005), where the EHH and rEHH of a particular core haplotype t are calculated as follows:

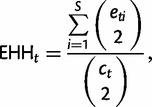where c is the number of samples of a particular core haplotype, e is the number of samples of a particular extended haplotype, and S is the number of unique extended haplotypes (Sabeti 2005).

The rEHH is 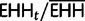. And, is the decay of EHH on all other core haplotypes combined:

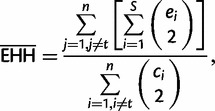where n is the number of different core haplotypes (Sabeti 2005).

For the purpose of this article, the core haplotypes of interest are defined by the presence or absence of a single SNP.

Supplementary Material

Supplementary figures S1–S5 and tables S1–S6 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).