Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Apr 23;4:4755. doi: 10.1038/srep04755

Enabling an Integrated Rate-temporal Learning Scheme on Memristor

Wei He 1,4, Kejie Huang 2,4, Ning Ning 1, Kiruthika Ramanathan 1, Guoqi Li 3, Yu Jiang 1, JiaYin Sze 1, Luping Shi 3,a, Rong Zhao 2,b, Jing Pei 3
PMCID: PMC3996481  PMID: 24755608

Abstract

Learning scheme is the key to the utilization of spike-based computation and the emulation of neural/synaptic behaviors toward realization of cognition. The biological observations reveal an integrated spike time- and spike rate-dependent plasticity as a function of presynaptic firing frequency. However, this integrated rate-temporal learning scheme has not been realized on any nano devices. In this paper, such scheme is successfully demonstrated on a memristor. Great robustness against the spiking rate fluctuation is achieved by waveform engineering with the aid of good analog properties exhibited by the iron oxide-based memristor. The spike-time-dependence plasticity (STDP) occurs at moderate presynaptic firing frequencies and spike-rate-dependence plasticity (SRDP) dominates other regions. This demonstration provides a novel approach in neural coding implementation, which facilitates the development of bio-inspired computing systems.

Our brain performs various cognitive tasks and outperforms the state-of-the-art von Neumann-based digital computer in many domains1,2. Brain inspired approach is one of the research directions to sustain the continuous performance improvement when downscaling of CMOS technology approaches its limits3,4,5. Despite the tremendous progress in VLSI technologies, it is still an insurmountable challenge to simulate our brain at the scale of 100 billion neurons and 100 trillion synapses using purely silicon-based devices6,7,8. It is widely agreed that the synapse - a biological connection between two neurons that allows information to flow from one to the other - is essential in mediating the processes of memory, learning and cognition9. A ubiquitous property of synapse is the ability to keep track of the activity history by shaping its plasticity, which is encoded via various forms of activity-dependent learning rules. Though the biological mechanism underlying the synaptic behaviors is still under debate, the identified parameters that influence synaptic plasticity including pre- and postsynaptic spiking interval10,11,12, spiking rate13,14, postsynaptic voltage15,16, dendritic location17,18, and postsynaptic depolarization19,20 have been reported. Generally, spiking-time-dependent plasticity (STDP), often interpreted as the “first law” of synaptic plasticity, focuses on the spike timing differences between the pre- and postsynaptic neurons in modifying the synaptic weight10,11,12,21. Apart from STDP, rate-dependent plasticity learning rule, which is termed as spike-driven rate-based plasticity13,22,23,24,25 or spike-rate-dependent plasticity (SRDP)26, expresses the dependence on spike frequency. Furthermore, in vivo experiments reveal that spike time- and spike rate-dependent plasticity integrate together as a function of presynaptic firing frequency14,27. When presynaptic neuron fires at moderate rates (10–20 Hz), STDP learning rule mostly occurs27. Outside of the moderate frequency region, spike rate-based synaptic learning rule governs the plasticity induction and is independent of pre- and postsynaptic spiking interval10,14,28. This integrated rate-temporal learning scheme is widely believed to play an important role in neural signal processing and information storage29,30,31. However, to our best knowledge, such learning scheme has not been realized on any devices.

Recent advancements in memristor (also termed as memristive device)32,33,34 have provided a strategic opportunity for advancing the development in neuromorphic engineering. This is attributed to the unique properties of the memristor including non-volatile storage, nano scale size, analog behaviors, and its ability to remember the history via the modulation of its internal state35,36. It sparks a new wave of enthusiasm in developing solid-state analog synaptic devices37,38,39,40,41,42,43. In this paper, we propose a novel way to emulate the dual coding (rate and temporal) learning scheme on a memristor by customizing the presynaptic spiking waveforms. This new proposal, relying on analog properties of memristor, can be easily implemented into neural circuits.

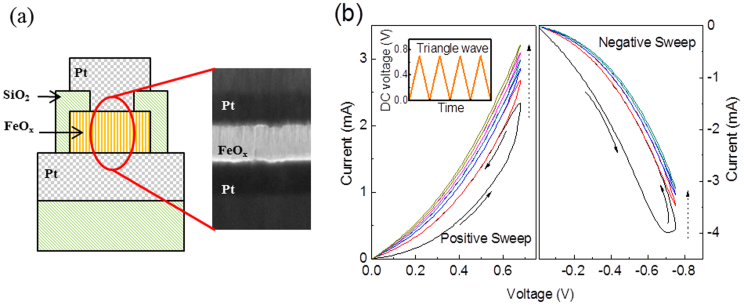
Compared with mass storage applications, neuromorphic applications set special requirements on the memristor. It desires reliable analog properties, such as non-abrupt switching transition, continuously distributed resistance states, and repeatable behavior. In this paper, iron oxide is chosen as the resistance switching layer of memristor and its properties will be discussed first. The memristor, consisting of a sandwich-like structure of Pt/iron oxide/Pt, as shown in Fig. 1(a), was fabricated. The device size was patterned to be 0.25 μm2. The iron oxide layer (50 nm) was sputtered in a high vacuum chamber from an iron oxide compound target and the deposition temperature is below 300°C, which is compatible with semiconductor backend process specification. Based on X-ray photoelectron spectroscopy (XPS) analysis (Supplementary information), the majority compound inside the sputtered film is FeO.

Figure 1.

Figure 1

Open in a new tab

(a) A schematic illustration of the iron oxide memristor device and cross-section view of a real device conducted in transmission electron microscopy (TEM). (b) Current-voltage (I-V) curves of memristor under multiple triangle-shapes DC sweeps. A bipolar behavior and continuous distribution of resistance states are demonstrated.

The iron oxide memristor was first investigated under DC mode. When inputting a triangle-wave shape DC voltage to memristor, the I–V curve in each sweeping cycle appears a banana-shape like hysteresis loop in both positive sweep (left plot) and negative sweep (right plot), as shown in Fig. 1(b). As the number of cycles increases, the conductance increases or decreases monotonically and consecutively. Compared to other reports of analog memristors37,40, the iron oxide memristor exhibits two main differences. First, the adjacent sweeping curves just coincide with each other at the low voltage region and there is no overlapping, indicating improved data retention. This coincidence region also shows a square law relationship between current and voltage (Supplementary information), which indicates a space-charge-limited current (SCLC) conduction mechanism44. Second, there is no fluctuation or abrupt change in I–V curves during sweeping, implying a continuous distribution of resistance states.

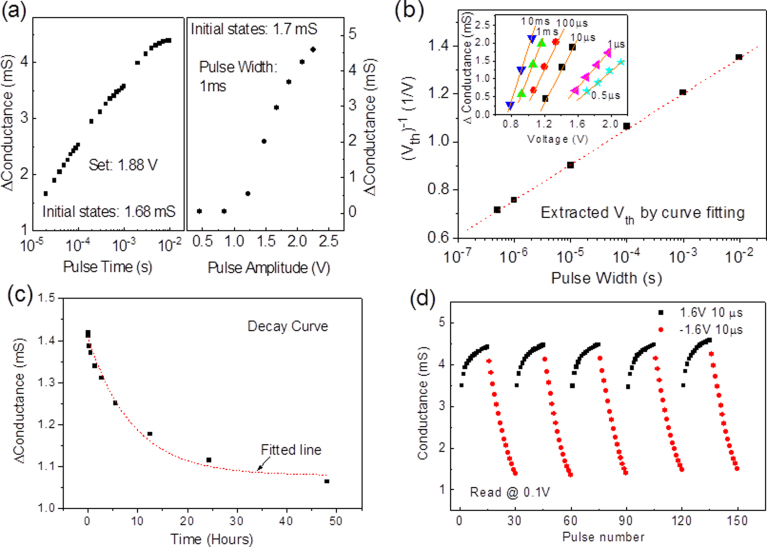
The programming characteristics of the set and reset operation were investigated under pulse mode. When the pulse amplitude is fixed during the set operation, as shown in the left plot of Fig. 2(a), a logarithmic relationship between the changes of conductance and pulse width is observed. On the other hand, when the pulse width is fixed, it exhibits an approximate linear relationship between the pulse amplitude and the change of conductance when the pulse amplitude above the threshold, as illustrated in the right plot of Fig. 2(a). In summary, voltage amplitude has more impact on the weight change of memristor than pulse width.

Figure 2.

Figure 2

Open in a new tab

(a) The impact of built-in conductance under varying pulse width and pulse amplitude. Left plot is under fixed positive amplitude (~1.88 V) and right plot is under fixed pulse width (1 ms). The built-in conductance was read at 0.1 V after each pulsing. (b) The relationship between threshold voltage and pulse width. Inset: threshold voltages extracted under linear fitting. (c) The decay performance of iron oxide-based memristor. (d) An illustration of repeatability of iron oxide memristor under consecutive pulse trains. Each of positive/negative pulse train consists of 15 pulses.

It is also found that the threshold voltage of the iron oxide memristor is pulse-width dependent. When varying the pulse width, the onset of conduction change is varied. By linearly fitting the measurement points, as shown in the inset of Fig. 2(b), the threshold voltages under different pulse widths can be extracted. A higher threshold voltage is accompanied by a shorter pulse width. The threshold voltages are compiled in Fig. 2(b). The figure shows an inversely linear relationship between threshold voltage and logarithm of pulse width. This indicates that if the pulse width is shrunk to nanosecond scale, a much higher voltage is required in order to move the built-in conductance, which makes the memristor robust to circuit glitches. In addition, if the memristor is heavily stressed, the memory window can be as large as 19 folds.

The memristor takes more than 4 months to decay to half of the memory window and several years to return to the starting point, as shown in the inset of Fig. 2(c). The strong retention loss reported from WOx memristor37 has not been observed in the iron oxide memristor. Based on the exponential decay function proposed by Hermann Ebbinghaus Inline graphic, the relative strength (S) of iron oxide memristor is fitted to be 8.9, as shown in Fig. 2(c), and the decay curve is not related to the pulse numbers. In addition, according to the report from Wickliffe C. Abraham in 2003 that “LTP (Long term potentiation) can last for hours, days or even months, and usually follows an exponential decay”45, the iron oxide-based memristor that retains the resistance for months can act as a long-term synapse in a neuromorphic circuit.

In order to form the analog memristor, a high voltage forming process is required, as illustrated in Supplementary Fig. S2. After the forming process, the memristor devices all exhibit similar memory window, despite the device size varying from 0.25 μm2 to 16 μm2, which implies a formation of conducting filament46. Besides, the non-linear I–V curve at low electric field region discussed above suggests that the memristor works under the condition of filament rupture. The condition of rupture point determines the resistance changing behavior.

Thus far, the characteristics of the iron oxide memristor have been analyzed. With proper initialization, the memory device can be repeatedly switched back and forth, as shown in Fig. 2(d). Compared to other reported memristors40,47,48, the iron oxide-based memristor demonstrates improved controllability during programming and improved repeatability between different pulse trains. By fully utilizing these analog behaviors, the iron oxide memristor can be used to emulate the synaptic learning rules.

Unlike STDP synaptic learning rule, the SRDP synaptic learning rule has not been demonstrated using memristor. Several papers reported frequency dependence of memristor that different programming frequencies lead to much different decay curves38,49,50,51. This behaviour is used to mimic the transition of short-term memory to long-term memory. However, it cannot be used to emulate the SRDP learning rule. Because SRDP requires bidirectional changing plasticity at different frequency region - low frequency induces LTD (decrease of plasticity) and high frequency induces LTP (increase of plasticity). In order to realize this bidirectional changing behaviour, we propose a novel way by engineering the input waveforms, which not only realizes SRDP, but further integrates with STDP together as a whole to achieve a bio-plausible integrated learning scheme.

The presynaptic spike is customized by drawing inspiration from the firing behavior of biological neurons. A typical biological neural firing curve is shown in the bottom left of Fig. 3(a)52. Based on this biological firing curve, a similar shape of presynaptic spike is constructed. As shown in the bottom right of Fig. 3(a), the presynaptic spike consists of two pulses. One is a short and high-amplitude pulse, followed by a relatively wide and low-amplitude pulse in the opposite direction. Construction of both negative and positive pulses in one presynaptic spike aims to realize bidirectional weight change when the presynaptic firing frequency varies. Using a simple circuit (supplementary document), this tailored presynaptic spike can be easily realized with a normal pulse input.

Figure 3.

Figure 3

Open in a new tab

(a) A simple illustration of neuron, synapse and neural spike. The customized spike (bottom right plot) is inspired by the biological firing curve (bottom left plot). (b) An illustration of spike waveforms at different presynaptic firing frequency. (c) An emulated of SRDP learning rule on iron oxide memristor. (d) The reported biological SRDP curve26.

In order to match the plasticity changing direction that low frequency induces long-term depression (LTD), the presynaptic spike shape used during the test is upside-down. That is, the short pulse has negative amplitude (−1.8 V), followed by the positive low amplitude (0.5 V), as shown in Fig. 3(b). This large negative amplitude (−1.8 V) decreases the memristor conductance greatly and the other half of the spike - low-amplitude positive pulse (0.5 V) has negligible impact on the memristor because it is below the threshold voltage. Thus, the overall effect of presynaptic spike decreases the conductivity, which realizes LTD at the low spike rate condition (<5 kHz). When the spike rate is above 5 kHz, the positive and negative pulses of presynaptic spikes overlap each other, thus cancelling the negative amplitude, resulting in a smaller decrease in conductance. Even higher presynaptic frequency, such as 20 kHz, further cancels the negative amplitude, as well as accumulates the positive pulses to be far above positive threshold voltage, causing a significant increase in memristor conductance. An illustration of the above discussed waveforms is shown in Fig. 3(b), using 2.5, 10 and 20 kHz presynaptic spike frequency as examples. When these presynaptic spikes are input into the iron oxide memristor, a frequency dependent plasticity behavior is demonstrated, as shown in Fig. 3(c), that low frequency of presynaptic spikes decreases the conductivity (LTD), and high frequency spikes increase the conductivity (LTP). This frequency dependent behavior matches the biological report of SRDP26, which is redrawn in Fig. 3(d).

Furthermore, the spiking-time-dependent plasticity (STDP) learning rule is also demonstrated using the same presynaptic spike trains. Similar to literature reports39,40,41,51,53,54, a special tailored pulse train (termed as STDP pulse train) with varying voltage amplitudes is constructed in order to correlate the change of conductance with pre- and postsynaptic firing interval (Δt = tpre − tpost), as shown in Fig. 4(a). The reason of using various pulse amplitudes in constructing the STDP pulse train instead of pulse widths is due to the higher sensitivity of the pulse amplitude of the memristor. The STDP pulse train consists of 8 pulses: 4 positive pulses followed by 4 negative pulses. All pulses have the same pulse width (4 μs) and the same intervals (4 μs). The center point of STDP pulse train is aligned with the rising edge of the presynaptic spike.

Figure 4.

Figure 4

Open in a new tab

(a) An example of pulsing scheme for the realization of STDP learning rule. (b) A schematic illustration of synapse circuit to achieve dual coding learning scheme. (c) A typical STDP learning rule emulated using iron oxide memristor at 10 kHz presynaptic firing frequency. (d) A summary of learning rule integration when varying presynaptic firing frequency. It shows that STDP learning rule only happens at the moderate frequency region and other regions are dominated by the SRDP learning rule.

Besides, inspired by the refractory period and back-propagation effect, an operational schematic of synapse is illustrated in Fig. 4(b) to realize the STDP learning rule. The refractory period refers to the biological information block period that is caused by the sodium ion channels inactivation. During this period, neuron does not fire again irrespective of incoming stimulus and resets itself to resting potential52. A switch (K1 switch) is used to realize and emulate the refractory period in our proposal. Unless the post-neuron fires, the iron oxide memristor connects the pre-synaptic neuron and post-synaptic neuron directly, enabling the information to pass through. Once the post-synaptic neuron fires, this firing information back-propagates to K1 switch and triggers it switching to STDP waveform terminal for a short period (8 μs) – refractory period. During this period, the information from presynaptic neuron will be blocked and the postsynaptic neuron will reset its potential to initial condition. At the same time, the presynaptic spike will overlap with the STDP pulses to modify the conductivity of the memristor – inducing the plasticity change.

A typical STDP is demonstrated in Fig. 4(c) at 10 kHz presynaptic frequency. Here, we assume nine-times firing of pre-synaptic neuron results in one time firing of post-synaptic neuron and the voltage drop on memristor is clamped to 2.5 V to avoid the breakdown of the memristor device. As shown in Fig. 4(c), when pre-synaptic neuron fires before post-synaptic neuron (Δt > 0), LTP is induced. Otherwise, LTD occurs. Moreover, the smaller of the pre- and post-synaptic firing interval results in a larger change of conductivity, and vice versa. However, when the pre-synaptic neuron fires at other frequency region (e.g. 2.5 kHz, 20 kHz), the STDP behavior is not observed regardless of the pre- and post-synaptic firing interval. This is due to the canceling effect between the STDP pulse train and presynaptic neural spikes (supplementary information). The frequency-dependent behaviors are summarized in Fig. 4(d), showing that STDP only happens at the moderate firing rate region (ranging from 8 kHz to 10 kHz in our test, as highlighted in Fig. 3(c)). Outside the moderate region, higher firing rates only lead to an increase of conductivity (LTP) and lower firing rate causes a decrease in conductivity (LTD). These observations are consistent with biological reports27, demonstrating a dual coding learning scheme on a single nano device. It is necessary to point out that constant inputting firing rates are used during the learning rule illustration which is to simplify the analysis. However, the input neuron spikes can be inconsistent and discrete like reality. By using the waveform generation block (supplementary information), the inconsistent and discrete spikes can be easily transformed into the tailored waveform for the learning rules implementation.

It should be noted that the response of biological neurons is not uniform, but is variable and is often modeled by a statistical distribution, i.e, Poissonian, in literatures55. Devices emulating synaptic properties need to consider the robustness against non-uniform neural stimulus. Our proposal of dual coding learning scheme is robust to the variation of the presynaptic input. When the presynaptic firing frequency is slightly varied, or even one spike is missed or is inserted owing to system instability, the learning scheme will tolerate these fluctuations and output the similar results, as long as the errors are not critical. (supplementary information).

The conductance variations from device to device also exist. For example, under the same pulse width condition (0.1 ms), the threshold voltages of most devices fall in the range of 0.9 ± 0.1 V. Such variations, we believe, would not be a great obstacle in neuromorphic implementation because the variation of synapses has also been observed in human brain which does not affect cognition56,57. Currently, there are two ways to deal with such variations. Simeon Bamford et al. reported that STDP is a homeostatic process which is unsupervised and self-contained. It can reduce variations in performance caused by both mismatch in fabrication and inhomogeneity in the electronic devices58. The other way proposed by Sadique Sheik et al is a totally different way59. Rather than attempting to reduce the device mismatch, he proposed to utilize these mismatches present in VLSI chips to model biological differences, such as the variations of axonal propagation delays. In this novel approach, a certain range of mismatches and variations is desirable.

It is known that different parts of the brain use different combinations of learning mechanisms. For example, our visual recognition uses spatio-temporal based learning rule and our aural recognition uses frequency based learning rule. In the grand challenge of cognitive systems, it is necessary to emulate a wide plethora of learning mechanisms to facilitate the development of the whole spectrum of cognitive functions. To this effect, we expect that our dual coding learning scheme could provide a platform for the development of neural coding technology in hierarchical structure. On the other hand, from the engineering point of view, there arises the question of whether the sole implementation of paired-based STDP learning rule, which has been reported by several groups39,40,41,42,60,61, is enough to build a functional neural circuit. We find there are two quandaries that are hard to deal with. First, at the condition of high frequency, the learning windows of LTP and LTD will overlap each other. The post-synaptic spike located inside this overlapping region would have difficulties in identifying the proper actions. Second, when a neuron has multiple inputs, the disturbance of alien spike from different synapse may induce an undesired synaptic weight change which is in conflict with its historical contributions. Therefore, the paired-based STDP learning rule is not enough to alleviate these quandaries and spike rate dependence should be considered. In short, the dual coding learning scheme should be highly desired in the implementation of neural circuits.

In summary, based on the good analog properties exhibited from the iron oxide-based memristor, an integrated rate-temporal learning scheme is demonstrated. This emulated learning scheme is robust to the input frequency variations as well as missing spikes. We expect that the implementation of dual coding learning scheme may greatly facilitate the development of neuromorphic circuits towards real cognition.

Author Contributions

W.H. proposed and designed the experiments, and drafted the manuscript. K.H. proposed and designed the electric circuit. N.N., K.R., G.L., R.Z. and J.P. carried out the theoretical analysis. W.H., K.H., Y.J., J.S. and R.Z. did the experiments. L.S. directed the projects and provided overall guidance throughout. All authors contributed to the results analysis and reviewed the manuscript.

Supplementary Material

Supplementary Information

Enabling an Integrated Rate-temporal Learning Scheme on Memristor

srep04755-s1.pdf (408.9KB, pdf)

References

  1. Markram H. The Human Brain Project. Sci. Am. 306, 50–55 (2012). [DOI] [PubMed] [Google Scholar]
  2. Berger T., Levy W. B. & Xing J. in 2011 49th Annual Conf. on Comm., Control, and Comp. (Allerton) 1737–1742 (IEEE). [Google Scholar]
  3. Douglas R., Mahowald M. & Mead C. Neuromorphic analogue VLSI. Annu. Rev. Neurosci. 18, 255–281 (1995). [DOI] [PubMed] [Google Scholar]
  4. Boahen K. Neuromorphic microchips. Sci. Am. 292, 56–63 (2005). [DOI] [PubMed] [Google Scholar]
  5. Sarpeshkar R. Ultra low power bioelectronics: fundamentals, biomedical applications, and bio-inspired systems. (Cambridge University Press, 2010). [Google Scholar]
  6. Indiveri G. et al. Neuromorphic silicon neuron circuits. Front. Neurosci. 5, 1–23 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Basu A., Shuo S., Zhou H., Hiot Lim M. & Huang G. B. Silicon spiking neurons for hardware implementation of extreme learning machines. Neurocomputing 102, 125–134 (2012). [Google Scholar]
  8. Modha D. S. et al. Cognitive computing. Commun. ACM 54, 62–71 (2011). [Google Scholar]
  9. McClelland J. L., McNaughton B. L. & O'Reilly R. C. Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychol. Rev. 102, 419 (1995). [DOI] [PubMed] [Google Scholar]
  10. Markram H., Lübke J., Frotscher M. & Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 (1997). [DOI] [PubMed] [Google Scholar]
  11. Bi G. & Poo M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Zhang L. I., Tao H. W., Holt C. E., Harris W. A. & Poo M. A critical window for cooperation and competition among developing retinotectal synapses. Nature 395, 37–44 (1998). [DOI] [PubMed] [Google Scholar]
  13. Kempter R., Gerstner W. & Hemmen J. L. Intrinsic stabilization of output rates by spike-based Hebbian learning. Neural Comput. 13, 2709–2741 (2001). [DOI] [PubMed] [Google Scholar]
  14. Sjöström P. J., Turrigiano G. G. & Nelson S. B. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164 (2001). [DOI] [PubMed] [Google Scholar]
  15. Linden D. J. The Return of the Spike: Review Postsynaptic Action Potentials and the Induction of LTP and LTD. Neuron 22, 661–666 (1999). [DOI] [PubMed] [Google Scholar]
  16. Golding N. L., Staff N. P. & Spruston N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 418, 326–331 (2002). [DOI] [PubMed] [Google Scholar]
  17. Froemke R. C., Poo M.-M. & Dan Y. Spike-timing-dependent synaptic plasticity depends on dendritic location. Nature 434, 221–225 (2005). [DOI] [PubMed] [Google Scholar]
  18. Letzkus J. J., Kampa B. M. & Stuart G. J. Learning rules for spike timing-dependent plasticity depend on dendritic synapse location. J. Neurosci. 26, 10420–10429 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lisman J. & Spruston N. Postsynaptic depolarization requirements for LTP and LTD: a critique of spike timing-dependent plasticity. Nat. Neurosci. 8, 839–841 (2005). [DOI] [PubMed] [Google Scholar]
  20. Turrigiano G. G. & Nelson S. B. Homeostatic plasticity in the developing nervous system. Nat. Rev. Neurosci. 5, 97–107 (2004). [DOI] [PubMed] [Google Scholar]
  21. Watt A. J. & Desai N. S. Homeostatic plasticity and STDP: keeping a neuron's cool in a fluctuating world. Front. Synaptic Neurosci. 2, 1–16 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fusi S., Annunziato M., Badoni D., Salamon A. & Amit D. J. Spike-driven synaptic plasticity: theory, simulation, VLSI implementation. Neural Comput. 12, 2227–2258 (2000). [DOI] [PubMed] [Google Scholar]
  23. Van Rossum M. C. W., Bi G. & Turrigiano G. Stable Hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Gerstner W. & Kistler W. M. Mathematical formulations of Hebbian learning. Biol. Cybern. 87, 404–415 (2002). [DOI] [PubMed] [Google Scholar]
  25. Bush D., Philippides A., Husbands P. & O'Shea M. Reconciling the STDP and BCM models of synaptic plasticity in a spiking recurrent neural network. Neural Comput. 22, 2059–2085 (2010). [DOI] [PubMed] [Google Scholar]
  26. Rachmuth G., Shouval H. Z., Bear M. F. & Poon C. S. A biophysically-based neuromorphic model of spike rate-and timing-dependent plasticity. Proc. Natl. Acad. Sci. USA 108, E1266–E1274 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Feldman D. E. The Spike-Timing Dependence of Plasticity. Neuron 75, 556–571 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wittenberg G. M. & Wang S. S. H. Malleability of spike-timing-dependent plasticity at the CA3-CA1 synapse. J. Neurosci. 26, 6610–6617 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. O'Keefe J. & Burgess N. Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus 15, 853–866 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Araki O. & Aihara K. Dual information representation with stable firing rates and chaotic spatiotemporal spike patterns in a neural network model. Neural Comput. 13, 2799–2822 (2001). [DOI] [PubMed] [Google Scholar]
  31. Pearson M. J. et al. Implementing spiking neural networks for real-time signal-processing and control applications: a model-validated FPGA approach. IEEE T Neural Networ. 18, 1472–1487 (2007). [DOI] [PubMed] [Google Scholar]
  32. Chua L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 18, 507–519 (1971). [Google Scholar]
  33. Chua L. Resistance switching memories are memristors. Appl. Phys. A: Mater. Sci. Process. 102, 765–783 (2011). [Google Scholar]
  34. Strukov D. B., Snider G. S., Stewart D. R. & Williams R. S. The missing memristor found. Nature 453, 80–83 (2008). [DOI] [PubMed] [Google Scholar]
  35. Yang J. J., Strukov D. B. & Stewart D. R. Memristive devices for computing. Nat. Nanotech. 8, 13–24 (2012). [DOI] [PubMed] [Google Scholar]
  36. Valov I. et al. Nanobatteries in redox-based resistive switches require extension of memristor theory. Nat. Commun. 4, 1771 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Chang T. et al. Synaptic behaviors and modeling of a metal oxide memristive device. Appl. Phys. A: Mater. Sci. Process. 102, 857–863 (2011). [Google Scholar]
  38. Ohno T. et al. Short-term plasticity and long-term potentiation mimicked in single inorganic synapses. Nat. Mater. 10, 591–595 (2011). [DOI] [PubMed] [Google Scholar]
  39. Choi S. J. et al. Synaptic behaviors of a single metal-oxide-metal resistive device. Appl. Phys. A: Mater. Sci. Process. 102, 1019–1025 (2011). [Google Scholar]
  40. Jo S. H. et al. Nanoscale memristor device as synapse in neuromorphic systems. Nano lett. 10, 1297–1301 (2010). [DOI] [PubMed] [Google Scholar]
  41. Seo K. et al. Analog memory and spike-timing-dependent plasticity characteristics of a nanoscale titanium oxide bilayer resistive switching device. Nanotechnology 22, 254023 (2011). [DOI] [PubMed] [Google Scholar]
  42. Snider G. S. in NANOARCH '08. 85–92 (IEEE). [Google Scholar]
  43. Pickett M. D., Medeiros-Ribeiro G. & Williams R. S. A scalable neuristor built with Mott memristors. Nat. Mater. (2012). [DOI] [PubMed] [Google Scholar]
  44. Grinberg A. A., Luryi S., Pinto M. R. & Schryer N. L. Space-charge-limited current in a film. IEEE Trans. Electon Dev. 36, 1162–1170 (1989). [Google Scholar]
  45. Abraham W. C. & Williams J. M. Properties and mechanisms of LTP maintenance. The Neuroscientist 9, 463–474 (2003). [DOI] [PubMed] [Google Scholar]
  46. Park G.-S. et al. In situ observation of filamentary conducting channels in an asymmetric Ta2O5 − x/TaO2 − x bilayer structure. Nat. Commun. 4, 10.1038/ncomms3382 (2013). [DOI] [PubMed] [Google Scholar]
  47. Jeong H. Y., Lee J. Y., Ryu M. K. & Choi S. Y. Bipolar resistive switching in amorphous titanium oxide thin film. Phys. Status Solidi RRL 4, 28–30 (2010). [Google Scholar]
  48. Jo S. H., Kim K. H. & Lu W. High-density crossbar arrays based on a Si memristive system. Nano lett. 9, 870–874 (2009). [DOI] [PubMed] [Google Scholar]
  49. Chang T., Jo S. H. & Lu W. Short-Term Memory to Long-Term Memory Transition in a Nanoscale Memristor. ACS nano 5, 7669–7676 (2011). [DOI] [PubMed] [Google Scholar]
  50. Li S. et al. Synaptic plasticity and learning behaviours mimicked through Ag interface movement in an Ag/conducting polymer/Ta memristive system. Journal of Materials Chemistry C 1, 5292–5298 (2013). [Google Scholar]
  51. Wang Z. Q. et al. Synaptic learning and memory functions achieved using oxygen ion migration/diffusion in an amorphous InGaZnO memristor. Advanced Functional Materials 22, 2759–2765 (2012). [Google Scholar]
  52. Kandel E. R., Schwartz J. H. & Jessell T. M. Principles of neural science. 4th edn, (McGraw-Hill New York, 2000). [Google Scholar]
  53. Yu S., Wu Y., Jeyasingh R., Kuzum D. & Wong H. P. An Electronic Synapse Device Based on Metal Oxide Resistive Switching Memory for Neuromorphic Computation. IEEE T Electron Dev. 58, 2729–2737 (2011). [Google Scholar]
  54. Chang T., Sheridan P. & Lu W. in 2012 13th International Workshop on Cellular Nanoscale Networks and Their Applications (CNNA). 1–3 (IEEE). [Google Scholar]
  55. Kumar A., Rotter S. & Aertsen A. Spiking activity propagation in neuronal networks: reconciling different perspectives on neural coding. Nat. Rev. Neurosci. 11, 615–627 (2010). [DOI] [PubMed] [Google Scholar]
  56. Qu L., Akbergenova Y., Hu Y. & Schikorski T. Synapse-to-synapse variation in mean synaptic vesicle size and its relationship with synaptic morphology and function. J. Comp. Neurol. 514, 343–352 (2009). [DOI] [PubMed] [Google Scholar]
  57. Harris K. & Sultan P. Variation in the number, location and size of synaptic vesicles provides an anatomical basis for the nonuniform probability of release at hippocampal CA1 synapses. Neuropharmacology 34, 1387–1395 (1995). [DOI] [PubMed] [Google Scholar]
  58. Bamford S. A., Murray A. F. & Willshaw D. J. Silicon synapses self-correct for both mismatch and design inhomogeneities. Electron. Lett. 48, 360–361 (2012). [Google Scholar]
  59. Sheik S., Chicca E. & Indiveri G. Exploiting device mismatch in neuromorphic VLSI systems to implement axonal delays. IJCNN 2012, 1–6 (2012). [Google Scholar]
  60. Kuzum D., Jeyasingh R. G. D., Lee B. & Wong H. S. P. Nanoelectronic programmable synapses based on phase change materials for brain-inspired computing. Nano lett. 12, 2179–2186 (2011). [DOI] [PubMed] [Google Scholar]
  61. Indiveri G., Chicca E. & Douglas R. A VLSI array of low-power spiking neurons and bistable synapses with spike-timing dependent plasticity. IEEE T Neural Networ. 17, 211–221 (2006). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Enabling an Integrated Rate-temporal Learning Scheme on Memristor

srep04755-s1.pdf (408.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES