The effect of fast and slow motor unit activation on whole-muscle mechanical performance: the size principle may not pose a mechanical paradox

Abstract

The output of skeletal muscle can be varied by selectively recruiting different motor units. However, our knowledge of muscle function is largely derived from muscle in which all motor units are activated. This discrepancy may limit our understanding of in vivo muscle function. Hence, this study aimed to characterize the mechanical properties of muscle with different motor unit activation. We determined the isometric properties and isotonic force–velocity relationship of rat plantaris muscles in situ with all of the muscle active, 30% of the muscle containing predominately slower motor units active or 20% of the muscle containing predominately faster motor units active. There was a significant effect of active motor unit type on isometric force rise time (p < 0.001) and the force–velocity relationship (p < 0.001). Surprisingly, force rise time was longer and maximum shortening velocity higher when all motor units were active than when either fast or slow motor units were selectively activated. We propose this is due to the greater relative effects of factors such as series compliance and muscle resistance to shortening during sub-maximal contractions. The findings presented here suggest that recruitment according to the size principle, where slow motor units are activated first and faster ones recruited as demand increases, may not pose a mechanical paradox, as has been previously suggested.

1. Introduction

Skeletal muscle converts metabolic energy into the mechanical output required for all movement. In order to meet this demand, muscle must be capable of graded force production with variable force development and strain rates. This can be achieved by altering motorneuron firing rate [1] and recruiting motor units with different mechanical and metabolic properties [2]. While much consideration has been given to the effect of motorneuron firing rate [3–9], the effect of recruiting different motor units has received relatively little attention. Vertebrate motor units (single motorneurons and associated muscle fibres) vary from slow to fast. Motorneuron diameter, force rise and relaxation rate, peak shortening velocity and metabolic energy consumption increase along this gradient [10–12]. The recruitment of these different motor unit types generally follows the size principle, whereby motor units are recruited from slow to fast due to differences in size, and therefore excitability, of motorneurons [13–15]. However, deviations from the size principle have been reported, with motor units being recruited in response to mechanical demand, rather than according to motorneuron size, in some situations (for review, see [16]). The existence of motor unit recruitment strategies means that the number and functional characteristics of active motor units will vary across locomotor tasks.

The number and type of motor units active have major implications for the mechanical output of a muscle. However, much of our understanding of the properties of muscle that are key to locomotor performance, such as the rate of force development and the force–velocity relationship, comes from studies of maximally activated whole muscles and isolated muscle fibres in vitro [17–21]. Relatively little is known about muscle performance in response to activation of sub-sets of motor units. The findings of studies of maximally activated muscles are commonly used in Hill-type muscle models to predict in vivo muscle forces [22,23] and mapped to muscle length changes measured during movement to understand muscle function [24]. While this approach may often provide useful information, the disparity between the number and type of motor units active in vitro and in the relevant locomotor condition may reduce the accuracy of such predictions [25] and limit the insight into muscle function that can be gained.

The aims of our study were therefore to determine the rate of force development, defined as the isometric force rise time, and force–velocity properties of a muscle in response to activation of all muscle fibres and the selective activation of sub-populations of either faster or slower motor units. Studies of single fast and slow fibres, and whole muscles containing predominantly fast or slow motor units, show that isometric force rise time is shorter [12,20,21], maximum shortening velocity higher and the curvature of the force–velocity relationship lower in faster fibres [12,17,18,20]. The implications of a thought experiment [26] suggested that the maximum shortening velocity of a whole muscle will reflect that of the fastest active fibres. Hence, we hypothesized that (i) isometric force rise time would be longer when slow motor units were selectively activated than when all and faster motor units were activated, and (ii) shortening velocity would be lower, and the curvature of the force–velocity relationship greater, when slow motor units were selectively activated than when all or fast motor units were activated.

2. Material and methods

Experiments were conducted on the plantaris muscles of male Sprague Dawley rats (Rattus norvegicus; n = 10; approx. age three to four months; body mass 403 ± 20 g; Charles River, Wilmington, MA). The plantaris was chosen as it is the most heterogeneous of the rat ankle extensors [27–30] and shows the greatest variation in recruitment pattern in vivo [31,32]. Estimates of fibre type composition range from 5 to 9% type I, 11 to 63% type IIa, 31 to 38% IIx and 46 to 47% IIb [27–30].

Rats were anaesthetized using 2% isoflurane, and the distal end of the plantaris was isolated and its tendon connected, via a stainless steel hook, to the lever arm of a muscle ergometer (series 305B-LR; Aurora Scientific Inc., Aurora, Ontario, Canada). The femur was clamped to a rigid frame. The calcaneus was cut to free the distal end of the muscle, and the sciatic nerve exposed and transected. A nerve cuff containing a stimulus, ground and blocking electrode was placed around the nerve, with the blocking electrode closest to the muscle, and a bipolar silver-wire electrode [33] implanted into the muscle belly. Rat body temperature was maintained using a heat pad and lamp. Muscle and nerve were kept warm and moist by immersing the hind limb in a pool of mineral oil, the temperature of which was maintained at 31 ± 1°C using a heat lamp.

Supra-maximal stimuli were applied to the sciatic nerve to generate isometric tetani (train duration, 320 ms; pulse duration, 0.25 ms; frequency, 80 Hz; amplitude, 3 V). Generation of stimulus pulse and simultaneous logging (5000 Hz) of force (F), length (L) and electromyography (EMG) data were done using a custom-built virtual instrument and A/D board (Labview v. 11 and NI UBS-6343; National Instruments, Austin, TX) and stimulation unit (S48; Grass, West Warwick, RI). A force–length curve was constructed [20,34] and optimal length (L₀) defined as the length corresponding to the right-hand edge of the plateau; all subsequent contractions were performed at this length.

Isometric tetani were performed using different stimulation condition that aimed to activate different motor unit types (figure 1). A supra-maximal stimulus (3 V; supra-max) was used as above to activate all motor units. Selective activation of different types of motor units exploited the fact that the largest, lowest-resistance motorneurons innervate the fastest motor units [10,35]; application of a given voltage will generate a larger current in the larger motorneurons supplying faster motor units. A sub-maximal stimulus (approx. 1 V; sub-max) was used to activate only the fastest motor units as it generated sufficient current to trigger an action potential only in these motorneurons [13]. A high-frequency sine wave, of appropriate amplitude, applied to the nerve will block conduction in motorneurons [36–38]. Generation of sufficient current to block conduction will occur at a lower amplitude in larger motorneurons. Application of a supra-maximal stimulus (3 V) and a high-frequency sine wave of appropriate amplitude (10–20 kHz, 2–5 V; 3311A, Hewlett Packard, Palo Alto, CA; block), from the blocking electrode, was used to trigger an action potential in all motorneurons but then block conduction in larger motorneurons, so activating only slower motor units. Hence, supra-max, sub-max and block stimulation conditions aimed to activate all, predominately faster or predominately slower motor units, respectively. Peak isometric force (F₀) in each condition was recorded and converted to peak isometric stress (σ₀) [30,34] and the time taken to reach half F₀ (force rise time_50%) was calculated.

Figure 1.

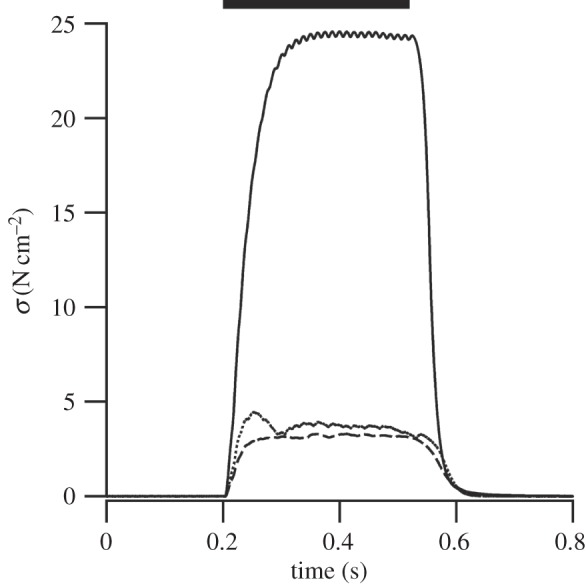
Example isometric tetani. Muscle stress (σ) in response to a supra-max (solid), sub-max (dashed) and block (dotted) stimuli. Timing and duration of the stimulus is denoted by the thick black bar.

After-loaded isotonic contractions, using the above stimulation conditions, were used to determine muscle force–velocity properties (see [20,34] for details) of the rat plantaris when all and predominately faster or predominately slower motor units were activated. The order of stimulation conditions was randomized and the experiment terminated once peak isometric force fell below 80% of its maximum. Relative force (F/F₀) was calculated from the force during a shortening contraction and the peak isometric force generated in that stimulation condition. Length was converted to strain ((L−L₀)/L₀) and differentiated with respect to time to determine shortening velocity (V) in fibre lengths per second (L₀ s⁻¹). Relative force was plotted against velocity and a hyperbolic-linear curve fitted to the data [18] (IGOR Pro v. 6.1.2.1; Wavemetrics, Lake Oswego, OR). Maximum shortening velocity (V_max) was determined by extrapolation of this relationship to zero force. The power ratio, a dimensionless measure of the curvature of the force–velocity relationship, was calculated as

where P is the maximum power taken from the force–velocity curve [18].

EMG signals were recorded simultaneously with force and length, amplified (500×) and filtered (band-pass 30–3000 Hz; P5 series pre-amplifier; Grass). In order to confirm activation of desired fibre type, wavelet analysis and principal component analysis were performed on EMG signals, and mean frequency and angle θ calculated (see [31–33,37,39–41] for details). As the frequency characteristics of the myoelectric signal are indicative of active motor unit type [37,42,43], a higher mean frequency and lower θ reflect a greater contribution of faster motor units [31,32,37,41].

One-way ANOVAs or generalized linear models (GLMs) were used, as appropriate (Fligner–Killeen tests used to assess the homogeneity of variances), to determine whether there were significant differences in σ₀, force rise time_50%, mean EMG frequency and θ with the activation of different motor unit types (supra-max, sub-max and block conditions). Tukey's honest significant difference tests or multiple comparisons of means using Tukey's contrasts were used, as appropriate, to determine where significant differences between conditions arose. All force–velocity data were combined and a single curve fitted for each stimulation condition. Generalized linear models were used to determine whether there were significant effects of stimulation condition on the relationship between force and velocity. Mixed-effect models were used to determine the effect of the level of activation of the muscle, independent of stimulation condition, on force rise time_50% and the force–velocity relationship [44].

3. Results and discussion

This study aimed to characterize the mechanical properties of the rat plantaris muscle in response to selective activation of different motor unit types using different stimulation conditions. Stimulation condition has a significant effect on maximum isometric stress (p < 0.001), with the muscle producing 20.0 ± 3.1% and 30.4 ± 5.7% of σ₀ obtained using the supra-max condition in the sub-max and block conditions, respectively (figure 2; all data are presented as mean ± s.e.m.; raw values for each individual can be seen in the electronic supplementary material). However, in order to interpret whether these lower stresses reflect selective activation of the desired motor units, we must consider the frequency content of the EMG signal. There was a significant effect of stimulation condition on mean frequency (p = 0.05) and θ (p < 0.05). Mean frequency was highest in the sub-max condition and lowest in the block condition, and θ lowest in the sub-max condition and highest in the block condition (figure 3). Higher mean frequency and lower θ reflect a greater contribution of high-frequency components in the EMG signal, indicative of a relatively higher number of faster motor units activated [31,32,37,41]. Therefore, if we define the level of activation of the muscle as the isometric stress relative to isometric stress in the supra-maximal conditions; the combined stress and EMG data suggest that the sub-max condition activates 20% of the muscle containing predominately faster motor units and the block condition activates 30% of the muscle containing predominately slower motor units. It should be noted that, given the fibre type composition of the muscle and level of activation, some faster (probably type IIa) motor units must be activated in the block condition. However, the frequency content of the EMG signal demonstrates that there are relatively more slow motor units active in the block than the supra-max condition, indicating that this condition does achieve some degree of selective recruitment. The difference in θ observed between sub-max and block conditions is comparable with the range observed over the course of a stride in a running rat [32], suggesting that the level of selectivity in activation of fast and slow motor units achieved here, while undoubtedly not absolute, is representative of the level of selective recruitment used in vivo.

Figure 2.

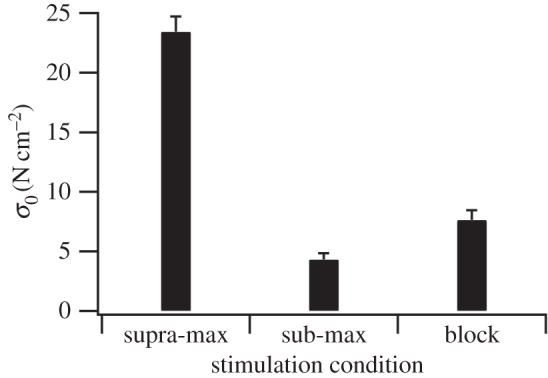
The effect of stimulation condition on peak isometric stress. Peak isometric stress (σ₀) varied with stimulation condition (p < 0.001), with there being significant differences between all conditions (p < 0.05; n = 10, 10, 7 for supra-max, sub-max and block, respectively).

Figure 3.

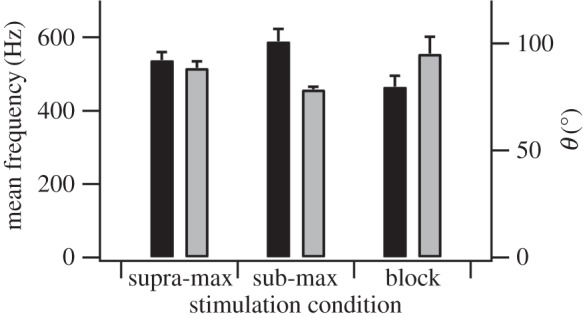
The effect of stimulation condition on the mean frequency and θ. Stimulation condition has a significant effect on the mean frequency (black; p = 0.05) and θ (grey; p < 0.05). Mean frequency is significantly higher (p < 0.05) and θ significantly lower (p < 0.05) in the sub-max condition than in the blocked condition (n = 9, 5 and 4 for supra-max, sub-max and block conditions, respectively).

From our prior understanding of the properties of single fast and slow fibres, and muscle containing predominately faster or slower motor units, we expected isometric force to rise more slowly when slow motor units were activated than when all or fast motor units were activated [12,20,21]. However, while there was a significant effect of stimulation condition (and therefore motor unit type activated) on isometric force rise time_50% (p < 0.001), the differences are not in the direction we predicted (figure 4). Force rise time was longest when all motor units were active (supra-max), and shorter when both predominately faster (sub-max) and slower (block) motor units were selectively activated (figure 4). It could be suggested that the inclusion of some faster motor units in the block condition could account for the similarity of the rate of force rise time between sub-max and block conditions. However, were active motor unit type the only factor altering force rise time, we would expect the inclusion of increasing numbers of faster motor units in the block condition to decrease force rise time to a minimum of that seen in the supra-max condition. The lower force rise time seen in the block condition compared with the supra-max condition suggests that there is an effect obscuring that of active motor unit type. We propose that this could be an effect of the absolute level of activation. This is supported by the finding that there is a significant effect of the level of activation of the muscle on force rise time independent of stimulation condition used, and so motor unit type activated (p < 0.001). We propose that the effect of the level of muscle activation on force rise time may be explained by the effects of series compliance. While external tendon was removed from the preparation, significant internal tendon [30] and other compliant elements remained. Hence, when force was generated, muscle fibres will have shortened as compliant elements stretched despite the entire preparation remaining isometric. Assuming linear elastic properties and constant shortening velocity, higher activation levels will have meant that muscle fibres shortened more and so took a longer time to reach an isometric state where peak force could be generated.

Figure 4.

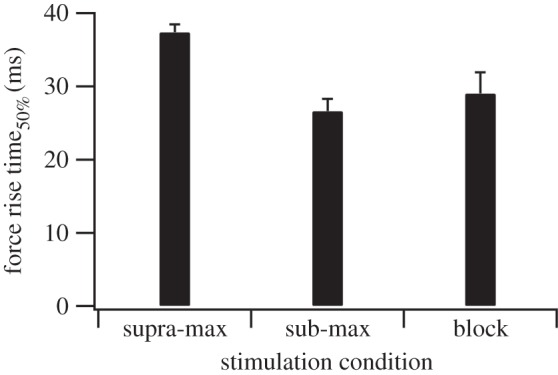
The effect of stimulation condition on force rise time. Force rise time_50% varied with stimulation condition (p < 0.001), being significantly higher in the supra-max condition than in either the sub-max (p < 0.05) or block conditions (p < 0.05). There was no difference between sub-max and block conditions (p = 0.65; n = 10, 10, 7 for supra-max, sub-max and block, respectively).

From our prior understanding of the force–velocity properties of single fibres and muscle containing predominately fast or slow motor units, we predicted that the force–velocity relationship would be the same when all motor units were activated and fast motor units were selectively activated, but that shortening velocity would be lower and curvature of the force–velocity relationship greater when slower motor units were selectively activated [12,17,18,20]. However, while there was a significant effect of stimulation condition on the force–velocity relationship (p < 0.001; figure 5), it was not in the direction we predicted. Maximum shortening velocity was greatest (3.52 L₀ s⁻¹) and power ratio the lowest (0.11), reflecting the highest degree of curvature, when all motor units (supra-max) were active. Maximum shortening velocity was lower and power ratio higher when both predominately faster (sub-max; 1.34 L₀ s⁻¹ and 0.21, respectively) and slower (block; 1.87 L₀ s⁻¹ and 0.15, respectively) motor units were selectively activated (figure 5). As with force rise time, there was a significant effect of the level of muscle activation on the whole muscle force–velocity relationship independent of stimulation condition used, and therefore motor unit type activated (p < 0.001). This suggests that, under these conditions, the level of muscle activation also has a considerable effect on the force–velocity relationship, to the extent that it masks any potential effect of active motor unit type. This reduction in maximum shortening velocity and curvature appears to have been observed previously in the isotonic, but interestingly not isovelocity [3,4], force–velocity relationships where muscle is sub-maximally activated using reduced stimulation frequency [5,6].

Figure 5.

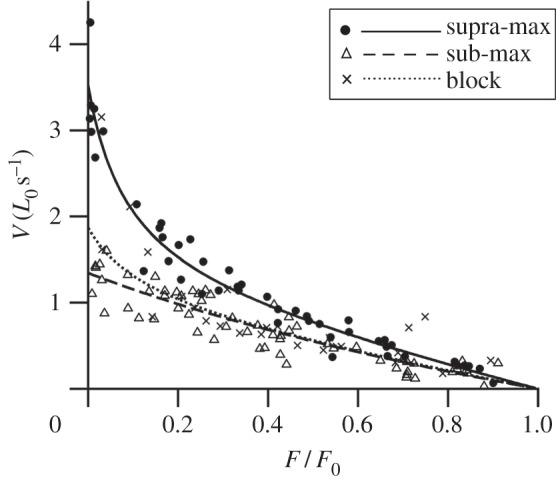
The effect of stimulation condition on the whole muscle force–velocity relationship. There is a significant effect of the stimulation condition on the force–velocity relationship (p < 0.001). The force–velocity data for each condition were fitted with hyperbolic-linear equations [18] which are displayed as solid and dashed lines (n = 9, 10 and 7 for supra-max, sub-max and block conditions, respectively).

We propose that the dependence of the force–velocity relationship on the level of activation may be explained by the resistance of the muscle to deformation. When muscle is activated, contractile elements develop longitudinal force that can cause muscle to shorten. However, in order to shorten, work must be done to overcome the elastic, viscous and inertial resistance to shortening resulting from factors such as the radial expansion of connective tissue layers and myofilament lattice, movement of intracellular fluid, and acceleration of the muscle mass. This may result in a depression of shortening velocity. This effect is likely to be greatest when contractile element force is low, as occurs with sub-maximal activation and at low relative forces, and resistance to shortening is high, as occurs at higher shortening velocities. Hence, we would expect the depression of shortening velocity to increase with decreasing activation level, decreasing relative force and increasing shortening velocity during isotonic contractions, but to be absent during isovelocity contractions where external work is done to overcome resistance to shortening. This is consistent with our findings (figure 5) and in comparison with previous studies [3–6].

Our interpretation of the effects of selective activation of different motor unit types on force rise time and muscle force–velocity properties suggests that the physical properties of the muscle, such as resistance to shortening and compliance, can have substantial effects on the mechanical output of the muscle. We propose that they can obscure differences in the contractile element properties of active motor unit type during sub-maximal contractions. While these results are specific to this muscle, which contains a high proportion of fast twitch motor units [27–30], stimulated at a tetanic frequency, we do not feel that either of these factors can explain the results presented here. It is conceivable that in a muscle with a larger proportion of slow twitch fibres, thereby allowing recruitment of only these motor units, there would be a slight difference between sub-max and block conditions. However, given the predominance of slow motor units recruited in the block condition, we feel that differences due to this would be small compared with the large differences seen between maximally and partially activated conditions. Given the similar effect of partial activation due to low stimulation frequency on muscle force–velocity properties observed, it seems unlikely that altering stimulus frequency would have significant effects beyond increasing the differences between maximally and partially activated muscle due to greater differences in activation level. Hence, we believe the dominance of the effect of the level of activation over that of fibre type is likely to be seen across muscles and has relevance to in vivo conditions.

This effect of partial activation of the muscle is crucial to our understanding of muscle function; much of our current understanding comes from the maximally activated muscle or isolated single fibres, and muscle models typically consider muscle fibres to be massless, independent actuators. These results highlight that the mechanical properties of maximally activated muscle are not necessarily representative of sub-maximally activated muscle, reiterate the presence [7] and functional consequences [8,9] of mechanical coupling between fibres, and suggest that the physical properties of muscle may have significant effects on muscle mechanical output, modifying and potentially obscuring any effect of activating different motor unit types. These results suggest that an understanding of the interaction between contractile element properties, level of activation and the physical properties of muscle is likely to be essential if we are to understand whole-muscle function during physiologically relevant, sub-maximal contractions. The presence of this interaction may also help to explain observed principles of motor unit recruitment [13–15].

Motor unit recruitment appears to have its basis in the size principle. Slow motor units, with higher post-synaptic motorneuron excitability, are activated first, and faster motor units recruited as activation intensity increases [13–15]. This is an inherently appealing theory as it suggests that smooth, graded force production may be achieved as a consequence of the basic properties of the motorneurons with no requirement for higher-level control. However, it has been suggested that it presents a mechanical [45,46], and potentially also an energetic, paradox. Slow motor units will be active during rapid sub-maximal contractions, thus consuming metabolic energy without significantly contributing to mechanical output. This may be somewhat avoided by the potential to deviate from the size principle to better meet the mechanical demands of a task [16,31,32,40,41,47–49]. However, despite the apparent paradox, the size principle does seem to be broadly adhered to in the majority of cases [14,15,48,50–55].

The results of our study may help to explain this discrepancy. We have demonstrated that activating predominately faster motor units does not necessarily result in faster rates of force development or higher shortening velocities. Hence, at low activation levels, an animal is likely to achieve a similar mechanical output regardless of whether fast or slow motor units are activated (figures 4 and 5). However, the selective activation of fast motor units would require the animal to use a more complex control strategy and would incur a higher metabolic cost, increasing the energy consumed to complete a given task. This is not to say that adherence to the size principle necessarily provides the best mechanical output in all situations; factors such as the proportion of different motor unit types within the muscle, the level of activation and the existence of any compartmentalization of motor unit type may mean that deviation from the size principle can sometimes offer mechanical and energetic advantages. However, our findings indicate that adherence to the size principle may provide not only a simple control strategy but also the best mechanical and energetic performance, helping to explain why it is so often adhered to.

Animals were housed and handled in accordance with U.S. Public Health Service Policy for the humane care and use of laboratory animals, and all protocols were approved by Harvard Animal Care and Use Committee.

Funding statement

Financial support was provided by NIH AR055648 to A.A.B. and J.M.W.