Abstract
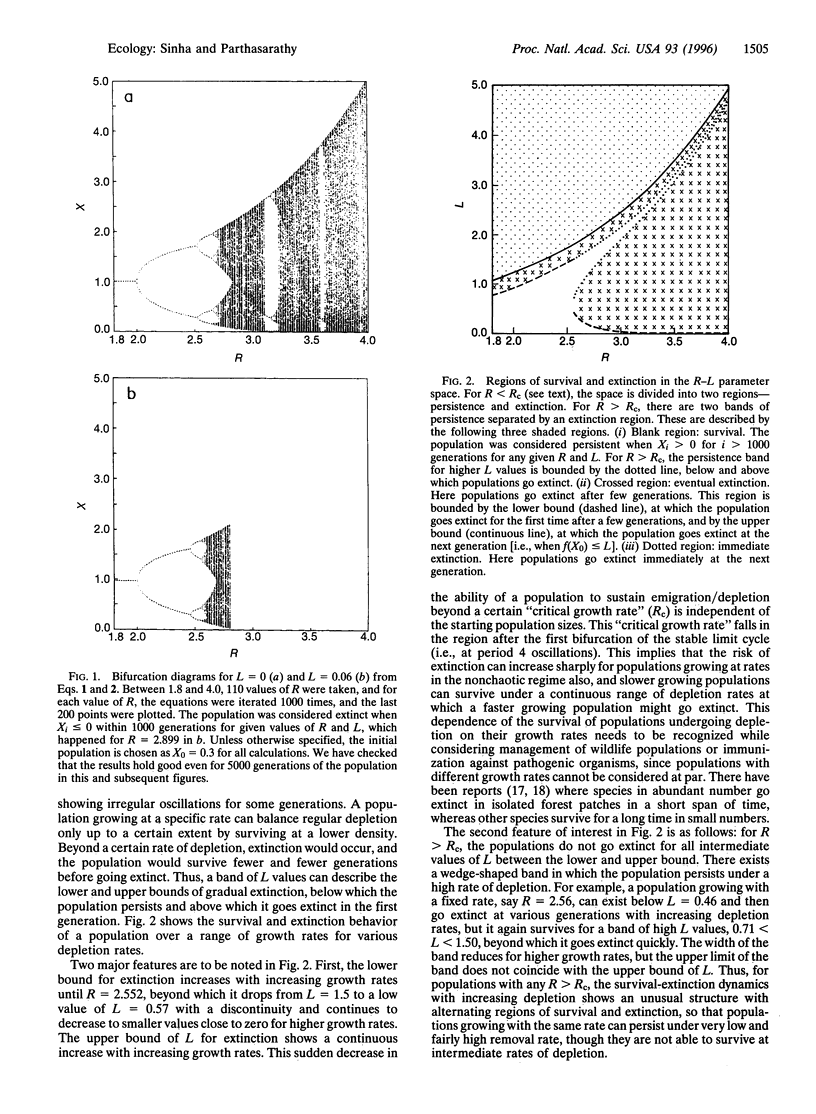
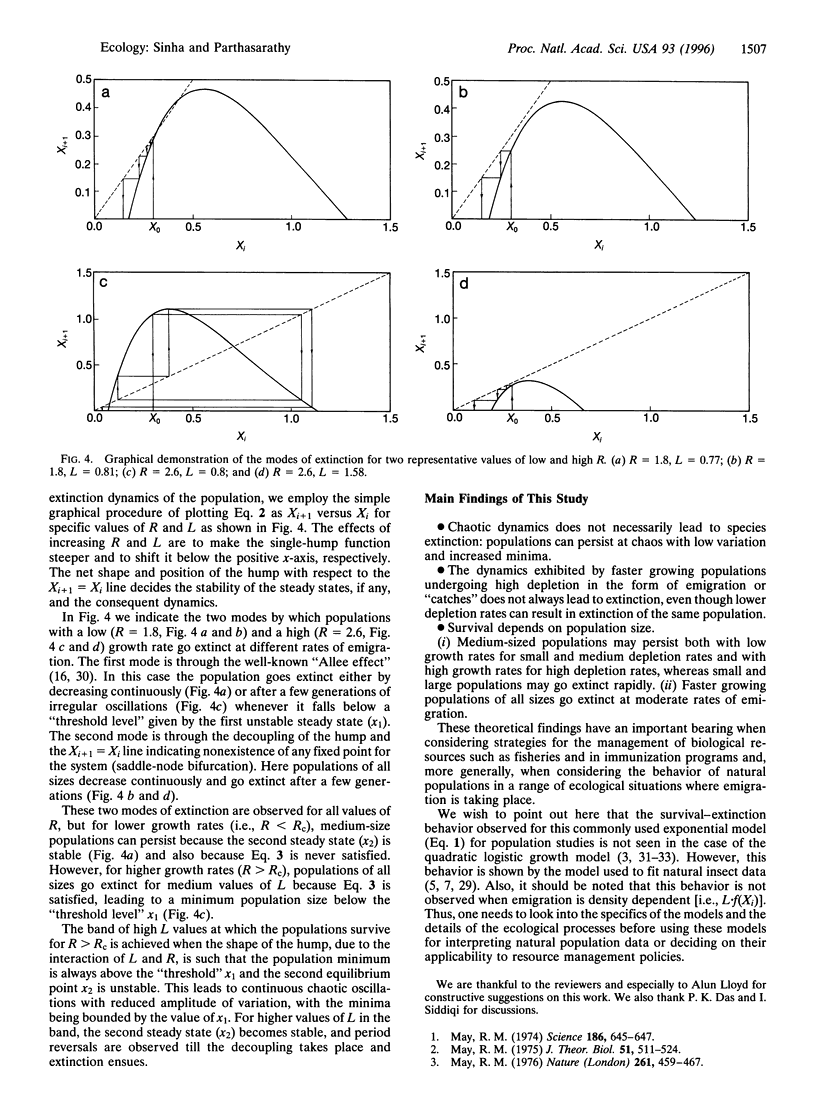
Studies on natural populations and harvesting biological resources have led to the view, commonly held, that (i) populations exhibiting chaotic oscillations run a high risk of extinction; and (ii) a decrease in emigration/exploitation may reduce the risk of extinction. Here we describe a simple ecological model with emigration/depletion that shows behavior in contrast to this. This model displays unusual dynamics of extinction and survival, where populations growing beyond a critical rate can persist within a band of high depletion rates, whereas extinction occurs for lower depletion rates. Though prior to extinction at lower depletion rates the population exhibits chaotic dynamics with large amplitudes of variation and very low minima, at higher depletion rates the population persists at chaos but with reduced variation and increased minima. For still higher values, within the band of persistence, the dynamics show period reversal leading to stability. These results illustrate that chaos does not necessarily lead to population extinction. In addition, the persistence of populations at high depletion rates has important implications in the considerations of strategies for the management of biological resources.
Full text
PDF


Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Allen J. C., Schaffer W. M., Rosko D. Chaos reduces species extinction by amplifying local population noise. Nature. 1993 Jul 15;364(6434):229–232. doi: 10.1038/364229a0. [DOI] [PubMed] [Google Scholar]
- Beddington J. R., May R. M. Harvesting natural populations in a randomly fluctuating environment. Science. 1977 Jul 29;197(4302):463–465. doi: 10.1126/science.197.4302.463. [DOI] [PubMed] [Google Scholar]
- Hanski I., Turchin P., Korpimäki E., Henttonen H. Population oscillations of boreal rodents: regulation by mustelid predators leads to chaos. Nature. 1993 Jul 15;364(6434):232–235. doi: 10.1038/364232a0. [DOI] [PubMed] [Google Scholar]
- Leigh E. G., Jr The average lifetime of a population in a varying environment. J Theor Biol. 1981 May 21;90(2):213–239. doi: 10.1016/0022-5193(81)90044-8. [DOI] [PubMed] [Google Scholar]
- May R. M. Biological populations obeying difference equations: stable points, stable cycles, and chaos. J Theor Biol. 1975 Jun;51(2):511–524. doi: 10.1016/0022-5193(75)90078-8. [DOI] [PubMed] [Google Scholar]
- May R. M. Biological populations with nonoverlapping generations: stable points, stable cycles, and chaos. Science. 1974 Nov 15;186(4164):645–647. doi: 10.1126/science.186.4164.645. [DOI] [PubMed] [Google Scholar]
- May R. M. Simple mathematical models with very complicated dynamics. Nature. 1976 Jun 10;261(5560):459–467. doi: 10.1038/261459a0. [DOI] [PubMed] [Google Scholar]
- Parthasarathy S, Sinha S. Controlling chaos in unidimensional maps using constant feedback. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1995 Jun;51(6):6239–6242. doi: 10.1103/physreve.51.6239. [DOI] [PubMed] [Google Scholar]
- Schaffer W. M., Kot M. Nearly one dimensional dynamics in an epidemic. J Theor Biol. 1985 Jan 21;112(2):403–427. doi: 10.1016/s0022-5193(85)80294-0. [DOI] [PubMed] [Google Scholar]
- Sugihara G., Grenfell B., May R. M. Distinguishing error from chaos in ecological time series. Philos Trans R Soc Lond B Biol Sci. 1990 Nov 29;330(1257):235–251. doi: 10.1098/rstb.1990.0195. [DOI] [PubMed] [Google Scholar]
- Sugihara G., May R. M. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature. 1990 Apr 19;344(6268):734–741. doi: 10.1038/344734a0. [DOI] [PubMed] [Google Scholar]
- Yorke J. A., Nathanson N., Pianigiani G., Martin J. Seasonality and the requirements for perpetuation and eradication of viruses in populations. Am J Epidemiol. 1979 Feb;109(2):103–123. doi: 10.1093/oxfordjournals.aje.a112666. [DOI] [PubMed] [Google Scholar]


