Abstract
Neural ensembles oscillate across a broad range of frequencies and are transiently coupled or “bound” together when people attend to a stimulus, perceive, think and act. This is a dynamic, self-assembling process, with parts of the brain engaging and disengaging in time. But how is it done? The theory of Coordination Dynamics proposes a mechanism called metastability, a subtle blend of integration and segregation. Tendencies for brain regions to express their individual autonomy and specialized functions (segregation, modularity) coexist with tendencies to couple and coordinate globally for multiple functions (integration). Although metastability has garnered increasing attention, it has yet to be demonstrated and treated within a fully spatiotemporal perspective. Here, we illustrate metastability in continuous neural and behavioral recordings, and we discuss theory and experiments at multiple scales suggesting that metastable dynamics underlie the real-time coordination necessary for the brain's dynamic cognitive, behavioral and social functions.
Introduction
Today we know that neurons fire and we know that they are connected. We don't know how they act in concert to govern behavior, the essential question in treating neurological disease and mental-health disorders.
Paul G. Allen and Francis S. Collins (2013)
The life of a brain is marked by a vast number of ongoing electrical and chemical processes spanning multiple spatial and temporal scales (Pritchard, 1992; Linkenkaer-Hansen et al., 2001; Kozma et al., 2005; Honey et al., 2007; Plenz and Chialvo, 2009; Werner, 2010; Lowen et al., 1997) that both arise from and modulate interactions with the body and the environment (Edelman, 1999; Thompson and Varela, 2001; Sporns, 2003; Kiebel et al., 2008; see also Longtin et al., 2003). Such processes take place in a network of cells whose organization emerges at multiple levels, as a result of phylogeny and ontogeny (Deacon, 1990; Krubitzer, 2009; Zhang and Poo, 2001; Chklovskii et al., 2004; Casanova et al., 2007; see also Kaiser et al., 2010). In such complex systems, space and time co-mingle; not much is to be gained by treating them separately or in turn. An obstacle to understanding the brain resides in our difficulty to incorporate both spatial and temporal dimensions in a common theoretical and analytical framework (Elbert and Keil, 2000; Tognoli and Kelso, 2013; Kelso, 1995; Kelso et al., 2013). Resulting from complex interactions in space-time, the coordinative ‘acting in concert’ behavior of neural ensembles lies between the dual poles of segregation (tendencies for neural ensembles to diverge and function independently) and integration (tendencies for neural ensembles to converge and work together) (Tononi et al., 1994; Kelso, 1991; 1992; 1995; Friston, 1997; Sporns et al., 2004; Kelso and Tognoli, 2007; Pitti et al., 2008). Such coordination happens dynamically, with ensembles of various sizes coming together and disbanding incessantly (Eguíluz et al., 2005; Kozma et al., 2005; Plenz and Chialvo, 2009).
The theoretical framework elaborated here is called Coordination Dynamics (Kelso; 1995; 2009; Fuchs and Jirsa, 2007; Tschacher and Dauwalder, 2003; see also von der Malsburg et al., 2010 for a related ‘dynamic coordination’ view). Originally grounded in the concepts and methods of self-organized pattern formation in physics, chemistry and biology (Haken, 1983) and the tools of nonlinear dynamical systems, Coordination Dynamics embraces both spontaneous self-organizing tendencies and the need to guide or direct such tendencies in specific ways. In Coordination Dynamics, the system’s parts and processes communicate via mutual information exchange, and information is meaningful and specific to the forms coordination takes. Coordination Dynamics seeks to identify and then track the temporal evolution of coordination or collective states, emergent quantities that specify how the linkage between components and processes changes over time. The rationale behind this perspective is that the function of a complex biological system lies in the interaction between (context-sensitive) components (see also Pattee, 1976; Miller and Phelps, 2010). In an open, non-equilibrium system, in which many components have the opportunity to interact, some ordering in space and time emerges spontaneously due to self-organization (Kelso and Haken, 1995; Laughlin and Pines, 2000). As a consequence, pattern formation and change may take the form of lower dimensional dynamics (Haken, 1983; Kelso, 2009; Schöner and Kelso, 1988), a plus in the case of large systems (e.g. ~1010–1011 neurons, Williams and Herrup, 1988; Lent et al., 2012).
In Coordination Dynamics, coordination variables are key quantities that specify functionally meaningful collective behaviors such as pattern generation in neural circuits (Grillner, 1975; Kelso, 1984; 1991; Marder, 2001; Schöner and Kelso, 1988; Yuste et al., 2005). Coordination variables span domains or sub-domains (components, processes, events): they may encompass entities that are often assumed to be incommensurable (Kelso, 2009; Tognoli et al., 2011). In the complex systems of living things, coordination variables are not known in advance but have to be found and their dynamics identified (Kelso, 1995; Kelso et al., 2013). Since component behavior on one level is an interaction among components at a level below, Coordination Dynamics is both level-dependent (in an operational sense, e.g. in terms of choosing levels of description—the scientist’s prerogative) and level-independent (in its search for principles and mechanisms that transcend levels). As a result, Coordination Dynamics seeks an understanding of brain function that cuts across scales and levels of description—from individual neurons to minds and their social fabric (see also Akil, et al., 2011; Sporns, 2010).
In its current form, the theory of Coordination Dynamics describes three qualitatively distinct collective behaviors (or schemes) in which integration and segregation come into play. The first two exist for components that are coupled, i.e. there is exchange of information and/or matter between the components, directly or indirectly, and irrespective of a (synchronized) collective outcome. The first scheme couples components whose intrinsic dynamics is similar. Attractors (dynamical structures in which the set of trajectories of a system converge to and persist in a given state) are created in the components’ coordination dynamics. As a result, neural oscillations may be trapped in states of phase- and frequency locking (Okuda and Kuramoto, 1991). If more than one state exists in the latent dynamical structure of the system (a condition called bi- or multistability) brain dynamics may switch states under the effect of a perturbation, input or fluctuations (Briggman and Kristan, 2008; Deco and Jirsa, 2012; Schöner and Kelso, 1988). Signature features of such phase transitions have been observed and modeled (Fuchs et al., 1992; Haken et al., 1985; Kelso et al., 1991; 1992; Kelso, 2010; Meyer-Lindenberg et al., 2002). In a second scheme, the components are also coupled. However, they differ enough in their intrinsic dynamics that they can no longer reconcile their behavior through the mechanism of phase-locking. With the disappearance of the attractors, there is no longer any phase- and frequency-locking behavior. Since the components are coupled however they still influence each other, expressing their relationship in a temporally structured behavior in which lingering in quasi-synchrony (integrative tendencies) and escaping from one another (segregation tendencies) coexist. This is called metastability (Kelso et al., 1990; Kelso, 1995; 2008; Kelso and Tognoli, 2007). Integrative tendencies are strongest during moments of quasi-synchrony or dwells: participating neural ensembles support a collective behavior. Segregative tendencies are observed as a kind of escape behavior: neural ensembles diverge and are removed from the collective effort. In the third and final scheme, the components do not exchange any information; they are completely autonomous and hence behave in total neglect of each other’s behavior. Any integrative or segregative tendency disappears, only independent behavior remains according to each component’s intrinsic dynamics. In nature, though symmetries are broken or lowered all the time, it is difficult for the parts to be perfectly isolated from one another: coupling tendencies may be vanishingly small and indirect, in effect approaching asymptotically the dynamics of uncoupled components.
The purest form of integration (order, synchronization through phase- and frequency-locking) has received by far the most attention in the literature (Ermentrout and Kopell, 1991; Bressler and Kelso, 2001; Bressler and Tognoli, 2006; Fries, 2005; Singer, 2005; Singer and Gray, 1995; Varela et al., 2001; Uhlhaas et al., 2009; Wang, 2010). The less orderly segregation (also called phase scattering, e.g. Rodriguez et al., 1999), however essential to function, has largely remained out of focus (Tognoli and Kelso, 2013; Kelso, 1995). As a consequence, large portions of data –those not matching the dominant thinking- tend to be under-recognized, if not ignored. This blind spot may be costly on both empirical and theoretical fronts: key aspects of the system’s functioning behavior may be left out. A comprehensive view of how the brain works should not be partial to either integration or segregation but recognize the interplay of both tendencies and their dynamics (Kelso, 1991; 1995; Kelso and de Guzman, 1991; Kelso and Engstrøm, 2006; Kelso and Tognoli, 2007; Sporns, 2010; Tononi et al., 1994; Tsuda and Fujii, 2004; Tsuda, 2009).
Coordination Dynamics builds upon the fact that oscillations and cycles are ubiquitous in nature (Eigen and Schuster, 1979; Yates and Iberall, 1973; Prigogine, 1977; Winfree, 2002). Many readers will be familiar with Huygens's famous discovery in 1665 that pendulum clocks coupled weakly through a shared medium mutually entrain into a collective behavior called “sympathy” -- or phase-locking in modern parlance- (see e.g. Bennett et al., 2002). Rhythms are also rife in the nervous system (Freeman, 1975; Grillner, 1975; Basar, 2004; Llinas, 1988; Buzsáki, 2006; Von der Malsburg et al., 2010): they are supported by numerous mechanisms (e.g. Buzsáki, 2006; Grillner, 1975; Llinas, 1988) and are deemed to be of clinical significance (e.g. Buzsáki and Watson, 2012; Uhlhaas et al., 2009). In the brain, across a broad range of frequencies, oscillations exhibit relationships to multiple processes of cognition, emotion and action (e.g. Ward, 2003; Basar, 2004; Bressler and Tognoli, 2006; Engel et al., 2010; Fries, 2005, Wang, 2010 for reviews). Because many functionally relevant neural ensembles are governed by oscillatory dynamics, a meaningful coordination variable is the relative phase ϕ, which is capable of tracking the competition of integrative and segregative tendencies over time When integrative tendencies predominate, the current ordering among components persists, and ϕ’s future values remain identical to the ones present. Alternatively, when segregative tendencies take over, the system is allowed to change, as does ϕ when it departs from a changeless (horizontal) trajectory.
Viewed from the perspective of Coordination Dynamics, the emerging picture is that of a brain in constant flux, its dynamic ensembles ever rearranging themselves as processes unfold that weave immediate and past events at numerous temporal and spatial scales. Here, we will discuss the complementary nature of integration and segregation, from the standpoint of theory, neural dynamics and function (behavior, cognition). We will proceed from a simpler view of coordination in a pair of oscillating components (thus emphasizing the temporal aspect) before extending the picture to incorporate metastability in a fully complex spatiotemporal perspective.
I. Metastability: A temporal perspective
a. Models
The coordination dynamics of complex, nonlinear systems does not necessarily fulfill expectations drawn only from knowledge of component properties and their coupling (Mazzochi, 2008; Motter, 2010). Moreover, the effects that emerge may seem paradoxical. For instance, it has been shown that oscillators with different intrinsic frequencies can synchronize (Kelso et al., 1990), whereas oscillators with (quasi-) identical intrinsic frequencies can exhibit partial or complete desynchronization (Kuramoto and Battogtokh, 2002). Metastability is a fundamental concept to grasp the behavior of complex systems theoretically and empirically (Friston, 1997; Kelso, 1995). It provides a description of the influence exerted by interconnected parts and processes when pure synchronization—phase and frequency-locking--does not exist. In Coordination Dynamics, such synchronization corresponds to, e.g. stable fixed points of collective states. By the word “metastability”, we mean that the system’s dynamics resides beyond such attractor-bearing regimes. As a result, components are able to affect each other’s destiny without being trapped in a sustained state of synchronization, a collective state where no new information can be created (Kelso, 1995; Kelso and Tognoli, 2007).
To illustrate the concepts, we consider the collective behavior of a pair of coupled oscillations (x1 and x2) that can exhibit phase- and frequency locking, metastability or individually autonomous behavior depending on coupling strength (embodied in parameters a and b in eq.1 below) and constitutive differences in their intrinsic frequencies (δω = ωx1 − ωx2). If left to themselves with no stimulation, the (intrinsically nonlinear) oscillators are capable of self-sustaining periodic behavior (a property motivated by the brain’s ongoing dynamics, e.g. Llinas, 1988; Buzsáki, 2006) and their (nonlinear) coupling obeys equation 1. As discussed above, to study the dynamics of the system’s collective behavior, we will focus on the relative phase ϕ = ϕx1 − ϕx2 and its rate of change over time ϕ̇. Eq. 1 also includes a noise term (Schöner et al., 1986) which is not essential for the emergence of metastable behavior though it can allow the system to discover (and in fact stabilize) new states. For further details about the components and their coupling, we refer the reader to (Fuchs, 2013; Liese and Cohen, 2005; Haken et al., 1985; Kelso et al., 1990).
| (eq.1) |
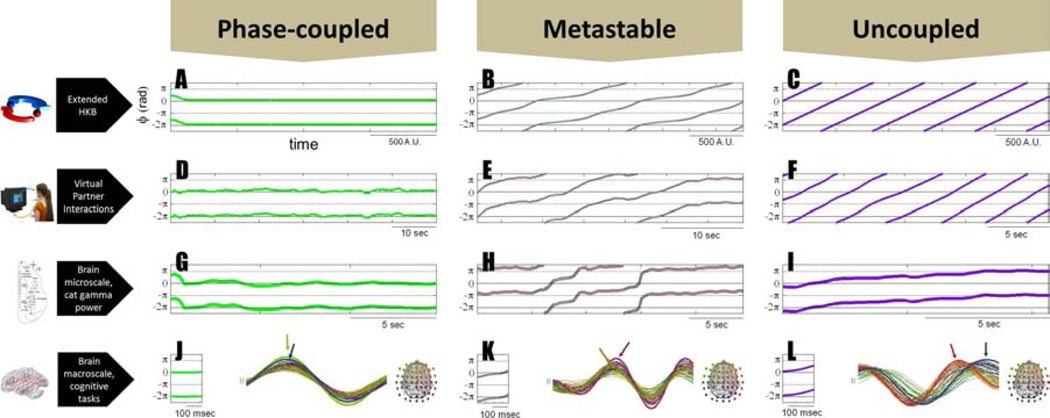
Figure 1A–C presents the relative phase dynamics (ϕ as a function of time) of a pair of oscillations under three qualitatively different parameter regimes, all belonging to the functional repertoire of eq. 1. Figure 1A shows an example of phase-locked oscillations, which have been abundantly theorized about as a basis for integration in the brain (e.g. Fries, 2005; Singer and Gray, 1995; Varela et al., 2001). Intrinsic frequencies are close to each other (δω small) or identical, and even when there is weak coupling, the relative phase heads toward a constant value ϕ, that is: ϕ(t + τ) ~ ϕ(t) as τ → ∞. Note that the individual phases ϕx1 and ϕx2 do not need to be (and in the most general case are not) identical (a situation wherein phases are both locked and coincident; also known as zero-lag synchrony), and that in this model the lag between phase-locked oscillations (ϕx1 − ϕx2) does not result from delays between the oscillators: it emerges predominantly from broken symmetry in the oscillators’ intrinsic dynamics (δω ≠ 0), or in other words, it is a manifestation of differential pulls simultaneously exerted by the components on each other. Figure 1C presents the limit case of oscillations with no coupling (a and b=0). Oscillator frequencies persist with a difference δω and the relative phase ϕ = ϕx1 − ϕx2 drifts with a constant slope dϕ / dt. This phase wrapping behavior only exists if components are completely isolated from one another (an idealized condition that is not met in nature), and especially not in the brain which exchanges information within itself and with its surroundings that include other human beings. Figure 1B illustrates metastable dynamics, with its characteristically non-uniform relative phase trajectory. In the metastable regime, integrative and segregative tendencies coexist. Integrative tendencies are accentuated near particular values of ϕ when each oscillator is maximally attuned to the other’s behavior. Mathematically, such tendencies exist near the fixed points of phase-locking that were annihilated through a saddle-node or tangent bifurcation. The periods when integrative tendencies dominate are called dwells and are revealed by the near-horizontal segments of the relative phase trajectory (tendency for changelessness). Segregative tendencies are manifest when the relative phase “escapes” (drifting segments that express change in the system’s coordination). Persistence of dwells can vary from long (approaching Figure 1A) to vanishingly short (approaching Figure 1C; see e.g. Kelso and Tognoli, 2007). Shorter dwells are associated with lesser symmetry in the components and/or weaker coupling. Through the dynamical interplay of coupling and broken symmetry manifested in dwells and escapes the system is able to realize both the parts’ tendency to behave as an integrated unit and their tendency to express individual dispositions. From these dual or complementary tendencies, functional complexity emerges (Kelso, 1995; Kelso and Engstrøm, 2006).
Figure 1. Patterns of coordination transcend multiple levels.
Coordination dynamics is shown in models (A–C), behavioral data (D–F), and neurophysiological data (G–L). Plots show the coordination variable phi as a function of time. The left column includes samples of relative phase observed during phase-locked coordination (note establishment of states, revealed by persistent horizontal trajectories). Right column shows uncoupled behaviors (note the constant change of the relative phase, called wrapping). Center column shows metastability in which the relative phase exhibits characteristic dwell and escape tendencies, manifested in the alternating mixture of quasi stable and wrapping epochs. See details in text.
The living brain never finds itself frozen for any length of time in a particular coordination state (Tognoli and Kelso, 2009; Kelso, 1995; 2010; see also e.g. Gusnard and Raichle, 2001; Rabinovich et al., 2008), although it might be desirable that some parts of the system dwell over longer time-scales (for instance, in some memory processes) than others (say, perception). In the present context, three mechanisms are capable of changing a system’s coordination. The first is bifurcation and requires that a control parameter (such as the concentration of a neuromodulator, cf. Briggman and Kristan, 2008) crosses a critical threshold causing the system to lose a preexisting attractor. If the system were locked in this lost attractor prior to bifurcation, a new dynamics may be chosen (e.g. selecting another attractor or a regime without any attractive states). The second mechanism of change requires perturbation, noise or energy input to transiently destabilize the coordination dynamics. If this event occurs with sufficient magnitude, and if the coordination dynamics is multistable (Kelso, 2012), both brain and behavior may switch to another coordination state (Kelso, 1984; 2010; Kelso et al., 1991; 1992; Meyer-Lindenberg et al., 2002; Schöner and Kelso, 1988). Such transition behaviors may be facilitated by criticality, the poising of the system at the border between order and disorder (Chialvo, 2010; Plenz and Thiagarian, 2007; Plenz and Chialvo, 2009). Finally, in metastable dynamics, there are no attractors in the system and no energy expenditure is necessary for self-organized tendencies to be visited in turn. Change and persistence are intimately linked in this transient regime. Both the duration of transient functional groupings and the presence of escape tendencies depend entirely on the dynamical structure of the system (see also Briggman and Kristan, 2008; Prinz, Bucher and Marder, 2004; Rabinovich et al., 2008; Cabral et al., 2011). Note that noise is critical for transitions in multistable regimes at rest, but it is not strictly necessary for the emergence of spatiotemporal patterns of the metastable type. Therefore, we will not enter into further details with respect to the issue of noise (but see, e.g. Tsuda and Fujii, 2004; Ghosh et al., 2008; Deco and Jirsa, 2012).
b. Functional evidence
The brain is an open system with respect to energy, matter and information flows. Some have pointed out that the brain’s fundamental raison d’être is to deal with the informational complexity surrounding the organism (e.g. Holloway, 1967; Chialvo, 2010). It is generally agreed that information exchange between brain and environment varies from minimal (e.g. the brain temporarily left to its own intrinsic dynamics, Gusnard and Raichle, 2001; Yuste et al., 2005; Lundervold et al., 2010) to strong and focal (e.g. in paradigms evoking neural responses to sudden and isolated stimuli). If the natural behavior of the brain is to be uncovered empirically and understood theoretically, care has to be taken to express the full spectrum of self-organizing processes. In the following, we present evidence for the emergence and evolution of metastable coordination dynamics in a wide variety of contexts.
Figure 1D–F presents samples of collective perceptuo-motor behavior. Humans have the potential to engage in coordination dynamics that is bistable at low movement frequencies and monostable at high ones (Haken et al., 1985; Kelso, 1984); and further, in intermittent or metastable collective behavior (Kelso et al., 1990; Kelso and de Guzman, 1991). In Kelso et al. (2009), a virtual partner or human dynamic clamp was designed—along the lines used in cellular neuroscience--and the coordination dynamics between human and virtual partner studied. To investigate the emerging coordination dynamics, both partners were given opposite goals: the human to stabilize inphase and the virtual partner to stabilize antiphase coordination. A range of dynamical behaviors was observed modulated by experimental conditions (reciprocity of coupling and movement frequency) including sustained states of locking (D), transient behaviors (E) akin to metastable dynamics observed in models (B) and unlocked behavior (F).
Similar results were observed in human sensorimotor behavior when subjects: 1) coordinate movement with periodic auditory and tactile (Lagarde and Kelso, 2006; Assisi et al., 2005b) as well as visual stimuli (Kelso et al., 1990), 2) in bimanual coordination (Banerjee et al., 2012) and 3) spontaneous social coordination between pairs of subjects (Tognoli, 2008; Tognoli et al., 2007, Oullier et al., 2008; Schmidt and Richardson, 2008). The tasks employed continuous (as compared to discrete) behavior, because discrete behaviors express the transients that occur as the system’s coordination behavior approaches a new attractor or a new landscape of attracting tendencies. Such transient behaviors are more difficult to decipher from the relative phase dynamics because of their brevity (which prevents persistence or repetition of a pattern to be observed). Some ambiguities ensue, for instance the transient observed at the onset of a phase-locked regime shares features with a metastable regime (see Kelso and Tognoli, 2007, figure 2), and may be mistakenly confused with the latter in brief windows of observation. Elsewhere, one of us has presented a treatment of how discrete dynamics relates to continuous dynamics (Jirsa and Kelso, 2005). Overall, these results suggest that across a broad range of very different behavioral systems the interplay of integration and segregation is visible in their coordination dynamics. Our interpretation is that the blend of integration and segregation opens up more potentialities for the performance of meaningful behaviors than synchronization, per se. Following the same line of thought we turn to neurophysiological coordination dynamics.
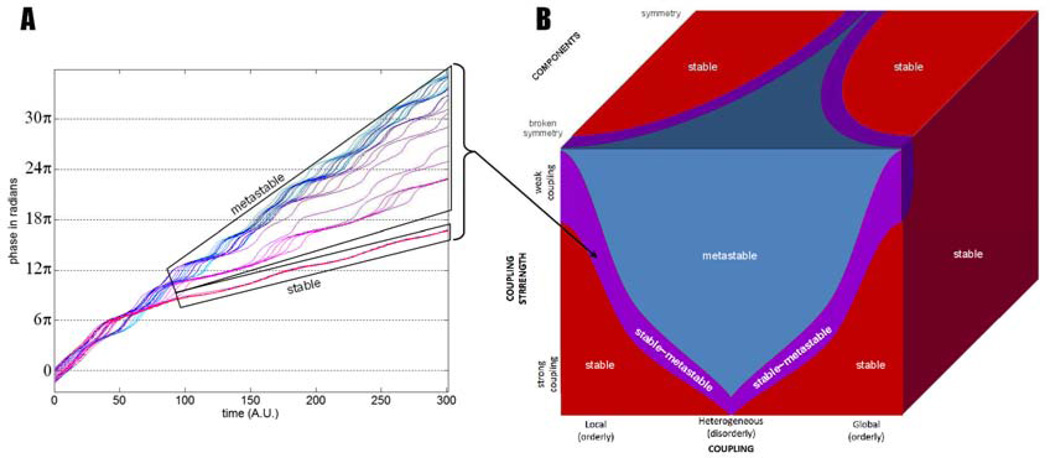
Figure 2. Coexisting phase synchrony and metastability.
In A, a “chimera” regime is shown, with time on the horizontal axis (arbitrary units) and unwrapped phase on the vertical axis. Having switched to a problem with N 2 elements, we now represent the oscillators’ individual phase (N trajectories) rather than the relative phase (which would suffer a combinatorial explosion with N! trajectories). Furthermore, we unwrap the phase trajectories to avoid the graphical confusion that would arise from wrapped phase intersections. In such graphs of individual phases, integrative tendencies are discovered when trajectories run parallel for a given length of time; trajectories that ascend with different slopes reveal segregation. The time series depict dynamics of oscillators governed by equation 2 above. After an initial transient, the group of oscillators remains perpetually in synchrony (lower box annotated “stable” that stacks the joint phase-trajectory of one third of the oscillators). An “incoherent” group coexists (upper box). Its dynamics consists of a series of escape (segregative tendencies) interspersed with periods of dwells (integrative tendencies), that are typical of metastability. Note undulations in the phase dynamics of the stable components. This undulation both depends on and affects the behavior of the “escapers”, determining their velocity and escape probability in space and time (not shown, see Tognoli and Kelso, 2013). B shows a conceptual ‘big picture’ illustration of the parameter regimes of coordination dynamics - observed for components ranging from similar to different, and coupled with varying strength and heterogeneity. Strong and symmetrical coupling in similar components gives rise to stable behavior, whereas weaker coupling, and/or lesser symmetry in the components and their coupling gives rise to metastability. A hybrid stable~metastable regime exists at the fringe between the two, as exemplified in A.
c. Neurophysiological evidence
Neural ensembles must work in a coordinated fashion at different spatial scales. Such ensembles produce extracellular fields that can be recorded at suitable temporal resolution using electrophysiological techniques. Figures 1G–I present samples of collective behavior between the gamma power of two neural populations in the cat’s brain at rest (after data published by Popa et al., 2009, figure 3, F2–F3). The two populations are reported to be coordinated antiphase with each other (Popa et al., 2009). In 1G, an episode is shown during which changes in gamma power in both ensembles are synchronized. In 1H, an episode is shown during which the gamma power collective dynamics appears to be metastable, with tendencies for quasi-synchrony (mainly antiphase in this particular sample) alternating with tendencies for segregation. In 1I, an episode of quasiunlocked gamma power change is shown. Similar coordination dynamics are observed at the macroscale in a variety of behavioral and mental tasks, for instance during movement arrest tasks (see figure 1 J–L, after data from Tognoli and Kelso, 2009), with EEG patterns drawn on the right (note phase aggregates indicated by colored arrows which are subject to relative phase analysis), and their respective episodes of relative phase on the left that shows locking, metastability or quasi-independence, albeit in shorter durations, because, we hypothesize, macroscopic data are made up of many more components than their mesoscopic and microscopic subsystems, and there are proportionally more opportunities for the dynamics to be reorganized (see also section II.d).
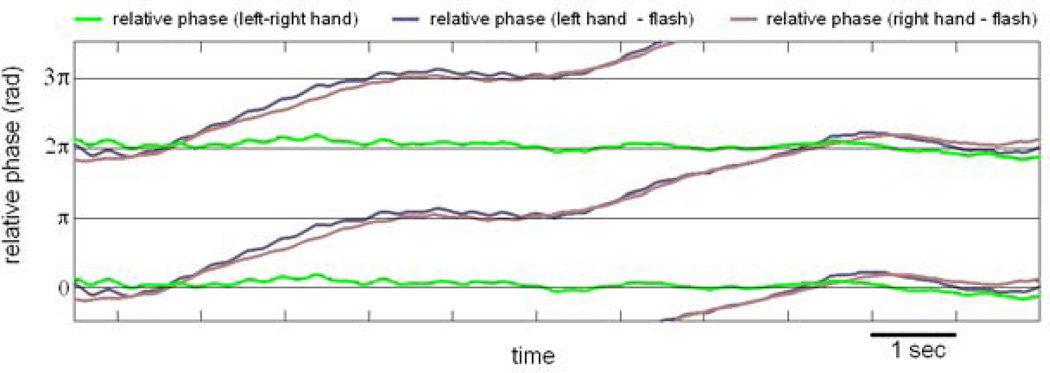
Figure 3. A behavioral “chimera”.
Shown is the relative phase among three pairs of components, left and right index fingers and a periodically flashing light that served as a pacing stimulus. Left and right fingers sustained a state of phase locking (persistently horizontal relative phase trajectory, in green), while at the same time the relative phases between each finger and the pacing stimulus alternated between dwells and escapes, in a manner typical of metastability (pink and blue trajectories).
d. The big picture: life of the brain
In previous sections, we have described the coordination dynamics of behavioral and neural variables in selected time windows. For clarity of exposition, the latter were framed to reveal only a single type of collective behavior that conforms to models known to be governed by state-transitions and metastability. The goal however was not to dichotomize the different organization schemes, for instance to decide which is the dominant modus operandi of the brain. Rather the aim is to formalize the different types of coordination behavior as different outcomes of the same dynamical design. Through examples taken at various neural and behavioral levels, we have posited the plausibility of each scheme on given occasions. For instance, we have shown that gamma power in the “anticorrelated network” of the resting brain (Popa et al., 2009) in reality appears intermittently anticorrelated (figure 1H), as well as “in-correlated” (figure 1G) and almost unlocked (figure 1I). A variety of forms of coordination are revealed if the system is observed on appropriate timescales. The scientific goal, of course, is to synthesize multiple and partial descriptions of the system’s behavior with a single coherent account (see Schmitt, 1978).
Thus far, our emphasis was predominantly on the temporal course of coordination. We presented examples in which the system was parsimoniously described using two interacting components or processes: spatial aspects were largely ignored. More typically, however, neural ensembles that are temporarily locked together may segregate or differentiate later on, each to engage in distinct neural groups. In the following, we extend the picture to include interaction between multiple neural ensembles and elaborate their full spatiotemporal dynamics.
II. Metastability: A spatiotemporal perspective
The brain does not work as a group of context-free local subsystems that respond to or anticipate events and then return to some homeostatic equilibrium until another functional demand arises (Lloyd, 2000; Tsuda and Fujii, 2004; Tognoli and Kelso, 2013). Neural ensembles are continuously engaged in multiple interactions, and changes occurring at any place in the network may ripple through and affect each and every ensemble, with time scales that span from near-instantaneous to long, and with coupling strengths from strong to minimal (Kelso, 1995). The coupling is never null, since there is no island in the brain (see also figure 5 in Izhikevich and Edelman, 2008 for a related account).
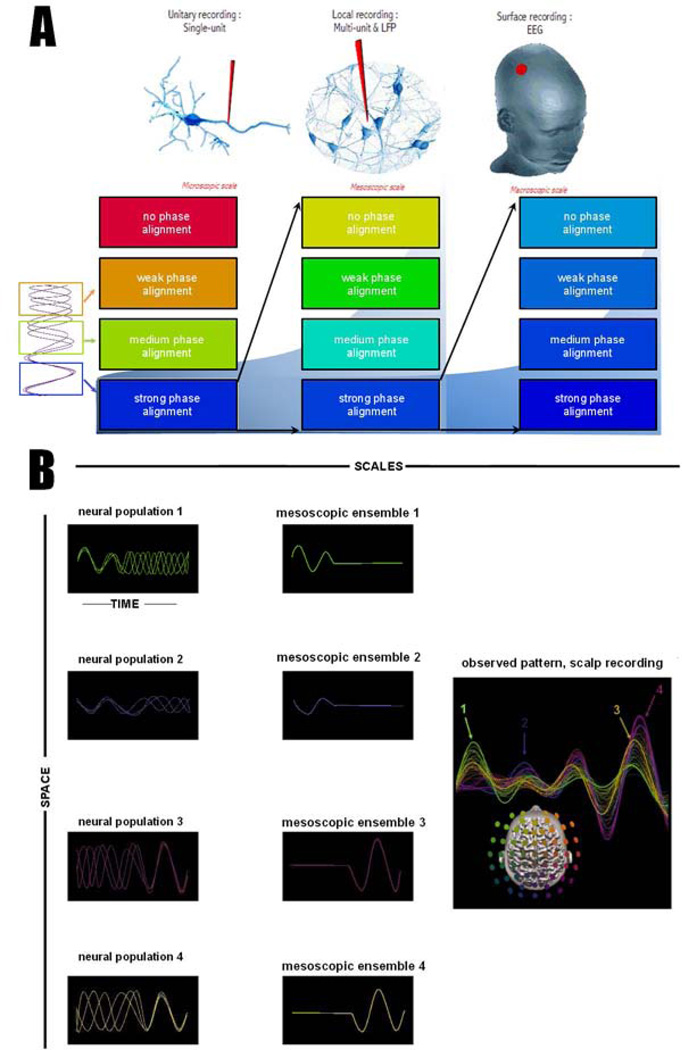
Figure 5. Narrowing the focus of coordination dynamics across scales of observation.
(A) illustrates three levels of recording of oscillatory activity: the hypothetical recording of individual neurons (left), local population recording of multiple neurons, for instance as Local Field Potentials (LFP) or intracranial EEG (iEEG)(center) and the global activity captured for instance with high density magnetic (MEG) or electric (EEG) sensor arrays (right). At each upper spatial scale, only the orderly most aspects of neural organization from the lower scale are observable. An example is outlined in figure 5B: when patterns have misaligned phase relationships (left columns), their population signal cancels (middle column) and disappears from the upper scales. The result resembles a state transition regime, although it is more plausible that a single spatiotemporally metastable regime without state transitions spans the entire episode.
That the brain is able to unfold such a variety of behavior over time demonstrates a fundamental point: the many interactions among components are not fixed (Ingber, 1981; Fuchs et al., 1992; Kelso and Fuchs, 1995; see also Tsuda, 2001). Brain regions engage and disengage constantly with each other. This is observed both during intensive information exchange with the environment (e.g. Hoshi and Tamura, 1997; Rabinovich et al., 2008), and when the brain operates more on the side of a closed system at rest (Gong et al., 2003; Kaplan et al., 2005; Honey et al., 2007; Ito et al., 2007).
At least two challenges need to be confronted for a deeper understanding of the self-organizing brain. One is a comprehensive description of the system’s spatiotemporal dynamics. Due to emergent properties of complex systems, such a description must go beyond the analysis of specialized brain regions and neural ensembles, per se (Kelso, 1995; Schierwagen, 2009, see also Bullock et al., 2005; Honey et al., 2009). A second challenge is to capture the essence of functional interactions within the brain and between the brain, body and environment. In this respect, the concepts of propagation (temporal order) and synchronization (spatial order) have received most theoretical and empirical scrutiny. Notice, however, that propagation and synchronization are limit cases of orderly behavior; as argued in section I a mixture of integration and segregation is needed to achieve complexity. In the quest to understand the self-organizing brain in space and time, we will discuss the grey areas lying between these two well-defined processes of synchronization and propagation (Tognoli and Kelso, 2013). To do so, we examine the basic building blocks of coordination dynamics presented in section I, and their interplay in space-time in systems composed of multiple components.
a. Models
Many models have been designed in an attempt to understand the complexity of the brain (Sporns, 2010). Modeling studies frequently explore parametrically the effect of coupling strength. Perhaps for convenience of dealing with orderly collective behaviors, more often than not they emphasize strong coupling: the system’s parameter space is divided between stable and “unstable” regions often with a focus on the former (but see recent work that focuses on the interface between stable and unstable regions, e.g. Ghosh et al., 2008; Cabral et al., 2011; Deco and Jirsa, 2012). What we pursue here is a theoretically valid description of brain function in which both integration and segregation are considered on an equal footing. As in section 1, metastable régimes that express both integrative and segregative tendencies lie in between complete synchronization (typically the result of strong and homogeneous coupling in a collection of identical oscillators) and complete independence (which, we submit, is only attained in idealized uncoupled systems).
In addition to régimes in which all interactions obey one of the four classes described in section 1 (phase-locking, phase transitions, metastability and independence) the existence of mixed regimes –or chimera- has been demonstrated (Kuramoto and Battogtokh, 2002; Abrams and Strogatz, 2006; Laing, 2009; Martens, 2010; Shanahan, 2010). That is, phase-locking is observed over certain regions of the system –those in which coupling is stronger- and an “incoherent” behavior is observed for other regions where coupling is weaker. An example of such coordination dynamics with components obeying equation 2 (after Kuramoto and Battogtokh, 2002) is presented in figure 2A.
| (eq.2) |
where ϕ is the time (t) and space (x)-dependent phase of oscillators x arranged in a circular, one dimensional domain (a ring), G is a nonlocal coupling function (forcing mean field) that is distance dependent, α is a phase constant parameter describing the exponential rate of spatial decay of the forcing mean field and ω is a parameter describing oscillator frequency (see Kuramoto and Battogtokh, 2002 for details).
Figure 2A shows that the so-called “incoherent” group is not composed of independent oscillators (see upper box). For shorter or longer periods of time, every oscillator from this group displays episodes of dwell interspersed with periods of escape, essentially revealing the same integrative~segregative tendencies as in figure 1B. Thus, the dynamics of this model reveals co-existing synchrony and metastability. Coordination is intermediary between synchrony, in which every component is phase-locked, and another core metastable group in which all the components exhibit dual tendencies for integration and segregation (Figure 2B).
The metastable régimes proper (blue part of figure 2B), or the so-called “incoherent” region of the mixed régime (in the purple part of figure 2B) have the richest dynamics in space and time. Sets of oscillatory components that dwell together and exert their mutual integrative tendencies are not fixed a priori, or organized in predetermined and immutable “networks”: they are dynamically arranged and rearranged under the influence of their own history. As the system evolves, many opportunities are created for the components to interact with each other in distinct coordination ensembles, and all of this, without need for external input—which may be viewed as shaping the coordination dynamics. An intriguing possibility is that such dynamic reorganization in space-time could explain how information flows from one region to another. The strict concept of propagation is untenable in a complex and nonlinear system such as the brain. Spatiotemporal metastability, we propose, is the missing conceptual link between propagation (orderly collective behavior in time) and synchronization (orderly collective behavior in space).
Metastable régimes are found in systems with weak coupling, and they are favored by broken symmetry, a property that introduces “frustration” in the system and expresses more fully its non-equilibrium nature. In models, broken symmetry can be manipulated in a variety of ways, for instance at the level of components or their coupling (e.g. Omata et al., 1988; Kuramoto and Battogtokh, 2002; Assisi et al., 2005a, see also Breakspear et al., 2010; Cabral et al., 2011). Figure 2B shows a conceptual illustration of metastability in a parameter space varying coupling strength, component and coupling asymmetry. Broken symmetry (Kelso, 1995; Kelso and Tognoli, 2007) and complexity are pervasive properties of brain networks (Sporns, 2010). It appears that the dynamical mechanism of metastability--a subtle blend of broken symmetry and coupling-- is more suited to the empirical facts than synchronization per se. In the following, we discuss behavioral and neurophysiological evidence supporting the hypothesis that the brain’s spatiotemporal behavior is governed by metastable coordination dynamics.
b. Functional evidence
Once again we exploit non-equilibrium steady-states to allow sufficient time for the system to self-organize and reveal its dynamical properties. We also favor studies of movement because they provide overt measures of brain function continuously over time (an invaluable feature for the study of a system’s coordination dynamics). Moreover, a great benefit is the potential to observe and measure the (often distributed) parts and their interaction over time, which is less accessible in the brain. In Jeka et al., (1993), coordination between all four limbs, the arms and the legs, was studied in humans. Subjects were able to stabilize certain patterns of coordinated behavior. Stable patterns were observed with all four limbs locked in phase or with subgroups of two or three limbs locked inphase within a group and antiphase between-groups. These stable regimes evoke the red region of figure 2B and suggest the presence of strong coupling and sufficient symmetry in the four-limb system. This example and others exemplify stable states of phase locking in both space and time (see also Schöner et al., 1990; Golubitsky et al., 1999).
Further, coexisting synchrony and metastability were also sought. In a task of visually-paced bimanual coordination for example, subjects were instructed to coordinate both left and right finger movements with the onset of a flash of light emitted periodically by a diode placed in front of them (Kelso, 1984; Banerjee et al., 2012). Both experiment and theory conceive of the sensory input from the metronome as a control parameter that drives the system beyond instability to discover new coordination states (Haken et al., 1985; Jirsa et al., 1998; Kelso, 1984; Kelso et al., 1990; Schöner and Kelso, 1988; Schöner et al., 1986). The experimental arrangement affords a unique possibility to test the interplay of the coupling between the two hands and the coupling between each hand and environmental signals. One might hypothesize that the coupling between left and right hands is stronger than the coupling between hands and rhythmic visual stimuli, thereby providing a combination of symmetry (left and right hands) and symmetry breaking (hands with visual stimulus) for a chimera régime to emerge. As this task was a natural place to seek a chimera’s empirical footprints, we reexamined the data of Banerjee et al., (2012). At high frequency, mixed coordination dynamics composed of phase locking and metastability was observed (Figure 3). That is, left and right hand movements were phase-locked, and at the same time, the relative phase between the hands and visual stimuli exhibited bistable attracting tendencies, alternating near inphase and near antiphase. The collective dynamics of this experimental model system is a clear instance of mixed (chimera) dynamics presented in section II.a (see purple region of figure 2B). Taken together, such functional evidence demonstrates that stable and metastable dynamics belong to the basic repertoire of human behavior. It also shows a way to study both integration and segregation at once--an important methodological and theoretical advantage when it comes to understanding the spatiotemporal organization of complex systems like the brain.
c. Neurophysiological evidence
Piecemeal instances of synchronization, metastability and quasi-independence are readily observed in electrophysiological recordings (figure 1), but now, following the taxonomy of section II.a (figure 2B), we ask whether complete synchronization, mixed synchronization~metastability and complete metastablity exist in the spatiotemporal dynamics of the brain. We consider two levels of observation, the microscale with individual neurons as functional units, and the mesoscale at the level of neural ensembles. At the microscale, Shoham et al. (2006) have shown that a large number of neurons are silent, at least at time scales relevant to electrophysiological studies. This observation precludes complete synchronization as a dominant modus operandi of neural populations. At the mesoscopic level, the idea of widespread neural synchronization, often considered in generalized epileptic seizures, has been rebutted (Garcia-Dominguez et al., 2005; Milton et al., 2007; Lehnertz, 2008). Thus, at both microscopic and mesoscopic scales, there are strong hints that the brain always remains less than completely synchronized. This is in agreement with the hypothesis that the brain realizes its complexity by living between order and disorder (Chialvo, 2010 see also Atlan, 1986), where it can realize its dual tendencies for integration and segregation (Kelso, 1995; Kelso and Tognoli, 2007; Tononi et al., 1994).
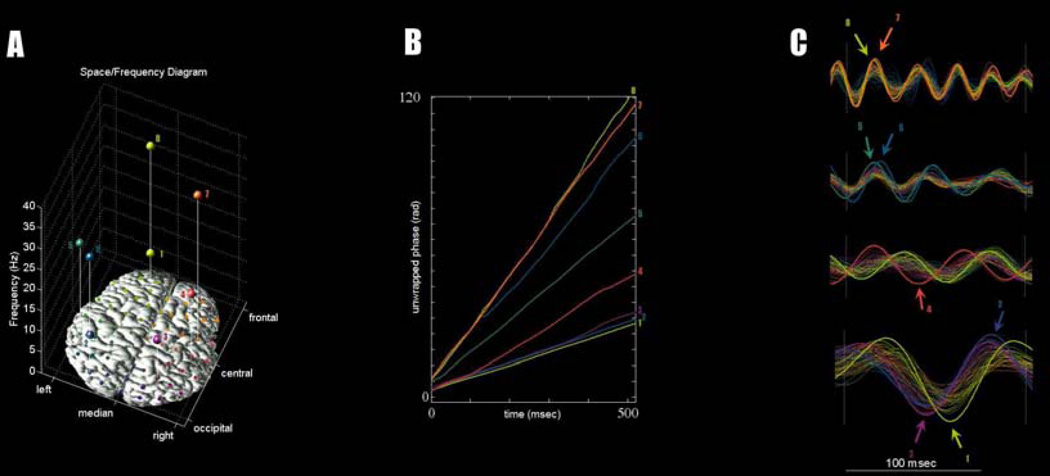
Alternatively, we turn to the issues of stable~metastable and fully metastable coordination. Figure 4B shows the phase trajectory of a set of neural ensembles captured during waking activity with EEG (data after Tognoli and Kelso, 2009, Fig.4). In this example, a spectral scanning analysis revealed eight ensembles spread across a range of frequencies (Figure 4A, C). Their coordination dynamics is further investigated in Figures 4B, D. As in Figure 2A, in Figure 4B integrative tendencies are manifested by phase trajectories running parallel to one another and segregative tendencies are seen as divergent phase trajectories. During this episode, we observe transiently formed groups that may either be synchronous or engaged in a metastable dwell. In contrast with the simple model represented in Figure 2A, we observed three characteristic properties of brain self-organization. First, multiple organized groups were simultaneously present: for instance, Figure 4 exhibits a group of three local ensembles locked in the alpha band (ensembles 1–3), an additional two ensembles transiently locked in the gamma band (ensembles 7–8), and three other ensembles exhibiting lesser phase interactions with the others (ensembles 4–6). Second, the synchronized cores are not composed of fixed groups of neurons: from moment to moment, the organized core(s) change, suggesting that coherent activity organizes into different sub-networks of the brain over time. Finally, the duration and strength of integrative tendencies observed between different groups was much weaker than the example shown in Figure 2A, suggesting that brain self-organization among neural ensembles is characterized by weak coupling. The idea of maximizing point-to-point information exchange is a potent assumption in systems neuroscience (e.g. Huang and Stevens, 1997). Accordingly, it may seem that weak coupling is a less favorable design for an efficient brain. In the present view however, weak coupling is a key factor that introduces flexibility and complexity in the system, rather than being an obstacle to the realization of function (see also Hoppensteadt and Izhikevich, 1997; Thiele, 2009; Ponzi and Wickens, 2010).
Figure 4. Dynamic coordination of eight neural ensembles observed in a momentary episode of waking brain EEG activity.
(A) scalp topography (projected on x-y axes) and center frequency (z-axis) of each ensemble. (B) unwrapped phase trajectories of each ensemble. Note similarities with Figure 2A. (C) ensemble oscillations in the time domain using adapted bandpass filters. Two organized groups are simultaneously present, one involving three ensembles in the alpha band (identified with numbers 1,2,3 throughout the figure); and the other involving two other ensembles in the gamma band (7,8).
d. Intermittently visible neural ensembles
In the previous section we stressed that a sparse number of ensembles is expressed at any given instant. For them, after a brief episode of existence and interaction, they lose coordination or disappear. At first, this is compatible with the idea that neural groups are engaged then disengaged, a few at a time. Theoretically, this finding is akin to state transition theories of brain function (régimes with attractors); methodologically, it led us to develop a framework for sequencing dynamic patterns from spatiotemporally recorded neurophysiological activity (Tognoli and Kelso, 2009, see also Lehmann, 1990; Kaplan et al., 2005; Abeles et al., 1995; Freeman and Holmes, 2005; Nikolaev et al., 2010; Alba et al., 2010). The inference that transitions exist at the level of cortical sources because we can see transitions in EEG measurements is simple enough. Deeper insight is gained when a forward model of the brain’s many superimposed electromagnetic sources is taken into account (see, e.g. Murzin, et al., 2013).
In reflecting on the principles of brain function, we are concerned with a signal arising from neuronal transactions of electrical charges which, though distinct from the observable signal recorded with our measuring instruments, relate in a systematic manner. Since we record from spatially discrete samples, a first principle to keep in mind is that sensor proximity to the originating neural population does not guarantee that its activity is maximally represented at that sensor (see, e.g. Tognoli and Kelso, 2009, fig. 3A). Nonetheless, there are sensors Sk that carry the greatest signal from a given neural ensemble k when the latter is singly active. The relationship between sources k and sensors Sk, can be specified by a forward model. However, in the presence of multiple and changing activities, no sensor provides faithful information on neural ensemble dynamics: all recorded dynamical properties (from phase, to amplitude, frequency and topography) are modified by the mixing of electrical patterns from multiple neural populations in the conductive medium of the brain (Tognoli and Kelso, 2009).
From a viewpoint that separates observable and true dynamical properties of neural ensembles, state-transitions observed in EEG and LFP recordings (STobs) cannot be taken at face value since they are the indirect manifestation of the dynamical organization of their originating neural ensembles. The issue can be turned the other way around, however, by examining which neural organizations appear as state transitions in neurophysiological recordings. One is a dynamics of states and transitions in the coordination dynamics of neural ensembles (STtrue→STobs); another is the regime of metastability (Mtrue→STobs) (see also Kelso and Tognoli, 2007 for other empirical similitudes between state-transitions and metastability). A spatiotemporally metastable system bears as sources the transient, many-sized and variously-lasting phase aggregates of its neural ensembles. From the viewpoint of sensor signals, metastable sources also exhibit formation and dissolution of spatiotemporally coherent patterns, resembling states and state transitions when seen from a single level of description.
The main variables that predict neural oscillations’ visibility at a higher level of observation are the size of the originating ensemble (not shown) and the degree of phase alignment (Figure 5A, see also Tognoli and Kelso, 2009). Phase alignment can be strong or weak in both régimes of phase locking and metastability. A synchronous regime may have a weak phase alignment due to a non-null relative phase. As for metastability, its phase alignment increases and decreases intermittently as a result of the continuous transactions between segregative and integrative tendencies, see e.g. Kelso and Tognoli, 2007). On the leftmost part of figure 5A, a neural population animated by metastable dynamics is illustrated. It goes through cycles of phase alignments (dwells, blue insert) and phase scattering (escape, orange insert). In an ideal, spatially dense and non-intrusive microscopic recording, all aspects of this organization are potentially observable (Figure 5A, left column). However, as one moves upward to mesoscopic and macroscopic recordings, only the orderly-most aspects of microscopic dynamics are visible. This is illustrated in figure 5B, with 4 neural populations that alternate phase alignment and phase scattering. To a casual observer interpreting the macroscopic signal shown on the right, it would seem that populations 1 and 2 are present in the first part of the epoch and recede in the second (and vice-versa for populations 3 and 4). The observed dynamics resembles two successive states of organization separated by a transition. The microscopic signal however (figure 5B left) hints at a spatiotemporally metastable dynamics, the segregative tendencies of which result in intermittent disappearance of the meso- and macroscopic observables.
We hypothesize that intermittent macroscopic dynamics resembling state transitions appears in records of brain activity as a result of spatiotemporal metastability. Note that neither level of observation is sufficient in itself to shed light on the comprehensive organization of the brain (micro- and mesoscopic recordings because of their limited spatial sampling and meso- and macroscopic recordings for their myopia on some aspects of microscopic organization). As a consequence, Coordination Dynamics advocates investigational strategies that traverse scales as a way to circumvent limitations of electrophysiological techniques and reveal the full self-organization of the brain (see also Grillner et al., 2005; Akil et al., 2011; Kelso et al., 1999; Kelso et al., 2013).
Conclusions and Future Directions
From the theory of transiently synchronized neural assemblies (e.g. Friston, 2000; Kelso, 1995; Varela et al., 2001), the concept of phase-locking has taken center place in the study of brain function. However, the all-important “transient” has not received the attention that it might have, perhaps because truly dynamical approaches of continuous brain activity are not yet in widespread use (but see e.g. Lehmann, 1990; Kaplan et al., 2005; Kelso et al., 1991; Tognoli and Kelso, 2009). That is, innumerably more efforts have been undertaken to describe phase- and frequency locking than its transience. From the perspective of Coordination Dynamics, there are objectionable consequences to a “locked” brain that is separated from unlocking mechanisms. As the word “locking” readily suggests, a brain that is a prisoner to itself is maladaptive: it is easy to see how useful functional patterns could be preserved, but this happens at the cost of brain dynamics being in a frozen state and secluded from ongoing events happening both internally and externally (Kelso and Tognoli, 2007). Here, we have exposed a key mechanism of brain coordination dynamics -metastability- in which temporary persistence of integrative tendencies fully co-exists with segregation over space, and within and across frequency bands and time scales. Metastability results from broken symmetry (i.e. constitutive differences) in a system of (nonlinearly) coupled (nonlinear) oscillatory processes, the latter representing a core dynamical description of coordinated brain and behavioral activity. It cannot be overemphasized that metastability corresponds to a régime devoid of stable coordination states. Nevertheless, attractive tendencies that enable cooperative behavior among neural regions still persist. Segregation is also functionally meaningful: it allows the transient expression of independent, modular-like behavior and enhances informational complexity. Further, in the present spatiotemporal view of metastability, timely release of neural ensembles from their coherent groups provides them with the opportunity to re-associate with other groups, a characteristic that is essential for flexible brain function and behavior.
Through theory and experimental evidence, we have tried to show how mechanisms of synchronization (attractors) and metastability (no attractors, only attracting tendencies) share the common ability to produce cooperation between neural ensembles. We have also emphasized that the two concepts and their realizations in data have differences (and complementarities, cf. Grossberg, 2000; Kelso, 1995; Kelso and Engstrøm, 2006). Most importantly, metastable coordination dynamics leads to a system that can change itself from within even in the absence of inputs or noise. For a brain that is not purely reflexive and stimulus-driven, but endowed with temporally structured intrinsic activity (see section II.a), this is an important property to have: changes in brain spatiotemporal patterns that occur spontaneously at rest naturally belong to the intrinsic dynamical repertoire of the metastable brain.
In support of the existence of metastability in the brain, we have described characteristic dwell and escape dynamics at two spatial scales. Such findings are fully compatible with a working brain whose ensembles entail chimera, metastability and both. Furthermore, we have discussed how the superposition of electrical fields from metastable neural ensembles may result in apparently discontinuous dynamics resembling state transitions, exactly of the kind widely observed (Figure 5). This analysis argues for increased effort to build multiscale experimental frameworks as a way to enhance further understanding of the metastable brain (see also Grillner et al., 2005; Akil et al 2011; Alivisatos et al., 2013 for related accounts). We expect the mechanism of metastability to be realized at multiple levels (from molecules to minds), provided that the basic conditions of weak coupling and broken symmetry are met.
On a broader note, for the metastable brain active, dynamic processes like “perceiving”, “attending”, “remembering,” and “deciding” are not restricted to particular brain locations, but rather emerge as dynamic patterns of interaction among widely distributed neural ensembles, and in general between human beings and their worlds. Metastability offers scientific grounds for how cognitive processes come and go fluidly as the brain expresses both an interactive integrative dynamic and an individualistic segregative dynamic (Kello, 2013). Metastable coordination dynamics is more in tune with William James’ (James, 1890) beautiful metaphor of the stream of consciousness as the flight of a bird whose life journey consists of ‘perchings’ (phase gathering, integrative tendencies) and ‘flights’ (phase scattering, segregative tendencies). Both tendencies appear to be crucial for a dynamic brain in action.
Finally, in specifying metastable brain dynamics in time and space simultaneously, we witness the emergence of spatiotemporal complexity: the irregular contours of coherent neural ensembles in space-time are thereby revealed. Such complex spatiotemporal behaviors are a challenge for neuroscientists: when viewed from a piecemeal spatial or temporal scope, a distorted picture of neural coordination is obtained, and critical aspects of brain self-organization are concealed. A truly integrated spatiotemporal account is attained through a thorough embrace of brain coordination dynamics: how neurons and neural ensembles “act in concert” requires the systematic unfolding of dwell-escape choreography in space-time to identify the dynamic signatures of healthy, adaptive brain function and its less adaptive counterparts.
Highlights.
-
-
A dynamical account of brain coordination whose key feature is metastability
-
-
Metastability is a blend of both integration and segregation observed on many scales
-
-
Both spatial and temporal dimensions are incorporated in a common framework
-
-
Spatiotemporal metastability may act as a fundamental coordinating mechanism
Acknowledgments
This work was supported by grants from the National Institute of Mental Health (MH080838), the National Science Foundation (BCS0826897), the US Office of Naval Research (N000140910527), the Chaire d’Excellence Pierre de Fermat and the Davimos Family Endowment for Excellence in Science. An early version of the research “Spatiotemporal metastability: design for a brain” (Program # 343.16) was presented by J.A.S. Kelso and E. Tognoli at the Society for Neuroscience Meeting in San Diego, Nov., 13–17, 2010. Suggestions on the manuscript by Christopher Beetle are gratefully acknowledged. We also thank two anonymous reviewers for their helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
The authors do not have any financial conflict of interest that might be construed to influence the results or interpretation of the present manuscript.
References
- Abeles M, Bergman H, Gat I, Meilijson I, Seidemann E, Tishby N, Vaadia E. Cortical activity flips among quasi-stationary states. Proc Natl Acad Sci U S A. 1995;92(19):8616–8620. doi: 10.1073/pnas.92.19.8616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abrams DM, Strogatz SH. Chimera states in rings of nonlocally coupled oscillators. Int J Bifurcat Chaos. 2006;16:21–37. [Google Scholar]
- Akil H, Martone ME, Van Essen DC. Challenges and opportunities in mining Neuroscience data. Science. 2011;331(6018):708–712. doi: 10.1126/science.1199305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alba A, Marroquín JL, Arce-Santana E, Harmony T. Classification and interactive segmentation of EEG synchrony patterns. Pattern Recognit. 2010;43(2):530–544. [Google Scholar]
- Allen PG, Collins FS. Toward the final frontier: the human brain. Wall St J (East Ed) 2013 Apr 8; 2013. [Google Scholar]
- Alivisatos AP, Chun M, Church GM, Greenspan RJ, Roukes ML, Yuste R. The brain activity map project and the challenge of functional connectomics. Neuron. 2012;74(6):970–974. doi: 10.1016/j.neuron.2012.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assisi CG, Jirsa VK, Kelso JAS. Synchrony and clustering in heterogeneous networks with global coupling and parameter dispersion. Phys Rev Lett. 2005a;94(1):018106. doi: 10.1103/PhysRevLett.94.018106. [DOI] [PubMed] [Google Scholar]
- Assisi CG, Jirsa VK, Kelso JAS. Dynamics of multifrequency coordination using parametric driving: theory and experiment. Biol Cybern. 2005b;93(1):6–21. doi: 10.1007/s00422-005-0558-y. [DOI] [PubMed] [Google Scholar]
- Atlan H. Entre le Cristal et la Fumée. Paris: Seuil; 1979. [Google Scholar]
- Banerjee A, Tognoli E, Kelso JAS, Jirsa VK. Spatiotemporal reorganization of large-scale neural assemblies mediates bimanual coordination. Neuroimage. 2012;62(3):1582–1592. doi: 10.1016/j.neuroimage.2012.05.046. [DOI] [PubMed] [Google Scholar]
- Başar E. Memory and Brain Dynamics: Oscillations Integrating Attention, Perception, Learning, and Memory. Boca Raton, Fla.: CRC Press; 2004. [Google Scholar]
- Bennett M, Schatz MF, Rockwood H, Wiesenfeld K. Huygens's clocks. Philos Trans R Soc Lond A. 2002;458:563–579. [Google Scholar]
- Breakspear M, Heitmann S, Daffertshofer A. Generative models of cortical oscillations: neurobiological implications of the Kuramoto model. Front Hum Neurosci. 2010;4:190. doi: 10.3389/fnhum.2010.00190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler SL, Kelso JAS. Cortical coordination dynamics and cognition. Trends Cogn Sci. 2001;5(1):26–36. doi: 10.1016/s1364-6613(00)01564-3. [DOI] [PubMed] [Google Scholar]
- Bressler SL, Tognoli E. Operational principles of neurocognitive networks. Int J Psychophysiol. 2006;60:139–148. doi: 10.1016/j.ijpsycho.2005.12.008. [DOI] [PubMed] [Google Scholar]
- Briggman KL, Kristan WB. Multifunctional pattern-generating circuits. Annu Rev Neurosci. 2008;31:271–294. doi: 10.1146/annurev.neuro.31.060407.125552. [DOI] [PubMed] [Google Scholar]
- Bullock TH, Bennett VL, Johnston D, Josephson R, Marder E, Fields D. The neuron doctrine, redux. Science. 2005;310(5749):791–793. doi: 10.1126/science.1114394. [DOI] [PubMed] [Google Scholar]
- Buzsáki G. Rhythms of the Brain. Oxford: Oxford University Press; 2006. [Google Scholar]
- Buzsáki G, Watson BO. Brain rhythms and neural syntax: implications for efficient coding of cognitive content and neuropsychiatric disease. Dialogues Clin Neurosci. 2012;14(4):345–367. doi: 10.31887/DCNS.2012.14.4/gbuzsaki. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabral J, Hugues E, Sporns O, Deco G. Role of local network oscillations in resting-state functional connectivity. Neuroimage. 2011;57(1):130–139. doi: 10.1016/j.neuroimage.2011.04.010. [DOI] [PubMed] [Google Scholar]
- Casanova MF, Trippe J, Switala A. Temporal continuity to the vertical organization of the human neocortex. Cereb Cortex. 2007;17(1):130–137. doi: 10.1093/cercor/bhj134. [DOI] [PubMed] [Google Scholar]
- Chialvo DR. Emergent complex neural dynamics. Nat Phys. 2010;6:744–750. [Google Scholar]
- Chklovskii DB, Mel BW, Svoboda K. Cortical rewiring and information storage. Nature. 2004;431(7010):782–788. doi: 10.1038/nature03012. [DOI] [PubMed] [Google Scholar]
- Deacon TW. Rethinking mammalian brain evolution. Am Zool. 1990;30:629–705. [Google Scholar]
- Deco G, Jirsa VK. Ongoing cortical activity at rest: criticality, multistability, and ghost attractors. J Neurosci. 2012;32(10):3366–3375. doi: 10.1523/JNEUROSCI.2523-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelman GM. Building a picture of the brain. Ann N Y Acad Sci. 1999;882:68–89. doi: 10.1111/j.1749-6632.1999.tb08535.x. [DOI] [PubMed] [Google Scholar]
- Eguíluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Phys Rev Lett. 2005;94(1):018102. doi: 10.1103/PhysRevLett.94.018102. [DOI] [PubMed] [Google Scholar]
- Eigen M, Schuster P. The Hypercycle: A Principle of Natural Self-Organization. Berlin: Springer-Verlag; 1979. [DOI] [PubMed] [Google Scholar]
- Elbert T, Keil A. Cognitive neuroscience: imaging in the fourth dimension. Nature. 2000;404(6773):29–31. doi: 10.1038/35003682. [DOI] [PubMed] [Google Scholar]
- Engel AK, Friston K, Kelso JAS, Konig P, Kovacs I, MacDonald A, Miller EK, Phillips WA, Silverstein SM, Tallon-Baudry C, et al. Coordination in behavior and cognition. In: Von der Malsburg C, Phillips WA, Singer W, editors. Dynamic Coordination in the Brain. Cambridge, Mass: MIT Press; 2010. pp. 267–299. [Google Scholar]
- Ermentrout GB, Kopell N. Multiple pulse interactions and averaging in systems of coupled neural oscillators. J Math Biol. 1991;29(3):195–217. [Google Scholar]
- Freeman WJ. Mass Action in the Nervous System. New York: Academic Press; 1975. [Google Scholar]
- Freeman WJ, Holmes MD. Metastability, instability, and state transition in neocortex. Neural Netw. 2005;18(5–6):497–504. doi: 10.1016/j.neunet.2005.06.014. [DOI] [PubMed] [Google Scholar]
- Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn Sci. 2005;9(10):474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Transients, metastability, and neuronal dynamics. Neuroimage. 1997;5(2):164–171. doi: 10.1006/nimg.1997.0259. [DOI] [PubMed] [Google Scholar]
- Friston KJ. The labile brain. I. Neuronal transients and nonlinear coupling. Philos Trans R Soc Lond B Biol Sci. 2000;355(1394):215–236. doi: 10.1098/rstb.2000.0560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs A, Jirsa VK, et al. Coordination: Neural, Behavioral and Social Dynamics. Berlin, Heidelberg: Springer; 2007. [Google Scholar]
- Fuchs A, Kelso JAS, Haken H. Phase transitions in the human brain: spatial mode dynamics. Int J Bifurcat Chaos. 1992;2(4):917–939. [Google Scholar]
- Fuchs A. Nonlinear Dynamics in Complex Systems. Berlin, Heidelberg: Springer; 2013. [Google Scholar]
- Garcia-Dominguez L, Wennberg R, Gaetz W, Cheyne D, Snead OC, III, Perez Velazquez JL. Enhanced synchrony in epileptiform activity? local versus distant synchronization in generalized seizures. J Neurosci. 2005;25(35):8077–8084. doi: 10.1523/JNEUROSCI.1046-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A, Rho Y, McIntosh AR, Kötter R, Jirsa VK. Noise during rest enables the exploration of the brain's dynamic repertoire. PLoS Comput Biol. 2008;4(10):e1000196. doi: 10.1371/journal.pcbi.1000196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golubitsky M, Stewart I, Buono P-L, Collins JJ. Symmetry in locomotor central pattern generators and animal gaits. Nature. 1999;401(6754):693–695. doi: 10.1038/44416. [DOI] [PubMed] [Google Scholar]
- Gong P, Nikolaev A, van Leeuwen C. Scale-invariant fluctuations of dynamical synchronization in human brain electrical activity. Neurosci Lett. 2003;336:33–36. doi: 10.1016/s0304-3940(02)01247-8. [DOI] [PubMed] [Google Scholar]
- Grillner S. Locomotion in vertebrates: central mechanisms and reflex interaction. Physiol Rev. 1975;55(2):247–304. doi: 10.1152/physrev.1975.55.2.247. [DOI] [PubMed] [Google Scholar]
- Grillner S, Kozlov A, Hellgren Kotaleski J. Integrative neuroscience: linking levels of analyses. Curr Opin Neurobiol. 2005;15(5):614–621. doi: 10.1016/j.conb.2005.08.017. [DOI] [PubMed] [Google Scholar]
- Grossberg S. The complementary brain: a unifying view of brain specialization and modularity. Trends Cogn Sci. 2000;4(6):233–246. doi: 10.1016/s1364-6613(00)01464-9. [DOI] [PubMed] [Google Scholar]
- Gusnard DA, Raichle ME. Searching for a baseline: Functional imaging and the resting human brain. Nat Rev Neurosci. 2001;2(10):685–694. doi: 10.1038/35094500. [DOI] [PubMed] [Google Scholar]
- Haken H. Springer Series in Synergetics. Berlin: Springer; 1983. Synergetics: an Introduction. [Google Scholar]
- Haken H, Kelso JAS, Bunz H. A theoretical model of phase transitions in human hand movements. Biol Cybern. 1985;51(5):347–356. doi: 10.1007/BF00336922. [DOI] [PubMed] [Google Scholar]
- Holloway RL. The evolution of the human brain: some notes toward a synthesis between neural structure and the evolution of complex behavior. Gen Syst XII. 1967:3–19. [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meulic R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci U S A. 2009;106(6):2035–2040. doi: 10.1073/pnas.0811168106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Kötter R, Breakspear M, Sporns O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc Natl Acad Sci U S A. 2007;104(24):10240–10245. doi: 10.1073/pnas.0701519104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoppensteadt FC, Izhikevich EM. Weakly Connected Neural Networks. New York, Berlin: Springer; 1997. [Google Scholar]
- Hoshi Y, Tamura M. Near-infrarerd optical detection of sequential brain activation in the prefrontal cortex during mental tasks. Neuroimage. 1997;5(4 Pt 1):292–297. doi: 10.1006/nimg.1997.0270. [DOI] [PubMed] [Google Scholar]
- Huang EP, Stevens CF. Estimating the distribution of synaptic reliabilities. J Neurophysiol. 1997;78(6):2870–2880. doi: 10.1152/jn.1997.78.6.2870. [DOI] [PubMed] [Google Scholar]
- Ingber L. Towards a unified brain theory. J Soc Biol Struct. 1981;4(3):211–224. [Google Scholar]
- Ito J, Nikolaev AR, van Leeuwen C. Dynamics of spontaneous transitions between global brain states. Hum Brain Mapp. 2007;28(9):904–913. doi: 10.1002/hbm.20316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM, Edelman GM. Large-scale model of mammalian thalamocortical systems. Proc Natl Acad Sci USA. 2008;105(9):3593–3598. doi: 10.1073/pnas.0712231105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James W. The Principles of Psychology. New York: Dover Publications; 1890. [Google Scholar]
- Jeka JJ, Kelso JAS, Kiemel T. Spontaneous transitions and symmetry: Pattern dynamics in human four limb coordination. Hum Mov Sci. 1993;12:627–651. [Google Scholar]
- Jirsa VK, Fuchs A, Kelso JAS. Connecting cortical and behavioral dynamics: bimanual coordination. Neural Comput. 1998;10(8):2019–2045. doi: 10.1162/089976698300016954. [DOI] [PubMed] [Google Scholar]
- Jirsa VK, Kelso JAS. The excitator as a minimal model for the coordination dynamics of discrete and rhythmic movements. J Mot Behav. 2005;37(1):35–51. doi: 10.3200/JMBR.37.1.35-51. [DOI] [PubMed] [Google Scholar]
- Kaiser M, Hilgetag CC, Kotter R. Hierarchy and dynamics of neural networks. Front Neuroinform. 2010;4:112. doi: 10.3389/fninf.2010.00112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplan AY, Fingelkurts AA, Fingelkurts AA, Borisov SV, Darkhovsky BS. Nonstationary nature of the brain activity as revealed by EEG/MEG: Methodological, practical and conceptual challenges. Signal Processing. 2005;85(11):2190–2212. [Google Scholar]
- Kello C. Critical branching neural networks. Psychol Rev. 2013;120:23–254. doi: 10.1037/a0030970. [DOI] [PubMed] [Google Scholar]
- Kelso JAS. Phase transitions and critical behavior in human bimanual coordination. Am J Physiol Regul Integr Comp Physiol. 1984;15:R1000–R1004. doi: 10.1152/ajpregu.1984.246.6.R1000. [DOI] [PubMed] [Google Scholar]
- Kelso JAS, DelColle J, Schöner G. Action-Perception as a pattern formation process. In: Jeannerod M, editor. Attention and Performance XII. Hillsdale, NJ: Erlbaum; 1990. pp. 139–169. [Google Scholar]
- Kelso JAS, de Guzman GC. An intermittency mechanism for coherent and flexible brain and behavioral function. In: Requin J, Stelmach GE, editors. Tutorials in Motor Neuroscience. Dordrecht: Kluwer; 1991. pp. 305–310. [Google Scholar]
- Kelso JAS. Behavioral and neural pattern generation: The concept of Neurobehavioral Dynamical System (NBDS) In: Koepchen HP, Huopaniemi T, editors. Cardiorespiratory and Motor Coordination. Berlin: Springer-Verlag; 1991. pp. 224–238. [Google Scholar]
- Kelso JAS, Bressler SL, Buchanan S, de Guzman GC, Ding M, Fuchs A, Holroyd T. Cooperative and critical phenomena in the human brain revealed by multiple SQUIDS. In: Duke D, Pritchard W, editors. Measuring Chaos in the Human Brain. New Jersey: World Scientific; 1991. pp. 97–112. [Google Scholar]
- Kelso JAS, Bressler SL, Buchanan S, de Guzman GC, Ding M, Fuchs A, Holroyd T. A phase transition in human brain and behavior. Phys Lett A. 1992;169(3):134–144. [Google Scholar]
- Kelso JAS. Coordination dynamics of human brain and behavior. Springer Proc in Physics. 1992;69:223–234. [Google Scholar]
- Kelso JAS, Fuchs A. Self-organizing dynamics of the human brain: Critical instabilities and Sil'nikov chaos. Chaos. 1995;5(1):64–69. doi: 10.1063/1.166087. [DOI] [PubMed] [Google Scholar]
- Kelso JAS. Dynamic Patterns: The Self-Organization of Brain and Behavior. Cambridge, Mass: MIT Press; 1995. [Google Scholar]
- Kelso JAS, Haken H. New laws to be expected in the organism: synergetics of brain and behavior. In: Murphy M, O'Neill L, editors. What is Life? The Next 50 Years. Cambridge: Cambridge University Press; 1995. pp. 137–160. [Google Scholar]
- Kelso JAS, Fuchs A, Jirsa VK. Traversing scales of brain and behavioral organization. I–III. In: Uhl C, editor. Analysis of Neurophysiological Brain Functioning. Berlin: Springer-Verlag; 1999. pp. 73–125. [Google Scholar]
- Kelso JAS, Engstrøm DA. The Complementary Nature. Cambridge, MA: The MIT Press; 2006. [Google Scholar]
- Kelso JAS, Tognoli E. Toward a complementary neuroscience: metastable coordination dynamics of the brain. In: Kozma R, Perlovsky L, editors. Neurodynamics of Cognition and Consciousness. Heidelberg: Springer; 2007. pp. 39–60. [Google Scholar]
- Kelso JAS. Haken-Kelso-Bunz model. Scholarpedia J. 2008;3(10):1612. [Google Scholar]
- Kelso JAS. Coordination Dynamics. In: Meyers RA, editor. Encyclopedia of Complexity and System Science. Heidelberg: Springer; 2009. pp. 1537–1564. [Google Scholar]
- Kelso JAS, de Guzman GC, Reveley C, Tognoli E. Virtual Partner Interaction (VPI): exploring novel behaviors via coordination dynamics. PLoS ONE. 2009;4(6):e5749. doi: 10.1371/journal.pone.0005749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelso JAS. Instabilities and phase transitions in human brain and behavior. Front Hum Neurosci. 2010;4:23. doi: 10.3389/fnhum.2010.00023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelso JAS. Multistability and metastability: Understanding dynamic coordination in the brain. Philos Trans R Soc Lond B Biol Sci. 2012;367(1591):906–918. doi: 10.1098/rstb.2011.0351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelso JAS, Dumas G, Tognoli E. Outline of a general theory of behavior and brain coordination. Neural Networks Neural Netw. 2013;37(25th Commemorative Issue):120–131. doi: 10.1016/j.neunet.2012.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiebel SJ, Daunizeau J, Friston KJ. A hierarchy of time-scales and the brain. PLoS Comput Biol. 2008;4(11):e1000209. doi: 10.1371/journal.pcbi.1000209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozma R, Puljic M, Balister P, Bollobás B, Freeman WJ. Phase transitions in the neuropercolation model of neural populations with mixed local and non-local interactions. Biol Cybern. 2005;92(6):367–379. doi: 10.1007/s00422-005-0565-z. [DOI] [PubMed] [Google Scholar]
- Krubitzer LA. In search of a unifying theory of complex brain evolution. The year in cognitive neuroscience, Ann N Y Acad Sci. 2009;1156:44–67. doi: 10.1111/j.1749-6632.2009.04421.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuramoto Y, Battogtokh D. Coexistence of coherence and incoherence in nonlocally coupled phase oscillators: a soluble case. Nonlin Phenom Complex Syst. 2002;5(4):380–385. [Google Scholar]
- Lagarde J, Kelso JAS. Binding of movement, sound and touch: Multimodal coordination dynamics. Exp Brain Res. 2006;173(4):673–688. doi: 10.1007/s00221-006-0410-1. [DOI] [PubMed] [Google Scholar]
- Laing CR. Chimera states in heterogeneous networks. Chaos. 2009;19:013113. doi: 10.1063/1.3068353. [DOI] [PubMed] [Google Scholar]
- Laughlin RB, Pines D. The theory of everything. Proc Natl Acad Sci U S A. 2000;97(1):28–31. doi: 10.1073/pnas.97.1.28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann D. Brain electric microstates and cognition: the atoms of thought. In: John ER, editor. Machinery of the Mind. Boston: Birkhäuser; 1990. pp. 209–224. [Google Scholar]
- Lehnertz K. Epilepsy and nonlinear dynamics. J Biol Phys. 2008;34(3):253–266. doi: 10.1007/s10867-008-9090-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lent R, Azevedo FA, Andrade-Moraes CH, Pinto AV. How many neurons do you have? Some dogmas of quantitative neuroscience under revision. European J Neurosci. 2012;35(1):1–9. doi: 10.1111/j.1460-9568.2011.07923.x. [DOI] [PubMed] [Google Scholar]
- Liese T, Cohen A. Nonlinear oscillators at our fingertips. Am Math Mon. 2005;114:14–28. [Google Scholar]
- Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ. Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci. 2001;21(4):1370–1377. doi: 10.1523/JNEUROSCI.21-04-01370.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R. The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science. 1988;242(4886):1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- Lloyd D. Virtual lesions and the not-so-modular brain. J Int Neuropsychol Soc. 2000;6:627–635. doi: 10.1017/s1355617700655121. [DOI] [PubMed] [Google Scholar]
- Longtin A, Laing C, Chacron MJ. Correlations and memory in neurodynamical systems. In: Rangarajan G, Ding M, editors. LNP. Vol. 621. Berlin: Springer-Verlag; 2003. pp. 286–308. [Google Scholar]
- Lowen SB, Cash SS, Poo MM, Teich MC. Quantal neurotransmitter secretion rate exhibits fractal behavior. J Neurosci. 1997;17(15):5666–5677. doi: 10.1523/JNEUROSCI.17-15-05666.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lundervold A. On consciousness, resting state fMRI and neurodynamics. Nonlinear Biomed Phys. 2010;4(S1):S9. doi: 10.1186/1753-4631-4-S1-S9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martens EA. Chimeras in a network of three oscillator populations with varying network topology. Chaos. 2010;20(4):043122–043122. doi: 10.1063/1.3499502. [DOI] [PubMed] [Google Scholar]
- Marder E. Moving rhythms. Nature. 2001;410(6830):755. doi: 10.1038/35071196. [DOI] [PubMed] [Google Scholar]
- Mazzocchi F. Complexity in biology. EMBO Rep. 2008;9(1):10–14. doi: 10.1038/sj.embor.7401147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer-Lindenberg A, Ziemann U, Hajak G, Cohen L, Berman KF. Transitions between dynamical states of differing stability in the human brain. Proc Natl Acad Sci U S A. 2002;99(17):10948–10953. doi: 10.1073/pnas.162114799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller EK, Phelps EA. Current opinion in Neurobiology-- Cognitive Neuroscience 2010. Curr Opin Neurobiol. 2010;20(2):141–142. doi: 10.1016/j.conb.2010.03.008. [DOI] [PubMed] [Google Scholar]
- Milton JG, Chkhenkeli SA, Towle VL. Brain connectivity and the spread of epileptic seizures. In: Jirsa VK, McIntosh AR, editors. Handbook of Brain Connectivity. Berlin, Heidelberg: Springer; 2007. pp. 477–503. [Google Scholar]
- Motter AE. Nonlinear dynamics: spontaneous synchrony breaking. Nat Phys. 2010;6:164–165. [Google Scholar]
- Murzin V, Fuchs A, Kelso JAS. Detection of correlated sources in EEG using a combination of beamforming and surface Laplacian methods. J Neurosci Methods. 2013;218(1):96–102. doi: 10.1016/j.jneumeth.2013.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikolaev AR, Gepshtein S, Gong P, van Leeuwen Duration of coherence intervals in electrical brain activity in perceptual organization. Cereb Cortex. 2010;20(2):365–382. doi: 10.1093/cercor/bhp107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okuda K, Kuramoto Y. Mutual entrainment between populations of coupled oscillators. Progress of Theoretical Physics. 1991;86(6):1159–1176. [Google Scholar]
- Omata S, Yamaguchi Y, Shimizu H. Entrainment among coupled limit cycle oscillators with frustration. Physica D. 1988;31(3):397–408. [Google Scholar]
- Oullier O, de Guzman GC, Jantzen KJ, Lagarde J, Kelso JAS. Social coordination dynamics: Measuring human bonding. Soc Neurosci. 2008;3(2):178–192. doi: 10.1080/17470910701563392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pattee HH. Physical theories of biological coordination. In: Grene M, Mendelsohn E, editors. Topics in the Philosophy of Biology. Vol. 27. Boston: Reidel; 1976. pp. 153–173. [Google Scholar]
- Pitti A, Lungarella M, Kuniyoshi Y. Metastability and functional integration in anisotropically coupled map lattices. Eur Phys J B. 2008;63(2):239–243. [Google Scholar]
- Plenz D, Chialvo DR. Scaling properties of neuronal avalanches are consistent with critical dynamics. 2009 arXiv 0912.5369v1. [Google Scholar]
- Plenz D, Thiagarian T. The organizing principles of neuronal avalanche activity; Cell assemblies and cortex. Trends Neurosci. 2007;30:101–110. doi: 10.1016/j.tins.2007.01.005. [DOI] [PubMed] [Google Scholar]
- Ponzi A, Wickens J. Sequentially Switching Cell Assemblies in Random Inhibitory Networks of Spiking Neurons in the Striatum. J Neurosci. 2010;30(17):5894–5911. doi: 10.1523/JNEUROSCI.5540-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popa D, Popescu AT, Paré D. Contrasting activity profile of two distributed cortical networks as a function of attentional demands. J Neurosci. 2009;29(4):1191–1201. doi: 10.1523/JNEUROSCI.4867-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prigogine I. Time, structure and fluctuations. [8 December 1977];Nobel Lecture. 1977 :263–264. Chemistry. [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat Neurosci. 2004;7(12):1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Pritchard WS. The brain in fractal time: 1/f-like power spectrum scaling of the human electroencephalogram. Int J Neurosci. 1992;66(1–2):119–129. doi: 10.3109/00207459208999796. [DOI] [PubMed] [Google Scholar]
- Rabinovich MI, Huerta R, Varona P, Afraimovich VS. Transient cognitive dynamics, metastability, and decision making. PLoS Comput Biol. 2008;4(5):e1000072. doi: 10.1371/journal.pcbi.1000072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez E, George N, Lachaux JP, Martinerie J, Renault B, Varela FJ. Perception's shadow: long-distance synchronization of human brain activity. Nature. 1999;397(6718):430–433. doi: 10.1038/17120. [DOI] [PubMed] [Google Scholar]
- Schierwagen A. Brain complexity: analysis, models and limits of understanding. In: Mira J, et al., editors. IWINAC 2009, part I, LNCS. Vol. 5601. Berlin: Springer-Verlag; 2009. pp. 195–204. [Google Scholar]
- Schmidt RC, Richardson MJ. Dynamics of interpersonal coordination. In: Fuchs A, Jirsa VK, editors. Coordination: Neural, Behavioral and Social Dynamics. Berlin: Springer-Verlag; 2008. pp. 283–308. [Google Scholar]
- Schmitt FO. Introduction. In: Edelman GM, Mountcastle VB, editors. The Mindful Brain. Cambridge, Mass: The MIT Press; 1978. pp. 1–6. [Google Scholar]
- Schöner G, Haken H, Kelso JAS. A stochastic theory of phase transitions in human hand movement. Biol Cybern. 1986;53(4):247–257. doi: 10.1007/BF00336995. [DOI] [PubMed] [Google Scholar]
- Schöner G, Kelso JAS. Dynamic pattern generation in behavioral and neural systems. Science. 1988;239(4847):1513–1520. doi: 10.1126/science.3281253. [DOI] [PubMed] [Google Scholar]
- Schöner G, Jiang W-Y, Kelso JAS. A synergetic theory of quadrupedal gaits and gait transitions. J Theor Biol. 1990;142(3):359–391. doi: 10.1016/s0022-5193(05)80558-2. [DOI] [PubMed] [Google Scholar]
- Shoham S, O'Connor DH, Segev R. How silent is the brain: is there a “dark matter” problem in neuroscience? J Comp Physiol A Neuroethol Sens Neural Behav Physiol. 2006;192(8):777–784. doi: 10.1007/s00359-006-0117-6. [DOI] [PubMed] [Google Scholar]
- Shanahan M. Metastable chimera states in community structured oscillator networks. Chaos. 2010;20(1):013108. doi: 10.1063/1.3305451. [DOI] [PubMed] [Google Scholar]
- Singer W. The brain - an orchestra without a conductor. [3/2005];Max Planck Research. 2005 [Google Scholar]
- Singer W, Gray CM. Visual feature integration and the temporal correlation hypothesis. Annu Rev Neurosci. 1995;18:555–586. doi: 10.1146/annurev.ne.18.030195.003011. [DOI] [PubMed] [Google Scholar]
- Sporns O. Network analysis, complexity and brain function. Complexity. 2003;8(1):56–60. [Google Scholar]
- Sporns O. Networks of the Brain. Cambridge, Mass: MIT press; 2010. [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC. Organization, development and function of complex brain networks. Trends Cogn Sci. 2004;8(9):418–425. doi: 10.1016/j.tics.2004.07.008. [DOI] [PubMed] [Google Scholar]
- Thiele A. Optimizing brain processing. Nat Neurosci. 2009;12:1359–1360. doi: 10.1038/nn1109-1359. [DOI] [PubMed] [Google Scholar]
- Thompson E, Varela FJ. Radical embodiment: Neural dynamics and consciousness. Trends Cogn Sci. 2001;5(10):418–425. doi: 10.1016/s1364-6613(00)01750-2. [DOI] [PubMed] [Google Scholar]
- Tognoli E, de Guzman GC, Kelso JAS. Interacting humans and the dynamics of their social brains. In: Wang R, Gu F, editors. Advances in Cognitive Neurodynamics (II) Dordrecht: Springer Netherlands; 2011. pp. 139–143. [Google Scholar]
- Tognoli E, Kelso JAS. Brain coordination dynamics: true and false faces of phase synchrony and metastability. Prog Neurobiol. 2009;87(1):31–40. doi: 10.1016/j.pneurobio.2008.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tognoli E. EEG coordination dynamics: neuromarkers of social coordination. In: Fuchs A, Jirsa VK, editors. Coordination: Neural, Behavioral and Social Dynamics. Berlin: Springer; 2008. pp. 309–323. [Google Scholar]
- Tognoli E, Kelso JAS. On the brain's dynamical complexity: Coupling and causal influences across spatiotemporal scales. In: Yamaguchi Y, editor. Advances in Cognitive Neurodynamics (III) Dordrecht: Springer Netherlands; 2013. pp. 259–265. [Google Scholar]
- Tognoli E, Lagarde J, de Guzman GC, Kelso JAS. The phi complex as a neuromarker of human social coordination. Proc Natl Acad Sci U S A. 2007;104(19):8190–8195. doi: 10.1073/pnas.0611453104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tononi G, Sporns O, Edelman GM. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc Natl Acad Sci U S A. 1994;91(11):5033–5037. doi: 10.1073/pnas.91.11.5033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tschacher W, Dauwalder JP. The Dynamical Systems Approach to Cognition: Concepts and Empirical Paradigms Based on Self-Organization, Embodiment and Coordination Dynamics. Singapore: World Scientific Press; 2003. [Google Scholar]
- Tsuda I. Toward an interpretation of dynamic neural activity in terms of chaotic dynamical systems. Behav Brain Sci. 2001;24(5):793–810. doi: 10.1017/s0140525x01000097. [DOI] [PubMed] [Google Scholar]
- Tsuda I, Fujii H. A complex systems approach to an interpretation of dynamic brain activity I: chaotic itinerancy can provide a mathematical basis for information processing in cortical transitory and nonstationary dynamics. In: Érdi P, Esposito A, Marinaro M, Scarpetta S, editors. Computational Neuroscience: Cortical Dynamics. Berlin, Heidelberg: Springer; 2004. pp. 109–128. [Google Scholar]
- Tsuda I. Hypotheses on the functional roles of chaotic transitory dynamics. Chaos. 2009;19:015113-1–015113-10. doi: 10.1063/1.3076393. [DOI] [PubMed] [Google Scholar]
- Uhlhaas PJ, Pipa G, Lima B, Melloni L, Neuenschwander S, Nikolić D, Singer W. Neural synchrony in cortical networks: history, concept and current status. Front Integr Neurosci. 2009;3:17. doi: 10.3389/neuro.07.017.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varela FJ, Lachaux J-P, Rodriguez E, Martinerie J. The brainweb: Phase synchronization and large-scale integration. Nat Rev Neurosci. 2001;2(4):229–239. doi: 10.1038/35067550. [DOI] [PubMed] [Google Scholar]
- Von der Malsburg C, Phillips WA, Singer W, et al. Dynamic Coordination in the Brain: From Neurons to Mind, Strüngmann Forum Report. Vol. 5. Cambridge, MA: MIT Press; 2010. [Google Scholar]
- Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90(3):1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward LM. Synchronous neural oscillations and cognitive processes. Trends Cogn Sci. 2003;7(12):553–559. doi: 10.1016/j.tics.2003.10.012. [DOI] [PubMed] [Google Scholar]
- Werner G. Fractals in the nervous system: conceptual implications for Theoretical Neuroscience. Front. Physiol. 2010;2010:1–15. doi: 10.3389/fphys.2010.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams RW, Herrup K. The control of neuron number. Annu Rev Neurosci. 1988;11:423–453. doi: 10.1146/annurev.ne.11.030188.002231. [DOI] [PubMed] [Google Scholar]
- Winfree AT. On emerging coherence. Science. 2002;298(5602):2336–2337. doi: 10.1126/science.1072560. [DOI] [PubMed] [Google Scholar]
- Yates FE, Iberall AS. Temporal and hierarchical organization in biosystems. In: Urquart J, Yates FE, editors. Temporal Aspects of Therapeutics. New York: Plenum; 1973. pp. 17–34. [Google Scholar]
- Yuste R, MacLean JN, Smith J, Lansner A. The cortex as a central pattern generator. Nat Rev Neurosci. 2005;6(6):477–483. doi: 10.1038/nrn1686. [DOI] [PubMed] [Google Scholar]
- Zhang LI, Poo M. Electrical activity and the development of neural circuits. Nat Neurosci. 2001;4(11):1207–1214. doi: 10.1038/nn753. [DOI] [PubMed] [Google Scholar]