An updated model for nitrate uptake modelling in plants. I. Functional component: cross-combination of flow–force interpretation of nitrate uptake isotherms, and environmental and in planta regulation of nitrate influx

Abstract

Background and Aims

In spite of major breakthroughs in the last three decades in the identification of root nitrate uptake transporters in plants and the associated regulation of nitrate transport activities, a simplified and operational modelling approach for nitrate uptake is still lacking. This is due mainly to the difficulty in linking the various regulations of nitrate transport that act at different levels of time and on different spatial scales.

Methods

A cross-combination of a Flow–Force approach applied to nitrate influx isotherms and experimentally determined environmental and in planta regulation is used to model nitrate in oilseed rape, Brassica napus. In contrast to ‘Enzyme–Substrate’ interpretations, a Flow–Force modelling approach considers the root as a single catalytic structure and does not infer hypothetical cellular processes among nitrate transporter activities across cellular layers in the mature roots. In addition, this approach accounts for the driving force on ion transport based on the gradient of electrochemical potential, which is more appropriate from a thermodynamic viewpoint.

Key Results and Conclusions

Use of a Flow–Force formalism on nitrate influx isotherms leads to the development of a new conceptual mechanistic basis to model more accurately N uptake by a winter oilseed rape crop under field conditions during the whole growth cycle. This forms the functional component of a proposed new structure–function mechanistic model of N uptake.

INTRODUCTION

Under current agronomic systems nitrogen is one of the key macronutrients in plant nutrition that limits potential yield (Tilmann, 1999; Gregory and George, 2011). To date, N inputs have been applied in massive quantities to match crop N demand and thus to maximize crop production. However, lack of accuracy in N fertilization application has an economic cost for farmers and an environmental cost (e.g. fossil energy waste in manufacturing N fertilizers and N leaking from fields through leaching and volatalizing). Therefore, new cultural practices related to fine-tuning of N fertilizer applications are critical with regard to climate change. In this context, soil–plant processes of N cycling are of great importance. Among them, nitrate uptake processes have been intensively studied at field (Colnenne et al., 1998; Devienne-Barret et al., 2000), plant and root (Laîné et al., 1995; Faure-Rabasse et al., 2002; Lemaire et al., 2013), and cellular and molecular levels (Good et al., 2004; Garnett et al., 2009) over the last three decades. Yet, integration of these non-intersecting domains remains challenging due to the plant models and the time and space scales used for such studies. Hence, modelling has been considered a powerful tool to develop a scaling-up approach that will account for all levels of regulation. Although major breakthroughs have been achieved, a plant nitrogen uptake model based upon mechanistic processes and related regulation that is able to predict N uptake under field conditions for a broad range of soil–climate conditions is still lacking (Barber, 1995a; Tinker and Nye, 2000a; Ma et al., 2008).

So far, prediction of N intake under field conditions in most of the agronomic models taking into account root nitrate uptake activity has been resolved by adjusting the nitrate kinetic data acquired in controlled conditions through ‘Enzyme–Substrate’ formalism proposed by Epstein's interpretation and by taking into account or ignoring ion diffusion and mass flow equations in soil (Barber, 1995a; Le Bot et al., 1997; Tinker and Nye, 2000b, c; Malagoli et al., 2004, 2008; Ma et al., 2008).

Initially Epstein's interpretation comes from the following question: is it possible to deduce the molecular and structural characteristics of the transport system or mechanisms from the kinetic data or, reciprocally, to calculate usable parameters of absorption from knowledge of the molecular and structural characteristics of the root? This question remains unresolved because of an over-simplification of the structural complexity of the root catalytic structure involved in nitrate uptake (Forde and Clarkson, 1999; Tinker and Nye, 2000b; Touraine et al., 2001). Indeed, molecular characterization of the different nitrate transporters involved in the root catalytic structure and mutant analyses were unable to answer this question and fill this gap, although they have increased the knowledge of N uptake complexity at the molecular level (Filleur et al., 2001; Liu and Tsay, 2003; Li et al., 2007). As an example, the recent discovery and involvement of CLC and NAXT genes in addition to NRT2 and NRT1 nitrate transporter genes have further increased the root catalytic structure and complicated interpretation in root nitrate transport and homeostasis (De Angeli et al., 2009; Monachello et al., 2009; Segonzac et al., 2011; Léran et al., 2013).

To overcome this issue and reconcile agronomic and physiological points of view, in our updated version of the nitrate uptake model, we propose to use a more realistic approach for modelling N intake under field conditions from nitrate uptake kinetics. We update the basic version of the model proposed by Malagoli et al. (2004) by removing the Enzyme–Substrate theory and by using the Flow–Force theory applied to Flow–Force nitrate influx kinetics proposed by Thellier (1970, 1971, 1973, 2012) and Thellier et al. (2009) in combination with effects of exogenous endogenous factors on the regulation of nitrate influx.

Flow–Force theory is preferred for several reasons. It is based on thermodynamic and Ohm's law and uses kinetic data from many ions so that general parameters such as ion flux and root conductance can be assessed (Thellier, 1970, 1971, 1973, 2012; Thellier et al., 2009). Moreover, this approach implicitly stated that ion transport is caused by the functioning of the overall root catalytic structure formed by a complex of transporters. It assumed implicitly that these transporters can be arranged in parallel and/or series in the different cell layers of the mature root and can interact with each other. For nitrate, even without taking into account biochemical, thermodynamic and electrophysiological justifications, molecular and physiological lines of evidence support this interpretation. Indeed, molecular analyses in rice and Arabidopsis have revealed that nitrate transporters mainly involved in nitrate uptake such as NRT1·1 and NRT2·1 are inserted in parallel and not in series in the different cell layers of the mature root (Guo et al., 2001, 2002; Nazoa et al., 2003; Remans et al., 2006a, b; Girin et al., 2007; Feng et al., 2011). This location contradicts the one-root-membrane hypothesis with nitrate transporters inserted in series proposed by Epstein (Epstein et al., 1963; Epstein, 1966, 1972; Crawford and Glass, 1998) or inserted in series and in parallel in plasma membrane and tonoplast of the epidermal layer proposed by Torii and Laties (1966). Secondly, in Brassica napus plants, K¹⁵NO₃ labelling for nitrate influx rate measurements (5 min) revealed that more than 40–60 % of ¹⁵N is translocated to the shoot throughout a daily period whatever the nitrate concentrations used, 100 µm or 5 mm (Supplementary Data Fig. S1). Likewise, daily measurements showed that 80 % of ¹⁵N is translocated to the shoot in seedlings treated from 0·05 to 20 mm external nitrate concentrations (Le Ny et al., 2013). This demonstrated that nitrate influx rate corresponds to measurements of whole root conductance for nitrate caused by nitrate transporters inserted in the overall root cell layers rather than a specific activity measurement of a nitrate transport system at the epidermal cell layer (one-root-membrane hypothesis). Thirdly, there is little certainty about the transporters and mechanisms involved in nitrate loading into the xylem and unloading into the leaf cells and what regulations are implicated in the rate of these transfers (Köhler et al., 2002; Li et al., 2010; Segonzac et al., 2011). Indeed, a previous physiological study in soybean plants has shown that NO₃⁻ uptake is uncoupled from NO₃⁻ translocation and that the diurnal changes of nitrate uptake are independent of root nitrate contents (Delhon et al., 1995). These results are in agreement with the positive feedback regulation of the xylem-quickly activating anion conductance (X-QUAC) observed in xylem–parenchyma protoplasts prepared from roots of barley plants (Köhler et al., 2002). Likewise, large fluctuations in nitrate concentrations of xylem sap during the night or under low transpiring conditions would be buffered by the strong nitrate uptake capacities of leaf cells (Nikolic et al., 2012) as well as their large capacities for nitrate storage and assimilation (Le Ny et al., 2013; Leblanc et al., 2013).

Furthermore, local parameters of root nitrate uptake are probably not uniform over longer distances of the different root segments depending on properties and root age (Eshel and Waisel, 1973; Nazoa et al., 2003; Eissenstat and Volder, 2005; Sorgona et al., 2011; Chen and Brassard, 2013). Thus, plasmodesmata frequency involved in the symplastic hypothesis of ion transport decreased along the root axis and root hair cells became symplastically isolated with root age (Duckett et al., 1994; Zhu et al., 1998a, b). As a consequence, an Enzyme–Substrate approach cannot account for root heterogeneity.

Most models for nitrate uptake under field conditions have used only one or two reference isotherms with constant I_max and V_max according to the Michaelis–Menten equation of Epstein's interpretation (Barber, 1995b; Le Bot et al., 1997; Tinker and Nye, 2000a; Ma et al., 2008). Generally, these reference isotherms are established in specific experimental conditions of temperature, pH, pressure and photosynthetically active radiation (PAR) (and determined in plants of specific age and N status). Alternatively, it is well established that variations of temperature, for example, or the combination of duration and concentrations of nitrate pretreatment induced variations in nitrate influx kinetics (Torii and Laties, 1966; Siddiqi et al., 1989, 1990; Laîné et al., 1994; Macduff et al., 1997). Accordingly, the level of influx given by the root catalytic structure for a given nitrate external concentration is not fixed but fluctuates according to the variations of exogenous and in planta factors. Hence, it is not realistic to use only one or two reference kinetics to model nitrate uptake during a whole growth cycle when environmental and endogenous factors vary continuously. To take these fluctuations into account, effects of exogenous (temperature and PAR) and endogenous (day–night cycle and ontogenesis) factors on nitrate influx have been combined with the Flow–Force theory. Compared with our previous modelling approach, this cross-combination avoids use of the inducible component of the nitrate influx kinetics (Malagoli et al., 2004, 2008), which is a characteristic of all agronomic models (Barber, 1995a, b; Le Bot et al., 1997; Tinker and Nye, 2000b; Ma et al., 2008).

The present study proposes a new conceptual framework that combines Flow–Force interpretation of nitrate uptake kinetics and short- and long-term regulation of nitrate influx to build new mechanistic models of N uptake in crop plants. This allowed a complete rebuilding of the functional component of the N uptake model proposed by Malagoli et al. (2004).

MATERIALS AND METHODS

Plant culture conditions for temperature, PAR and light/darkness on K¹⁵NO₃ influx

Seeds of oil seed rape (Brassica napus L. ‘Capitol’) were germinated and grown in hydroponic conditions in greenhouse (Malagoli et al., 2004). The basic medium contained 1 mm KNO₃, 0·4 mm KH₂PO₄, 0·15 mm K₂HPO₄, 1 mm K₂SO₄, 0·5 mm MgSO₄, 3 mm CaCl₂, 0·2 mm Fe–Na EDTA, 14 µm H₃BO₃, 5 µm MnSO₄, 3 µm ZnSO₄, 0·7 µm CuSO₄, 0·7 µm (NH₄)₆Mo₇O₂₄ and 0·1 µm CoCl₂ and was renewed every 2 day. pH was maintained at 6·5 ± 0·5 by adding CaCO₃ (200 mg L⁻¹). Phytor lamps (150 µmol m⁻² s⁻¹ at the canopy height) supplemented the PAR of natural light for 16 h d⁻¹. The thermoperiod was 24 ± 1 °C (day) and 18 ± 1 °C (night). Then, 15-d-old seedlings were transferred in a climatic chamber for 1 week at 300 µmol m⁻² s⁻¹ of PAR (provided by high-pressure sodium lamps) for 16 h d⁻¹. The thermoperiod was 20 ±1 °C (day) and 15 ± 1 °C (night). Before influx measurements with K¹⁵NO₃⁻ at 100 µm or 5 mm for 5 min, three batches of 25 seedlings each were acclimated over 1·5 h in a nutrient solution containing either 100 µm or 5 mm of non-labelled KNO₃ (for details see Malagoli et al., 2004).

Plant material and growth conditions for ontogenetic effect on K¹⁵NO₃ influx

Vernalized plants from the field plot of Saint-Aubin d'Arquenay (Normandie, France) were harvested at the C2 stage (according to a phenological scale established by the Bayer, BASF, Ciba and Hoechst companies) and screened for their root diameter (0·6–1 cm) before being acclimated in a growth chamber under hydroponic conditions described in the section above (Beuve et al., 2004). Indeed, the two experiments of Beuve et al. (2004) and Malagoli et al. (2004) were conducted at the same time and in the same climatic chamber. Nine homogeneous plants for each developmental stage of growth cycle (D1, D2, E, F, G2, G3, G4) were used to measure K¹⁵NO₃ influx either at 100 µm or at 5 mm.

Estimate of daily accumulation of K¹⁵NO₃ in seedlings grown in Petri dishes

Seeds were treated for germination according to Leblanc et al. (2008). After 48 h in the dark at room temperature, four seedlings were screened through their radicle length (5–6 mm), then transferred to new Petri dishes (12 × 12 cm) filled with 50 mL of solidified agar culture medium as presented above. Liquid medium was supplemented with K¹⁵NO₃ (Atom% ¹⁵N: 1 %) as the sole nitrogen source at external nitrate concentrations indicated for each individual experiment (from 0·05 to 20 mm). Liquid medium was solidified with 0·8 % (w/v) agar (Sigma A-7002, St Louis, MO, USA), pH 6·75. Then, Petri dishes were half sealed with adhesive tape. Dishes were placed vertically in a growth chamber at 22 °C under a 16/8-h light/dark regime with a light intensity of 200 µmol m⁻² s⁻¹. Daily accumulation of ¹⁵N in the seedlings was determined between 96 and 120 h for the different nitrate treatments to calculate net uptake of ¹⁵NO₃⁻ (for details see Le Ny et al., 2013).

MODEL DESCRIPTION

New assumptions of the model

Most of the main assumptions needed to run the model are referred to in Malagoli et al. (2004), such as a lack of explicit interactions among environmental and endogenous factors. Moreover, the N uptake model does not account for abiotic (water shortage, occurrence of macro- or micro-element deficiency) or biotic (weeds, pests) constraints. By contrast to the model proposed by Malagoli et al. (2004), assumptions of the updated version are that there is no transport system for nitrate but that there exists a single root catalytic structure formed by a complex of nitrate transporters (CNT) inserted in the membranes of the different root cell layers. Whereas nitrate transport systems HATS and LATS (high and low affinity transport) systems are defined according to their affinities and activities, the CNT results from the coupling of different transporters belonging to different families, such as NRT2, NRT1, NAXT and CLC with low and high affinities for nitrate. Moreover, the nitrate transporters of the CNT are arranged in series and/or in parallel in the root membranes along the radial structure from epidermis to pericycle rather than just inserted into epidermis as proposed for HATS and LATS (Crawford and Glass, 1998). The CNT is characterized by a conductance that can be up- or down-regulated (efficiency) depending on nitrate external concentration and environmental and endogenous factors. Such an assumption is more in line with recent physiological and molecular evidence, as shown in the Introduction and Results.

Linearization of nitrate influx response curves with external nitrate concentrations

The original model was based upon processes involved in nitrate root transport that were formalized by kinetic equations derived from fitting response curves of nitrate influx to external nitrate concentrations with rectangular hyperbolas (Faure-Rabasse et al., 2002; Malagoli et al., 2004). In the present revised version, external nitrate concentrations were expressed on a logarithmic scale to linearize the response curves, according to the Flow–Force theory from Thellier et al. (2009) and Thellier (2012). This resulted in a linear equation describing the catalytic activity of the CNT in the mature root for low and high external nitrate concentrations (Table 1). This is the core of the functional model presented here.

Table 1.

Plant and soil parameters used for N uptake model calculations

(a) Plant parameter
ln K′	1·81 µmol g−1 root d.wt h−1
L′	6·41 µmol nitrate
Soil parameter
Temperature below which no uptake occurs	4 °C

(b) Fertilization level
Growth stage	N0 (0 kg N ha−1)	N1 (135 kg N ha−1)	N2 (273 kg N ha−1)
D1 (visible inflorescence)	598	668	754
D2 (beginning of extension of floral peduncle)	668	754	793
E (extension of floral peduncle)	700	780	815
F2 (mid-flowering)	791	843	905
G2 (beginning of pod filling)	843	905	960
G4 (pod mid-filling)	1513	1513	1514
G5 (end of pod filling)	1691	1691	1691

Introduction of temperature, PAR and developmental stage effects on nitrate influx rates

As in Malagoli et al. (2004), response curves of nitrate influx to variations in the studied factors were formalized through polynomial equations. In the original version, two polynomial equations were determined to fit response curves of nitrate influx at either 100 µm or 5 mm external nitrate concentrations. In this new version, a single equation able to adjust nitrate influx variations within the range of tested external nitrate concentrations (from 100 µm to 5 mm) was chosen (see Figs 3a, 4a, 6a, Supplementary Data Fig. S2a. and Table 2) for each studied factor (temperature, PAR and development stage). Each equation can be written as follows:

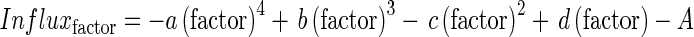(1)

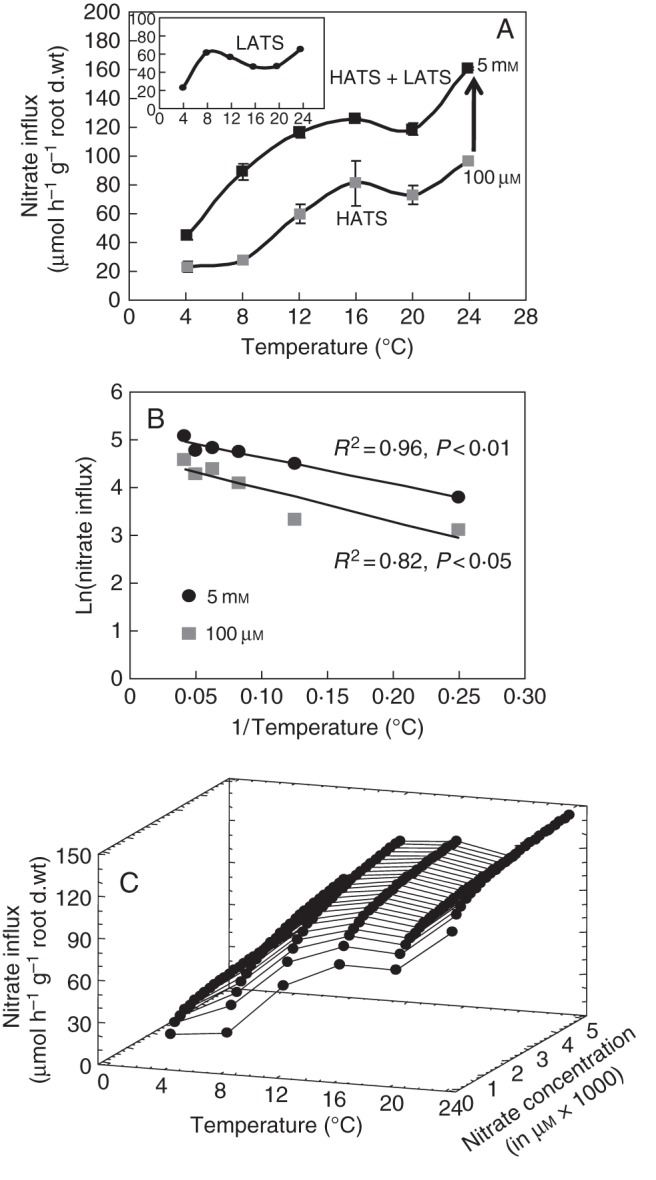
with (1) ‘factor’ corresponding to temperature (in °C) or PAR (μmol m² s⁻¹) or development stage (in degree-days, °Cd) and (2) ‘A’ depending on external nitrate concentrations according to the following formula:

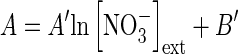(2)

where [NO₃⁻]_ext corresponds to soil nitrate concentrations (Table 2). This approach allows cross-combining of the effects on root nitrate influx of external nitrate concentrations and endogenous and environmental factors. It assumes that interpolation within the range of tested nitrate concentrations (from 100 µm to 5 mm) is linear when a logarithmic transformation is applied (Table 2).

Fig. 3.

Reinterpretation of the temperature effect on nitrate influx rate. (A) Previous interpretation in the changes of nitrate influx rate as a function of root temperature (Malagoli et al., 2004). Inset: LATS activity obtained by subtracting HATS activity from HATS + LATS activity. (B) Arrhénius diagram deduced from nitrate influx variations. (C) Three-dimensional plot of the temperature effect on nitrate influx variations based on reinterpretation of nitrate uptake kinetics and deduced from the Arrhénius diagram, electrophysiological studies (Glass et al., 1992) and Thellier's transformation (see Fig. 1C, D). Vertical bars indicate SD for n = 3 when larger than the symbol.

Table 2.

Adjusted equations describing variations of influx for CNT as a function of external nitrate concentrations.

	Equation
Effects
Day/night cycle	DI (time, [NO3–]ext) = ∫024 P(t, [NO3−]ext) dt = (820·3526 × ln[NO3−]ext –1904·853) × A1
	A1 = average duration of daily photoperiod for each month/duration of maximum photoperiod
Temperature	Influx = 0·0062(Temp)4 – 0·3299 (Temp)3 + 5·8057(Temp)2 – 32·0379999999(Temp) + Atemp
PAR	Influx = –0·0013(PAR)2 + 0·8714(PAR) + APAR
Ontogenesis: N0 (0 kg N ha−1)	Influx = –4·77661035 × 10−7(x4) + 1·3589613637003 × 10−3(x3) –1·45765833536765(x2) + 698·10207537693(x) – AN0
N1 (135 kg N ha−1)	Influx = –3·9039142 × 10−6(x3) – 7·14109674786 × 10−3(x2) + 17·6158328191565(x) – AN1
N2 (273 kg N ha−1)	Influx = 2·4592397142 × 10−5(x3) – 8·52408758764510−2(x2) + 90·5915208183033(x) – AN2
Logarithmic functions applied to polynomial constants: Atemp, Apar AN0, AN1 and AN2
Temperature	ATemperature= 11·528562 × ln[NO3−]ext + 1·80901
PAR	APAR = 48·138776 × ln[NO3−]ext – 195·687257
Ontogenesis: N0 (0 kg N ha−1)	AN0 = –35·06881 × ln[NO3−]ext + 12 5788·56955
N1 (135 kg N ha−1)	AN1= –35·06881 × ln[NO3−]ext + 7478·87153
N2 (273 kg N ha−1)	AN2 = –35·06881 × ln[NO3−]ext + 30445·47938
Standard influx (SI)
Day/night cycle	SI =20·045 × ln[NO3−]ext + 9·84524
Temperature	SI = 8·04443 × ln[NO3−]ext + 44·32403
PAR	SI = 56·23689 × ln[NO3−]ext – 58·98044
Ontogenesis	SI =14·71106 × ln[NO3−]ext – 48·55693

Influx rate standardization among the controlled physiological experiments

To compare and to normalize the different influx rate values obtained after factor applications among the different controlled experiments, standard conditions were defined as follows: 12:00 H for light/darkness cycle under a 16/8-h photoperiod regime, 20 °C for root temperature under 300 µmol s⁻¹ m⁻² PAR and at the B4 stage (scale of Bayer, BASF, Ciba and Hoechst companies) for ontogeny (i.e. four-leaf stage). These conditions allowed the measurement of a standard influx (SI) for each studied factor. Then, the ratio U_i (known as the uniformization factor) between the polynomial equation (see eqn 1) and the SI value allows normalization of the different influx values in the controlled experiments by accounting only for the variation in nitrate influx. In this updates version, the SI value was not set to either 100 µm or 5 mm nitrate concentrations, but is changed along a nitrate concentration gradient ranging from 100 µm to 5 mm according to the following relationship:

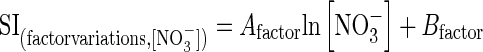(3)

Endogenous (day/night, ontogeny) and environmental (temperature, PAR) factors were introduced into the model by multiplying kinetic equations by the uniformization factor (U_i). Each U_i is defined as the ratio between the equation describing nitrate influx rate variation for each factor and the SI value. This can be summed-up as follows:

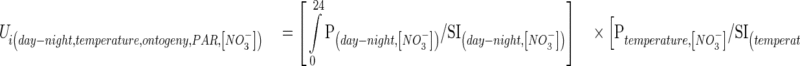(4)

where U_i (ranging from 0 to 1; unitless) is a uniformization factor allowing normalization of influx measurements in response to the studied factors (temperature, PAR, ontogenesis and day–night cycles) among the different laboratory experiments at the ith °Cd. P are the polynomial functions established for each studied factor (day–night, PAR, temperature, ontogeny) that give the influx value for given values of the studied factor and soil nitrate concentration.

RESULTS

Application of the Flow–Force interpretation to NO₃⁻ uptake

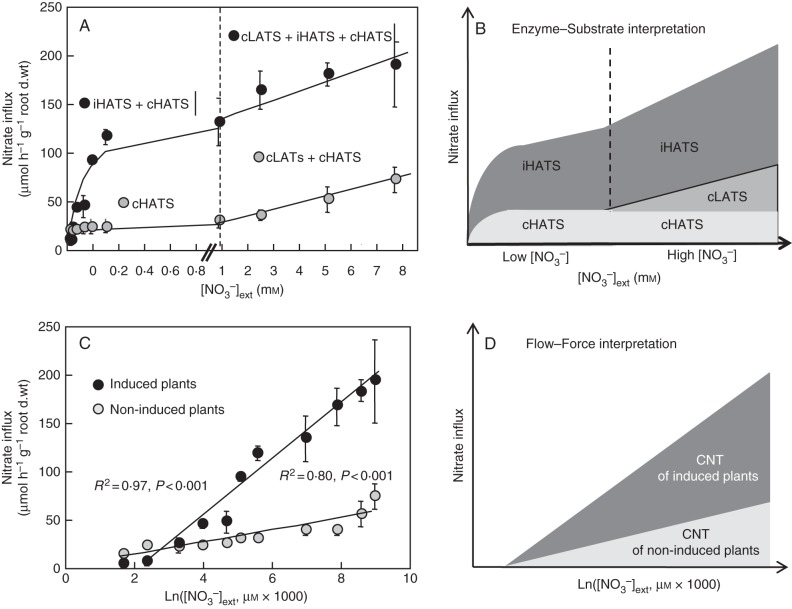
The Enzyme–Substrate interpretation hypothesizes that nutrient uptake by the root is formally equivalent to a catalysis reaction by an enzyme system through Michaelis and Menten type functioning (Epstein and Hagen, 1952; Epstein, 1953, 1966). Following this interpretation, three discrete transport systems in the nitrate uptake process were deduced in roots of Brassica napus plants (Faure-Rabasse et al., 2002; Fig. 1A): the constitutive and inducible high affinity transport system (cHATS and iHATS) and the constitutive low affinity transport system (cLATS; Fig. 1A, B).

Fig. 1.

Transformation of ‘Enzyme–Substrate’ formalism to the ‘Flow–Force’ formalism of nitrate uptake kinetics in winter oilseed rape (Brassica napus ‘Capitol’) seedlings. (A,B) ‘Enzyme–Substrate’ formalism and interpretation. Two-week-old seedlings were N deprived for 1 week before measurements (non-induced plants) or being transferred over 24 h in 1 mm NO₃⁻ before measurements (induced plants) in increasing external concentrations. High-affinity nitrate influx was measured at 100 µm ¹⁵NO₃⁻ whereas low-affinity nitrate uptake was measured at 5 mm ¹⁵NO₃⁻. iHATS and cHATS, inducible and constitutive high affinity nitrate transport systems; cLATS, constitutive low affinity nitrate transport system. In (B), cLATS is obtained after subtraction of theoretical calculated iHATS + cHATS influx at 100 mm ¹⁵NO₃⁻. (C,D) Flow–Force formalism and interpretation. The original data of Faure-Rabasse et al. (2002) were plotted in the system of coordinate {J(NO₃⁻)_ext = L′ ln K′ [NO₃⁻]_ext} according to Thellier et al. (2009) and fitted to straight line for induced and non-induced plants. The estimates for J(NO₃⁻)_ext = 0 are 1·44 and 2·09 mm of (NO₃⁻)_ext and slopes of the curve L′_N03⁻ are 6·31 and 28·07 for non-induced and induced plants, respectively. CNT, complex of nitrate transporters in multiple root cell layers. Vertical bars indicate SD for n = 3 when larger than the symbol.

Here, the Flow–Force transformation was applied to nitrate uptake processes in B. napus. This alternative approach to ion-uptake kinetics developed by Thellier (1970, 1971, 1973, 2012) and Thellier et al. (2009) is based on the Flow–Force relationships of non-equilibrium thermodynamics of irreversible processes and analyses the dual mechanisms of influx kinetics of a substrate S (NO₃⁻, K⁺, Na⁺, sucrose, etc.) without invoking the concept of the carrier site. In this formalism, the inward or outward flow (J_S) of S, which is dependent on the ratio between external and internal S concentration, is considered to be formally equivalent to an electric intensity where the magnitude is given by

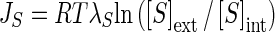(5)

in which R is the gas constant (8·314 J mol⁻¹ K⁻¹), T is the absolute temperature in degrees Kelvin, λ_S relates the flow to the force acting on the exchange of substrate S, and [S]_ext and [S]_int are the external and internal concentrations of substrate S. RTλ_S can be replaced by L′ corresponding to the overall conductance of the root system that groups these parameters and remains constant as long as the system is close to equilibrium. As noted for silicon uptake, and uptake data of many authors when the system is in a steady state, nutrient flows along the radial root gradient can be linearly linked to external nutrient concentration (Thellier et al., 2009; Thellier, 2012). Accordingly, reprocessing the nitrate influx dataset from Faure-Rabasse et al. (2002) transforms the biphasic responses of nitrate influx rates of induced and non-induced plants along an increasing nitrate concentration gradient (Fig. 1A) into two linear approximation curves. The curve's equations are equivalent to

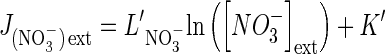(6)

where 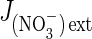is the nitrate influx, L′_NO3^– is the slope of the straight line (reflecting overall conductance of the root system for nitrate) and K′ is the ordinate at the origin (when the y-value = 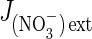= 0) corresponding to a thermodynamic parameter (Thellier et al., 2009; Thellier, 2012). The subscript ext (external) or int (internal) indicates the direction of substrate flow. Indeed, increasing external concentration of the substrate in the medium induces influx whereas increasing internal concentration of the substrate in the root induces efflux. In conclusion, these two linear curves allow contrasted conductance values to be distinguished (slope of the curves and then different catalytic efficiencies; Fig. 1C) for nitrate in induced and non-induced plants.

Flow–Force transformation defines a root catalytic structure formed by a CNT but not nitrate transport systems such as HATS and LATS

Compared with Epstein's interpretation, the mathematical Flow–Force transformation of nitrate influx erases the biphasic response observed along increasing external nitrate concentration gradients in induced and non-induced plants (Fig. 1A, C). Hence, deduction of the type of transporters (high- or low-affinity) involved in the nitrate uptake process (Fig. 1A, D) is not permitted by the Flow–Force interpretation. It can only be deduced from this interpretation that nitrate conductance of the root is due to functioning of a complex of nitrate transporters (CNT) inserted into different cell layers of mature roots to form a catalytic structure operating with variable efficiencies at the overall root system level (Thellier, 1970, 1973, 2012; Thellier et al., 2009). Recent molecular studies have validated this interpretation. Indeed, the biphasic pattern in nitrate uptake transporter depends on the phosphorylation state at threonine 101 of the NRT1·1 nitrate transporter (Ho et al., 2009; Hu et al., 2009). Thus, under low external nitrate concentrations, the NRT1·1 transporter is phosphorylated and then functions as a high-affinity nitrate transporter (Liu and Tsay, 2003). However, under high external nitrate concentration, the NRT1·1 transporter is dephosphorylated and it acts as a low-affinity nitrate transporter. Moreover, recent studies have shown that CBL–CIPK signalling network is involved in the primary nitrate response and induced biphasic pattern in gene expression of NRT1·1 and NRT2·1 nitrate transporters (Ho et al., 2009; Hu et al., 2009). These molecular findings invalidate the existence of two distinct transport systems operating at low and high affinity for nitrate derived from the Epstein interpretation (Siddiqi et al., 1989, 1990; Kronzucker et al., 1995a, b). Compared with the Enzyme–Substrate interpretation, the Flow–Force approach cannot infer whether there is a parallel and/or series arrangement of carriers, or their number, affinity and/or coupling.

Histochemical approaches reveal parallel and series arrangements of the CNT within the root cell layers and support the Flow–Force interpretation

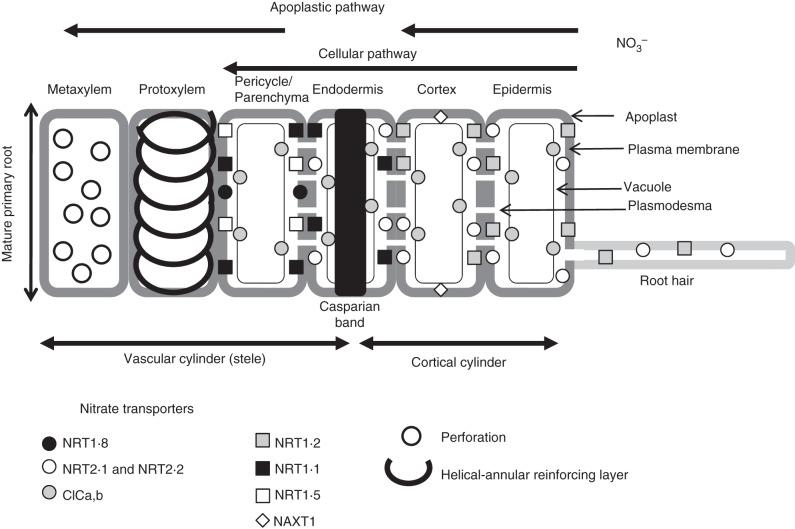
Recent observations from in situ hybridization and histochemical GUS and GFP activities in pNRT::GUS and pNRT::GFP transgenic Arabidopsis seedlings showed localization of transporters of the AtNRT1 and AtNRT2 families at the root cellular level (Guo et al., 2002; Nazoa et al., 2003; Chopin et al., 2007; Girin et al., 2007; Orsel et al., 2007; Lin et al., 2008; Feng et al., 2011). These data are summarized in Fig. 2. They reveal that NRT2·1 is predominantly localized in the outer layers of the mature root (i.e. root hair, epidermis and cortex) whereas NRT1 transporters are mainly sited in the inner root layers. NRT1·2 is found in the root hair, cortex and endoderma whereas NRT1·5 and NRT1·1 are localized to the endoderma and pericycle. Such differential localization of nitrate transporters along the mature root radius strengthens the hypothesis of ‘parallel and/or series’ arrangement of a CNT for the NRT1 and NRT2 families across multiple root cell layers in the mature root. Accordingly, these data argue against the one-root-membrane hypothesis of the Enzyme–Substrate interpretation in which all the carriers (HATS and LATS) are inserted independently under a parallel arrangement into the epidermal root tissue with no clear spatial interaction or complementary action (Crawford and Glass, 1998). Hence, the multiple root cell layer arrangement revealed by histochemical approaches is consistent with a fine coupling and tuning among transporters depending on the external soil nitrate concentrations. Such assumptions fit more accurately within the Flow–Force theory.

Fig. 2.

Schematic localization of the nitrate transporters involved in nitrate transport, nitrate efflux and homeostasis in the mature roots of Arabidopsis. The location of the NRT transporters from NRT1 and NRT2 families has been deduced from in situ hybridization and GUS and GFP activities from transformed seedlings with pNRT::GUS and pNRT::GFP or pCLC-b::GFP and pNAXT1::GFP constructs (from Guo et al., 2001, 2002; Nazoa et al., 2003; De Angeli et al., 2006; Remans et al., 2006a, b; Girin et al., 2007; Orsel et al., 2007; Chopin et al., 2007; Lin et al., 2008; Li et al., 2010; Von der Fecht-Bartenbach et al., 2010).

Cross-combination of the Flow–Force theory with effects of temperature and PAR on nitrate influx

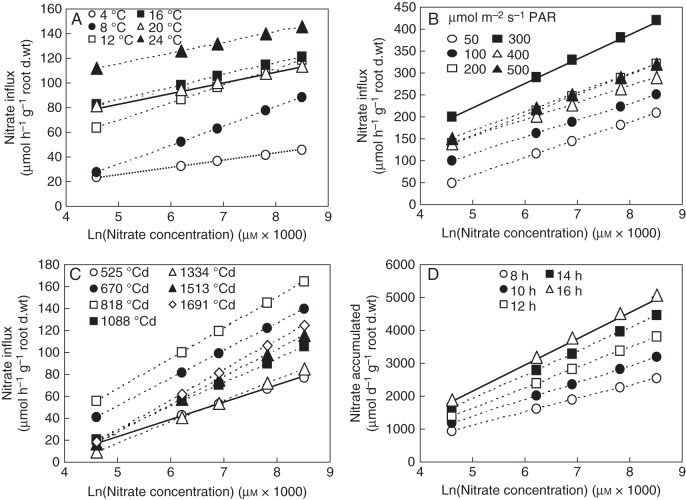
The Enzyme–Substrate interpretation of environmental variables such as temperature and PAR effects on nitrate uptake used in the previous model version is no longer valid and must be revisited. Indeed, in previous interpretations, polynomial response curves were based on the existence of nitrate transport systems and through a subtraction of the HATS value from the HATS + LATS value as presented in Fig. 3A (inset). In light of the Flow–Force theory, a closer examination of the response curves of root nitrate influx to environmental variables revealed that their overall patterns are parallel at both 100 µm and 5 mm external nitrate concentrations (Fig. 3A and Supplementary Data S2; Malagoli et al., 2004). This parallel relationship is also reinforced by the Arrhenius diagram obtained by plotting the logarithm of the nitrate influx rate versus 1/root temperature at 100 µm and 5 mm external nitrate concentrations (Fig. 3B). Moreover, the parallelism of the two linear curves strengthens the observation that root conductance for nitrate is not changed by temperature, but also indicates that the increase in nitrate influx for a given conductance of the CNT between 100 µm and 5 mm is not accompanied by modifications in membrane properties such as conformational change of the lipid chains. This suggests that temperature modifications are not associated with qualitative changes in catalytic efficacy of nitrate root carriers, but are rather associated with quantitative changes such as the number of carriers (Thellier et al., 2009; Thellier, 2012). Based upon such observations, it is possible to cross-combine the transformation of nitrate influx kinetics with the effects of temperature on nitrate influx (Fig. 3C):

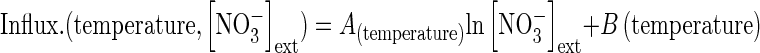(7)

Parallel relationships established at 100 µm and 5 mm external nitrate concentrations for the PAR effect were interpreted and integrated into the model in a similar manner (Supplementary Data Fig. S2).

Cross-combination of Flow–Force theory and effects of endogenous factors on nitrate influx

As for environmental factors, variations of nitrate influx were also monitored during the day–night and ontogenetic cycles to cross-combine the polynomial response curves of nitrate influx with Flow–Force kinetics (Figs 4A and 6A). In contrast to temperature and PAR effects that modify nitrate transport through energetic considerations such as sugar allocation to the roots and ATP production, these effects are more difficult to interpret. Indeed, they result from pleiotropic effects of nitrate influx regulations that operate at two scales: time and space. Moreover, interpretation of the ontogenetic effect requires an accurate definition of plant developmental stages (vegetative versus reproductive) under different fertilization levels.

Fig. 4.

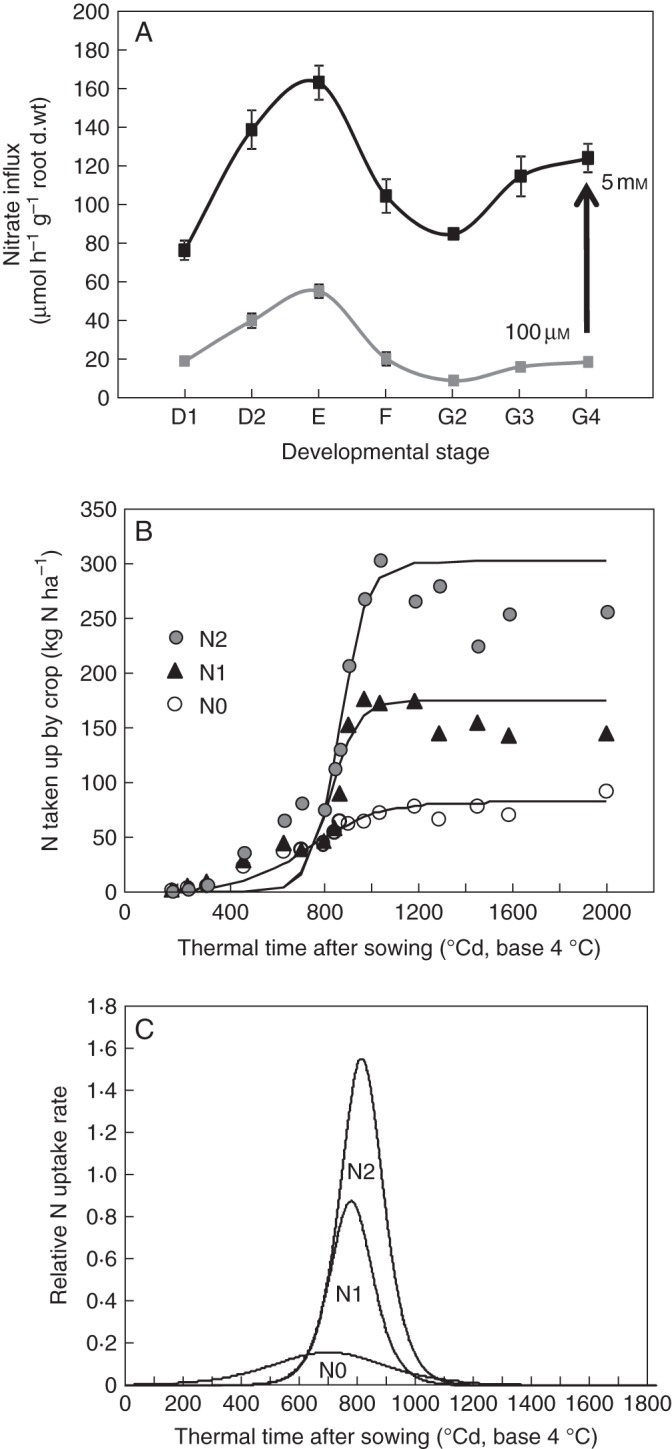
Determination on the duration and onset of developmental stages during the growth cycle. (A) New measurements in changes of nitrate influx rate as a function of developmental stages from Beuve et al. (2004). (B) Fitting of the quantity in total N exported plotted against thermal time with logistic curves for the three levels of fertilization. (C) Relative N accumulation derived from the logistic curves. Vertical bars indicate SD for n = 3 when larger than the symbol.

Nitrate influx variations during the time course of the ontogenetic cycle revealed parallel relationships

In the new model version, the nitrate influx response curve during the time course of the growth cycle was obtained from a parallel experiment realized under the same controlled conditions with the same genotype (Fig. 4A) but conducted independently of the previous published results (Malagoli et al., 2004). In this experiment, the different developmental stages have been accurately determined when sampling before measuring nitrate influx rates under controlled conditions (Beuve et al., 2004). As previously observed for temperature and PAR, influx rate variations at 100 µm and 5 mm followed a parallel pattern (Fig. 4A). Based on this parallel relationship, it was possible to cross-combine the Flow–Force kinetics with effects of ontogenetic cycle on nitrate influx.

However, it is critical to set the timing of the development stages accurately between controlled and field conditions as under field conditions three levels of nitrogen fertilization (N0, 0 kg N ha⁻¹; N1, 135 kg N ha⁻¹; N2, 272 kg N ha⁻¹) have been used. Hence, plants field-grown under contrasting N input levels do not have the same nitrogen status. To determine accurately the timing of the development stages for each level of N fertilization from Grignon/Châlons/Laon/Reims field experiment data (Gosse et al., 1999), logistic curves describing the total amount of N exported by the crop (Fig. 4B) plotted against thermal time for every N fertilization level as previously done by Barraclough (1989) were derived. This method allowed us to determine the time of maximum N uptake during accumulation of N during stem and inflorescence elongation (Fig. 4C, Table 1). This thermal time was set at 700, 780 and 815 °Cd for N0, N1 and N2 fertilization treatments, respectively (Table 1). The result clearly indicates a shift in the timing of developmental stage appearance among N fertilization treatments compared with a previous modelling approach (Malagoli et al., 2004). The matching of thermal time to developmental stage for every level of N fertilization was obtained by assuming that the maximum N uptake rate during stem elongation (field conditions) was concomitant with the maximum nitrate influx rate measured under controlled conditions (Fig. 4A), which corresponds to stage E (end of stem elongation and beginning of inflorescence extension). Eventually, as carried out above for the temperature effect, the nitrate influx rate response curve during the development cycle and between the 100 µm and 5 mm nitrate levels (Fig. 5) was calculated according to the Flow–Force theory:

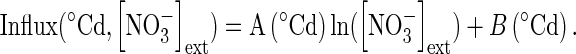(8)

Fig. 5.

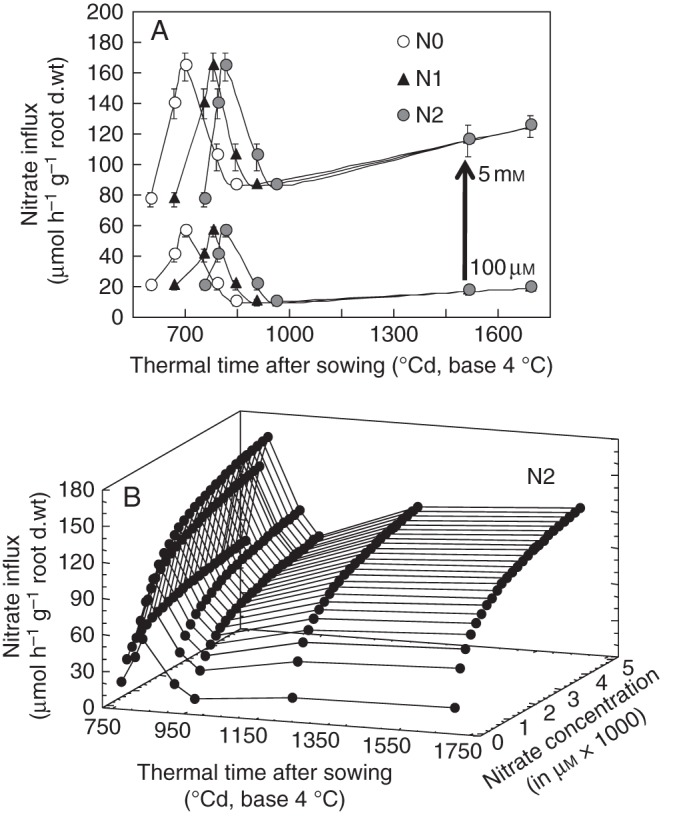
Reinterpretation of the ontogenetic effect on nitrate influx variations in winter oilseed rape (Brassica napus ‘Capitol’) plants. (A) Estimation of nitrate influx variations at different development stages (ontogenetic effect) under three N fertilization levels (N0, 0 kg ha⁻¹; N1, 135 kg ha⁻¹; N2, 272 kg ha⁻¹). (B) Three-dimensional plots of the ontogenetic effects for N2 fertilization level based on the reinterpretation in nitrate uptake kinetics from Thellier's transformation (see Fig. 1C, D). Vertical bars indicate SD for n = 3 when larger than the symbol.

Introduction of ontogenetic variations in nitrate uptake with nitrate concentrations changes greatly improved the updated version of the model and allowed a more accurate change in the time scale of N accumulation from days to months (Table 2).

The lack of parallel relationships in nitrate influx variations during the day/night cycle have been resolved by operating the change in time scale for modelling

In contrast to other effects on nitrate influx (temperature, PAR and ontogenetic cycle), variations in the nitrate influx rate during the 16/8-h day/night cycle showed no strictly parallel responses at 100 µm and 5 mm (Fig. 6A). Indeed, nitrate uptake exhibited two peaks during the light period at 5 mm nitrate treatment compared with at 100 µm (Fig. 6A). These two peaks in nitrate uptake are frequently observed but remain unclear and under debate (Pearson and Steer, 1977; Hansen, 1980; Steingrover et al., 1986; Delhon et al., 1995; Macduff et al., 1997; Macduff and Bakken, 2003). Whatever the daily regulation involved, it was assumed, as for the other factors studied, that a parallel relationship in nitrate influx exists between plants treated at 100 µm and 5 mm nitrate. Hence, changes in the polynomial relationships for different external nitrate concentrations between 100 µm and 5 mm nitrate were deformed on the basis of a logarithmic function (Influx (time, concentration) = A(time) ln [NO₃⁻]_ext + B(time)) according to the Flow–Force approach (Fig. 6B). Then, integration values of each polynomial curve for a given external nitrate concentration during the daily period were adjusted with the following logarithmic equation

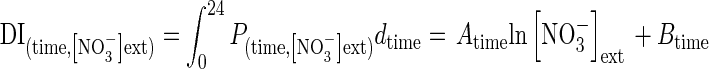(9)

to calculate the daily accumulation of nitrate for a given external concentration [in which time is expressed in d⁻¹ (24 h⁻¹), and DI is daily influx]. To verify the validity of this relationship experimentally, seedlings of the same genotype were supplied with a wide range of K¹⁵NO₃ concentrations (from 0·05 to 20 mm) over 5 d at 20 °C on agar plates. The response curve of daily accumulation of ¹⁵N to external nitrate concentrations was very close to the mathematical estimation based on the cross-combination between Flow–Force theory and day–night influx variations (Fig. 6C). This result supports our assumption that cross combining changes in external nitrate concentrations and daily variations in nitrate influx is relevant. Hence, daily changes in the model were adjusted by taking into account variations in soil nitrate concentrations, rather than just from two nitrate concentrations: 100 µm and 5 mm. Introduction of daily variations in nitrate uptake with nitrate concentrations changes strongly improved the updated version of the model and allowed a more accurate change in the time scale of N accumulation from minutes to hours and hours to days (Table 2).

Fig. 6.

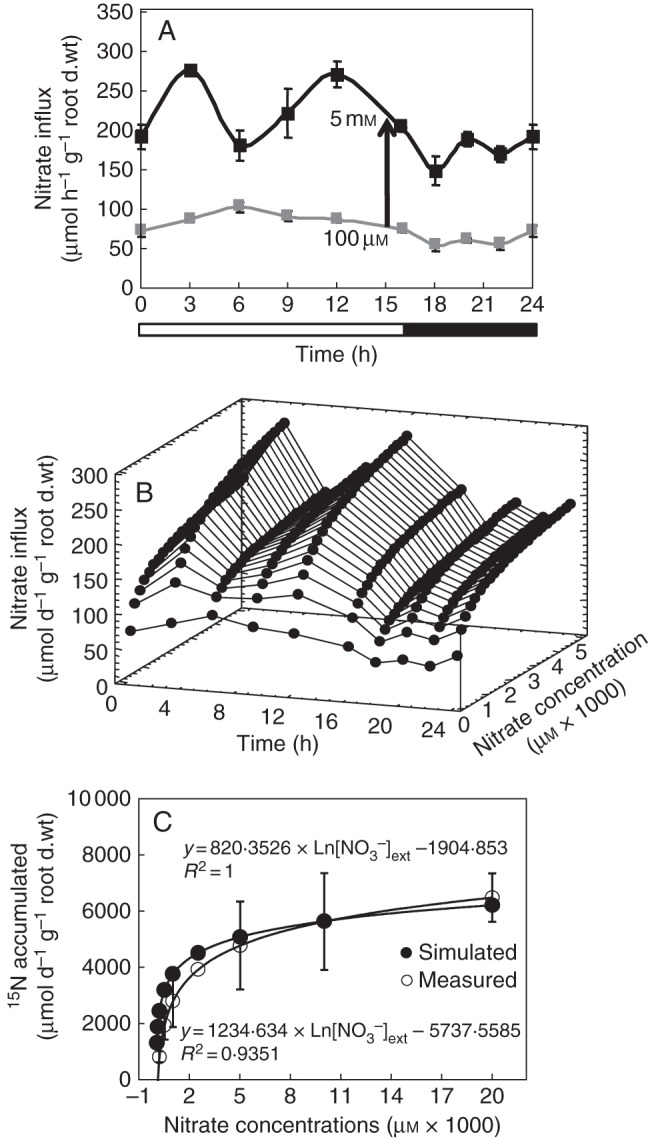
Reinterpretation of changes in nitrate influx variations during the light–dark cycle. (A) Variations of nitrate influx during the light–dark cycle after 100 µm and 5 mm external nitrate concentration treatment in 15-d-old plants growing under hydroponic conditions. (B) Three-dimensional plot of the light/dark nitrate influx variations as a function of time and nitrate concentrations based upon a mathematical reinterpretation in nitrate uptake kinetics from Thellier's transformation (see Fig. 1C, D). (C) Comparison of the estimates (A) and measured daily ¹⁵N accumulation variations in response to external nitrate concentrations. Experimental data were obtained from 5-d-old seedlings grown in agar plate with different external nitrate concentrations from 0·05 to 20 mm. Values are the average (±SE) of four replicates with four seedlings for each replicate.

DISCUSSION

Flow–Force mathematical transformation: a more suitable interpretation for modelling root nitrate uptake

Compared with the Enzyme–Substrate interpretation, the Flow–Force approach to nitrate influx kinetics appears to be an alternative and consistent choice to model overall properties of nitrate uptake (Baker, 1988; Thellier, 2012). Indeed, the Flow–Force interpretation considers only nitrate uptake kinetics at the level of the overall root system with no insight on microscopic complexity (number of carriers, affinity and/or coupling between carriers). The Flow–Force equation is analogous to an electrical model (Ohm's law) in which an ion current (ion flow) along the root radius results from the product of root conductance and driving forces (Thellier, 1970, 1971, 1973, 2012). Recently, it has been successfully applied to silicon uptake (Thellier et al., 2009). In a similar manner, Flow–Force formalism was originally proposed by Dainty (1963, 1969a) for root water uptake and has been helpful to better understand water transport in plants (Fiscus and Kramer, 1975; Kramer, 1983; Steudle, 2000a, b), despite the complexity of the differential localization and regulation activities of plant root aquaporins (Maurel, 2007).

In fact, the stated purpose of the Enzyme–Substrate interpretation, first proposed by Epstein and co-workers (Epstein and Hagen, 1952; Epstein, 1953, 1966), was to characterize carriers involved in uptake processes to access values of parameters such as number, affinity (K_m) and saturation rate (V_m). However, mathematical adjustment of the experimental data for ion influx rate with hyperbolas did not match all underlying enzymatic and thermodynamic assumptions of a complex structure such as a root. As suggested by Dainty (1969b): ‘It is rather surprising that such a mixed cell population (root organ) should obey such Michaelis-Menten law, with a single value of K_m’; and by Tinker and Nye (2000b): ‘The initial justification for using this Michaelis-Menten type of equation to express the isotherms was that the uptake was enzyme-catalyzed, but it is clear that the whole uptake process for an entire plant is too complex for such a simple view … The justification is therefore empirical’. Furthermore, this formalism is inconsistent with the general theory of driving force on ion transport in plant cells based on the gradient of electrochemical potential (Dainty, 1969b). Thus, biphasic kinetics for potassium and nitrate uptake was explained by the involvement of two distinct transport systems with different affinities for potassium and nitrate (Epstein, 1966; Siddiqi et al., 1989, 1990; Kronzucker et al., 1995a, b; Faure-Rabasse et al., 2002). However, recent molecular findings for nitrate and potassium uptake reject and blur this microscopic distinction between HATS and LATS (Liu and Tsay, 2003; Ho et al., 2009; Coskun et al., 2013). Indeed, the NRT1·1 nitrate transporter is a dual-affinity transporter depending on the phosphorylated state of threonine 101. Moreover, as shown in Fig. 2, recent findings based upon localization of nitrate transporters in the mature root and nitrate influx analyses of nitrate transporter mutants (Filleur et al., 2001; Li et al., 2007) have highlighted the coupling between NRT1·1 and NRT2·1 in Arabidopsis (Krouk et al., 2006; Wang et al., 2009; Le Ny et al., 2013). They also in part revealed mechanisms involved in the tight temporal and spatial coordination among location, expression regulation and coupling of nitrate transporters NRT1 and NRT2 with other root nitrate carriers such as CLC and NAXT transporters (Monachello et al., 2009). Indeed, if we know that the biphasic pattern of NRT1·1 and NRT2·1 gene expression is under the control of a CBL–CIPK signalling cascade via the primary effect of nitrate, we do not know if this signalling network is also involved in expression of the CLC and NAXT genes (Ho et al., 2009; Hu et al., 2009). These recent advances clearly demonstrate that the Enzyme–Substrate interpretation can no longer be used to model root nitrate uptake in crop species at the whole root physiological level.

Application of the Flow–Force theory for root NO₃⁻ uptake modelling

Here Flow–Force theory was applied to nitrate from nitrate influx kinetics to model root uptake in B. napus during the whole growth cycle. The Flow–Force interpretation allowed us to model changes in nitrate influx levels of the mature root without explicitly involving one or several hypothetical nitrate transporters or referring to constitutive and inducible components. Hence, Flow–Force theory does not allow us to deduce the type of transporters involved in the nitrate uptake process, but rather only describes that the macroscopic parameter such as nitrate conductance is due to functioning of a CNT inserted into different cell layers of mature roots to form a catalytic structure (Thellier, 1970, 1971, 1973, 2009). Accordingly, an increase in the nitrate conductance can occur through (1) addition of new transporters, (2) a change in the activity (affinity) of individual transporters and/or (3) coupling among several carriers in the different cell layers. These changes can be caused by the interactions among shoot N demand, N supply to the root (soil nitrate concentrations), period of the day–night or ontogenetic cycles and changes in environmental factor values (temperature and PAR). Indeed, this nitrate uptake kinetic interpretation makes no assumptions and no deduction of the transport mechanisms involved within a complex tissue structure such as the root (see Fig. 2). From a physiological and molecular viewpoint this interpretation is more straightforward as well as more consistent with recent molecular advances such as the discovery and involvement of CLC genes in root nitrate transport and homeostasis or NAXT and NRT1·1 genes in root nitrate efflux (Geelen et al., 2000; De Angeli et al., 2009; Monachello et al., 2009; Segonzac et al., 2011; Léran et al., 2013).

Furthermore, owing to the redundancy in nitrate transporter genes in polyploid crop species (rice, wheat and oilseed rape), the Flow–Force approach appears more convenient for modelling nitrate uptake at the whole plant level. Indeed, compared with Arabidopsis, attempts to suppress specifically one or several nitrate transporters by mutant approaches to decipher carriers involved in nitrate influx appears to be impossible because of the redundancy of gene function, coupling and/or compensation mechanisms among nitrate transporters that can induce lethality or pleiotropic effects. As an illustration, in Arabidopsis, mutants of nitrate transporters NRT2·1, NRT2·2 and NRT1·1 mainly involved in absorption show that influx of nitrate at low and high concentrations is not abolished (Filleur et al., 2001; Liu and Tsay, 2003; Li et al., 2007). This demonstrates the complexity of the root catalytic structure for nitrate uptake.

Nitrate uptake kinetics are provided by a single root catalytic structure and vary considerably depending on endogenous and exogenous factors

In the previous modelling approach, the relative contribution of both constitutive and inducible components of HATS and LATS regulated by soil nitrate concentrations was over-estimated (Malagoli et al., 2004, 2008). Indeed, the cHATS and iHATS as well as cLATS and iLATS were considered to function simultaneously during nitrate uptake on a root dry weight basis in a defined soil layer. However, this situation is not realistic when considering the Enzyme–Substrate interpretation. Indeed, the iHATS component arises from the increase in cHATS activity for nitrate influx after a combination of concentration and duration of nitrate pretreatment (Siddiqi et al., 1989; Okamoto et al., 2003). As a result, depending on root pretreatment and plant N status, cHATS and iHATS cannot function simultaneously for the same root segments in the same soil layer because they represent two different nitrate uptake potentials. The same reasoning will apply with the Flow–Force kinetic interpretation, in which inducible behaviour of nitrate transport depends not only on changes in external nitrate concentration but also on root temperature and plant N status (Fig. 1C). Hence, the different nitrate uptake potentials depending on endogenous and exogenous factors were taken into account by the cross-combination of Flow–Force theory and the effects of environmental and in planta factors. This is one of the critical improvements in comparison with the previous modelling approach because it avoids an important overestimation of total N taken up by plants. In other words, it is not realistic to build an N uptake model based only on one or two velocity equations as reference, such as in all current models (Le Bot et al., 1997; Tinker and Nye, 2000b; Ma et al., 2008). Indeed, it is well established that influx kinetics varies considerably with temperature, PAR, time of the day–night period, root age and N status.

Cross-combination of Flow–Force theory with endogenous and environmental effects on nitrate influx does not modify nitrate conductance

The linear increase in nitrate influx for a given conductance over a wide range of external nitrate concentrations (0–10 mm) deduced from Flow–Force mathematical transformation led to a re-examination of the effects of endogenous and environmental factors (Malagoli et al., 2004). Indeed, a closer examination of nitrate influx variations measured at 100 µm and 5 mm [NO₃⁻]_ext for endogenous and environmental factors clearly showed a parallel pattern for a given root nitrate conductance. This demonstrated that the level of nitrate influx for a given value of applied factors depends directly on external nitrate concentrations without a large change in root conductance. Hence, for each factor, it was then possible to cross-combine effects of (1) external nitrate concentrations and (2) studied factors on variations of nitrate influx as presented in Fig. 7. This illustrates that the I_max value of the nitrate influx rate oscillates up and down, depending on the endogenous or exogenous factor values for a given external nitrate concentration (Supplementary Data Fig. S3). In fact, there is no absorption kinetic of nitrate used as reference with static parameters (V_m and K_m) throughout the growth cycle, as defined in most current agronomic models (Ma et al., 2008). Figure 7 is another type of representation that combines the effects of studied factors and external nitrate concentrations, as previously plotted through 3D curves (i.e. Figs 3C, 6B, 7C and Supplementary Data Fig. S3). This interpretation led to an important modification in the integration of in planta and environmental factor effects in the model (Table 2). It allows the construction of a model with influx response curves representing all physiological situations encountered by plants at different external nitrate concentrations and for different values of environmental and endogenous factors.

Fig. 7.

Cross-combined effects of endogenous and environmental factors and nitrate external concentrations on ¹⁵NO₃ influx in winter oilseed rape (Brassica napus ‘Capitol’) plants. (A) Effects of temperature variations along with increasing external nitrate concentration on nitrate influx. (B) Effects of PAR variations along with increasing external nitrate concentration on nitrate influx. (C) Effects of ontogenetic variations during growth cycle on nitrate influx for N2 fertilization level (272 kg N ha⁻¹). (D) Effects of the day length on day/night nitrate accumulation along with increasing external nitrate concentration on nitrate influx. Solid lines represent the influx for standard conditions (B₄ stage, 20 °C, 300 µmol m² s⁻¹ PAR, 16/8-h regimen) and dotted lines represent influx variations for other endogenous and environmental conditions.

Other effects that influence nitrate absorption rate

In this model, the combination of mass flow and diffusion providing nitrate to the root are not limiting processes because the soil water content values are close to field capacity and hardly change. Because nitrate is highly mobile in the soil, nitrate uptake is greatly influenced by water movement and water uptake by plants (Barber, 1995c; Tinker and Nye, 2000c). Hence, there is a clear need for experiments in which nutrient and water uptake are measured simultaneously, as proposed by Roose and Fowler (2004) for water and phosphate uptake. However, in this last modelling approach, nutrient uptake is always based on Michaelis–Menten formalism (Roose and Fowler, 2004). In the Flow–Force approach presented here, the close relationship between the thermodynamic formalisms for ions and water uptake should provide a new conceptual basis to build models to improve simultaneous modelling of water and nutrient uptake in relation to changes in soil water content (Dainty, 1963, 1969a; Fiscus and Kramer, 1975; Thellier et al., 2009).

Finally, the reciprocal dynamic relationships between root branching and ion uptake rate may be of major importance for our understanding on ion uptake (Roose and Fowler, 2004; Biondini, 2008; Lemaire et al., 2013). Indeed, when the exchange of isotopes is performed over a longer period, the validity of the flux analyses must take into account the effects of nutrient status, development of root branching structure, and heterogeneity and ageing of the cells along the roots axes (Bhat et al., 1979; Barber, 1995b; Okamoto et al., 2003; Lemaire et al., 2013). Thus, in long-term experiments (weeks to months), B. napus plants supplied with a solution of constant nitrate concentration from 1 µm to 10 mm showed a continuous collapse in nitrate influx rate recalculated on a root length basis (μmol N h⁻¹ cm⁻¹ root, Bhat et al., 1979). As yet, no wholly acceptable hypothesis has been advanced to explain this down-regulation in nitrate influx rate when plant N demand is always important (Barber, 1995b; Gao et al., 1998; Okamoto et al., 2003; Eissenstat and Volder, 2005). Intriguingly, recalculation of nitrate uptake rate on a Flow–Force basis for roots of different ages showed linear behaviour for changes of nitrate influx rate from 1 µm to 10 mm consistent with the Flow–Force theory (Bhat et al., 1979). Therefore, further studies are needed with tracer experiments to decipher this behaviour for different ions such as N, P, K and S to integrate the effects of root age and root structural changes in new conceptual structure–function N uptake models, as done in our companion paper (Malagoli and Le Deunff, 2014).

In conclusion, this new conceptual framework has many important implications at both the physiological and the agronomical levels for current modelling of nitrate uptake. Indeed, our demonstration clearly showed that the cross-combination of Flow–Force mathematical fitting of nitrate uptake kinetics with short-term environmental effects and long-term developmental effects on nitrate influx are more consistent for modelling nitrate uptake (Malagoli and Le Deunff, 2014). Because Flow–Force interpretation infers neither the hypothetical cellular processes within the root cell layers nor the type of carriers involved, but only the efficiency of the root catalytic structure (macroscopic parameters L′ and K′), it describes more accurately the nitrate uptake at enzymatic and thermodynamic levels than the Enzyme–Substrate interpretation. Furthermore, the transformation of hyperbolic and linear ¹⁵NO₃⁻ response curves of nitrate influx isotherms to an increasing nitrate concentration gradient into a linear curve by a simple abscissa change from an arithmetic to a logarithmic scale is easy and convenient. However, a linear equation for nitrate uptake provided by the Flow–Force theory is not sufficient to refine agronomic models to predict in a more realistic manner the amount of N taken up in relation to soil nitrate availability. Indeed, the variations of nitrate influx caused by the effects of environmental and endogenous factors and expressed by polynomial curves must also be taken into account by cross-combination. Even if underground structural localization and coupling between nitrate carriers are not clearly determined at the molecular and cellular levels by this approach, it refines a new realistic and mechanistic basis to design future functional components of agronomic models to predict quantitative N taken up by crops plants under field conditions throughout the growth cycle. Finally, this model should be tested with data collected under different soil and climate conditions to validate whether it can be applied to other species. At first approximation, it is likely that the model will account for changes in climate conditions as these variables partly drive N uptake in the model. However, coupling a root submodel able to simulate soil nitrate supply (for instance based upon mineralization of organic matter and soil properties as in the Azodyn model; Laurent and Mary, 1992; Jeuffroy and Recous, 1999) may improve the use and feasibility of this approach. Similarly, the transposition of the model to other species requires measuring the values of polynomial curve parameters of nitrate influx rate in response to the effects of environmental and in planta factors.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Figure S1: percentage of ¹⁵N translocation to the shoot after 5 min supply with 100 µm or 5 mm K¹⁵NO₃ for different times over the day. Figure S2: reinterpretation of the PAR effect on nitrate influx rate. Figure S3: variations of NO₃⁻ influx simulated by the model in the presence and absence of different regulation.